Optica: Capitulo7-problemas

Problemas capítulo 7 Óptica Hecht, La superposición de Ondas.

Ejercicios resueltos sobre La superposición de Ondas. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema.

Algunas ediciones del Hecht, tienen distintas numeraciones para problemas idénticos.

---

4ta Edición en Ingles

Ejercicio 7.3 4ta Edición en Ingles

Muestre cuando las dos ondas de la ecuación 7.5 (Optica, Hecht, 4a ed) están en fase, la amplitud resultante al cuadrado, es un máximo igual a $(E_{01}+E_{02})^2$, y cuando están fuera de fase, es un mínimo igual a $(E_{01}-E_{02})^2$.

Solución

La ecuación 7.5 nos da las dos ondas

$E_1=E_{01}\text{sen}(\omega t+\alpha_1)$ y $E_2=E_{02}\text{sen}(\omega t+\alpha_2)$

Apliquemos la ecuación 7.9 para la amplitud resultante al cuadrado $E_0^2$

$E_0^2=E_{01}^2+E_{02}^2+2E_{01}E_{02}\text{cos}(\alpha_2-\alpha_1)$

Primero cuando están en fase $\alpha_1=\alpha_2$.

$E_0^2=E_{01}^2+E_{02}^2+2E_{01}E_{02}\text{cos}(0)=E_{01}^2+E_{02}^2+2E_{01}E_{02}$

Por lo que

$E_0^2=(E_{01}+E_{02})^2$ Es un máximo pues el coseno no toma valores más grandes que $1$

Ahora cuando están fuera de fase $\alpha_2-\alpha_1=\pi$

$E_0^2=E_{01}^2+E_{02}^2+2E_{01}E_{02}\text{cos}(\pi)=E_{01}^2+E_{02}^2-2E_{01}E_{02}$

Por lo que

$E_0^2=(E_{01}-E_{02})^2$ Es un mínimo pues coseno no toma valores más pequeños que $-1$

---

Realizado por: UsuarioFlor Ivon Vivar

---

Ejercicio 7.30* 4ta Edición en Ingles

Usando la ecuación de dispersión:

$n^{2}(\omega)= 1+ \frac{N{g_e}^2}{\epsilon_{0}m_e} \sum_{j}[\frac{f_{j}}{\omega_{0_j}}^2 - \omega^{2}] $-----(1)

Mostrar que la velocidad de grupo esta dada por: $v_{g}= \frac{c}{1 + Nq_{e}/2\varepsilon_{0}m_{e}\omega^{2}}$------(2)

Para ondas electromagnéticas de frecuencias altas (e.g., rayos X). Mantener en cuenta que como las $f_{j}$ son factores de peso, entonces $\sum_{j}f_{j}=1$.

Solución

Tomando en cuenta el hecho de que se trata de ondas electromagnéticas de alta frecuencia, entonces $\omega>>\omega_{0j}$ y de la ecuación (1) podemos despreciar el término $\omega_{0j}$, por lo que (1) queda como sigue: $n^2(w)\thickapprox 1 - \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}\omega^2}\sum_{j}f_{j}$

Pero $\sum_{j}f_{j}=1$ entonces la última ecuación queda como:

$n^2(w)\thickapprox 1 - \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}\omega^2}$------(3)

Entonces,

$n(w)\thickapprox \sqrt {1 - \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}\omega^2}}$------(4)

Usando la expansión binomial,

$\sqrt{1-x} = 1 - \frac{1}{2x} - \frac{1}{8x^{2}} - ...$

Con $x= \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}\omega^2}$ y despreciando términos mayores e iguales que $\omega^{4}$, obtenemos que n($\omega$) es aproximadamente:

$n(\omega)=1 - \frac{N{q_{e}}^2}{2\varepsilon_{0}m_{e}\omega^2}$------(5)

Utilizando la relación:

$v_{g}= \frac{c}{n_{g}}$------(6)

Con $v_{g}$ la velocidad de grupo y $n_{g}$ el índice de grupo de refracción definido como:

$n_{g}= n(\nu) + \nu\frac{dn(\nu)}{d\nu}$

siendo $\nu$ la frecuencia de la onda, sin embargo a $n_{g}$ la escribiremos en terminos de $\omega$:

$\omega= 2\pi\nu ; \longrightarrow \frac{dn}{d\nu}= \frac{dn}{\omega}\frac{d\omega}{d\nu}, \therefore n_{g}(\omega)= n(\omega) + \omega\frac{dn}{\omega}$

$n_{g}(\omega)= n(\omega) + \omega\frac{dn}{d\omega}$------(7)

y,

$\frac{dn(\omega)}{d\omega}= \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}{\omega}^{3}}$

Sustituyendo todo en (6) llegamos a que la velocidad de grupo $v_{g}$ es:

$v_{g}= \frac{c}{1 + Nq_{e}/2\varepsilon_{0}m_{e}\omega^{2}}$

como se pedía en el problema.

---

Realizado por: Usuarios LeonardoFR (discusión), Usuario:Pedro J. Julián

---

Ejercicio 7.35 4ta Edición en Ingles

Tome la función $f\left(\theta \right)=\theta ^{2}$ en el intervalo $0<\theta <2\pi$ & que sea $2\pi$ periódica. Muestre que su expansión en serie de Fourier es:

$f\left(\theta \right)={\frac {4\pi ^{2}}{3}}+\sum _{m=1}^{\infty }\left({\frac {4\cos(m\theta )}{m^{2}}}-{\frac {4\pi \sin(m\theta )}{m}}\right)$

Solución 

Teorema(serie de Fourier trigonométrica). Sea f una función definida en $-l<x<l$, si:

$a_{0}={\frac {1}{2l}}\int _{-l}^{l}f(x)dx$

$b_{n}={\frac {1}{l}}\int _{-l}^{l}f(x)\cos({\frac {n\pi x}{l}})dx,n=1,2,3...$

$a_{n}={\frac {1}{l}}\int _{-l}^{l}f(x)\sin({\frac {n\pi x}{l}})dx,n=1,2,3...$

Entonces la serie

$a_{0}+\sum _{n=1}^{\infty }\left(b_{n}\cos({\frac {n\pi x}{l}})+a_{n}\sin({\frac {n\pi x}{l}})\right)$

converge a f(x).

Sin embargo, tomaremos un corolario del teorema anterior (caso $l=\pi$), para ello basta aplicar una traslación $T:\Re \rightarrow \Re$ dada por:

$T(\theta ):=\left({\frac {2x-2\pi }{2\pi }}\right)\pi$......(1)

Así, tomamos a la función $g(x):=f(\theta =x-\pi )=(x+\pi )^{2}$ en el intervalo $-\pi <x<\pi$.

Observe que $g(x+2\pi )=\left((x+2\pi )+\pi \right)^{2}=((x+\pi )+2\pi )^{2}:=(\theta +2\pi )^{2}=f(\theta +2\pi ){\stackrel {\mathrm {hip} }{=}}f(\theta ):=g(x)$, bajo (1), pues T es una biyección. Esto indica que la periodicidad se sigue conservando aún al aplicar T.

Entonces, sea que $g(x)$ y, por tanto, $f(\theta )$, admite una expansión en serie de Fourier, tenemos que:

$a_{0}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }g(x)dx={\frac {1}{2\pi }}\int _{-\pi }^{\pi }{\frac {1}{3}}\left({\dfrac {d}{dx}}(x-\pi )^{3}\right)dx={\frac {4}{3}}\pi ^{2}$

$a_{n}={\frac {1}{\pi }}\int _{-\pi }^{pi}(x+\pi )^{2}\sin(nx)dx={\frac {1}{\pi }}[\int _{-\pi }^{\pi }x^{2}\sin(nx)dx+\int _{-\pi }^{\pi }2x\pi \sin(nx)dx+\int _{-\pi }^{\pi }\pi ^{2}\sin(nx)dx]$

Donde la primer integral y la tercera se anulan, pues, son funciones impares definidas en un intervalo simétrico. Por lo que:

$a_{n}=-{\frac {4}{n}}\pi \cos(n\pi )=-{\frac {4}{n}}\pi$ si n es par .

$a_{n}=-{\frac {4}{n}}\pi \cos(n\pi )={\frac {4}{n}}\pi$ si n es impar.

Análogamente,

$b_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }(x+\pi )^{2}\cos(nx)dx$. Obteniendo:

$b_{n}={\frac {4}{n^{2}}}\cos(n\pi )={\frac {4}{n^{2}}}$ si n es par.

$b_{n}={\frac {4}{n^{2}}}\cos(n\pi )=-{\frac {4}{n^{2}}}$ si n es impar.

Entonces:

$g(x)=(x+\pi )^{2}={\frac {4}{3}}\pi ^{2}+\sum _{n_{par}}^{\infty }\left(-{\frac {4}{n}}\pi \sin(nx)+{\frac {4}{n^{2}}}\cos(nx)\right)+\sum _{n_{impar}}^{\infty }\left({\frac {4}{n}}\pi \sin(nx)-{\frac {4}{n^{2}}}\cos(nx)\right)$

Por fin:

$g(x=\theta -\pi )=\theta ^{2}=f(\theta )={\frac {4}{3}}\pi ^{2}+\sum _{n_{par}}^{\infty }\left(-{\frac {4}{n}}\pi \sin(n(\theta -\pi ))+{\frac {4}{n^{2}}}\cos(n(\theta -\pi ))\right)+\sum _{n_{impar}}^{\infty }\left({\frac {4}{n}}\pi \sin(n(\theta -\pi ))-{\frac {4}{n^{2}}}\cos(n(\theta -\pi ))\right)$.

Con $\sin(n\theta -n\pi )=\sin(n\theta )\cos(n\pi )-\cos(n\theta )\sin(n\pi )=\sin(n\theta )$ si n es par.

$\sin(n\theta -n\pi )=\sin(n\theta )\cos(n\pi )-\cos(n\theta )\sin(n\pi )=-\sin(n\theta )$ si n es impar.

& $\cos(n\theta -n\pi )=\cos(n\theta )\cos(n\pi )+\sin(n\theta )\sin(n\pi )=\cos(n\theta )$ si n es par.

$\cos(n\theta -n\pi )=\cos(n\theta )\cos(n\pi )+\sin(n\theta )\sin(n\pi )=-\cos(n\theta )$ si n es impar.

Por lo que:

$f(\theta )=\theta ^{2}={\frac {4}{3}}\pi ^{2}+\sum _{n_{par}}^{\infty }\left(-{\frac {4}{n}}\pi \sin(n\theta )+{\frac {4}{n^{2}}}\cos(n\theta )\right)+\sum _{n_{impar}}^{\infty }\left(-{\frac {4}{n}}\pi \sin(n\theta )+{\frac {4}{n^{2}}}\cos(n\theta )\right)$. Es decir:

$f\left(\theta \right)={\frac {4\pi ^{2}}{3}}+\sum _{n=1}^{\infty }\left({\frac {4\cos(n\theta )}{n^{2}}}-{\frac {4\pi \sin(n\theta )}{n}}\right)$

---

Realizado por: UsuarioDiego de la Cruz López

---

3ra Edición en Español

Ejercicio 7.1 3ra Edición en Español

Determine la resultante de la superposición de las ondas paralelas $E_1=E_{01} \sin{\left(\omega t + \varepsilon_1\right)}$ y $E_2=E_{02} \sin{\left(\omega t + \varepsilon_2\right)}$ cuando $\omega=120\pi, E_{01}=6, E_{02}=8, \varepsilon_1=0$ y $\varepsilon_2=\pi/2$. Represente gráficamente cada función y la resultante.

Solución:

Se requiere calcular la amplitud y la fase de la resultante:

$E_0^2=E_{01}^2+E_{02}^2+E_{01}E_{02}\cos{(\varepsilon_2-\varepsilon_1)}$

$\Rightarrow E_0^2=36+64+2\times 6 \times 8 \times \cos{\pi/2}=100$

$\therefore E_0=10$

$\tan{\alpha}=\frac{E_{01}\sin{\varepsilon_1}+E_{02}\sin{\varepsilon_2}}{E_{01}\cos{\varepsilon_1}+E_{02}\cos{\varepsilon_2}}=\frac{E_{02}}{E_{01}}=\frac{8}{6}$

$\therefore \alpha =0.93$

Finalmente la resultante queda como:

$E=E_0\sin{(\omega t+\alpha)}$

$E=10\sin{(120\pi t+0.93)}$

---

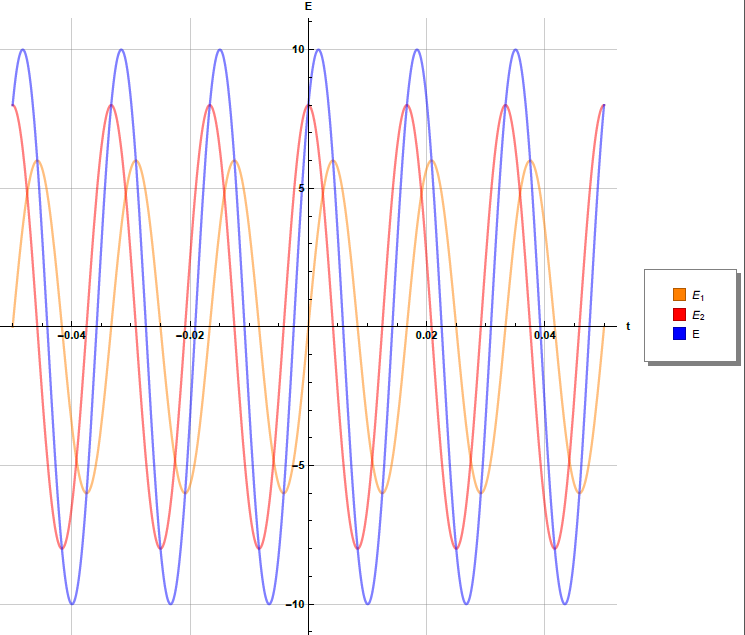
Realizado por: Usuario Sergio

---

Ejercicio 7.2 3ra Edición en Español

Considerando la sección 7.1 suponga que empezamos el análisis con el fin de calcular $E=E_{1}+E_{2}$ con dos funciones coseno $E_{1}=E_{01} \cos \left(\omega t + \alpha _{1} \right)$ y $E_{02}=\cos \left(\omega t + \alpha _{2}\right)$. Para facilitar algo la tarea, sea $E_{01}=E_{02}$ y $\alpha _{1}=0$. Sume las dos ondas algebraicamente y utilice la conocida identidad trigonométrica $\cos \theta + \sin \phi = 2 \cos \frac{1}{2} \left(\theta + \phi \right) \cos \frac{1}{2} \cos \left(\theta - \phi \right) $ para demostrar que $E=E_{0}\cos \left(\omega t + \alpha\right)$, donde $E_{0}=2E_{01}\cos \alpha_{2}$ y $\alpha = \frac{\alpha_{2}}{2}$.

Solución

Sumando $E_{1}$ con $E_{2}$ obtenemos

$E_{1}+E_{2}=E_{01}\cos \omega t + E_{01}\cos \left(\omega t + \alpha_{2} \right) $

aquí aplicamos la hipótesis dada en el problema $E_{01}=E_{02}$ entonces obtenemos

$E_{1}+E_{2}=E_{01}\left( \cos \omega t + \cos \left( \omega t + \alpha_{2}\right) \right)$

ahora si hacemos el cambio de variable $\omega t = \theta$ y $\omega t +\alpha_{2}=\phi$ y empleamos la identidad trigonométrica dada en el problema obtenemos

$E_{1}+E_{2}=2E_{01}\cos\frac{\alpha}{2}\cos \left(\omega t + \alpha_{2}\right)$

Si hacemos que $E_{0}=2E_{01}\cos\frac{\alpha}{2}$ y $ \alpha_{2}=\alpha$ y sustituimos en nuestra ecuación anterior tenemos $E_{1} + E_{2}= E_{0} \cos \left( \omega t + \alpha \right)$

---

Realizado por: Usuario: Jesús Flores Ortega

---

Ejercicio 7.7 3ra Edición en Español

Utilizando las ecuaciones 7.9, 7.10 y 7.11 muestre que la resultante de las dos ondas

$E_{1}=E_{01}sen\left[\omega t-k(x+\Delta x)\right]$

$E_{2}=E_{01}sen\left[\omega t-kx\right]$

es

$ E = 2 E_{01} cos\left(\dfrac{k \Delta x}{2}\right) \sin\left[\omega t - k\left(x+\dfrac{\Delta x}{2}\right)\right] $

Solución:

De las ondas 1 y 2 tenemos que $\alpha _{1}=-k(x+\Delta x)$ y $\alpha _{2}=-kx$. La ecuación 7.9 es

$ E_0^2 = E_{01}^2 + E_{02}^2 + 2 E_{01} E_{02} cos(\alpha_2 - \alpha_1) $

y nos da la amplitud de la onda resultante, calculando para nuestro caso tenemos

$E_{0}^{2}=E_{01}^{2}+E_{01}^{2}+2E_{01}^{2}cos\left[-kx+k(x+\Delta x)\right]=2E_{01}^{2}+2E_{01}^{2}cos(k\Delta x)=2E_{01}^{2}\left[1+cos(k\Delta x)\right]=4E_{01}^{2}cos^{2}\left({\dfrac {k\Delta x}{2}}\right)$

Donde se ha utilizado la identidad trigonométrica

$cos^{2}\left({\dfrac {x}{2}}\right)={\dfrac {1+cosx}{2}}$

Ahora para calcular la fase de la onda resultante utilizamos la ecuación 7.10 que es

$tan\alpha ={\dfrac {E_{01}sen\alpha _{1}+E_{02}sen\alpha _{2}}{E_{01}cos\alpha _{1}+E_{02}cos\alpha _{2}}}$

y en nuestro caso

$tan\alpha ={\dfrac {E_{01}sen[-k(x+\Delta x)]+E_{01}sen(-kx)}{E_{01}cos[-k(x+\Delta x)]+E_{01}cos(-kx)}}={\dfrac {sen[-k(x+\Delta x)]+sen(-kx)}{cos[-k(x+\Delta x)]+cos(-kx)}}$

y definiendo $\eta \equiv -k(x+\Delta x)$ y $\theta \equiv -kx$ tenemos

$tan\alpha ={\dfrac {sen\eta +sen\theta }{cos\eta +cos\theta }}=tan\left({\dfrac {\eta +\theta }{2}}\right)$

Donde la igualdad final se cumple gracias a una identidad trigonométrica, por lo que la fase de la onda resultante será

$\alpha ={\dfrac {\eta +\theta }{2}}=-k\left[x+{\dfrac {\Delta x}{2}}\right]$

Y la relación 7.11 es

$E=E_{0}sen(\omega t+\alpha )$

por lo que nuestra onda resultante queda como

$E=2E_{01}^{2}cos^{2}\left({\dfrac {k\Delta x}{2}}\right)sen\left[\omega t-k\left(x+{\dfrac {\Delta x}{2}}\right)\right]$

---

Realizado por: Ivan de Jesús Pompa García (discusión) 21:00 5 nov 2018 (CST)

---

Ejercicio 7.8 3ra Edición en Español

Sume directamente las dos ondas del problema 7.7 para encontrar la misma solución.

Solución

Primero, renombremos los argumentos de la siguiente forma:

$a=wt-kx$ y $b=k\Delta x$.

Entonces las expresiones de los campos serán de la forma

$E_{1}=E_{0}sen(a-b)$ $E_{2}=E_{0}sen(a)$

Por tanto, al tener la suma de los campos.

$E_{t}=E_{1}+E_{2}=E_{0}sen(a-b)+E_{0}sen(a)=E_{0}[sen(a-b)+sen(a)]$

Asi que sólo los debemos enfocar en la suma trigonométrica. Entonces:

$sen(a-b)+sen(a)=[sen(a)cos(b)-sen(b)cos(a)+sen(a)$

Factorizando $sen(a)$:

$sen(a)[cos(b)+1]-sen(b)cos(a)$

Recordando dos identidades trigonométricas importantes que son:

$cos^{2}(b)=1/2[1+cos(b)]$ → $cos(b)+1=2cos^{2}(b)$ y $sen(b)=2sen(b/2)cos(b/2)$.

Entonces:

$sen(a)[cos(b)+1]-sen(b)cos(a)=sen(a)[2cos^{2}(b/2)]-[2sen(b/2)cos(b/2)]cos(a)$

Ahora factorizando $2cos(b/2)$ llegamos a:

$2cos(b/2){sen(a)cos(b/2)-cos(a)sen(b/2)}=2cos(b/2)[sen(a-b/2)]$

Por lo tanto:

$E_{t}=E_{0}2cos(b/2)[sen(a-b/2)]$

Finalmente, regresando a las variables originales.

$E_{t}=E_{0}2cos(k\Delta x/2)[sen(wt-kx-k\Delta x/2)]=E_{0}2cos(k\Delta x)/2)[sen(wt-k[x+\Delta x/2)])]$.

---

Realizado por: Fernando Valencia Hernández

---

Ejercicio 7.9 3ra Edición en Español

Utilice la representación compleja para calcular la resultante de $E=E_1+E_2$ donde

$E_1=E_0cos{(kx\ +\ \omega t)\ \ \ \ \ \ \ \ \ }$

$E_2=-E_0cos{(kx\ -\ \omega t)\ \ \ \ \ \ \ }$

Describa la onda.

Solución:

${Re(e}^{i(kx+\omega t)})=cos{(kx+\omega t)\ \ }$

${Re(e}^{i(kx-\omega t)})=cos{(kx-\omega t)\ \ }$

$E=E_1+E_2=E_0cos{(kx\ +\ \omega t)\ \ - E_0cos{(kx\ -\ \omega t)\ \ \ \ \ \ \ }\ \ \ \ \ }$

${E=E_0Re(e}^{i(kx+\omega t)})-E_0\ {Re(e}^{i(kx-\omega t)})$

${E=E_0Re(e}^{i(kx+\omega t)}-e^{i(kx-\omega t)})$

${E=E_0Re[e^{ikx}(e}^{i\omega t}-e^{-i\omega t)})]=E_0 Re\left [ 2i e^{ikx} \sin(\omega t) \right ]$

Donde se uso que:

$\sin z=\frac{e^{iz}-e^{-iz}}{2i}$

$E=E_0Re[2i\cos{(kx})\sin{(\omega t)}-2\sin{(kx)}\sin{(\omega t)}]$

Conclusión

Por lo tanto

$E=-2E_0\sin{(kx)}\sin{(\omega t)}$. Onda estacionaria con nodo en $x=0$

---

Realizado por: Usuario Verenisse

---

5ta Edición en Ingles

Ejercicio 7.27 5ta Edición en Ingles

Usar la relación ${ \frac {1}{v_g}} = { \frac {dk}{dv}}$, probando que:

${ \frac {1}{v_g}} = { \frac {1}{v}}$ - ${ \frac {\upsilon}{v^2}} * { \frac {dv}{d\upsilon}}$

Solución

Dado que ${ \frac {1}{v_g}} = { \frac {dk}{dv}}$....(1)

K denota el número de onda  : K = ${ \frac {1}{\lambda}}$

ya que ${\upsilon}=v{\lambda}$

${\lambda}$=${ \frac {\upsilon}{v}}$

${ \frac {1}{\lambda}}$=${ \frac {v}{\upsilon}}$

así que K=${ \frac {v}{\upsilon}}$

Así de la ecua 1 se obtiene:

${ \frac {1}{v_g}}= { \frac {d}{dv} { \frac {v}{\upsilon}}}$

Por diferenciación parcial respecto a las ${\upsilon}$ que obtenemos

${ \frac {1}{v_g}}={ \frac {1}{v}}{ \frac {d\upsilon}{dv}}+v{ \frac {d}{dv}}{ \frac {1}{v}}$

${ \frac {1}{v_g}}={ \frac {1}{v}}+v{ \frac {-1}{v^2}}{ \frac {d\upsilon}{dv}}$

${ \frac {1}{v_g}}={ \frac {1}{v}}-{ \frac {\upsilon}{v^2}}{ \frac {dv}{d\upsilon}}$

por lo que queda probado.

---

Realizado por: Usuario:Luisa Alejandra Vega Sanchez

---

Ejercicio 7.29 5ta Edición en Ingles

La velocidad de propagación de una onda de superficie en un líquido de profundidad mucho mayor que $\lambda$ viene dada por:

$v={\sqrt {{\frac {g\lambda }{2\pi }}+{\frac {2\pi \Upsilon }{\rho \lambda }}}}$

donde g = aceleración de la gravedad, $\lambda$ = longitud de onda, $\rho$ = densidad, $\Upsilon$ = tensión superficial. Calcule la velocidad de grupo de un pulso en el límite de longitud de onda larga (se denominan ondas de gravedad).

Solución:

Para longitudes de onda grandes, notemos que el segundo término de la suma dentro de la raíz es despreciable :

${\frac {2\pi \Upsilon }{\rho \lambda }}$

Entonces la velocidad de propagación de una onda de superficie se convierte en:

$v={\sqrt {\frac {g\lambda }{2\pi }}}$ ........(1)

EL número de onda esta dada,por:

$k={\frac {2\pi }{\lambda }}$ ................(2)

Sustituyendo la ecuación (2) en (1), la velocidad de propagación:

$v={\sqrt {\frac {g}{k}}}$.................(3)

De la relación entre la velocidad de grupo y velocidad de propagación es:

${v}_{g}=v+k{\frac {dv}{dk}}$.............(4)

Donde ${v}_{g}$, es la velocidad de grupo.

De la ecuación (3):

${\frac {dv}{dk}}={\frac {d}{dk}}\left({\sqrt {\frac {g}{k}}}\right)$

${\frac {dv}{dk}}={\sqrt {g}}{\frac {d}{dk}}\left({k}^{-{\frac {1}{2}}}\right)$

${\frac {dv}{dk}}={\sqrt {g}}\left(-{\frac {1}{2}}\right)\left({k}^{-{\frac {3}{2}}}\right)$

${\frac {dv}{dk}}={\sqrt {g}}\left(-{\frac {1}{2}}\right){\frac {1}{k{\sqrt {k}}}}$

${\frac {dv}{dk}}=\left(-{\frac {1}{2k}}\right){\sqrt {\frac {g}{k}}}$

Sustituyendo (3) en la última expresión:

${\frac {dv}{dk}}=\left(-{\frac {v}{2k}}\right)$..........(5)

Sustituyendo (5) en (4):

${v}_{g}=v+k\left({\frac {-v}{2k}}\right)$

Reduciendo, tenemos que la velocidad de grupo es:

${v}_{g}=v-{\frac {v}{2}}$

${v}_{g}={\frac {v}{2}}$

---

Realizado por: Luis Manuel Chávez Antonio

---

Ejercicio 7.30 5ta Edición en Ingles

Demuestre que la velocidad de grupo puede escribirse como:

$v_{g}=v-\lambda {\frac {dv}{d\lambda }}$

Solución:

La expresión de la velocidad de grupo se puede escribir como:

$v_{g}=v+{\frac {kdv}{dk}}$

Donde:

$v_{g}$ es la velocidad de grupo

$v$ es la velocidad de fase

$k$ es el numero de onda

La expresión de numero de onda se puede escribir como:

$k={\frac {2\pi }{\lambda }}$

Donde $\lambda$ es la longitud de onda

La expresion de velocidad de grupo se puede escribir como:

$v_{g}=v+k{\frac {dv}{dk}}$

$v_{g}=v+k\left({\frac {dv}{d\lambda }}\right)\left({\frac {d\lambda }{dk}}\right)$

La expresión del numero de onda se diferencia con respecto a la longitud de onda como:

$k={\frac {2\pi }{\lambda }}$

${\frac {dk}{d\lambda }}=-2\pi \left({\frac {1}{\lambda ^{2}}}\right)$

${\frac {d\lambda }{dk}}=-{\frac {\lambda ^{2}}{2\pi }}$

Sustituimos ${\frac {d\lambda }{dk}}$ en la expresión anterior.

$v_{g}=v+k\left({\frac {dv}{d\lambda }}\right)\left({\frac {d\lambda }{dk}}\right)$

$v_{g}=v+k\left({\frac {dv}{d\lambda }}\right)\left(-{\frac {\lambda ^{2}}{2\pi }}\right)$

$v_{g}=v-{\frac {\lambda ^{2}k}{2\pi }}\left({\frac {dv}{d\lambda }}\right)$

Sustituimos ${\frac {2\pi }{\lambda }}$ por $k$ en la expresión anterior:

$v_{g}=v-{\frac {\lambda ^{2}}{2\pi }}\left({\frac {2\pi }{\lambda }}\right)\left({\frac {dv}{d\lambda }}\right)$

$v_{g}=v-\lambda \left({\frac {dv}{d\lambda }}\right)$

Por lo tanto $v_{g}=v-\lambda \left({\frac {dv}{d\lambda }}\right)$

---

Realizado por: UsuarioEnrique Ortiz Martinez

---

Ejercicio 7.36 5ta Edición en Ingles

---

Demuestre que la velocidad de grupo puede escribirse como:

${\upsilon }_{g}={\frac {c}{n}}+{\frac {\lambda c}{{n}^{2}}}{\frac {dn}{d\lambda }}$

Solución:

La velocidad de grupo esta dada por:

${v}_{g}=v+{\frac {kdv}{dk}}$.......(1)

y sabemos que por regla de la cadena podemos escribir:

${\frac {dv}{dk}}={\frac {dv}{dn}}{\frac {dn}{dk}}$.......(2)

sabemos que la velocidad de la luz en un medio de refracción n es :

$v={\frac {c}{n}}$ donde c= velocidad de la luz en el vació

derivando con respecto a n tenemos:

${\frac {dv}{dn}}={\frac {-c}{{n}^{2}}}$

sustituyendo este valor en la ecuación (2) obtenemos:

${\frac {dv}{dk}}={\frac {-c}{{n}^{2}}}{\frac {dn}{dk}}$....(3)

y utilizando regla de la cadena tenemos :

${\frac {dn}{dk}}={\frac {d\lambda }{dk}}{\frac {dn}{d\lambda }}$....(4)

sabemos que la constante de propagación esta dada por:

$k={\frac {2\pi }{\lambda }}$

${\frac {dk}{d\lambda }}={\frac {d}{d\lambda }}\left({\frac {2\pi }{\lambda }}\right)$

${\frac {dk}{d\lambda }}=-{\frac {2\pi }{{\lambda }^{2}}}$

${\frac {d\lambda }{dk}}=-{\frac {{\lambda }^{2}}{2\pi }}$

sustituyendo este valor en la ecuación (4) obtenemos que :

${\frac {dn}{dk}}=-{\frac {{\lambda }^{2}}{2\pi }}{\frac {dn}{d\lambda }}$....(5)

sustituyendo la ecuación (5) en la ecuación (3) obtenemos:

${\frac {dv}{dk}}={\frac {-c}{{n}^{2}}}\left({\frac {{-\lambda }^{2}}{2\pi }}\right){\frac {dn}{d\lambda }}$

${\frac {dv}{dk}}=\left({\frac {{c\lambda }^{2}}{2\pi {n}^{2}}}\right){\frac {dn}{d\lambda }}$

sustituyendo este valor en la ecuación (1) obtenemos:

${v}_{g}=v+k\left({\frac {{c\lambda }^{2}}{2\pi {n}^{2}}}\right){\frac {dn}{d\lambda }}$

donde sabemos que $v={\frac {c}{n}}$, $k={\frac {2\pi }{\lambda }}$

sustituyendo en lo anterior tenemos:

${v}_{g}={\frac {c}{n}}+{\frac {2\pi }{\lambda }}\left({\frac {{c\lambda }^{2}}{2\pi {n}^{2}}}\right){\frac {dn}{d\lambda }}$

${v}_{g}={\frac {c}{n}}+\left({\frac {\lambda c}{{n}^{2}}}\right){\frac {dn}{d\lambda }}$

Como podemos el problema queda demostrado

---

Realizado por: UsuarioRuben Espinosa Guzman

---

Ejercicio 7.38 5ta Edición en Ingles

Para una onda que se propaga en una estructura periódica para la cual $\omega (k)=2{\omega }_{0}\sin {\left({kl}/{2}\right)}$, determine las velocidades de fase y de grupo. Escriba el primer termino como una función seno.

Solución:

Para una onda periódica $\omega (k)=2{\omega }_{0}\sin {\left({kl}/{2}\right)}$ ...$(1)$

Esa es la frecuencia angular de la onda, es una función de constante de propagación.

Sabemos que la velocidad de fase es $v={\frac {\omega }{k}}$

$v={\frac {2{\omega }_{0}\sin {\left({kl}/{2}\right)}}{k}}$

Y la velocidad de grupo ${v}_{g}={\frac {d\omega }{dk}}$

${v}_{g}={\frac {d}{dk}}\left(2{\omega }_{0}\sin {\left({kl}/{2}\right)}\right)$

${v}_{g}=2{\omega }_{0}\left[\cos {\left({kl}/{2}\right)}\left({\frac {l}{2}}\right)\right]$

${v}_{g}={\omega }_{0}l\left[\cos {\left({kl}/{2}\right)}\right]$

Recordando lo siguiente: $\sin {\left({\frac {\pi }{2}}+\theta \right)}=\cos {\left(\theta \right)}$

$\therefore {v}_{g}={\omega }_{0}l\sin {\left[{\frac {\pi }{2}}+\left({\frac {kl}{2}}\right)\right]}$

---

Realizado por: Luis Gutiérrez Melgarejo

---

Ejercicio 7.39 5ta Edición en Ingles

Un gas o plasma ionizado es un medio dispersivo para las ondas EM. Dado que la ecuación de dispersión es:

${\omega }^{2}={\omega }_{p}^{2}+{c}^{2}{k}^{2}$

donde ${\omega }_{p}^{2}$ es la constante de plasma frecuencial. Determinar expresiones tanto para la fase como para el grupo de velocidades y demostrar que: ${v{v}_{g}}={c}^{2}$.

Solución:

sabemos que k= constante de propagación, ademas la velocidad de fase se expresa como: $v={\frac {\omega }{k}}$

entonces ${\frac {\sqrt {{\omega }_{p}^{2}+{c}^{2}{k}^{2}}}{k}}$

= ${\sqrt {\frac {{\omega }_{p}^{2}+{c}^{2}{k}^{2}}{{k}^{2}}}}$

= ${\sqrt {{\frac {{\omega }_{p}^{2}}{{k}^{2}}}+{c}^{2}}}$ ...(1)

la velocidad de grupo viene dada por: ${v}_{g}={\frac {d\omega }{dk}}$ ...(2)

tenemos: ${\omega }^{2}={\omega }_{p}^{2}+{c}^{2}{k}^{2}$

derivando obtenemos: $2\omega {\frac {d\omega }{dk}}{=c}^{2}2k$

= ${\frac {d\omega }{dk}}={\frac {{c}^{2}k}{\omega }}$ sea ${\omega }_{p}$ una constante

de la ecuación (2): ${v}_{g}={\frac {{c}^{2}k}{\omega }}$

y ya que $v={\frac {\omega }{k}}$ entonces: ${v}_{g}={\frac {{c}^{2}}{v}}$

sustituyendo ecuación (1) en lo anterior: ${v}_{g}={\frac {{c}^{2}}{\sqrt {{\frac {{\omega }_{p}^{2}}{{k}^{2}}}+{c}^{2}}}}$ ...(3)

ahora multiplicando (1) y (3)

${v\bullet v}_{g}={\frac {{c}^{2}}{\sqrt {{\frac {{\omega }_{p}^{2}}{{k}^{2}}}+{c}^{2}}}}\bullet {\sqrt {{\frac {{\omega }_{p}^{2}}{{k}^{2}}}+{c}^{2}}}$

${v{v}_{g}}={c}^{2}$.

por tanto queda probado.

---

Realizado por: Usuario Salvador Morales Carranza

---

Ejercicio 7.41 5ta Edición en Ingles

Determine analíticamente la resultante cuando las dos funciones $E_1=2E_0 \cos (\omega t)$ y $E_2=\frac{1}{2}E_0 \sin (2\omega t) $ se superponen. Dibuje $E_1$ , $E_2$ y $E=E_1+E_2$ ¿La resultante es periódica? Si lo es ¿Cuál es su periodo en términos de $\omega$?

Solución:

Realizamos la suma de las dos funciones :

$E=E_1+E_2=2E_0 \cos (\omega t)+\frac{1}{2}E_0 \sin (2\omega t)$

Se hace uso de la identidad trigonométrica : $\sin(2 \theta)=2 \sin \theta \cos \theta $

$E= 2 E_0 \cos ( \omega t ) + \frac{1}{2} E_0 2 \cos (\omega t) \sin (\omega t) $

$E=E_0 \sin \omega t \cos \omega t +2 E_0 \cos \omega t$

$E=E_0 \cos \omega t (1+ \sin (\omega t))$

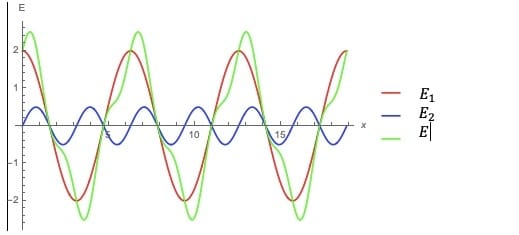
Se dice que una función f es periódica con período P mayor que cero si cumple que:

$f(t+P)=f(t)$

Así que sustituimos $t$ por ($t+P$) en $E$

$E_0 \cos \omega (t+P) (1+ \sin (\omega (t+P)))$

Usamos la identidad trigonométrica de del coseno de una suma : $\cos (a+b)= \cos a \cos b- \sin a \sin b$

$E_0 \left( \cos (\omega t) \cos (\omega P) - \sin (\omega t) \sin (\omega P) \right) (1+ \sin (\omega (t+P))) $

Para que se cumpla la igualdad :

$E_0 \left( \cos (\omega t) \cos (\omega P) - \sin (\omega t) \sin (\omega P) \right) (1+ \sin (\omega (t+P))) = E_0 \cos \omega t (1+ \sin (\omega t ))$

Se requiere que se cumplan simultáneamente:

$\cos (\omega P)=1$

$\sin (\omega P)=0$

Por lo tanto $P=2 \pi n$

Podemos afirmar entonces que la función resultante es periódica, por periodo $P=2 \pi n$

---

Realizado por: Aurea Espin (discusión) 23:36 10 nov 2018 (CST)

---