Bienvenidos. En esta página pueden dejar las soluciones a sus problemas del Hecht- Capítulo 4,
con el siguiente formato:
Ejercicio 4.4 (Hecht, Optics 4 ed.)
La ecuación de un oscilador amortiguado es
 .....(1)
.....(1)
a) Explique el significado de cada término
b) Sea  y
y  , donde
, donde  y
y  son cantidades reales. Sustituir en la ecuación (1) y probar que
son cantidades reales. Sustituir en la ecuación (1) y probar que
![x_{0}=\frac{q_{e}E_{0}}{m_{e}}\frac{1}{[(\omega_{0}^{2}-\omega^{2})^{2} + (\gamma\omega)^{2}]^{\frac{1}{2}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5a0dac1bd4a66e54ca5363aa36b4637169c7ba13)
c) Derive una expresión para la fase retardada, , y discuta cómo varía conforme
, y discuta cómo varía conforme  se encuentra en los regímenes:
se encuentra en los regímenes:  ,
,  ,
, 
Solución
a) La ecuación (1) surge de considerar en la segunda ley de Newton fuerzas disipadoras causadas ya sea, por ejemplo, un medio. La ecuación (1) considera el movimiento de un electrón en una sola dirección, en este caso, la dirección x. El primer término de la ecuación, , es simplemente la masa del electrón por su aceleración; el segundo término,
, es simplemente la masa del electrón por su aceleración; el segundo término,  , indica la fuerza resistiva causada por el medio, la cual, tiene una dependencia proporcional (por el factor
, indica la fuerza resistiva causada por el medio, la cual, tiene una dependencia proporcional (por el factor  ) a la velocidad del electrón; el tercer término,
) a la velocidad del electrón; el tercer término,  , subraya a la fuerza restitutiva (tipo ley de Hook) causante de que el electrón oscile, cuya frecuencia angular de oscilación es
, subraya a la fuerza restitutiva (tipo ley de Hook) causante de que el electrón oscile, cuya frecuencia angular de oscilación es  ; finalmente, el término
; finalmente, el término  indica la fuerza que siente la partícula cargada (electrón) debido a un campo eléctrico externo dependiente del tiempo, es un factor de forzamiento causado por una fuerza externa.
indica la fuerza que siente la partícula cargada (electrón) debido a un campo eléctrico externo dependiente del tiempo, es un factor de forzamiento causado por una fuerza externa.
b) Ahora, si  , entonces
, entonces
 ;
;

y si  , tenemos que, al sustituir en la ecuación (1):
, tenemos que, al sustituir en la ecuación (1):
![[-m_{e}\omega^{2}x_{0} + im_{e}\gamma\omega x_{0} + m_{e}\omega_{0}^{2}x_{0}]\exp(i\left(\omega t-\alpha\right))=q_{e}E_{0}\exp(i\omega t)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d87afdc94dc7cadef2b6bb78a23cda20d4adf728)
realizando más manipulaciones algebraicas, obtenemos:

pero, dos números complejos son iguales si, y sólo si, sus partes reales son iguales y sus partes imaginarias también, es decir:
 .....(2)
.....(2)
&  .....(3)
.....(3)
aprovechándonos de la identidad pitagórica de las funciones trigonométricas, elevamos al cuadrado las ecuaciones (2) y (3), y las sumamos:

por supuesto que la cantidad  es positiva definida, por lo que, al sacar la raíz cuadrada a ambos lados de la ecuación previa, nos quedamos únicamente con la raíz positiva, obteniendo así:
es positiva definida, por lo que, al sacar la raíz cuadrada a ambos lados de la ecuación previa, nos quedamos únicamente con la raíz positiva, obteniendo así:
![x_{0}=\frac{q_{e}E_{0}}{m_{e}}\frac{1}{[(\omega_{0}^{2}-\omega^{2})^{2} + (\gamma\omega)^{2}]^{\frac{1}{2}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5a0dac1bd4a66e54ca5363aa36b4637169c7ba13)
c) Retomando las ecuaciones (2) y (3), podemos formar el siguiente cociente:
 . De aquí que:
. De aquí que:
 .....(4)
.....(4)
La ecuación (4) nos dice la relación entre el ángulo retardado  y la frecuencia de forzamiento
y la frecuencia de forzamiento  . Consideremos los casos siguientes:
. Consideremos los casos siguientes:
i) 
 . Definamos la cantidad adimensional
. Definamos la cantidad adimensional  . Observamos que
. Observamos que  va lineal en
va lineal en  , por lo que
, por lo que

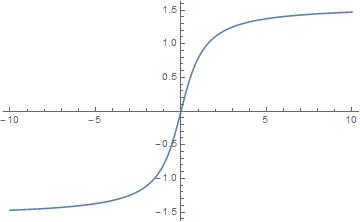
ii)  .
.
En el  , por lo que
, por lo que  y
y  .(El límite de
.(El límite de  dependerá si
dependerá si  se acerca a
se acerca a  por la izquierda o por la derecha. Se tomó el caso cuando
por la izquierda o por la derecha. Se tomó el caso cuando  se acerca por la derecha).
se acerca por la derecha).
iii) 
 . Lo cual implica que:
. Lo cual implica que:

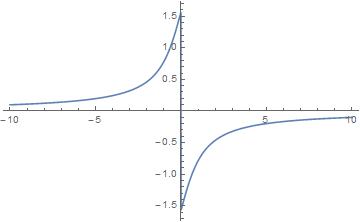
--Diego de la Cruz López
Ejercicio 4.45
Un rayo láser incide en la interfaz entre el aire y algunos dieléctricos de índice n. Para valores pequeños de  muestre que
muestre que  , Usa esto y la ec. (4.42) para establecer que en una incidencia casi normal
, Usa esto y la ec. (4.42) para establecer que en una incidencia casi normal

- Solución:
- Tenemos los siguientes datos conocidos:
- Indice de refracción del aire
 es: 1
es: 1
- Indice de refracción del dieléctrico
 es :
es :
- Ángulo de incidencia =

- Ángulo de refracción =

- Aplicando la ley de Snell:


- Para valores pequeños de theta, tenemos las siguientes relaciones:


- La Ecuación (1) se reduce:

- De la última expresión tenemos:

- Ahora ocupando la ecuación 4.42 y considerando
 muy pequeñas :
muy pequeñas :

- Haciendo la consideración:

- ocupando
 , y sustituyendo en la ultima ecuación:
, y sustituyendo en la ultima ecuación:

- Factorizando


- Reduciendo:

- Finalmente tenemos:

- --Luis Manuel Chávez Antonio
Ejercicio 4.64
Verifique que:
 .........[4.49]
.........[4.49]
para  en una interfaz de vidrio crown y aire
en una interfaz de vidrio crown y aire 
- Solución:
Datos:
Angulo de incidencia  = 30°
= 30°
Indice de refracción del cristal  = 1.52
= 1.52
Indice de refracción del aire = 1
Angulo de transmisión 
Usando la ley de Snell obtenemos:




En angulo de transmisión  sera:
sera:


El componente perpendicular del coeficiente de transmisión es:




Ahora, la componente perpendicular del coeficiente de reflexión es:



Al sumar los valores de  y
y  obtenemos:
obtenemos:
![t_{\perp }+(-r_{\perp })=0.7514+[-(-0.2486)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d3a5b6542f6c89ba86b59539af1351a8c69d7b73)


Por lo tanto 
- --Enrique Ortiz Martinez
Ejercicio 4.21
Trace un gráfico de θ_i con respecto a θ_t para una frontera aire-vidrio donde  . Discuta la forma de la curva.
. Discuta la forma de la curva.
Solución:
- La ecuación de la refracción de Snell está dada por:
Error al representar (error de sintaxis): n_i sin(θ_i )=n_t sin(θ_t )
- Pero n_i=1
- Por lo tanto
Error al representar (error de sintaxis): n_i sin(θ_i )=n_t sin(θ_t )
Despejando θ_t se tiene que
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): θ_t=sin^(-1)(sinθ_i /n_t )
En este caso se realizan cambios de 2 grados de diferencia, se tuvo la siguiente gráfica
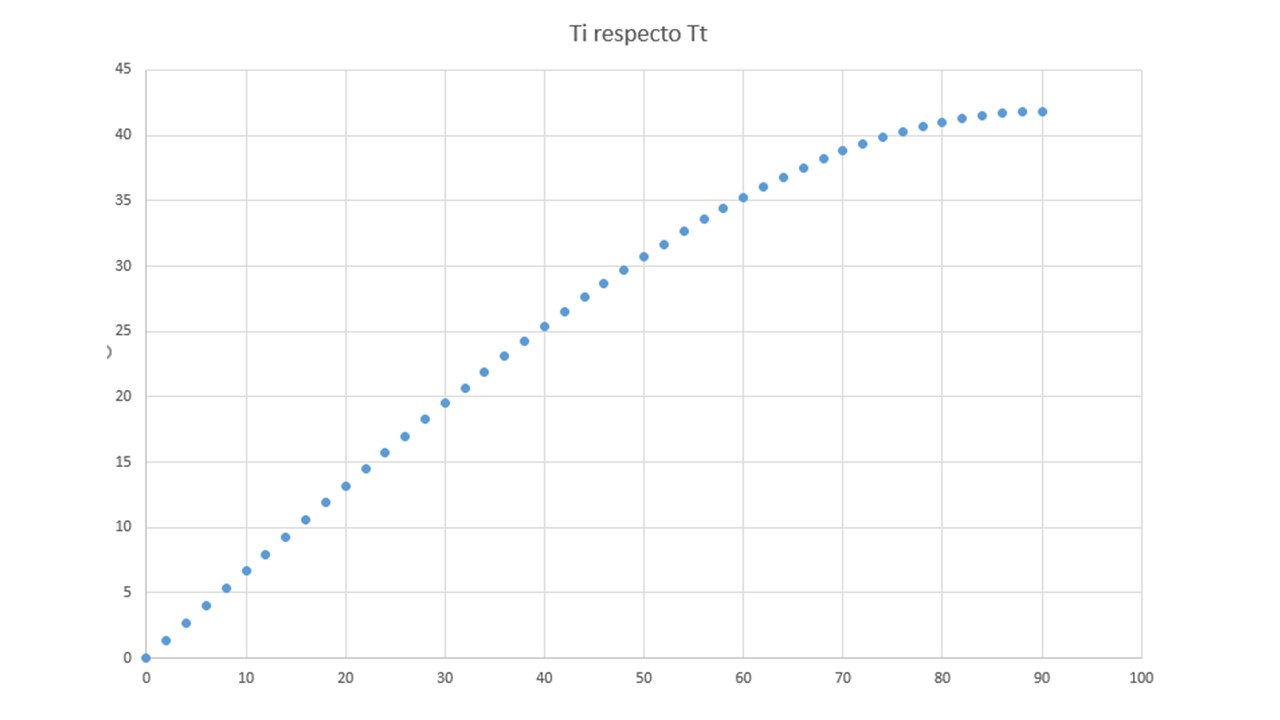
Podemos observar que a pesar que al comparar los ángulos, se puede apreciar que los valores tienden a un número que en este caso es aproximadamente 42°. Esto se podría interpretar como el ángulo máximo que puede tomar el haz, en este caso, en el agua.
Los datos están en el siguiente documento.
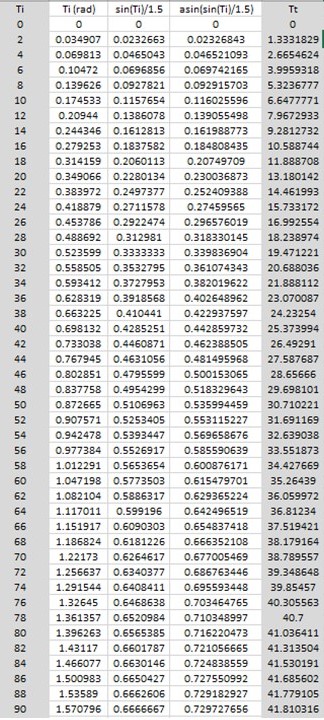
--Fernando Valencia Hernández
Problema 4.72
Mostrar que:

Y

Solución:
La componente perpendicular de la transmitancia  esta dada por:
esta dada por:

Pero el coeficiente de amplitud de transmisión es:


Sustituyendo el valor calculado de  en la Ec.
en la Ec.  , se obtiene:
, se obtiene:

De la ley de Snell 

Sustituyendo el valor de  de la Ec.
de la Ec.  en la Ec.
en la Ec.  , obtenemos:
, obtenemos:



Comprobando que:

Del mismo modo podemos proceder para el comportamiento paralelo de  , se la siguiente manera:
, se la siguiente manera:
El comportamiento paralelo de la transmitancia  , se expresa como:
, se expresa como:

Pero sabemos que la amplitud del coeficiente de transmisión es:


Sustituyendo el valor de  , en la Ec.
, en la Ec.  , obtenemos:
, obtenemos:

De la Ec. 




Comprobando que:

--Luis Gutiérrez Melgarejo
Problema 4.63
Prueba que  para todo
para todo  , primero de las condiciones de frontera y después de las ecuaciones de Fresnel.
, primero de las condiciones de frontera y después de las ecuaciones de Fresnel.
Solucion:
Podemos notar que la continuidad de los componentes tangenciales de  analizando cualquier limite en cualquier punto , el campo tangencial en el medio incidente es igual al del medio de transmisión.
analizando cualquier limite en cualquier punto , el campo tangencial en el medio incidente es igual al del medio de transmisión.
 Así obtenemos:
Así obtenemos:
![{ \left[ { E }_{ 0i } \right] }_{ \perp }+{ \left[ { E }_{ 0r } \right] }_{ \perp }={ \left[ { E }_{ 0t } \right] }_{ \perp }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d9f008db9dc5f19ef46754cc5cbfdd1cbbebb0a0)
![{ \left[ { E }_{ 0t } \right] }_{ \perp }-{ \left[ { E }_{ 0r } \right] }_{ \perp }={ \left[ { E }_{ 0i } \right] }_{ \perp }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/eca104bdadf7549e988ea0913e6694465455353e)
Dividimos cada término con el ![{ \left[ { E }_{ 0i } \right] }_{ \perp }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9be52078c54d1c08bd5f83cb071560ac700a2139) para obtener:
para obtener:
![{ \left[ \frac { { E }_{ 0t } }{ { E }_{ 0i } } \right] }_{ \perp }-{ \left[ \frac { { E }_{ 0r } }{ { E }_{ 0i } } \right] }_{ \perp }={ \left[ \frac { { E }_{ 0i } }{ {E}_{ 0i } } \right] }_{ \perp }\quad](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d45c1e6d723eebd1f5016888fffef0116533cab0)
![{ \left[ \frac { { E }_{ 0t } }{ { E }_{ 0i } } \right] }_{ \perp }-{ \left[ \frac { { E }_{ 0r } }{ { E }_{ 0i } } \right] }_{ \perp }=1\quad \quad \quad](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f9123a97fd10eafb3ec4028f8b9b378e3904a4d6)
Sabemos que ![\left[ \frac { { E }_{ 0t } }{ { E }_{ 0i } } \right]_{ \perp }=](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/09a9d1068c77a54eba62ea6352920cb5f8cd95fb) Amplitud del coeficiente de transmisión
Amplitud del coeficiente de transmisión y también podemos notar que el cociente
y también podemos notar que el cociente ![\left[ \frac { { E }_{ 0r } }{ { E }_{ 0i } } \right] _{ \perp }=](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0990b13297897cbc62c01ec90c3bbb0b186db3fd) Amplitud del coeficiente de reflexión
Amplitud del coeficiente de reflexión
Dado las dos aseveraciones anteriores podemos dar por echo entonces que:


Por lo tanto esta probado
Otro camino para la comprobación anterior es la siguiente:
Sabemos que el cociente de reflexión de amplitud es:

Y por otro lado el coeficiente de transmisión de amplitud es:




Utilizando la fórmula de suma y diferencia Bhaskara Acharya :




--Ruben Espinosa Guzmán
Ejercicio 4.68
muestra que los ángulos de polarización para la reflexión interna y externa en una interfaz dada son complementarios, es decir,
si el indice de refracción de las regiones incidente y transmitida es  respectivamente y
respectivamente y  es el angulo de polarización, entonces
es el angulo de polarización, entonces

llamemos para la reflexion interna  ....(1)
....(1)
llamemos para la reflexion externa  ....(2)
....(2)
de las ecuaciones (1) y (2) obtenemos...



al multiplicar cruzado obtenemos:




si la suma de su angulo de polarización de la reflexión interna  y el angulo de polarización externa
y el angulo de polarización externa  son
son  entonces complementarios.
entonces complementarios.
 el angulo de polarización de la reflexión interna
el angulo de polarización de la reflexión interna  y el angulo de polarización de reflexión externa
y el angulo de polarización de reflexión externa  son complementarios.
son complementarios.
 queda probado.
queda probado.
--Salvador Alejandro Morales Carranza
Ejercicio 4.51
Utilizando las ecuaciones de Fresnel, demuestre que :
$ r_{\perp} = \frac{ \cos \theta_i - \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}{ \cos \theta_i + \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}$
$r_{\parallel} = \frac{n_{ti}^2 \cos \theta_i - \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}{ n_{ti}^2\cos \theta_i + \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}$
- Solución:
Los coeficientes de reflexión en medios deieléctricos son:
$ r_{\perp} =\frac{n_i \cos \theta_i- n_t \cos \theta_t}{n_i \cos \theta_i+ n_t \cos \theta_t} $
$r_{\parallel} =\frac{n_t\cos \theta_i- n_i\cos \theta_t}{n_i \cos \theta_i+ n_t \cos \theta_t} $
Haciendo uso de la relación pitagórica : $\sin^2 \theta+ \cos^2 \theta=1$ podemos reescribir $ \cos \theta_t $ y $ \cos \theta_i $
$\cos \theta_t= \sqrt{ 1 - \sin^2 \theta_t}$
Y por Ley de Snell:
$\sin \theta_t= \frac{n_i}{n_t} \sin \theta_i$
elevamos al cuadrado:
$\sin^2 \theta_t= \frac{n_i^2}{n_t^2} \sin^2 \theta_i$
$\sin^2 \theta_i= \frac{n_t^2}{n_i^2} \sin^2 \theta_t$
Al hacer la sustitución llegamos a una expresión para $\cos \theta_t $ que involucra a $\sin \theta_i $
$\cos \theta_t= \sqrt{ 1 -\frac{n_i^2}{n_t^2} \sin ^2 \theta_i}$
con :$ \frac{n_t}{n_i} \equiv n_{ti}$
$\cos \theta_t= \sqrt{ n_{ti}^2- \sin ^2 \theta_i}$
Sustituimos en la ecuación para $ r_{\perp}$ y obtenemos:
$ r_{\perp} = \frac{ \cos \theta_i - \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}{ \cos \theta_i + \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}$
Para $ r_{\parallel}$
$ \cos \theta_t= \sqrt{ \frac {1}{n_{ti}^2}- \sin ^2 \theta_i}$
Multiplicamos y dividimos por $ n_{ti}^2$
y reescribimos $ r_{\parallel}$
$r_{\parallel} = \frac{n_{ti}^2 \cos \theta_i - \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}{ n_{ti}^2\cos \theta_i + \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}$
Aurea Espin (discusión) 00:13 29 oct 2018 (CDT)
Ejercicio 4.59
Utilice la ecuación 4.42 y la expansión en serie de la función seno para establecer que en una incidencia cercana a la normal podemos obtener una mejor aproximación que la del problema 4.45.
- Solución:
Ahora bien, el desarrollo en serie de Taylor para el seno está dado por

lo que puede ser escrito como
![sen \theta = \theta \left[1 - \dfrac{1}{3!}\theta^2 + \dfrac{1}{5!}\theta^4-\cdots\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6a5cd98879e571f43fd2667f59f57d2ca11ab53a)
Y de la ley de Snell  obtenemos
obtenemos
![\theta_t \left[1-\dfrac{1}{6}\theta_t^2+\cdots\right] = \dfrac{1}{n}\theta_i \left[1-\dfrac{1}{6}\theta_i^2+\cdots\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c1224e9018b3df5e6c2ef10eb91dd5d45f40dfe0)
Del desarrollo binomial conocemos que  y como los ángulos son pequeños despreciamos los términos de los ángulos en potencias mayores a dos:
y como los ángulos son pequeños despreciamos los términos de los ángulos en potencias mayores a dos:
![\theta_t = \dfrac{1}{n}\theta_i \left[1-\dfrac{1}{6}\theta_i^2\right] \left[1+\dfrac{1}{6}\theta_t^2\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f3a3ace80a281eed31f51e498802d03bacd4df94)
La ley de Snell cuando el medio del rayo incidente es el vacío nos dice que para cuando los ángulos son  entonces
entonces  , entonces sustituyendo al ángulo transmitido en términos del incidente
, entonces sustituyendo al ángulo transmitido en términos del incidente
![\theta_t = \dfrac{1}{n}\theta_i \left[1-\dfrac{1}{6}\theta_i^2\right] \left[1+\dfrac{1}{6n^2}\theta_i^2\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ce055fe2b2f351af5ea99ee427e5af7b01c37ec0)
Y realizando el producto
![\theta_t = \dfrac{\theta_i}{n} \left[1+\dfrac{1}{6n^2}\theta_i^2 -\dfrac{1}{6}\theta_i^2 - \dfrac{1}{36n^2}\theta_i^4 \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/db549e7f61a3d16f5e88f4c5b7d3abb104e372dd)
que tomando en cuenta que despreciamos términos en los ángulos mayores a potencias de dos
![\theta_t = \dfrac{\theta_i}{n} \left[1-(n^2-1) \dfrac{\theta_i^2}{6n^2}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/162b54e7b070a41c5e7ae530f32f077b0afc0457)
de donde es fácil ver que
![\theta_i \pm \theta_t = \theta_i \pm \dfrac{\theta_i}{n} \left[1-(n^2-1) \dfrac{\theta_i^2}{6n^2}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5b904313922ce0a7ad9ae9bd9f6e996b0213af92)
que puede reescribirse como
![\theta_i \pm \theta_t = \theta_i \left[1 \pm \dfrac{1}{n} \left(1-(n^2-1) \dfrac{\theta_i^2}{6n^2}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c3a27b83349f19b2773ad7d57eb7fa02ebf64513)
La ecuación 4.42 es

Y con la expansión del seno y el resultado anterior queda como

Ivan de Jesús Pompa García (discusión) 19:32 5 nov 2018 (CST)
Ejercicio 4.11
Calcule el ángulo de transmisión para un rayo en el aire inicialmente a $30°$ en un bloque de vidrio crown $(n_v=1.52)$.
- $n_i\sin{\theta_i}{=n}_t\sin{\theta_t}$
- donde $n_i=1$ y $n_v=n_t$
- $sin30°=(1.52)sinθt$
- $\theta_t=\sin^{-1}{(0.5/1.52)}$
- $\theta_t=19.20°$
--Verenisse
Ejercicio 4.25
comenzando con la ley de snell, pruebe que la ecuación vectorial de la refracción tiene la forma:
ntkt-niki=$n_t\cos{\theta_t}{-n}_i\cos{\theta_i}$
partiendo de : $n_i\sin{\theta_i}{=n}_t\sin{\theta_t}{,n_i}( k_{i} X {u_n}){=n}_t{,n_t}( {k_t} X {u_n})$
donde: k_{i},k_{t} son los vectores unitarios de propagación
Así
${n_t}( k_{t} X {u_n}) -{n_i}( k_{i} X {u_n})=0$
$({n_t} k_{t} {-n_i} k_{i}) x U{n}=0$
dejando:
${n_t} k_{t}{-n_i} k_{i}$=${\gamma}$=${\gamma_{u_n}}$
donde
${\gamma}$ es referido como el astigmático constante, tambien
${\gamma}$ es la diferencia entre las proyecciones de ${n_t} k_{t} y { n_i} k_{i}$ en ${u_n}$
En otras palabras, es el producto punto entre ${\gamma}$ y ${u_n}$:
por lo que
${\gamma}$ =$n_t\cos{\theta_t}{-n}_i\cos{\theta_i}$
--[[Usuario:|Luisa Alejandra Vega S.]]
Ejercicio 4.32
Derivar la ley de refracción, $\theta_i=\theta_f$, usando cálculo para minimizar el tiempo de tránsito como lo requiere el principio de Fermat.
- --Solución--
Con ayuda de la siguiente figura, podremos hacer el problema.
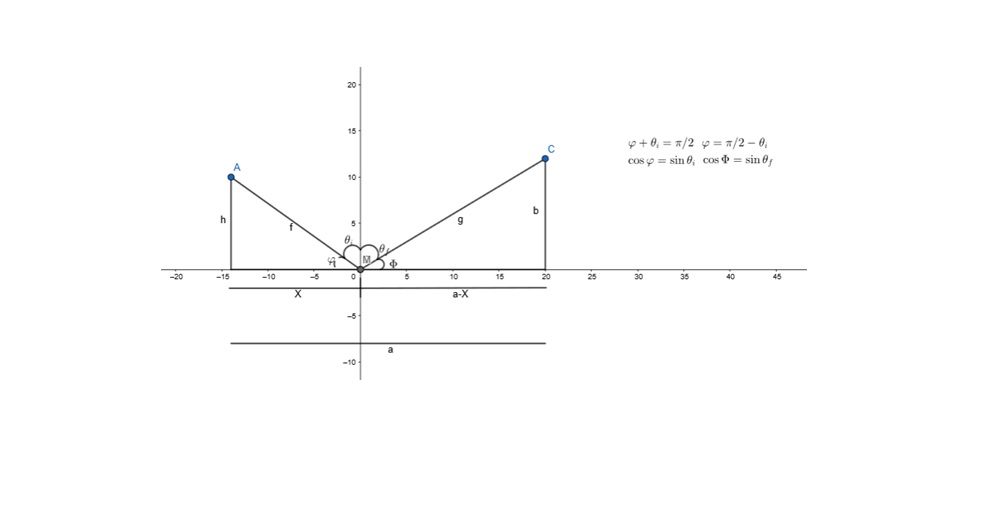
- Definimos a la longitud de camino óptico como:
$LOP=nAB + nBC$ ; n es el índice de refracción del medio. En este caso es el mismo porque el medio es el mismo.
- Por trigonometría sabemos que:
$AM=(h^2 + x^2)^{1/2}$ y;
- $MC=(b^2+(a-x)^2)^{1/2}$ ; Por lo tanto la longitud de camino óptico es:
- $LOP= n(h^2 + x^2)^{1/2} + n(b^2+(a-x)^2)^{1/2}$ ; Como queremos minimizar el tránsito de $LOP$, entonces debemos sacar la derivada respecto de x, a $LOP$ e igualarla a 0.
- $d/dx(LOP)= d/dx[n(h^2 + x^2)^{1/2} + n(b^2+(a-x)^2)^{1/2}]=0$
Entonces:
- $\frac{d}{dx}[n(h^2 + x^2)^{1/2} + n(b^2+(a-x)^2)^{1/2}]= n(h^2+ x^2)^{-1/2}x + n(b^2+ (a-x)^2)^{-1/2}(x-a)=0$
Por lo tanto:
- $n[(h^2+ x^2)^{-1/2}x - (b^2+ (a-x)^2)^{-1/2}(a-x)]=0$ ó
- $\frac{x}{(h^2+ x^2)^{1/2}} - \frac{a-x}{(b^2+ (a-x)^2)^{1/2}}= 0$
- Pero si nos fijamos de nuevo en la figura, observamos que:
- $\frac{x}{(h^2+ x^2)^{1/2}}= \sin\theta_i$ y;
- $\frac{a-x}{(b^2+ (a-x)^2)^{1/2}}= \sin\theta_r$ Por lo tanto:
- $\sin\theta_i= \sin\theta_r$ $\Leftrightarrow$ $\theta_i=\theta_f$.
- --[[Usuario:|Pedro J. Julian.]]
Ejercicio 4.43
Deduzca las ecuaciones (4.42) a (4.45) para $r_{\perp}$, $r_{\parallel}$, $t_{\perp}$, $t_{\parallel}$
$r_{\perp}=-\frac{\sin{(\theta_i-\theta_t)}}{\sin{(\theta_i+\theta_t)}}$ ...$(4.42)$
$r_{\parallel}=+\frac{\tan{(\theta_i-\theta_t)}}{\tan{(\theta_i+\theta_t)}}$ ...$(4.43)$
$t_{\perp}=+\frac{2\sin{\theta_t}\cos{\theta_i}}{\sin{(\theta_i+\theta_t)}}$ ...$(4.44)$
$t_{\parallel}=+\frac{2\sin{\theta_t}\cos{\theta_i}}{\sin{(\theta_i+\theta_t)}\cos{(\theta_i-\theta_t)}}$ ...$(4.45)$
- Solución:
- Partiendo de las ecuaciones de Fresnel y el índice de refracción relativo $n_{ti}=\frac{n_t}{n_i}=\frac{\sin{\theta_i}}{\sin{\theta_t}}$
- $r_{\perp}=\frac{n_i\cos{\theta_i}-n_t\cos{\theta_t}}{{n_i\cos{\theta_i}+n_t\cos{\theta_t}}}=\left(\frac{1/n_i}{1/n_i}\right)\frac{n_i\cos{\theta_i}-n_t\cos{\theta_t}}{{n_i\cos{\theta_i}+n_t\cos{\theta_t}}}=\frac{\frac{n_i}{n_i}\cos{\theta_i}-\frac{n_t}{n_i}\cos{\theta_t}}{{\frac{n_i}{n_i}\cos{\theta_i}+\frac{n_t}{n_i}\cos{\theta_t}}}=\left(\frac{\sin{\theta_t}}{\sin{\theta_t}}\right)\frac{\cos{\theta_i}-\frac{\sin{\theta_i}}{\sin{\theta_t}}\cos{\theta_t}}{{\cos{\theta_i}-\frac{\sin{\theta_i}}{\sin{\theta_t}}\cos{\theta_t}}}=\frac{\sin{\theta_t}\cos{\theta_i}-\sin{\theta_i}\cos{\theta_t}}{\sin{\theta_t}\cos{\theta_i}+\sin{\theta_i}\cos{\theta_t}}=-\frac{\sin{\theta_i}\cos{\theta_t}-\sin{\theta_t}\cos{\theta_i}}{\sin{\theta_t}\cos{\theta_i}+\sin{\theta_i}\cos{\theta_t}}$
- utilizando la identidad trigonométrica $\sin{(a\pm b)}=\sin{a}\cos{b}\pm \cos{a}\sin{b}$
$\therefore r_{\perp}=-\frac{\sin{(\theta_i-\theta_t)}}{\sin{(\theta_i+\theta_t)}}$
- $t_{\perp}=\frac{2 n_i \cos{\theta_i}}{n_i\cos{\theta_i}+n_t\cos{\theta_t}}=\frac{2 \frac{n_i}{n_t} \cos{\theta_i}}{\frac{n_i}{n_t}\cos{\theta_i}+\cos{\theta_t}}=\frac{2 \sin{\theta_t} \cos{\theta_i}\frac{1}{\sin{\theta_i}}}{\frac{\sin{\theta_t}}{\sin{\theta_i}}\cos{\theta_i}+\cos{\theta_t}}=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_t}\cos{\theta_i}+\sin{\theta_i}\cos{\theta_t}}$
- $\therefore t_{\perp}=+\frac{2\sin{\theta_t}\cos{\theta_i}}{\sin{(\theta_i+\theta_t)}}$
- $r_{\parallel}=\frac{n_t\cos{\theta_i}-n_i\cos{\theta_t}}{{n_t\cos{\theta_i}+n_i\cos{\theta_t}}}=\frac{\sin{\theta_i}\cos{\theta_i}-\sin{\theta_t}\cos{\theta_t}}{\sin{\theta_t}\cos{\theta_t}+\sin{\theta_i}\cos{\theta_i}}$
- Poniendo los senos y cosenos en términos de exponenciales:
- $r_{\parallel}=\frac{\left(\frac{e^{i\theta_i}-e^{-i\theta_i}}{2i}\right)\left(\frac{e^{i\theta_i}+e^{-i\theta_i}}{2}\right)-\left(\frac{e^{i\theta_t}-e^{-i\theta_t}}{2i}\right)\left(\frac{e^{i\theta_t}+e^{-i\theta_t}}{2}\right)}{\left(\frac{e^{i\theta_i}-e^{-i\theta_i}}{2i}\right)\left(\frac{e^{i\theta_i}+e^{-i\theta_i}}{2}\right)+\left(\frac{e^{i\theta_t}-e^{-i\theta_t}}{2i}\right)\left(\frac{e^{i\theta_t}+e^{-i\theta_t}}{2}\right)}=\frac{\left(e^{i\theta_i}-e^{-i\theta_i}\right)\left(e^{i\theta_i}+e^{-i\theta_i}\right)-\left(e^{i\theta_t}-e^{-i\theta_t}\right)\left(e^{i\theta_t}+e^{-i\theta_t}\right)}{\left(e^{i\theta_i}-e^{-i\theta_i}\right)\left(e^{i\theta_i}+e^{-i\theta_i}\right)+\left(e^{i\theta_t}-e^{-i\theta_t}\right)\left(e^{i\theta_t}+e^{-i\theta_t}\right)}$
- al realizar los productos se obtiene:
- $r_{\parallel}=\frac{e^{2i\theta_i}-e^{-2i\theta_i}-e^{2i\theta_t}+e^{-2i\theta_i}}{e^{2i\theta_i}-e^{-2i\theta_i}+e^{2i\theta_t}-e^{-2i\theta_t}}$
- sumando y restando $\theta_i$ y $\theta_t$ a los argumentos de las exponenciales y separandolas como producto de exponenciales:
- $r_{\parallel}= \frac{e^{i(\theta_i+\theta_t+\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t+\theta_i-\theta_t)}-e^{i(\theta_t+\theta_i+\theta_t-\theta_i)}+e^{-i(\theta_t+\theta_i+\theta_t-\theta_i)}}{e^{i(\theta_i+\theta_t+\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t+\theta_i-\theta_t)}+e^{i(\theta_t+\theta_i+\theta_t-\theta_i)}-e^{-i(\theta_t+\theta_i+\theta_t-\theta_i)}}$
- $=\frac{e^{i(\theta_i+\theta_t)}e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t)}e^{-i(\theta_i-\theta_t)}-e^{i(\theta_i+\theta_t)}e^{-i(\theta_i-\theta_t)}+e^{-i(\theta_i+\theta_t)}e^{i(\theta_i-\theta_t)}}{e^{i(\theta_i+\theta_t)}e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t)}e^{-i(\theta_i-\theta_t)}+e^{i(\theta_i+\theta_t)}e^{-i(\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t)}e^{i(\theta_i-\theta_t)}}$
- factorizando términos semejantes:
$r_{\parallel}=\frac{e^{i(\theta_i+\theta_t)}\left(e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i-\theta_t)}\right)+e^{-i(\theta_i+\theta_t)}\left(e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i-\theta_t)}\right)}{e^{i(\theta_i+\theta_t)}\left(e^{i(\theta_i-\theta_t)}+e^{-i(\theta_i-\theta_t)}\right)-e^{-i(\theta_i+\theta_t)}\left(e^{i(\theta_i-\theta_t)}+e^{-i(\theta_i-\theta_t)}\right)}=\frac{\left(e^{i(\theta_i+\theta_t)}+e^{-i(\theta_i+\theta_t)}\right)\left(e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i-\theta_t)}\right)}{\left(e^{i(\theta_i+\theta_t)}-e^{-i(\theta_i+\theta_t)}\right)\left(e^{i(\theta_i-\theta_t)}+e^{-i(\theta_i-\theta_t)}\right)}$
- regresando a senos y cosenos:
$r_{\parallel}=\frac{\left(2\cos{(\theta_i+\theta_t)}\right)\left(2i\sin{(\theta_i-\theta_t)}\right)}{\left(2\cos{(\theta_i-\theta_t)}\right)\left(2i\sin{(\theta_i+\theta_t)}\right)}=\frac{\left(\cos{\theta_i+\theta_t}\right)\left(\sin{\theta_i-\theta_t}\right)}{\left(\sin{\theta_i+\theta_t}\right)\left(\cos{\theta_i-\theta_t}\right)}$
- $\therefore r_{\parallel}=+\frac{\tan{(\theta_i-\theta_t)}}{\tan{(\theta_i+\theta_t)}}$
- $t_\parallel=\frac{2 n_i \cos{\theta_i}}{n_i\cos{\theta_t}+n_t\cos{\theta_i}}=\frac{2 n_{it} \cos{\theta_i}}{n_{it}\cos{\theta_t}+\cos{\theta_i}}=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_t}\cos{\theta_t}+\sin{\theta_i}\cos{\theta_i}}=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_t}\cos{\theta_t}\left(\sin^2 \theta_i+\cos^2 \theta_i \right)+\sin{\theta_i}\cos{\theta_i}\left(\sin^2\theta_t+\cos^2 \theta_t\right)}$
- $=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_i}^2\sin{\theta_t}\cos{\theta_t}+\cos{\theta_i}^2\sin{\theta_t}\cos{\theta_t}+\sin{\theta_t}^2\sin{\theta_i}\cos{\theta_i}+\cos{\theta_t}^2\sin{\theta_i}\cos{\theta_i}}$
- $=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_i}\cos{\theta_t}\sin{\theta_i}\sin{\theta_t}+\sin{\theta_i}\cos{\theta_t}\cos{\theta_i}\cos{\theta_t}+\cos{\theta_i}\sin{\theta_t}\sin{\theta_i}\sin{\theta_t}+\cos{\theta_i}\sin{\theta_t}\cos{\theta_i}\cos{\theta_t}}$
- $=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_i}\cos{\theta_t}\left(\sin{\theta_i}\sin{\theta_t}+\cos{\theta_i}\cos{\theta_t}\right)+\cos{\theta_i}\sin{\theta_t}\left(\sin{\theta_i}\sin{\theta_t}+\cos{\theta_i}\cos{\theta_t}\right)}$
- $=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\left(\sin{\theta_i}\cos{\theta_t}+\cos{\theta_i}\sin{\theta_t}\right)\left(\sin{\theta_i}\sin{\theta_t}+\cos{\theta_i}\cos{\theta_t}\right)}$
- $\therefore t_{\parallel}=+\frac{2\sin{\theta_t}\cos{\theta_i}}{\sin{(\theta_i+\theta_t)}\cos{(\theta_i-\theta_t)}}$
--Sergio






![x_{0}=\frac{q_{e}E_{0}}{m_{e}}\frac{1}{[(\omega_{0}^{2}-\omega^{2})^{2} + (\gamma\omega)^{2}]^{\frac{1}{2}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5a0dac1bd4a66e54ca5363aa36b4637169c7ba13)














![[-m_{e}\omega^{2}x_{0} + im_{e}\gamma\omega x_{0} + m_{e}\omega_{0}^{2}x_{0}]\exp(i\left(\omega t-\alpha\right))=q_{e}E_{0}\exp(i\omega t)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d87afdc94dc7cadef2b6bb78a23cda20d4adf728)

























































![t_{\perp }+(-r_{\perp })=0.7514+[-(-0.2486)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d3a5b6542f6c89ba86b59539af1351a8c69d7b73)


































![{ \left[ { E }_{ 0i } \right] }_{ \perp }+{ \left[ { E }_{ 0r } \right] }_{ \perp }={ \left[ { E }_{ 0t } \right] }_{ \perp }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d9f008db9dc5f19ef46754cc5cbfdd1cbbebb0a0)
![{ \left[ { E }_{ 0t } \right] }_{ \perp }-{ \left[ { E }_{ 0r } \right] }_{ \perp }={ \left[ { E }_{ 0i } \right] }_{ \perp }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/eca104bdadf7549e988ea0913e6694465455353e)
![{ \left[ { E }_{ 0i } \right] }_{ \perp }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9be52078c54d1c08bd5f83cb071560ac700a2139)
![{ \left[ \frac { { E }_{ 0t } }{ { E }_{ 0i } } \right] }_{ \perp }-{ \left[ \frac { { E }_{ 0r } }{ { E }_{ 0i } } \right] }_{ \perp }={ \left[ \frac { { E }_{ 0i } }{ {E}_{ 0i } } \right] }_{ \perp }\quad](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d45c1e6d723eebd1f5016888fffef0116533cab0)
![{ \left[ \frac { { E }_{ 0t } }{ { E }_{ 0i } } \right] }_{ \perp }-{ \left[ \frac { { E }_{ 0r } }{ { E }_{ 0i } } \right] }_{ \perp }=1\quad \quad \quad](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f9123a97fd10eafb3ec4028f8b9b378e3904a4d6)
![\left[ \frac { { E }_{ 0t } }{ { E }_{ 0i } } \right]_{ \perp }=](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/09a9d1068c77a54eba62ea6352920cb5f8cd95fb)

![\left[ \frac { { E }_{ 0r } }{ { E }_{ 0i } } \right] _{ \perp }=](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0990b13297897cbc62c01ec90c3bbb0b186db3fd)




























![sen \theta = \theta \left[1 - \dfrac{1}{3!}\theta^2 + \dfrac{1}{5!}\theta^4-\cdots\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6a5cd98879e571f43fd2667f59f57d2ca11ab53a)

![\theta_t \left[1-\dfrac{1}{6}\theta_t^2+\cdots\right] = \dfrac{1}{n}\theta_i \left[1-\dfrac{1}{6}\theta_i^2+\cdots\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c1224e9018b3df5e6c2ef10eb91dd5d45f40dfe0)

![\theta_t = \dfrac{1}{n}\theta_i \left[1-\dfrac{1}{6}\theta_i^2\right] \left[1+\dfrac{1}{6}\theta_t^2\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f3a3ace80a281eed31f51e498802d03bacd4df94)


![\theta_t = \dfrac{1}{n}\theta_i \left[1-\dfrac{1}{6}\theta_i^2\right] \left[1+\dfrac{1}{6n^2}\theta_i^2\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ce055fe2b2f351af5ea99ee427e5af7b01c37ec0)
![\theta_t = \dfrac{\theta_i}{n} \left[1+\dfrac{1}{6n^2}\theta_i^2 -\dfrac{1}{6}\theta_i^2 - \dfrac{1}{36n^2}\theta_i^4 \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/db549e7f61a3d16f5e88f4c5b7d3abb104e372dd)
![\theta_t = \dfrac{\theta_i}{n} \left[1-(n^2-1) \dfrac{\theta_i^2}{6n^2}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/162b54e7b070a41c5e7ae530f32f077b0afc0457)
![\theta_i \pm \theta_t = \theta_i \pm \dfrac{\theta_i}{n} \left[1-(n^2-1) \dfrac{\theta_i^2}{6n^2}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5b904313922ce0a7ad9ae9bd9f6e996b0213af92)
![\theta_i \pm \theta_t = \theta_i \left[1 \pm \dfrac{1}{n} \left(1-(n^2-1) \dfrac{\theta_i^2}{6n^2}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c3a27b83349f19b2773ad7d57eb7fa02ebf64513)

