Optica: Capitulo4-problemas

Bienvenidos. En esta página pueden dejar las soluciones a sus problemas del Hecht- Capítulo 4, con el siguiente formato:

Problema 1

Planteamiento del problema

Solución

y su respectiva firma

--Gael

---

Ejercicio 4.45

---

Un rayo láser incide en la interfaz entre el aire y algunos dieléctricos de índice n. Para valores pequeños de ${\theta }_{i}$ muestre que ${\theta }_{t}={\frac {{\theta }_{i}}{n}}$, Usa esto y la ec. (4.42) para establecer que en una incidencia casi normal ${\left\lceil {-r}_{\bot }\right\rceil }_{{\theta }_{i}\sim 0}={\frac {n-1}{n+1}}$

Solución:

Tenemos los siguientes datos conocidos:

Indice de refracción del aire ${n}_{i}$ es: 1

Indice de refracción del dieléctrico ${n}_{t}$ es :$n$

Ángulo de incidencia = ${\theta }_{i}$

Ángulo de refracción = ${\theta }_{t}$

Aplicando la ley de Snell:

${n}_{i}sin{\theta }_{i}={n}_{t}sin{\theta }_{t}$

$sin{\theta }_{i}=nsin{\theta }_{t}\quad ......(1)$

Para valores pequeños de theta, tenemos las siguientes relaciones:

$sin{\theta }_{t}={\theta }_{i}$

$sin{\theta }_{t}={\theta }_{t}$

La Ecuación (1) se reduce:

$n{\theta }_{t}={\theta }_{i}$

De la última expresión tenemos:

${\theta }_{t}={\frac {{\theta }_{i}}{n}}$

Ahora ocupando la ecuación 4.42 y considerando ${\theta }_{i}$ muy pequeñas :

${r}_{\bot }=-{\frac {sin({\theta }_{i}-{\theta }_{t})}{sin({\theta }_{i}+{\theta }_{t})}}\quad .....(a)$

Haciendo la consideración:

${r}_{\bot }={\frac {({\theta }_{t}-{\theta }_{i})}{({\theta }_{i}+{\theta }_{t})}}$

ocupando ${\theta }_{t}={\frac {{\theta }_{i}}{n}}$ , y sustituyendo en la ultima ecuación:

${r}_{\bot }={\frac {({\frac {{\theta }_{i}}{n}}-{\theta }_{i})}{({\theta }_{i}+{\frac {{\theta }_{i}}{n}})}}$

Factorizando ${\theta }_{i}$

${r}_{\bot }={\frac {{\theta }_{i}({\frac {1}{n}}-1)}{{\theta }_{i}(1+{\frac {1}{n}})}}$

Reduciendo:

${r}_{\bot }={\frac {(1-n)}{(1+n)}}$

Finalmente tenemos:

${\left(-{r}_{\bot }\right)}_{{\theta }_{i}\approx 0}={\frac {n-1}{n+1}}$

--Luis Manuel Chávez Antonio

---

Ejercicio 4.64

---

Verifique que:

$t_{\perp }+(-r_{\perp })=1$.........[4.49]

para $\theta _{i}=30$ en una interfaz de vidrio crown y aire $(n_{ti}=1.52)$

Solución:

Datos:

Angulo de incidencia $(\theta _{i})$ = 30°

Indice de refracción del cristal $(n_{f})$ = 1.52

Indice de refracción del aire = 1

Angulo de transmisión $(\theta _{t})$

Usando la ley de Snell obtenemos:

${\frac {sen(\theta _{i})}{sen(\theta _{t})}}={\frac {n_{t}}{n_{i}}}$

${\frac {sen(30)}{sen(\theta _{t})}}=1.52$

${\frac {0.5}{sen(\theta _{t})}}=1.52$

$sen(\theta _{t})={\frac {0.5}{1.52}}$

En angulo de transmisión $(\theta _{t})$ sera:

$\theta _{t}=sen^{-1}\left({\frac {0.5}{1.52}}\right)$

$\theta _{t}=19.2$

El componente perpendicular del coeficiente de transmisión es:

$t_{\perp }={\frac {2n_{i}cos(\theta _{i})}{n_{i}cos(\theta _{i})+n_{f}cos(\theta _{t})}}$

$t_{\perp }={\frac {2cos(30)}{cos(30)+(1.52)cos(19.2)}}$

$t_{\perp }={\frac {(2)(0.86)}{(0.86)+(1.52)(0.94)}}$

$t_{\perp }=0.7514$

Ahora, la componente perpendicular del coeficiente de reflexión es:

$r_{\perp }={\frac {n_{i}cos(\theta _{i})-n_{t}cos(\theta _{t})}{n_{i}cos(\theta _{i})+n_{t}cos(\theta _{t})}}$

$r_{\perp }={\frac {(0.86)-(1.52)(0.94)}{(0.86)+(1.52)(0.94)}}$

$r_{\perp }=-0.2486$

Al sumar los valores de $t_{\perp }$ y $r_{\perp }$ obtenemos:

$t_{\perp }+(-r_{\perp })=0.7514+[-(-0.2486)]$

$t_{\perp }+(-r_{\perp })=0.7514+0.2486$

$t_{\perp }+(-r_{\perp })=1$

Por lo tanto $t_{\perp }+(-r_{\perp })=1$

--Enrique Ortiz Martinez

---

Ejercicio 4.21

Trace un gráfico de θ_i con respecto a θ_t para una frontera aire-vidrio donde $n_{v}a=1.5$. Discuta la forma de la curva.

Solución:

La ecuación de la refracción de Snell está dada por:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): n_i sin⁡(θ_i )=n_t sin⁡(θ_t )

Pero n_i=1

Por lo tanto

Error al representar (error de sintaxis): n_i sin⁡(θ_i )=n_t sin⁡(θ_t )

Despejando θ_t se tiene que Error al representar (error de sintaxis): θ_t=sin^(-1)⁡(sin⁡θ_i /n_t )

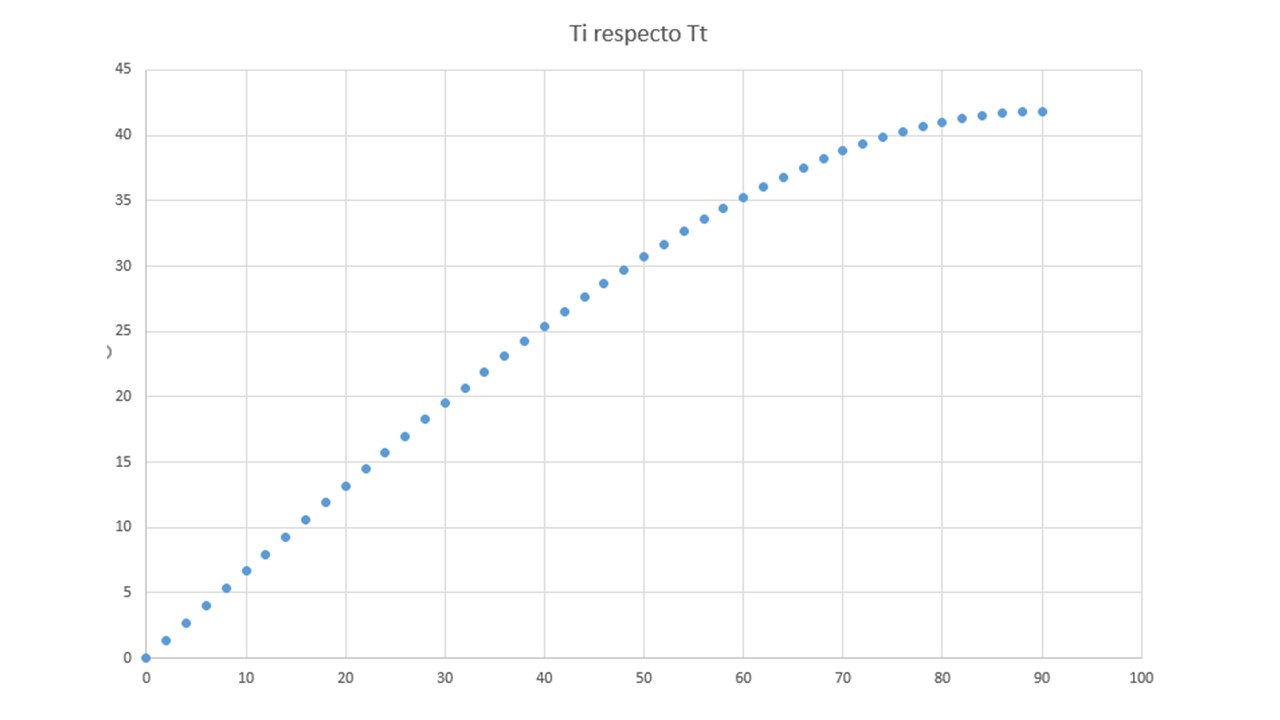
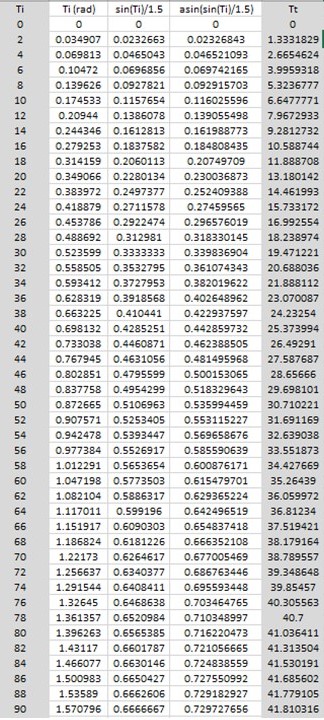
En este caso se realizan cambios de 2 grados de diferencia, se tuvo la siguiente gráfica

Podemos observar que a pesar que al comparar los ángulos, se puede apreciar que los valores tienden a un número que en este caso es aproximadamente 42°. Esto se podría interpretar como el ángulo máximo que puede tomar el haz, en este caso, en el agua.

Los datos están en el siguiente documento.

--Fernando Valencia Hernández

---

Problema 4.72

---

Mostrar que: ${T}_{\parallel }={\frac {\sin {2{\theta }_{i}}\sin {2{\theta }_{t}}}{\sin ^{2}{({\theta }_{i}+{\theta }_{t})}\cos ^{2}{({\theta }_{i}-{\theta }_{t})}}}$

Y

${T}_{\bot }={\frac {\sin {2{\theta }_{i}}\sin {2{\theta }_{t}}}{\sin ^{2}{({\theta }_{i}+{\theta }_{t})}}}$

Solución:

La componente perpendicular de la transmitancia $T$ esta dada por: ${T}_{\bot }=\left({\frac {{n}_{t}\cos {{\theta }_{t}}}{{n}_{i}\cos {{\theta }_{i}}}}\right){t}_{\bot }^{2}\quad ......\left(1\right)$

Pero el coeficiente de amplitud de transmisión es:

${t}_{\bot }={\frac {2\sin {{\theta }_{t}}\cos {{\theta }_{i}}}{\sin {({\theta }_{i}+{\theta }_{t})}}}$

${t}_{\bot }^{2}={\frac {4\sin ^{2}{{\theta }_{i}}\cos ^{2}{{\theta }_{t}}}{\sin ^{2}{({\theta }_{i}+{\theta }_{t})}}}$

Sustituyendo el valor calculado de ${t}_{\bot }^{2}$ en la Ec. $\left(1\right)$, se obtiene:

${T}_{\bot }=\left({\frac {{n}_{t}\cos {{\theta }_{t}}}{{n}_{i}\cos {{\theta }_{i}}}}\right)\left({\frac {4\sin ^{2}{{\theta }_{i}}\cos ^{2}{{\theta }_{t}}}{\sin ^{2}{({\theta }_{i}+{\theta }_{t})}}}\right)\quad ......\left(2\right)$

De la ley de Snell ${n}_{i}\sin {{\theta }_{i}}={n}_{t}\cos {{\theta }_{t}}$

${\frac {{n}_{t}}{{n}_{i}}}={\frac {\sin {{\theta }_{i}}}{\sin {{\theta }_{t}}}}\quad ......\left(3\right)$

Sustituyendo el valor de ${\frac {{n}_{t}}{{n}_{i}}}$ de la Ec. $\left(3\right)$ en la Ec. $\left(2\right)$, obtenemos:

${T}_{\bot }=\left({\frac {\sin {{\theta }_{i}}}{\sin {{\theta }_{t}}}}{\frac {\cos {{\theta }_{t}}}{\cos {{\theta }_{i}}}}\right)\left({\frac {4\sin ^{2}{{\theta }_{i}}\cos ^{2}{{\theta }_{t}}}{\sin ^{2}{({\theta }_{i}+{\theta }_{t})}}}\right)$

${T}_{\bot }={\frac {4\sin {{\theta }_{t}}\cos {{\theta }_{t}}\sin {{\theta }_{i}}\cos {{\theta }_{i}}}{\sin ^{2}{({\theta }_{i}+{\theta }_{t})}}}$

${T}_{\bot }=\left({\frac {\left(2\sin {{\theta }_{t}}\cos {{\theta }_{t}}\right)\left(2\sin {{\theta }_{i}}\cos {{\theta }_{i}}\right)}{\sin ^{2}{({\theta }_{i}+{\theta }_{t})}}}\right)$

Comprobando que:

${T}_{\bot }={\frac {\sin {2{\theta }_{i}}\sin {2{\theta }_{t}}}{\sin ^{2}{({\theta }_{i}+{\theta }_{t})}}}$

Del mismo modo podemos proceder para el comportamiento paralelo de $T$, se la siguiente manera:

El comportamiento paralelo de la transmitancia $T$, se expresa como:

${T}_{\parallel }=\left({\frac {{n}_{t}\cos {{\theta }_{t}}}{{n}_{i}\cos {{\theta }_{i}}}}\right){t}_{\parallel }^{2}\quad ......\left(4\right)$

Pero sabemos que la amplitud del coeficiente de transmisión es:

${t}_{\parallel }={\frac {2\sin {{\theta }_{t}}\cos {{\theta }_{i}}}{\sin {{(\theta }_{i}+{\theta }_{t})}\cos {({{\theta }_{i}-\theta }_{t})}}}$

${{t}_{\parallel }^{2}}={\frac {4\sin ^{2}{{\theta }_{t}}\cos ^{2}{{\theta }_{i}}}{\sin ^{2}{{(\theta }_{i}+{\theta }_{t})}\cos ^{2}{{(\theta }_{i}-{\theta }_{t})}}}$

Sustituyendo el valor de ${t}_{\parallel }^{2}$, en la Ec. $\left(4\right)$, obtenemos:

${T}_{\parallel }=\left({\frac {{n}_{t}\cos {{\theta }_{t}}}{{n}_{i}\cos {{\theta }_{i}}}}\right)\left({\frac {4\sin ^{2}{{\theta }_{t}}\cos ^{2}{{\theta }_{i}}}{\sin ^{2}{{(\theta }_{i}+{\theta }_{t})}\cos ^{2}{{(\theta }_{i}-{\theta }_{t})}}}\right)$

De la Ec. $\left(3\right)$

${\frac {{n}_{t}}{{n}_{i}}}={\frac {\sin {{\theta }_{i}}}{\sin {{\theta }_{t}}}}$

${T}_{\parallel }=\left({\frac {\sin {{\theta }_{i}}}{\sin {{\theta }_{t}}}}{\frac {\cos {{\theta }_{t}}}{\cos {{\theta }_{i}}}}\right)\left({\frac {4\sin ^{2}{{\theta }_{t}}\cos ^{2}{{\theta }_{i}}}{\sin ^{2}{{(\theta }_{i}+{\theta }_{t})}\cos ^{2}{{(\theta }_{i}-{\theta }_{t})}}}\right)$

${T}_{\parallel }=\left({\frac {4\sin {{\theta }_{i}}\sin {{\theta }_{t}}\cos {{\theta }_{i}}\cos {{\theta }_{t}}}{\sin ^{2}{{(\theta }_{i}+{\theta }_{t})}\cos ^{2}{{(\theta }_{i}-{\theta }_{t})}}}\right)$

${T}_{\parallel }=\left({\frac {(2\sin {{\theta }_{i}}\sin {{\theta }_{t})(2}\cos {{\theta }_{i}}\cos {{\theta }_{t}})}{\sin ^{2}{{(\theta }_{i}+{\theta }_{t})}\cos ^{2}{{(\theta }_{i}-{\theta }_{t})}}}\right)$

Comprobando que:

${T}_{\parallel }={\frac {\sin {2{\theta }_{i}}\sin {2{\theta }_{t}}}{\sin ^{2}{({\theta }_{i}+{\theta }_{t})}\cos ^{2}{({\theta }_{i}-{\theta }_{t})}}}$

--Luis Gutiérrez Melgarejo

---

Problema 4.63

---

Prueba que ${t}_{\perp }+(-{r}_{\perp })=1$ para todo ${\theta }_{i}$ , primero de las condiciones de frontera y después de las ecuaciones de Fresnel.

Solucion:

Podemos notar que la continuidad de los componentes tangenciales de ${\overrightarrow {E}}$ analizando cualquier limite en cualquier punto , el campo tangencial en el medio incidente es igual al del medio de transmisión.

$\therefore$ Así obtenemos:

${\left[{E}_{0i}\right]}_{\perp }+{\left[{E}_{0r}\right]}_{\perp }={\left[{E}_{0t}\right]}_{\perp }$

${\left[{E}_{0t}\right]}_{\perp }-{\left[{E}_{0r}\right]}_{\perp }={\left[{E}_{0i}\right]}_{\perp }$

Dividimos cada término con el ${\left[{E}_{0i}\right]}_{\perp }$ para obtener:

${\left[{\frac {{E}_{0t}}{{E}_{0i}}}\right]}_{\perp }-{\left[{\frac {{E}_{0r}}{{E}_{0i}}}\right]}_{\perp }={\left[{\frac {{E}_{0i}}{{E}_{0i}}}\right]}_{\perp }\quad$

${\left[{\frac {{E}_{0t}}{{E}_{0i}}}\right]}_{\perp }-{\left[{\frac {{E}_{0r}}{{E}_{0i}}}\right]}_{\perp }=1\quad \quad \quad$

Sabemos que $\left[{\frac {{E}_{0t}}{{E}_{0i}}}\right]_{\perp }=$Amplitud del coeficiente de transmisión$=t_{\perp }$ y también podemos notar que el cociente $\left[{\frac {{E}_{0r}}{{E}_{0i}}}\right]_{\perp }=$Amplitud del coeficiente de reflexión$={r}_{\perp }$

Dado las dos aseveraciones anteriores podemos dar por echo entonces que:

$t_{\perp }-r_{\perp }=1$

$\therefore \quad \quad t_{\perp }+\left(-r_{\perp }\right)=1$

Por lo tanto esta probado

Otro camino para la comprobación anterior es la siguiente:

Sabemos que el cociente de reflexión de amplitud es:

$r_{\perp }=-{\frac {sen({\theta }_{i}-{\theta }_{t})}{sen({\theta }_{i}+{\theta }_{t})}}$

Y por otro lado el coeficiente de transmisión de amplitud es:

$t_{\perp }={\frac {2sen({\theta }_{t})cos({\theta }_{i})}{sen({\theta }_{i}+{\theta }_{t})}}$

$\rightarrow \quad \quad t_{\perp }-r_{\perp }={\frac {2sen({\theta }_{t})cos({\theta }_{i})}{sen({\theta }_{i}+{\theta }_{t})}}-\left(-{\frac {sen({\theta }_{i}-{\theta }_{t})}{sen({\theta }_{i}+{\theta }_{t})}}\right)$

$\quad \quad t_{\perp }-r_{\perp }={\frac {2sen({\theta }_{t})cos({\theta }_{i})}{sen({\theta }_{i}+{\theta }_{t})}}+\left({\frac {sen({\theta }_{i}-{\theta }_{t})}{sen({\theta }_{i}+{\theta }_{t})}}\right)$

$\quad \quad t_{\perp }-r_{\perp }={\frac {2sen({\theta }_{t})cos({\theta }_{i})+sen({\theta }_{i}-{\theta }_{t})}{sen({\theta }_{i}+{\theta }_{t})}}$

Utilizando la fórmula de suma y diferencia Bhaskara Acharya :

$\quad t_{\perp }-r_{\perp }={\frac {2sen({\theta }_{t})cos({\theta }_{i})+sen({\theta }_{i})cos({\theta }_{t})-sen({\theta }_{t})cos({\theta }_{i})}{sen({\theta }_{i}+{\theta }_{t})}}$

$\quad \quad t_{\perp }-r_{\perp }={\frac {sen({\theta }_{t})cos({\theta }_{i})+sen({\theta }_{i})cos({\theta }_{t})}{sen({\theta }_{i}+{\theta }_{t})}}$

$\quad \quad t_{\perp }-r_{\perp }={\frac {sen({\theta }_{i}+{\theta }_{t})}{sen({\theta }_{i}+{\theta }_{t})}}$

$\quad \therefore \quad \quad t_{\perp }-r_{\perp }=1$

--Ruben Espinosa Guzmán

---

Ejercicio 4.68

---

muestra que los ángulos de polarización para la reflexión interna y externa en una interfaz dada son complementarios, es decir,${\theta }_{p}+{\theta }_{p}^{\prime }={90}^{\circ }$

si el indice de refracción de las regiones incidente y transmitida es ${n}_{i}\quad y\quad {n}_{t}$ respectivamente y ${\theta }_{p}$ es el angulo de polarización, entonces

${\theta }_{p}={\frac {{n}_{t}}{{n}_{i}}}$

llamemos para la reflexion interna ${\theta }_{p}={\frac {{n}_{t}}{{n}_{i}}}$ ....(1)

llamemos para la reflexion externa ${{\theta }^{\prime }}_{p}={\frac {{n}_{t}}{{n}_{i}}}$ ....(2)

de las ecuaciones (1) y (2) obtenemos...

$tan{{\theta }^{}}_{p}={\frac {1}{\frac {{n}_{i}}{{n}_{t}}}}$

$tan{{\theta }^{}}_{p}={\frac {1}{tan{\theta }_{p}^{\prime }}}$

${\frac {sen{\theta }_{p}}{cos{\theta }_{p}}}={\frac {cos{\theta }_{p}^{\prime }}{sen{\theta }_{p}^{\prime }}}$

al multiplicar cruzado obtenemos:

$sen{\theta }_{p}sen{\theta }_{p}^{\prime }=cos{\theta }_{p}cos{\theta }_{p}^{\prime }$

$sen{\theta }_{p}sen{\theta }_{p}^{\prime }-cos{\theta }_{p}cos{\theta }_{p}^{\prime }=0$

$cos{(\theta }_{p}^{\prime }+{\theta }_{p})=0$

${(\theta }_{p}^{\prime }+{\theta }_{p})={90}^{\circ }$

si la suma de su angulo de polarización de la reflexión interna ${\theta }_{p}$ y el angulo de polarización externa ${(\theta }_{p}^{\prime }$ son ${90}^{\circ }$ entonces complementarios.

$\therefore$ el angulo de polarización de la reflexión interna ${\theta }_{p}$ y el angulo de polarización de reflexión externa ${\theta }_{p}^{\prime }$ son complementarios.

$\therefore$ queda probado.

--Salvador Alejandro Morales Carranza

---

Ejercicio 4.51

---

Utilizando las ecuaciones de Fresnel, demuestre que :

$ r_{\perp} = \frac{ \cos \theta_i - \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}{ \cos \theta_i + \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}$

$r_{\parallel} = \frac{n_{ti}^2 \cos \theta_i - \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}{ n_{ti}^2\cos \theta_i + \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}$

Solución:

Los coeficientes de reflexión en medios deieléctricos son:

$ r_{\perp} =\frac{n_i \cos \theta_i- n_t \cos \theta_t}{n_i \cos \theta_i+ n_t \cos \theta_t} $

$r_{\parallel} =\frac{n_t\cos \theta_i- n_i\cos \theta_t}{n_i \cos \theta_i+ n_t \cos \theta_t} $

Haciendo uso de la relación pitagórica : $\sin^2 \theta+ \cos^2 \theta=1$ podemos reescribir $ \cos \theta_t $ y $ \cos \theta_i $

$\cos \theta_t= \sqrt{ 1 - \sin^2 \theta_t}$

Y por Ley de Snell:

$\sin \theta_t= \frac{n_i}{n_t} \sin \theta_i$

elevamos al cuadrado:

$\sin^2 \theta_t= \frac{n_i^2}{n_t^2} \sin^2 \theta_i$

$\sin^2 \theta_i= \frac{n_t^2}{n_i^2} \sin^2 \theta_t$

Al hacer la sustitución llegamos a una expresión para $\cos \theta_t $ que involucra a $\sin \theta_i $

$\cos \theta_t= \sqrt{ 1 -\frac{n_i^2}{n_t^2} \sin ^2 \theta_i}$

con :$ \frac{n_t}{n_i} \equiv n_{ti}$

$\cos \theta_t= \sqrt{ n_{ti}^2- \sin ^2 \theta_i}$

Sustituimos en la ecuación para $ r_{\perp}$ y obtenemos:

$ r_{\perp} = \frac{ \cos \theta_i - \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}{ \cos \theta_i + \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}$

Para $ r_{\parallel}$

$ \cos \theta_t= \sqrt{ \frac {1}{n_{ti}^2}- \sin ^2 \theta_i}$

Multiplicamos y dividimos por $ n_{ti}^2$

y reescribimos $ r_{\parallel}$

$r_{\parallel} = \frac{n_{ti}^2 \cos \theta_i - \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}{ n_{ti}^2\cos \theta_i + \sqrt{ n_{ti}^2 - \sin^2 \theta_i }}$

Aurea Espin (discusión) 00:13 29 oct 2018 (CDT)

---

Ejercicio 4.59

Utilice la ecuación 4.42 y la expansión en serie de la función seno para establecer que en una incidencia cercana a la normal podemos obtener una mejor aproximación que la del problema 4.45, que es

---

---

Ejercicio 4.11

---

Calcule el ángulo de transmisión para un rayo en el aire inicialmente a $30°$ en un bloque de vidrio crown $(n_v=1.52)$.

$n_i\sin{\theta_i}{=n}_t\sin{\theta_t}$

donde $n_i=1$ y $n_v=n_t$

$sin30°=(1.52)sinθt$

$\theta_t=\sin^{-1}{(0.5/1.52)}$

$\theta_t=19.20°$

--Verenisse

Ejercicio 4.25

comenzando con la ley de snell, pruebe que la ecuación vectorial de la refracción tiene la forma:

ntkt-niki=$n_t\cos{\theta_t}{-n}_i\cos{\theta_i}$

partiendo de : $n_i\sin{\theta_i}{=n}_t\sin{\theta_t}{,n_i}( k_{i} X {u_n}){=n}_t{,n_t}( {k_t} X {u_n})$

donde: k_{i},k_{t} son los vectores unitarios de propagación

Así

${n_t}( k_{t} X {u_n}) -{n_i}( k_{i} X {u_n})=0$

$({n_t} k_{t} {-n_i} k_{i}) x U{n}=0$

dejando:

${n_t} k_{t}{-n_i} k_{i}$=${\gamma}$=${\gamma_{u_n}}$

donde

${\gamma}$ es referido como el astigmático constante, tambien ${\gamma}$ es la diferencia entre las proyecciones de ${n_t} k_{t} y { n_i} k_{i}$ en ${u_n}$

En otras palabras, es el producto punto entre ${\gamma}$ y ${u_n}$:

por lo que

${\gamma}$ =$n_t\cos{\theta_t}{-n}_i\cos{\theta_i}$

--[[Usuario:|Luisa Alejandra Vega S.]]

Ejercicio 4.32

Derivar la ley de refracción, $\theta_i=\theta_f$, usando cálculo para minimizar el tiempo de tránsito como lo requiere el principio de Fermat.

--Solución--

Con ayuda de la siguiente figura, podremos hacer el problema.

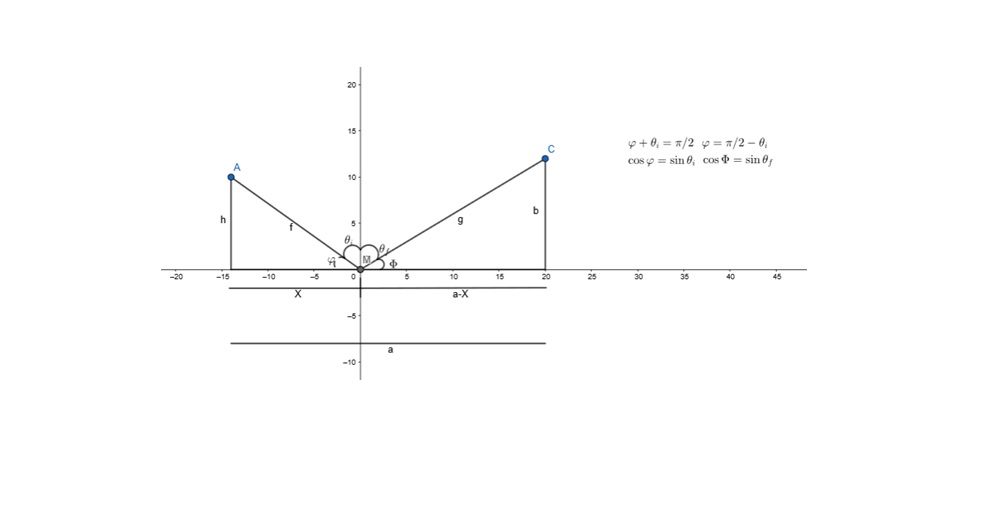
Definimos a la longitud de camino óptico como:

$LOP=nAB + nBC$ ; n es el índice de refracción del medio. En este caso es el mismo porque el medio es el mismo.

Por trigonometría sabemos que:

$AM=(h^2 + x^2)^{1/2}$ y;

$MC=(b^2+(a-x)^2)^{1/2}$ ; Por lo tanto la longitud de camino óptico es:

$LOP= n(h^2 + x^2)^{1/2} + n(b^2+(a-x)^2)^{1/2}$ ; Como queremos minimizar el tránsito de $LOP$, entonces debemos sacar la derivada respecto de x, a $LOP$ e igualarla a 0.

$d/dx(LOP)= d/dx[n(h^2 + x^2)^{1/2} + n(b^2+(a-x)^2)^{1/2}]=0$

Entonces:

$\frac{d}{dx}[n(h^2 + x^2)^{1/2} + n(b^2+(a-x)^2)^{1/2}]= n(h^2+ x^2)^{-1/2}x + n(b^2+ (a-x)^2)^{-1/2}(x-a)=0$

Por lo tanto:

$n[(h^2+ x^2)^{-1/2}x - (b^2+ (a-x)^2)^{-1/2}(a-x)]=0$ ó

$\frac{x}{(h^2+ x^2)^{1/2}} - \frac{a-x}{(b^2+ (a-x)^2)^{1/2}}= 0$

Pero si nos fijamos de nuevo en la figura, observamos que:

$\frac{x}{(h^2+ x^2)^{1/2}}= \sin\theta_i$ y;

$\frac{a-x}{(b^2+ (a-x)^2)^{1/2}}= \sin\theta_r$ Por lo tanto:

$\sin\theta_i= \sin\theta_r$ $\Leftrightarrow$ $\theta_i=\theta_f$.

--[[Usuario:|Pedro J. Julian.]]

Ejercicio 4.43

---

Deduzca las ecuaciones (4.42) a (4.45) para $r_{\perp}$, $r_{\parallel}$, $t_{\perp}$, $t_{\parallel}$

  $r_{\perp}=-\frac{\sin{(\theta_i-\theta_t)}}{\sin{(\theta_i+\theta_t)}}$ ...$(4.42)$
  
  $r_{\parallel}=+\frac{\tan{(\theta_i-\theta_t)}}{\tan{(\theta_i+\theta_t)}}$ ...$(4.43)$
  
  $t_{\perp}=+\frac{2\sin{\theta_t}\cos{\theta_i}}{\sin{(\theta_i+\theta_t)}}$ ...$(4.44)$
  
  $t_{\parallel}=+\frac{2\sin{\theta_t}\cos{\theta_i}}{\sin{(\theta_i+\theta_t)}\cos{(\theta_i-\theta_t)}}$ ...$(4.45)$

Solución:

Partiendo de las ecuaciones de Fresnel y el índice de refracción relativo $n_{ti}=\frac{n_t}{n_i}=\frac{\sin{\theta_i}}{\sin{\theta_t}}$

$r_{\perp}=\frac{n_i\cos{\theta_i}-n_t\cos{\theta_t}}{{n_i\cos{\theta_i}+n_t\cos{\theta_t}}}=\left(\frac{1/n_i}{1/n_i}\right)\frac{n_i\cos{\theta_i}-n_t\cos{\theta_t}}{{n_i\cos{\theta_i}+n_t\cos{\theta_t}}}=\frac{\frac{n_i}{n_i}\cos{\theta_i}-\frac{n_t}{n_i}\cos{\theta_t}}{{\frac{n_i}{n_i}\cos{\theta_i}+\frac{n_t}{n_i}\cos{\theta_t}}}=\left(\frac{\sin{\theta_t}}{\sin{\theta_t}}\right)\frac{\cos{\theta_i}-\frac{\sin{\theta_i}}{\sin{\theta_t}}\cos{\theta_t}}{{\cos{\theta_i}-\frac{\sin{\theta_i}}{\sin{\theta_t}}\cos{\theta_t}}}=\frac{\sin{\theta_t}\cos{\theta_i}-\sin{\theta_i}\cos{\theta_t}}{\sin{\theta_t}\cos{\theta_i}+\sin{\theta_i}\cos{\theta_t}}=-\frac{\sin{\theta_i}\cos{\theta_t}-\sin{\theta_t}\cos{\theta_i}}{\sin{\theta_t}\cos{\theta_i}+\sin{\theta_i}\cos{\theta_t}}$

utilizando la identidad trigonométrica $\sin{(a\pm b)}=\sin{a}\cos{b}\pm \cos{a}\sin{b}$

$\therefore r_{\perp}=-\frac{\sin{(\theta_i-\theta_t)}}{\sin{(\theta_i+\theta_t)}}$

$t_{\perp}=\frac{2 n_i \cos{\theta_i}}{n_i\cos{\theta_i}+n_t\cos{\theta_t}}=\frac{2 \frac{n_i}{n_t} \cos{\theta_i}}{\frac{n_i}{n_t}\cos{\theta_i}+\cos{\theta_t}}=\frac{2 \sin{\theta_t} \cos{\theta_i}\frac{1}{\sin{\theta_i}}}{\frac{\sin{\theta_t}}{\sin{\theta_i}}\cos{\theta_i}+\cos{\theta_t}}=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_t}\cos{\theta_i}+\sin{\theta_i}\cos{\theta_t}}$

$\therefore t_{\perp}=+\frac{2\sin{\theta_t}\cos{\theta_i}}{\sin{(\theta_i+\theta_t)}}$

$r_{\parallel}=\frac{n_t\cos{\theta_i}-n_i\cos{\theta_t}}{{n_t\cos{\theta_i}+n_i\cos{\theta_t}}}=\frac{\sin{\theta_i}\cos{\theta_i}-\sin{\theta_t}\cos{\theta_t}}{\sin{\theta_t}\cos{\theta_t}+\sin{\theta_i}\cos{\theta_i}}$

Poniendo los senos y cosenos en términos de exponenciales:

$r_{\parallel}=\frac{\left(\frac{e^{i\theta_i}-e^{-i\theta_i}}{2i}\right)\left(\frac{e^{i\theta_i}+e^{-i\theta_i}}{2}\right)-\left(\frac{e^{i\theta_t}-e^{-i\theta_t}}{2i}\right)\left(\frac{e^{i\theta_t}+e^{-i\theta_t}}{2}\right)}{\left(\frac{e^{i\theta_i}-e^{-i\theta_i}}{2i}\right)\left(\frac{e^{i\theta_i}+e^{-i\theta_i}}{2}\right)+\left(\frac{e^{i\theta_t}-e^{-i\theta_t}}{2i}\right)\left(\frac{e^{i\theta_t}+e^{-i\theta_t}}{2}\right)}=\frac{\left(e^{i\theta_i}-e^{-i\theta_i}\right)\left(e^{i\theta_i}+e^{-i\theta_i}\right)-\left(e^{i\theta_t}-e^{-i\theta_t}\right)\left(e^{i\theta_t}+e^{-i\theta_t}\right)}{\left(e^{i\theta_i}-e^{-i\theta_i}\right)\left(e^{i\theta_i}+e^{-i\theta_i}\right)+\left(e^{i\theta_t}-e^{-i\theta_t}\right)\left(e^{i\theta_t}+e^{-i\theta_t}\right)}$

al realizar los productos se obtiene:

$r_{\parallel}=\frac{e^{2i\theta_i}-e^{-2i\theta_i}-e^{2i\theta_t}+e^{-2i\theta_i}}{e^{2i\theta_i}-e^{-2i\theta_i}+e^{2i\theta_t}-e^{-2i\theta_t}}$

sumando y restando $\theta_i$ y $\theta_t$ a los argumentos de las exponenciales y separandolas como producto de exponenciales:

$r_{\parallel}= \frac{e^{i(\theta_i+\theta_t+\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t+\theta_i-\theta_t)}-e^{i(\theta_t+\theta_i+\theta_t-\theta_i)}+e^{-i(\theta_t+\theta_i+\theta_t-\theta_i)}}{e^{i(\theta_i+\theta_t+\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t+\theta_i-\theta_t)}+e^{i(\theta_t+\theta_i+\theta_t-\theta_i)}-e^{-i(\theta_t+\theta_i+\theta_t-\theta_i)}}$

$=\frac{e^{i(\theta_i+\theta_t)}e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t)}e^{-i(\theta_i-\theta_t)}-e^{i(\theta_i+\theta_t)}e^{-i(\theta_i-\theta_t)}+e^{-i(\theta_i+\theta_t)}e^{i(\theta_i-\theta_t)}}{e^{i(\theta_i+\theta_t)}e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t)}e^{-i(\theta_i-\theta_t)}+e^{i(\theta_i+\theta_t)}e^{-i(\theta_i-\theta_t)}-e^{-i(\theta_i+\theta_t)}e^{i(\theta_i-\theta_t)}}$

factorizando términos semejantes:

$r_{\parallel}=\frac{e^{i(\theta_i+\theta_t)}\left(e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i-\theta_t)}\right)+e^{-i(\theta_i+\theta_t)}\left(e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i-\theta_t)}\right)}{e^{i(\theta_i+\theta_t)}\left(e^{i(\theta_i-\theta_t)}+e^{-i(\theta_i-\theta_t)}\right)-e^{-i(\theta_i+\theta_t)}\left(e^{i(\theta_i-\theta_t)}+e^{-i(\theta_i-\theta_t)}\right)}=\frac{\left(e^{i(\theta_i+\theta_t)}+e^{-i(\theta_i+\theta_t)}\right)\left(e^{i(\theta_i-\theta_t)}-e^{-i(\theta_i-\theta_t)}\right)}{\left(e^{i(\theta_i+\theta_t)}-e^{-i(\theta_i+\theta_t)}\right)\left(e^{i(\theta_i-\theta_t)}+e^{-i(\theta_i-\theta_t)}\right)}$

regresando a senos y cosenos:

$r_{\parallel}=\frac{\left(2\cos{(\theta_i+\theta_t)}\right)\left(2i\sin{(\theta_i-\theta_t)}\right)}{\left(2\cos{(\theta_i-\theta_t)}\right)\left(2i\sin{(\theta_i+\theta_t)}\right)}=\frac{\left(\cos{\theta_i+\theta_t}\right)\left(\sin{\theta_i-\theta_t}\right)}{\left(\sin{\theta_i+\theta_t}\right)\left(\cos{\theta_i-\theta_t}\right)}$

$\therefore r_{\parallel}=+\frac{\tan{(\theta_i-\theta_t)}}{\tan{(\theta_i+\theta_t)}}$

$t_\parallel=\frac{2 n_i \cos{\theta_i}}{n_i\cos{\theta_t}+n_t\cos{\theta_i}}=\frac{2 n_{it} \cos{\theta_i}}{n_{it}\cos{\theta_t}+\cos{\theta_i}}=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_t}\cos{\theta_t}+\sin{\theta_i}\cos{\theta_i}}=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_t}\cos{\theta_t}\left(\sin^2 \theta_i+\cos^2 \theta_i \right)+\sin{\theta_i}\cos{\theta_i}\left(\sin^2\theta_t+\cos^2 \theta_t\right)}$

$=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_i}^2\sin{\theta_t}\cos{\theta_t}+\cos{\theta_i}^2\sin{\theta_t}\cos{\theta_t}+\sin{\theta_t}^2\sin{\theta_i}\cos{\theta_i}+\cos{\theta_t}^2\sin{\theta_i}\cos{\theta_i}}$

$=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_i}\cos{\theta_t}\sin{\theta_i}\sin{\theta_t}+\sin{\theta_i}\cos{\theta_t}\cos{\theta_i}\cos{\theta_t}+\cos{\theta_i}\sin{\theta_t}\sin{\theta_i}\sin{\theta_t}+\cos{\theta_i}\sin{\theta_t}\cos{\theta_i}\cos{\theta_t}}$

$=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\sin{\theta_i}\cos{\theta_t}\left(\sin{\theta_i}\sin{\theta_t}+\cos{\theta_i}\cos{\theta_t}\right)+\cos{\theta_i}\sin{\theta_t}\left(\sin{\theta_i}\sin{\theta_t}+\cos{\theta_i}\cos{\theta_t}\right)}$

$=\frac{2 \sin{\theta_t} \cos{\theta_i}}{\left(\sin{\theta_i}\cos{\theta_t}+\cos{\theta_i}\sin{\theta_t}\right)\left(\sin{\theta_i}\sin{\theta_t}+\cos{\theta_i}\cos{\theta_t}\right)}$

$\therefore t_{\parallel}=+\frac{2\sin{\theta_t}\cos{\theta_i}}{\sin{(\theta_i+\theta_t)}\cos{(\theta_i-\theta_t)}}$

--Sergio