Diferencia entre revisiones de «Ondas: probs c4»
(Optics Eugene Hecht, with contributions by Alfred Zajac Ejercicio 4.16.) |
|||
| Línea 182: | Línea 182: | ||
y usando como ejemplo una lámina de vidrio analizamos: | y usando como ejemplo una lámina de vidrio analizamos: | ||
[[Archivo:Diagrama2.jpg| | [[Archivo:Diagrama2.jpg|300px|thumb|left|Análisis]] | ||
| Línea 218: | Línea 218: | ||
Ejercicio resuelto por --[[Usuario:Luis Velázquez|Luis Velázquez]] ([[Usuario discusión:Luis Velázquez|discusión]]) 07:24 27 mar 2015 (CDT) | Ejercicio resuelto por --[[Usuario:Luis Velázquez|Luis Velázquez]] ([[Usuario discusión:Luis Velázquez|discusión]]) 07:24 27 mar 2015 (CDT) | ||
---- | |||
==Problema 4.16== | |||
''' Obtener la ley de reflexión, <math>\theta_{i} = \theta{r}</math>, usando para el cálculo el tiempo de mínima transmisión, como requerimiento por el principio de Fermat''' | |||
Lo que nos dice el principio de Fermat: | |||
El trayecto seguido por la luz al propagarse de un punto a otro es tal que el tiempo empleado en recorrerlo es estacionario respecto a posibles variaciones de la trayectoria | |||
Dicho de otra manera, el tiempo de transmisión que sigue la luz para recorrer un medio tiene que ser el mínimo. | |||
[[Archivo:Ley de reflexión.png|250px]] | |||
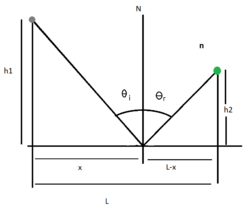
En la imagen anterior representa la trayectoria de un haz de luz en un medio homogéneo en donde es reflejado totalmente, la representación nos servirá para deducir las expresiones de reflexión. | |||
Primero para el tiempo que se observa que el tiempo que dura la luz para ir del objeto gris al objeto verde es: | |||
<math>T= \frac{d_{1}}{C}+\frac{d_{2}}{C}</math> | |||
donde <math>C</math> es la velocidad de la luz y <math>T=t_{1}+t_{2}</math>, por lo tanto podemos deducir que: | |||
<math>CT=d_{1} +d_{2}= \sqrt{h_{1}^2+x^2}+\sqrt{h_{2}^2+(L-x)^2}</math> | |||
Usando el principio de Fermat donde nos dice que: | |||
<math>C \frac{dt}{dx}= 0</math> | |||
Aplicando la primera derivada con respecto de la posición tenemos que: | |||
<math>C \frac{dt}{dx}= \frac{d ( \sqrt{h_{1}^2+x^2})}{dx}+\frac{d( \sqrt{h_{2}^2+(L-x)^2})}{dx}=0</math> | |||
Desarrollando tenemos que: | |||
<math>\frac{x}{\sqrt{h_{1}^2+x^2}}-\frac{L-x}{\sqrt{h_{2}^2+(L-x)^2}}=0</math> | |||
Por trigonometría tenemos que: | |||
<math>sen(\theta_{i})=\frac{x}{\sqrt{h_{1}^2+x^2}} </math> | |||
Y: | |||
<math>sen(\theta_{r})= \frac{L-x}{\sqrt{h_{2}^2+(L-x)^2}}</math> | |||
Por lo tanto obtenemos que: | |||
<math>Sen(\theta_{i})-Sen(\theta_{r})=0</math> | |||
De donde podemos concluir, usando el principio de Fermat que: | |||
<math>Sen(\theta_{i})=Sen(\theta_{r})</math> | |||
Sí y sólo si: | |||
<math>\theta_{i}=\theta_{r}</math> | |||
Hecho por --[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 17:44 29 mar 2015 (CDT) | |||
Revisión del 17:44 29 mar 2015
Vibraciones y Ondas
Problemas capítulo 4. Óptica - Hecht
Problema 4.1
Work your away through an argument using dimensional analysis to establish the $\lambda^{-4}$ dependence of the percentage of light scattered in Rayleigh Scattering. Let $E_{0i}$ and $E_{0s}$ be the incident and scattered amplitudes, the latter at a distance r from the scatterer. Assame $ E_{0s}\varpropto E_{0i}$ and $E_{0s}\varpropto \dfrac{1}{r}$. Furthermore, plausibly assume that the scattered amplitude is proportional to the volume. V, of the scatterer, within limits the is reasonable. Determine the units of the constant of proportionality.
Para relacionando la distancia r con la amplitud y su proporcionalidad con el volumen, utilizaremos la siguiente ecuación, la cual es adimencional.
$$\dfrac{VK}{r}$$
Sí $E_{0s}\varpropto\dfrac{1}{r}$ y $ E_{0s}\varpropto E_{0i}$
Entonces $$E_{0s}\varpropto \dfrac{VE_{0i}}{r}= \dfrac{K V E_{0i}}{r}$$
Así que K tiene las unidades de $(\lambda)_{2}$ $$K= (\lambda)^{-2}$$
Y esto se puede comprobar por: $$\dfrac{I_{i}}{I_{s}}\varpropto K^{2}\varpropto \lambda ^{-4}$$
--Esther Sarai (discusión) 23:34 28 mar 2015 (CDT)Esther Sarai Garcia
Problema 4.5
Un haz de microondas planas de 12 cm incide en la superficie de un dieléctrico a 45°. Si $n_{ti}=4/3$ calcule a) la longitud de onda en el medio transmisor, y b) el ángulo $\theta_{t}$
Solución:
De la ley de Snell \[ n_i sin\theta_i = n_t sin\theta_t \] Tenemos: \[\frac{n_t}{n_i}=\frac{sin\theta_i}{sin\theta_t}=n_{ti}...(1)\]
Tambien sabemos que: \[ n=\frac{C}{v}...(2) \]
y
\[ v=\lambda \nu...(3) \]
Por lo que (1) puede escribirse como:
\[n_{ti} = \frac{\frac{C}{v_t}}{\frac{C}{n_i}}=\frac{v_i}{v_t}=\frac{\lambda_i}{\lambda_t}...(3)\]
Despejando:
\[ \lambda_t = \frac{\lambda_i}{n_{ti}}=\frac{12cm}{4/3} \]
\[ \lambda_t=9cm \]
De (1)
\[sin\theta_i = n_{ti}sin\theta_t\]
\[ \theta_t =angsin \frac{sin\theta_i}{n_{ti}}=angsin \frac{sin45^{o}}{4/3} \]
\[ \theta_t = 32.02^{o} \]
Resuelto por: --Luis Santos (discusión) 14:31 28 mar 2015 (CDT)
Problema 4.6
Un haz láser muy estrecho incide bajo un ángulo de $58^o$ sobre un espejo horizontal. El haz de luz reflejado incide en una pared en un punto situado a 5 metros de distancia del punto de incidencia donde el haz de luz chocó con el espejo. ¿A qué distancia, medida horizontalmente, está la pared de ese punto de incidencia?.
Como bien sabemos, los ángulos de inicidencia y reflexión(o refracción) se miden respecto a la normal a la superficie, por lo que si el láser incide con un ángulo $\alpha_i = 58^o$, entonces el ángulo reflejado, por la ley de reflexión que nos dice que el ángulo reflejado es igual al rayo incidente, será $\alpha_r = 58^o$.
Además, se forma un triángulo rectángulo entre las dos trayectorias del rayo(incidente y reflejado) y la distancia $d$ horizontal del punto de incidencia y el punto donde el láser toca la pared. Por lo que, utilizando trigonometría básica, tenemos:
Entonces, la distancia, medida horizontalmente, de la pared al punto de incidencia es de: $d \approx 4.24m$.
Ivan de Jesús Pompa García (discusión) 01:09 27 mar 2015 (CDT)
Problema 4.8
Calcule el ángulo de transmisión para un rayo en el aire incidente a $30^o$ en un bloque de vidrio-crown($n_v = 1,52$).
La Ley de Snell-Descartes nos dice que:
Por lo que despejando para $\alpha_t$:
donde $n_i$ es el ángulo de incidencia, en este caso $\alpha_i = 30^o$ y $n_i$ es el índice de refracción del aire, que es $n_i \approx 1$. Entonces, sustituyendo:
Por lo que, el ángulo de transmisión buscado es: $\alpha_t = 19^o 7'$.
Ivan de Jesús Pompa García (discusión) 01:52 27 mar 2015 (CDT)
Problema 4.12
Luz de longitud de onda $600nm$ en el vacío entra a un bloque de vidrio donde $n_v = 1.5$. Calcule su longitud de onda en el vidrio. ¿De qué color aparecerá para alguien que está simergido en el vidrio(véase tabla 3.4)?.
Tomemos la relación (2.19) del libro:
Error al representar (función desconocida «\hspace»): v = \lambda \nu \hspace{20pt} \cdots \hspace{20pt} (2.19)
En el vacío, la ecuación (2.19) se convierte, con $\lambda_0$ la longitud de onda la luz en el vacío, en:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): c = \lambda \nu \Rightarrow \nu = \dfrac{c}{\lambda_0} = \dfrac{3x10^8 m/s}{6x10^{-7} m}\\ \therefore \nu = 5x10^{14} Hz
Ahora bien, el índice de refracción del vidrio es $n_v = 1.5$, por lo que utilizando la definición, tenemos que:
Error al representar (error de sintaxis): n_v = \dfrac{c}{v} \Rightarrow v = \dfrac{c}{n_v} = \dfrac{3x10^8 m/s}{1.5} \\ \therefore v = 2x10^8 m/s
Ahora, reutilizando la ecuación (2.19):
Error al representar (error de sintaxis): v = \lambda_v \nu \Rightarrow \lambda_v = \dfrac{v}{\nu} = \dfrac{2x10^8 m/s}{5x10^{14} Hz} \\ \therefore \lambda_v = 4x10^{-7} m = 400 nm
Ahora, la tabla (3.4) del libro de texto, nos dice que para el color violeta el rango de longitudes de onda es $455nm-390nm$, por lo que para una persona sumergida en el vidrio, el rayo de luz le parecerá violeta.
Ivan de Jesús Pompa García (discusión) 01:40 27 mar 2015 (CDT)
Problema 4.18
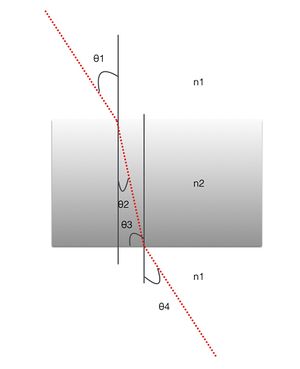
Show analytically that a beam entering a planar transparent plate , as in figure , emerges parallel to displacement of the beam . Incidentally, the incoming and outgoing rays would be parallel even for a stack of plates of different material
Muestra analíticamente que un haz de entrar en una placa transparente planar , como en la figura , emerge paralelo al desplazamiento de la viga. Por cierto, los rayos entrantes y salientes serían paralelas incluso para una pila de placas de material diferente.
Solución
Partiendo de la ley de Snell
y usando como ejemplo una lámina de vidrio analizamos:
, Error al representar (error de sintaxis): \theta 1=45^º
, Error al representar (error de sintaxis): \theta 2=27.7^º
ahora sabemos queError al representar (error de sintaxis): \theta 2=27.7^º
y analizando
y
por triángulos semejantes sabemos que
Error al representar (error de sintaxis): \theta 3=62.3^º
volviendo a aplicar ley de Snell
y obtenemos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \theta 4=45^º
Así queda demostrado que el rayo incidente y el saliente son paralelos por que
es igual a
Ejercicio resuelto por --Luis Velázquez (discusión) 07:24 27 mar 2015 (CDT)
Problema 4.16
Obtener la ley de reflexión, , usando para el cálculo el tiempo de mínima transmisión, como requerimiento por el principio de Fermat
Lo que nos dice el principio de Fermat: El trayecto seguido por la luz al propagarse de un punto a otro es tal que el tiempo empleado en recorrerlo es estacionario respecto a posibles variaciones de la trayectoria
Dicho de otra manera, el tiempo de transmisión que sigue la luz para recorrer un medio tiene que ser el mínimo.
En la imagen anterior representa la trayectoria de un haz de luz en un medio homogéneo en donde es reflejado totalmente, la representación nos servirá para deducir las expresiones de reflexión. Primero para el tiempo que se observa que el tiempo que dura la luz para ir del objeto gris al objeto verde es: donde es la velocidad de la luz y , por lo tanto podemos deducir que:
Usando el principio de Fermat donde nos dice que: Aplicando la primera derivada con respecto de la posición tenemos que: Desarrollando tenemos que: Por trigonometría tenemos que: Y: Por lo tanto obtenemos que: De donde podemos concluir, usando el principio de Fermat que: Sí y sólo si:
Hecho por --Pablo (discusión) 17:44 29 mar 2015 (CDT)