Ondas: probs c4

Problemas capítulo 4 Óptica Hecht, Propagación de la Luz

Ejercicios resueltos acerca de la propagación de la luz. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema.

Algunas ediciones del Hetch, tienen distintas numeraciones para problemas identicos.

Primeras Ediciones (1°,2°,3°) en Ingles.

Problema 4.11 (hecht 1ra ed.)

La ecuación $E(x,t)=10^{-3}cos(5\times10^{10}t-200x)$, en unidades del SI, representa la propagación del campo eléctrico de una onda electromagnética plana por un medio determinado. Este campo eléctrico está confinado en el plano XY.

a)Calcula la frecuencia y la longitud de onda de esa onda electromagnética.

b)Determina el índice de refracción del medio.

c)Escribe la expresión del campo magnético de la onda e indica en que plano está confinado.

Inciso a

La expresión general de un campo eléctrico es:

\[ E(x,t)=E_{0}cos(\omega t-kx) \]

Comparando las expresión del campo dada y general podemos obtener que:

$\omega=5\times10^{10}\frac{rad}{seg}=2\pi(\upsilon)$

pero,

\[ \omega=2\pi(\upsilon)\Longrightarrow\upsilon=\frac{\omega}{2\pi}=\frac{5\times10^{10}\frac{rad}{seg}}{2\pi}=8\times10^{9}Hz \]

La velocidad de propagación es:

\[ V=\lambda\upsilon=\frac{\omega}{k}=\frac{5\times10^{10}\frac{rad}{seg}}{200m^{-1}}=2.5\times10^{8}\frac{m}{seg} \]

Conocemos también $k$, por lo que,

\[ k=\frac{2\pi}{\lambda}\Longrightarrow\lambda=\frac{2\pi}{k}=\frac{2\pi}{200m^{-1}}=3.1\times10^{-2}m \]

Donde $\lambda$ es la longitud de onda.

Inciso b

Y el índice de refracción del medio es:

\[ n=\frac{c}{V}=\frac{3\times10^{8}\frac{m}{seg}}{2.5\times10^{8}\frac{m}{seg}}=1.2 \]

Inciso c

Las ondas que describen los campos eléctrico y magnético están en fase y sus módulos están relacionados por:

\[ E_{0}=VB_{0}\longrightarrow(2.5\times10^{8}\frac{m}{seg})B_{0}=10^{-3} \]

\[ \Longrightarrow B_{0}=4\times10^{12}T \] Por lo tanto, la ecuación del campo magnético es:

\[ B(x,t)=4\times10^{12}cos(5\times10^{10}t-200x) \]

Está confinado en el plano ZX los vectores $\overrightarrow{B}$ y $\overrightarrow{E}$ son perpendiculares entre sí y perpendiculares a la dirección de propagación.

---

Realizado por: A. Martín R. Rabelo (discusión) 18:42 30 mar 2015 (CDT)

---

Problema 4.26 3ra Edición

Calcular el angulo critico mas allá del cual hay reflexión total interna en la interfase aire-vidrio. Compare este problema con el problema 4.8

Procedimiento

Se da en el problema $n_{g}=1.5$ el indice de refracción del vidrio. Ademas sabiendo que el indice de refracción del aire es casi 1.0 y usando la relación:

$\theta _{c}=\arcsin \left({\frac {n_{2}}{n_{1}}}\right)$

con $n_{2}<n_{1}$

se tiene:

$\theta _{c}=\arcsin \left({\frac {1.0}{1.5}}\right)=46{\text{°}}$

Conclusión

En el problema 4.8 se tiene que si el angulo del rayo incidente es de 45° el primer angulo refractado también sera de 45° por ser estos complementarios y a partir de esto los segundos ángulos incidentes y refractado también tienen 45°, así que el diagrama en ese problema se ajusta a este problema eligiendo el primer angulo incidente de 45°

---

Realizado por: Uziel Sanchez Gutierrez (discusión) 18:46 30 mar 2015 (CDT) Hecho por Uziel Sanchez Gutierrez

---

4ta Edición en Ingles.

Problema 4.15 4ta Edición

Luz de longitud de onda $600nm$ en el vacío entra a un bloque de vidrio donde $n_v = 1.5$. Calcule su longitud de onda en el vidrio. ¿De qué color aparecerá para alguien que está sumergido en el vidrio(véase tabla 3.4)?.

Procedimiento 

Tomemos la relación (2.19) del libro:

$ v = \lambda \nu \hspace{20pt} \cdots \hspace{20pt} (2.19) $

En el vacío, la ecuación (2.19) se convierte, con $\lambda_0$ la longitud de onda la luz en el vacío, en:

$ c = \lambda \nu \Rightarrow \nu = \dfrac{c}{\lambda_0} = \dfrac{3x10^8 m/s}{6x10^{-7} m}\\ \therefore \nu = 5x10^{14} Hz $

Ahora bien, el índice de refracción del vidrio es $n_v = 1.5$, por lo que utilizando la definición, tenemos que:

$ n_v = \dfrac{c}{v} \Rightarrow v = \dfrac{c}{n_v} = \dfrac{3x10^8 m/s}{1.5} \\ \therefore v = 2x10^8 m/s $

Conclusión

Ahora, reutilizando la ecuación (2.19):

$ v = \lambda_v \nu \Rightarrow \lambda_v = \dfrac{v}{\nu} = \dfrac{2x10^8 m/s}{5x10^{14} Hz} \\ \therefore \lambda_v = 4x10^{-7} m = 400 nm $

Ahora, la tabla (3.4) del libro de texto, nos dice que para el color violeta el rango de longitudes de onda es $455nm-390nm$, por lo que para una persona sumergida en el vidrio, el rayo de luz le parecerá violeta.

---

Realizado por: Ivan de Jesús Pompa García (discusión) 01:40 27 mar 2015 (CDT)

---

Problema 4.32 4ta Edición

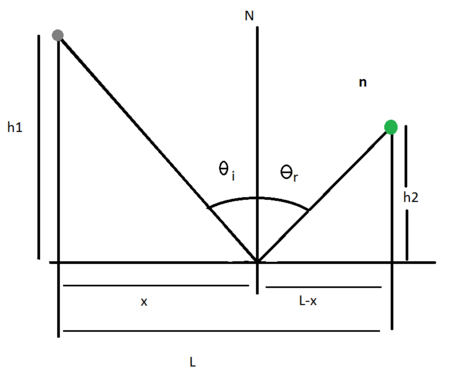
Obtener la ley de reflexión, $\theta _{i}=\theta {r}$, usando para el cálculo el tiempo de mínima transmisión, como requerimiento por el principio de Fermat

Lo que nos dice el principio de Fermat:

El trayecto seguido por la luz al propagarse de un punto a otro es tal que el tiempo empleado en recorrerlo es estacionario respecto a posibles variaciones de la trayectoria

Dicho de otra manera, el tiempo de transmisión que sigue la luz para recorrer un medio tiene que ser el mínimo.

En la imagen anterior representa la trayectoria de un haz de luz en un medio homogéneo en donde es reflejado totalmente, la representación nos servirá para deducir las expresiones de reflexión.

Primero para el tiempo que se observa que el tiempo que dura la luz para ir del objeto gris al objeto verde es:

$T={\frac {d_{1}}{C}}+{\frac {d_{2}}{C}}$

donde $C$ es la velocidad de la luz y $T=t_{1}+t_{2}$, por lo tanto podemos deducir que:

$CT=d_{1}+d_{2}={\sqrt {h_{1}^{2}+x^{2}}}+{\sqrt {h_{2}^{2}+(L-x)^{2}}}$

Usando el principio de Fermat donde nos dice que:

$C{\frac {dt}{dx}}=0$ Aplicando la primera derivada con respecto de la posición tenemos que: $C{\frac {dt}{dx}}={\frac {d({\sqrt {h_{1}^{2}+x^{2}}})}{dx}}+{\frac {d({\sqrt {h_{2}^{2}+(L-x)^{2}}})}{dx}}=0$ Desarrollando tenemos que: ${\frac {x}{\sqrt {h_{1}^{2}+x^{2}}}}-{\frac {L-x}{\sqrt {h_{2}^{2}+(L-x)^{2}}}}=0$ Por trigonometría tenemos que: $sen(\theta _{i})={\frac {x}{\sqrt {h_{1}^{2}+x^{2}}}}$ Y: $sen(\theta _{r})={\frac {L-x}{\sqrt {h_{2}^{2}+(L-x)^{2}}}}$ Por lo tanto obtenemos que: $Sen(\theta _{i})-Sen(\theta _{r})=0$

Conclusión

De donde podemos concluir, usando el principio de Fermat que:

$Sen(\theta _{i})=Sen(\theta _{r})$

Sí y sólo si: $\theta _{i}=\theta _{r}$

---

Hecho por :Pablo (discusión) 17:44 29 mar 2015 (CDT)

---

Problema 4.34 4ta Edición

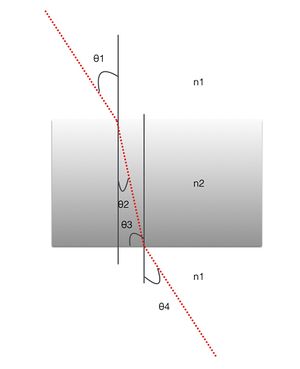
Muestra analíticamente que un haz de entrar en una placa transparente planar , como en la figura , emerge paralelo al desplazamiento de la viga. Por cierto, los rayos entrantes y salientes serían paralelas incluso para una pila de placas de material diferente.

Cristal

Solución

Partiendo de la ley de Snell

$n_{1}\sin \theta _{0}=n_{2}\sin \theta _{t}$

y usando como ejemplo una lámina de vidrio analizamos:

Análisis

$n1=1$, $\theta_1=45^°$

$n2=1.52$, $\theta_2=27.7^°$

${\frac {n_{1}}{n_{2}}}\sin \theta _{1}=\sin \theta _{2}$

Ahora sabemos que $\theta_2=27.7^°$

y analizando

$\theta_3$ y $\theta_4$

Por triángulos semejantes sabemos que

$\theta_3=62.3^°$

Volviendo a aplicar ley de Snell

$ \frac{n_2}{n_1 }\sin \theta_3 = \sin \theta_4 $

y obtenemos

$\theta_4=45^°$

Así queda demostrado que el rayo incidente y el saliente son paralelos por que

$\theta_4$ es igual a $\theta_1$

---

Ejercicio resuelto por --Luis Velázquez (discusión) 07:24 27 mar 2015 (CDT)

---

Problema 4.66 4ta Edición

Demostrar que los ángulos de polarización para la reflexión interna y externa en la interfaz dada son complementarios que es $\theta p + \theta'p = 90 $

De la figura 4.61, se muestran 2 reflexiones :

Figura 4.61

Procedimiento

1ra reflexión: $\theta r=\theta i$

2da reflexión: $\phi r=\phi i$

Siendo $\theta r$ y $\phi i$ ángulos complementarios

$\theta r+\phi i={\frac {\pi }{2}}$

---

Realizado por: Luisa Alejandra Vega Sanchez (discusión) 18:38 30 mar 2015 (CDT)luisa alejandra vega sanchez

---

5ta Edición en Ingles.

Problema 4.1 5ta Edición

Work your away through an argument using dimensional analysis to establish the $\lambda^{-4}$ dependence of the percentage of light scattered in Rayleigh Scattering. Let $E_{0i}$ and $E_{0s}$ be the incident and scattered amplitudes, the latter at a distance r from the scatterer. Assame $ E_{0s}\varpropto E_{0i}$ and $E_{0s}\varpropto \dfrac{1}{r}$. Furthermore, plausibly assume that the scattered amplitude is proportional to the volume. V, of the scatterer, within limits the is reasonable. Determine the units of the constant of proportionality.

Traducción

Trabaja a tu manera haciendo un análisis dimensional, para establecer la $\lambda^{-4}$ dependencia del porcentaje de luz dispersada en la dispersión de Rayleigh. Sean $E_{0i}$ y $E_{0s}$ la amplitud incidente y dispersada, este último a una distancia r del dispersor. De igual forma $ E_{0s}\varpropto E_{0i}$ y $E_{0s}\varpropto \dfrac{1}{r}$. Además, suponga plausiblemente que la amplitud dispersada es proporcional al volumen. V, del dispersor, dentro de los límites que sea razonable. Determine las unidades de la constante de proporcionalidad.

Procedimiento

Para relacionando la distancia r con la amplitud y su proporcionalidad con el volumen, utilizaremos la siguiente ecuación, la cual es adimensional.

$\dfrac{VK}{r}$

Sí $E_{0s}\varpropto\dfrac{1}{r}$ y $ E_{0s}\varpropto E_{0i}$

Entonces $E_{0s}\varpropto \dfrac{VE_{0i}}{r}= \dfrac{K V E_{0i}}{r}$

Así que K tiene las unidades de $(\lambda)_{2}$

$K= (\lambda)^{-2}$

Conclusión 

Y esto se puede comprobar por:

$\dfrac{I_{i}}{I_{s}}\varpropto K^{2}\varpropto \lambda ^{-4}$

---

Realizado por: Esther Sarai (discusión) 23:34 28 mar 2015 (CDT)Esther Sarai Garcia

---

Problema 4.3 5ta Edición

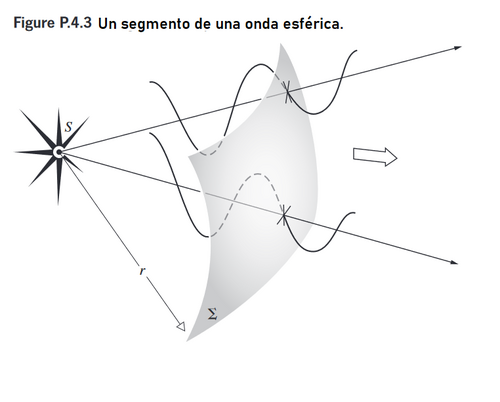
La figura P.4.3 representa la luz que emerge de una fuente puntual . Muestra tres representaciones diferentes de transmisión de energía radiante hacia el exterior. Identifique cada uno y discutir su relación con los demás

Figura P.4.3

Solución: 

Los sinusoides representan el campo , en este caso el campo E de la perturbación. El frente de onda es una superficie de fase constante y se reúne cada sinusoide en el mismo punto ( misma fase) en su desarrollo. Las líneas radiales externas son rayos y están por todas partes perpendicular a los frentes de onda.

---

Ejercicio resuelto por: Rosario Maya (discusión) 02:22 30 mar 2015 (CDT)

---

Problema 4.4 5ta Edición

La ecuación para un oscilador amortiguado impulsado es

$m_{e}\ddot{x}+m_{e}\gamma\dot{x}+m_{e}\omega_{0}^{2}x=q_{e}E(t)$

(a)Explique el significado de cada termino.

(b) sea $​​E=E_{0}e^{i\omega t}$ y $x=x_{0}e^{i(\omega t-\alpha)}$, donde $E_{0}$ y $x_{0}$ son cantidades reales.

Sustituya en las expresiones anteriores y demostrar que

$x_{0}=\frac{q_{e}E_{0}}{m_{e}}\frac{1}{\left[(\omega_{0}^{2}-\omega^{2})^{2}+\gamma^{2}\omega^{2}\right]^{1/2}}$

Inciso a

En el lado izquierdo son la inercia , fuerza de arrastre , y los términos de la fuerza elástica ; en el lado derecho es la fuerza motriz eléctrica.

Inciso b

$x_{o}(-\omega^{2}+\omega_{0}^{2}+i\gamma\omega)=(q_{e}E_{0}/m_{e})e^{i\alpha}$

Elevando al cuadrado de ambos lados tenemos

$x_{0}^{2}\left[(\omega_{0}^{2}-\omega^{2})^{2}+\gamma^{2}\omega^{2}\right]=\left(q_{e}E_{0}/m_{e}\right)^{2}$

despejando $x_{0}$

y tomando la raíz cuadrada de ambos lados

$x_{0}=\frac{q_{e}E_{0}}{m_{e}}\frac{1}{\left[(\omega_{0}^{2}-\omega^{2})^{2}+\gamma^{2}\omega^{2}\right]^{1/2}}$

(c) Derivar la expresión para el retraso de fase , $\alpha$, y discutir cómo un varía como $\omega$ va de $\omega\ll\omega_{0}$ para $\omega\gg\omega_{0}$.

Como para $\alpha$, dividir las partes imaginarias de ambos lados de la primera ecuación anterior,

a saber

$x_{0}\gamma\omega=\left(q_{e}E_{0}/m_{e}\right)sin\alpha$

la parte real

$x_{0}(\omega_{0}^{2}-\omega^{2})=\left(q_{e}E_{0}/m_{e}\right)cos\alpha$

se obtiene

$\alpha=\arctan\left[\gamma\omega/(\omega_{0}^{2}-\omega^{2})\right]$

$\alpha$ oscila de 0 a $\frac{\pi}{2}$ a $\pi$

---

Resuelto por: Rosario Maya (discusión) 03:32 30 mar 2015 (CDT)

---

Problema 4.4 Versión alternativa

La ecuación del oscilador forzado amortiguado es

$m_{e}{\ddot {x}}+m_{e}\gamma {\dot {x}}+m_{e}\omega ^{2}x=q_{e}E(t)$........(1)

Sea $E=E_{0}Exp(i\omega t)$ y sea $X=x_{0}Exp(\omega t-\alpha )$

sustituir estos valores en la ecuación (1) y demuestre que

$x_{0}={\frac {q_{e}E_{0}}{m_{e}}}{\frac {1}{(\omega _{0}^{2}-\omega +\gamma ^{2}\omega ^{2})}}$

primero se deriva la expresión $x=x_{0}expi(\omega t-\alpha )$

quedando ${\dot {x}}=\omega x_{0}expi(\omega t-\alpha )$

y derivamos otra vez y queda

${\ddot {x}}\omega ^{2}expi(\omega t-\alpha )$

Así que sustituimos en la ecuación (1)

y se tiene

$x_{0}={\frac {q_{e}E_{0}}{m_{e}}}[(\omega _{0}^{2}-\omega ^{2})+\gamma ^{2}\omega ^{2}]^{1/2}$

Que es la expresión buscada.

---

Realizado por: Hector resendiz Héctor Reséndiz (discusión) 16:46 30 mar 2015 (CDT)

---

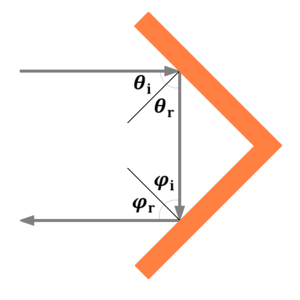
Problema 4.8 5ta Edición

Figura 4.8.

En la figura 4.8 se muestran las dos reflexiones del un rayo luminoso. En la primera reflexión, $ \theta_r=\theta_i $, y en la segunda reflexión, $ \varphi_r=\varphi_i $.

De la figura se concluye que $\theta_r$ y $\varphi_i$ son ángulos complementarios, i.e.,

\[ \theta_r+\varphi_i =\frac{\pi}{2} \] \[ \Longrightarrow \quad \theta_r+\varphi_r =\frac{\pi}{2} \] \[ \Longrightarrow \quad \varphi_r=\frac{\pi}{2}-\theta_r \] \[ \therefore \quad \varphi_r=\frac{\pi}{2}-\theta_i \]

Es decir, el ángulo saliente de la segunda reflexión $\varphi_r$, es complementario con el ángulo incidente en la primera reflexión $\theta_i$.

---

Problema realizado por: Adolfo Calderón Alcaraz (discusión) 14:06 30 mar 2015 (CDT)

---

3ra Edición en Español.

Problema 4.2 3ra Edición en español

Un haz reflector blanco cruza un gran volumen que contiene una mezcla de gas molecular tenue de la mayoría de oxígeno y nitrógeno. Comparar la cantidad relativa de dispersión para el ( 580nm) componente amarillo con el de la ( 400nm) componente violeta

Solución 

Donde:

Longitud de onda amarilla $\lambda_{y}= 580nm$

Longitud de onda violeta $\lambda_{v}= 400nm$

Conclusión

El grado de dispersión de Rayleigh que sufre un rayo de luz depende del tamaño de las partículas y de la longitud de onda de la luz, en concreto, del coeficiente de dispersión y por lo tanto la intensidad de la luz dispersada depende inversamente de la cuarta potencia de la longitud de onda, relación conocida como Ley de Rayleigh $\frac{1}{\lambda^{4}}$

Pero $\lambda_{y}=1.45\lambda_{v}$ y así $\frac{1}{\lambda^{4}{}_{y}}=\left(\frac{1}{1.45\lambda_{v}}\right)^{4}$ de ahí violeta se dispersa $\left(1.45\right)^{4}=4.42$ veces más intensamente que el amarillo. La proporción de amarillo a violeta es 22.6 %

---

Ejercicio Resuelto por: Rosario Maya (discusión) 01:51 30 mar 2015 (CDT)

---

Problema 4.8 3ra Edición en español

Calcule el ángulo de transmisión para un rayo en el aire incidente a $30^o$ en un bloque de vidrio-crown($n_v = 1,52$).

Procedimiento

La Ley de Snell-Descartes nos dice que:

$n_{i}\sin \alpha _{0}=n_{v}\sin \alpha _{t}$

Por lo que despejando para $\alpha_t$:

$\sin \alpha _{t}={\dfrac {n_{i}}{n_{v}}}\sin \alpha _{0}$

Donde $n_i$ es el ángulo de incidencia, en este caso $\alpha_i = 30^o$ y $n_i$ es el índice de refracción del aire, que es $n_i \approx 1$. Entonces, sustituyendo:

$\sin \alpha _{t}={\dfrac {1}{1.52}}\sin(30^{0})\Rightarrow \sin \alpha _{t}=(0.66)\left({\dfrac {1}{2}}\right)\Rightarrow \alpha _{t}=\arcsin(0.33)\approx 19^{o}7'$

Por lo que, el ángulo de transmisión buscado es: $\alpha_t = 19^o 7'$.

---

Realizado por: Ivan de Jesús Pompa García (discusión) 01:52 27 mar 2015 (CDT)

---

Problema 4.6 3ra Edición en español

Un haz láser muy estrecho incide bajo un ángulo de $58^o$ sobre un espejo horizontal. El haz de luz reflejado incide en una pared en un punto situado a 5 metros de distancia del punto de incidencia donde el haz de luz chocó con el espejo. ¿A qué distancia, medida horizontalmente, está la pared de ese punto de incidencia?.

Procedimiento

Como bien sabemos, los ángulos de incidencia y reflexión(o refracción) se miden respecto a la normal a la superficie, por lo que si el láser incide con un ángulo $\alpha_i = 58^o$, entonces el ángulo reflejado, por la ley de reflexión que nos dice que el ángulo reflejado es igual al rayo incidente, será $\alpha_r = 58^o$.

Además, se forma un triángulo rectángulo entre las dos trayectorias del rayo(incidente y reflejado) y la distancia $d$ horizontal del punto de incidencia y el punto donde el láser toca la pared. Por lo que, utilizando trigonometría básica, tenemos:

$\sin(58^o) = \dfrac{d}{5m} \Rightarrow d = (5m) \sin(58^o)$

Entonces, la distancia, medida horizontalmente, de la pared al punto de incidencia es de: $d \approx 4.24m$.

---

Realizado por: Ivan de Jesús Pompa García (discusión) 01:09 27 mar 2015 (CDT)

---

Problema 4.9 3ra Edición en español

Un rayo de luz amarilla en el aire, procedente de una lámpara de descarga de sodio, cae sobre la superficie de un diamante en el aire a 45°. Si a esa frecuencia nd =2.42, calcule la desviación angular sufrida en la transmisión.

Solución

Se tiene que la relación del indice de refracción es de la forma:

$n_{ti}={\frac {n_{t}}{n_{i}}}={\frac {\lambda _{i}}{\lambda _{t}}}=2.42$

Entonces, si:

${\frac {n_{t}}{n_{i}}}=2.42\Rightarrow {\frac {n_{i}}{n_{t}}}={\frac {1}{2.42}}$

Ahora la Ley de Snell nos dice:

$n_{ti}={\frac {sen\theta _{i}}{sen\theta _{t}}}$

donde $n_{ti}={\frac {n_{t}}{n_{i}}}$, entonces:

${\frac {n_{t}}{n_{i}}}={\frac {sen\theta _{i}}{sen\theta _{t}}}\Rightarrow n_{i}sen\theta _{i}=n_{t}sen\theta _{t},$

despejamos $\theta _{t}$ que es el ángulo de transmisión sobre la superficie del diamante, y se tiene:

$\theta _{t}=sen^{-1}\left[{\frac {n_{i}}{n_{t}}}sen\theta _{i}\right],$

sustituyendo los valores proporcionados pro el problema:

$\theta_{t} = sen^{-1} \left[\frac{sen45\text{\textdegree}}{2.42}\right] $

$\theta_{t} = sen^{-1} \left(0.2921\right) = 16.98° $

por lo tanto:

La desviación angular es 45°- 16.98° = 28.02°

Que es el ángulo de desviación angular sufrida en la transmisión.

---

Elaborado por: Ricardo García HernándezRicardo Garcia Hernandez (discusión) 00:32 30 mar 2015 (CDT)

---

Problema 4.11 3ra Edición en español

Un haz de microondas planas de 12 cm incide en la superficie de un dieléctrico a 45°. Si $n_{ti}=4/3$ calcule a) la longitud de onda en el medio transmisor, y b) el ángulo $\theta_{t}$

Inciso a

De la ley de Snell \[ n_i sin\theta_i = n_t sin\theta_t \] Tenemos:

\[\frac{n_t}{n_i}=\frac{sin\theta_i}{sin\theta_t}=n_{ti}...(1)\]

También sabemos que:

\[ n=\frac{C}{v}...(2) \]

y

\[ v=\lambda \nu...(3) \]

Por lo que (1) puede escribirse como:

\[n_{ti} = \frac{\frac{C}{v_t}}{\frac{C}{n_i}}=\frac{v_i}{v_t}=\frac{\lambda_i}{\lambda_t}...(3)\]

Despejando:

\[ \lambda_t = \frac{\lambda_i}{n_{ti}}=\frac{12cm}{4/3} \]

\[ \lambda_t=9cm \]

Inciso b

De (1)

\[sin\theta_i = n_{ti}sin\theta_t\]

\[ \theta_t =angsin \frac{sin\theta_i}{n_{ti}}=angsin \frac{sin45^{o}}{4/3} \]

\[ \theta_t = 32.02^{o} \]

---

Resuelto por: Luis Santos (discusión) 14:31 28 mar 2015 (CDT)

---

Ejercicios Adicionales

Ejercicio adicional, propagación de luz

Un lente convergente de 10 cm, de longitud focal forma una imagen de un objeto situado del lente a  :

(a) 30 cm (b)10 cm (c) 5 cm

Encontrar la distancia a la imagen y describir la imagen en cada caso.

La ecuación del lente delgado puede utilizarse para determinar la distancia a la imagen :

${\frac {1}{P}}+{\frac {1}{q}}={\frac {1}{F}}$

${\frac {1}{30}}+{\frac {1}{q}}={\frac {1}{10}}$

Inciso a

q= 15 cm

el signo positivo indica que la imagen es real. El aumento es:

${\frac {q}{p}}={\frac {-15}{30}}=-0.5$

de este modo la imagen a reducido su tamaño a la mitad y el signo negativo de M indica que la imagen esta invertida.

Inciso b

Ningún calculo es necesario para este caso, ya que, se sabe que cuando el objeto se pone en el punto focal, la imagen se forma en el infinito. Esto se puede verificar sustituyendo P=10 en la ecuación del lente.

Inciso c

A continuación nos movemos dentro del punto focal, hasta una distancia del objeto de 5cm. En este caso, la ecuación del lente delgado produce :

${\frac {1}{5}}+{\frac {1}{9}}={\frac {1}{10}}$

q= -10cm

$M={\frac {-q}{p}}=-({\frac {-10}{5}}=2$

La distancia a la imagen negativa nos indica que es virtual. La imagen se ha alargado y el signo positivo para M nos señala que la imagen esta de pie.

---

Realizado por: Luisa Alejandra Vega Sanchez (discusión) 00:43 30 mar 2015 (CDT)luisa alejandra vega sanchez

---