Ondas: planas

Introducción

Por efecto de la vibración, su energía se transmite de partícula a partícula. Ya que siempre hay el mismo número de partículas en los planos siguientes, por lo que : la $\textbf{intensidad}$ en una $\textbf{onda plana}$ permanece constante a medida que se propaga.

Ya que aunque no tienen una existencia física real, nos ayudan a representar con una buena aproximación de las ondas esféricas cuando estamos lejos de las fuentes que las originan ya que podemos sustituir la superficie esférica por su plano tangente.

Existen casos donde la ecuación de onda se puede resolver directamente. Por ejemplo en coordenadas cartesianas, cuando no existe variación respecto a $x$ y $y$ la ecuación de onda tiene la solución conocida de ondas planas unidimensionales.

Archivo:Ondasplanas.jpg

Fig. 0 Ondas planas

Este es el ejemplo más sencillo de onda tridimensional. Existe en un instante dado cuando todas las superficies sobre las cuales una perturbación tiene fase constante, forman un conjunto de planos, cada uno generalmente perpendicular a la dirección de propagación.

Fig. 1 Onda plana con movimiento en dirección $\hat k$

Forma Vectorial

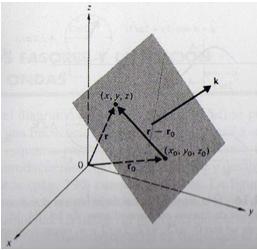
Para deducir la expresión matemática de un plano perpendicular a un vector dado k y que pasa a través de algún punto $(x_{0},y_{0},z_{0})$, primero se escribe el vector de posición en coordenadas cartesianas, en términos de los vectores unitarios de la base.

Fig. 2 Vectores unitarios en el plano cartesiano

$\textbf{r}=x \hat{\mathbf{e}}_x+y \hat{\mathbf{e}}_y+z \hat{\mathbf{e}}_z$

Comienza en el origen arbitrario $\textbf{0}$ y termina en el punto $(x,y,z)$ que en este caso será cualquier lugar en el espacio.

sabemos por la ecuación del plano que un vector único paralelo a un plano no basta para definir la dirección del plano, pero un vector perpendicular al plano sí la especifica. Así un plano en el espacio esta determinado por un punto $(x_{0},y_{0}.z_{0})$ en el plano y un vector kque es ortogonal al plano. Este vector ortogonal k se llama vector normal. Sea $(x,y,z)$ un punto arbitrario en el plano, y sean $\mathbf {r_{0}}$ y $\mathbf {r}$ los vectores de posición $P_{0}yP$. Entonces, el vector $\mathbf {r} -\mathbf {r_{0}}$ esta representado por $P_{0}P$. El vector normal $\mathbf {k}$ es ortogonal a cada vector en un plano determinado. En particular, $\mathbf {k}$ es ortogonal a $\mathbf {r} -\mathbf {r_{0}}$ ver (fig 1) por lo que tenemos

$(\textbf{r}-\textbf{r}_{0})=(x-x_{0})\hat{\mathbf{e}}_x+(y-y_{0})\hat{\mathbf{e}}_y+(z-z_{0})\hat{\mathbf{e}}_z$

Estableciendo

\begin{equation} (\textbf{r}-\textbf{r}_{0})\cdot\textbf{k}=0 \end{equation}

obligando al vector $(\textbf{r}-\textbf{r}_{0})$ a barrer un plano perpendicular a k, al ir adquiriendo su punto extremo $( x ,y, z )$ todos los valores permitidos.

Con

\begin{equation} \textbf{k}=k\hat{\mathbf{e}}_x+k\hat{\mathbf{e}}_y+k\hat{\mathbf{e}}_z \end{equation}

la ecuación (1) puede expresarse como

\begin{equation} k_{x}(x-x_{0}) + k_{y}(y-y_{0}) + k_{z}(z-z_{0})=0 \end{equation}

o como

\begin{equation} k_{x}x + k_{y}y + k_{z}z =0 \end{equation}

donde

\begin{equation} a = k_{x}x_{0} + k_{y}y_{0} + k_{z}z_{0}\ =constante \end{equation}

La forma más concisa de la ecuación de un plano perpendicular a $k$ es entonces

\begin{equation} \textbf{k}\cdot\textbf{r}= constante = a \end{equation}

El plano es el lugar de todos los puntos cuyos vectores de posición tienen cada uno la misma proyección en la dirección de $\textbf{k}$

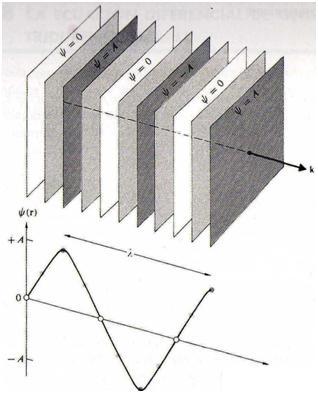
Ahora podemos construir un conjunto de planos sobre los cuales $\psi(\textbf{r})$ varía de manera sinusoidal en el espacio, es decir

\begin{equation} \psi(\textbf{r})=A Sen (\textbf{k}\cdot\textbf{r}) \end{equation}

\begin{equation} \psi(\textbf{r})=A Cos (\textbf{k}\cdot\textbf{r}) \end{equation}

o

\begin{equation} \psi(\textbf{r})=A e^{i\textbf{k}\cdot\textbf{r}} \end{equation}

Por todas estas expresiones $\psi ({\textbf {r}})$ se mantiene constante sobre cada plano definido por ${\textbf {k}}\cdot {\textbf {r}}=constante$. Como estamos analizando las funciones armónicas, deberían repetirse en el espacio después de un desplazamiento de $\lambda$ en la dirección de k. En la figura se representa esta clase de expresión. Del infinito número de planos se han dibujado sólo unos pocos, cada uno con una $\psi ({\textbf {r}})$ diferente. Los planos deberían también haberse dibujado con una extensión espacial infinita, ya que no se han puesto límites a ${\textbf {r}}$. La perturbación ocupa claramente todo el espacio.

Fig. 3 repetición en el espacio después de un desplazamiento de $\lambda$ en la dirección $\hat k$

La naturaleza repetitiva espacial de estas funciones armónicas se puede expresar por

\begin{equation} \psi(\textbf{r})=\psi(\textbf{r}+\frac{\lambda\textbf{r}}{k}) \end{equation}

Donde $k$ es la magnitud de $\textbf{k}$ y $\textbf{k}/{k}$ es un vector unitario paralelo a él.

En la forma exponencial, esto equivale a

$Ae^{i{\textbf {k}}\cdot {\textbf {r}}}=Ae^{i{\textbf {k}}\cdot {\textbf {r}}+\lambda {\textbf {k}}/k)}=Ae^{i{\textbf {k}}\cdot {\textbf {r}}}e^{i\lambda {k}}$

Para que sea cierto, debemos tener

$e^{i\lambda {k}}=1=e^{i2\pi }$

Por consiguiente

$\lambda {k}=2\pi$

y

$k=2\pi /\lambda$

El vector k, cuya magnitud es el número de propagación $k$, se llama vector de onda o de propagación. Ver ondas: vector de onda

En cualquier punto fijo del espacio donde r es constante, la fase es constante y también lo es $\psi ({\textbf {r}})$; en resumen, los planos están inmóviles. Para hacer que se muevan, $\psi ({\textbf {r}})$ debe hacerse variar en el tiempo, algo que puede lograrse introduciendo la dependencia del tiempo en una forma análoga a la de una onda unidimensional.

Aquí entonces

\begin{equation} \psi(\textbf{r},t)=Ae^{i(\textbf{k}\cdot\textbf{r}\pm\omega{t})} \end{equation}

donde $A,\omega ,yk$ son constantes. Mientras que esta perturbación viaja a lo largo de la dirección k, podemos asignarle una fase correspondiente en cada punto en el espacio y en el tiempo. En cualquier instante, las superficies que unen todos los puntos de igual fase se conocen como frentes de onda . Obsérvese que la función de onda tendrá un valor constante sobre el frente de onda solamente si la amplitud A tiene un valor fijo en todos los puntos del frente de onda. Por lo general, A es una función de r y puede que no sea constante en todo el espacio o en todo un frente de onda. En este último caso, la onda se dice inhomogénea.

La velocidad de fase vease ondas: velocidad de fase de una onda plana dada por la ecuación 10 es equivalente a la velocidad de propagación del frente de onda. En la figura 4 la componente escalar de r en la dirección de k es $r_{k}$. La perturbación en un frente de onda es constante, de manera que al cabo de un tiempo dt, si el frente recorre una distancia $d_{rk}$ a lo largo de k, debemos tener

\begin{equation} \psi(\textbf{r},t)=\psi(r_{k}+d_{rk},t+dt)=\psi(r_{k},t) \end{equation}

En forma exponencial, sería

\begin{equation} Ae^{i(\textbf{k}\cdot\textbf{r}\pm\omega{t})}=Ae^{i(kr_{k}+kdr_{k}\pm\omega{t}\pm\omega {dt})}=Ae^{i(kr_{k}\pm\omega{t})} \end{equation}

Por consiguiente

$kdr_{k}=\pm \omega {dt}$

La magnitud de la velocidad de la onda, $dr_{k}/dt$ es

\begin{equation} \frac{dr_{k}}{dt}=\pm\frac{\omega}{k}=\pm{v} \end{equation}

Podriamos haber anticipado este resultado girando el sistema coordenado de la figura 4 de tal forma quek fuera paralelo al eje x. Para esa orientación

$\psi ({\textbf {r}},t)=Ae^{i(kx\pm \omega {t}}$

ya que ${\textbf {k}}\cdot {\textbf {r}}=kr_{k}=kx$. La onda ha sido reducida efectivamente de esa manera a la perturbación unidimensional de la que ya se habló.

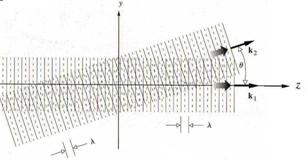
Ahora, considerense dos ondas de la figura 4; ambas tienen la misma longitud de onda $\lambda$ de tal manera que $k_{1}=k_{2}=k=2\pi /\lambda$. La onda 1 que se propaga a lo largo del eje z puede escribirse

$\psi _{1}=A_{1}cos({\frac {2\pi }{\lambda }}z-\omega {t})$

Fig. 5 Dos ondas superpuestas de la misma longitud de onda moviendose en direcciones diferentes

donde, puesto que ${\textbf {k}}_{1}$ y ${\textbf {r}}$ son paralelos ${\textbf {k}}_{1}\cdot {\textbf {r}}=kz=(2\pi /\lambda )z$. De forma análoga, para la onda 2, ${\textbf {k}}_{2}\cdot {\textbf {r}}=k_{z}z+k_{y}y=(kcos\theta )z+(ksen\theta )$.

$\psi _{2}=A_{2}cos[{\frac {2\pi }{\lambda }}(zcos\theta +ysen\theta )-\omega {t}]$

La onda armónica plana a menudo se escribe en coordenadas cartesianas como

\begin{equation} \psi(x,y,z,t)=Ae^{i(k_{x}x+k_{y}y+k_{z}z\pm\omega{t})} \end{equation}

o

\begin{equation} \psi(x,y,z,t)=Ae^{i[k(\alpha{x}+\beta{y}+\gamma{z}\pm\omega{t})]} \end{equation}

donde $\alpha$, $\beta$ y $\gamma$ son los cosenos directores de $k$. En términos de sus componentes, la magnitud del vector de propagación esta dado por

\begin{equation} \textbf{k}=k=(k_{x}^{2}+k_{y}^{2}+k_{z}^{2})^{1/2} \end{equation}

y por supuesto

\begin{equation} \alpha^{2}+ \beta ^{2}+ \gamma^{2}=1 \end{equation}

Hemos examinado ondas planas poniendo de relieve particularmente las funciones armónicas. La ondas sinusoidales pueden generarse de manera relativamente simple, usando alguna forma de oscilador armónico. cualquier onda tridimensional puede expresarse como una combinación de ondas planas, cada una con amplitud y dirección de propagación distintas.

Campo Electromagnético

Consideraremos una región en la cual hay conductividad despreciable, permitividad $\epsilon_0$ $\epsilon_r$ y permeabilidad $\mu_0$. En la región mencionada existe un campo electromagnético variable en el tiempo y la fuente del campo está fuera de la región.

De este modo podemos describir en la región, las ecuaciones de Maxwell como:

\begin{equation} \nabla \cdot \textbf{E} = 0 \end{equation}

\begin{equation} \nabla \times \textbf{E} = -\mu_0 \frac{\partial \textbf{H}}{\partial t } \end{equation}

\begin{equation} \nabla \cdot \textbf{H} = 0 \end{equation}

\begin{equation} \nabla \times \textbf{H} = \epsilon_0 \epsilon_r \frac{\partial \textbf{E}}{\partial t } \end{equation}

Usemos el rotacional de la Ecuación (20) y su resultado sustituimos la ecuación (19) y (22). Así obtenemos la ecuación de onda para $\textbf{E}$

\begin{equation} \nabla^2 \textbf{E}-\mu_0 \epsilon_0 \epsilon_r \frac{\partial^2 \textbf{E}}{\partial t^2 } = 0 \end{equation}

Análogamente podemos obtener la ecuación de onda para $\textbf{H}$

\begin{equation} \nabla^2 \textbf{H}-\mu_0 \epsilon_0 \epsilon_r \frac{\partial^2 \textbf{H}}{\partial t^2 } = 0 \end{equation}

Si $\textbf{E}$ y $\textbf{H}$ varían sinusoidalmente en el tiempo, puede escribirse:

\begin{equation} \textbf{E} (r,t) = Re [\tilde{E} (r) e^{j \omega t}] \end{equation}

\begin{equation} \textbf{H} (r,t) = Re [\tilde{H} (r) e^{j \omega t}] \end{equation}

donde $\tilde{E}(r)$ y $\tilde{H}(r)$ son los fasores asociados a $E(r, t)$ y $H(r, t)$. Si sustituimos (25) y (26) en (19) a (22), se obtiene la forma fasorial de las ecuaciones de Maxwell:

\begin{equation} \nabla \cdot \tilde{E} = 0 \end{equation}

\begin{equation} \nabla \times \tilde{E} = -j \omega \mu_0 \tilde{H} \end{equation}

\begin{equation} \nabla \cdot \tilde{H} = 0 \end{equation}

\begin{equation} \nabla \times \tilde{H} = j \omega \epsilon_0 \epsilon_r \tilde{E} \end{equation}

y si sustituimos (25) y (26) en las ecuaciones (23) y (24), se obtienen las ecuaciones de Helmholtz para $\tilde{E}(r)$ y $\tilde{H}(r)$, dadas por: