Diferencia entre revisiones de «Investigacion: RO18O»
| (No se muestran 232 ediciones intermedias de 14 usuarios) | |||
| Línea 3: | Línea 3: | ||
[[categoría:Investigacion]] | [[categoría:Investigacion]] | ||
[[categoría:Cursos]] | [[categoría:Cursos]] | ||
---- | ---- | ||
= Quiralidad Óptica y su interacción con la materia = | |||
El objetivo de esta información es mostrar una introducción y generar ideas elementales de qué teoría y qué se deben usar para explicar el efecto de la quiralidad óptica ya que puede ser bastante engorroso mostrar paso a paso los desarrollos matemáticos. | El objetivo de esta información es mostrar una introducción y generar ideas elementales de qué teoría y qué se deben usar para explicar el efecto de la quiralidad óptica ya que puede ser bastante engorroso mostrar paso a paso los desarrollos matemáticos. | ||
| Línea 120: | Línea 122: | ||
Es fácil ver que cuando las energías van teniendo casi la misma intensidad, la taza de asimetría aumenta mucho. Esto se le conoce como onda estacionaria superquiral. La presente teoría está limitada a efectos quirales donde el campo EM no es tan intenso, es decir, el material responde linealmente con dicho campo. Otro detalle a tomar en cuenta que se deberá contemplar los momentos cuadrupolares para moléculas que sean del tamaño aproximadamente de la longitud de onda del campo EM. | Es fácil ver que cuando las energías van teniendo casi la misma intensidad, la taza de asimetría aumenta mucho. Esto se le conoce como onda estacionaria superquiral. La presente teoría está limitada a efectos quirales donde el campo EM no es tan intenso, es decir, el material responde linealmente con dicho campo. Otro detalle a tomar en cuenta que se deberá contemplar los momentos cuadrupolares para moléculas que sean del tamaño aproximadamente de la longitud de onda del campo EM. | ||
==Bibliografía== | |||
Yiqiao Tang and Adam E. Cohen, ''Optical quirality and interaction with Matter'' (Harvard University, Massachusetts, 2010) | Yiqiao Tang and Adam E. Cohen, ''Optical quirality and interaction with Matter'' (Harvard University, Massachusetts, 2010) | ||
| Línea 126: | Línea 128: | ||
--[[Usuario:Onáfeder|Fernando Valencia Hernández]] | --[[Usuario:Onáfeder|Fernando Valencia Hernández]] | ||
=Polarización= | |||
== Introducción == | == Introducción == | ||
| Línea 152: | Línea 153: | ||
[[Archivo:002_unpolar.jpg|300px|thumb|center| Luz no Polarizada: Representación de cada una de las polarizaciones, la suma de todas ellas dará como resultado una polarización neta]] | [[Archivo:002_unpolar.jpg|300px|thumb|center| Luz no Polarizada: Representación de cada una de las polarizaciones, la suma de todas ellas dará como resultado una polarización neta]] | ||
====Animación==== | |||
http://www.geocities.ws/fisica1y2/interactivas2/polarizacion/polarizacion.html | |||
== Luz Linealmente Polarizada == | == Luz Linealmente Polarizada == | ||
| Línea 254: | Línea 258: | ||
<math>\vec{\mathbf{E}}=2E_{0}\hat i cos(kz - \omega t) \qquad( | <math>\vec{\mathbf{E}}=2E_{0}\hat i cos(kz - \omega t) \qquad(11)</math> | ||
== Luz Elípticamente Polarizada == | == Luz Elípticamente Polarizada == | ||
| Línea 263: | Línea 267: | ||
La '''polarización elíptica''' se presenta cuando las componentes <math>\textstyle{E_x}</math> y <math>\textstyle{E_y}</math> se encuentran desfasadas un valor <math>\varepsilon</math> arbitrario, y a su vez presentan una amplitud arbitraria. | La '''polarización elíptica''' se presenta cuando las componentes <math>\textstyle{E_x}</math> y <math>\textstyle{E_y}</math> se encuentran desfasadas un valor <math>\varepsilon</math> arbitrario, y a su vez presentan una amplitud arbitraria. | ||
<math> E_{x}(z,t)=E_{0x} \cos(kz- \omega t) </math> | <math> E_{x}(z,t)=E_{0x} \cos(kz- \omega t) \qquad(12) </math> | ||
<math> E_{y}(z,t)=E_{0y}\cos(kz- \omega t+ \epsilon) </math> | <math> E_{y}(z,t)=E_{0y}\cos(kz- \omega t+ \epsilon) \qquad(13) </math> | ||
Para encontrar una ecuación independiente del espacio y del tiempo | Para encontrar una ecuación independiente del espacio y del tiempo | ||
| Línea 290: | Línea 294: | ||
-2(\frac{E_{y}}{E_{0y}})(\frac{E_{x}}{E_{0x}})\cos \epsilon= | -2(\frac{E_{y}}{E_{0y}})(\frac{E_{x}}{E_{0x}})\cos \epsilon= | ||
\sin^{2}\epsilon </math> | \sin^{2}\epsilon \qquad(14)</math> | ||
Aqui <math>\epsilon</math> es la diferencia de fase relativa entre las ondas. | Aqui <math>\epsilon</math> es la diferencia de fase relativa entre las ondas. | ||
| Línea 297: | Línea 301: | ||
En este caso, si pudiéramos observar las oscilaciones del campo eléctrico en un haz de luz linealmente polarizada, viniendo de frente (saliendo de la pantalla), entonces el movimiento descrito sería en la mayoría de los casos elíptico. | En este caso, si pudiéramos observar las oscilaciones del campo eléctrico en un haz de luz linealmente polarizada, viniendo de frente (saliendo de la pantalla), entonces el movimiento descrito sería en la mayoría de los casos elíptico. | ||
En general, los ejes principales de la elipse no están en las direcciones x e y. Al utilizar una transformación (rotación) del sistema de coordenadas, podemos diagonalizar la ecuación <math>(14)</math>: | |||
[[Archivo:poleliptica.PNG|center]] | |||
Sean x' y y' el nuevo conjunto de ejes a lo largo de los ejes principales de la elipse. Entonces la ecuación de la elipse en este nuevo sistema de coordenadas se convierte en: | |||
<math>{ \left( \frac { { E }_{ \grave { x } } }{ a } \right) }^{ 2 }+{ { \left( \frac { { E }_{ \grave { y } } }{ b } \right) } }^{ 2 }=1</math> | |||
donde a y b son las longitudes de los semiejes principales de la elipse, y <math>{ E }_{ \grave { x } }</math>y <math>{ E }_{ \grave { y } }</math> son los componentes del vector del campo eléctrico en este sistema de coordenadas principal. | |||
Sea <math>\Phi </math> el ángulo entre el eje x' y el eje x. Entonces las longitudes de los ejes principales están dadas por: | |||
<math>{ a }^{ 2 }={ E }_{ 0x }^{ 2 }{ cos }^{ 2 }\Phi +{ E }_{ 0y }^{ 2 }{ sin }^{ 2 }\Phi +2{ E }_{ 0x }{ E }_{ 0y }cos\varepsilon { sin }\Phi cos\Phi </math> | |||
<math>b^{ 2 }={ E }_{ 0x }^{ 2 }{ sin }^{ 2 }\Phi +{ E }_{ 0y }^{ 2 }{ cos }^{ 2 }\Phi -2{ E }_{ 0x }{ E }_{ 0y }cos\varepsilon { sin }\Phi cos\Phi </math> | |||
El ángulo <math>\Phi </math> se puede expresar en términos de <math>{ E }_{ 0x }</math>, <math>{ E }_{ 0y }</math> y <math>cos\varepsilon </math> como: | |||
<math>Tan2\Phi =\frac { 2{ E }_{ 0x }{ E }_{ 0y }cos\varepsilon }{ { { E }_{ 0x } }^{ 2 }-{ { E }_{ 0y } }^{ 2 } } </math> | |||
Es importante tener en cuenta que <math>\Phi +\frac { \pi }{ 2 } </math> también es una solución, si <math>\Phi </math>es una solución de la ecuación. | |||
Dirección de la revolución de una polarización elíptica | |||
La dirección de la revolución de una polarización elíptica está determinada por el signo de <math>sin\varepsilon </math>. El punto final del vector del campo eléctrico girará en el sentido de las agujas del reloj si <math>sin\varepsilon </math> > 0, y en el sentido contrario a las agujas del reloj si <math>sin\varepsilon </math> <0. | |||
La siguiente figura muestra cómo cambia la elipse de polarización al variar la diferencia de fase δ. | |||
[[Archivo:Modeloelip.PNG|center]] | |||
==Polarizadores dicroicos.== | ==Polarizadores dicroicos.== | ||
| Línea 320: | Línea 361: | ||
[[Archivo:PolarizacionH.jpg|300px|thumb|center||Lamina H.]] | [[Archivo:PolarizacionH.jpg|300px|thumb|center||Lamina H.]] | ||
====Polarizadores en un reloj(Animación)==== | |||
https://www.vascak.cz/data/android/physicsatschool/templateimg.php?s=opt_polarizacefiltr&l=es | |||
====Figura activa con dos polarizadores==== | |||
http://micro.magnet.fsu.edu/primer/java/polarizedlight/filters/index.html | |||
====Vídeo de polarización==== | |||
https://www.youtube.com/watch?v=82Cux9Q9afk | |||
==Polarizadores de reflexión:== | ==Polarizadores de reflexión:== | ||
| Línea 343: | Línea 397: | ||
==El vector de Stokes== | ==El vector de Stokes== | ||
== | El vector de Stokes | ||
El vector de Stokes es un conjunto de números, se aplica igualmente a luz polarizada, a luz parcialmente polarizada y a la luz no polarizada. Inventado en 1852 por el físico británico G.G Stokes, proporciona el método más sencillo para predecir el resultado de superponer dos haces incoherentes. | |||
Más importante aún es el hecho de que el vector de Stokes de un método numérico simple para predecir cómo se afecta un haz por efecto de un polarizador o un retardador. La especificación del haz emergente se determina multiplicando el vector de Stokes que representa el haz incidente por una matriz que representa al polarizador o retardador. | |||
<math>1</math>La intensidad total de la luz (polarizada + no polarizada) <math>{ S }_{ 0 }</math> | |||
<math>2</math>La intensidad de la polarización lineal horizontal o vertical <math>{ S }_{ 1 }</math> | |||
<math>3</math>La intensidad de la polarización lineal + 45 ° o -45 ° <math>{ S }_{ 2 }</math> | |||
<math>4</math>La intensidad de polarización circular derecha o izquierda <math>{ S }_{ 3 }</math> | |||
La intensidad de la parte polarizada de la onda de luz viene dada por: | |||
<math>I_{ polarizda }=\sqrt { { s }_{ 1 }^{ 2 }+{ s }_{ 2 }^{ 2 }+{ s }_{ 3 }^{ 2 } } </math> | |||
La intensidad total <math>{ s }_{ 0 }</math> es: | |||
<math>{ s }_{ 0 }=I_{ polarizda }+{ I }_{ no\quad polarizada }=\sqrt { { s }_{ 1 }^{ 2 }+{ s }_{ 2 }^{ 2 }+{ s }_{ 3 }^{ 2 } } +{ I }_{ no\quad polarizado }</math> | |||
Así: | |||
<math>s_{ 0 }^{ 2 }={ s }_{ 1 }^{ 2 }+{ s }_{ 2 }^{ 2 }+{ s }_{ 3 }^{ 2 }</math> (Luz completamente polarizada) | |||
<math>s_{ 0 }^{ 2 }>{ s }_{ 1 }^{ 2 }+{ s }_{ 2 }^{ 2 }+{ s }_{ 3 }^{ 2 }</math> (Luz parcialmente polarizado y no polarizado) | |||
Para representar (14) en términos de los observables del campo óptico, debemos tomar un promedio durante el tiempo de observación. | |||
Dado que la vibración es tan rápida, el tiempo de observación puede verse como infinito. Pero, dado que <math>{ E }_{ x }(t)</math> y <math>{ E }_{ y }(t)</math> son periódicos, en realidad podemos promediar (14) solo en un solo período de oscilación. | |||
El tiempo promedio está representado por los corchetes angulares <...>, por lo que (14) puede escribirse como: | |||
<math>\frac { \left< { E }_{ x }^{ 2 }(t) \right> }{ { E }_{ 0x }^{ 2 } } +\frac { \left< { E }_{ y }^{ 2 }(t) \right> }{ { E }_{ 0y }^{ 2 } } -2\frac { \left< { E }_{ y }(t){ E }_{ x }(t) \right> }{ { E }_{ 0y }(t){ E }_{ 0x }(t) } cos\varepsilon ={ sin }^{ 2 }\varepsilon </math> ....(14) | |||
dónde | |||
<math>\left< { E }_{ y }(t){ E }_{ x }(t) \right> ={ Lim }_{ T\longrightarrow \infty }\frac { 1 }{ T } \int _{ 0 }^{ T }{ { E }_{ y }(t){ E }_{ x }(t)dt } </math> .....(15) | |||
Luego multiplicamos (14) por <math>{ { 4E }_{ 0x } }^{ 2 }{ { E }_{ 0y } }^{ 2 }</math> , y luego obtenemos: | |||
<math>{ { 4E }_{ 0y } }^{ 2 }\left< { E }_{ x }^{ 2 }(t) \right> +{ { 4E }_{ 0x } }^{ 2 }\left< { E }_{ y }^{ 2 }(t) \right> -8{ E }_{ 0y }(t){ E }_{ 0x }(t)\left< { E }_{ y }(t){ E }_{ x }(t) \right> cos\varepsilon ={ (2{ E }_{ 0y }(t){ E }_{ 0x }(t){ sin }\varepsilon ) }^{ 2 }</math> ......(16) | |||
De (1) y (2), podemos encontrar los valores promedio de la ecuación (16) usando la ecuación (15): | |||
<math>\left< { E }_{ x }^{ 2 }(t) \right> =\frac { 1 }{ 2 } { { E }_{ 0x } }^{ 2 }</math> ......(17) | |||
<math>\left< { E }_{ y }^{ 2 }(t) \right> =\frac { 1 }{ 2 } { { E }_{ 0y } }^{ 2 }</math> .......(18) | |||
<math>\left< { E }_{ y }(t){ E }_{ x }(t) \right> =\frac { 1 }{ 2 } { { E }_{ 0x } }{ { E }_{ 0y } }cos\varepsilon </math> .......(19) | |||
Sustituyendo (17), (18), (19) en (16) y obtenemos: | |||
<math>{ { 2E }_{ 0x } }^{ 2 }{ { E }_{ 0y } }^{ 2 }+{ { 2E }_{ 0x } }^{ 2 }{ { E }_{ 0y } }^{ 2 }-{ ({ { 2E }_{ 0x } }{ { E }_{ 0y } }cos\varepsilon ) }^{ 2 }={ (2{ E }_{ 0y }{ E }_{ 0x }{ sin }\varepsilon ) }^{ 2 }</math> ....(20) | |||
Como queremos expresar el resultado final en términos de intensidad, podemos sumar y restar la cantidad <math>{ { E }_{ 0x } }^{ 4 }+{ { E }_{ 0y } }^{ 4 }</math> al lado izquierdo de (20); Haciendo esto se obtienen cuadrados perfectos. | |||
Entonces podemos obtener: | |||
<math>{ { ({ E }_{ ox }^{ 2 } }{ +{ { E }_{ oy }^{ 2 } } }) }^{ 2 }-{ { { ({ E }_{ ox }^{ 2 } } }{ -{ { E }_{ oy }^{ 2 } } }) }^{ 2 }-{ ({ { 2E }_{ 0x } }{ { E }_{ 0y } }cos\varepsilon ) }^{ 2 }={ (2{ E }_{ 0y }{ E }_{ 0x }{ sin }\varepsilon ) }^{ 2 }</math> .....(21) | |||
Escribimos las cantidades dentro de los paréntesis como: | |||
<math>{ S }_{ 0 }={ { E }_{ ox }^{ 2 } }{ +{ { E }_{ oy }^{ 2 } } }</math> ......(22) | |||
<math>{ S }_{ 1 }={ { E }_{ ox }^{ 2 } }{ -{ { E }_{ oy }^{ 2 } } }</math> .......(23) | |||
<math>{ S }_{ 2 }={ { { 2E }_{ 0x } }{ { E }_{ 0y } }cos\varepsilon }</math> .......(24) | |||
<math>{ S }_{ 3 }={ { { 2E }_{ 0x } }{ { E }_{ 0y } }sin\varepsilon }</math> ........(25) | |||
Tenga en cuenta que S_0 , S_1 , S_2 , S_3 son cantidades promediadas en el tiempo realizadas en un intervalo de tiempo T_D que es la constante de tiempo característica del proceso de detección | |||
Luego reescribimos (21) como: | |||
<math>{ S }_{ 0 }^{ 2 }={ S }_{ 1 }^{ 2 }+{ S }_{ 2 }^{ 2 }+{ S }_{ 3 }^{ 2 }</math> ...(26) | |||
Las cuatro ecuaciones (22), (23), (24) y (25) son los parámetros de polarización de Stokes para una onda plana . | |||
Nota: | |||
Los parámetros de Stokes se expresan en términos de intensidades (que podemos medir) | |||
Los parámetros de Stokes son cantidades reales (en lugar de números complejos como en las matrices de Jones) | |||
Basándonos en la desigualdad de Schwartz, podemos decir que para cualquier estado de luz polarizada: | |||
<math>{ S }_{ 0 }^{ 2 }\ge { S }_{ 1 }^{ 2 }+{ S }_{ 2 }^{ 2 }+{ S }_{ 3 }^{ 2 }</math> | |||
En (17), la igualdad es verdadera para la luz completamente polarizada, y la desigualdad es verdadera para la luz parcialmente polarizada o no polarizada. | |||
GRADO DE POLARIZACIÓN (DOP) EN TÉRMINOS DE PARÁMETROS DE STOKES | |||
Podemos usar los parámetros de Stokes para describir el grado de polarización para cualquier estado de polarización (completamente polarizado, parcialmente polarizado y no polarizado). | |||
El grado de polarización P se define como (basado en la intensidad de la luz): | |||
<math>P=\frac { { I }_{ polarizado } }{ { I }_{ Total } } =\frac { \sqrt { { S }_{ 1 }^{ 2 }+{ S }_{ 3 }^{ 2 }+{ S }_{ 2 }^{ 2 } } }{ { S }_{ 0 } } </math> | |||
Entonces el significado de P es: | |||
P = 1 ---> luz completamente polarizada | |||
P = 0 ---> luz no polarizada | |||
0 < P <1 ---> luz parcialmente polarizada | |||
EJEMPLOS DE PARÁMETROS DE STOKES PARA LUZ COMPLETAMENTE POLARIZADA | |||
Ahora discutimos los parámetros de Stokes para algunos casos especiales. | |||
1. LUZ LINEALMENTE POLARIZADA HORIZONTALMENTE (LHP) | |||
Para este caso, no hay componente de campo vertical, por lo que <math>{ E }_{ 0y }=0</math>. De (22), (23), (24) y (25) obtenemos: | |||
<math>{ S }_{ 0 }={ E }_{ 0x }^{ 2 }</math> | |||
<math>{ S }_{ 1 }={ E }_{ 0x }^{ 2 }</math> | |||
<math>{ S }_{ 2 }=0</math> | |||
<math>{ S }_{ 3 }=0</math> | |||
2. LUZ LINEALMENTE POLARIZADA VERTICALMENTE (LVP) | |||
Para este caso, no hay componente de campo horizontal, por lo que <math>{ E }_{ 0x }=0</math>. De (22) a (25) obtenemos: | |||
<math>{ S }_{ 0 }={ E }_{ 0y }^{ 2 }</math> | |||
<math>{ S }_{ 1 }={ -E }_{ 0y }^{ 2 }</math> | |||
<math>{ S }_{ 2 }=0</math> | |||
<math>{ S }_{ 3 }=0</math> | |||
3. LINEAL + 45 ° LUZ POLARIZADA (L +45) | |||
Las condiciones para obtener luz polarizada lineal de + 45 ° son: | |||
<math>{ E }_{ 0x }={ E }_{ 0y }={ E }_{ 0 } </math> y <math>\varepsilon =0</math> | |||
Esto significa que esta polarización es una superposición de campos horizontales y verticales en fase, de igual amplitud. Con (22) a (25), obtenemos: | |||
<math>{ S }_{ 0 }={ 2E }_{ 0 }^{ 2 }</math> | |||
<math>{ S }_{ 1 }=0</math> | |||
<math>{ S }_{ 2 }={ 2E }_{ 0 }^{ 2 }</math> | |||
<math>{ S }_{ 3 }=0</math> | |||
4. LINEAL -45 ° LUZ POLARIZADA (L -45) | |||
Las condiciones para obtener luz polarizada lineal de -45 ° son: | |||
<math>{ E }_{ 0x }={ E }_{ 0y }={ E }_{ 0 } </math> y <math>\varepsilon =180°</math> | |||
Entonces obtenemos: | |||
<math>{ S }_{ 0 }={ 2E }_{ 0 }^{ 2 }</math> | |||
<math>{ S }_{ 1 }=0</math> | |||
<math>{ S }_{ 2 }={- 2E }_{ 0 }^{ 2 }</math> | |||
<math>{ S }_{ 3 }=0</math> | |||
LUZ CIRCULARMENTE POLARIZADA DERECHA (RCP) | |||
Las condiciones para obtener una luz polarizada circularmente correcta son: | |||
<math>{ E }_{ 0x }={ E }_{ 0y }={ E }_{ 0 } </math> y <math>\varepsilon =90°</math> | |||
Entonces obtenemos: | |||
<math>{ S }_{ 0 }={ 2E }_{ 0 }^{ 2 }</math> | |||
<math>{ S }_{ 1 }=0</math> | |||
<math>{ S }_{ 2 }=0</math> | |||
<math>{ S }_{ 3 }={ 2E }_{ 0 }^{ 2 }</math> | |||
LUZ CIRCULARMENTE POLARIZADA IZQUIERDA (LCP) | |||
Las condiciones para obtener luz polarizada circularmente a la izquierda son: | |||
<math>{ E }_{ 0x }={ E }_{ 0y }={ E }_{ 0 } </math> y <math>\varepsilon =-90°</math> | |||
Entonces obtenemos: | |||
<math>{ S }_{ 0 }={ 2E }_{ 0 }^{ 2 }</math> | |||
<math>{ S }_{ 1 }=0</math> | |||
<math>{ S }_{ 2 }=0</math> | |||
<math>{ S }_{ 3 }={ -2E }_{ 0 }^{ 2 }</math> | |||
7. LUZ POLARIZADA ELÍPTICAMENTE | |||
Los parámetros de Stokes para luz polarizada elípticamente en general son como la definición: | |||
Aplicaciones: | |||
El resultado de combinar dos haces incoherentes se halla sumando los dos vectores de Stokes adecuados. | |||
Considérese, por ejemplo,la suma de un haz polarizado horizontalmente de intensidad uno y un haz polarizado circularmente en sentido derecho de intensidad tres. Los vectores correspondientes son ( 1,1,0,0) y (3,0,0,3),hay que notar los vectores los pusimos horizontal solo para ahorrar espacio. | |||
La suma obtenida añadiendo los números situados en lugares correspondientes es (4,1,0,3). Este vector resultante significa que la intensidad del haz resultante es 4, ya que el primer número es 4. | |||
El modelo seccional elíptico tiene gran parecido con un círculo, ya que la magnitud del último número es grande y el sentido circular de la elipse es hacia la derecha, pues el último número es positivo. La elipse es más horizontal que vertical, ya que el segundo número es positivo. El grado de polarización es | |||
<math>\frac { { \left( { 1 }^{ 2 }+{ 0 }^{ 2 }+{ 3 }^{ 2 } \right) }^{ \frac { 1 }{ 2 } } }{ 4 } </math> | |||
o sea 79 por ciento. | |||
Otro ejemplo es la combinación de dos haces polarizados horizontal y verticalmente que son incoherentes y de intensidad unidad. sus vectores son (1,1,0,0) y (1,-1,,0,0), en tanto que la suma es (2,0,0,0). Este representa un haz no polarizado, pues los últimos tres números son cero. | |||
==EL vector de Jones== | |||
El vector de de Jones, inventado en 1941 por un físico americano de 25 años, R.Clark Jones, es superior al vector de Stokes en algunos sentidos, pero inferior a otros. Es superior en el sentido de que es aplicable a la adición de haces coherentes. Es inferior en el sentido de que no puede aplicarse a la luz no polarizada o parcialmente polarizada y en que, además, utiliza números complejos. | |||
Dado que la luz se compone de campos eléctricos y magnéticos oscilantes, Jones razonó que la forma más natural de representar la luz es en términos del vector de campo eléctrico. | |||
Cuando se escribe como un vector de columna, este vector se conoce como un vector de Jones y tiene la forma: | |||
<math> \hat E= \ \begin {bmatrix} { E }_{ x }(t)\\ { E }_{ y }(t)\end {bmatrix}</math> | |||
Donde <math>{ E }_{ x }\left( t \right) </math> y <math>{ E }_{ y }\left( t \right) </math> son los componentes escalares instantáneos del campo eléctrico. Nota que estos valores pueden ser números complejos, por lo que la información de amplitud y fase es presente. A menudo, sin embargo, no es necesario conocer las amplitudes y fases exactas de los componentes del vector. Por lo tanto los vectores de Jones pueden ser normalizados y en fase común, los factores pueden ser descuidados. Esto resulta en una pérdida de información, pero puede simplificar enormemente expresiones. Por ejemplo, los siguientes vectores contienen diversos grados de información, pero son todas las representaciones vectoriales de Jones para el mismo estado de polarización: | |||
<math> \ \ \begin {bmatrix} { E }_{ 0 }{ e }^{ i\phi }\\ { E }_{ 0 }{ e }^{ i\psi }\end {bmatrix}</math> <math>\longrightarrow </math> <math> \ \ \begin {bmatrix} { e }^{ i\phi }\\ { e }^{ i\psi }\end {bmatrix}</math> <math>\longrightarrow </math> <math> \ \ \begin {bmatrix} 1\\ { e }^{ i(\psi -\phi ) }\end {bmatrix}</math> | |||
Tenga en cuenta que se dice que un vector complejo se normaliza cuando el producto punto del vector con su conjugado complejo produce un valor de unidad. | |||
En la mayoría de los casos, se elige la base para el vector de Jones como los estados de polarización lineal horizontal y vertical. En este caso las representaciones de estos dos estados son: | |||
<math> \ E_h = \ \begin {bmatrix} { E }_{ x }(t)\\ 0\end {bmatrix}</math> y <math> \ E_v= \ \begin {bmatrix} 0\\ { E }_{ y }(t)\end {bmatrix}</math> | |||
o, en forma normalizada, | |||
<math> \ E_h = \ \begin {bmatrix} 1\\ 0\end {bmatrix}</math> y <math> \ E_v= \ \begin {bmatrix} 0\\1\end {bmatrix}</math> | |||
Donde <math>{ E }_{ h }</math> y <math>{ E }_{ v }</math> representan la luz polarizada horizontal y verticalmente, respectivamente. La suma de dos haces de luz coherentes viene dada por la suma de sus componentes correspondientes del vector de Jones, por lo que la suma de <math>{ E }_{ h }</math> y <math>{ E }_{ v }</math>cuando <math>{ E }_{ v }={ E }_{ h }</math> viene dada por : | |||
<math> \ E_45°= \ \begin {bmatrix} { E }_{ x }(t)\\ { E }_{ x }(t)\end {bmatrix}</math> <math>\Rightarrow </math> <math> \ E_45° = \frac { 1 }{ \sqrt { 2 } } \ \begin {bmatrix} 1\\ 1\end {bmatrix}</math> | |||
donde la flecha indica normalización. Tenga en cuenta que esta es la representación de la polarización. Estado en el que el campo eléctrico está orientado en un ángulo de 45 grados con respecto a la estados base. Otros dos estados de polarización comunes son circular derecho y circular izquierdo. En ambos casos los dos componentes tienen la misma amplitud,pero tienen una diferencia de fase de 90°. Así, la representación vectorial de Jones para la derecha-circular es | |||
<math> \ E_R=\ \begin {bmatrix} { E }_{ 0 }{ e }^{ i\phi }\\ { E }_{ 0 }{ e }^{ i(\phi -\frac { \pi }{ 2 } ) }\end {bmatrix}</math> | |||
Normalizando esta expresión y factorizando un factor de fase constante <math>{ e }^{ i\phi }</math>: | |||
<math> \ E_R=\frac { 1 }{ \sqrt { 2 } } \begin {bmatrix}\\ 1\\ { e }^{ -i\frac { \pi }{ 2 } }\end {bmatrix}</math> <math>=</math> <math> \ \frac { 1 }{ \sqrt { 2 } } \begin {bmatrix}\\ 1\\ -i\end {bmatrix}</math> | |||
Del mismo modo, la representación normalizada para la luz circular izquierda es: | |||
<math> \ E_L=\frac { 1 }{ \sqrt { 2 } } \begin {bmatrix}\\ 1\\ { e }^{ i\frac { \pi }{ 2 } }\end {bmatrix}</math> <math>=</math> <math> \ \frac { 1 }{ \sqrt { 2 } } \begin {bmatrix}\\ 1\\ i\end {bmatrix}</math> | |||
La intensidad del haz es proporcional a la suma de los cuadrados de las magnitudes de los elementos. Si cada elemento del vector se multiplica por 4,la intensidad aumenta por un factor de 16. | |||
Aplicaciones: Una aplicación sencilla del vector de Jones es la predicción del resultado de componer dos haces coherentes. | |||
Considérese un haz polarizado horizontalmente de intensidad 1 y otro verticalmente polarizado de intensidad de 16 veces mayor. Los haces se suponen coherentes y de la misma fase. | |||
Los vectores correspondientes son <math> \ \ \begin {bmatrix} 1\\0\end {bmatrix}</math> y <math> \ \ \begin {bmatrix} 0\\ 4\end {bmatrix}</math> El resultado de componer los dos haces se encuentra sumando los vectores. La suma es <math> \ \ \begin {bmatrix} 1\\ 4\end {bmatrix}</math> | |||
Este corresponde a un haz linealmente polarizado a un angulo dado por <math>arctan\left( \frac { 4 }{ 1 } \right) </math>; esto es ,76°. La intensidad esta dada por <math>{ (1) }^{ 2 }+{ (4) }^{ 2 }</math> osea 17. | |||
A continuación, consideremos un haz de luz representado por el vector de Jones | |||
<math> \hat E_i= \ \begin {bmatrix} { E }_{ ix }(t)\\ { E }_{ iy }(t)\end {bmatrix}</math> | |||
incidente en un dispositivo óptico. La luz interactuará con el dispositivo, y el nuevo estado de polarización de la luz al salir del dispositivo será: | |||
<math> \hat E_t= \ \begin {bmatrix} { E }_{ tx }(t)\\ { E }_{ ty }(t)\end {bmatrix}</math> | |||
El acoplamiento entre estos dos vectores se puede describir completamente mediante un conjunto de cuatro coeficientes de acuerdo con el siguiente par de ecuaciones lineales: | |||
<math>{ E }_{ tx }=a{ E }_{ ix }+b{ E }_{ iy }</math> | |||
<math>{ E }_{ ty }=c{ E }_{ ix }+d{ E }_{ iy }</math> | |||
Estas dos ecuaciones pueden reescribirse usando la notación matricial como | |||
<math>\overrightarrow { { E }_{ t } } =\overrightarrow { J } \overrightarrow { { E }_{ i } } </math> | |||
dónde | |||
<math> \hat J= \ \begin {bmatrix} a & b \\ c & d \end {bmatrix}</math> | |||
Es la matriz de Jones del dispositivo óptico. Una lista de matrices de Jones para algunos dispositivos ópticos comunes aparece en la Tabla 1. Es posible representar el paso de un haz de luz a través de múltiples dispositivos como la multiplicación de matrices de Jones. Tenga en cuenta que las matrices no conmutan, como se ilustra en el siguiente ejemplo. Supongamos una señal de entrada polarizada horizontalmente, y veamos su propagación a través de dos dispositivos, un polarizador lineal orientado a y una placa de cuarto de onda con su eje vertical rápido. Si la luz pasa a través del polarizador primero, seguido por la placa de onda, tenemos: | |||
<math> \hat E_t= \ \begin {bmatrix} 1 & 0 \\ 0 & -i \end {bmatrix}</math> <math> \ \ \begin {bmatrix} 1 & 1 \\ 1 & 1 \end {bmatrix}</math> <math> \ \ \begin {bmatrix} 1 \\ 0 \end {bmatrix}</math> | |||
<math> \hat E_t= \ \begin {bmatrix} 1 & 0 \\ 0 & -i \end {bmatrix}</math> <math> \ \ \begin {bmatrix} 1 \\ 1 \end {bmatrix}</math> | |||
<math> \hat E_t= \ \begin {bmatrix} 1 \\ -i\end {bmatrix}</math> | |||
donde hemos descuidado los factores de amplitud y fase comunes por simplicidad. La salida es polarizado circularmente a la derecha. | |||
Si bien la multiplicación de matrices no es conmutativa, es asociativa, por lo que una cadena de múltiples matrices de Jones que representan varios dispositivos se puede multiplicar para obtener una sola matriz de Jones que describe el sistema óptico en su conjunto. Por lo tanto, es posible condensar las propiedades de N dispositivos ópticos que actúan en serie hasta una sola matriz simplemente multiplicando las matrices de Jones de los dispositivos: | |||
[[Archivo:Matones.PNG|center]] | |||
==Cómo funcionan las gafas 3-D== | |||
Visualización en 3-D | |||
En una sala de cine, la razón por la que usas gafas 3-D es para introducir diferentes imágenes en tus ojos como lo hace un View-Master. En realidad, la pantalla muestra dos imágenes y las gafas hacen que una de las imágenes entre en un ojo y la otra en el otro. Hay dos sistemas comunes para hacer esto: | |||
Rojo / Verde o Rojo / Azul | |||
Aunque el sistema rojo / verde o rojo / azul ahora se usa principalmente para efectos de televisión en 3D, y se usó en muchas películas antiguas en 3D. En este sistema, se muestran dos imágenes en la pantalla, una en rojo y la otra en azul (o verde). Los filtros en las gafas permiten que solo una imagen entre en cada ojo, y su cerebro hace el resto. Realmente no puede tener una película en color cuando está usando el color para proporcionar la separación, por lo que la calidad de la imagen no es tan buena como con el sistema polarizado. | |||
Polarización | |||
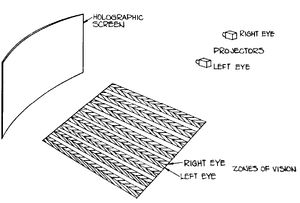
En Disney World , Universal Studios y otros lugares tridimensionales, el método preferido utiliza lentes polarizados porque permiten la visualización del color. Dos proyectores sincronizados proyectan dos vistas respectivas en la pantalla, cada una con una polarización diferente. Las gafas permiten solo una de las imágenes en cada ojo porque contienen lentes con polarización diferente. | |||
Como se había dicho anteriormente un filtro polarizador tiene pequeñas líneas paralelas grabadas en él, un poco como las lamas de un conjunto de persianas venecianas. Esto significa que solo permitirá que la luz vibre en un plano particular a través. | |||
Al igual que en el antiguo estilo 3D, la película se graba utilizando dos lentes de cámara, sentados uno al lado del otro. Pero en el cine, los dos carretes de película se proyectan a través de diferentes filtros polarizados. Así que las imágenes destinadas a los ojos izquierdos de los espectadores están polarizadas en un plano horizontal, mientras que las imágenes destinadas a sus ojos derechos están polarizadas en un plano vertical. Las gafas de los espectadores de cine usan los mismos filtros polarizadores para separar las dos imágenes nuevamente, dando a cada ojo una perspectiva ligeramente diferente y engañando al cerebro para que "vea" el planeta Pandora de Avatar. | |||
[[Archivo:Avatar.PNG|center]] | |||
En un par de gafas digitales 3D, cada lente está polarizada de manera diferente. En algunas gafas, hay una diferencia de 90 grados en la polarización. Otros utilizan diferentes alineaciones de polarización circular. La pantalla está especialmente diseñada para mantener la polarización correcta cuando la luz de los proyectores rebota en ella. En lugar de verse como una malla de rojo y verde, las películas que usan esta tecnología parecen normales, pero borrosas, cuando se ven sin gafas. | |||
[[Archivo:Lentes polarizados.PNG|center]] | |||
==Referencia== | |||
"Óptica.". E. Hecht, A. Zajac. Ed. Addison Wesley, 2000 | |||
"Luz Polarizada". WILLIAM A. SHURCLIFF. Ed.Reverté Mexicana, 1968 | |||
"Polarized Light:Production and Use". W.A. SHURCLIFF, Harvard University Press,1962. | |||
E. Collett, Field Guide to Polarization, SPIE Press, Bellingham, WA (2005). | |||
[[Usuario:Luis Chávez|Luis Manuel Chávez Antonio]] | [[Usuario:Luis Chávez|Luis Manuel Chávez Antonio]] | ||
---- | ---- | ||
==Ondas | |||
=Ondas Electromagnéticas en medios conductores y no conductores= | |||
Una de las consecuencias mas importantes de las ecuaciones de Maxwell es la deducción de las ecuaciones de propagación de ondas electromagnéticas en un medio ó en el vacío. Entonces partiremos de éstas para derivar las ecuaciones de las ondas electromagnéticas tanto para el campo eléctrico $\vec{\textbf{E}}$ como para el campo magnético $\vec{\textbf{B}}$. A continuación se escriben las ecuaciones de Maxwell en ausencia de fuentes $\rho$=0, y $\vec{\textbf{J}}$ como respuesta de medios conductores. | |||
\begin{center}\textbf{Ecuaciones de Maxwell} \end{center} | |||
<math>\mathbf{\nabla} \cdot \mathbf E = \mathbf 0........(1)</math>: | |||
<math>\mathbf{\nabla} \cdot \mathbf B = \mathbf 0.........(2)</math>: | |||
<math>\mathbf{\nabla} \times \mathbf E = - \frac{\partial \mathbf B}{\partial t}...........(3)</math>: | |||
<math>\mathbf{\nabla} \times \mathbf H = \vec{\textbf{J}} + \frac{\partial\vec{\textbf{D}}}{\partial{t}}.........(4)</math> | |||
:Con $\vec{\textbf{D}}$ y $\vec{\textbf{H}}$ la intensidad del campo eléctrico y magnético, respectivamente. | |||
Los campos que cumplen las ecuaciones anteriores también cumplen con ecuaciones constitutivas que cambian dependiendo para que medio se aplican. Para este caso sólo consideraremos medios lineales, isótropicos, homogeneos y no dispersivos, los cuales se ajustan a las siguientes ecuaciones constitutivas | |||
:<math>\vec{\textbf{D}}=\varepsilon \vec{\textbf{E}}.........(5)</math> | |||
:<math>\vec{\textbf{H}}=\frac{\vec{\textbf{B}}}{\mu}.......(6)</math> | |||
:Ahora se podrán derivar las ecuaciones de onda correspondientes al campo eléctrico y magnético. Si aplicamos el rotor a la ecuación (4), obtendremos: | |||
:<math>\nabla \times (\nabla \times \vec{\textbf{H}})= \nabla \times \vec{\textbf{J}} + \nabla \times (\frac{\partial\vec{\textbf{D}}}{\partial{t}}).....(7)</math> | |||
:Pero como $\vec{\textbf{J}}$ es respuesta del medio entonces: | |||
<math>\vec{\textbf{J}}=\sigma\vec{\textbf{E}}........(8)</math> | |||
:Que es la ley de Ohm para medios lineales. Entonces la ecuación (7) queda como: | |||
<math>\nabla \times (\nabla \times \vec{\textbf{H}})= \sigma\nabla \times \vec{\textbf{E}} + \nabla \times (\frac{\partial\vec{\textbf{D}}}{\partial{t}})</math>.......(9) | |||
Aprovechando la identidad vectorial: | |||
<math>\nabla \times (\nabla \times \vec{\textbf{A}})= \nabla \cdot (\nabla \cdot \vec{\textbf{A}}) - | |||
{\nabla}^{2}\vec{\textbf{A}}</math> | |||
y la ecuación (5) llegamos a la siguiente ecuación: | |||
<math>\nabla \cdot (\nabla \cdot \vec{\textbf{H}})= {\nabla}^{2}\vec{\textbf{H}} + \sigma\nabla \times \vec{\textbf{E}} + \varepsilon \frac{\partial}{\partial{t}} \nabla \times \vec{\textbf{E}}.....(10)</math> | |||
De las ecuaciones (2) y (3) se sigue que de la ecuación (10) sólo queda: | |||
<math>{\nabla}^{2}\vec{\textbf{H}}= \sigma\mu\frac{\partial}{\partial{t}}\vec{\textbf{H}} + \varepsilon\mu\frac{{\partial}^{2}}{\partial{{t}^{2}}}\vec{\textbf{H}}.........(11)</math> | |||
:Entonces la ecuación de onda para $\vec{\textbf{H}}$ queda de la siguiente manera: | |||
<math>{\nabla}^{2}\vec{\textbf{H}}(\vec{\textbf{r}},t) - \sigma\mu\frac{\partial}{\partial{t}}\vec{\textbf{H}}(\vec{\textbf{r}},t) - \varepsilon\mu\frac{{\partial}^{2}}{\partial{{t}^{2}}}\vec{\textbf{H}}(\vec{\textbf{r}},t) = 0......(12)</math> | |||
:Análogamente para la ecuación de onda de $\vec{\textbf{E}}$ pero esta vez aplicando el rotor a la ecuación (3), y siguiendo los pasos que se describieron arriba, llegaríamos a: | |||
<math>{\nabla}^{2}\vec{\textbf{E}}(\vec{\textbf{r}},t) - \sigma\mu\frac{\partial}{\partial{t}}\vec{\textbf{E}}(\vec{\textbf{r}},t) - \varepsilon\mu\frac{{\partial}^{2}}{\partial{{t}^{2}}}\vec{\textbf{E}}(\vec{\textbf{r}},t) = 0....(13)</math> | |||
\begin{center}\textbf{Ondas Electromagnéticas Monocromáticas} \end{center} | |||
Las ondas electromagnéticas son soluciones de las ecuaciones (12) y (13). Para este caso vamos a considerar sólo ondas electromagnéticas monocromáticas, esto quiere decir que estas ondas sólo poseen una frecuencia.\\ | |||
Podemos suponer una dependencia temporal armónica en la solución a (12): | |||
<math>\vec{\textbf{E}}(\vec{\textbf{r}},t)= \vec{\textbf{E}}_w(\vec{\textbf{r}})e^{-i{\omega}t}......(14)</math> | |||
Siempre teniendo en cuenta que la parte real de $\vec{\textbf{E}}(\vec{\textbf{r}},t)$ tendrá significado físico. Si sustituimos (14) en (12): | |||
<math>\frac{\partial}{\partial{t}}\vec{\textbf{E}}(\vec{\textbf{r}},t)= -iw\vec{\textbf{E}}_w(\vec{\textbf{r}})e^{-iwt}= -i\omega\vec{\textbf{E}}(\vec{\textbf{r}},t) ----> \frac{\partial}{\partial{t}}= -i\omega ; \frac{{\partial}^{2}}{\partial{t}^{2}}= (-i\omega)^{2}= {-\omega}^{2}</math>, Por lo tanto: | |||
<math>e^{i{\omega}t}{\nabla}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + e^{i{\omega}t}\varepsilon\mu{\omega}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + e^{i{\omega}t}i\sigma\mu\omega\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})=0</math> | |||
Entonces (12) queda como: | |||
<math>{\nabla}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + \varepsilon\mu{\omega}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + i\sigma\mu\omega\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})=0........(15)</math> | |||
:Similarmente para $\vec{\textbf{H}}(\vec{\textbf{r}},t)$, tenemos: | |||
<math>\vec{\textbf{H}}(\vec{\textbf{r}},t)= \vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})e^{-i{\omega}t}.......(16)</math> | |||
:<math>{\nabla}^{2}\vec{\textbf{H}}_{\omega}(\vec{\textbf{r}}) + \varepsilon\mu{\omega}^{2} \vec{\textbf{H}}_{\omega}(\vec{\textbf{r}}) + i\sigma\mu\omega \vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})= 0........(17)</math> | |||
Ambas soluciones deben satisfacer las ecuaciones de Maxwell: | |||
<math>\nabla \cdot \vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})= 0</math>: | |||
<math>\nabla \cdot \vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})=0</math> | |||
:<math>e^{-i{\omega}t}\nabla \times \vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})= i\mu\omega\vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})e^{-i{\omega}t}</math> -----> <math>\nabla \times \vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})= i\mu\omega\vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})</math> | |||
:Y: | |||
<math>e^{-i{\omega}t}\nabla \times \vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})= \sigma\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})e^{-i{\omega}t} - i\varepsilon\omega\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})e^{-i{\omega}t} ----> \nabla \times \vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})= -i\omega(\varepsilon + i\sigma/{\omega})\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})</math> | |||
:Ó para mayor comodidad podemos escribir la última ecuación como: | |||
<math>\nabla \times \vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})= -i\epsilon\omega\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) ------> \epsilon= \varepsilon + i\sigma/{\omega}</math> | |||
: | |||
: | |||
\begin{center}\textbf{Condiciones de frontera para los campos} \end{center}: | |||
:Para continuar es necesario establecer las condiciones de frontera que deberan obedecer las ondas electromagnéticas al pasar de un medio a otro. | |||
: | |||
[[File:Condiciones de frontera radiación.png|Condiciones de frontera radiación]] | |||
: | |||
: | |||
Considerando la figura 1, y utilizando la ecuación (2): | |||
<math>\nabla \cdot \vec{\textbf{B}} = 0 ---> B_{1n}=B_{2n}</math>: | |||
Esto quiere decir que la componente normal de la inducción magnética no cambia al pasar de un medio a otro. Utilizando la ecuación (3): | |||
:<math>\nabla \times \vec{\textbf{E}} = -\frac{\partial\vec{\textbf{B}}}{\partial{t}} ----> \oint_c\vec{\textbf{E}} \cdot \vec{\textbf{dl}}= - \int_s\frac{\partial\vec{\textbf{B}}}{\partial{t}} \cdot \hat{\textbf{n}}da</math>: | |||
: | |||
En el último paso se utilizó el teorema de Stokes para pasar de una formulación diferencial a una integral de la ecuación (3). | |||
:Si $\frac{\partial\vec{\textbf{B}}}{\partial{t}}$ es finita, su flujo tiende a ser 0 para cuando $\textbf{h}$--->0 y entonces: | |||
:<math>\oint_c\vec{\textbf{E}} \cdot \vec{\textbf{dl}}=0 \longrightarrow E_{it}=E_{2t}</math> | |||
:Lo que se interpreta como que en la superficie de separación la componente tangencial del campo eléctrico no cambia. | |||
:\begin{center}\textbf{Ondas planas en medios no conductores} \end{center}: | |||
: | |||
:Para medios no conductores podemos hacer $\sigma=0$ en la ecuación (15): | |||
:<math>{\nabla}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + \varepsilon\mu{\omega}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})=0----(18)</math> | |||
:(18) es la ecuación de Helmholtz vectorial. Proponemos una solución para (18) de tal forma que tenga amplitud compleja: | |||
:<math>\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})= \vec{\textbf{E}}_{0}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}------(19)</math> | |||
:$\vec{\kappa}$ es el vector de propagación de la onda, cuyas componentes [$\kappa_{x},\kappa_{y},\kappa_{z}$] están por determinar. | |||
:Ahora sustituimos (19) en (18): | |||
: | |||
: | |||
:<math>{\nabla}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})= {\nabla}^{2}\vec{\textbf{E}}_{0}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}= \vec{\textbf{E}}_{0}{\nabla}^{2}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}</math> | |||
:Pero ${\nabla}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}= i\vec{\kappa}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}$ ; por lo que podemos identificar :${\nabla}= i\vec{\kappa}$ ; \therefore ${\nabla}^{2}=(i\vec{\kappa}) \cdot (i\vec{\kappa})= -\kappa^{2}$. Por lo que (18) que como sigue: | |||
:<math>-\kappa^{2}\vec{\textbf{E}}_{0}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}} + \varepsilon\mu{\omega}^{2}\vec{\textbf{E}}_{0}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}=0</math> ó: | |||
:<math>\vec{\textbf{E}}_{0}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}( -\kappa^{2} + \varepsilon\mu{\omega}^{2})=0</math> ----(20) | |||
: | |||
:Como $\vec{\textbf{E}}_{0}$ no puede ser 0, entonces encontramos una relación de dispersión para $\kappa$, por lo que $\kappa= \kappa(\omega)$: | |||
:<math>-\kappa^{2} + \varepsilon\mu{\omega}^{2}= 0 \longrightarrow \kappa= (\mu\varepsilon)^{1/2}\omega-----(21)</math> | |||
Para medios lineales, homogéneos, isótropos y no dispersivos: | |||
:<math>\varepsilon\neq \varepsilon(\omega), \mu\neq \mu(\omega)</math> | |||
:También supondremos medios no magnéticos: | |||
:<math>\mu= \mu_{0}</math> | |||
: | |||
:Para el medio no conductor, establecemos la relación entre la permitividad de éste y su constante dieléctrica cómo: | |||
:<math>\varepsilon= k\varepsilon_{0}-----(22)</math> | |||
:Con k la constante dieléctrica del medio no conductor. Sustituyendo (22) en (21): | |||
:<math>\kappa= (k\varepsilon_{0}\mu_{0})^{1/2}\omega</math>: | |||
:Tomando en cuenta que $c= \frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}}$ es la velocidad de la luz en el vacío, podemos escribir la relación anterior en terminos de c: | |||
:<math>\kappa= \sqrt{k}(\frac{\omega}{c})-----(23)</math> | |||
:De aquí se define el índice de refracción de un medio: | |||
:<math>n= \sqrt{k}-----(24)</math>: | |||
Por lo tanto (23) se convierte en: | |||
:<math>\kappa= n\frac{\omega}{c}-------(25)</math> | |||
:Retomando la propuesta de (14) como solución a la ecuación de onda completa, y sustituyendo (19) en (14): | |||
:<math>\vec{\textbf{E}}(\vec{\textbf{r}},t)= \vec{\textbf{E}}_{0}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}e^{-i{\omega}t}</math> | |||
:Entonces, | |||
:<math>\vec{\textbf{E}}(\vec{\textbf{r}},t)= \vec{\textbf{E}}_{0}e^{i(\vec{\kappa} \cdot \vec{\textbf{r}} - {\omega}t)}-------(26)</math> | |||
:De igual manera para (16): | |||
:<math>\vec{\textbf{H}}(\vec{\textbf{r}},t)= \vec{H_{0}}e^{i(\vec{\kappa} \cdot \vec{\textbf{r}} - {\omega}t)}----(27)</math> | |||
: | |||
: | |||
:Si el vector de propagación $\vec{\kappa}$ lo escribimos como $ \vec{\kappa}= \kappa\hat{u}$, donde $\hat{u}$ es el vector unitario en la misma dirección que $\vec{\kappa}$, entonces podemos escribir a $\vec{\kappa} \cdot \vec{\textbf{r}}$ como: | |||
:<math>\vec{\kappa} \cdot \vec{\textbf{r}}= \kappa\hat{u} \cdot \vec{\textbf{r}}= \kappa\xi</math> | |||
Siendo $\xi$ la proyección de $\vec{\textbf{r}}$ en la dirección de $\vec{\kappa}$. Con esto (26) se escribiría como: | |||
:<math>\vec{\textbf{E}}(\vec{\textbf{r}},t)= \vec{\textbf{E}}_{0}e^{i(\kappa\xi - \omega{t})}= \vec{\textbf{E}}_{0}e^{i\kappa(\xi- \frac{\omega}{\kappa}{t})}-------(28)</math> | |||
: | |||
:(28) es de la forma $f= f(x- vt)$ siendo v la velocidad a la que se propaga la onda. Entonces tanto $\vec{\textbf{E}}(\vec{\textbf{r}},t)= \vec{\textbf{E}}_{0}e^{i(\vec{\kappa} \cdot \vec{\textbf{r}} - {\omega}t)}$ como $\vec{\textbf{H}}(\vec{\textbf{r}},t)= \vec{H_{0}}e^{i(\vec{\kappa} \cdot \vec{\textbf{r}} - {\omega}t)}$ representan una onda que se propaga en la dirección $\vec{\kappa}$, con velocidad $\frac{\omega}{\kappa}$. | |||
:\begin{center}\textbf{Relación entre campos} \end{center} | |||
:Para encontrar la relación entre los campos, tomaremos la parte espacia de (26) y (27): | |||
:<math>\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})= \vec{\textbf{E}}_{0}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}</math> | |||
:Igualmente para $\vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})$: | |||
:<math>\vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})= \vec{\textbf{H}}_{0}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}</math> | |||
:De la ecuación (1), tenemos: | |||
:<math>i\vec{\kappa} \cdot \vec{\textbf{E}}_{0}= \longrightarrow \vec{\kappa}\perp\vec{\textbf{E}}_{0}-------(29)</math> | |||
:De igual manera, de la ecuación (2): | |||
:<math>\vec{\kappa} \cdot \vec{\textbf{H}}_{0}= 0 \longrightarrow \vec{\kappa}\perp\vec{\textbf{H}}_{0}---------(30)</math> | |||
:y, de la ecuación (3) vemos que también $\vec{\textbf{H}}_{0}$ es perpendicular a $\vec{\textbf{E}}_{0}$: | |||
:<math>\nabla \times \vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})= i\mu_{0}\omega\vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})= i\vec{\kappa} \times \vec{\textbf{E}}_{0}= i\mu_{0}\omega\vec{\textbf{H}}_{0}</math> | |||
:Entonces la relación anterior queda como: | |||
:<math>\vec{\textbf{H}}_{0}= \frac{1}{\mu_{0}\omega}\vec{\kappa} \times \vec{\textbf{E}}_{0}----(31)</math> | |||
:Y de la ecuación (4): | |||
:<math>\nabla \times \vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})= -i\varepsilon\omega\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})</math> | |||
:Se llega a: | |||
:<math>\vec{\textbf{E}}_{0}= -\frac{1}{\varepsilon\omega}\vec{\kappa} \times \vec{\textbf{H}}_{0}--------(32)</math> | |||
:Con lo que se concluye que en una onda electromagnética, los campos eléctricos y magnéticos son ortogonales a lo largo del camino de la onda y que éstos a su vez son ortogonales a la dirección de propagación. | |||
:\begin{center}\textbf{Propagación de ondas planas en medios conductores} \end{center} | |||
:Para el caso de medios conductores consideramos a $\sigma$ diferente de 0, medios no magnéticos($\mu= \mu_{0}$) y medios no dispersivos($\varepsilon= k\varepsilon_{0}$). Tomando la parte espacial de la ecuación de onda y las consideraciones de arriba($\sigma\neq 0, {\mu= \mu_{0}}, y {\varepsilon= k\varepsilon_{0}}$) , la ecuación (15) se reescribe como: | |||
:<math>{\nabla}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + k\varepsilon_{0}\mu_{0}{\omega}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + i\sigma\mu_{0}\omega\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})=0</math> | |||
:Con <math>\vec{\textbf{E}}(\vec{\textbf{r}},t)= \vec{\textbf{E}}_w(\vec{\textbf{r}})e^{-i{\omega}t}</math> como solución a la ecuación de onda completa. Cómo <math>c= \frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}}</math>, la ecuación de arriba se puede escribir como: | |||
:<math>{\nabla}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + (k\frac{{\omega}^{2}}{c^{2}} + i\omega\sigma\mu_{0})\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})-------(33)</math> | |||
:De (33) podemos hacer un poco de álgebra para acomodarla un poco más simple: | |||
:<math>{\nabla}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + (k + i\mu_{0}\sigma\omega\frac{c^{2}}{\omega^{2}})\frac{\omega^{2}}{c^{2}}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})=0</math> ; pero como <math>c= \frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}}</math>, entonces: | |||
:<math>{\nabla}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + (k + \frac{i\mu_{0}\sigma}{\omega\varepsilon_{0}\mu_{0}})\frac{\omega^{2}}{c^2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})=0</math> | |||
:Aquí hacemos la definición siguiente: | |||
:<math> \delta= (k + \frac{i\mu_{0}\sigma}{\sigma\varepsilon_{0}\mu_{0}})----------(34)</math> | |||
:Entonces (33) es: | |||
:<math>{\nabla}^{2}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}}) + \frac{\delta\omega^{2}}{c^{2}}\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})=0-------(35)</math> | |||
:Proponemos como solución a la ecuación (35) una relación de la forma: | |||
:<math>\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})= \vec{\textbf{E}}_{0}e^{i\vec{\textbf{k}} \cdot \vec{\textbf{r}}}------(36)</math> | |||
:Con $\vec{\textbf{k}}$ un vector de onda complejo, de la forma <math>\vec{\textbf{k}}= \vec{k}_{r} + i\vec{k}_{i}</math>. | |||
Ahora para poder sustituir (36) en (35), establecemos las mismas relaciones que para (19): | |||
:<math>\nabla= i\vec{\textbf{k}}</math> , Entonces ---> <math>\nabla^2= -\vec{\textbf{k}} \cdot \vec{\textbf{k}}</math>. | |||
:Y sustituyendo en (35): | |||
:<math>(-\vec{\textbf{k}} \cdot \vec{\textbf{k}} + \frac{\delta\omega^{2}}{c^2})\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})= 0</math> | |||
:Como $\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})$ no puede ser 0, entonces de la relación anterior obtenemos una relación de dispersión: | |||
<math>-\vec{\textbf{k}} \cdot \vec{\textbf{k}} + \frac{\delta\omega^{2}}{c^2}= 0------(37)</math> | |||
:Por lo tanto siguiendo los mismos pasos que cuando no había medios conductores: | |||
:<math> | |||
\mid\vec{\textbf{k}}\mid= \frac{\omega}{c}(\sqrt{\delta})-------(38)</math> | |||
:De igual forma que cuando no había medio conductor, se define: | |||
:<math>g= \sqrt{\delta} ; g= \sqrt{k + i\frac{\sigma}{\varepsilon_0\omega}}------(39)</math> | |||
:Siendo g un número complejo podemos usar el álgebra compleja para separar de g su parte real y su parte imaginaria, si hacemos <math>g= n + i\eta</math>, entonces: | |||
:<math>g^2= (n^2 - \eta^2) + 2in\eta-------(40)</math> | |||
:Igualando (40) con el cuadrado de (39): | |||
:<math>(n^2 - \eta^2) + 2in\eta= k + i\frac{\sigma}{\varepsilon_{0}\omega}----(41)</math> | |||
:Igualando las partes reales e imaginarias de la ecuación (41): | |||
:<math>(n^2 - \eta^2)= k---(42)</math> | |||
:Para la parte real y para la parte imaginaria: | |||
:<math>2n\eta= \frac{\sigma}{\varepsilon_{0}\omega}----(43)</math> | |||
:Podemos despejar de (43) a "eta" y sustituirla en (42), lo que nos va a llevar a una ecuación de grado cuarto para n, por lo que usando la fórmula general para encontrar soluciones de segundo grado podremos encontrar una solución para n^{2}: | |||
:<math>n^{2} - \frac{\sigma^{2}}{4\varepsilon_{0}^{2}\omega^{2}n^{2}}= k------(44)</math> | |||
:Multiplicando a (44) por n^2: | |||
:<math>({n^{2}})^{2} - \frac{\sigma^2}{4\varepsilon_{0}^{2}\omega^{2}}- kn^2=0-------(45)</math> | |||
:Usando la formula general de segundo grado para resolver (45) con <math>x= n^{2}</math>, da como solución: | |||
:<math>n^{2}= \frac{k}{2} \pm 1/2\sqrt{k^{2} + \frac{\sigma^2}{\varepsilon_{0}^2\omega^2}}</math> | |||
:En la ultima relación de arriba sólo vamos a tomar el signo positivo porque la $n$ tiene que ver con índices ópticos que por lo general sólo son positivos: | |||
:<math>n^{2}= \frac{k}{2} + 1/2\sqrt{k^{2} + \frac{\sigma^2}{\varepsilon_{0}^2\omega^2}}</math> | |||
:Usando el mismo procedimiento para encontrar $eta^2$: | |||
:<math>\eta^{2}= -\frac{k}{2} + 1/2\sqrt{k^{2} + \frac{\sigma^2}{\varepsilon_{0}^2\omega^2}}</math> | |||
:Sacando raíz cuadrada a las dos ultimas relaciones de arriba, encontramos a $n$ y $\eta$: | |||
:<math>n= \sqrt{\frac{k}{2} + 1/2\sqrt{k^{2} + \frac{\sigma^2}{\varepsilon_{0}^2\omega^2}}}-----(46)</math> | |||
:<math>\eta= \sqrt{-\frac{k}{2} + 1/2\sqrt{k^{2} + \frac{\sigma^2}{\varepsilon_{0}^2\omega^2}}}-------(47)</math> | |||
:Por lo tanto de (38) y (39), con <math>g= n + i\eta</math>: | |||
:<math>\mid\vec{\textbf{k}}\mid= \sqrt{\delta}(\frac{\omega}{c})= (n + i\eta)(\frac{\omega}{c})= \mid\vec{k}_{r}\mid + i\mid\vec{k}_{i}\mid-------(48)</math> | |||
:Igualando la parte real e imaginaria: | |||
:<math>\mid\vec{k}_{r}\mid= \frac{n\omega}{c} </math> y, <math>\mid\vec{k}_{i}\mid= \frac{\eta\omega}{c}</math>---------(49) | |||
:Al valor de $\mid\vec{k}_{i}\mid$ es a lo que en la literatura se le conoce como constante de atenuación ó efecto piel. | |||
:Retomando la solución completa espacial-temporal $\vec{\textbf{E}}(\vec{\textbf{r}},t)$: | |||
:<math>\vec{\textbf{E}}(\vec{\textbf{r}},t)= \vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})e^{i{\omega}t}</math> | |||
:Pero <math>\vec{\textbf{E}}_{\omega}= \vec{\textbf{E}}_{0}e^{i\vec{\textbf{k}} \cdot \vec{\textbf{r}}}</math> con <math>\vec{\textbf{k}}= \vec{k}_{r} + i\vec{k}_{i}</math> una cantidad compleja. Por lo que la solución $\vec{\textbf{E}}(\vec{\textbf{r}},t)$ se escribe como: | |||
<math>\vec{\textbf{E}}(\vec{\textbf{r}},t)= \vec{E_{0}}e^{-\vec{k}_{i} \cdot \vec{\textbf{r}}}e^{i(\vec{k}_{r} \cdot \vec{\textbf{r}} - \omega{t})}--------(50)</math> | |||
:Entonces $\vec{\textbf{E}}(\vec{\textbf{r}},t)$ es una onda plana que se propaga en dirección de $\vec{k}_{r}$ pero con amplitud decreciente en la dirección de $\vec{k}_{i}$ | |||
:\begin{center}\textbf{Ecuaciones de Fresnel para medios conductores} \end{center} | |||
De la ecuación (39) y en analogía con (24), podemos definir a (39) como el índice de refracción del medio conductor. Éste es un número complejo que tiene que ver con la conductividad del conductor. Por lo tanto podemos considerar para el caso dieléctrico-conductor a las mismas ecuaciones de Fresnel que se derivan para dieléctrico-dieléctrico (ver capitulo 18, sección 2 de Reitz & Milford, fundamentos de la teoría electromagnética, cuarta edición) pero con índice de refracción del segundo medio complejo. Entonces de estas ecuaciones (dieléctrico-dieléctrico) que son: | |||
Para polarización del campo eléctrico perpendicular al plano de incidencia: | |||
:$\textbf{r}_{s}= \frac{n_{1}cos\theta_{1} - n_{2}cos\theta_{2}}{n_{1}cos\theta_{1} + n_{2}cos\theta_{2}}$----------(51) | |||
:$\textbf{t}_{s}= \frac{2n_{1}cos\theta_{1}}{n_{1}cos\theta_{1} + n_{2}cos\theta_{2}}$---------(52) | |||
:$\textbf{r}_{s}$ y $\textbf{t}_{s}$ son los coeficientes de fresnel para la onda reflejante y transmitida, respectivamente y $n_{1}$ el índice de refracción del medio 1, y $\theta_{1}$ el ángulo que hace el vector de propagación con la normal a la interfaz entre los dos medios. | |||
Para polarización del campo eléctrico polarizado paralelamente al plano de incidencia: | |||
:$\textbf{r}_{p}= \frac{n_{2}cos\theta_{1} - n_{1}cos\theta{2}}{n_{2}cos\theta_{1} + n_{1}cos\theta_{2}}$-------------(53) | |||
:$\textbf{t}_{p}= \frac{2n_{1}cos\theta{1}}{n_{2}cos\theta_{1} + n_{1}cos\theta_{2}}$-------------------(54) | |||
:Para dieléctrico-conductor por lo tanto, proponemos: | |||
:$\textbf{r´}_{s}= \frac{n_{1}cos\theta_{1} - gcos\gamma}{n_{1}cos\theta_{1} + gcos\gamma}$--------------(55) | |||
:$\textbf{t´}_{s}= \frac{2n_{1}cos\theta_{1}}{n_{1}cos\theta_{1} + gcos\gamma}$-----------------(56) | |||
:$\textbf{r´}_{p}= \frac{gcos\theta_{1} - n_{1}cos\gamma}{gcos\theta_{1} + n_{1}cos\gamma}$-------------(57) | |||
:$\textbf{t´}_{p}= \frac{2n_{1}cos\theta{1}}{gcos\theta_{1} + n_{1}cos\gamma}$----------------(58) | |||
:Con $"g"$ como se definió en (39) y $cos\gamma$ otro número complejo para considerar el caso mas general. Así $gcos\gamma$ es un número complejo. Haciendo $gcos\gamma= \alpha + i\xi$ y elevando al cuadrado ambos miembros: | |||
:$g^{2}cos^{2}\gamma= \alpha^{2} - \xi^{2} + 2i\alpha\xi$ ; $g= \sqrt{k + i\frac{\sigma}{\varepsilon_{0}\omega}}$ | |||
:Por lo tanto: | |||
:$(k + i\frac{\sigma}{\varepsilon_{0}\omega})(1 - sen^{2}\gamma)= \alpha^{2} - \xi^{2} + 2i\alpha\xi$------------(59) | |||
:Si se cumple la ley de Snell para este caso $n_{1}cos\theta_{1}= gsen\gamma$ entonces de (59) igualando parte real e imaginaria obtenemos: | |||
$k + n_{1}^{2}sen^{2}\gamma= \alpha^{2} - \xi^{2}$ y; $ \frac{\sigma}{\varepsilon_{0}\omega}= \alpha\xi$-----------(60) | |||
:Entonces de (60) se sigue que $\alpha= \sqrt{\xi^{2} +k + n_{1}^{2}sen^{2}\gamma}$ y sustituyendo $\alpha$ en la otra ecuación, tenemos: | |||
:$\xi^{4} + \xi^{2}(k - n_{1}^{2}sen^{2}\theta_{1}) - \frac{\sigma^{2}}{\varepsilon^{2}\omega^{2}}$--------------(61) | |||
:Resolviendo a (61) para $\xi^{2}$ por la fórmula general tenemos que $\xi$ es: | |||
:$\xi= \sqrt{-\frac{1}{2}(k - n_{1}sen^{2}\theta) + \frac{1}{2}\sqrt{(k^{2} - n_{1}^{2}sen^{2}\theta_{1})^{2} + (\frac{2\sigma}{\varepsilon\omega})^{2}}}$--------------------(62) | |||
:Siguiendo el mismo procedimiento para encontrar a $\alpha$ obtenemos que: | |||
:$\alpha= \sqrt{\frac{1}{2}(k + n_{1}^{2}sen^{2}\theta_{1} + \sqrt{(-k -n_{1}^{2}sen^{2}\theta_{1})^{2} - (\frac{2\sigma}{\varepsilon_{0}\omega})^{2}})}$-------------------(63) | |||
:Por lo tanto despejando y sustituyendo $gcos\gamma= \alpha + i\xi$ con $\alpha$ y $\xi$ definidos como en (62) y (63) se obtendrían los nuevos coeficientes de Fresnel complejos para las ondas transmitidas y reflejadas del campo eléctrico. Así las amplitudes del campo eléctrico polarizado perpendicularmente son: | |||
:$\vec{{E}_{0 rs}}(\vec{r})= {r´}_{s}\vec{E}_{0}-------------(64)$ | |||
:$\vec{E}_{0 ts}(\vec{r})= {t´}_{s}\vec{E}_{0}------------------(65)$ | |||
:Y para las amplitudes del campo eléctrico polarizado paralelamente: | |||
:$\vec{E}_{0 rp}(\vec{r})= {r´}_{p}\vec{E}_{0}-------------(66)$ | |||
:$\vec{E}_{0 tp}(\vec{r})= {t´}_{p}\vec{E}_{0}----------------(67)$ | |||
:Con $\vec{E}_{0 r}(\vec{r})$ y $\vec{E}_{0 t}(\vec{r})$ la amplitud reflejada y transmitida respectivamente. | |||
==Referencias== | |||
:Introduction To Electrodynamics -Griffiths | |||
:Foundations Of Electromagnetic Theory - Reitz & Milford | |||
[[Usuario:Pedro J. Julián]] | |||
---- | |||
= Esparcimiento Estático de Luz (SLS) = | |||
== Introducción == | |||
El esparcimiento electromagnético es un fenómeno que se da cuando un campo incidente interactúa con la materia. Esta interacción se da a escalas similares a las de la longitud de onda incidente. | |||
Debido a la heterogeneidad de la materia a esa escala, la luz se esparcirá en direcciones distintas a las consideradas por la reflexión y la refracción. | |||
Si consideramos la naturaleza molecular de los materiales con los que interactúa la luz, entonces debemos tomar en cuenta que están presentes cargas negativas y positivas en su misma constitución aunque, en promedio, la mayoría de los cuerpos son neutros. | |||
Tratando a la luz como una onda electromagnética debemos observar que las cargas presentes en la estructura interna de los cuerpos pueden y tendrán una interacción real con el campo luminoso. Para fines prácticos podemos considerar que la componente magnética del campo que genera a la luz es despreciable debido a que las fuerzas (fuerzas de Lorentz) que ocasiona este son muy pequeñas comparadas con las fuerzas eléctricas (fuerzas de Coulomb) provocadas por la misma luz. Esto debido a que la fuerza magnética es | |||
<math display="block">\label{eq:fuerza_lorentz} | |||
\mathbf{F}_m = q\mathbf{v} \times \mathbf{B}</math> | |||
donde <math display="inline">\mathbf{v}</math> es la velocidad a la que se mueve la carga, que en este caso al estar ligada a la estructura atómica será, en magnitud, mucho menor que <math display="inline">c</math> (<math display="inline">v<<c</math>) y entonces la fuerza magnética será muy pequeña. Por otro lado al considerar la fuerza eléctrica | |||
<math display="block">\label{eq:fuerza_coulomb} | |||
\mathbf{F}_e = q\mathbf{E}</math> | |||
vemos que la fuerza generada por el campo eléctrico es directamente proporcional al mismo y cuya constante de proporcionalidad es la carga. Es por ello que en este tratamiento supondremos que la luz está compuesta únicamente por campos eléctricos. | |||
Ahora bien, la interacción del campo eléctrico de la luz con los componentes del material donde incide puede observarse de manera somera en la figura [[#fig:campodipolo|[fig:campodipolo]]]. | |||
[[File:campodipolo.png|frame|none|alt=|caption Interacción del campo eléctrico de la luz con una partícula induciendo un dipolo.<span label="fig:campodipolo"></span>]] | |||
Sabemos que la interacción del campo eléctrico con una partícula cargada es tal que tiende a alejarla o a acercarla dependiendo su naturaleza (signo). Como el campo es oscilatorio tendrá el efecto de <span>''acercar hacia él''</span> un tipo de carga a un tiempo <math display="inline">t</math> y a alejar al mismo tipo de carga a un tiempo <math display="inline">t+\lambda/(2c)</math>, es decir, cuando haya pasado media longitud de onda. | |||
Esta interacción del campo con las cargas genera un dipolo eléctrico temporal (inducido). Sabemos que no está presente de manera permanente en el material sino que es generado por la acción del campo eléctrico incidente. | |||
Un dipolo eléctrico está compuesto de dos cargas de igual magnitud pero de signo contrario que se encuentran separadas por una distancia <math display="inline">d</math>. Si se toma el vector <math display="inline">\mathbf{d}</math> como una cantidad vectorial que va de la carga positiva a la negativa y cuya longitud es la separación entre las cargas (<math display="inline">d</math>), entonces se define el momento dipolar eléctrico como | |||
<math display="block">\label{eq:momento_dipolar_electrico} | |||
\mathbf{p} = q \cdot \mathbf{d}</math> | |||
Una cantidad que relaciona al campo eléctrico y al momento dipolar es la <span>'''polarizabilidad'''</span> eléctrica que se define como | |||
<math display="block">\label{eq:polarizabilidad_electrica} | |||
\alpha = \dfrac{p}{E}</math> | |||
Lo que nos dice la proporción entre la magnitud del dipolo eléctrico inducido y el campo eléctrico que lo generó. De manera intuitiva, la polarizabilidad puede entenderse como la tendencia de una distribución de cargas a ser modificada en su configuración por un campo eléctrico externo. | |||
En el caso en el que el dipolo es dependiente del tiempo, como en este caso, suele escribirse como | |||
<math display="block">\label{eq:momento_dipolar_m} | |||
\mu = \mu_0 \cos(\omega t - kx)</math> | |||
con <math display="inline">\mu_0 = qd</math>. Entonces podemos escribir a la polarizabilidad como | |||
<math display="block">\label{eq:polarizabilidad_m} | |||
\alpha = \dfrac{\mu}{E}</math> | |||
y con ello | |||
<math display="block">\mu = \mu (t) = \alpha E = E_0 \cos (\omega t - kz) = \mu_0 \cos (\omega t - kz)</math> | |||
== Esparcimiento debido a una sola molécula == | |||
Si queremos encontrar la magnitud del campo producido por la dispersión de la luz debido a una molécula a cierta distancia <math display="inline">r</math> de esta debemos considerar al dipolo inducido que irradia en cierta dirección. Para realizar esto tomamos al dipolo como un dipolo Hertziano, es decir, una corriente oscilante en una pequeña longitud. La teoría electromagnética nos dice que la radiación esparcida por una sola partícula será (figura [[#fig:scat1|[fig:scat1]]]) | |||
[[File:scat1.png|frame|none|alt=|caption Esparcimiento del campo incidente por una única molécula.<span label="fig:scat1"></span>]] | |||
<math display="block">E_{s,1} (r) = E_0 \left(\dfrac{\pi \alpha \sin \phi}{r \lambda^2}\right) \cos(\omega t - kr)</math> | |||
Sabemos que la irradiancia de un campo eléctrico está dada por | |||
<math display="block">\label{eq:irradiancia} | |||
I(r) = \left<S\right>_T = \left<\epsilon_0 c E^2\right>_T = \dfrac{1}{2}c\epsilon_0 E_0^2</math> | |||
donde <math display="inline">E_0</math> es la amplitud del campo. Por lo que la irradiancia de la luz esparcida será | |||
<math display="block">I_{s,1} (r) = \dfrac{1}{2} \epsilon_0 c E_0^2 \left(\dfrac{\pi \alpha \sin \phi}{r \lambda^2}\right)^2</math> | |||
y como la irradiancia del campo incidente es | |||
<math display="block">I_0 = \dfrac{1}{2} \epsilon_0 c E_0^2</math> | |||
entonces | |||
<math display="block">\label{eq:i_s1} | |||
I_{s,1} (r) = I_0 \dfrac{\pi^2 \alpha^2 \sin^2 \phi}{r^2 \lambda^4}</math> | |||
[[File:kq.png|frame|none|alt=|caption Esquema de la interacción del campo con la partícula.<span label="fig:kq"></span>]] | |||
Resulta conveniente definir el llamado vector de esparcimiento <math display="inline">\mathbf{q}</math>. Este es un vector que se encuentra en función del vector de onda y por lo mismo apuntará en la dirección de propagación de la luz. Si consideramos que la luz incidente tiene un vector de onda <math display="inline">\mathbf{k}_i</math> y la luz esparcida <math display="inline">\mathbf{k}_s</math> entonces el vector de esparcimiento será | |||
<math display="block">\label{eq:q} | |||
\mathbf{q} = \mathbf{k}_s - \mathbf{k}_i</math> | |||
Para obtener la longitud del vector <math display="inline">\mathbf{q}</math> utilizamos el hecho de que, si bien los vectores de las ondas incidente y esparcida son distintos, sus magnitudes son iguales y están dadas por | |||
<math display="block">\label{eq:numero_onda} | |||
k = \dfrac{2\pi}{\lambda}</math> | |||
Si la longitud de <math display="inline">q</math> es <math display="inline">2a</math> y el ángulo entre <math display="inline">\mathbf{k}_s</math> y <math display="inline">\mathbf{k}_i</math> es <math display="inline">\theta</math> podemos obtener de la figura [[#fig:kaq|[fig:kaq]]]. | |||
[[File:kaq.png|frame|none|alt=|caption Diagrama con los vectores de onda incidente y esparcido.<span label="fig:kaq"></span>]] | |||
<math display="block">\label{eq:a_distancia} | |||
a = k \sin \dfrac{\theta}{2}</math> | |||
De la longitud de <math display="inline">q</math> y las ecuaciones [[#eq:numero_onda|[eq:numero_onda]]] y [[#eq:a_distancia|[eq:a_distancia]]] llegamos a que la longitud del vector <math display="inline">q</math> es | |||
<math display="block">q = \dfrac{4\pi}{\lambda} \sin \dfrac{\theta}{2}</math> | |||
que escrito en términos de la longitud de onda del vacío es | |||
<math display="block">q = \dfrac{4\pi n}{\lambda_0} \sin \dfrac{\theta}{2}</math> | |||
== Esparcimiento de una onda por dos partículas pequeñas == | |||
En el caso de dos ondas esparcidas generadas por dos partículas distintas pero que fueron impactadas por el mismo campo incidente podemos utilizar a los campos esparcidos en su forma compleja para simplificar los cálculos. Esto es | |||
<math display="block">E_1 = E_{0,1} e^{i(\omega t - \mathbf{R} \cdot \mathbf{k}_s)} \\ | |||
E_2 = E_{0,1} e^{i(\omega t - \mathbf{R} \cdot \mathbf{k}_s) + \Delta \phi}</math> | |||
donde <math display="inline">\mathbf{R}</math> es la distancia entre la partícula y el detector. Entre los campos sólo hay una diferencia de fase <math display="inline">\Delta \phi</math> y el campo total está dado por la suma. Además en este caso | |||
<math display="block">E_{0,1} = E_0 \left(\dfrac{\pi \alpha \sin \phi}{r \lambda^2}\right)</math> | |||
entonces la irradiancia total es | |||
<math>I_T = \dfrac{1}{2} \epsilon_0 c |E|^2 </math> | |||
<math>\qquad = \dfrac{1}{2} \epsilon_0 c |E_1 + E_2|^2 </math> | |||
<math>\qquad = \dfrac{1}{2} \epsilon_0 c |E_1 + E_2| \cdot |E_1^* + E_2^*| </math> | |||
<math>\qquad = \dfrac{1}{2} \epsilon_0 c \left[E_{0,1} e^{i(\omega t - \mathbf{R} \cdot \mathbf{k}_s)} + E_{0,1} e^{i(\omega t - \mathbf{R} \cdot \mathbf{k}_s) + \Delta \phi}\right] \cdot \left[E_{0,1} e^{-i(\omega t - \mathbf{R} \cdot \mathbf{k}_s)} + E_{0,1} e^{-i(\omega t - \mathbf{R} \cdot \mathbf{k}_s) + \Delta \phi}\right]</math> | |||
<math>\qquad = \dfrac{1}{2} \epsilon_0 c E_{0,1}^2 \left[1 + e^{i\Delta \phi} + e^{-i\Delta \phi} + 1\right]</math> | |||
<math>\qquad = \dfrac{1}{2} \epsilon_0 c E_{0,1}^2 \left[2 + 2\cos \Delta \phi\right]</math> | |||
<math>\qquad = \epsilon_0 c E_{0,1}^2 \left[1 + \cos \Delta \phi\right]</math> | |||
Utilizando la expresión [[#eq:i_s1|[eq:i_s1]]] obtenemos finalmente la irradiancia total de la luz esparcida por dos partículas, que es | |||
<math display="block">I_T = 2 I_{s,1} \left[1 + \cos \Delta \phi\right]</math> | |||
== Esparcimiento de una onda por n partículas pequeñas == | |||
Tenemos ahora <math display="inline">n</math> partículas pequeñas que forman una molécula más grande como puede ser un aminoácido o un monosacárido. Denotaremos a las partículas por un subíndice <math display="inline">i</math> y tendremos <math display="inline">n</math> de ellas, es decir <math display="inline">i=1,2,3,\ldots,n</math>. Sus campos eléctricos esparcidos se denotarán con <math display="inline">E_{s,i}</math>, sus respectivas fases están dadas por <math display="inline">\phi_i</math> y el campo total dispersado estará dado por la superposición de todos ellos, a saber | |||
<math display="block">E_{s,n} = \sum_{j=1}^n E_{s,j} = \sum_{j=1}^n E_{0,1} e^{i(\omega t + \phi_j)}</math> | |||
[[File:nint.png|frame|none|alt=|caption Representación de las partículas que conforman a una molécula de mayor tamaño.<span label="fig:nint"></span>]] | |||
Siguiendo los procedimientos expuestos anteriormente, debemos ahora calcular la irradiancia total generada por todos los campos esparcidos, esto es | |||
<math>I_{s,n} = \dfrac{1}{2}\epsilon_0 c E_{s,n} E_{s,n}^*</math> | |||
<math>\qquad = \dfrac{1}{2}\epsilon_0 c \left(\sum_{j=1}^n E_{0,1} e^{i(\omega t + \phi_j)}\right) \left(\sum_{k=1}^n E_{0,1} e^{-i(\omega t + \phi_k)}\right) </math> | |||
<math>\qquad = \dfrac{1}{2}\epsilon_0 c E_{0,1}^2 \sum_{j=1}^n \sum_{k=1}^n e^{i(\omega t + \phi_j)} e^{-i(\omega t + \phi_k)} </math> | |||
<math>\qquad = \dfrac{1}{2}\epsilon_0 c E_{0,1}^2 \sum_{j=1}^n \sum_{k=1}^n e^{i(\omega t + \phi_j) -i(\omega t + \phi_k)} </math> | |||
<math>\qquad = \dfrac{1}{2}\epsilon_0 c E_{0,1}^2 \sum_{j=1}^n \sum_{k=1}^n e^{i(\phi_j - \phi_k)} </math> | |||
<math>\qquad = \dfrac{1}{2}\epsilon_0 c E_{0,1}^2 \sum_{j=1}^n \sum_{k=1}^n \left[\cos(\phi_j - \phi_k) + i \sin(\phi_j - \phi_k)\right]</math> | |||
Es claro que cuando <math display="inline">j=k</math> entonces <math display="inline">\sin(\phi_j - \phi_k) = \sin(0) = 0</math>. Luego utilizando que la función <math display="inline">\sin(-x)=-\sin(x)</math>, es decir, que el seno es una función impar, vemos que todas las contribuciones son nulas debido a que <math display="inline">\sin(\phi_j - \phi_k) = -\sin(\phi_k - \phi_j)</math>. Como ejemplo (caso particular) tomemos <math display="inline">j=2</math> y <math display="inline">k=3</math> esto contribuye con <math display="inline">\sin(\phi_2 - \phi_3)</math>; pero en el punto donde <math display="inline">j=3</math> y <math display="inline">k=2</math> tenemos <math display="inline">\sin(\phi_3 - \phi_2) = -\sin(\phi_2 - \phi_3)</math> por lo que ambas se anulan. Lo anterior nos lleva a que la irradiancia total generada por <math display="inline">n</math> partículas es | |||
<math display="block">I_{s,n} = \dfrac{1}{2}\epsilon_0 c E_{0,1}^2 \sum_{j=1}^n \sum_{k=1}^n \cos(\phi_j - \phi_k)</math> | |||
que escrita en términos de la irradiancia esparcida debida a una sóla partícula arroja | |||
<math display="block">\label{eq:isn} | |||
I_{s,n} = I_{s,1} \sum_{j=1}^n \sum_{k=1}^n \cos(\phi_j - \phi_k)</math> | |||
Ahora consideramos que la longitud de onda de la luz es mucho mayor que el tamaño de las moléculas. Es decir, si la molécula tiene un tamaño <math display="inline">d</math> y <math display="inline">k</math> es el número de onda, entonces | |||
<math display="block">\label{eq:rdga01} | |||
d \cdot k = d \dfrac{2\pi}{\lambda} \approx 0</math> | |||
Con lo anterior es razonable suponer ahora a las diferencias de fase como | |||
<math display="block">\label{eq:rdga02} | |||
|\phi_j - \phi_k| \approx 0</math> | |||
Las ecuaciones [[#eq:rdga01|[eq:rdga01]]], [[#eq:rdga02|[eq:rdga02]]] y el hecho de que consideremos al campo dispersado total como la superposición de todos los campos dispersados provenientes de cada una de las moléculas que forman el sistema en estudio constituyen la llamada <span>'''Aproximación Rayleigh-Debye-Gans'''</span> o por sus siglas en inglés <span>'''RDGA'''</span>. | |||
Retomando la expresión [[#eq:isn|[eq:isn]]] con la aproximación [[#eq:rdga02|[eq:rdga02]]] obtenemos que <math display="inline">\cos(\phi_j - \phi_k) \approx \cos(0) = 1</math> | |||
<math display="block">\label{eq:isn_app} | |||
I_{s,n} \approx n^2 I_{s,1}</math> | |||
donde <math display="inline">n</math> es el número de partículas, pero también si <math display="inline">M</math> es la masa molecular de la molécula y <math display="inline">M_1</math> es la masa molecular de una componente de la molécula | |||
<math display="block">\label{eq:n_mol} | |||
n = \dfrac{M}{M_1}</math> | |||
== Esparcimiento por partículas idénticas == | |||
Tomaremos <math display="inline">N</math> partículas idénticas en un volumen <math display="inline">V</math> como las estudiadas en la sección anterior. Utilizando un procedimiento similar al anterior calculamos la irradiancia total generada por las <math display="inline">N</math> partículas idénticas | |||
<math display="block">I_{s,T} = I_{s,n} \sum_{j=1}^N \sum_{k=1}^N \cos(\phi_j - \phi_k)</math> | |||
[[File:next.png|frame|none|alt=|caption Representación de las partículas que se encuentran dentro de un volumen <math display="inline">V</math>.<span label="fig:next"></span>]] | |||
En el caso particular del <span>'''SLS'''</span> estamos interesados en el promedio de esta cantidad | |||
<math display="block">\left<I_{s,T}\right> = I_{s,n} \sum_{j=1}^N \sum_{k=1}^N \left<\cos(\phi_j - \phi_k)\right></math> | |||
Ninguna de las partículas tiene un movimiento en una dirección preferencial ni una velocidad definida y sus movimientos son completamente independientes entre sí. Debido a los movimientos al azar de todas las partículas tenemos que si <math display="inline">k \neq j</math> | |||
<math display="block">\left<\cos(\phi_j - \phi_k)\right> = 0</math> | |||
y sólo quedará la contribución de <math display="inline">j=k</math> que será | |||
<math display="block">\left<\cos(\phi_j - \phi_k)\right> = \left<\cos(0)\right> = 1</math> | |||
con lo que la irradiancia total media para <math display="inline">N</math> moléculas idénticas compuestas por <math display="inline">n</math> elementos cada una es | |||
<math display="block">\label{eq:i_st} | |||
\left<I_{s,T}\right> = N I_{s,n}</math> | |||
Si tomamos ahora la expresión [[#eq:i_s1|[eq:i_s1]]] podemos ver que | |||
<math display="block">I_{s,1} \propto \dfrac{I_0}{r^2}</math> | |||
y si introducimos una constante de proporcionalidad | |||
<math display="block">\label{eq:k_is1} | |||
I_{s,1} = K \dfrac{I_0}{r^2}</math> | |||
con | |||
<math display="block">\label{eq:k} | |||
K \equiv \dfrac{\pi^2 \alpha^2 \sin^2 \phi}{\lambda^4}</math> | |||
Consideremos ahora la concentración molar <math display="inline">c</math> de la solución | |||
<math display="block">c = \dfrac{N}{N_A V}</math> | |||
donde <math display="inline">N_A</math> es el número de Avogadro y <math display="inline">N</math> el número de partículas contenidas en el volumen <math display="inline">V</math>, por lo que | |||
<math display="block">N = N_A \cdot V \cdot c</math> | |||
entonces con [[#eq:n_mol|[eq:n_mol]]] la ecuación [[#eq:isn_app|[eq:isn_app]]] se escribe como | |||
<math display="block">I_{s,n} \approx n^2 I_{s,1} = \dfrac{M^2}{M_1^2} I_{s,1}</math> | |||
Estas relaciones las aplicacmos nn la ecuación [[#eq:i_st|[eq:i_st]]] | |||
<math display="block">\left<I_{s,T}\right> = N I_{s,n} = N_A \cdot V \cdot c \cdot \dfrac{M^2}{M_1^2} I_{s,1}</math> | |||
Además la concentración <math display="inline">C</math> está dada por | |||
<math display="block">C = c \cdot M</math> | |||
entonces | |||
<math display="block">\left<I_{s,T}\right> = N_A \cdot V \cdot C \cdot \dfrac{M}{M_1^2} I_{s,1}</math> | |||
que con [[#eq:k_is1|[eq:k_is1]]] | |||
<math display="block">\label{eq:ist_final01} | |||
\left<I_{s,T}\right> = \dfrac{1}{r^2} KI_0VCM</math> | |||
y definiendo la proporción de Rayleigh en términos de <math display="inline">q</math> | |||
<math display="block">\label{eq:rayleigh_q} | |||
R(q) \equiv \dfrac{I_{s,T}(q) r^2}{I_0 V(q)}</math> | |||
vemos que podemos escribir a [[#eq:ist_final01|[eq:ist_final01]]] como | |||
<math display="block">\label{eq:ist_final} | |||
R(q) = KCM</math> | |||
== Soluciones con mayor concentración == | |||
Las expresiones anteriores son aproximaciones razonables cuando se tienen soluciones con concentraciones pequeñas. Esto es razonable debido a la consideración de que los movimientos de las partículas del soluto son independientes y no existe interacción entre ellas. | |||
Con el fin de obtener una generalización se define el factor estático de estructura como | |||
<math display="block">\label{eq:s} | |||
S(q) = \dfrac{1}{N} \sum_{j=1}^N \sum_{k=1}^N \left<\cos(\phi_j - \phi_k)\right></math> | |||
Generalizando la expresión [[#eq:ist_final|[eq:ist_final]]] | |||
<math display="block">\label{eq:rayleigh_qs} | |||
R(q) = KCM\cdot S(q)</math> | |||
observemos que para el caso de una solución diluída volvemos al caso en el que la doble suma tiene como valor final a <math display="inline">N</math> y entonces <math display="inline">S(q)=1</math> recuperando la expresión para la proporción de Rayleigh escrita en [[#eq:rayleigh_q|[eq:rayleigh_q]]]. | |||
La ecuación [[#eq:rayleigh_qs|[eq:rayleigh_qs]]] puede ser escrita como | |||
<math display="block">\dfrac{KC}{R(q)} = \dfrac{1}{M S(q)}</math> | |||
Para encontrar <math display="inline">S(q)</math> debemos hacer uso de la ley límite de van’t Hoff para la presión osmótica <math display="inline">\Pi</math>, es decir | |||
<math display="block">\label{eq:vant_hoff} | |||
\lim_{C\rightarrow 0} \dfrac{\Pi}{C} = \dfrac{\partial \Pi}{\partial C} = \dfrac{RT}{M}</math> | |||
donde <math display="inline">R</math> es la constante universal de los gases ideales. Usando ahora el teorema del virial para la presión osmótica en términos de la concentración | |||
<math display="block">\label{eq:pi_virial} | |||
\dfrac{\Pi}{RT} = \dfrac{1}{M}C + A_2 C^2 + A_3 C^3 + \cdots</math> | |||
que derivando respecto a la concentración nos da | |||
<math display="block">\dfrac{1}{RT} \dfrac{\partial \Pi}{\partial C} = \dfrac{1}{M} + 2 A_2 C + 3A_3 C^2 + \dots</math> | |||
llegando a | |||
<math display="block">\dfrac{KC}{R(q)} = \dfrac{1}{M} + 2 A_2 C + 3A_3 C^2 + \dots</math> | |||
con lo que | |||
<math display="block">S(q) = \left[1+2 A_2 M C + 3A_3 M C^2 + \dots\right]^{-1}</math> | |||
== Factor de forma == | |||
Se discutió el caso para partículas mucho más pequeñas que la longitud de onda de la luz incidente. Para el caso en el que las partículas no cumplen esta condición y tienen formas simétricas como esferas o cilindros, se debe definir una función llamada factor de forma <math display="inline">P(q)</math> que puede verse como una irradiancia normalizada debido a que las partículas que no son mucho más pequeñas que la longitud de onda de la luz incidente tendrán máximos y mínimos de irradiancia esparcida. | |||
<math display="block">P(q) = \dfrac{I_s(q)}{I_s(0)}</math> | |||
donde <math display="inline">I_s(0)</math> puede verse como una constante de normalización que se obtiene al esparcir luz a un ángulo nulo respecto a la incidencia, lo que implica que <math display="inline">q=0</math>. De modo experimental esto tiene que conseguirse por extrapolación. Si <math display="inline">I_s(0)</math> se ve como la irradiancia esparcida por moléculas infinitamente pequeñas entonces puede utilizarse [[#eq:isn|[eq:isn]]] y para <math display="inline">I_s(q)</math> se usa [[#eq:isn_app|[eq:isn_app]]], por lo que | |||
<math display="block">P(q) = \left<\dfrac{I_{s,1}\sum_{j=1}^n \sum_{k=1}^n\cos(\phi_j - \phi_k)}{I_{s,1} n^2}\right> = \dfrac{1}{n^2} \sum_{j=1}^n \sum_{k=1}^n \left<\cos(\phi_j - \phi_k)\right></math> | |||
Para calcular el promedio es conveniente utilizar que <math display="inline">\phi_j - \phi_k = \mathbf{r}_{jk} \cdot \mathbf{q}</math> donde el subíndice <math display="inline">jk</math> indica entré qué partículas se tiene la distancia. Y por la definición de producto punto tenemos | |||
<math display="block">\mathbf{r}_{jk} \cdot \mathbf{q} = r_{jk}q \cdot \cos(\theta)</math> | |||
e integrando en coordenadas polares para considerar todas las posibles orientaciones de las moléculas | |||
<math display="block">\left<\cos(r_{jk}q \cdot \cos(\theta))\right> = \dfrac{1}{4\pi}\int_0^{2\pi} \int_0^\pi \cos(r_{jk}q \cdot \cos(\theta)) \sin \theta d\theta d\phi = \dfrac{\sin(q r_{jk})}{q r_{jk}}</math> | |||
por lo que el factor de forma será finalmente | |||
<math display="block">\label{eq:factor_forma} | |||
P(q) = \dfrac{1}{n^2} \sum_{j=1}^n \sum_{k=1}^n \dfrac{\sin(q r_{jk})}{q r_{jk}}</math> | |||
En la figura [[#fig:tablapq|[fig:tablapq]]] se presentan valores típicos del factor de forma. | |||
[[File:tablapq.png|frame|none|alt=|caption Factores de forma usuales dentro de la aproximación RGDA.<span label="fig:tablapq"></span>]] | |||
Ahora es posible escribir | |||
<math display="block">R(q) = KCMP(q)</math> | |||
y vemos que si <math display="inline">q<<1</math> lo que implica que el ángulo de esparcimiento es muy pequeño entonces <math display="inline">P(q)\approx 1</math> y entonces se recupera la expresión [[#eq:rayleigh_q|[eq:rayleigh_q]]]. Además es posible definir un peso molecular aparente | |||
<math display="block">M_{app} = M P(q)</math> | |||
que en el caso en el que <math display="inline">P(q) = 1</math> entonces se tendrá el peso molecular real. | |||
== Aproximación de Guinier == | |||
Observando la ecuación del factor de forma [[#eq:factor_forma|[eq:factor_forma]]] vemos que cuando el argumento de la función seno es pequeño podemos aproximar utulizando su serie de Taylor, esto es | |||
<math display="block">\dfrac{\sin(qr_{jk})}{qr_{jk}} \approx \dfrac{qr_{jk} - (qr_{jk})^3/3! + \cdots}{qr_{jk}} = 1- \dfrac{1}{3!} (qr_{jk})^2 + \cdots</math> | |||
con el desarrollo anterior podemos simplificar de manera aproximada el factor de forma | |||
<math>P(q) \approx \dfrac{1}{n^2} \sum_{j=1}^n \sum_{k=1}^n \left[1 - \dfrac{1}{6} (qr_{jk})^2\right] </math> | |||
<math>\qquad = \dfrac{1}{n^2} \sum_{j=1}^n \sum_{k=1}^n 1 - \dfrac{q^2}{6n^2} \sum_{j=1}^n \sum_{k=1}^n r_{jk}^2 </math> | |||
<math>\qquad = 1 - \dfrac{1}{3} q^2 \left(\dfrac{1}{2n^2} \sum_{j=1}^n \sum_{k=1}^n r_{jk}^2\right)</math> | |||
de donde se toma el término final en paréntesis y se define | |||
<math display="block">\label{eq:radio_giro} | |||
R_g^2 \equiv \dfrac{1}{2n^2} \sum_{j=1}^n \sum_{k=1}^n r_{jk}^2</math> | |||
El radio de giro <math display="inline">R_g</math> sirve como una medida de la longitud de la cadena de partículas que se estudia. Puede verse como la distancia que hay entre el eje de giro y una masa puntual. | |||
Con estos resultados podemos escribir la llamada <span>'''aproximación de Debye'''</span> que es | |||
<math display="block">\label{eq:debye} | |||
P(q) \approx - \dfrac{1}{3}q^2 R_g^2</math> | |||
== Referencias == | |||
''Óptica, Tercera Edición; Eugene Hecht''.<br /> | |||
720pp, Addison-Wesley Iberoamericana, Madrid, España, 2000. | |||
''Light Scattering Demystified: Theory and Practice; Lars <span>Ø</span>gendal''.<br /> | |||
125pp. Internet Publication, University of Copenhagen, Denmark, 2017. | |||
''An Atmospheric Radiative Transfer Primer; R. G. Grainer''.<br /> | |||
Internet Publication Draft, Oxford University, 2013. | |||
''Handbook of Polymer Synthesis, Characterization, and Processing; Editors: Enrique Saldívar‐Guerra & Eduardo Vivaldo‐Lima''.<br /> | |||
'''Chapter 18: Light Scattering and its Applications in Polymer Characterization; Roberto Alexander-Katz'''.<br /> | |||
pp 367-389. John Wiley & Sons Inc. USA. 2013. | |||
''Physical Chemistry of Macromolecules; Charles Tanford''.<br /> | |||
724 pp. John Wiley & Sons Inc, New York, USA, 1961. | |||
[[Usuario:Ivan de Jesús Pompa García|Ivan de Jesús Pompa García]] ([[Usuario discusión:Ivan de Jesús Pompa García|discusión]]) 15:53 27 nov 2018 (CST) | |||
---- | |||
---- | |||
=Metodo de matrices para optica geometrica = | |||
== ''Introducción''' == | |||
Cuando el sistema óptico consta de varios elementos, por ejemplo, las cuatro o cinco lentes que constituyen una lente fotográfica, necesitamos un enfoque sistemático que facilite el análisis. Si bien limitamos nuestro análisis a los rayos paraxiales, este método sistemático se maneja bien con el método de matrices. Ahora presentamos un tratamiento de imágenes que emplea matrices para describir cambios en la altura y el ángulo de un rayo a medida que progresa a través de reflexiones y refracciones sucesivas a través de un sistema óptico. Mostramos que, en el enfoque paraxial, los cambios en altura y dirección de un rayo se pueden expresar mediante ecuaciones lineales que hacen posible este enfoque de matriz. Al combinar matrices que representan refracciones individuales, reflexiones y traslaciones, un sistema óptico dado puede representarse por una matriz única, a partir de la cual se pueden deducir las propiedades esenciales del sistema óptico compuesto. El método se presta a técnicas informáticas para rastrear un rayo a través de un sistema óptico de complejidad arbitraria. La figura 4 muestra el progreso de un solo rayo a través de un sistema óptico arbitrario. El rayo se describe a una distancia <math>{ x }_{ 0 } </math> de la primera superficie refractiva en términos de su altura <math>{ y }_{ 0 } </math> y el ángulo de pendiente <math>{ \alpha }_{ 0 }</math> con respecto al eje óptico. Los cambios de ángulo se producen en cada refracción, como en los puntos 1 a 5, y en cada reflexión, como en el punto 6. La altura del rayo cambia durante las traslaciones entre estos puntos. Estamos buscando un procedimiento que nos permita calcular la altura y el ángulo de inclinación del rayo en cualquier punto del sistema óptico, por ejemplo, en el punto <math> T</math> , a una distancia <math>{ x }_{ 7 } </math> del espejo. En otras palabras, dados los datos de entrada <math> ({ y }_{ 0 },{ \alpha }_{ 0 })</math> en el punto <math>0</math>, deseamos predecir valores de <math> ({ y }_{ 7 },{ \alpha }_{ 7 })</math> en el punto <math>7</math> como datos de salida. | |||
[[Archivo:1.22.jpg|thumb|center|'''Fig.4''' Pasos para trazar un rayo a través de un sistema óptico,el progreso de un rayo puede ser descrito por cambios en su elevacion y dirección]] | |||
== '''La traslación de matriz''' == | |||
Considere una traslación simple del rayo en un medio homogéneo, como en la Figura 5. Deje que el progreso axial del rayo sea <math>L</math>, como se muestra, de modo que en el punto 1, la elevación y la dirección del rayo estén dadas por "coordenadas" entrada <math> { y }_{ 1} </math> y <math>{ \alpha }_{ 1 }</math>, respectivamente. | |||
[[Archivo:2.jpg|thumb|center|'''Fig.5''' Traslación simple de un rayo ]] | |||
<math>{ \alpha }_{ 1 }={ \alpha }_{ 0 }</math> y <math> { y }_{ 1 }={ y }_{ 0 }+L(tan{ \alpha }_{ 0 })</math> | |||
Estas ecuaciones se pueden poner en una forma ordenada | |||
<math>{ y }_{ 1 }=(1){ y }_{ 0 }+(L){ \alpha }_{ 0 } </math> | |||
<math> { \alpha }_{ 1 }=(0){ y }_{ 0 }+(1){ \alpha }_{ 0 }</math> | |||
Donde la aproximación paraxial <math>tan{ \alpha }_{ 0 }\cong { \alpha }_{ 0 } </math> ha sido usada. En notación matricial, se escriben las dos ecuaciones entonces: | |||
<math> \ \begin {bmatrix} { y }_{ 1 } \\ { \alpha }_{ 1 }\end {bmatrix}=\ \begin {bmatrix} 1 & L \\ 0 & 1 \end {bmatrix}\ \begin {bmatrix} { y }_{ 0 } \\ { \alpha }_{ 0 }\end {bmatrix}</math> | |||
La matriz 2 X 2 de traslación de rayo representa el efecto de la tralacion en un rayo. Los datos de entrada <math> ({ y }_{ 0 },{ \alpha }_{ 0 })</math> son modificados por la matriz de transferencia de rayos para producir datos de salida correctos <math> ({ y }_{ 1 },{ \alpha }_{ 1 })</math> | |||
== '''La matriz de refracción''' == | |||
Consideramos a continuación la refracción de un rayo en una interfaz esférica que separa los medios de los índices de refracción <math>n</math> y <math>n´</math>, como se muestra en la Figura 6. Necesitamos relacionar las coordenadas del rayo <math>({y´},{\alpha´ })</math> después de la refracción con las anteriores a la refracción, <math>({y},{\alpha })</math> Dado que la refracción se produce en un punto, no hay cambios en la elevación, <math>y=y´</math> | |||
El ángulo <math>{\alpha´ }</math>, por otro lado, es, mediante el uso de las aproximaciones de un angulo pequeño y observando la figura tomaron los valores siguientes: | |||
[[Archivo:1.23.jpg|thumb|center|'''Fig.6''' Refracción de un rayo en una interfaz esférica]] | |||
<math> { \alpha }´ =\theta´-\phi =\theta´-\frac { y }{ R } </math> | |||
<math>{ \alpha }=\theta -\phi \quad =\theta -\frac { y }{ R } </math> | |||
Incorporando la forma paraxial de la ley de Snell tenemos | |||
<math>n\theta =n´\theta´</math> | |||
Entonces tenemos: | |||
<math>\alpha´=\left( \frac { n }{ n´ } \right) \theta -\frac { y }{ R } =\left( \frac { n }{ n´ } \right) \left( \alpha +\frac { y }{ R } \right) -\frac { y }{ R } </math> | |||
Simplificando tenemos : | |||
<math>\alpha ´=\left( \frac { \\ 1 }{ R } \right) \left( \frac { n }{ n´ } -1 \right) y+\left( \frac { n }{ n´ } \right) \alpha </math> | |||
Las ecuaciones lineales apropiadas son: | |||
<math>y´=(1)y+(0)\alpha </math> | |||
<math>\alpha ´=\left\lfloor \left( \frac { 1 }{ R } \right) \left( \frac { n }{ n´ } -1 \right) \right\rfloor y+\left( \frac { n }{ n´ } \right) \alpha </math> | |||
O, en forma de matriz: | |||
<math> \ \begin {bmatrix} y´ \\ \alpha ´ \end {bmatrix}=\ \begin {bmatrix} 1 & 0 \\ \left( \frac { 1 }{ R } \right) \left( \frac { n }{ n´ } -1 \right) & \frac { n }{ n´ } \end {bmatrix}\ \begin {bmatrix} y \\ \alpha \end {bmatrix}</math> | |||
Aquí, usamos una convención de signos para R, si la superficie es cóncava, es negativa y si R es positivo tendremos una superficie convexa. Además, al permitir <math>R\rightarrow \infty </math>, se obtiene la matriz de refracción adecuada para una interfaz plana (superficie plana). | |||
== '''La matriz de reflexión.''' == | |||
Finalmente, consideramos la reflexión en una superficie esférica, ilustrada en la Figura 7. En este caso consideraremos, un espejo cóncavo, R, por la explicación anterior vemos entonces que R debe tomar valores negativos. Necesitamos agregar una convención de signos para los ángulos que describen las direcciones de los rayos. Los ángulos se consideran positivos para todos los rayos que apuntan hacia arriba, ya sea antes o después de una interacción en este caso será una reflexión; Los ángulos para los rayos que apuntan hacia abajo se consideran negativos. La convención de signos se resume en el recuadro de la misma Figura. | |||
De la geometría de la figura 7, ambos <math>\alpha´</math> y <math>\alpha</math> son positivos | |||
[[Archivo:1.25.jpg|thumb|center|'''Fig.7''' Reflejo de un rayo en una superficie esférica.Ilustra la convencion de signos para los angulos de los rayos.]] | |||
<math>\alpha =\theta +\phi =\theta +\frac { y }{ -R } </math> | |||
y <math>\alpha ´=\theta ´-\phi =\theta ´-\frac { y }{ -R } </math> | |||
Donde hemos realizado las aproximaciones de ángulos pequeños que hemos tomado anteriormente. Usando estas relaciones junto con la ley de reflexión, <math>\theta =\theta ´</math>, | |||
<math>\alpha ´=\theta ´+\frac { y }{ -R } =\theta +\frac { y }{ R } =\alpha +\frac { 2y }{ R } </math> | |||
Y así, las dos ecuaciones lineales deseadas son: | |||
<math>y´=\left( 1 \right) y+(0)\alpha </math> | |||
<math>\alpha ´=\left( \frac { 2 }{ R } \right) y+(1)\alpha </math> | |||
En su forma de matriz es: | |||
<math> \ \begin {bmatrix} y´ \\ \alpha´ \end {bmatrix}=\ \begin {bmatrix} 1 & 0 \\ \frac { 2 }{ R } & 1 \end {bmatrix}\ \begin {bmatrix} y \\ \alpha \end {bmatrix}</math> | |||
== '''Matrices de lente grueso y lente delgado.''' == | |||
Construimos ahora una matriz que representa la acción de una lente gruesa sobre un rayo de luz. En general, asumimos diferentes medios en lados opuestos de la lente, con índices de refracción <math>n</math> y <math>n´</math> , como se muestra en la Figura 8. Al atravesar la lente, el rayo sufre dos refracciones y una traslación, pasos para los cuales ya hemos derivado matrices. . Refiriéndonos a la Figura 8, donde hemos elegido por simplicidad una lente con un radio de curvatura positivo, podemos escribir, simbólicamente, | |||
[[Archivo:1.26.jpg|thumb|center|'''Fig.8''' El progreso de un rayo a través de una lente gruesa]] | |||
<math> \ \begin {bmatrix} { y }_{ 1 } \\ { \alpha }_{ 1 }\end {bmatrix}={ M }_{ 1 } \ \begin {bmatrix} { y }_{ 0 } \\ { \alpha }_{ 0 }\end {bmatrix}</math> (para la primera refracción) | |||
<math> \ \begin {bmatrix} { y }_{ 2 } \\ { \alpha }_{ 2 }\end {bmatrix}={ M }_{ 2 } \ \begin {bmatrix} { y }_{ 1 } \\ { \alpha }_{ 1 }\end {bmatrix}</math> (para la traslación) | |||
<math> \ \begin {bmatrix} { y }_{ 3 } \\ { \alpha }_{ 3 }\end {bmatrix}={ M }_{ 3 } \ \begin {bmatrix} { y }_{ 2 } \\ { \alpha }_{ 2 }\end {bmatrix}</math> (para la segunda refracción) | |||
Juntando los resultados anteriores tenemos: | |||
<math> \ \begin {bmatrix} { y }_{ 3 } \\ { \alpha }_{ 3 }\end {bmatrix}={ M }_{ 3 }{ M }_{ 2 }{ M }_{ 1 } \ \begin {bmatrix} { y }_{ 0 } \\ { \alpha }_{ 0 }\end {bmatrix}</math> | |||
Evidentemente, toda la lente gruesa se puede representar por una matriz <math>M={ M }_{ 3 }{ M }_{ 2 }{ M }_{ 1 }</math>. Recordando que la multiplicación de matrices es asociativa pero no conmutativa, se debe mantener el orden descendente. Las matrices individuales operan en el rayo de luz en el mismo orden en que las acciones ópticas correspondientes influyen en el rayo de luz cuando atraviesa el sistema. Generalizando, la ecuación matricial que representa cualquier número N de traslaciones, reflexiones y refracciones están dada por: | |||
<math> \ \begin {bmatrix} { y }_{ f } \\ { \alpha }_{ f }\end {bmatrix}={ M }_{ N }{ M }_{ N-1 }...........{ M }_{ 1 } \ \begin {bmatrix} { y }_{ 0 } \\ { \alpha }_{ 0 }\end {bmatrix}</math>....................(1) | |||
La matriz de la transferencia de rayos que representa todo el sistema óptico es: | |||
<math>M={ M }_{ N }{ M }_{ N-1 }...........{ M }_{ 1 }</math>........................(2) | |||
Primero aplicamos este resultado a la lente gruesa de la Figura 8, cuyo índice es <math>{ n }_{ L }</math> y cuyo grosor para los rayos paraxiales es<math>t</math>. La aproximación correcta para una lente delgada se realiza al tener<math>t\rightarrow 0</math>. Permitiendo que <math>\Re </math> represente una matriz de refracción y <math>L </math> represente una matriz de traslación, la matriz para la lente gruesa es, por la Ec. (2), la matriz compuesta por: | |||
<math>M={ \Re }_{ 2 }L { \Re }_{ 1 }</math> | |||
Sustituyendo tenemos: | |||
<math> M =\ \begin {bmatrix} 1 & 0 \\ \frac { { n }_{ L }-n´ }{ n´{ R }_{ 2 } } & \frac { { n }_{ L } }{ n´ } \end {bmatrix}\ \begin {bmatrix} 1 & t \\ 0 & 1 \end {bmatrix}\ \begin {bmatrix} 1 & 0 \\ \frac { { n-n }_{ L } }{ { n }_{ L }R_{ 1 } } & \frac { n }{ { n }_{ L } } \end {bmatrix}</math>.......................(3) | |||
Para los casos en donde t es despreciable (t=0) y donde los lentes están rodeados por el mismo medio en cualquier lado (n=n´): | |||
<math> M =\ \begin {bmatrix} 1 & 0 \\ \frac { { n }_{ L }-n }{ n{ R }_{ 2 } } & \frac { { n }_{ L } }{ n} \end {bmatrix}\ \begin {bmatrix} 1 & 0 \\ 0 & 1 \end {bmatrix}\ \begin {bmatrix} 1 & 0 \\ \frac { { n-n }_{ L } }{ { n }_{ L }R_{ 1 } } & \frac { n }{ { n }_{ L } } \end {bmatrix}</math>..........................(4) | |||
Simplificando la ecuación anterior tenemos: | |||
<math> M =\ \begin {bmatrix} 1 & 0 \\ \frac { n_{ L }-n }{ n } \left( \frac { 1 }{ { R }_{ 2 } } -\frac { 1 }{ { R }_{ 1 } } \right) & 1 \end {bmatrix}</math> | |||
El elemento de matriz en la primera columna, segunda fila, puede expresarse en términos de la longitud focal de la lente, mediante las características que rigen el lente | |||
<math>\frac { 1 }{ f } =\frac { { n }_{ L }-n }{ n } \left( \frac { 1 }{ { R }_{ 1 } } -\frac { 1 }{ { R }_{ 2 } } \right) </math> | |||
Para que la matriz de transferencia de rayos del lente delgado sea simplemente: | |||
<math> M =\ \begin {bmatrix} 1 & 0 \\ \frac {- 1 }{ f } & 1 \end {bmatrix}</math> | |||
<math> f </math> se toma como positivo para una lente convexa y negativo para una lente cóncava. | |||
A continuación, se muestra una tabla resumiendo los resultados anteriores (matrices de transferencia de rayos simples) | |||
[[Archivo:1.27.jpg|thumb|center|'''Tabla''']] | |||
== '''Sistema de matriz de rayos de transferencia''' == | |||
Al combinar matrices individuales apropiadas en el orden apropiado, de acuerdo con la ec. (2), es posible expresar cualquier sistema óptico mediante una sola matriz 2 x 2, que llamamos matriz del sistema. | |||
'''Ejemplo:''' | |||
Encuentre la matriz del sistema para la lente gruesa de la Figura 8, cuya matriz antes de la multiplicación se expresa mediante la ecuación. (3), y especifique la lente gruesa exactamente eligiendo <math> { R }_{ 1 }=45cm </math>,<math> { R }_{ 2 }=30cm </math>, <math> t=5cm </math>, <math> { n }_{ L }=1.60 </math> y <math> n=n´=1 </math> | |||
Solución: | |||
<math> M =\ \begin {bmatrix} 1 & 0 \\ \frac { 1 }{ 50 } & 1.6 \end {bmatrix}\ \begin {bmatrix} 1 & 5 \\ 0 & 1 \end {bmatrix}\ \begin {bmatrix} 1 & 0 \\ -\frac { 1 }{ 120 } & \frac { 1 }{ 1.6 } \end {bmatrix}</math> | |||
Simplificando tenemos: | |||
<math> M =\ \begin {bmatrix} \frac { 23 }{ 24 } & \frac { 25 }{ 8 } \\ \frac { 7 }{ 1200 } & \frac { 17 }{ 16 } \end {bmatrix}</math> | |||
Los elementos de esta matriz de rayos de transferencia compuesto, usualmente se refieren a la forma simbolica: | |||
<math> M =\ \begin {bmatrix} A & B \\ C & D \end {bmatrix}</math> | |||
Describe las propiedades relevantes del sistema óptico. Teniendo en cuenta que los valores particulares de los elementos de la matriz de un sistema dependen de la ubicación del rayo en la entrada y la salida. En el caso de la lente gruesa que se acaba de calcular, el plano de entrada se eligió en la superficie izquierda de la lente y el plano de salida se eligió en la superficie derecha. Si cada uno de estos planos se mueve a cierta distancia de la lente, la matriz del sistema también incluirá una matriz de traslación inicial y una final que incorpore estas distancias. Los elementos de la matriz cambian y la matriz del sistema ahora representa este "sistema" ampliado. En cualquier caso, el determinante de la matriz del sistema tiene una propiedad muy útil: | |||
<math> Det M= AD-BC=\frac { { n }_{ 0 } }{ { n }_{ f } } </math>.....................(5) | |||
donde <math> { n }_{ o }</math>, y <math> { n }_{ f}</math> son los índices de refracción de los medios iniciales y finales del sistema óptico. La prueba de esta afirmación sigue al notar primero que el determinante de todas las matrices de transferencia de rayos individuales en la Tabla 1 tienen valores de <math> n/n´</math> o unidad y utilizando el teorema de que el determinante de un producto de matrices es igual al producto de los determinantes. Esto quiere decir, si <math>M={ M }_{ 1 }{ M }_{ 2 }{ M }_{ 3 }.......{ M }_{ N }</math>, entonces: | |||
<math>Det(M)=Det({ M }_{ 1 })Det({ M }_{ 2 }{ )Det(M }_{ 3 }).......Det({ M }_{ N })</math> | |||
Al formar este producto, usando determinantes de matrices de transferencia de rayos, todos los índices de refracción intermedios se cancelan, y nos queda la relación <math>\frac { { n }_{ 0 } }{ { n }_{ f } } </math>, como se indica en la ecuación (5) La mayoría de las veces, como en el caso del ejemplo de lente gruesa,<math>{ n }_{ 0 }</math> y <math>{ n }_{ f }</math> se refieren al aire, y <math>Det (M)</math> es la unidad. La condición expresada por la ec. (5) es útil para verificar la exactitud de los cálculos que producen una matriz del sistema. | |||
== '''Importancia de los elementos de la matriz del sistema''' == | |||
Examinamos ahora las implicaciones que siguen cuando cada uno de los elementos de la matriz a su vez es cero. En forma simbólica, tenemos, desde la ec. (1), | |||
<math> \ \begin {bmatrix} { y }_{ f } \\ { \alpha }_{ f } \end {bmatrix}=\ \begin {bmatrix} A & B \\ C & D \end {bmatrix}\ \begin {bmatrix} { y }_{ 0 } \\ { \alpha }_{ 0 } \end {bmatrix}</math> | |||
Lo que equivale a las relaciones algebraicas | |||
<math>{ y }_{ f }=A{ y }_{ 0 }+B{ \alpha }_{ 0 }</math> | |||
<math>{ \alpha }_{ f }=C{ y }_{ 0 }+D{ \alpha }_{ 0 }</math> | |||
1.D = 0. En este caso, <math>{ \alpha }_{ f }=C{ y }_{ 0 }</math>, independientemente de <math>{ \alpha }_{ 0 }</math>. Como <math>{ y }_{ 0 }</math> es fijo, esto significa que todos los rayos estarán en el punto en el plano de entrada y tendrán el mismo ángulo en el plano de salida, independientemente de sus ángulos en la entrada. Como se muestra en la Figura 9a, el plano de entrada coincide así con el primer plano focal del sistema óptico. | |||
2.A = 0.Este caso es muy parecido al anterior. Aquí <math>{ y }_{ f }=B{ \alpha }_{ 0 }</math> implica que <math>{ y }_{ f }</math> es independiente de <math>{ y }_{ 0 }</math>, de modo que todos los rayos que salen del plano de entrada en el mismo ángulo, independientemente de la altitud, llegan a la misma altitud y al plano de salida. Como se muestra en la Figura 9b, el plano de salida funciona así como el segundo plano focal. | |||
3.B = 0. Entonces <math>{ y }_{ f }=A{ y }_{ 0 }</math>, independientemente de <math>{ \alpha }_{ 0 }</math>. Por lo tanto, todos los rayos desde un punto en altura <math>{ y }_{ 0 }</math> en el plano de entrada llegan al mismo punto de altura <math>{ y }_{ f }</math> en el plano de salida. Los puntos se relacionan con el objeto y los puntos de imagen, como se muestra en la Figura 9c, y los planes de entrada y salida correspondientes a los planos conjugados para el sistema óptico. También, como <math>A=\frac { { y }_{ f } }{ { y }_{ 0 } } </math>,el elemento matriz A representa la extensión lineal. | |||
4.C = 0. Ahora <math>{ \alpha }_{ f }=D{ \alpha }_{ 0 }</math>, independientemente de <math>{ y }_{ 0 }</math>. Este caso es análogo al caso 3, con direcciones que reemplazan las alturas de los rayos. Los rayos entrantes, todos desde una dirección, ahora producen rayos de salida paralelos en alguna otra dirección. Además, <math>D=\frac { { \alpha }_{ f } }{ { \alpha }_{ 0 } } </math> es el aumento angular. Un sistema para el cual C=0 a veces se llama "sistema telescópico", porque un telescopio admite rayos paralelos en su objetivo y emite rayos paralelos para verlos | |||
[[Archivo:1.28.jpg|thumb|center|'''Figura.9'' Diagrama que ilustran el significado de la desaparición de elementos específicos de la matriz del sistema.(a)Cuando D=0, el plano de entrada corresponde al primer plano focal del sistema óptico.(b)Cuando A=0,el plano de salida corresponde al segundo plano focal del sistema óptico.(c)Cuando B=0,el plano de salida es el plano de la imagen conjugado con el plano de entrada y A es la ampliación lineal.(d)Cuando C=0,un haz paralelo de rayos en el plano de entrada es paralelo en el plano de salida y D es la ampliación angular]] | |||
A continuación, mostraremos un ejemplo sencillo para esclarecer la construcción de matrices para un arreglo óptico. | |||
Ejemplo: | |||
Colocamos un objeto pequeño en el eje a una distancia de 16 cm del extremo izquierdo de una varilla larga de plástico con un extremo esférico pulido de radio de 4 cm, como se indica en la Figura 10, el índice de refracción del plástico es de 1,50 y el objeto está en el aire. Deje que la imagen desconocida se forme en el plano de referencia de salida, a una distancia x de la tapa esférica. Queremos determinar la distancia de la imagen x y la ampliación lateral m. La matriz del sistema que conecta el objeto y los planos de imagen consiste en el producto de tres matrices, (1) que corresponden a una traslación <math>{ L }_{ 1 } </math> en el aire del objeto a la varilla, (2) una refracción <math>\Re </math> en la superficie esférica, y (3 ) una traslación <math>{ L }_{ 2 } </math> en plástico a la imagen. | |||
[[Archivo:1.29.jpg|thumb|center|'''Figura.10'' Esquema que define un ejemplo para los métodos de matriz de transferencia de rayos]] | |||
'''Solución:''' | |||
Recuerde tomar las matrices en orden inverso y trabajar en cm y así tenemos | |||
<math>M={ L }_{ 2 }\Re { L }_{ 1 }</math> | |||
Sustituyendo tenemos: | |||
<math> M =\ \begin {bmatrix} 1 & x \\ 0 & 1 \end {bmatrix}\ \begin {bmatrix} 1 & 0 \\ \frac { 1-1.50 }{ 4(1.50) } & \frac { 1 }{ 1.50 } \end {bmatrix}\ \begin {bmatrix} 1 & 16 \\ 0 & 1 \end {bmatrix}</math> | |||
<math> M =\ \begin {bmatrix} 1-\frac { x }{ 12 } & 16-\frac { 2x }{ 3 } \\ -\frac { 1 }{ 12 } & 1 \end {bmatrix}</math> | |||
con la cantidad desconocida x incorporada en los elementos de la matriz. De acuerdo con esta discusión, cuando B = 0, el plano de salida es el plano de la imagen, de modo que la distancia de la imagen x se determina configurando | |||
<math>16-\frac { 2x }{ 3 } =0</math> | |||
ó <math>x=24cm</math> | |||
Además, el aumento lineal viene expresado por el valor del elemento A: | |||
<math>m=A=1-\frac { x }{ 12 } =-1</math> | |||
Concluimos que la imagen ocurre 24 cm dentro de la varilla, está invertida y tiene el mismo tamaño lateral que el objeto. Esto ilustra cómo se puede usar la matriz del sistema para encontrar ubicaciones y tamaños de imágenes, aunque esto generalmente se puede hacer más rápidamente utilizando las fórmulas de imágenes gaussianas derivadas anteriormente. | |||
== '''Cálculo de un sistema óptico complejo ''' == | |||
Se construirá un sistema óptico que esta conformado por tres lentes cóncavos-convexos,se encuentran a una cierta distancia uno del otro y el medio de propagación es el aire , en la siguiente tabla se muestra el arreglo del sistema óptico que queremos estudiar: | |||
[[Archivo:Mathe0.jpg|thumb|center]] | |||
Como se explico anteriormente en el desarrollo del método de matrices, debemos de construir inicialmente una matriz total la cual representara las interacciones ópticas para una sola lente la cual es: | |||
<math>{ M }_{ LEN }={ M }_{ R }{ M }_{ T }{ M }_{ R }</math> | |||
donde: | |||
<math>{ M }_{ LEN }=</math>la matriz toda del lente | |||
<math>{ M }_{ R }=</math>la matriz referente a la primera interacción óptica la cual es una refracción | |||
<math>{ M }_{ T }=</math>la matriz referente a la segunda interacción óptica la cual es una traslación | |||
<math>{ M }_{ R }=</math>la matriz referente a la tercera interacción óptica la cual es una refracción | |||
Posteriormente, ya que se construyo una matriz que represente las interacciones ópticas de un lente podemos construir la matriz total final la cual asume todas las interacciones del sistema; tenemos entonces: | |||
<math>{ M }_{ Tot }={ M }_{ 3 }{ T }_{ 3 }{ M }_{ 2 }{ T }_{ 2 }{ M }_{ 1 }</math> | |||
donde: | |||
<math>{ M }_{ Tot }=</math>la matriz total del sistema óptico | |||
<math>{ M }_{ 3 }=</math>la matriz toda del lente 3 | |||
<math>{ T }_{ 3 }=</math>la matriz de traslación debido al recorrido del rayo del lente 3 al 2 | |||
<math>{ M }_{ 2 }=</math>la matriz toda del lente 2 | |||
<math>{ T }_{ 2 }=</math>la matriz de traslación debido al recorrido del rayo del lente 2 al 1 | |||
<math>{ M }_{ 1 }=</math>la matriz toda del lente 1 | |||
Calculando la matriz total del sistema óptico tenemos: | |||
<math> M =\ \begin {bmatrix} 0.93233 & 22.2198 \\ -0.0108425 & 0.812518 \end {bmatrix}</math> | |||
podemos notar que el termino negativo es el inverso negativo de la distancia focal dando así una longitud focal de d=93.23 mm | |||
Como podemos ver con ayuda de mathematicas podemos realizar el calculo de la matriz total con mucha facilidad por lo que estudiaremos la dependencia de la distancia focal para dos casos. | |||
'''Primer caso:''' | |||
Se dejara la distancia del lente 3 fija y se ira alejo la segunda lente de la primera. | |||
El incremento de la distancia entre las lentes se ira aumentando en 0.01mm y para cada incremento se calculara la matriz total del sistema para obtener una distancia focal. | |||
Dando así como resultado la disminución de la distancia focal al aumentar la separación entre los lentes ,como puede comprobarse en la Fig. 1, donde se gráfica la dependencia de la distancia focal en función de la variación de la distancia entre las lentes el cual nos dice que a mayor distancia entre los lentes menor sera la distancia focal del sistema total. | |||
[[Archivo:Mathe1.jpg|thumb|center]] | |||
'''Segundo caso:''' | |||
En este caso disminuiremos el radio de las lentes pero solo en los planos de entrada, donde el decremento de los radios se ira disminuyendo en 0.01mm y para cada decremento se calculara la matriz total del sistema para obtener una distancia focal. | |||
El caso de disminución de los radios de curvatura se presenta en la Fig. 2, donde se grafica la dependencia de la distancia focal de las variaciones de los radios de curvatura de las lentes. En el mismo es posible comprobar que el aumento de los radios aumenta la distancia focal. | |||
[[Archivo:Mathe2.jpg|thumb|center]] | |||
== Referencias == | |||
''Óptica, Tercera Edición; Eugene Hecht''.<br /> | |||
720pp, Addison-Wesley Iberoamericana, Madrid, España, 2000. | |||
"Introduction to Modern Optics;Grant R. Fowles,Dover Publications,1989" | |||
"Physical optics;S. A. Akhmanov, S. Yu. Nikitin,Clarendon Press; Oxford University Press,1997" | |||
"Principles of applied optics [1 ed.];Partha P. Banerjee, Ting-Chung PoonAksen Associates; Irwin,1991" | |||
"Principles of optics;Max Born, Emil Wolf,Cambridge University Press,1999" | |||
[[Usuario:Ruben Espinosa|Ruben Espinosa Guzman]] | |||
---- | |||
=='''Fenómeno de Gibbs'''== | |||
=='''Fenomeno de Gibbs para funciones con saltos'''== | |||
'''Función Signo''' | |||
Consideremos la función f(x)=sgn(x) para <math> x\in(-\pi,\pi) </math>. | |||
Que su serie de Fourier es | |||
<math> \frac { 4 }{ \pi } \sum _{ k=0 }^{ \infty }{ \frac { \sin (2k+1)x }{ 2k+1 } } </math> ... (1) | |||
Usando el siguiente teorema | |||
'''Teorema 1.''' ''Sea f una función integrable en <math> (-\pi,\pi) </math> que tiene derivadas laterales en un punto <math> x_{0} </math> en el sentido mencionado. Entonces, la serie de Fourier de f converge en <math> x_{0} </math> a <math> (f(x_{ 0 }+)+f(x_{ 0 }-))/2</math>.'' | |||
Que asegura que la serie de Fourier converge a la función en <math> (-\pi,\pi) </math> (definiendo el signo de 0 como 0). La convergencia no puede ser uniforme porque el limite no es una función continua, aunque si es uniforme en <math> \left[\delta,\pi-\delta\right] </math> para cualquier <math> \delta>0 </math>. | |||
Y que a su vez lo anterior es asegurado por el siguiente teorema | |||
'''Teorema 2.''' ''Sea f continua, con derivada continua a trozos y acotada en un intervalo <math> \left[a,b\right]\subset\left[-\pi,\pi\right] </math>. Entonces la serie de Fourier de f converge a f uniformemente en <math> \left[a+\delta,b-\delta\right] </math> para <math> \delta>0 </math>.'' | |||
Por lo tanto, si tomamos <math> \epsilon>0 </math>, existe <math> N_{0} </math> de modo que las sumas parciales de la serie de Fourier satisfacen <math> |S_{N}f(x)-1|<\epsilon </math>, para todo <math> N\geq N_{0} </math> y <math> x\in\left[\delta,\pi-\delta\right] </math>. | |||
Por otra parte, esta claro que en <math> \left(0,\delta\right)</math> las sumas parciales tienen que formar valores entre 0 y 1. | |||
[[Archivo:Grafica_1._gibbs.png|thumb|center|''Figura 1: '' Grafica de <math>{ S }_{ 9 }</math>.]] | |||
La figura 1 muestra la gráfica de la suma parcial <math> S_{9}</math> de la serie de Fourier. Solo en la zona central de cada intervalo esta relativamente cerca de los valores de f. Con mas sumas la aproximación sera mejor | |||
[[Archivo:Grafica_2.1._gibbs.png|thumb|center|''Figura 2: '' Grafica de <math>{ S }_{19 }</math>.]] | |||
En la gráfica de <math> S_{19}</math> (figura 2) vemos que la aproximación mejora en la zona central pero no se rebaja el ”pico” que por encima de 1 aparece para los valores de la variable cercanos a 0 (y sus correspondientes simétricos). | |||
[[Archivo:Grafica_3.1._gibbs.png|thumb|center|''Figura 3: '' Detalle de la grafica de <math>{ S }_{ 29 }</math>, para valores de la función cercanos a 1.]] | |||
[[Archivo:Grafica_4._gibbs.png|thumb|center|''Figura 4: '' Detalle de la grafica de <math>{ S }_{ 100 }</math>, para valores de la función cercanos a 1.]] | |||
Aumentando el numero de sumandos de la suma parcial, la situación no cambia: la figura 3 muestra una amplificación de la gráfica para <math> S_{29} </math> y, sin embargo, el pico se mantiene. Este hecho, que puede resultar sorprendente, no se remedia añadiendo términos a la suma parcial (en la figura 4 se muestra <math> S_{100} </math>). En efecto, el valor máximo de la suma parcial <math> S_{N}f </math> en <math> \left(0,\delta\right) </math> no tiende a 1 cuando N tiende a infinito, sino al valor | |||
<math> \frac { 2 }{ \pi } \int _{ 0 }^{ \pi }{ \frac { \sin x }{ x } dx } =1.17897944... </math> ...(2) | |||
<math> S_{2N-1}f </math> corresponde a tomar la suma hasta k=N-1 en la ec. (1). Los máximos de <math> S_{2N-1}f </math> se encuentran en puntos que anulen a su derivada, que es | |||
<math> \frac { d }{ dx } S_{ 2N-1 }f(x)=\frac { 4 }{ \pi } \sum _{ k=0 }^{ N-1 }{ \cos (2k+1)x } =\frac { 4 }{ \pi } \frac { \sin 2Nx }{ \sin x } </math> ...(3) | |||
(La ultima igualdad se obtiene a partir de la formula <math> \cos\left(2k+1\right)x\sin </math> <math> x=\sin\left(2k+2\right)x-\sin2kx </math>, del mismo modo que en el calculo del núcleo de Dirichlet.) Esta revidad se anula en <math> \left(0,\pi\right) </math> en los ceros de <math> \sin2Nx </math> que son <math> x={ k\pi / }{ 2N },\quad k=1,2,...,2N-1 </math>. La segunda derivada tiene en sus puntos el signo de <math> \cos2Nx </math> de modo que corresponde alternativamente a máximos y mínimos locales, comenzando en un máximo. | |||
Como <math> S_{2N-1}f(0)=0 </math>, de la expresión (3) para la derivada de la suma parcial también se deduce | |||
<math> S_{ 2N-1 }f(x)=\frac { 4 }{ \pi } \int _{ 0 }^{ x }{ \frac { \sin 2Nt }{ \sin t } dt } </math> | |||
Utilizando esta expresión se pueden comprobar las sumas parciales en máximos sucesivos y se comprueba que el primer máximo, que se obtiene para <math> x={ \pi }{ /2N } </math>, es precisamente el máximo absoluto. Ahí es donde vamos a evaluar la suma parcial y calcular el limite, de modo que buscamos | |||
<math> \underset { N\rightarrow \infty }{ lim } S_{ 2N-1 }f\left( \frac { \pi }{ 2N } \right) =\underset { N\rightarrow \infty }{ lim } \frac { 4 }{ \pi } \sum _{ k=0 }^{ N-1 }{ \frac { \sin { \left( 2k+1 \right) } { 2N } }{ 2k+1 } } </math> ...(4) | |||
Consideramos la partición del intervalo <math> \left[0,\pi\right] </math> en N intervalos iguales determinada por los puntos <math> x_{ k }={ k }/{ N },\quad k=0,1,...,N </math>. Si escribimos ahora la suma de Riemann para la función <math> { \sin x }/{ x } </math> asociada a esta partición, con la función evaluada en el punto medio de cada uno de los intervalos, obtenemos precisamente el valor <math> S_{ 2N-1 }f\left( { \pi }{ /2N } \right) </math> multiplicado por <math> { \pi / }{ 2 } </math>. Como la función <math> { \sin x }{ /x } </math> es continua, el limite de sus sumas de Riemann cuando N tiende a infinito es su integral en <math> \left(0,\pi\right) </math>. Entonces el limite de <math> S_{ 2N-1 }f\left( { \pi }{ /2N } \right) </math> vendrá dado por el expresión (2). | |||
=='''Un importante ejemplo: la “función” delta de Dirac'''== | |||
En 1926, el físico ingles P.A.M Dirac, introdujo la “función” delta de dirac, en conexión con sus estudios sobre mecánica cuántica. Realmente no se trata de una función en el sentido ordinario del temrino, sino de una distribución. | |||
La delta de Dirac viene caracterizada por las siguientes propiedades | |||
1. <math>\delta (x)=0\quad si\quad x\neq 0</math> | |||
2. <math>\delta (0) </math> no esta definida. | |||
3. <math>\int { \delta (x)dx } =1</math>, siempre que el recinto de integración incluya x=0 | |||
4. <math>g(x</math>) es una función continua en <math>\Re</math>, entonces <math>\int { g(x)\delta (x)dx=g(0) }</math>. | |||
En la figura 6 representamos la delta de Dirac en un sentido figurado: la delta de Dirac puede interpretarse como una función que se anula en todos los puntos salvo en x=0, donde toma el valor infinito. | |||
Para <math>a\neq 0</math>, la función <math>\delta (x-a)</math>, seria la misma función o distribución pero trasladada a x=a. | |||
[[Archivo:Gibbs_6..png|thumb|center|''Figura 5: '' Delta de Dirac, <math>\delta (x)</math>.]] | |||
El concepto de la función delta de Dirac, también llamada función impulso unitario, resulta un modelo útil en situaciones en las que, por ejemplo, tenemos un sistema mecanico sobre el cual actua una fuerza externa de gran magnitud durante un breve instante de tiempo. En el caso extremos en el que esta fuerza estuviese concentrada en un punto, vendría representada por al delta de Dirac. | |||
La delta de dirac puede efectivamente entenderse como el limite de una sucesión de funciones que, con masa unidad, se concentran infinitamente en torno a un punto. En efecto, sea <math>f</math> una función regular tal que | |||
<math>f(x)=0,\quad si\quad \left| x \right| >1</math> | |||
<math>\int { f(x)dx=1 }</math> | |||
<math>f(x)\ge 0,\quad para\quad todo\quad x\in \Re</math> | |||
Consideremos ahora la sucesión de funciones: | |||
<math>{ f }_{ \epsilon }(x)=\frac { 1 }{ \epsilon } f\left( \frac { x }{ \epsilon } \right) </math> | |||
Este cambio de escala no altera la masa total de la función, puesto que: | |||
<math>\int { { f }_{ \epsilon }(x) } dx=\int { \frac { 1 }{ \epsilon } f\left( \frac { x }{ \epsilon } \right) } dx=\int { f(y) } dy=1</math> | |||
Sin embargo, a medida que <math>\epsilon</math> tiende a 0, el soporte de la función <math>{ f }_{ \epsilon }</math> se contrae puesto que | |||
<math>{ f }_{ \epsilon }(x)\rightarrow 0\quad si\quad |x|>\epsilon</math> | |||
En el limite, cuando <math>\epsilon \rightarrow 0</math>, las funciones <math>{ f }_{ \epsilon }</math>, cada vez mas concentradas, convergen a la delta de Dirac, puesto que | |||
<math>\int { { f }_{ \epsilon }(x)g(x)dx } =\frac { 1 }{ \epsilon } \int { f\left( \frac { x }{ \epsilon } \right) } dx=\int { f(x)g(x) } dx</math> | |||
<math>\rightarrow g(0)\int { f(x)dx } =g(0)=\int { g(x)\delta (x)dx }</math> | |||
Cuando <math>\epsilon \rightarrow 0</math>, para toda la función <math>g</math> continua y acotada. | |||
Vamos a calcular las sumas parciales de Fourier para la delta de Dirac. Pero, ¿cómo puede expresarse con una serie trigonométrica una “función” tan singular como la delta de Dirac?. | |||
En realidad, lo que se hara es calcular las sumas parciales de Fourier correspondientes a una determinada combinación lineal de deltas de Dirac. | |||
<math>\Delta x=\sum _{ z=par }^{ }{ \delta (x+2z) } -\sum _{ z=impar }^{ }{ \delta (x+2z) }</math> | |||
Que se obtiene al extender de manera periódica con periodo <math>2\pi</math> la “función” que coincide con la delta de Dirac | |||
<math>\delta (x) </math> en <math>x=0</math> y con <math>-\delta (x-\pi ) </math> en el punto <math>x=\pi</math>, es decir, que la <math>\delta</math> trasladada y cambiada de signo, la reflejada impar de la <math>\delta (x) </math>. Dicho de otra forma, la función que hemos llamado <math>\Delta x</math>, esta compuesta por: impulsos unitarios positivos en los múltiplos pares de <math>\pi</math>, es decir, puntos de la forma …, <math>2\pi ,\quad 0,\quad 2\pi ,\quad 4\pi…</math>; e impulsos unitarios negativos en los múltiplos impares de <math>\pi</math>, es decir, puntos de la forma, …, <math>-3\pi ,\quad -\pi ,\quad \pi ,\quad 3\pi, …</math>; La grafica de esta función se podria representar en la figura 7. | |||
[[Archivo:Gibbs_7..png|thumb|center|''Figura 6: '' "función" <math>\Delta (x)</math>.]] | |||
Aplicando las formulas para calcular los coeficientes de Fourier y teniendo en cuenta que <math>\Delta x</math>, es una función par | |||
<math>{ a }_{ k }=\frac { 1 }{ \pi } \int _{ -\pi }^{ \pi }{ \Delta x } cos(kx)dx=\frac { 2 }{ \pi } \int _{ -\pi }^{ \pi }{ \Delta x } cos(kx)dx</math> | |||
<math>=\int _{ 0 }^{ \pi }{ (\delta (x)-\delta (x-\pi ))cos(kx)dx } </math> | |||
<math>=\frac { 2 }{ \pi } (cos(0)-cos(k\pi )) </math> | |||
<math>=\frac { 2 }{ \pi } (1-(-{ 1 }^{ k })</math> | |||
<math>{ b }_{ k }=\frac { 1 }{ \pi } \int _{ -\pi }^{ \pi }{ \Delta x } sin(kx)dx=0</math> | |||
Por tanto, la suma parcial de Fourier para la función <math>\Delta x</math> queda | |||
<math>{ S }_{ \Delta ,N }(x)=\sum _{ k=0 }^{ N }{ \frac { 2 }{ \pi } (1-(-{ 1 }^{ k })) } cos(kx) </math> | |||
Que se puede expresar de la siguiente forma, dado que para los valores pares de <math>k</math> los sumandos se anulan: | |||
<math>{ S }_{ \Delta ,2n-1 }(x)=\frac { 4 }{ \pi } \sum _{ r=1 }^{ n }{ cos((2r-1)x) }</math> | |||
[[Archivo:Gibbs_8..png|thumb|center|''Figura 7: '' Suma de Fourier de <math>Delta (x)</math>, N=30.]] | |||
Los cálculos y graficas obtenidas requieren algunas observaciones: | |||
En primer lugar, con toda seguridad podemos afirmar lo siguiente | |||
<math>\frac { d }{ dx } [{ S }_{ 2n-1 }(x)]=\quad { S }_{ \Delta ,2n-1 }(x) </math> | |||
Lo cual nos hace pensar que, en cierto sentido, la derivada de la función salto, debe ser la “función” <math>\Delta x</math>. | |||
[[Archivo:Gibbs_9..png|thumb|center|''Figura 8: '' Suma de Fourier de <math>Delta (x)</math>, N=100.]] | |||
A partir de la observación anterior; si la derivada de las sumas parciales de la función salto son las sumas parciales de la delta de Dirac, entonces la integral de las sumas parciales de la delta serán las de la función salto, es decir | |||
<math>{ S }_{ 2n-1 }(x)=\int _{ 0 }^{ x }{ { S }_{ \Delta ,2n-1 }(t) } dt</math> | |||
Por otra parte, <math>{ S }_{ \Delta ,2n-1 }</math> admite una expresión mas comoda: | |||
<math>{ S }_{ \Delta ,2n-1 }(x)=\frac { 4 }{ \pi } \sum _{ r=1 }^{ n }{ cos((2r-1)x) }</math> | |||
<math>=\frac { 2 }{ \pi sin(x) } \sum _{ r=1 }^{ n }{ 2sin(x)cos((2r-1)x) }</math> | |||
<math>=\frac { 2 }{ \pi sin(x) } \sum _{ r=1 }^{ n }{ [sin(2rx)-sin(2(r-1)x)] } </math> | |||
<math>=\frac { 2 }{ \pi sin(x) } \left[ \sum _{ r=1 }^{ n }{ sin(2rx)- } \sum _{ r=0 }^{ n-1 }{ sin(2rx) } \right] </math> | |||
<math>=\frac { 2 }{ \pi } \frac { sin(2nx) }{ sin(x) }</math> | |||
Este hecho, nos proporciona la siguiente expresión para las sumas parciales de Fourier de la función salto | |||
<math>{ S }_{ 2n-1 }(x)=\frac { 2 }{ \pi } \int _{ 0 }^{ x }{ \frac { sin(2nt) }{ sin(t) } dt }</math> | |||
Mientras que | |||
<math>\frac { d }{ dx } [{ S }_{ 2n-1 }(x)]=\frac { 2 }{ \pi } \frac { sin(2nx) }{ sin(x) }</math> | |||
Se puede comprobar de esta forma, que los puntos críticos de las sumas parciales de la función salto son los ceros de las sumas parciales de la delta de Dirac. Es decir, que la altura que se alcanza en el primer máximo de la suma parcial de Fourier de la función salto, a la derecha de <math>x=0</math>, es la mitad del área por debajo del arco central de la grafica x. Es decir | |||
<math>{ S }_{ 2n-1 }\left( \frac { \pi }{ 2n } \right) =\frac { 2 }{ \pi } \int _{ 0 }^{ \frac { \pi }{ 2n } }{ \frac { sin(2nt) }{ sin(t) } dt }</math>. Pasando al limite cuando <math> n\rightarrow \infty</math>, necesariamente habremos de obtener el mismo valor | |||
<math>\int _{ 0 }^{ \frac { \pi }{ 2n } }{ \frac { sin(2nt) }{ sin(t) } dt } =\int _{ 0 }^{ \pi }{ \frac { sin(t) }{ t } dt } =si(\pi ) </math> | |||
En las graficas de las figuras x y Y parece observarse también algo parecido al fenómeno de Gibbs. Pero ahora es algo disinto a lo que ocurria con la función salto. En la función salto veíamos que las graficas de las sumas parciales excedían, o quedaban por debajo de la función de los alrededores de los puntos de discontinuidad. Aquí la situación es peor, porque esto ocurre no solo en las cercanías de <math>x=0</math> sino a lo largo de los puntos de continuidad de la función original, por ejemplo en los puntos de intervalo <math> (0,\pi ) </math>. Ademas esta situación no cambian aunque aumentos la cantidad de sumandos. ¿Cuál es la razón de este comportamiento tan anómalo? Simplemente, ahora ni siquiera tenemos convergencia puntual. En efecto, si tomamos por ejemplo, un punto <math>{ x }_{ 0 }\in (0,\pi </math> la función original valdrá <math>\Delta ({ x }_{ 0 })=0</math>. Sin embargo, la sucesión | |||
<math>{ S }_{ \Delta ,2n-1 }(x)=\frac { 2 }{ \pi } \frac { sin(2n{ x }_{ 0 }) }{ sin({ x }_{ 0 }) }</math> | |||
No converge cuando <math> n\rightarrow \infty</math>. De hecho, lo que courre es que la grafica de <math>{ S }_{ \Delta ,2n-1 }(x) </math> oscila entre las graficas de las dos funciones <math>y=\pm \frac { 2 }{ \pi } \frac { 1 }{ sin(x) }</math>, que acota superior e inferiormente a <math>{ S }_{ \Delta ,2n-1 }(x) </math>, es decir | |||
<math>\left| \frac { 2 }{ \pi } \frac { sin(2nx) }{ sin({ x }) } \right| \le \frac { 2 }{ \pi } \frac { 1 }{ \left| sin(x) \right| }</math> | |||
En la figura X hemos dibujado la grafica de la suma parcial de la delta de Dirac hasta el sumando N=50, en el intervalo <math>\left[ -\frac { \pi }{ 2 } ,\frac { \pi }{ 2 } \right] </math> junto con las graficas de las funciones <math>y=\pm \frac { 2 }{ \pi } \frac { 1 }{ sin(x) }</math>. | |||
[[Archivo:Gibbs_10..png|thumb|center|''Figura 9: '' "fenomeno de Gibbs" en delta Dirac, N=50 .]] | |||
Entonces, ¿Qué tipo de representación es la que producen las sumas parciales de Fourier para la delta de Dirac en la que ni siquiera hay convergencia puntual para los puntos de la continuidad? La respuesta es que si hay convergencia, pero es una convergencia especial, una convergencia “débil”: como hemos podido ver mas arriba, en la definición de la delta de Dirac, esta función no se define de una manera clásica, dando sus valores, sino mas bien a través de sus efectos sobre otras funciones en el sentido de las distribuciones. Y en este sentido, las sumas parciales de Fourier de la delta producen sobre otras funciones los mismos efectos, puesto que las oscilaciones se cancelan a través de la integración. | |||
=='''Método de sumacion de Fejér.'''== | |||
En 1903, el matemático húngaro L. Fejér. Propuso una nueva forma de sumas los términos de la serie de Fourier. Se trata de sumar los promedios de las sumas parciales y pasar al limite. Se obtiene asi una nueva sucesión de funciones que producen convergencia incluso en algunos casos en los que la serie original no la tiene. | |||
Veamos como se construye la suma fe Fejér a partir de las sumas parciales de Fourier se construirá una nueva sucesión con el promedio de las sumas parciales | |||
<math>{ \sigma }_{ M }=\frac { 1 }{ M+1 } \sum _{ N=0 }^{ M }{ \frac { { s }_{ 0 }(x)+{ s }_{ 1 }(x)+...+{ s }_{ M }(x) }{ M+1 } }</math> | |||
La suma de Fejér es entonces | |||
<math>s(x)=\lim _{ M\rightarrow \infty }{ { \sigma }_{ M }(x) }</math> | |||
En cuanto a la convergencia de la sima de Fejér se tiene el siguiente teorema | |||
'''Teorema de Fejér''' | |||
Sea <math>f(x) </math> definida en el intervalo <math> (-\pi ,\pi ) </math>. Si <math>f</math> es acotada, supones que es integrable; si no es acotada, suponemos que la integral <math>\int _{ -\pi }^{ \pi }{ f(x)dx }</math> es absolutamente convergente. Entonces para cualquier punto <math>x</math> del intervalo las sumas parciales de Fejér <math>{ \sigma }_{ M }(x) </math> converge a <math>\frac { 1 }{ 2 } (f(x+)+f(x-))</math>. | |||
Y como una consecuencia del Teorema de Fejér tenemos que, si <math>f(x) </math> es continua en <math> [a,b] </math>, entonces la sucesión de las medias aritméticas <math>{ \sigma }_{ 0 },{ \sigma }_{ 1 },{ \sigma }_{ 2 },...</math> converge uniformemente a <math>f(x) </math> en el interior del intervalo <math> (a,b) </math>. | |||
Obviamente, cuando <math>f</math> es continua en <math>x</math>, <math>\frac { 1 }{ 2 } (f(x+)+f(x-))=f(x) </math> y por tanto, <math>{ \sigma }_{ M }(x) </math> converge a <math>f(x) </math>. | |||
Esta es la versión mas clásica del teorema, utilizando la integral de Riemann. | |||
[[Archivo:Gibbs_11..png|thumb|center|''Figura 10: '' Sumación parcial de Fejér M=40.]] | |||
Lo primero que se observa en la nueva grafica es que ahora tenemos un tipo de convergencia distinta, de hecho ahora tenemos convergencia uniforme (según el teorema anterior) en el interior del intervalo <math> (0,\pi ) </math> ( y, por simetría, en <math> (-\pi ,0) </math>). Por otra parte se puede observar que la grafica de la suma de Fejér cae por debajo (en el <math>0<x<\pi</math>, y por encima de <math>-\pi <x<0</math>) de la grafica de <math>f(x) </math>. De hecho puede probarse que todas las sumas parciales de Fejér verifican <math>|{ \sigma }_{ M }(x)|<1</math>, es decir ahora no se produce el fenómeno de Gibbs y aunque la grafica sigue teniendo las mismas oscilaciones, ahora son mucho menores. | |||
=='''Fourier versus Fejér'''== | |||
Dibujando ahora las graficas de las sumas de Fourier y las de Fejér juntas. En la figura X, se han dibujado superpuestas, las graficas de las sumas parciales de Fourier y de Fejér hasta el sumando <math>N=11</math>, en el intervalo <math> [0,\pi ] </math>. En la figura X, se ha representado lo mismo, pero ahora en el intervalo <math> [-\pi ,\pi ] </math>. En ambas figuras se pueden observar como las sumas parciales de Fourier y las de Fejér parecen coincidir en algunos puntos críticos de las sumas de Fourier. En concreto en el intervalo <math> [0,\pi ] </math>, esto ocurre en los minimos y, debido a la simetría impar, en el intervalo <math> [-\pi ,0] </math>, ocurre en los máximos. | |||
[[Archivo:Gibbs_12..png|thumb|center|''Figura 11: '' Fourier versus Fejér, N=29.]] | |||
Viendo que este curioso fenómeno no es solo aparente, ni debido a los errores de redondeo, sino que courre de hecho: | |||
En primer lugar, si la N-ésima suma parcial de Fourier es | |||
<math>{ S }_{ N }=\frac { { a }_{ 0 } }{ 2 } +\sum _{ k=1 }^{ N }{ [{ a }_{ k }cos(kx)+b_{ k }sin(kx)] }</math> | |||
[[Archivo:Gibbs_13..png|thumb|center|''Figura 12: '' Fourier versus Fejér, N=11.]] | |||
Entonces la N-ésima suma parcial de Fejér es, a partir de su expresión antes dada, se puede escribir de la forma alternativa | |||
<math>{ \sigma }_{ N }(x)=\frac { { a }_{ 0 } }{ 2 } +{ \beta }_{ k }\sum _{ k=1 }^{ N }{ [{ a }_{ k }cos(kx)+b_{ k }sin(kx)] }</math> | |||
Donde <math>{ \beta }_{ k }=1-\frac { k }{ N+1 }</math> | |||
Para el caso particular de la función salto, estas expresiones se convierten en | |||
<math>{ S }_{ 2n-1 }(x)=\frac { 4 }{ \pi } \sum _{ r=1 }^{ n }{ \frac { 1 }{ 2r-1 } sin((2r-1)x) }</math> | |||
Y | |||
<math>{ \sigma }_{ 2n-1 }(x)=\frac { 4 }{ \pi } \sum _{ r=1 }^{ n }{ \left( 1-\frac { 2r-1 }{ 2n } \right) \frac { 1 }{ 2r-1 } sin((2r-1)x) }</math> | |||
Los puntos en que se cortan, han de ser soluciones de la ecuación | |||
<math>{ S }_{ 2n-1 }(x)-{ \sigma }_{ 2n-1 }(x)=0</math> | |||
Por otra parte, si estos puntos son máximos o minimos, es decir, puntos críticos, entonces también deben de satisfacer la ecuacion | |||
<math>\frac { d }{ dx } [{ S }_{ 2n-1 }(x)]=0</math> | |||
Reescribiendo la ecuación para la suma parcial de Fourier como | |||
<math>{ S }_{ 2n-1 }(x)-{ \sigma }_{ 2n-1 }(x)=\frac { 4 }{ \pi } \sum _{ r=1 }^{ n }{ \frac { 1 }{ 2n } sin((2r-1)x) } =0</math> | |||
Por tanto | |||
<math>\sum _{ r=1 }^{ n }{ sin((2r-1)x) } =0</math> | |||
Que se puede transformar de la siguiente manera | |||
<math>0=\sum _{ r=1 }^{ n }{ sin((2r-1)x) } =\frac { 1 }{ 2sin(x) } \sum _{ r=1 }^{ n }{ 2sin((2r-1)x)sin(x) }</math> | |||
<math>=\frac { 1 }{ 2sin(x) } \sum _{ r=1 }^{ n }{ [cos(2(r-1)x-cos(2x))] }</math> | |||
<math>=\frac { 1 }{ 2sin(x) } \left[ \sum _{ r=0 }^{ n-1 }{ cos(2rx)-\sum _{ r=1 }^{ n }{ (2rx) } } \right]</math> | |||
<math>=\frac { 1-cos(2nx) }{ 2sin(x) }</math> | |||
Ahora bien la solución de la ecuación | |||
<math>\frac { 1-cos(2nx) }{ 2sin(x) } =0</math> | |||
En el intervalo <math> (0,\pi ) </math> son los puntos de la forma | |||
<math>{ x }_{ 1 }=\frac { \pi }{ n } ,\quad { x }_{ 2 }=\frac { 2\pi }{ n } ,\quad ...,\quad { x }_{ n-1 }=\frac { (n-1)\pi }{ n }</math> | |||
Y es sencillo comprobar que estos puntos son precisamente los minimos de la función <math>{ S }_{ 2n-1 }(x)</math>, ya que sabemos que | |||
<math>\frac { d }{ dx } [{ S }_{ 2n-1 }(x)]=\frac { 2 }{ \pi } \frac { sin(2nx) }{ sin(x) }</math> | |||
Luego, efectivamente las graficas de las sumas parciales de Fourier y las de Fejér se cortan en los minimos de las primeras, en el intervalo <math>(0,\pi )</math> y, por la simetría, en los máximos del intervalo (<math>-\pi ,0) </math> (excepto en el caso <math>n=1</math>, en el que no hay ningún minimo en <math> (0,\pi ) </math>). | |||
[[Archivo:Gibbs_14..png|thumb|center|''Figura 13: '' Delta de Dirac. Fourier versus Fejér, N=30.]] | |||
=='''Otras funciones con saltos.'''== | |||
La propiedad que se ha probado para la función <math> f(x)=sgn(x) </math> en <math> x\in\left(-\pi,\pi\right) </math>, ocurre para cualquier función que tenga un salto, en el entorno de esta. Sea g una función discontinua en un punto <math> x_{0} </math>, en el que tiene un salto <math> g\left(x_{0}+\right)-g\left(x_{0}-\right)=2l </math>. La función <math> g-lf </math> es continua en <math> x_{0} </math> y, por lo tanto, el comportamiento de la serie de Fourier de g </math> en un entorno de <math> x_{0} </math> es el mismo que el de <math> lf </math>. Es decir, la diferencia entre el limite cuando N tiende a infinito del máximo de <math> S_{N}g </math> en un entorno de <math> x_{0} </math> y el mayor de los valores <math> g\left(x_{0}+\right) </math> y <math> g\left(x_{0}-\right) </math> es <math> 0.17897944...l </math> y lo mismo ocurre por debajo. Esta propiedad se llama ''fenómeno de Gibbs''. | |||
[[Archivo:Grafica_5._gibbs.png|thumb|center|''Figura 15: '' Grafica de <math>{ S }_{ 15 }</math> en medio periodo par la función impar de periodo <math>2\pi</math> que vale <math>\pi -x</math> en <math>\left( 0,\pi \right) </math>.]] | |||
En 1898 Michelson y Stratton diseñaron un analizador armónico que permitía hacer gráficas de las sumas parciales series de Fourier. Observaron que en esas gráficas aparecía un exceso sobre el valor máximo de la función cuando estaba cerca del salto y Michelson envió una carta a la revista Nature pidiendo una explicación para el fenómeno. Durante los años 1898 y 1899 hubo varios artículos sobre el tema en la revista y finalmente fue Gibbs quien en 1899 aclaro la situación. El nombre de fenómeno de Gibbs es debido a bôcher. | |||
Posteriormente se descubrió que ya en 1848 Wilbraham había publicado un articulo titulado On a certain periodic (Cambridge Dublin Math. J. 3, 1848) en el que había descubierto el fenómeno. Wilbraham estudiaba la serie | |||
<math> \sum _{ k=0 }^{ \infty }{ \left( -1 \right) ^{ k }\frac { \cos \left( 2k+1 \right) x }{ 2k+1 } } </math> | |||
Que corresponde a un función que vale <math> { \pi / }{ 4 }</math> entre <math> -\pi /2</math> y <math> \pi /2</math> y -<math> \pi /4</math> en el resto del periodo y que aparece en el libro de Fourier; indica que erróneamente algunos autores dicen que las sumas parciales están comprendidas entre <math> \pi /4</math> y <math> -\pi /4</math>, demuestra que no es así y obtiene el valor exacto del exceso. | |||
=='''Referencias'''== | |||
''A source Book in Classical Analysis'', Editado por G. Birkhoff (Harvard University Press, 1973). | |||
G. Bachmann, L. Narici y E. Beckenstein, ''Function Fourier and wavelet analysis'', Springer-Verlag, New York, 2002. | |||
Gerald B. Folland, ''Fourier analysis and it's applications'', Wadsworth & Brooks, California, 1992. | |||
[[Usuario:Luis Gutierrez|Luis Gutiérrez Melgarejo]] | |||
---- | |||
= aproximación de ondas esféricas a planas. = | |||
== Introducción. == | |||
de todas las ondas tridimencionales la onda plana es la única que puede moverse a lo largo de su dirección sin cambiar su perfil (armónica o no),aunque se ve claro que esta idea es incompleta. De la misma forma se puede definir una onda como una solucion cualquiera de la ecuación diferencial de onda. Necesitaremos una ecuación tridimensional lo cual no sera difícil de conseguir. | |||
== Onda plana. == | |||
Entraremos en la definición de onda plana. | |||
En la física de propagación de ondas (especialmente en campos y ondas electromagnéticas), una onda plana o también llamada onda monodimensional, es una onda de frecuencia constante cuyos frentes de onda (superficies con fase constante) son planos paralelos de amplitud constante normales al vector velocidad de fase. Es decir, son aquellas ondas que se propagan en una sola dirección a lo largo del espacio. | |||
[[Imagen:Planas.jpeg]] fig(1) | |||
Este es el ejemplo más sencillo de onda tridimensional. Existe en un instante dado cuando todas las superficies sobre las cuales una perturbación tiene fase constante, forman un conjunto de planos, cada uno generalmente perpendicular a la dirección de propagación. | |||
[[Imagen:111.jpg]] fig (2) | |||
Para deducir la expresión matemática de un plano perpendicular a un vector dado '''k''' y que pasa a través de algún punto <math>(x_{0},y_{0},z_{0})</math>, primero se escribe el vector de posición en coordenadas cartesianas, en términos de los vectores unitarios de la base. | |||
[[Imagen:fig 10.jpg]] fig (3) | |||
<math>\textbf{r}=x \hat{\mathbf{e}}_x+y \hat{\mathbf{e}}_y+z \hat{\mathbf{e}}_z</math> | |||
Comienza en algún origen arbitrario '''O''' y termina en el punto <math>(x,y,z)</math> que, por el momento debe ser cualquier lugar en el espacio. | |||
sabemos por la ecuación del plano que un vector único paralelo a un plano no basta para definir la dirección del plano, pero un vector perpendicular al plano sí la especifica. Así un plano en el espacio esta determinado por un punto <math>(x_0,y_0.z_0)</math> en el plano y un vector '''k'''que es ortogonal al plano. Este vector ortogonal '''k''' se llama '''vector normal'''. Sea <math>(x, y, z)</math> un punto arbitrario en el plano, y sean <math>\mathbf{r_0}</math> y <math>\mathbf{r}</math> los vectores de posición <math>P_0 y P</math>. Entonces, el vector <math>\mathbf{r}-\mathbf{r_0}</math> esta representado por <math>P_0P</math>. El vector normal <math>\mathbf{k}</math> es ortogonal a cada vector en un plano determinado. En particular, <math>\mathbf{k}</math> es ortogonal a <math>\mathbf{r}-\mathbf{r_0}</math> ver (fig 1) por lo que tenemos | |||
<math>(\textbf{r}-\textbf{r}_{0})=(x-x_{0})\hat{\mathbf{e}}_x+(y-y_{0})\hat{\mathbf{e}}_y+(z-z_{0})\hat{\mathbf{e}}_z</math> | |||
Estableciendo | |||
<math>(\textbf{r}-\textbf{r}_{0})\cdot\textbf{k}=0</math> (1) | |||
obligando al vector <math>(\textbf{r}-\textbf{r}_{0})</math> a barrer un plano perpendicular a '''k''', al ir adquiriendo su punto extremo <math>( x ,y, z )</math> todos los valores permitidos. | |||
Con | |||
<math>\textbf{k}=k\hat{\mathbf{e}}_x+k\hat{\mathbf{e}}_y+k\hat{\mathbf{e}}_z</math> (2) | |||
la ecuación (1) puede expresarse como | |||
<math> k_{x}(x-x_{0}) + k_{y}(y-y_{0}) + k_{z}(z-z_{0})=0 </math> (3) | |||
o como | |||
<math> k_{x}x + k_{y}y + k_{z}z =0 </math> (4) | |||
donde | |||
<math>a = k_{x}x_{0} + k_{y}y_{0} + k_{z}z_{0}\ =constante </math> (5) | |||
La forma más concisa de la ecuación de un plano perpendicular a '''k''' es entonces | |||
<math>\textbf{k}\cdot\textbf{r}=constante=a</math> | |||
El plano es el lugar de todos los puntos cuyos vectores de posición tienen cada uno la misma proyección en la dirección de <math>\textbf{k}</math>. | |||
Ahora podemos construir un conjunto de planos sobre los cuales <math>\psi(\textbf{r})</math> varía de manera sinusoidal en el espacio, es decir | |||
consideremos: | |||
<math>\psi(\textbf{r})=A e^{i\textbf{k}\cdot\textbf{r}} </math> ec(6) | |||
Por todas estas expresiones <math>\psi(\textbf{r})</math> se mantiene constante sobre cada plano definido por <math>\textbf{k}\cdot\textbf{r}=constante</math>. Como estamos analizando las funciones armónicas, deberían repetirse en el espacio después de un desplazamiento de <math>\lambda</math> en la dirección de '''k'''. En la figura se representa esta clase de expresión. Del infinito número de planos se han dibujado sólo unos pocos, cada uno con una <math>\psi(\textbf{r})</math> diferente. Los planos deberían también haberse dibujado con una extensión espacial infinita, ya que no se han puesto límites a <math>\textbf{r}</math>. La perturbación ocupa claramente todo el espacio. | |||
[[Imagen:fig 9.jpg]] fig (4) | |||
La naturaleza repetitiva espacial de estas funciones armónicas se puede expresar por | |||
<math>\psi(\textbf{r})=\psi(\textbf{r}+\frac{\lambda\textbf{r}}{k}) </math> (7) | |||
Donde <math>k </math> es la magnitud de <math>\textbf{k}</math> y <math>\textbf{k}/{k}</math> es un vector unitario paralelo a él. | |||
[[Imagen:999.jpg]]fig (5) | |||
En la forma exponencial, esto equivale a | |||
<math>A e^{i\textbf{k}\cdot\textbf{r}} =Ae^{i\textbf{k}\cdot\textbf{r}+\lambda\textbf{k}/k)}=A e^{i\textbf{k}\cdot\textbf{r}} e^{i\lambda{k}}</math> | |||
Para que sea cierto, debemos tener | |||
<math>e^{i\lambda{k}}=1=e^{i2\pi}</math> | |||
Por consiguiente | |||
<math>\lambda{k}=2\pi</math> | |||
y | |||
<math>k=2\pi/\lambda</math> | |||
El vector '''k''', cuya magnitud es el número de propagación <math>k</math>, se llama vector de onda o de propagación. Ver [[ondas: vector de onda]] | |||
En cualquier punto fijo del espacio donde '''r''' es constante, la fase es constante y también lo es <math>\psi(\textbf{r})</math>; en resumen, los planos están inmóviles. Para hacer que se muevan, <math>\psi(\textbf{r})</math> debe hacerse variar en el tiempo, algo que puede lograrse introduciendo la dependencia del tiempo en una forma análoga a la de una onda unidimensional. | |||
Aquí entonces | |||
<math>\psi(\textbf{r},t)=Ae^{i(\textbf{k}\cdot\textbf{r}\pm\omega{t})}</math> ec(8) | |||
sin embargo, hemos examinado las ondas planas poniendo de relieve que son funciones armónicas, no obstante cualquier onda tridimensional puede expresarse como una combinación de ondas planas. | |||
Involucraremos a la ecuación de onda tridimensional que tiene la siguiente forma: | |||
<math>{ \triangledown }^{ 2 }=\frac { { \partial }^{ 2 } }{ { { \partial x }^{ 2 } } } +\frac { { \partial }^{ 2 } }{ { { \partial y }^{ 2 } } } +\frac { { \partial }^{ 2 } }{ { { \partial z }^{ 2 } } } ={ \triangledown }^{ 2 }\Psi =\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 }\Psi }{ { { \partial t }^{ 2 } } } </math> | |||
Regresando a la onda plana, esta queda de la siguiente manera: | |||
<math>\Psi (x,y,z)=A{ e }^{ ik(\alpha x+\beta y+\gamma z+vt) }</math> | |||
Son ambas soluciones de onda plana que tendrían la siguiente forma: | |||
<math>\Psi (x,y,z)=f(\alpha x+\beta y+\gamma z+vt)\quad y\quad \Psi (x,y,z)=g(\alpha x+\beta y+\gamma z-vt)</math> | |||
Donde las funciones f y g son diferenciables 2 veces son arbitrarias y no necesitan se prescisamente armonicas. | |||
== Ondas esfericas. == | |||
Hay situaciones físicas en las que podremos sacar mas provecho utilizando otro tipo de coordenadas | |||
Considérese ahora una fuente puntual de luz, la radiación que procede de ella fluye directamente hacia afuera, se dice que es isotropa y que son esferas concentricas los frentes de onda. | |||
en términos de coordenadas esféricas polares, el operador laplaciano es: | |||
<math>{ \triangledown }^{ 2 }=\frac { 1 }{ { r }^{ 2 } } \frac { { \partial } }{ \partial { r } } \left( { r }^{ 2 }\frac { \partial }{ \partial r } \right) +\frac { 1 }{ { r }^{ 2 }sen\theta } \frac { \partial }{ \partial \theta } \left( sen\theta \frac { \partial }{ \partial \theta } \right) +\frac { 1 }{ { r }^{ 2 }{ sen }^{ 2 }\theta } \frac { { \partial }^{ 2 } }{ \partial { \phi }^{ 2 } } </math> | |||
Ahora las coordenadas(x,y,z) son: <math>x=rsen\theta cos\phi ,\quad y=rsen\theta sen\phi \quad y\quad z=rcos\theta </math> | |||
como estamos considerando ondas que son simétricas no dependeran de ángulos solo la parte radial, por tanto: <math>\Psi (r)=\Psi (\theta ,\phi ,r)=\psi (r)</math> ec(9) | |||
[[Imagen:ondas es.jpg]] fig(6) | |||
Entonces el laplaciano queda de la siguiente forma: | |||
<math>{ \triangledown }^{ 2 }\Psi (r)=\frac { 1 }{ { r }^{ 2 } } \frac { \partial }{ \partial r } \left( { r }^{ 2 }\frac { \partial \Psi }{ \partial r } \right) </math>, lo cual es: <math>{ \triangledown }^{ 2 }\Psi (r)=\frac { 1 }{ { r } } \frac { { \partial }^{ 2 } }{ \partial { r }^{ 2 } } (r\Psi )</math> | |||
También esta ecuación diferencial de onda se puede escribir como: <math>\frac { 1 }{ { r } } \frac { { \partial }^{ 2 } }{ \partial { r }^{ 2 } } (r\Psi )=\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } </math> | |||
Al multiplicar ambos lados por r, obtenemos: <math>\frac { { \partial }^{ 2 } }{ \partial { r }^{ 2 } } (r\Psi )=\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 } }{ { \partial t }^{ 2 } } (r\Psi )</math> | |||
Observamos que esta expresión es ahora la ecuación de onda unidimensional, donde la variable espacial es r. la solución seria entonces: <math>r\Psi (r,t)=f(r-vt)=\frac { f(r-vt) }{ r } </math> ec(10) | |||
Esto representa una onda esférica que progresa radialmente hacia afuera, aunque también la siguiente solución es valida: <math>r\Psi (r,t)=\frac { g(r+vt) }{ r } </math>, que en este caso la onda esta convergiendo hacia el origen. | |||
Un caso especial de la solución general es la suma de las 2 soluciones con sus respectivas constantes es la onda esférica armónica: | |||
<math>\Psi (r,t)=\frac { A }{ r } cosk\left( r+vt \right) \quad o\quad \Psi (r,t)=\frac { A }{ r } cosk\left( r-vt \right) </math> ec(11) | |||
Donde la constante A se denomina la intensidad de la fuente. para cualquier valor fijo del tiempo, esto representa una agrupación de esferas concentricas que abarcan todo el espacio. Cada frente de onda o superficie de fase constante esta dado por | |||
<math>kr=constante</math>. | |||
[[Imagen:ondas esfericas.jpg]] fig(7) | |||
nos damos cuenta que la amplitud de onda esférica depende explicitamente de r, y este termino con exponente negativo sirve como atenuación. A diferencia de la onda plana que aumenta su amplitud, esta disminuye consecuente en su propagación. | |||
La siguiente figura muestra el siguiente hecho, cuando un frente de onda esférico se propaga hacia afuera, su radio aumenta a una distancia considerable de su fuente, una pequeña área de frente se aproximara a una porción de una onda plana. | |||
[[Imagen:Planas.jpeg]] fig(8) | |||
nos damos cuenta que la ecuación de la onda plana no tiene un factor de atenuación como la ecuación de onda esférica. | |||
<math>\Psi (r,t)=\frac { A }{ r } cosk\left( r+vt \right) \quad o\quad \Psi (r,t)=\frac { A }{ r } cosk\left( r-vt \right) </math> si nosotros consideramos una distancia muy grande de la fuente (r muy grande) | |||
entonces | |||
<math>\Psi (r,t)=\frac { A }{ r } cosk\left( r+vt \right) \quad o\quad \Psi (r,t)=\frac { A }{ r } cosk\left( r-vt \right) \widetilde { = } A{ e }^{ i(k\bullet r+\omega t) }</math> ec(12) | |||
que es la ecuación de una onda plana, como se había comentado esta es la única onda que no cambia mientras se propaga. | |||
=='''Referencias'''== | |||
''A source Book in Classical Analysis'', Editado por G. Birkhoff (Harvard University Press, 1973). | |||
''Óptica, Tercera Edición; Eugene Hecht''.<br /> | |||
720pp, Addison-Wesley Iberoamericana, Madrid, España, 2000. | |||
Gerald B. Folland, ''Fourier analysis and it's applications'', Wadsworth & Brooks, California, 1992. | |||
[[Usuario:salvadormorales|Salvador Morales Carranza]] | |||
---- | |||
---- | |||
= Formulación Covariante de los campos electromagnéticos. = | |||
== Introducción. == | |||
La fórmula fundamental en Mecánica Clásica, <math> \vec{F}=m\vec{a} </math>, es ''aproximadamente'' correcta, pues, no presenta los efectos que se producen al considerar grandes velocidades. Por lo cual, la Mecánica Clásica requiere de una reformulación, actualmente dada por la ''Teoría de la Relatividad''. Con esto uno puede decir que la Mecánica Clásica obedece los principios de la relatividad. Surge la pregunta: ¿La Electrodinámica obedece los principios de la relatividad?. La respuesta es que sí y , de hecho, no requiere de una reformulación como en el caso de la Mecánica Clásica. | |||
En la Mecánica Clásica, los conceptos de ''espacio'' y ''tiempo'' son completamente separables, esto es porque se toma al tiempo como una cantidad absoluta, independiente del sistema de referencia. Está implícito en Clásica que la "acción a distancia" debido a , ya sea, fuerzas gravitacionales o electromagnéticas, se transmite de manera instantánea. Esto deja ''invariante'' a las leyes de la Mecánica Clásica ante ''transformaciones Galileanas'': | |||
'''I.1''' | |||
:<math> x'=x-vt </math> | |||
:<math> y'=y </math> | |||
:<math> z'=z </math> | |||
:<math> t'=t </math> | |||
[[Archivo:Transformación_de_Galileo.gif]] | |||
Siendo las variables primadas descritas en un sistema de referencia <math> O' </math> que se mueve a velocidad <math> v </math> respecto a un sistema <math> O </math> (comúnmente a estas traslaciones sobre un eje, en este caso el eje x, se les conoce como "boost" en x), ambos sistemas son inerciales. | |||
De '''I.1''', se observa que el elemento de longitud entre puntos son el mismo para ambos sistemas de referencia: | |||
:<math> ds^{2}=\sum_{j}^{3} (dx_{j})^{2}=\sum_{j}^{3} (dx'_{j})^{2} =ds'^{2} </math>.....'''I.2''' | |||
En el caso de <math> \Re^{2} </math> (''Plano Euclidiano''), la ecuación '''I.2''' se reescribe en forma matricial como: | |||
<math> ds^{2}= \ \begin {bmatrix} dx & dy \end {bmatrix}\begin {bmatrix} 1 & 0 \\ 0 & 1 \end {bmatrix}\ \begin {bmatrix} dx \\ dy \end {bmatrix}</math>; | |||
siendo | |||
:<math> \delta^{i}_{j}=\begin {bmatrix} 1 & 0 \\ 0 & 1 \end {bmatrix} </math>.....'''I.3''' | |||
la ''métrica'' en el plano Euclidiano. | |||
También, se observa que de '''I.1''' que <math> \vec{F}_{j}=m\frac{d^{2}x_{j}}{dt^{2}}=m\frac{d^{2}x'_{j}}{dt^{2}}=\vec{F}'_{j}, j=x,y,z </math>. | |||
Sin embargo, las ecuaciones de Maxwell no son invariantes ante ''I.1''. Para visualizar dicho acervo, consideremos la ecuación de onda para un potencial: | |||
:<math> \nabla^{2}\Phi=-\frac{1}{c^{2}}\frac{\partial^{2}\Phi}{\partial t^{2}}=0 </math>.....'''I.4''' | |||
pero bajo '''I.1''', tenemos que: | |||
:<math> \frac{\partial^{2}}{\partial (x_{1})^{2}}=\frac{\partial^{2}}{\partial (x'_{1})^{2}} </math>; | |||
:<math> \frac{\partial^{2}}{\partial (x_{2})^{2}}=\frac{\partial^{2}}{\partial (x'_{2})^{2}} </math>; | |||
:<math> \frac{\partial^{2}}{\partial (x_{3})^{2}}=\frac{\partial^{2}}{\partial (x'_{3})^{2}} </math>; | |||
:<math> \frac{\partial }{\partial t}=\frac{\partial }{\partial t'}-v\frac{\partial }{\partial x'_{3}} </math>; | |||
:<math> \frac{\partial^{2}}{\partial t^{2}}=\frac{\partial^{2}}{\partial t'^{2}}+v^{2}\frac{\partial^{2}}{\partial (x'_{3})^{2}}-2v\frac{\partial^{2}}{\partial t'\partial x'_{3}} </math> | |||
por lo que '''I.4''' transforma como: | |||
:<math> \nabla '^{2}\Phi - \frac{1}{c^{2}}\frac{\partial^{2}\Phi}{\partial t'^{2}}-\frac{v^{2}}{c^{2}}\frac{\partial^{2}\Phi}{\partial (x'_{3})^{2}}+\frac{2v}{c^{2}}\frac{\partial^{2}\Phi}{\partial t'\partial x'_{3}}=0 </math>.....'''I.5''' | |||
'''I.5''' no describe la propagación de una onda electromagnética en la manera que describe Albert Einstein en sus postulados de la teoría de la relatividad. Entonces, la electrodinámica no es consistente con la invarianza de Galileo. Sin embargo las leyes de Maxwell son invariantes ante ''transformaciones de Lorentz'': | |||
:<math> x'^{\mu}=\sum_{\nu =0}^{3} \Lambda^{\mu}_{\nu}x^{\nu} </math>.....'''I.6''' | |||
Dicha transformación ('''I.6''') es una transformación ortogonal en el espacio de ''Minkowski'', con: | |||
:<math> \Lambda^{\mu}_{\nu}:= \ \begin {bmatrix} \gamma & -\gamma\beta & 0 & 0 \\ -\gamma\beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end {bmatrix} </math>.....'''I.7''' la matriz de transformación de Lorentz y, | |||
<math> \gamma = \frac{1}{\sqrt{1-\beta^{2}}} </math> & <math> \beta =\frac{v}{c} </math> ; ''c'' la velocidad de la luz. | |||
Cuando una ecuación que expresa una relación física es transformada de un sistema de referencia a otro bajo '''I.6''', se dice que dicha ecuación es ''covariante'' si su forma permanece sin cambio. | |||
De lo anterior, uno puede encontrar las ''coordenadas espacio-tiempo'' de un "boost en <math> x' </math>" de un sistema <math> S' </math> que se mueve a velocidad <math> v </math> respecto de un sistema <math> S </math>, introduciendo la coordenada <math> x^{0}= ct </math>: | |||
'''I.7''' | |||
:<math> x'^{0}=\gamma (x^{0}-\beta x^{1}) </math> | |||
:<math> x'^{1}=\gamma (x^{1}-\beta x^{0}) </math> | |||
:<math> x'^{2}=x^{2} </math> | |||
:<math> x'^{3}= x^{3} </math> | |||
los índices 1,2 y 3 corresponden a las coordenadas x,y y z respectivamente. | |||
Entonces, '''I.6''' muestra la forma en cómo transformar de un sistema en el espacio de Minkowski, en el cual se definen 4-vectores (vectores de 4 entradas): | |||
:<math> (x^{0},x^{1},x^{2},x^{3}) </math> | |||
en otro. | |||
'''I.7''' se obtienen al considerar los efectos que se dan en la ''teoría de la relatividad especial'' en las ecuaciones '''I.1''', por ejemplo, a la ecuación <math> t'=t </math> debe ser reemplazada por una regla que incorpore los efectos de ''dilatación del tiempo'', la ''relatividad de la simultaneidad'', y la ''no sincronización '' de relojes en movimiento relativo. Lo anterior implicará entonces una modificación también a la ecuación <math> x'=x-vt </math> | |||
En éste espacio, existe una analogía con el producto punto del espacio euclidiano, la única diferencia radica en que la componente de índice cero aparece un signo menos: | |||
<math> -a^{0}b^{0} + a^{1}b^{1} + a^{2}b^{2} + a^{3}b^{3} </math>.....'''I.8''' | |||
'''I.8''' es el 4-dimensional producto escalar, de hecho, es un ''invariante'' (para el "boost en x") bajo transformaciones de Lorentz, como lo es el producto punto en el espacio euclidiano bajo transformaciones de Galileo ('''I.2'''). | |||
Es importante aquí introducir la distinción entre un vector covariante (<math> a_{\mu} </math>) y un vector contravariante (<math> a^{\mu} </math>), ya que, difieren sólo en el signo de la componente cero: | |||
<math> a_{\mu}=(a_{0},a_{1},a_{2},a_{3})=(-a^{0},a^{1},a^{2},a^{3}) </math> | |||
formalmente esto es: | |||
:<math> a_{\mu}=\sum_{\nu =0}^{3} g_{\mu\nu}a^{\nu} </math>.....'''I.9''' | |||
con <math> g_{\mu\nu}= \ \begin {bmatrix} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end {bmatrix} </math> la métrica de Minkowski que es un análogo a '''I.3'''. | |||
Pero ¿qué es este espacio de Minkowski?. Bueno, si uno desea representar el movimiento de una partícula, lo normal es graficar dicho movimiento en un diagrama posición contra tiempo. En dichos diagramas la velocidad se lee como la pendiente de la recta tangente en un punto de la curva. Por esta razón, dicha técnica también se conserva en relatividad, sólo que el eje que representa al tiempo (o mejor dicho <math> x^{0}=ct </math>) es el eje vertical. La velocidad será entonces el recíproco de la pendiente de la recta tangente en un punto de la curva. Una partícula en reposo está representada por una línea vertical; un fotón, viajando a la velocidad de la luz es descrito por una línea de 45 grados; y un cohete espacial viajará a una velocidad intermedia siguiendo una linea de pendiente <math> \frac{c}{v}=\frac{1}{\beta} </math>. Llamamos a dichos diagramas ''diagramas de Minkowski''. | |||
[[Archivo:Cono-de-luz1.png]] | |||
Justo aquí entra el gran dilema de Albert Einstein: ¿qué hay que corregir, la Mecánica de Newton o la Electrodinámica de Maxwell? | |||
== Preliminares. == | |||
'''1.1 Nota.'''Los valores de los índices que tomaremos correrán sobre el conjunto <math> \{1,2,...\} </math> | |||
'''1.2 Acuerdo'''(Convención de suma). Si un índice está repetido en un término dentro de una expresión matemática, ésto indica que hay una suma sobre ''todos'' los valores de dicho índice. | |||
'''1.3 Definición.''' Un conjunto de <math> n^{r+s} </math> funciones <math> T^{h_{1}...h_{r}}_{k_{1}...k_{s}}(x^{q}) </math> se dice que constituyen las componentes de un campo tensorial de tipo <math> (r,s) </math> sobre una variedad <math> X_{n} </math>, si, bajo la transformación de coordenadas: | |||
:<math> \bar{x}^{j}=\bar{x}^{j}(x^{h}) </math>, | |||
estas funciones transforman de acuerdo a la regla: | |||
:<math> \bar{T}^{j_{1}...j_{r}}_{l_{1}...l_{s}}(\bar{x}^{p})=\frac{\partial\bar{x}^{j_{1}}}{\partial x^{h_{1}}}...\frac{\partial\bar{x}^{j_{r}}}{\partial x^{h_{r}}}.\frac{\partial x^{k_{1}}}{\partial\bar{x}^{h_{1}}}...\frac{\partial x^{k_{s}}}{\partial\bar{x}^{l_{s}}}T^{h_{1}...h_{r}}_{k_{1}...k_{s}}(x^{q}). </math> | |||
el rango de dicho tensor es <math> r+s </math>. | |||
En el caso especial de 1.1, tenemos los siguientes tensores: | |||
:<math> \bar{A}^{j}=\frac{\partial\bar{x}^{j}}{\partial x^{h}}A^{h} </math>, vector contravariante (tensor de tipo (1,0)); | |||
:<math> \bar{C}^{j}=\frac{\partial x^{h}}{\partial\bar{x}^{j}}C_{h} </math>, vector covariante (tensor de tipo (0,1)); | |||
:<math> \bar{T}^{j}_{l}=\frac{\partial\bar{x}^{j}}{\partial x^{h}}\frac{\partial x^{k}}{\partial\bar{x}^{l}}T^{h}_{k} </math>, tensor de tipo (1,1). | |||
De hecho, uno puede probar que la ''delta de Kronecker'' <math> \bar{\delta}^{j}_{l} </math> es un tensor de tipo (1,1). | |||
Tensores de tipo (0,0) se les denomina escalares o ''invariantes''. | |||
'''1.4 Definición.'''Siempre es posible multiplicar tensores de tipo arbitrarios en un punto P sobre <math> X_{n} </math> componente a componente. Más precisamente, la multiplicación de las componentes de dos tensores de tipo <math> (r_{1},s_{2}) </math> & <math> (r_{2},s_{2}) </math> en P da un tensor de tipo <math> (r_{1}+r_{2},s_{1}+s_{2}) </math> en P. | |||
'''1.5 Definición.''' Considérese un tensor de orden <math> (r,s) </math>, la contracción de dicho tensor se forma tomando la suma sobre un par de índices, uno contravariante y uno covariante. El tensor resultante de la contracción es un tensor de tipo <math> (r-1,s-1) </math> (ordenes menor que el original). | |||
'''1.6 Definición.''' Se dice que un tensor es simétrico si al permutar un par de sus superíndices (o un par de sus subíndices) las componentes de dicho tensor permanecen si cambio. Se dice que un tensor es anti-simétrico si al permutar un par de sus superíndices (o un par de sus subíndices) las componentes de dicho tensor se multiplican por -1. | |||
== Ecuaciones de Maxwell en forma covariante. == | |||
'''Nota.''' Las unidades que vamos a utilizar serán las unidades ''Gaussianas'' para los campos. | |||
Los índices que vamos a utilizar corren sobre <math> \{0,1,2,3\} </math> siendo 0 correspondiente a la coordenada temporal y las restantes correspondientes a las coordenadas espaciales x,y,z. | |||
Buscamos escribir una acción (escalar) para el campo electromagnético covariante, es decir: | |||
:<math> S=\int d^{4}x\mathcal{L}(E,B,\dot{E},\dot{B};t) </math>.....'''3.1''' | |||
siendo <math> \mathcal{L} </math> análoga a la ''lagrangiana'' en Mecánica Clásica, salvo que <math> \mathcal{L} </math> se le denomina ''densidad lagrangiana'' debido a sus unidades <math> [\mathcal{L}]=\frac{1}{L^{3}} </math>. | |||
Los campos que vamos a utilizar para nuestro propósito son los auxiliares: <math> (\phi ,\vec{A}) </math>, que satisfacen las constricciones: | |||
:<math> \vec{B}=\nabla\times\vec{A} </math> & <math> \vec{E}=-\frac{\partial\vec{A}}{\partial t}-\nabla\phi </math> | |||
Construyamos el ''cuadripotencial'' <math> A^{\mu}(x^{\nu}):=(\phi ,\vec{A}) </math> y a su vez construyamos una matriz: | |||
:<math> F^{\mu\nu}(x^{\alpha}):=\partial^{\mu}A^{\nu}-\partial^{\nu}A^{\mu} </math>..... '''3.2''' | |||
A '''3.2''' se le conoce como ''tensor de intensidad de campo''. | |||
De '''3.2''', observamos que: | |||
:<math> F^{\mu\nu}= \ \begin {bmatrix} 0 & \frac{E^{1}}{c} & \frac{E^{2}}{c} & \frac{E^{3}}{c} \\ -\frac{E^{1}}{c} & 0 & B^{3} & -B^{2} \\ -\frac{E^{2}}{c} & -B^{3} & 0 & B^{1} \\ -\frac{E^{3}}{c} & B^{2} & -B^{1} & 0 \end {bmatrix} </math> | |||
A partir de '''3.2''' podemos definir su ''dual'' como: | |||
:<math> \ast F^{\mu\nu}:=\frac{1}{2}\epsilon^{\mu\nu\alpha\beta}F_{\alpha\beta} </math>.....'''3.3''' | |||
Lo que se realiza en '''3.3''' es que cambia al campo magnético <math> B^{j} </math> por el campo eléctrico <math> -\frac{E^{j}}{c} </math> y al campo eléctrico <math> \frac{E^{k}}{c} </math> por el campo magnético <math> B^{k} </math> para <math> 0\leq j,k\leq 3 </math> | |||
Con '''3.2''' y '''3.3''' podemos construir escalares para '''3.1''', ya que, ésta es un escalar, sin embargo, no todas las opciones que se nos puedan presentar pueden ser utilizadas para nuestro propósito, por ejemplo, entre estas opciones tenemos: | |||
:<math> F^{\mu\nu}F_{\mu\nu} </math>.....'''3.4''' | |||
& | |||
:<math> F^{\mu\nu}\ast F_{\mu\nu} </math>.....'''3.5''' | |||
pero '''3.5''' es un ''pseudoescalar''. No hay otra opción para '''3.1''' que utilizar '''3.4''', ya que funciona perfecto para nuestro propósito( uno puede verificar realizando el producto de matrices y convencerse que '''3.4''' dará órdenes cuadráticos en los campos, por lo que, al hacer la variación, estos órdenes se reducirán a orden lineal en los campos, como debe ser según las ecuaciones de Maxwell),entonces: | |||
:<math> S=\int d^{4}x(-\frac{1}{16\pi} F^{\mu\nu}F_{\mu\nu}) </math>.....'''3.6''' | |||
Para considerar fuentes de campo, acoplamos con un "término de interacción": <math> -\frac{1}{c}j^{\mu}A_{\mu} </math>. Entonces: | |||
:<math> S=\int d^{4}x(-\frac{1}{16\pi} F^{\mu\nu}F_{\mu\nu}-\frac{1}{c}j^{\mu}A_{\mu}) </math>.....'''3.7''' | |||
Variando '''3.7''', arribamos a las ''ecuaciones de Euler-Lagrange''(para no cargar con notación, quitemos por el momento las constantes <math> \frac{1}{16\pi}</math> & <math> \frac{1}{c}</math>) | |||
:<math> \frac{\partial\mathcal{L}}{\partial A_{\nu}}-\partial _{\mu}(\frac{\partial\mathcal{L}}{\partial (\partial _{\mu}A_{\nu})})=0 </math> | |||
Calculemos: <math> \frac{\partial\mathcal{L}}{\partial A_{\nu}}=\frac{\partial}{\partial A_{\nu}}(-j^{\mu}A_{\mu})=-j^{\mu}\delta^{\nu}_{\mu}=-j^{\nu} </math>.Entonces: | |||
:<math> \frac{\partial\mathcal{L}}{\partial (\partial _{\mu}A_{\nu})}=\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}[-\frac{1}{4}g^{\alpha\rho}g^{\beta\sigma}F_{\rho\sigma}F_{\alpha\beta}]=-\frac{1}{4}g^{\alpha\rho}g^{\beta\sigma}[F_{\rho\sigma}\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}F_{\alpha\beta} + (\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}F_{\rho\sigma})F_{\alpha\beta}] </math>. | |||
Observe que aquí bajamos los índices del tensor <math> F^{\mu\nu} </math>, para ello utilizamos la ecuación '''I.9''' y el hecho de que <math> F^{\mu\nu} </math> es un tensor de tipo (2,0), por lo que para bajar sus índices recurrimos a la métrica de Minkowski. | |||
Donde: | |||
:<math>\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}F_{\alpha\beta}=\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}(\partial_{\alpha}A_{\beta}-\partial_{\beta}A_{\alpha})=\delta^{\mu}_{\alpha}\delta^{\nu}_{\beta}-\delta^{\mu}_{\beta}\delta^{\nu}_{\alpha} </math> | |||
& | |||
:<math>\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}F_{\rho\sigma}=\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}(\partial_{\rho}A_{\sigma}-\partial_{\sigma}A_{\rho})=\delta^{\mu}_{\rho}\delta^{\nu}_{\sigma}-\delta^{\mu}_{\sigma}\delta^{\nu}_{\rho} </math>. | |||
Así: | |||
:<math> g^{\alpha\rho}g^{\beta\sigma}\delta^{\mu}_{\alpha}\delta^{\nu}_{\beta}-g^{\alpha\rho}g^{\beta\sigma}\delta^{\mu}_{\beta}\delta^{\nu}_{\alpha}=g^{\mu\rho}g^{\nu\sigma}-g^{\nu\rho}g^{\mu\sigma} </math> | |||
:<math> g^{\alpha\rho}g^{\beta\sigma}\delta^{\mu}_{\rho}\delta^{\nu}_{\sigma}-g^{\alpha\rho}g^{\beta\sigma}\delta^{\mu}_{\sigma}\delta^{\nu}_{\rho}=g^{\alpha\mu}g^{\beta\nu}-g^{\alpha\nu}g^{\beta\mu}</math> | |||
Ahora, multiplicando por <math> F_{\rho\sigma} </math> & <math> F_{\alpha\beta}</math> las ecuaciones anteriores respectivamente obtenemos: | |||
:<math> F_{\rho\sigma}(g^{\mu\rho}g^{\nu\sigma}-g^{\nu\rho}g^{\mu\sigma})=F^{\mu\nu}-F^{\nu\mu} </math> | |||
& | |||
:<math> (g^{\alpha\mu}g^{\beta\nu}-g^{\alpha\nu}g^{\beta\mu})F_{\alpha\beta}=F^{\mu\nu}-F^{\nu\mu} </math> | |||
De lo anterior: <math>\frac{\partial\mathcal{L}}{\partial (\partial _{\mu}A_{\nu})}=-\frac{1}{4}[F^{\mu\nu}-F^{\nu\mu}]-\frac{1}{4}[F^{\mu\nu}-F^{\nu\mu}]=-\frac{1}{2}(F^{\mu\nu}-F^{\nu\mu})=-\frac{1}{2}(F^{\mu\nu}-(-F^{\mu\nu}))=-F^{\mu\nu} </math>. | |||
Finalmente: | |||
:<math> -j^{\nu}-\partial_{\mu}(-F^{\mu\nu})=0 </math> | |||
entonces: | |||
:<math> \partial_{\mu}F^{\mu\nu}=j^{\nu} </math>.....'''3.8''' | |||
'''Nota.''' Retomando las constantes: | |||
:<math> \frac{\partial F^{\mu\nu}}{\partial x^{\mu}}=\frac{4\pi}{c}j_{\mu} </math>. | |||
con <math> j^{\nu}=(\rho,\vec{J}) </math>. Sin embargo '''3.8''' representa la ''Ley de Gauss'' & ''Ley de Ampere-Maxwell''. Para determinar las otras leyes, debemos obtener una expresión como '''3.8''' para el dual de <math> F^{\mu\nu} </math>, es decir: | |||
:<math> \partial_{\mu}\ast F^{\mu\nu}=0 </math>.....'''3.9''' | |||
'''3.9''' representa la ''inexistencia de monopolos magnéticos'' & ''Ley de Faraday''. | |||
Las ecuaciones '''3.8''' & '''3.9''' no presentan distinción entre derivadas temporales ni espaciales, pero respetan a las variables <math> \vec{x} </math> & <math> t </math> con igual importancia. Es por ello que las ecuaciones de Maxwell en esta forma se les conoce como ''ecuaciones de Maxwell en forma covariante''. | |||
Es inmediato de '''3.8''' que: | |||
:<math>\partial_{\alpha}\partial_{\mu}F^{\mu\nu}=\partial_{\alpha}j^{\nu} </math>, es decir: | |||
:<math> \partial_{\alpha}j^{\nu}=0 </math> | |||
la cual representa la ''ecuación de continuidad''. | |||
== Conclusiones. == | |||
El campo electromagnético, como cualquier otro campo que describa fenómenos físicos, debe respetar las simetrías y leyes de conservación impuestas por la estructura del espacio y tiempo. Como Einstein y Lorentz vislumbraron, el campo electromagnético respeta las simetrías del espacio-tiempo llamado Minkowski y no el espacio (y tiempo) galileano. Sin embargo, las ecuaciones de Maxwell no están escritas en forma manifiestamente covariante (como se ha mostrado anteriormente). Esto significa que no es muy claro cómo las ecuaciones de Maxwell transforman en diversos sistemas coordenados respetando la igualdad y dominio de las variables <math> \vec{x} </math> y <math> t </math>. Se requiere entonces un formalismo matemático para que las ecuaciones del Electromagnetismo sean independientes del sistema coordenado; que transformen bajo Lorentz de manera covariante: | |||
Bajo la regla <math> [F'^{\mu\nu}]:=F'=\Lambda F\Lambda^{t} </math> (donde <math>\Lambda^{t}</math> indica la transpuesta de la matriz de transformación de Lorentz) garantizamos que, como '''F''' contiene la información de los campos: | |||
:<math> F^{\mu\nu}:=\partial^{\mu}A^{\nu}-\partial^{\nu}A^{\mu} </math> en un sistema de referencia inercial <math> S </math> | |||
& | |||
:<math> F'^{\mu\nu}:=\partial^{\mu}A'^{\nu}-\partial^{\nu}A'^{\mu} </math> en un sistema de referencia inercial <math> S' </math> que se mueve respecto a S. | |||
== Referencias. == | |||
''Classical Electromagnetic Radiation''. Marion, J.B. and Heald, M.A. (Printed in the United States of America). | |||
''Introduction to Electrodynamics''. Griffiths, D.J. (Published by Pearson Education, Inc. 2013). | |||
''Tensors, Differential Forms, and Variational Principles''. Lovelock, D. and Rund, H. (Dover Publications, Inc., New York). | |||
[[Usuario:diegophy17|Diego de la Cruz López]] | |||
---- | |||
---- | |||
= Láser de Cristal Líquido = | |||
== Introducción == | == Introducción == | ||
Los láseres de cristal líquido son un tema en constante desarrollo dentro de los campos de materia blanda y óptica aplicada.Dichos láseres abarcan una multitud de características extraordinarias, incluida la capacidad de ajuste de frecuencia, gran área de coherencia y, en algunos casos, emisiones multidireccionales, además tienen la capacidad de combinar grandes potencias de salida con dimensiones de cavidad muy pequeñas, dos propiedades que tradicionalmente son incompatibles. | |||
== Cristal líquido == | |||
[[File:Neumatica.gif|thumb| Representación de las moléculas en los 3 estados de agregación]] | |||
El cristal líquido es un tipo de estado de agregación de la materia que presenta propiedades físicas tanto de la fase líquida como de la fase sólida, puesto que las moleculas de un cristal líquido pueden desplazarse unas con respecto a otras con facilidad como ocurre con los líquidos y sin embargo todas las moléculas de su estructura tienden a estar orientadas del mismo modo, como sucede en los sólidos . | |||
Se le atribuye su descubrimiento al biólogo Frederick Reinitzer, quien realizó el hallazgo de materia que parecía tener dos puntos de fusión mientras trabajaba con derivados del colesterol en el año de 1888. Hasta entonces , sólo se conocían tres fases de la materia. Reinitzer al observar el compuesto bajo el microscopio se percató de que este fluido denso mostraba una estructura interna hasta el momento desconocida ,además el compuesto tenía dos puntos de fusión; en el primero se fundía generando un fluido denso y opaco, pero a una segunda temperatura, más alta que la primera, éste se convertía en un líquido transparente más parecido al agua. | |||
Cabe mencionar que los cristales líquidos sólo mantienen su doble naturaleza en un determinado rango de temperaturas y presiones. A temperaturas altas o presiones bajas, el orden de la orientación da paso a las rotaciones moleculares aleatorias, con lo que deja de ser cristal líquido y se convierte en un líquido normal. | |||
En función de la forma de las moléculas que componen al cristal este puede presentar una o más fases intermedias (mesofases) desde el estado cristalino hasta el líquido. | |||
La mesofase de nuestro interes es la : quiral nemática o fase “colestérica”( por observarse por primera ves en compuestos derivados del colesterol), además de ser una de las más comunes, es la usada en los láseres de cristal líquido. En la fase quiral nemática las moléculas tienen un ordenamiento posicional en una estructura de capas. La quiralidad (es decir, que las moléculas no tengan planos internos de simetría) induce un giro azimutal finito de una capa a la siguiente, produciendo un giro en espiral del eje molecular a lo largo de la normal de la capa . | |||
La característica clave de la importancia de este material para la óptica es que l cuenta con la existencia de un intervalo de banda fotónica para luz visible | |||
== Banda fotónica == | |||
[[File:Bandafotonica.png|thumb|La Figura muestra las configuraciones y el espectro de transmisión para luz blanca de la fase Quiral Nemática (arriba) y la fase Quiral Esmética (abajo) ]] | |||
Es ampliamente conocido que todo cristal que presente una peridiocidad en su estructura atómica, posee la característica de que los electrones inmersos en su red interna experimentan la propiedad de tener su energía restringida a un rango de valores específicos.Esta restricción se debe a la existencia de bandas de energía prohibida, para la cuál el cristal rechaza la propagación de los electrones a través del medio. Análogamente, un material que presenta una peridiocidad en su constante dieléctrica posee la propiedad de rechazar la propagación de fotónes a través del mismo. Dichas bandas prohibidas dependen de varios factores estructurales del material. Dado que las bandas prohibidas en el material dependen de la periodicidad y variación de las propiedades dieléctricas del mismo, es lógico pensar que dichas bandas varían su posición y anchura dependiendo la dirección que se considere dentro del material, con lo cual una onda de una determinada frecuencia podrá atravesar el material sin ser rechazada por el mismo, en el caso de que incida en una dirección, mientras que puede ser rechazada totalmente en el caso de incidir en otra dirección, en la cual la frecuencia de la onda esté dentro de la banda prohibida. | |||
== Elementos presentes en el láser== | |||
Elementos básicos de un láser de cistal líquido | |||
Un láser típico, ya sea de cristal líquido o no consta de tres elementos básicos de operación : | |||
'''Cavidad resonante''': | |||
También llamada cavidad laser sirve para mantener la luz circulando a través del medio activo el mayor número de veces posible, generalmente está compuesta por dos espejos, pero en este caso son remplazados por un cristal líquido, lo que permite la selección de la longitud de onda de emisión y la polarización del medio laser activo | |||
'''El medio activo''': | |||
El medio láser activo es el medio material donde se produce la amplificación óptica, es dónde ocurren los procesos de excitación . En el caso de los láseres de cristal líquido el medio láser suele ser un tinte orgánico: rodamina, fluoresceína, cumarina , E- Stylbene , Umbeliferona, entre otros. | |||
'''Bombeo''': | |||
Para que el medio activo pueda amplificar la radiación, es necesario excitar sus niveles electrónicos o vibracionales de alguna manera. Comúnmente un haz de luz (bombeo óptico) de una lámpara de descarga u otro láser o una corriente eléctrica (bombeo eléctrico) son empleados para alimentar al medio activo con la energía necesaria. | |||
El bombeo óptico se utiliza habitualmente en láseres de estado sólido (cristales y vidrios) y láseres de colorante (líquidos y algunos polímeros) y el bombeo eléctrico es el preferido en láseres de semiconductor y de gas. | |||
==Sintonización del color== | |||
[[File:Campoelectrico.jpg|thumb|Alineación de la espiral y la dirección de emisión del láser ]] | |||
En particular, la sintonización del color del láser se puede lograr con los láseres de cristal líquido por la presencia de las antes mencionadas estructuras helicoidales de formación espontánea que provocan que el índice de refracción cambie periódicamente a lo largo del eje helicoidal del cristal y este se vuelva esencialmente un cristal fotónico. | |||
Para lograr un ajuste continuo de la longitud de onda del láser mediante un campo eléctrico variable, es esencial la alineación de la hélice, y el campo eléctrico en el mismo plano como se muestra en la figura: | |||
Se puede elegir cualquier cualquier valor de longitud de onda en el espectro en el espectro de luz visible | |||
==Características sobresalientes == | |||
En contraste con los láseres semiconductores, se puede elegir un rango más amplio de longitud de onda mediante el ajuste de la posición de la banda fotónica . | |||
Aún son un están en desarrollo, sin embargo se espera que combinen las mejores características de los láseres de tinte, gas y diodos: Los láseres de tinte se pueden ajustar para emitir diferentes longitudes de onda, pero son muy grandes. Los láseres de gas son potentes y estables, pero no se pueden sintonizar mientras que los láseres de diodo, son mucho más pequeños pero tampoco pueden sintonizarse. | |||
== Aplicaciones == | |||
Biomédica: el tamaño pequeño, el bajo costo y el bajo consumo de energía de láseres de este tipo ofrecen una variedad de ventajas al lograr hacer dispositivos de exámenes de detección oportuna de enfermedades “de bolsillo” pues podrían brindan lecturas inmediatas sin enviar una muestra a otro laboratorio. | |||
Médica: los láseres de cristal líquido muestran el potencial para ser utilizados en técnicas de microscopía y en terapia fotodinámica. | |||
Tecnología: las pantallas basadas en láser de cristal líquido ofrecen la mayoría de las ventajas de las pantallas de cristal líquido estándar, un control más preciso del color. Se planea que en los años siguientes los elementos individuales sean lo suficientemente pequeños como para actuar como píxeles . Un sistema en el que cada píxel es un único dispositivo sintonizado espacialmente podría evitar los largos tiempos de relajación de la sintonización dinámica, y podría emitir cualquier color utilizando el direccionamiento espacial y la misma fuente de bombeo monocromático. | |||
Detección ambiental: utilizando un material con un paso helicoidal altamente sensible a la temperatura, campo eléctrico, campo magnético o tensión mecánica, el cambio de color del láser de salida proporciona una medición simple y directa de las condiciones ambientales. | |||
== Referencias == | |||
S. M. Morris, A. D. Ford, C. Gillespie, M. N. Pivnenko, O. Hadeler, H. J. Coles, "The emission characteristics of liquid-crystal lasers," J. SID 14, 565-573 (2006). | |||
M. Ozaki, Y. Matsuhisa, Y. Inoue, H. Yoshida “Color-tunable liquid-crystal laser”, SPIE Newsroom. DOI: 10.1117/2.1200903.1554 . 24 April 2009 | |||
B. Maune, M. Loncar, J. Witzens, M. Hochberg, T. Baehr-Jones, D. Psaltis, Y. Qiu, and A. Scherer, "Liquid-crystal electric tuning of a photonic crystal laser", Appl. Phys. Lett. 85, 360-362 (2004). | |||
---- | |||
[[Usuario:Aurea Espin|Aurea Espin]] ([[Usuario discusión:Aurea Espin|discusión]]) 01:20 2 dic 2018 (CST) | |||
---- | |||
= Rerfracción en Metamateriales= | |||
== Introducción == | |||
Victor Veselago (1968), predijo las consecuencias de la interacción de la radiación electromagnética con un material hipotético de índice de refracción negativo, el resultado sería una refracción negativa contrario a lo observado en todos los materiales existentes. | |||
Los metamateriales son materiales construidos artificialmente que poseen propiedades electromagnéticas que no se encuentran normalmente en la naturaleza(permitividad eléctrica y permeabilidad magnética negativas). El estudio de estos materiales con propiedades electromagneticas particulares ha cobrado gran interes en los ultimos años, se utilizan en electronica para fabricación de antenas pequeñas de móviles o de satélites en los que se quieren agrupar un gran número de antenas en un espacio mínimo. | |||
Algunas propiedades electromagnéticas interesantes son: | |||
* Índice de refracción negativa. | |||
*Comportamiento diferente en las ecuaciones de Fresnel. | |||
*Comportamiento diferente en el ángulo crítico. | |||
[[File:Metamaterial.jpg|Metamaterial|500px|thumb|center|Figura 1. Ejemplo de metamaterial hecho a base de fibra de vidrio con celdas de cobre de 5 mm de lado]] | |||
== Propiedades de Metamateriales== | |||
===Índice de refracción negativa=== | |||
Cuando un haz de luz cruza la interfase entre diferentes materiales, su dirección de propagación es alterada, este cambio depende de los índices de refracción de los materiales por donde se propaga el rayo. Entre más grande sea la diferencia, mayor será la refracción del rayo. En todos los materiales conocidos a este fenómeno se le conoce como refracción positiva. | |||
En un metamaterial el rayo de luz refractado se curva hacia el mismo lado que el rayo incidente (medido en relación a la normal a la interfaz entre el metamaterial y el material normal). Ver ''Figura 2''. | |||
[[File:Comparación R.png|500px|thumb| center |Figura 2. a)Refracción Positiva b)Refracción Negativa]] | |||
===Ecuaciones de Fresnel=== | |||
Calculamos las ecuaciones de Fresnel para un metamaterial como se muestra en la ''figura 3'' | |||
[[File: | [[File:IndiceN.png|IndiceN|500px|thumb|center|Refracción Negativa]] | ||
== | |||
[[Usuario: | |||
<math>-\frac{B_i}{\mu_i}cos\theta_i + \frac{B_r}{\mu_i}cos\theta_r =-\frac{B_t}{\mu_t}cos\theta_t</math> | |||
<math>B_i=\frac{E_i}{v_i}</math> | |||
<math>B_r=\frac{E_r}{v_r}</math> | |||
<math>B_t=\frac{E_t}{v_t}</math> | |||
Pero $v_i=v_r$ y $\theta_i=\theta_r$ Pro lo cual la ecuación puede reescribirse como: | |||
<math>\frac{1}{\mu_i v_i}(E_i - E_r)cos\theta_i =\frac{1}{\mu_t v_t}E_t cos\theta_t</math> | |||
Y utilizando las ecuaciones | |||
<math>E_t = E_{0t}cos(k_t \cdot \omega_t t + \epsilon_t)</math> | |||
<math>E_r = E_{0r}cos(k_t \cdot \omega_r t + \epsilon_r)</math> | |||
<math>E_i = E_{0i}cos(k_i \cdot \omega_i t)</math> | |||
y recordado que los cosenos que aparecen son iguales entre si cuando y-0 se obtiene | |||
<math>\frac{n_i}{\mu_i}=(E_{0i} -E_{0r})cos\theta_i=\frac{n_t}{\mu_t}E_{0t}cos\theta_t</math> | |||
combinando con la ecuación | |||
<math>E_{0i}+E_{0r}=E_{0t}</math> | |||
Tenemos | |||
<math>\frac{n_i}{\mu_i}(E_{0i}-E_{0r})cos\theta_i=\frac{n_t}{\mu_t}(E_{0i}+E_{0r})cos\theta_t)</math> | |||
<math>E_{oi}(n_i cos\theta_i- n_2cos\theta_t)=E_{or}(n_i cos\theta_i + n_2cos\theta_t)</math> | |||
Entonces la ecuacion queda como | |||
<math>\frac{E_{or}}{E_{oi}}=\frac{n_i cos\theta_i+ n_2cos\theta_t}{n_i cos\theta_i- n_2cos\theta_t}</math> | |||
pero como $n_t<0$ entonces | |||
<math>r_{\| m}=\frac{E_{or}}{E_{oi}} = \frac{-n_2 cos \theta_i - n_1 cos\theta_t}{n_1 cos \theta_t + n_2 cos\theta_i}</math> | |||
Y de manera similar se calculan las demás. | |||
<math>t_{\bot m}=\frac{2n_1 cos \theta_i}{n_1 cos \theta_i - n_2 cos\theta_t}</math> | |||
<math>t_{\| m}=\frac{2n_1 cos \theta_i}{n_1 cos \theta_t - n_2 cos\theta_t} </math> | |||
<math>r_{\bot m}=\frac{n_1 cos \theta_i + n_2 cos\theta_t}{n_1 cos \theta_i - n_2 cos\theta_t}</math> | |||
A estas ecuaciones también se les llama ''coeficientes de amplitud de reflexión y transmisión'', en la parte inferior podemos encontar las ecuaciones de Fresnel para refracción positiva, casi no variaron con las ecuaciones para metamateriales. | |||
<math>t_{\bot}=\frac{2n_1 cos \theta_i}{n_1 cos \theta_i + n_2 cos\theta_t}</math> | |||
<math>t_{\|}=\frac{2n_1 cos \theta_i}{n_1 cos \theta_t + n_2 cos\theta_i}</math> | |||
<math>r_{\bot}=\frac{n_1 cos \theta_i - n_2 cos\theta_t}{n_1 cos \theta_i + n_2 cos\theta_t}</math> | |||
<math>r_{\|}=\frac{n_2 cos \theta_i - n_1 cos\theta_t}{n_1 cos \theta_t + n_2 cos\theta_i}</math> | |||
Las consecuencias de un índice de refracción negativo en las ecuaciones de fresnel, los coeficientes de transmisión y reflexión muestran diferencias físicas, esto es cambios de fase debido a que los valores de amplitud del campo son diferentes. | |||
Observamos que el comportamiento de los campos incidente, reflejado y transmitido cambian con respecto a medios homogéneos, por lo que las ecuaciones de fresnel deben modificarse para un metamaterial teniendo en cuenta la condición que $n_2 < 0$, de esta manera los coeficiente de amplitud de trasmisión y reflexión quedan expresados de la siguiente forma. | |||
===Ángulo Crítico=== | |||
El ángulo crítico también es conocido como el ángulo mínimo de incidencia en el cual se produce la reflexión interna total, este ángulo de incidencia se mide respecto a la normal de la separación de los medios. | |||
Ahora de la ley de Snell donde el ángulo de refracción o transmitido es $ \theta_t =90° $, el ángulo crítico $ \theta_c $ está dado por la siguiente expresión | |||
<math>\theta_c = arcsin \frac{n_1}{n_2}</math> | |||
Tambien sabemos que para ángulos de incidencia mayores que el ángulo crítico $\theta_i > \theta_c$ , el ángulo de refracción será mayor de $90°$, por lo cual el rayo no será refractado, ya que no pasa de un medio a otro, y por lo tanto se produce una reflexión total interna. Para metamateriales tenemos que la expresión para el ángulo crítico se modifica para | |||
obtener la siguiente forma(ver \textit{Figura 6}). | |||
<math>\theta_c = arcsin \left(-\frac{n_1}{n_2} \right)</math> | |||
[[File:AnguloC.png|AnguloC|500px|thumb|center|Ángulo crítico en un metamaterial]] | |||
== Como se hace un Metamaterial == | |||
Un metamaterial es aquel compuesto por más de dos materiales, esto implica tener un campo compuesto, como se muestra la \textit{figura 7}, esta es óptima para un metamaterial. En esta estructura veremos como al hacer incidir un haz de luz sobre una rejilla acoplada a una superficie plana, se exita un plasmon, apartir de este fenómeno es posible obtener refracción negativa (haz refractado), con plasmón se refiere a un plasma compuesto de electrones | |||
Un plasma es un conjunto de cargas eléctricas, las cuales pueden exhibir comportamientos armónicos al ser perturbadas por un campo electromagnético.Para el caso de los metales, algunos electrones pueden moverse libremente, por lo que en estos materiales | |||
se pueden producir plasmones | |||
[[File:Plamon.png|Plamon|500px|thumb|center|Material compuesto]] | |||
Otra forma de obtener este tipo de material es realizando un conjunto de elementos ordenados periódicamente, los cuales están diseñados para responder a la acción de un campo electromagnético. El tamaño y la separación deben ser mucho menor que la longitud de onda de la radiación electromagnética de interés para el estudio. Esto permitirá que la radiación incidente interaccione con el material artificial como si éste fuera homogéneo. De esta manera se puede reemplazar el sistema compuesto por un material continuo con parámetros $\epsilon$ y $\mu$, los cuales son la permitividad eléctrica y la permeabilidad magnética, respectivamente. | |||
==Aplicaciones== | |||
Los metamateriales como subsistemas se encuentran actualmente en diversas aplicaciones: las lentes corrientes tiene un índice de refracción positivo por lo cual son curvos, como en el caso de los telescopios o de los microscopios. Los metamateriales brindan la posibilidad de que estas lentes sean planas y puedan mejorar en un grado importante su eficacia permitiendo enfocar luz en áreas muy pequeñas (más pequeña que la longitud de onda de la luz), sin preocuparnos por su forma. | |||
Revolucionarán el campo de la óptica, permitirán el desarrollo de microscopios ultrapotentes, además de importantes avances en computación cuántica y paneles solares. | |||
Desarrollo de sistema capaz de transferir con mucha eficiencia la energía eléctrica entre dos circuitos separados, mediante el uso de metamateriales, permitiendo la deseada carga inalámbrica a distancias mayores de móviles, tabletas, etc. | |||
[[Usuario:Flor|Flor Ivon Vivar]] | |||
= Holografía = | |||
La holografía es la creación de imágenes fotográficas sin el uso de lentes. Un holograma es una estructura física que difracta la luz en una imagen, parece ser un patrón irreconocible de rayas y espirales, pero que, al iluminarlo con luz coherente, organiza la luz en una representación en tres dimensiones del objeto original. | |||
El termino "holograma" se puede referir a la película con la información codificada y también a la imagen resultante. | |||
La palabra holografía proviene de las palabras griegas ὅλος (holos; "todo") y γραφή (graphē; "escribir" o "dibujar"). | |||
[[Archivo:Holog.gif|thumb|upright|La información completa de la imagen queda registrada por cualquier parte del holograma.]] | |||
==Historia== | |||
===Dennis Gabor (1900-1979)=== | |||
Físico británico de origen húngaro, recibió el premio nobel en 1971. | |||
Interesado en la microscopía electrónica, con la que se mejoraba el poder de resolución de los mejores microscopios ópticos hasta cien veces, mas no se tenía la suficiente resolución para las redes cristalinas de los átomos. | |||
Podía compararse con perfección óptica el mejor objetivo del microscopio con una gota de lluvia. | |||
El trabajo teórico de O. Scherzer, predecía la imposibilidad de perfeccionarlas. | |||
El límite teórico para la resolución del objetivo estaba estimado en 4 Å, casi el doble del necesario para resolver las redes cristalinas de los átomos, mientras que en la práctica era de 12 Å. | |||
Estos límites son impuestos por la necesidad de restringir la apertura de los lentes a aproximadamente $5/1000$ rad, ángulo en el cual el error de aberración esférica es casi igual que el error de difracción. | |||
===La solución=== | |||
Un buen día en la Pascua de 1947, después de reflexionar sobre este problema, surgió en Dennis una solución, ''¿Por qué no tomar una mala imagen, pero que contenga ''toda'' la información, y corregirla por medios ópticos?'' | |||
Era claro que solo con haces coherentes de electrones esto podría hacerse, con ondas de electrones que tienen una fase definida. | |||
Una fotografía ordinaria pierde la fase completamente, solo graba las intensidades. ¡No es de extrañarse que se pierda la fase, si no hay nada con que compararla! Veamos que ocurre si le agregamos un estándar, un "fondo coherente". | |||
===Las limitaciones=== | |||
Como fuente de luz, se utilizaba una lampara de mercurio de alta presión, con una longitud de coherencia de $0.1 mm$. | |||
Para tener coherencia espacial, debían iluminar un agujero de $3\mu m$ de diámetro. | |||
Lo que permitía hacer hologramas de objetos con $1 cm$ de diámetro, con las que se obtenían microfotografías de $1 mm$ de diámetro, con una exposición de pocos minutos, en las emulsiones mas sensibles disponibles. Debido a la corta longitud de coherencia se limitaba a arreglar todo en un solo eje. Además del $efecto\, schlieren$, causante de perturbaciones aleatorias, había un defecto sistemático en las imágenes. La perturbación proviene del hecho que no es una sola imagen, si no dos, cada punto en el objeto emite una onda esférica secundaria, que interfiere con el fondo y produce un sistema de zonas de Fresnel circulares. | |||
Si se utiliza "holografía en línea", ambas imágenes están en línea, y se pueden separar enfocando, pero esta separación nunca es del todo perfecta, por que en general, la iluminación coherente deja una "estela". Este defecto se puede corregir utilizando el objetivo del microscopio en sentido opuesto en la reconstrucción. | |||
En los años siguientes se tuvo éxito mejorando el microscopio electrónico, pero finalmente, se tuvo que dejar el trabajo por las limitaciones de la época. | |||
Resultó que el microscopio electrónico aún estaba lejos del límite impuesto por las aberraciones ópticas, sufría de vibraciones, los campos magnéticos no se manejaban con la precisión requerida, la contaminación de la | |||
objeto y todo empeorado por las largas exposiciones requeridas en el débil haz coherente de electrones. | |||
==Idea básica de la holografía== | |||
[[Archivo:basid.jpg]] | |||
==Creación y reproducción de un holograma== | |||
Para el caso más simple donde solo hay un objeto puntual, la interferencia de la onda reflejada por el objeto y el fondo coherente u "onda de referencia" producirán franjas de interferencia, habrá máximos donde las ondas estén en fase. Registrando este patrón, e iluminándolo únicamente con el haz de referencia, la onda, en efecto, se haya en fase para la fuente de referencia A, pero como en las rendijas las fases son idénticas, también deben ser correcta para B; por lo tanto, la onda de B también de aparecer reconstruida. | |||
==La física de la holografía== | |||
===Interferencia=== | |||
[[Archivo:destru.gif|thumb|100px|right|Interferencia destructiva.]] | |||
[[Archivo:constru.gif|thumb|100px|left|Interferencia constructiva]] | |||
La holografía se basa en el principio de interferencia. Un holograma captura el patrón de interferencia producido por dos o más haces de luz coherente. Se hace incidir un haz directamente en la película y este actúa como referencia para la luz dispersada por el objeto iluminado. | |||
Debido a la superposición de dos o mas ondas, existen regiones donde se traslapan, cancelándose mutuamente parcial o totalmente, mientras que en otras regiones, las crestas y los valles resultantes son incluso mayores que las de cualquiera de las ondas constituyentes, después de la superposición, las ondas se separan y continúan sin verse afectadas. | |||
===Coherencia=== | |||
Coherencia, una relación fija entre la fase de ondas en un haz de una sola frecuencia. Dos haces de luz son coherentes cuando la diferencia de fase entre sus ondas es constante; son no coherentes si hay una relación de fase aleatoria o cambiante. Los patrones de interferencia estables se forman solo por la radiación emitida por fuentes coherentes, que generalmente se producen al dividir un haz en dos o más. Un láser, a diferencia de una fuente incandescente, produce un haz en el que todos los componentes tienen una relación fija entre sí. | |||
===Fotografía y revelado=== | |||
El medio de grabación debe poder resolver todas las franjas que surgen de la interferencia entre el objeto y el haz de referencia. Estas separaciones de franjas pueden variar desde decenas de micrómetros hasta menos de un micrómetro. La película fotográfica común tiene una respuesta muy baja o incluso nula en las frecuencias involucradas y no se puede usar para hacer un holograma. | |||
Si la respuesta no es plana sobre el rango de frecuencias espaciales en el patrón de interferencia, entonces la resolución de la imagen reconstruida también puede degradarse. | |||
===Difracción=== | |||
El patrón de luz y franjas oscuras que se observa cuando la luz pasa un obstáculo, es un ejemplo del fenómeno de difracción. La difracción es resultado de la superposición de ondas, es un efecto de interferencia. Cuando se obstruye una onda, las partes de la onda no obstruidas interfieren entre sí en una región del espacio más allá de la obstrucción. | |||
==Las matemáticas de la holografía== | |||
[[Archivo:3ab.jpg|thumb|300px|right|Creación de un holograma]] | |||
El tren de ondas difundido del objeto, que penetra a un ángulo $\theta$, produce la interferencia máxima en los puntos $A, B$ y $C$ | |||
La fase relativa $\phi$ de las dos ondas, que varía a lo largo de la película, puede escribirse como función de $x$. Dado que $\phi$ se cambia por 2$\pi$, conforme $x$ avanza a lo largo de $ \overline{AB}$, $\phi/2\pi=x/\overline{AB}$. Además $\sin \theta=\lambda/\overline{AB}$. | |||
$\therefore \phi(x)=\frac{2\pi x \sin \theta}{\lambda}$ | |||
Suponiendo que las dos ondas tienen la misma amplitud $E_0$, el campo resultante será: | |||
$E=2E_0\cos\frac{\phi}{2} \sin{\left(\omega t-kx-\frac{\phi}{2}\right)}$ | |||
y la distribución de la irradiancia, queda como: | |||
$I(x)=\frac{1}{2}c\varepsilon_0\left(2E_0\cos\frac{\phi}{2}\right)^2$ | |||
$I(x)=2c\varepsilon_0 E_0^2+2c\varepsilon_0 E_0^2\cos^2 \phi$ | |||
Obteniendo así una distribución de la irradiancia cosinusoidal en el plano de la película. | |||
Al emplear objetos aún más complejos, la fase relativa $\phi$ entre el objeto y las ondas de referencia variará punto por punto de manera más complicada. La diferencia de ángulo de fase $\phi$ está codificada en la configuración de las franjas, y la irradiancia de estas franjas también es alterada. | |||
Suponiendo que el plano $xy$ es el plano del holograma $\Sigma_H$. Entonces: | |||
$E_B(x,y)=E_{0B}\cos\left[2\pi \nu t+\phi(x,y)\right]$ | |||
describe el fondo plano u onda de referencia en $\Sigma_H$. Su amplitud $E_{0B}$, es constante, mientras que la fase depende de la posición. Si la onda estuviera orientada de tal manera que pudiera hacerse coincidir con $\Sigma_H$ por una sola rotación con un ángulo $\theta$ alrededor de $y$, la fase en cualquier punto del plano del holograma dependería de su valor de $x$. Así $\phi$ tendría otra vez la forma: | |||
$\phi=\frac{2\pi}{\lambda}x\sin\theta=kx\sin\theta$ | |||
La onda esparcida por el objeto puede expresarse como: | |||
$E_O(x,y)=E_{0O}(x,y)\cos\left[2\pi \nu t + \phi_O(x,y)\right]$ | |||
Se trata de una onda portadora modulada en amplitud y en fase que contiene toda la información disponible del objeto. | |||
Esta información está codificada en variaciones espaciales, y no temporales. Las dos ondas se superponen e interfieren para formar una distribución de irradiancia que se registra mediante la emulsión fotográfica. | |||
La irradiancia resultante, salvo una constante, es $I(x)=\langle{(E_B+E_O)^2}\rangle_T$ | |||
$I(x,y)=\frac{E_{0B}^2}{2}+\frac{E_{0O}^2}{2}+E_{0B}E_{0O}\cos(\phi-\phi_O)$ | |||
La visibilidad de las franjas en el plano del holograma es: | |||
$\mathscr{V}=\frac{2E_{0B}E_{0O}}{E_{0B}^2+E_{0O}^2}$ | |||
y contiene la información acerca de la amplitud de la onda objeto. | |||
El perfil de la transmisión de amplitud del holograma procesado puede establecerse proporcionalmente a $I(x)$, en ese caso la ''onda emergente final'', $E_F(x,y)$, es proporcional al producto $I(x,y)E_R(x,y)$, donde $E_R(x,y)$ es la ''onda de reconstrucción'' incidente en el holograma, entonces, si la onda de reconstrucción de frecuencia $\nu$ incide oblicuamente en $\Sigma_H$, como lo era la onda básica, se puede escribir como: | |||
$E_R(x,y)=E_{0R}\cos\left[2\pi\nu t+ \phi(x,y)\right]$ | |||
La onda final, salvo una constante multiplicativa es: | |||
$E_F(x,y)=\frac{1}{2}E_{0R}\left(E_{0B}^2+E_{0O}^2\right)\cos\left[2\pi\nu t+ \phi(x,y)\right]+ \frac{1}{2} E_{0R} E_{0B} E_{0O} \cos\left(2 \pi \nu t + 2\phi-\phi_0\right)+\frac{1}{2}E_{0R}E_{0B}E_{0O}\cos\left(2\pi \nu t + 2\phi-\phi_0\right)$ | |||
Tres términos describen la luz que emana del holograma; el primero se puede reescribir como: | |||
$\frac{1}{2}\left(E_{0B}^2E_{0O}^2\right)E_{0B}E_R(x,y)$ | |||
y es una versión de amplitud modulada de la reconstrucción de la onda. Cada parte del holograma funciona como una rejilla de difracción, y este es el de ''orden cero'', ya que no contiene información acerca de la fase de la onda objeto. | |||
Los otros términos son las ''ondas de banda lateral'', estas son las dos ondas de primer orden difractadas por el holograma. | |||
==Holografía a gran escala== | |||
[[Archivo:cine.jpg|300px|thumb|left]] | |||
Un esquema mas ambicioso, es cinematografía en tres dimensiones, sin el uso de los lentes polarizadores. | |||
La audiencia cubierta por zonas de visión, con el espaciamiento del ancho ocular, una | |||
para el ojo derecho y una para el izquierdo, con un espacio en blanco entre pares. Los ojos deben ver dos imágenes diferentes; un par estereoscópico. El espectador puede mover su cabeza un poco hacia la derecha o hacia la izquierda, o incluso cuando mueve un ojo en la zona en blanco, la imagen aparecerá más oscura pero no plana, porque un ojo tiene la impresión de "estereoscopia por defecto". | |||
Este problema es estrictamente insoluble con los medios ortodoxos de óptica, lentes, espejos, prismas. Se pueden hacer satisfactoriamente pantallas pequeñas para teatros pequeños, pero con pantallas grandes y teatros grandes, uno cae en una dilema. Si las lentes son grandes, se verán desde los asientos delanteros; si son pequeñas, no tendrán suficiente definición para los asientos traseros. | |||
La holografía puede resolver este problema, utilizando un proyector como fuente de referencia y, digamos, el sistema de zonas de visualización izquierda como objeto. La pantalla, cubierta con un emulsión, se convertirá automáticamente en un sistema óptico muy complicado, tal que cuando se proyecta una imagen desde el proyector, se verá solo desde las zonas de visión izquierda. | |||
Repitiendo el proceso con el proyector derecho, y las zonas de visualización derechas. | |||
Los hologramas muestran el fenómeno de la selectividad direccional. Si uno desplaza el iluminador de la posición original en un cierto ángulo, no habrá reflexión. Poniendo los dos proyectores en este ángulo el uno del otro, se tendrá que la imagen derecha no será vista por el ojo izquierdo y viceversa. | |||
Queda, por supuesto, una dificultad, y es que no se puede practicar holografía en la escala de un cine, y con una película tan grande como una pantalla. | |||
Pero esto también podría resolverse, haciendo la pantalla a partir de piezas pequeñas. | |||
Estas son algunas de las dificultades para realizar holografía a gran escala. | |||
==Referencias== | |||
Eugene Hecht, Óptica, 5° edición, Ed. Pearson, 2017. | |||
Dennis Gabor – Nobel Lecture. NobelPrize.org. Nobel Media AB 2018. Mon. 3 Dec 2018. <https://www.nobelprize.org/prizes/physics/1971/gabor/lecture/> | |||
[[Usuario:Sesebasi|Sesebasi]] ([[Usuario discusión:Sesebasi|discusión]]) 23:01 2 dic 2018 (CST) | |||
===Óptica de cristales líquidos nemáticos=== | |||
Los cristales líquidos fueron descubiertos alrededor del año 1888 por el botánico | |||
australiano Friedrich Rheinitzer al observar la composición cholesteric del benzoato, un | |||
poco después el físico alemán O. Lehmann sugiere el nombre de “cristal líquido” al observar | |||
la estructura cristalina de este. | |||
Los cristales líquidos son sustancias que presentan propiedades de sólidos y de líquidos al mismo tiempo. Existen tres tipos de cristales líquidos: liotrópicos, poliméricos y termotrópicos. Estos últimos son los más estudiados por sus propiedades ópticas y podemos clasificarlos a su vez en tres subtipos: nemáticos, colestéricos y esmécticos. Se diferencian por las distintas ordenaciones posibles de sus moléculas, que, en el caso de los nemáticos, suelen representarse por elipsoides de revolución capaces de interactuar entre sí debido a su carácter eléctrico dipolar. La fase nemática de los cristales líquidos se caracteriza por un orden orientacional de sus moléculas y por una movilidad traslacional muy semejante a la de un líquido. Las moléculas de cristal líquido nemático están orientadas en una dirección preferente, conocida como director. | |||
[[Archivo:director.jpg|thumb|center]] | |||
El cristal líquido es una estructura molecular que posee propiedades físicas tanto de sólidos como de líquidos. | |||
El material con el que está fabricado un cristal líquido, por lo general está compuesto de un alto número de moléculas anisotrópicas birrefringentes. | |||
Sus moléculas tienen una forma elipsoidal con una orientación ordenada a través de la estructura cristalina. Pero también tienen una viscosidad comparable con la de los líquidos; ya que cuando se le aplica una fuerza eléctrica externa al cristal líquido, cada molécula puede girar o rotar con respecto a otra molécula. | |||
Los cristales líquidos son un tipo especifico de moduladores espaciales de luz en dos dimensiones. | |||
En 1963 Williams descubre la propiedad moduladora que tienen los cristales líquidos, esto al hacer pasar luz a través del cristal liquido y estimular a este con una carga eléctrica. | |||
La configuración más utilizada en pantallas de cristal líquido es la nemática. Sus moléculas poseen una orientación paralela en todo el volumen del cristal. | |||
[[Archivo:cristal_liquido_nematico.jpg|thumb|center]] | |||
La estructura cristalina nemática posee propiedades ópticas importantes como lo es el giro de sus moléculas debido a una actividad óptica inducida. Que aparece cuando el cristal líquido nemático se coloca entre dos placas de vidrio pulidas con direcciones de pulidos diferentes. | |||
'''El giro molecular''' | |||
Es una propiedad de los cristales líquidos del tipo nemático. | |||
[[Archivo:Torcion_en_cristal_liquido_nematico.jpg|thumb|center]] | |||
Al iniciar el giro, el eje de la molécula se encuentra paralelo a la dirección de pulido del vidrio 1 y al finalizarse se encuentra paralelo a la dirección de pulido de vidrio 2. | |||
Los cristales líquidos tienes la propiedad de modificar la transmitancia al aplicarle un voltaje, con el cual creamos un campo eléctrico perpendicular a la ventana de vidrio. | |||
[[Archivo:cristal_liquido_con_voltaje.jpg|thumb|center]] | |||
Existirán entonces dipolos inducidos y la moléculas del cristal líquido experimentan pares de torsión que las llevan a alinearse con el campo a medida que aumenta el voltaje (a). | |||
Se reduce la birrefringencia | |||
:<math>∆𝑛=(𝑛_𝑒−𝑛_𝑜)</math> | |||
y la retardancia | |||
:<math>∆𝜑(𝑉,𝑇,𝜆_0 )=2𝜋/𝜆_0 𝑑 Δ𝑛(𝑉,𝑇,𝜆_0)</math> | |||
La retardancia máxima se obtiene cuando el voltaje aplicado es cero. Cuando V es grande, la retardancia es un mínimo de 30 nm. | |||
Este tipo de pantallas de cristal líquido, son usados generalmente en relojes digitales y calculadoras. | |||
[[Usuario:Verenisse|verenisse]] | |||
------------------------------------------------------------------------------------------------------------------------------------------------------------- | |||
===Óptica relativista=== | |||
'''introdución''' | |||
La pregunta, ¿ Cómo es el aspecto de las cosas cuando se mueven a velocidades relativistas ? logró resolverse gracias a lo trabajos de un colega de Einstein, Anton Lampa, de 1924 y de Penrose y Terrell, | |||
de 1959. | |||
La forma, posición y orientación de un objeto que se mueve a una velocidad cercana a la de la luz puede ser bastante diferente de lo que se vería a velocidades mas lentas. Estas deformaciones ópticas, conocidas como aberraciones, recuerdan a las imágenes que se producen en espejos curvos. Se debe a dos causas, compresión angular y distorsión. Por otro lado el color de los objetos puede variar debido al efecto Doppler. También la intensidad de luz que viene de objetos que se mueven a velocidades relativistas puede cambiar debido a una combinación de dilatación temporal y compresión angular. Así que la imagen del mundo que uno vería estaría afectado no solo por la contracción espacial y la dilatación temporal si no también por la velocidad finita de la luz. Las aberraciones el efecto Doppler y los cambios de intensidad son todos causados por la velocidad finita de la luz, el tema que trataremos aquí el el efecto Doppler. | |||
'''Efecto Doppler relativista''' | |||
El efecto Doppler se manifiesta en todo tipo de onda, incluyendo el sonido y la luz. En el caso del sonido, Por ejemplo, cuando un auto de carreras se acerca a nosotros, el ruido de su motor se escucha mas agudo, y cuando se aleja, el ruido es mas grave. Análogamente, cuando un objeto emite luz se acerca a nosotros la frecuencia de la luz aumenta, y al revés si se aleja. Con la luz, los cambios de frecuencia representan cambios de color. Un aumento de frecuencia de la luz produce un objeto azulado. Una disminución de la frecuencia hace que veamos los objetos mas rojizo. Se ha observado que la luz que llega de estrellas o galaxias lejanas es algo mas rojiza de lo que debería ser si estuvieran quietas. Del corrimiento al rojo de la luz, las observaciones de Edwin Hubble en 1920 nos permite deducir que las galaxias más lejanas se alejan de nosotros a gran velocidad. Estos resultados son una comprobación de la expansión del universo y su edad de 13.8 mil millones de años. | |||
Ahora matemáticamente, consideremos la ecuación de onda en dos marcos de referencia | |||
$ \Box \varphi = \Box^{\prime}\varphi\left(t^{\prime},x^{\prime}\right)=0$ | |||
donde | |||
$\Box =\frac{1}{c^{2}\partial t^{2}}-\vec \bigtriangledown \cdot \vec \bigtriangledown$ | |||
es el operador de d' Alembert, el cual es invariante a la transformaciones de Lorentz. | |||
Para una onda plana, la solución es | |||
$\varphi=A\exp i[\vec k \cdot \vec x - \omega t] $, | |||
donde $\vec k$ es el vector de onda y $\omega $ es la frecuencia angular. Como la ecuación de onda es invariante a transformaciones de Lorentz, también la fase lo es, es decir, | |||
$-\eta_{\nu \mu}k^{\mu}x^{\mu}=\vec k \cdot \vec x - \omega t= \vec k^{\prime}\cdot \vec x^{\prime}-\omega^{\prime}t^{\prime}$. | |||
Entonces $\vec k^{\mu}=\left(\omega/c,\vec k\right)$ se transforma igual que un cuadri-vector $x^{\\nu}=\left( ct,\vec x\right)$ de Lorentz, es decir, | |||
$\omega^{\prime}=\gamma\left(\omega-c\vec\beta\cdot\vec k\right)$ | |||
$\vec k^{\prime}=\vec k + \frac{\gamma-1}{v^{2}}\left(\vec v \cdot \vec k\right)\vec v-\gamma\vec v\frac{\omega}{c^{2}}$. | |||
Donde $\gamma=1/\sqrt{1-\beta^{2}}$ es el conocido factor de Lorentz. El cuatri-momento $p^{\mu}=\hbar k^{mu}$ lo obtenemos por la publicación de la constante de Planck $\hbar$ reducida. | |||
Por la ecuación de onda, la fórmula de dispersión | |||
$\vec k\cdot\vec k=\frac{\omega^{2}}{c^{2}}$ | |||
es valida en el vacio e invariante a las transformaciones de Lorentz. Ahora, supongamos que el vector de onda $\vec k$ forma un ángulo $\theta$ con la velocidad relativa entonces el producto escalar $\vec v \cdot \vec k=vk\cos \theta$ se puede simplificar. Por lo tanto | |||
$\omega^{\prime}= \gamma \omega \left(1-\beta\cos\theta\right)$, | |||
que es el efecto Doppler para la frecuencia angular $\omega=2\pi f$. | |||
Para el ángulo $\theta=0$ tenemos | |||
$\omega^{\prime}=\gamma \omega\left(1-\beta\right)=\frac{1-\beta}{\sqrt{\left(1-\beta\right)\left(1+\beta\right)}}\omega$ | |||
$=\sqrt{\frac{1-\beta}{1+\beta}}\omega=\omega/D$ | |||
que es conocido como el efecto Doppler longitudinal, donde | |||
$D=\sqrt{1+\beta}/\sqrt{1+\beta}$ | |||
es el factor de Doppler. | |||
El efecto Doppler transversal $\omega=\omega^{\prime}\sqrt{1-\beta^{2}}$ se puede deducir más fácilmente de la dilatación de el tiempo. A sugerencia de Einstein, en 1938, Ives y Stilwell fueron los primeros en comprobar experimentalmente este efecto con un haz de átomos excitados de hidrógeno. Para la longitud de onda $\lambda=c/f=2\pi c/\omega$ llegamos a una relación inversa | |||
$\lambda^{\prime}=\sqrt{\frac{1+\beta}{1-\beta}}\lambda=\sqrt{\frac{c+v}{c-v}}\lambda$. | |||
Donde el factor $D=\sqrt{\left(c+v\right)/\left(c-v\right)}$ de Doppler es independiente de la longitud de onda. La velocidad relativa de los objetos del cosmos se obtiene mediante la relación | |||
$1+z=\frac{\lambda^{\prime}}{\lambda}=1+\frac{\Delta\lambda}{\lambda}$ | |||
$=\sqrt{\frac{1+\beta}{1-\beta}}\simeq 1+\beta$ | |||
donde $z\equiv \Delta\lambda/\lambda$ corresponde a un corrimiento al rojo. Hay cuasares (fuentes brillantes llamados, casi estelares) tan lejos que tienen un valor $z>3$. | |||
==Bibliografía== | |||
Taylor John R., ''Mecánica clásica'' (Reverté, Barcelona, 2013) | |||
Eckehard W. Mielke, 'Relatividad Moderna'', CreateSpace, Amazon.com, | |||
ISBN-13: 9781512117820), 184 paginas. | |||
[[Usuario:Jesús|Jesús Flores Ortega]] | |||
---- | |||
Revisión actual - 19:32 4 dic 2018
Este espacio es para que desarrollen su tema de investigación.
Quiralidad Óptica y su interacción con la materia
El objetivo de esta información es mostrar una introducción y generar ideas elementales de qué teoría y qué se deben usar para explicar el efecto de la quiralidad óptica ya que puede ser bastante engorroso mostrar paso a paso los desarrollos matemáticos.
Un objeto quiral (en general en tres dimensiones) es un objeto tal que no se puede superponer con su imagen especular. En otras palabras, dichos objetos, por más que lo rotemos en distintos sentidos, nunca se obtendrá su imagen especular. El ejemplo clásico de un objeto quiral, son las manos. Uno puede hacer el simple experimento en intentar rotar y mover la mano (por ejemplo, la izquierda) para generar una imagen igual a la otra mano. Claramente nunca podrá quedar igual.
Ya que entendemos la definición de un objeto quiral, se define como enantiómeros, que son objetos con quiralidad opuesta (al superponerlos quedan de cierta forma en “sentidos opuestos”). En la física, dichos objetos enantiomerismo, generalmente son idénticos en sus magnitudes físicas como la densidad, peso molecular, entalpía de formación, frecuencias de vibración, etcétera
Para aterrizar los conceptos, la luz circularmente polarizada (LCP) es un objeto quiral. Y al tener una molécula quiral dicha molécula tendrá diferentes secciones rectas de absorción cuando se ilumina con LCP izquierda o ferecha.
En la ciencia, definen el factor de desimetría g que es la fracción entre las diferentes absorciones de luz. Cabe resaltar que este efecto de absorción de LCP no puede ser visible teóricamente con la expansión dipolar del sistema, sino que requiere expansión a primer orden de la forma ka~〖10〗^(-3) donde k es el el vector de la onda de luz mientras que a es el tamaño de la molécula.
Como nota para observar las dimensiones de dificultad de este tipo de estudios, cuando se tiene una onda electromagnética no plana que varía (aunque sea poco) sobre la distancia en dimensiones de la molécula, se tiene que los grados de desimetría dependen locamente, cosa que genera muchos problemas para el estudio de los mismos comparado con un campo homogéneo ya que para éste sucede lo mismo en cualquier punto del espacio de la molécula.
Para el estudio de las interacciones quirales, se una un pseudoescalar (cantidad que se comporta como escalar, pero cambia de signo bajo rotaciones impropias). En la literatura, Lipkin propuso la siguiente cantidad:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): C≡\frac{ϵ_0}{2}E∙∇×E+\frac{1}{2μ_0}B∙∇×B
Usando las ecuaciones de Maxwell podemos reescribir dicha ecuación de la siguiente forma:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): C=\frac{ϵ_0}{2}{-E∙\frac{∂B}{∂t}+B∙\frac{∂E}{∂t}}
Donde ϵ_0 y μ_0 es la permitibidad y permeabilidad en el vacío mientras que E y B son el campo eléctrico y magnético respectivamente.
Dicha cantidad C representa el grado de asimetría quiral de excitación para una molécula pequeña. La respuesta de éstas moléculas interactuando con una perturbación de un campo electromagnético (CEM) pueden ser obtenidos desde la teoría o desde el experimento. Una molécula sujeta a un CEM monocromático (una sola longitud de onda) genera un momento dipolar eléctrico p y un momento dipolar eléctrico m. dados por:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): m=χ'B'+iG'E'
NOTA IMPORTANTE: toda cantidad "primas", son valores complejos. Las cantidades α y χ. Son la polarización eléctrica y la susceptibilidad magnética respectivamente mientras que los campos eléctrico y magnético son campos locales de la molécula (ya que locálmente, en general dichos campos no son iguales). También cabe resaltar que solo las cantidades que pertenecen a los reales son las cantidades físicas.
Ahora consideremos los siguientes campos eléctrico y magnético:
y
Nota: el campo E posee paridad (inversión de coordenadas espaciales) par mientras que B es impar.
Entonces, la taza de excitación de la molécula, (suponiendo que interactúa con la LCP un tiempo razonablemente largo) está dada por el promedio temporal de:
Error al representar (error de sintaxis): A^{±}=<E∙''p''+B∙''m''>=\frac{\omega}{2}Im(E´*∙p'+B´*∙m')
Donde el asterisco implica el conjugado de dicho número complejo, las letras en cursiva implican la derivada respecto al tiempo y el signo ± representa la dirección de giro de la LCP (+ si es a la izquierdaq y - es a la derecha).
Usando las ecuaciones del momento dipolar eléctrico, magnético y desarrollando el álgebra, se puede llegar a:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): A^{±}=\frac{\omega}{2}(\alpha''ǀEǀ^{2}+χ''ǀBǀ^{2})±G'' \omega Im(E'*∙B')
los valores biprimados son de la forma:
En general, el valor de χes muy pequeño a comparación de la mayoría de las moléculas así que puede descartarse. Por otro lado, existe la identidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \omega Im(E'*∙B')=''B''∙E-''E''∙B y como las variables en cursiva son derivadas parciales respecto al tiempo, usamos las ecuaciones de Maxwell para poder reescribir dicha expresión de la siguiente forma:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): A^{±}=\frac{2}{ϵ_0}(\omega U_e\alpha ''∓CG'')<math> Donde: <math>U_e=\frac{ϵ_0}{4}ǀEǀ^{2} que el promedio temporal de la densidad de energía electríca.
Para una onda plana monocromática, el factor de desimetría está definido por:
Donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): A^{±} es la taza de absorción para cualquier par de ondas electromagnéticas con paridades intercambiadas. Sustituyendo la Error al representar (error de sintaxis): A^{±} que se acaba de encontrar en g, tenemos:
Este resultado nos muestra que la taza de excitación de una molécula pequeña es proporcional al producto de la quiralidad de la materia (primer fracción) y la quiralidad del campo EM (el término C).
Todo esto es para un material que no tiene alguna fuente o sumidero de quiralidad óptica, sin embargo, como un pequeño paréntesis, se puede ver que materiales tipo "Material currents" funcionan como fuente o sumidero. asi que tomando la derivada respecto al tiempo de C y usando las ecuaciones de Maxwell, tenemos que:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{dC}{dt}=\frac{∂C}{∂t}+\frac{1}{\mu_0}∇×F=-\frac{1}{2}(j∙∇×E+E∙∇×j)
Donde
Error al representar (error de sintaxis): F≡\frac{E×(∇×B)-B×(∇×E)}{2}
Que representa el flujo de quiralidad y podemos notar que tiene la misma estructura que el teorema del vector de Pointing, asi es como se deduce que el vector de Pointing
Error al representar (error de sintaxis): S=E×B
y la cantidad
Error al representar (error de sintaxis): j∙E
describe cómo estos materiales actúan como fuente o sumidero.
Regresando a la LCP, esta mejorada asimetría quiral tiene la información de los nodos de la onda estacionaria y las moléculas pequeñas que estén localizadas en estas regiones se predice que mostrarán una mejora en la asimetría quiral en su taza de excitación.
Como se sabe, una onda estacionaria está construída a partir de dos ondas que se contraponen y que tengan sentidos opuestos, misma frecuencia y un cambio pequeño entre sus intensidades.
Sea un campo eléctrico de una LCP en sentido izquierdo, que se mueve dederecha a izquierda, mientras que es el campo eléctrico de ootra LCP en sentido derecho propagandose de izquierda a derecha, y se asume que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): E_1 es ligeramente mayor que . Como se sabe, estas dos ondas genererán una interferencia entre los haces de luz, mientras que su densidad de energía está dada por:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): U_e(z)=\frac{ϵ_0}{2}[E_1^{2}+E_2^{2}-2E_1E_2cos(2kz)]
donde claramente, el mínimo de la energía es cuando . Por tanto, la densidad de energía mínima es:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): U_{e min}=\frac{ϵ_0}{2}[E_1-E_2]^{2}
Con esto y con las definiciones anteriores, se puede mostrar que el grado de asimetría quiral está dada por:
que es independiente de la posició. Entonces el valor de g será:
Y sustituyendo los valores encontrados, se llega a que:
El valor de g es máximo ya que como el valor de la densidad de energía era mínimo, y por propiedad elemental de una fracción, si el denominador es menor, el resultado será mayor.
Es fácil ver que cuando las energías van teniendo casi la misma intensidad, la taza de asimetría aumenta mucho. Esto se le conoce como onda estacionaria superquiral. La presente teoría está limitada a efectos quirales donde el campo EM no es tan intenso, es decir, el material responde linealmente con dicho campo. Otro detalle a tomar en cuenta que se deberá contemplar los momentos cuadrupolares para moléculas que sean del tamaño aproximadamente de la longitud de onda del campo EM.
Bibliografía
Yiqiao Tang and Adam E. Cohen, Optical quirality and interaction with Matter (Harvard University, Massachusetts, 2010)
Polarización
Introducción
Polarización y sencillez
hay varios tipos de sencillez que son familiares a los estudiantes de óptica. Por ejemplo, la sencillez respecto a la longitud de onda; un haz de luz blanca no es sencillo, pues incluye una gran variedad de longitudes de onda y un prisma puede dispersarlo, separándolo en un abanico de direcciones, cada una de las cuales corresponde a una sola longitud de onda. La sencillez puede ser aún mayor ; un haz puede subdividirse hasta que consista en una sola longitud de onda y una sola forma de polarización.

Una de las propiedades físicas de la luz es que puede ser polarizada. Siendo la luz un tipo de radiación electromagnética, posee tanto campo eléctrico como campo magnético; es precisamente su campo eléctrico el que produce el fenómeno de la polarización.
Un hecho notable acerca de las ondas luminosas es que son transversales. Los desplazamientos, de naturaleza electromagnética, no son a lo largo de la línea de propagación, sino perpendiculares a ella. Por ejemplo si la dirección de propagación es hacia el este, las vibraciones eléctricas pueden ser de arriba arriba-abajo, o de norte-sur, o a lo largo de cualquier otra línea perpendicular al eje este-oeste,(Fig.1) oscilando a medida que la luz avanza en el medio o en el vacío. Es debido a esto que a la luz se le considera una onda electromagnética transversal.
La orientación de las oscilaciones del campo eléctrico de la luz en el plano (si se considera al eje como el eje de la dirección de propagación) son las que generan el efecto de polarización. Para que la luz sea polarizada, el campo eléctrico debe vibrar principalmente en una dirección.
La mayoría de las fuentes de luz no se encuentran polarizadas, por ejemplo la luz natural, llamada así porque es la proveniente del sol, tiene todas las polarizaciones, esto quiere decir que a todo tiempo la suma de sus vectores de campo eléctrico tienen una cierta magnitud y sentido, la cual no tiene relación con cualquier otra polarización en cualquier tiempo o bien la polarización es aleatoria. Se puede hablar de luz no polarizada cuando ésta no es estrictamente monocromática y no es posible determinar si está polarizada o no. Es en el caso de la luz no polarizada donde no todos los átomos emiten luz en el mismo estado de polarización, por lo que el vector campo eléctrico vibra en todas las direcciones, cancelando el efecto de polarización.
Animación
http://www.geocities.ws/fisica1y2/interactivas2/polarizacion/polarizacion.html
Luz Linealmente Polarizada
Se dice que la luz es linealmente polarizada (o polarizada plana) cuando la componente-x y la componente-y del vector del campo eléctrico se encuentran en fase. Si pudiéramos observar las oscilaciones del campo eléctrico en un haz de luz linealmente polarizada, viniendo de frente (saliendo de la pantalla), entonces el movimiento descrito sería lineal, o una recta.
Tomando el plano como referencia, podemos considerar a las vibraciones del campo eléctrico (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \mathbf{E}
) en ese plano como una onda armónica simple, la cuál se propaga a lo largo de . El campo eléctrico va a oscilar en perpendicularmente a , a determinada frecuencia.
Análogamente, tomando el plano como referencia, se consideran de igual forma las vibraciones del campo eléctrico en ese plano como una onda armónica simple, que también se propaga a lo largo de , y cuyas oscilaciones se darán en perpendicularmente a .
Ambas ondas, matemáticamente, pueden se descritas por las siguientes ecuaciones.
.
En estas expresiones, es la diferencia de fase entre las ondas, las cuales viajan en dirección de . La amplitud de estas ondas puede ser diferente, y esta diferencia únicamente determina la dirección de la línea recta , en el caso que las amplitudes de campo sean iguales el anulo pormado sera de (o qué tanto se inclina en el plano ) que traza el vector del campo eléctrico mientras se propaga.
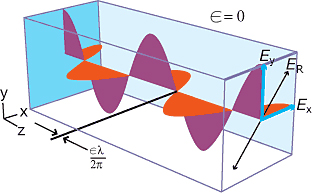
Hablando del campo eléctrico como una perturbación óptica, la suma vectorial de sus componentes produce un resultante.
Si es cero, o un múltiplo entero de , ambas componentes se dicen que se encuentran en fase. En ese caso, la suma vectorial de ambas sería.
Es la superposición de las ondas y (en fase) que resulta en la ecuación (4), con una amplitud fija igual a , lo cuál significa que la suma de ambas genera otra onda que también es linealmente polarizada.
Las magnitudes relativas de las componentes determinarán la orientación de la polarización, es decir:
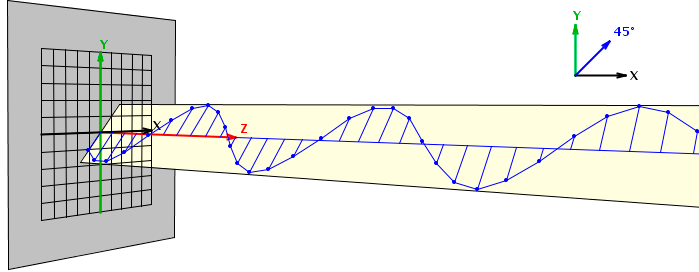
Luz Circularmente Polarizada
Cuando la luz es linealmente polarizada y se encuentran desfasadas por 90°, y cuando la amplitud de ambas es exactamente la misma,hablamos de polarización circular. En este caso, si pudiéramos observar las oscilaciones del campo eléctrico en un haz de luz linealmente polarizada, viniendo de frente (saliendo de la pantalla), entonces el movimiento descrito sería circular.
Bajo esta definición, las ondas en el eje-x y el eje-y que describen a este tipo de polarización pueden representarse matemáticamente por las siguientes ecuaciones
Donde la amplitud de y es la misma (). Por el desfase de 90°, la componente del campo eléctrico en el eje-y cambia de a , por lo que la fase debe ser equivalente a (con ,...).
Luego, la suma vectorial de las componentes en el eje-x () y el eje-y () es:
La polarización circular puede presentarse como polarización circular derecha y polarización circular izquierda. Los nombres sólo hacen referencia a la dirección en la que el campo eléctrico rota mientras la onda se propaga (dextrógiro, hacia la derecha es en sentido de las manecillas del reloj y levógiro hacia la izquierda en sentido opuesto a las manecillas del reloj).
Una forma de representar la polarización circular derecha es haciendo , a un valor arbitrario . En este caso, el vector del campo eléctrico quedaría en un eje de referencia situado en el primer cuadrante del plano , por lo que las componentes en el eje-x y en el eje-y quedarían así:
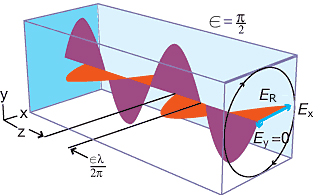
Si avanzamos en el tiempo de tal forma que ahora , obtenemos que y . Con esto podemos deducir que del eje de referencia, el campo eléctrico rotó de tal forma que ahora se encuentra sobre el eje-x, por lo que su dirección de rotación fue en sentido de las manecillas del reloj.
Para representar su caso opuesto (polarización circular izquierda), basta con tener una onda cuya ecuación corresponda a:
donde el signo negativo en el eje-y, a una fase de (con ,...), genera una rotación en sentido contrario a las manecillas del reloj.
Si sumamos las ecuaciones de polarización circular izquierda (10) y polarización circular derecha (7), podemos obtener una ecuación que representaría una onda linealmente polarizada:
Luz Elípticamente Polarizada
La polarización elíptica se presenta cuando las componentes y se encuentran desfasadas un valor arbitrario, y a su vez presentan una amplitud arbitraria.
Para encontrar una ecuación independiente del espacio y del tiempo (kz-ωt). Se busca el cociente y ocupando la propiedad para el coseno:
Error al representar (error de sintaxis): \frac{E _{y}}{E_{0y}} = \cos(kz − \omega t)\cos \epsilon − \sin(kz − \omega t)\sin \epsilon
ahora sustituyendo Error al representar (error de sintaxis): \frac{E_{x}}{E_{0X}} = \cos(kz − \omega t ) se tiene.
Error al representar (error de sintaxis): \frac{E_{y}}{E_{oy}} − \frac{E_{x}}{E_{0x}} \cos \epsilon = −\sin(kz − \omega t)\sin \epsilon
Con un poco de algebra y elevandoal cuadrado se obtiene.
Utilizando la identidad Error al representar (error de sintaxis): \sin^{2}\epsilon = 1 − \cos^{2}\epsilon
Aqui es la diferencia de fase relativa entre las ondas.
Si se puede considerar "arbitrario" como cualquier valor, entonces se pueden presentar los casos donde , (o múltiplos enteros de éste), así como cuando la amplitud de las componentes sea la misma. Es por esto que a la polarización lineal y polarización circular se les considera casos especiales de polarización elíptica, a pesar de que éstos no manifiesten estrictamente un movimiento elíptico.
En este caso, si pudiéramos observar las oscilaciones del campo eléctrico en un haz de luz linealmente polarizada, viniendo de frente (saliendo de la pantalla), entonces el movimiento descrito sería en la mayoría de los casos elíptico.
En general, los ejes principales de la elipse no están en las direcciones x e y. Al utilizar una transformación (rotación) del sistema de coordenadas, podemos diagonalizar la ecuación :
Sean x' y y' el nuevo conjunto de ejes a lo largo de los ejes principales de la elipse. Entonces la ecuación de la elipse en este nuevo sistema de coordenadas se convierte en:
donde a y b son las longitudes de los semiejes principales de la elipse, y y son los componentes del vector del campo eléctrico en este sistema de coordenadas principal.
Sea el ángulo entre el eje x' y el eje x. Entonces las longitudes de los ejes principales están dadas por:
El ángulo se puede expresar en términos de , y como:
Es importante tener en cuenta que también es una solución, si es una solución de la ecuación.
Dirección de la revolución de una polarización elíptica
La dirección de la revolución de una polarización elíptica está determinada por el signo de . El punto final del vector del campo eléctrico girará en el sentido de las agujas del reloj si > 0, y en el sentido contrario a las agujas del reloj si <0.
La siguiente figura muestra cómo cambia la elipse de polarización al variar la diferencia de fase δ.
Polarizadores dicroicos.
El artefacto que divide la luz no polarizada en dos componentes y descarta una, se llama polarizador. Si el proceso para separar es imperfecto, de modo que una fracción de la componente que no se desea, no se descarta, el polarizador se llama parcial. Existen muchos tipos de polarizadores que se pueden usar en muchos procesos de óptica: absorción, reflexión, refracción, o dispersión cualquiera de estos puede usarse para resolver un haz en componentes polarizadas. La clave para el proceso de polarización es la asimetría ( por ejemplo la asimetría estructural interna del polarizador, la asimetría, oblicuidad, de la armadura del polarizador o la asimetría de la dirección de visión relativa a la dirección de incidencia del haz, asimetría de en la absorción o dricroísmo.
El Polarizador de rejilla de alambre
Este aparato consta de un conjunto de finos alambres colocados paralelamente, siendo los alambres metálicos de gran conductividad para los campos eléctricos paralelos a ellos. Tales campos producen corrientes eléctricas en los alambres de forma que su energía se invierte en calor, debido a la pequeña pero significativa, resistencia eléctrica de los alambres. Sin embargo, debido a que en los espacios entre los alambres no hay conducción, no hay flujo de corriente perpendicular a ellos. Así, pues, los campos eléctricos perpendiculares a los alambres no producen corrientes ni pierden energía. Entonces, el colocar la rejilla de alambre frente a un haz no polarizado se disipa la energía de una de las componentes y permite la otra pasar casi sin disminución.
La Lámina H
Son largas y delgadas cadenas de Yodo, absorben las vibraciones eléctricas paralelas a su eje de alineación y transmiten libremente las vibraciones perpendiculares. Así el eje de transmisión es perpendicular a la dirección del estiramiento.En condiciones ideales se transmite el cincuenta por ciento de la potencia de un haz incidente. La componente de en una onda incidente, que es paralela a las moléculas, impulsa a los electrones, hace trabajo sobre ellos, y es fuertemente absorbida La hoja H es un polarizador muy efectivo sobre todo en el espectro visible pero es algo menos en el extremo azul. Cuando se observa una luz blanca brillante a través de un par de hojas H polaroides cruzadas, el color de extinción será un color azul profundo como resultado de esta fuga.
Polarizadores en un reloj(Animación)
https://www.vascak.cz/data/android/physicsatschool/templateimg.php?s=opt_polarizacefiltr&l=es
Figura activa con dos polarizadores
http://micro.magnet.fsu.edu/primer/java/polarizedlight/filters/index.html
Vídeo de polarización
https://www.youtube.com/watch?v=82Cux9Q9afk
Polarizadores de reflexión:
Casi cualquier objeto pulido, no metálico tiende a polarizar a luz que choca oblicuamente. Uno de los polarizadores de reflexión más sencillos es una placa de vidrio montada oblicuamente en el haz de luz dado. Cuando se monta la placa perpendicular al haz no hay polarización; todas las componentes de la luz se transmiten ( cerca del 92% por lo general) y el haz transmitido esta no polarizado. Cerca del 8 % se refleja y también es no polarizada.
Pero cuando la placa está inclinada, de modo que la asimetría del proceso de reflexión queda destruida, suceden cosas interesantes . El haz transmitido se halla parcialmente polarizado y el haz reflejado aún más.Las formas de polarización de los dos haces son ortogonales
Como se ve en la figura, para un caso particular, el caso en el que haz B1 incide a 56.3° de la normal en una placa de vidrio cuyo índice de reflexión es 1.5 .
se supondrá en primer lugar que el haz está 100 % polarizado linealmente y que la dirección de vibración eléctrica es paralela al plano del papel. Considérese enseguida al haz refractado B2 que penetra al vidrio y el B3 que está reflejado de la superficie superior.
El haz refractado tiene una dirección más inclinada que B1, como lo describe la ley de Snell, y las vibraciones en el haz refractado , B2, son paralelas exactamente a la dirección del haz reflejado, B3.
Y esto a su vez , significa que el haz reflejado, B3 no puede existir. No hay tal haz y ninguna energía puede fluir en esa dirección.
¿Por qué? porque , de acuerdo con la teoría electromagnética, la luz necesita una vibración transversal; sin embargo, en el punto en el que empieza la luz entrar al vidrio las vibraciones son exactamente paralelas a la dirección B3 y por tanto, no tiene componente que sea transversal a B3.
Finalmente supongase que el haz incidente B1 no esta polarizado. El haz reflejado consta, por tanto, de una segunda componente y tiene una polarización de 100 %. El transmitido también se polariza; por en un grado mucho menor y , por supuesto predomina la dirección de vibración ortogonal.
El único ángulo en el que el haz reflejado queda completamente polarizado es el que se conoce como de Brewster o ángulo de polarización. Esto es lo único que se necesita para producir un haz completamente polarizado, Conociendo el índice de refracción, n, de una placa de vidrio, plástico o algún material semejante, y conociendo la ley de Snell se puede calcular el ángulo de polarización; este resulta ser el ángulo cuya tangente es precisamente n, Así, pues, una placa de cloruro de plata n=2, tiene un ángulo de polarización de arco tan 2, o aproximadamente de 63°.
El agua tiene un índice de 1.33; por tanto la luz natural que se refleja a un arco tan 1.33, o aproximadamente a 53°, de la superficie de un estanque está completamente polarizada.
El vector de Stokes
El vector de Stokes
El vector de Stokes es un conjunto de números, se aplica igualmente a luz polarizada, a luz parcialmente polarizada y a la luz no polarizada. Inventado en 1852 por el físico británico G.G Stokes, proporciona el método más sencillo para predecir el resultado de superponer dos haces incoherentes.
Más importante aún es el hecho de que el vector de Stokes de un método numérico simple para predecir cómo se afecta un haz por efecto de un polarizador o un retardador. La especificación del haz emergente se determina multiplicando el vector de Stokes que representa el haz incidente por una matriz que representa al polarizador o retardador.
La intensidad total de la luz (polarizada + no polarizada)
La intensidad de la polarización lineal horizontal o vertical
La intensidad de la polarización lineal + 45 ° o -45 °
La intensidad de polarización circular derecha o izquierda
La intensidad de la parte polarizada de la onda de luz viene dada por:
La intensidad total es:
Así:
(Luz completamente polarizada)
(Luz parcialmente polarizado y no polarizado)
Para representar (14) en términos de los observables del campo óptico, debemos tomar un promedio durante el tiempo de observación.
Dado que la vibración es tan rápida, el tiempo de observación puede verse como infinito. Pero, dado que y son periódicos, en realidad podemos promediar (14) solo en un solo período de oscilación.
El tiempo promedio está representado por los corchetes angulares <...>, por lo que (14) puede escribirse como:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac { \left< { E }_{ x }^{ 2 }(t) \right> }{ { E }_{ 0x }^{ 2 } } +\frac { \left< { E }_{ y }^{ 2 }(t) \right> }{ { E }_{ 0y }^{ 2 } } -2\frac { \left< { E }_{ y }(t){ E }_{ x }(t) \right> }{ { E }_{ 0y }(t){ E }_{ 0x }(t) } cos\varepsilon ={ sin }^{ 2 }\varepsilon ....(14)
dónde
Error al representar (error de sintaxis): \left< { E }_{ y }(t){ E }_{ x }(t) \right> ={ Lim }_{ T\longrightarrow \infty }\frac { 1 }{ T } \int _{ 0 }^{ T }{ { E }_{ y }(t){ E }_{ x }(t)dt } .....(15)
Luego multiplicamos (14) por , y luego obtenemos:
Error al representar (error de sintaxis): { { 4E }_{ 0y } }^{ 2 }\left< { E }_{ x }^{ 2 }(t) \right> +{ { 4E }_{ 0x } }^{ 2 }\left< { E }_{ y }^{ 2 }(t) \right> -8{ E }_{ 0y }(t){ E }_{ 0x }(t)\left< { E }_{ y }(t){ E }_{ x }(t) \right> cos\varepsilon ={ (2{ E }_{ 0y }(t){ E }_{ 0x }(t){ sin }\varepsilon ) }^{ 2 }
......(16)
De (1) y (2), podemos encontrar los valores promedio de la ecuación (16) usando la ecuación (15):
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left< { E }_{ x }^{ 2 }(t) \right> =\frac { 1 }{ 2 } { { E }_{ 0x } }^{ 2 } ......(17)
Error al representar (error de sintaxis): \left< { E }_{ y }^{ 2 }(t) \right> =\frac { 1 }{ 2 } { { E }_{ 0y } }^{ 2 } .......(18)
Error al representar (error de sintaxis): \left< { E }_{ y }(t){ E }_{ x }(t) \right> =\frac { 1 }{ 2 } { { E }_{ 0x } }{ { E }_{ 0y } }cos\varepsilon .......(19)
Sustituyendo (17), (18), (19) en (16) y obtenemos:
....(20)
Como queremos expresar el resultado final en términos de intensidad, podemos sumar y restar la cantidad al lado izquierdo de (20); Haciendo esto se obtienen cuadrados perfectos.
Entonces podemos obtener:
.....(21)
Escribimos las cantidades dentro de los paréntesis como:
......(22)
.......(23)
.......(24)
........(25)
Tenga en cuenta que S_0 , S_1 , S_2 , S_3 son cantidades promediadas en el tiempo realizadas en un intervalo de tiempo T_D que es la constante de tiempo característica del proceso de detección
Luego reescribimos (21) como:
...(26)
Las cuatro ecuaciones (22), (23), (24) y (25) son los parámetros de polarización de Stokes para una onda plana .
Nota:
Los parámetros de Stokes se expresan en términos de intensidades (que podemos medir) Los parámetros de Stokes son cantidades reales (en lugar de números complejos como en las matrices de Jones)
Basándonos en la desigualdad de Schwartz, podemos decir que para cualquier estado de luz polarizada:
En (17), la igualdad es verdadera para la luz completamente polarizada, y la desigualdad es verdadera para la luz parcialmente polarizada o no polarizada.
GRADO DE POLARIZACIÓN (DOP) EN TÉRMINOS DE PARÁMETROS DE STOKES
Podemos usar los parámetros de Stokes para describir el grado de polarización para cualquier estado de polarización (completamente polarizado, parcialmente polarizado y no polarizado).
El grado de polarización P se define como (basado en la intensidad de la luz):
Entonces el significado de P es:
P = 1 ---> luz completamente polarizada
P = 0 ---> luz no polarizada
0 < P <1 ---> luz parcialmente polarizada
EJEMPLOS DE PARÁMETROS DE STOKES PARA LUZ COMPLETAMENTE POLARIZADA
Ahora discutimos los parámetros de Stokes para algunos casos especiales.
1. LUZ LINEALMENTE POLARIZADA HORIZONTALMENTE (LHP)
Para este caso, no hay componente de campo vertical, por lo que . De (22), (23), (24) y (25) obtenemos:
2. LUZ LINEALMENTE POLARIZADA VERTICALMENTE (LVP) Para este caso, no hay componente de campo horizontal, por lo que . De (22) a (25) obtenemos:
3. LINEAL + 45 ° LUZ POLARIZADA (L +45) Las condiciones para obtener luz polarizada lineal de + 45 ° son:
y
Esto significa que esta polarización es una superposición de campos horizontales y verticales en fase, de igual amplitud. Con (22) a (25), obtenemos:
4. LINEAL -45 ° LUZ POLARIZADA (L -45) Las condiciones para obtener luz polarizada lineal de -45 ° son:
y Error al representar (error de sintaxis): \varepsilon =180°
Entonces obtenemos:
LUZ CIRCULARMENTE POLARIZADA DERECHA (RCP) Las condiciones para obtener una luz polarizada circularmente correcta son:
y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \varepsilon =90°
Entonces obtenemos:
LUZ CIRCULARMENTE POLARIZADA IZQUIERDA (LCP) Las condiciones para obtener luz polarizada circularmente a la izquierda son:
y Error al representar (error de sintaxis): \varepsilon =-90°
Entonces obtenemos:
7. LUZ POLARIZADA ELÍPTICAMENTE Los parámetros de Stokes para luz polarizada elípticamente en general son como la definición:
Aplicaciones: El resultado de combinar dos haces incoherentes se halla sumando los dos vectores de Stokes adecuados. Considérese, por ejemplo,la suma de un haz polarizado horizontalmente de intensidad uno y un haz polarizado circularmente en sentido derecho de intensidad tres. Los vectores correspondientes son ( 1,1,0,0) y (3,0,0,3),hay que notar los vectores los pusimos horizontal solo para ahorrar espacio.
La suma obtenida añadiendo los números situados en lugares correspondientes es (4,1,0,3). Este vector resultante significa que la intensidad del haz resultante es 4, ya que el primer número es 4.
El modelo seccional elíptico tiene gran parecido con un círculo, ya que la magnitud del último número es grande y el sentido circular de la elipse es hacia la derecha, pues el último número es positivo. La elipse es más horizontal que vertical, ya que el segundo número es positivo. El grado de polarización es
o sea 79 por ciento.
Otro ejemplo es la combinación de dos haces polarizados horizontal y verticalmente que son incoherentes y de intensidad unidad. sus vectores son (1,1,0,0) y (1,-1,,0,0), en tanto que la suma es (2,0,0,0). Este representa un haz no polarizado, pues los últimos tres números son cero.
EL vector de Jones
El vector de de Jones, inventado en 1941 por un físico americano de 25 años, R.Clark Jones, es superior al vector de Stokes en algunos sentidos, pero inferior a otros. Es superior en el sentido de que es aplicable a la adición de haces coherentes. Es inferior en el sentido de que no puede aplicarse a la luz no polarizada o parcialmente polarizada y en que, además, utiliza números complejos.
Dado que la luz se compone de campos eléctricos y magnéticos oscilantes, Jones razonó que la forma más natural de representar la luz es en términos del vector de campo eléctrico.
Cuando se escribe como un vector de columna, este vector se conoce como un vector de Jones y tiene la forma:
Donde y son los componentes escalares instantáneos del campo eléctrico. Nota que estos valores pueden ser números complejos, por lo que la información de amplitud y fase es presente. A menudo, sin embargo, no es necesario conocer las amplitudes y fases exactas de los componentes del vector. Por lo tanto los vectores de Jones pueden ser normalizados y en fase común, los factores pueden ser descuidados. Esto resulta en una pérdida de información, pero puede simplificar enormemente expresiones. Por ejemplo, los siguientes vectores contienen diversos grados de información, pero son todas las representaciones vectoriales de Jones para el mismo estado de polarización:
Tenga en cuenta que se dice que un vector complejo se normaliza cuando el producto punto del vector con su conjugado complejo produce un valor de unidad. En la mayoría de los casos, se elige la base para el vector de Jones como los estados de polarización lineal horizontal y vertical. En este caso las representaciones de estos dos estados son:
y
o, en forma normalizada,
y
Donde y representan la luz polarizada horizontal y verticalmente, respectivamente. La suma de dos haces de luz coherentes viene dada por la suma de sus componentes correspondientes del vector de Jones, por lo que la suma de y cuando viene dada por :
Error al representar (error de sintaxis): \ E_45°= \ \begin {bmatrix} { E }_{ x }(t)\\ { E }_{ x }(t)\end {bmatrix}
Error al representar (error de sintaxis): \ E_45° = \frac { 1 }{ \sqrt { 2 } } \ \begin {bmatrix} 1\\ 1\end {bmatrix}
donde la flecha indica normalización. Tenga en cuenta que esta es la representación de la polarización. Estado en el que el campo eléctrico está orientado en un ángulo de 45 grados con respecto a la estados base. Otros dos estados de polarización comunes son circular derecho y circular izquierdo. En ambos casos los dos componentes tienen la misma amplitud,pero tienen una diferencia de fase de 90°. Así, la representación vectorial de Jones para la derecha-circular es
Normalizando esta expresión y factorizando un factor de fase constante :
Del mismo modo, la representación normalizada para la luz circular izquierda es:
La intensidad del haz es proporcional a la suma de los cuadrados de las magnitudes de los elementos. Si cada elemento del vector se multiplica por 4,la intensidad aumenta por un factor de 16. Aplicaciones: Una aplicación sencilla del vector de Jones es la predicción del resultado de componer dos haces coherentes. Considérese un haz polarizado horizontalmente de intensidad 1 y otro verticalmente polarizado de intensidad de 16 veces mayor. Los haces se suponen coherentes y de la misma fase.
Los vectores correspondientes son y El resultado de componer los dos haces se encuentra sumando los vectores. La suma es
Este corresponde a un haz linealmente polarizado a un angulo dado por ; esto es ,76°. La intensidad esta dada por osea 17.
A continuación, consideremos un haz de luz representado por el vector de Jones
incidente en un dispositivo óptico. La luz interactuará con el dispositivo, y el nuevo estado de polarización de la luz al salir del dispositivo será:
El acoplamiento entre estos dos vectores se puede describir completamente mediante un conjunto de cuatro coeficientes de acuerdo con el siguiente par de ecuaciones lineales:
Estas dos ecuaciones pueden reescribirse usando la notación matricial como
dónde
Es la matriz de Jones del dispositivo óptico. Una lista de matrices de Jones para algunos dispositivos ópticos comunes aparece en la Tabla 1. Es posible representar el paso de un haz de luz a través de múltiples dispositivos como la multiplicación de matrices de Jones. Tenga en cuenta que las matrices no conmutan, como se ilustra en el siguiente ejemplo. Supongamos una señal de entrada polarizada horizontalmente, y veamos su propagación a través de dos dispositivos, un polarizador lineal orientado a y una placa de cuarto de onda con su eje vertical rápido. Si la luz pasa a través del polarizador primero, seguido por la placa de onda, tenemos:
donde hemos descuidado los factores de amplitud y fase comunes por simplicidad. La salida es polarizado circularmente a la derecha.
Si bien la multiplicación de matrices no es conmutativa, es asociativa, por lo que una cadena de múltiples matrices de Jones que representan varios dispositivos se puede multiplicar para obtener una sola matriz de Jones que describe el sistema óptico en su conjunto. Por lo tanto, es posible condensar las propiedades de N dispositivos ópticos que actúan en serie hasta una sola matriz simplemente multiplicando las matrices de Jones de los dispositivos:
Cómo funcionan las gafas 3-D
Visualización en 3-D
En una sala de cine, la razón por la que usas gafas 3-D es para introducir diferentes imágenes en tus ojos como lo hace un View-Master. En realidad, la pantalla muestra dos imágenes y las gafas hacen que una de las imágenes entre en un ojo y la otra en el otro. Hay dos sistemas comunes para hacer esto:
Rojo / Verde o Rojo / Azul
Aunque el sistema rojo / verde o rojo / azul ahora se usa principalmente para efectos de televisión en 3D, y se usó en muchas películas antiguas en 3D. En este sistema, se muestran dos imágenes en la pantalla, una en rojo y la otra en azul (o verde). Los filtros en las gafas permiten que solo una imagen entre en cada ojo, y su cerebro hace el resto. Realmente no puede tener una película en color cuando está usando el color para proporcionar la separación, por lo que la calidad de la imagen no es tan buena como con el sistema polarizado.
Polarización
En Disney World , Universal Studios y otros lugares tridimensionales, el método preferido utiliza lentes polarizados porque permiten la visualización del color. Dos proyectores sincronizados proyectan dos vistas respectivas en la pantalla, cada una con una polarización diferente. Las gafas permiten solo una de las imágenes en cada ojo porque contienen lentes con polarización diferente.
Como se había dicho anteriormente un filtro polarizador tiene pequeñas líneas paralelas grabadas en él, un poco como las lamas de un conjunto de persianas venecianas. Esto significa que solo permitirá que la luz vibre en un plano particular a través.
Al igual que en el antiguo estilo 3D, la película se graba utilizando dos lentes de cámara, sentados uno al lado del otro. Pero en el cine, los dos carretes de película se proyectan a través de diferentes filtros polarizados. Así que las imágenes destinadas a los ojos izquierdos de los espectadores están polarizadas en un plano horizontal, mientras que las imágenes destinadas a sus ojos derechos están polarizadas en un plano vertical. Las gafas de los espectadores de cine usan los mismos filtros polarizadores para separar las dos imágenes nuevamente, dando a cada ojo una perspectiva ligeramente diferente y engañando al cerebro para que "vea" el planeta Pandora de Avatar.
En un par de gafas digitales 3D, cada lente está polarizada de manera diferente. En algunas gafas, hay una diferencia de 90 grados en la polarización. Otros utilizan diferentes alineaciones de polarización circular. La pantalla está especialmente diseñada para mantener la polarización correcta cuando la luz de los proyectores rebota en ella. En lugar de verse como una malla de rojo y verde, las películas que usan esta tecnología parecen normales, pero borrosas, cuando se ven sin gafas.
Referencia
"Óptica.". E. Hecht, A. Zajac. Ed. Addison Wesley, 2000
"Luz Polarizada". WILLIAM A. SHURCLIFF. Ed.Reverté Mexicana, 1968
"Polarized Light:Production and Use". W.A. SHURCLIFF, Harvard University Press,1962.
E. Collett, Field Guide to Polarization, SPIE Press, Bellingham, WA (2005).
Ondas Electromagnéticas en medios conductores y no conductores
Una de las consecuencias mas importantes de las ecuaciones de Maxwell es la deducción de las ecuaciones de propagación de ondas electromagnéticas en un medio ó en el vacío. Entonces partiremos de éstas para derivar las ecuaciones de las ondas electromagnéticas tanto para el campo eléctrico $\vec{\textbf{E}}$ como para el campo magnético $\vec{\textbf{B}}$. A continuación se escriben las ecuaciones de Maxwell en ausencia de fuentes $\rho$=0, y $\vec{\textbf{J}}$ como respuesta de medios conductores.
\begin{center}\textbf{Ecuaciones de Maxwell} \end{center}
:
:
:
- Con $\vec{\textbf{D}}$ y $\vec{\textbf{H}}$ la intensidad del campo eléctrico y magnético, respectivamente.
Los campos que cumplen las ecuaciones anteriores también cumplen con ecuaciones constitutivas que cambian dependiendo para que medio se aplican. Para este caso sólo consideraremos medios lineales, isótropicos, homogeneos y no dispersivos, los cuales se ajustan a las siguientes ecuaciones constitutivas
- Ahora se podrán derivar las ecuaciones de onda correspondientes al campo eléctrico y magnético. Si aplicamos el rotor a la ecuación (4), obtendremos:
- Pero como $\vec{\textbf{J}}$ es respuesta del medio entonces:
- Que es la ley de Ohm para medios lineales. Entonces la ecuación (7) queda como:
.......(9)
Aprovechando la identidad vectorial:
y la ecuación (5) llegamos a la siguiente ecuación:
De las ecuaciones (2) y (3) se sigue que de la ecuación (10) sólo queda:
- Entonces la ecuación de onda para $\vec{\textbf{H}}$ queda de la siguiente manera:
- Análogamente para la ecuación de onda de $\vec{\textbf{E}}$ pero esta vez aplicando el rotor a la ecuación (3), y siguiendo los pasos que se describieron arriba, llegaríamos a:
\begin{center}\textbf{Ondas Electromagnéticas Monocromáticas} \end{center}
Las ondas electromagnéticas son soluciones de las ecuaciones (12) y (13). Para este caso vamos a considerar sólo ondas electromagnéticas monocromáticas, esto quiere decir que estas ondas sólo poseen una frecuencia.\\ Podemos suponer una dependencia temporal armónica en la solución a (12):
Siempre teniendo en cuenta que la parte real de $\vec{\textbf{E}}(\vec{\textbf{r}},t)$ tendrá significado físico. Si sustituimos (14) en (12):
, Por lo tanto:
Entonces (12) queda como:
- Similarmente para $\vec{\textbf{H}}(\vec{\textbf{r}},t)$, tenemos:
Ambas soluciones deben satisfacer las ecuaciones de Maxwell:
:
- ----->
- Y:
- Ó para mayor comodidad podemos escribir la última ecuación como:
\begin{center}\textbf{Condiciones de frontera para los campos} \end{center}:
- Para continuar es necesario establecer las condiciones de frontera que deberan obedecer las ondas electromagnéticas al pasar de un medio a otro.
Considerando la figura 1, y utilizando la ecuación (2): : Esto quiere decir que la componente normal de la inducción magnética no cambia al pasar de un medio a otro. Utilizando la ecuación (3):
- :
En el último paso se utilizó el teorema de Stokes para pasar de una formulación diferencial a una integral de la ecuación (3).
- Si $\frac{\partial\vec{\textbf{B}}}{\partial{t}}$ es finita, su flujo tiende a ser 0 para cuando $\textbf{h}$--->0 y entonces:
- Lo que se interpreta como que en la superficie de separación la componente tangencial del campo eléctrico no cambia.
- \begin{center}\textbf{Ondas planas en medios no conductores} \end{center}:
- Para medios no conductores podemos hacer $\sigma=0$ en la ecuación (15):
- (18) es la ecuación de Helmholtz vectorial. Proponemos una solución para (18) de tal forma que tenga amplitud compleja:
- $\vec{\kappa}$ es el vector de propagación de la onda, cuyas componentes [$\kappa_{x},\kappa_{y},\kappa_{z}$] están por determinar.
- Ahora sustituimos (19) en (18):
- Pero ${\nabla}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}= i\vec{\kappa}e^{i\vec{\kappa} \cdot \vec{\textbf{r}}}$ ; por lo que podemos identificar :${\nabla}= i\vec{\kappa}$ ; \therefore ${\nabla}^{2}=(i\vec{\kappa}) \cdot (i\vec{\kappa})= -\kappa^{2}$. Por lo que (18) que como sigue:
- ó:
- ----(20)
- Como $\vec{\textbf{E}}_{0}$ no puede ser 0, entonces encontramos una relación de dispersión para $\kappa$, por lo que $\kappa= \kappa(\omega)$:
Para medios lineales, homogéneos, isótropos y no dispersivos:
- También supondremos medios no magnéticos:
- Para el medio no conductor, establecemos la relación entre la permitividad de éste y su constante dieléctrica cómo:
- Con k la constante dieléctrica del medio no conductor. Sustituyendo (22) en (21):
- :
- Tomando en cuenta que $c= \frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}}$ es la velocidad de la luz en el vacío, podemos escribir la relación anterior en terminos de c:
- De aquí se define el índice de refracción de un medio:
- :
Por lo tanto (23) se convierte en:
- Retomando la propuesta de (14) como solución a la ecuación de onda completa, y sustituyendo (19) en (14):
- Entonces,
- De igual manera para (16):
- Si el vector de propagación $\vec{\kappa}$ lo escribimos como $ \vec{\kappa}= \kappa\hat{u}$, donde $\hat{u}$ es el vector unitario en la misma dirección que $\vec{\kappa}$, entonces podemos escribir a $\vec{\kappa} \cdot \vec{\textbf{r}}$ como:
Siendo $\xi$ la proyección de $\vec{\textbf{r}}$ en la dirección de $\vec{\kappa}$. Con esto (26) se escribiría como:
- (28) es de la forma $f= f(x- vt)$ siendo v la velocidad a la que se propaga la onda. Entonces tanto $\vec{\textbf{E}}(\vec{\textbf{r}},t)= \vec{\textbf{E}}_{0}e^{i(\vec{\kappa} \cdot \vec{\textbf{r}} - {\omega}t)}$ como $\vec{\textbf{H}}(\vec{\textbf{r}},t)= \vec{H_{0}}e^{i(\vec{\kappa} \cdot \vec{\textbf{r}} - {\omega}t)}$ representan una onda que se propaga en la dirección $\vec{\kappa}$, con velocidad $\frac{\omega}{\kappa}$.
- \begin{center}\textbf{Relación entre campos} \end{center}
- Para encontrar la relación entre los campos, tomaremos la parte espacia de (26) y (27):
- Igualmente para $\vec{\textbf{H}}_{\omega}(\vec{\textbf{r}})$:
- De la ecuación (1), tenemos:
- De igual manera, de la ecuación (2):
- y, de la ecuación (3) vemos que también $\vec{\textbf{H}}_{0}$ es perpendicular a $\vec{\textbf{E}}_{0}$:
- Entonces la relación anterior queda como:
- Y de la ecuación (4):
- Se llega a:
- Con lo que se concluye que en una onda electromagnética, los campos eléctricos y magnéticos son ortogonales a lo largo del camino de la onda y que éstos a su vez son ortogonales a la dirección de propagación.
- \begin{center}\textbf{Propagación de ondas planas en medios conductores} \end{center}
- Para el caso de medios conductores consideramos a $\sigma$ diferente de 0, medios no magnéticos($\mu= \mu_{0}$) y medios no dispersivos($\varepsilon= k\varepsilon_{0}$). Tomando la parte espacial de la ecuación de onda y las consideraciones de arriba($\sigma\neq 0, {\mu= \mu_{0}}, y {\varepsilon= k\varepsilon_{0}}$) , la ecuación (15) se reescribe como:
- Con como solución a la ecuación de onda completa. Cómo , la ecuación de arriba se puede escribir como:
- De (33) podemos hacer un poco de álgebra para acomodarla un poco más simple:
- ; pero como , entonces:
- Aquí hacemos la definición siguiente:
- Entonces (33) es:
- Proponemos como solución a la ecuación (35) una relación de la forma:
- Con $\vec{\textbf{k}}$ un vector de onda complejo, de la forma .
Ahora para poder sustituir (36) en (35), establecemos las mismas relaciones que para (19):
- , Entonces ---> .
- Y sustituyendo en (35):
- Como $\vec{\textbf{E}}_{\omega}(\vec{\textbf{r}})$ no puede ser 0, entonces de la relación anterior obtenemos una relación de dispersión:
- Por lo tanto siguiendo los mismos pasos que cuando no había medios conductores:
- De igual forma que cuando no había medio conductor, se define:
- Siendo g un número complejo podemos usar el álgebra compleja para separar de g su parte real y su parte imaginaria, si hacemos , entonces:
- Igualando (40) con el cuadrado de (39):
- Igualando las partes reales e imaginarias de la ecuación (41):
- Para la parte real y para la parte imaginaria:
- Podemos despejar de (43) a "eta" y sustituirla en (42), lo que nos va a llevar a una ecuación de grado cuarto para n, por lo que usando la fórmula general para encontrar soluciones de segundo grado podremos encontrar una solución para n^{2}:
- Multiplicando a (44) por n^2:
- Usando la formula general de segundo grado para resolver (45) con , da como solución:
- En la ultima relación de arriba sólo vamos a tomar el signo positivo porque la $n$ tiene que ver con índices ópticos que por lo general sólo son positivos:
- Usando el mismo procedimiento para encontrar $eta^2$:
- Sacando raíz cuadrada a las dos ultimas relaciones de arriba, encontramos a $n$ y $\eta$:
- Por lo tanto de (38) y (39), con :
- Igualando la parte real e imaginaria:
- y, ---------(49)
- Al valor de $\mid\vec{k}_{i}\mid$ es a lo que en la literatura se le conoce como constante de atenuación ó efecto piel.
- Retomando la solución completa espacial-temporal $\vec{\textbf{E}}(\vec{\textbf{r}},t)$:
- Pero con una cantidad compleja. Por lo que la solución $\vec{\textbf{E}}(\vec{\textbf{r}},t)$ se escribe como:
- Entonces $\vec{\textbf{E}}(\vec{\textbf{r}},t)$ es una onda plana que se propaga en dirección de $\vec{k}_{r}$ pero con amplitud decreciente en la dirección de $\vec{k}_{i}$
- \begin{center}\textbf{Ecuaciones de Fresnel para medios conductores} \end{center}
De la ecuación (39) y en analogía con (24), podemos definir a (39) como el índice de refracción del medio conductor. Éste es un número complejo que tiene que ver con la conductividad del conductor. Por lo tanto podemos considerar para el caso dieléctrico-conductor a las mismas ecuaciones de Fresnel que se derivan para dieléctrico-dieléctrico (ver capitulo 18, sección 2 de Reitz & Milford, fundamentos de la teoría electromagnética, cuarta edición) pero con índice de refracción del segundo medio complejo. Entonces de estas ecuaciones (dieléctrico-dieléctrico) que son: Para polarización del campo eléctrico perpendicular al plano de incidencia:
- $\textbf{r}_{s}= \frac{n_{1}cos\theta_{1} - n_{2}cos\theta_{2}}{n_{1}cos\theta_{1} + n_{2}cos\theta_{2}}$----------(51)
- $\textbf{t}_{s}= \frac{2n_{1}cos\theta_{1}}{n_{1}cos\theta_{1} + n_{2}cos\theta_{2}}$---------(52)
- $\textbf{r}_{s}$ y $\textbf{t}_{s}$ son los coeficientes de fresnel para la onda reflejante y transmitida, respectivamente y $n_{1}$ el índice de refracción del medio 1, y $\theta_{1}$ el ángulo que hace el vector de propagación con la normal a la interfaz entre los dos medios.
Para polarización del campo eléctrico polarizado paralelamente al plano de incidencia:
- $\textbf{r}_{p}= \frac{n_{2}cos\theta_{1} - n_{1}cos\theta{2}}{n_{2}cos\theta_{1} + n_{1}cos\theta_{2}}$-------------(53)
- $\textbf{t}_{p}= \frac{2n_{1}cos\theta{1}}{n_{2}cos\theta_{1} + n_{1}cos\theta_{2}}$-------------------(54)
- Para dieléctrico-conductor por lo tanto, proponemos:
- $\textbf{r´}_{s}= \frac{n_{1}cos\theta_{1} - gcos\gamma}{n_{1}cos\theta_{1} + gcos\gamma}$--------------(55)
- $\textbf{t´}_{s}= \frac{2n_{1}cos\theta_{1}}{n_{1}cos\theta_{1} + gcos\gamma}$-----------------(56)
- $\textbf{r´}_{p}= \frac{gcos\theta_{1} - n_{1}cos\gamma}{gcos\theta_{1} + n_{1}cos\gamma}$-------------(57)
- $\textbf{t´}_{p}= \frac{2n_{1}cos\theta{1}}{gcos\theta_{1} + n_{1}cos\gamma}$----------------(58)
- Con $"g"$ como se definió en (39) y $cos\gamma$ otro número complejo para considerar el caso mas general. Así $gcos\gamma$ es un número complejo. Haciendo $gcos\gamma= \alpha + i\xi$ y elevando al cuadrado ambos miembros:
- $g^{2}cos^{2}\gamma= \alpha^{2} - \xi^{2} + 2i\alpha\xi$ ; $g= \sqrt{k + i\frac{\sigma}{\varepsilon_{0}\omega}}$
- Por lo tanto:
- $(k + i\frac{\sigma}{\varepsilon_{0}\omega})(1 - sen^{2}\gamma)= \alpha^{2} - \xi^{2} + 2i\alpha\xi$------------(59)
- Si se cumple la ley de Snell para este caso $n_{1}cos\theta_{1}= gsen\gamma$ entonces de (59) igualando parte real e imaginaria obtenemos:
$k + n_{1}^{2}sen^{2}\gamma= \alpha^{2} - \xi^{2}$ y; $ \frac{\sigma}{\varepsilon_{0}\omega}= \alpha\xi$-----------(60)
- Entonces de (60) se sigue que $\alpha= \sqrt{\xi^{2} +k + n_{1}^{2}sen^{2}\gamma}$ y sustituyendo $\alpha$ en la otra ecuación, tenemos:
- $\xi^{4} + \xi^{2}(k - n_{1}^{2}sen^{2}\theta_{1}) - \frac{\sigma^{2}}{\varepsilon^{2}\omega^{2}}$--------------(61)
- Resolviendo a (61) para $\xi^{2}$ por la fórmula general tenemos que $\xi$ es:
- $\xi= \sqrt{-\frac{1}{2}(k - n_{1}sen^{2}\theta) + \frac{1}{2}\sqrt{(k^{2} - n_{1}^{2}sen^{2}\theta_{1})^{2} + (\frac{2\sigma}{\varepsilon\omega})^{2}}}$--------------------(62)
- Siguiendo el mismo procedimiento para encontrar a $\alpha$ obtenemos que:
- $\alpha= \sqrt{\frac{1}{2}(k + n_{1}^{2}sen^{2}\theta_{1} + \sqrt{(-k -n_{1}^{2}sen^{2}\theta_{1})^{2} - (\frac{2\sigma}{\varepsilon_{0}\omega})^{2}})}$-------------------(63)
- Por lo tanto despejando y sustituyendo $gcos\gamma= \alpha + i\xi$ con $\alpha$ y $\xi$ definidos como en (62) y (63) se obtendrían los nuevos coeficientes de Fresnel complejos para las ondas transmitidas y reflejadas del campo eléctrico. Así las amplitudes del campo eléctrico polarizado perpendicularmente son:
- $\vec{{E}_{0 rs}}(\vec{r})= {r´}_{s}\vec{E}_{0}-------------(64)$
- $\vec{E}_{0 ts}(\vec{r})= {t´}_{s}\vec{E}_{0}------------------(65)$
- Y para las amplitudes del campo eléctrico polarizado paralelamente:
- $\vec{E}_{0 rp}(\vec{r})= {r´}_{p}\vec{E}_{0}-------------(66)$
- $\vec{E}_{0 tp}(\vec{r})= {t´}_{p}\vec{E}_{0}----------------(67)$
- Con $\vec{E}_{0 r}(\vec{r})$ y $\vec{E}_{0 t}(\vec{r})$ la amplitud reflejada y transmitida respectivamente.
Referencias
- Introduction To Electrodynamics -Griffiths
- Foundations Of Electromagnetic Theory - Reitz & Milford
Esparcimiento Estático de Luz (SLS)
Introducción
El esparcimiento electromagnético es un fenómeno que se da cuando un campo incidente interactúa con la materia. Esta interacción se da a escalas similares a las de la longitud de onda incidente.
Debido a la heterogeneidad de la materia a esa escala, la luz se esparcirá en direcciones distintas a las consideradas por la reflexión y la refracción.
Si consideramos la naturaleza molecular de los materiales con los que interactúa la luz, entonces debemos tomar en cuenta que están presentes cargas negativas y positivas en su misma constitución aunque, en promedio, la mayoría de los cuerpos son neutros.
Tratando a la luz como una onda electromagnética debemos observar que las cargas presentes en la estructura interna de los cuerpos pueden y tendrán una interacción real con el campo luminoso. Para fines prácticos podemos considerar que la componente magnética del campo que genera a la luz es despreciable debido a que las fuerzas (fuerzas de Lorentz) que ocasiona este son muy pequeñas comparadas con las fuerzas eléctricas (fuerzas de Coulomb) provocadas por la misma luz. Esto debido a que la fuerza magnética es
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:fuerza_lorentz} \mathbf{F}_m = q\mathbf{v} \times \mathbf{B}}
donde es la velocidad a la que se mueve la carga, que en este caso al estar ligada a la estructura atómica será, en magnitud, mucho menor que () y entonces la fuerza magnética será muy pequeña. Por otro lado al considerar la fuerza eléctrica
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:fuerza_coulomb} \mathbf{F}_e = q\mathbf{E}}
vemos que la fuerza generada por el campo eléctrico es directamente proporcional al mismo y cuya constante de proporcionalidad es la carga. Es por ello que en este tratamiento supondremos que la luz está compuesta únicamente por campos eléctricos.
Ahora bien, la interacción del campo eléctrico de la luz con los componentes del material donde incide puede observarse de manera somera en la figura [fig:campodipolo].
Sabemos que la interacción del campo eléctrico con una partícula cargada es tal que tiende a alejarla o a acercarla dependiendo su naturaleza (signo). Como el campo es oscilatorio tendrá el efecto de acercar hacia él un tipo de carga a un tiempo y a alejar al mismo tipo de carga a un tiempo , es decir, cuando haya pasado media longitud de onda.
Esta interacción del campo con las cargas genera un dipolo eléctrico temporal (inducido). Sabemos que no está presente de manera permanente en el material sino que es generado por la acción del campo eléctrico incidente.
Un dipolo eléctrico está compuesto de dos cargas de igual magnitud pero de signo contrario que se encuentran separadas por una distancia . Si se toma el vector como una cantidad vectorial que va de la carga positiva a la negativa y cuya longitud es la separación entre las cargas (), entonces se define el momento dipolar eléctrico como
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:momento_dipolar_electrico} \mathbf{p} = q \cdot \mathbf{d}}
Una cantidad que relaciona al campo eléctrico y al momento dipolar es la polarizabilidad eléctrica que se define como
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \label{eq:polarizabilidad_electrica} \alpha = \dfrac{p}{E}}
Lo que nos dice la proporción entre la magnitud del dipolo eléctrico inducido y el campo eléctrico que lo generó. De manera intuitiva, la polarizabilidad puede entenderse como la tendencia de una distribución de cargas a ser modificada en su configuración por un campo eléctrico externo.
En el caso en el que el dipolo es dependiente del tiempo, como en este caso, suele escribirse como
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \label{eq:momento_dipolar_m} \mu = \mu_0 \cos(\omega t - kx)}
con . Entonces podemos escribir a la polarizabilidad como
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \label{eq:polarizabilidad_m} \alpha = \dfrac{\mu}{E}}
y con ello
Esparcimiento debido a una sola molécula
Si queremos encontrar la magnitud del campo producido por la dispersión de la luz debido a una molécula a cierta distancia de esta debemos considerar al dipolo inducido que irradia en cierta dirección. Para realizar esto tomamos al dipolo como un dipolo Hertziano, es decir, una corriente oscilante en una pequeña longitud. La teoría electromagnética nos dice que la radiación esparcida por una sola partícula será (figura [fig:scat1])
Sabemos que la irradiancia de un campo eléctrico está dada por
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:irradiancia} I(r) = \left<S\right>_T = \left<\epsilon_0 c E^2\right>_T = \dfrac{1}{2}c\epsilon_0 E_0^2}
donde es la amplitud del campo. Por lo que la irradiancia de la luz esparcida será
y como la irradiancia del campo incidente es
entonces
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:i_s1} I_{s,1} (r) = I_0 \dfrac{\pi^2 \alpha^2 \sin^2 \phi}{r^2 \lambda^4}}
Resulta conveniente definir el llamado vector de esparcimiento . Este es un vector que se encuentra en función del vector de onda y por lo mismo apuntará en la dirección de propagación de la luz. Si consideramos que la luz incidente tiene un vector de onda y la luz esparcida entonces el vector de esparcimiento será
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:q} \mathbf{q} = \mathbf{k}_s - \mathbf{k}_i}
Para obtener la longitud del vector utilizamos el hecho de que, si bien los vectores de las ondas incidente y esparcida son distintos, sus magnitudes son iguales y están dadas por
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \label{eq:numero_onda} k = \dfrac{2\pi}{\lambda}}
Si la longitud de es y el ángulo entre y es podemos obtener de la figura [fig:kaq].
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \label{eq:a_distancia} a = k \sin \dfrac{\theta}{2}}
De la longitud de y las ecuaciones [eq:numero_onda] y [eq:a_distancia] llegamos a que la longitud del vector es
que escrito en términos de la longitud de onda del vacío es
Esparcimiento de una onda por dos partículas pequeñas
En el caso de dos ondas esparcidas generadas por dos partículas distintas pero que fueron impactadas por el mismo campo incidente podemos utilizar a los campos esparcidos en su forma compleja para simplificar los cálculos. Esto es
Error al representar (error de sintaxis): {\displaystyle E_1 = E_{0,1} e^{i(\omega t - \mathbf{R} \cdot \mathbf{k}_s)} \\ E_2 = E_{0,1} e^{i(\omega t - \mathbf{R} \cdot \mathbf{k}_s) + \Delta \phi}}
donde es la distancia entre la partícula y el detector. Entre los campos sólo hay una diferencia de fase y el campo total está dado por la suma. Además en este caso
entonces la irradiancia total es
Utilizando la expresión [eq:i_s1] obtenemos finalmente la irradiancia total de la luz esparcida por dos partículas, que es
Esparcimiento de una onda por n partículas pequeñas
Tenemos ahora partículas pequeñas que forman una molécula más grande como puede ser un aminoácido o un monosacárido. Denotaremos a las partículas por un subíndice y tendremos de ellas, es decir . Sus campos eléctricos esparcidos se denotarán con , sus respectivas fases están dadas por y el campo total dispersado estará dado por la superposición de todos ellos, a saber
Siguiendo los procedimientos expuestos anteriormente, debemos ahora calcular la irradiancia total generada por todos los campos esparcidos, esto es
Es claro que cuando entonces . Luego utilizando que la función , es decir, que el seno es una función impar, vemos que todas las contribuciones son nulas debido a que . Como ejemplo (caso particular) tomemos y esto contribuye con ; pero en el punto donde y tenemos por lo que ambas se anulan. Lo anterior nos lleva a que la irradiancia total generada por partículas es
que escrita en términos de la irradiancia esparcida debida a una sóla partícula arroja
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:isn} I_{s,n} = I_{s,1} \sum_{j=1}^n \sum_{k=1}^n \cos(\phi_j - \phi_k)}
Ahora consideramos que la longitud de onda de la luz es mucho mayor que el tamaño de las moléculas. Es decir, si la molécula tiene un tamaño y es el número de onda, entonces
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:rdga01} d \cdot k = d \dfrac{2\pi}{\lambda} \approx 0}
Con lo anterior es razonable suponer ahora a las diferencias de fase como
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:rdga02} |\phi_j - \phi_k| \approx 0}
Las ecuaciones [eq:rdga01], [eq:rdga02] y el hecho de que consideremos al campo dispersado total como la superposición de todos los campos dispersados provenientes de cada una de las moléculas que forman el sistema en estudio constituyen la llamada Aproximación Rayleigh-Debye-Gans o por sus siglas en inglés RDGA.
Retomando la expresión [eq:isn] con la aproximación [eq:rdga02] obtenemos que
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:isn_app} I_{s,n} \approx n^2 I_{s,1}}
donde es el número de partículas, pero también si es la masa molecular de la molécula y es la masa molecular de una componente de la molécula
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \label{eq:n_mol} n = \dfrac{M}{M_1}}
Esparcimiento por partículas idénticas
Tomaremos partículas idénticas en un volumen como las estudiadas en la sección anterior. Utilizando un procedimiento similar al anterior calculamos la irradiancia total generada por las partículas idénticas
En el caso particular del SLS estamos interesados en el promedio de esta cantidad
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left<I_{s,T}\right> = I_{s,n} \sum_{j=1}^N \sum_{k=1}^N \left<\cos(\phi_j - \phi_k)\right>}
Ninguna de las partículas tiene un movimiento en una dirección preferencial ni una velocidad definida y sus movimientos son completamente independientes entre sí. Debido a los movimientos al azar de todas las partículas tenemos que si
Error al representar (error de sintaxis): {\displaystyle \left<\cos(\phi_j - \phi_k)\right> = 0}
y sólo quedará la contribución de que será
Error al representar (error de sintaxis): {\displaystyle \left<\cos(\phi_j - \phi_k)\right> = \left<\cos(0)\right> = 1}
con lo que la irradiancia total media para moléculas idénticas compuestas por elementos cada una es
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:i_st} \left<I_{s,T}\right> = N I_{s,n}}
Si tomamos ahora la expresión [eq:i_s1] podemos ver que
y si introducimos una constante de proporcionalidad
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \label{eq:k_is1} I_{s,1} = K \dfrac{I_0}{r^2}}
con
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \label{eq:k} K \equiv \dfrac{\pi^2 \alpha^2 \sin^2 \phi}{\lambda^4}}
Consideremos ahora la concentración molar de la solución
donde es el número de Avogadro y el número de partículas contenidas en el volumen , por lo que
entonces con [eq:n_mol] la ecuación [eq:isn_app] se escribe como
Estas relaciones las aplicacmos nn la ecuación [eq:i_st]
Error al representar (error de sintaxis): {\displaystyle \left<I_{s,T}\right> = N I_{s,n} = N_A \cdot V \cdot c \cdot \dfrac{M^2}{M_1^2} I_{s,1}}
Además la concentración está dada por
entonces
Error al representar (error de sintaxis): {\displaystyle \left<I_{s,T}\right> = N_A \cdot V \cdot C \cdot \dfrac{M}{M_1^2} I_{s,1}}
que con [eq:k_is1]
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:ist_final01} \left<I_{s,T}\right> = \dfrac{1}{r^2} KI_0VCM}
y definiendo la proporción de Rayleigh en términos de
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:rayleigh_q} R(q) \equiv \dfrac{I_{s,T}(q) r^2}{I_0 V(q)}}
vemos que podemos escribir a [eq:ist_final01] como
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:ist_final} R(q) = KCM}
Soluciones con mayor concentración
Las expresiones anteriores son aproximaciones razonables cuando se tienen soluciones con concentraciones pequeñas. Esto es razonable debido a la consideración de que los movimientos de las partículas del soluto son independientes y no existe interacción entre ellas.
Con el fin de obtener una generalización se define el factor estático de estructura como
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:s} S(q) = \dfrac{1}{N} \sum_{j=1}^N \sum_{k=1}^N \left<\cos(\phi_j - \phi_k)\right>}
Generalizando la expresión [eq:ist_final]
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:rayleigh_qs} R(q) = KCM\cdot S(q)}
observemos que para el caso de una solución diluída volvemos al caso en el que la doble suma tiene como valor final a y entonces recuperando la expresión para la proporción de Rayleigh escrita en [eq:rayleigh_q].
La ecuación [eq:rayleigh_qs] puede ser escrita como
Para encontrar debemos hacer uso de la ley límite de van’t Hoff para la presión osmótica , es decir
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:vant_hoff} \lim_{C\rightarrow 0} \dfrac{\Pi}{C} = \dfrac{\partial \Pi}{\partial C} = \dfrac{RT}{M}}
donde es la constante universal de los gases ideales. Usando ahora el teorema del virial para la presión osmótica en términos de la concentración
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:pi_virial} \dfrac{\Pi}{RT} = \dfrac{1}{M}C + A_2 C^2 + A_3 C^3 + \cdots}
que derivando respecto a la concentración nos da
llegando a
con lo que
Factor de forma
Se discutió el caso para partículas mucho más pequeñas que la longitud de onda de la luz incidente. Para el caso en el que las partículas no cumplen esta condición y tienen formas simétricas como esferas o cilindros, se debe definir una función llamada factor de forma que puede verse como una irradiancia normalizada debido a que las partículas que no son mucho más pequeñas que la longitud de onda de la luz incidente tendrán máximos y mínimos de irradiancia esparcida.
donde puede verse como una constante de normalización que se obtiene al esparcir luz a un ángulo nulo respecto a la incidencia, lo que implica que . De modo experimental esto tiene que conseguirse por extrapolación. Si se ve como la irradiancia esparcida por moléculas infinitamente pequeñas entonces puede utilizarse [eq:isn] y para se usa [eq:isn_app], por lo que
Error al representar (error de sintaxis): {\displaystyle P(q) = \left<\dfrac{I_{s,1}\sum_{j=1}^n \sum_{k=1}^n\cos(\phi_j - \phi_k)}{I_{s,1} n^2}\right> = \dfrac{1}{n^2} \sum_{j=1}^n \sum_{k=1}^n \left<\cos(\phi_j - \phi_k)\right>}
Para calcular el promedio es conveniente utilizar que donde el subíndice indica entré qué partículas se tiene la distancia. Y por la definición de producto punto tenemos
Error al representar (error de sintaxis): {\displaystyle \mathbf{r}_{jk} \cdot \mathbf{q} = r_{jk}q \cdot \cos(\theta)}
e integrando en coordenadas polares para considerar todas las posibles orientaciones de las moléculas
Error al representar (error de sintaxis): {\displaystyle \left<\cos(r_{jk}q \cdot \cos(\theta))\right> = \dfrac{1}{4\pi}\int_0^{2\pi} \int_0^\pi \cos(r_{jk}q \cdot \cos(\theta)) \sin \theta d\theta d\phi = \dfrac{\sin(q r_{jk})}{q r_{jk}}}
por lo que el factor de forma será finalmente
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:factor_forma} P(q) = \dfrac{1}{n^2} \sum_{j=1}^n \sum_{k=1}^n \dfrac{\sin(q r_{jk})}{q r_{jk}}}
En la figura [fig:tablapq] se presentan valores típicos del factor de forma.
Ahora es posible escribir
y vemos que si lo que implica que el ángulo de esparcimiento es muy pequeño entonces y entonces se recupera la expresión [eq:rayleigh_q]. Además es posible definir un peso molecular aparente
que en el caso en el que entonces se tendrá el peso molecular real.
Aproximación de Guinier
Observando la ecuación del factor de forma [eq:factor_forma] vemos que cuando el argumento de la función seno es pequeño podemos aproximar utulizando su serie de Taylor, esto es
con el desarrollo anterior podemos simplificar de manera aproximada el factor de forma
de donde se toma el término final en paréntesis y se define
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \label{eq:radio_giro} R_g^2 \equiv \dfrac{1}{2n^2} \sum_{j=1}^n \sum_{k=1}^n r_{jk}^2}
El radio de giro sirve como una medida de la longitud de la cadena de partículas que se estudia. Puede verse como la distancia que hay entre el eje de giro y una masa puntual.
Con estos resultados podemos escribir la llamada aproximación de Debye que es
Error al representar (función desconocida «\label»): {\displaystyle \label{eq:debye} P(q) \approx - \dfrac{1}{3}q^2 R_g^2}
Referencias
Óptica, Tercera Edición; Eugene Hecht.
720pp, Addison-Wesley Iberoamericana, Madrid, España, 2000.
Light Scattering Demystified: Theory and Practice; Lars Øgendal.
125pp. Internet Publication, University of Copenhagen, Denmark, 2017.
An Atmospheric Radiative Transfer Primer; R. G. Grainer.
Internet Publication Draft, Oxford University, 2013.
Handbook of Polymer Synthesis, Characterization, and Processing; Editors: Enrique Saldívar‐Guerra & Eduardo Vivaldo‐Lima.
Chapter 18: Light Scattering and its Applications in Polymer Characterization; Roberto Alexander-Katz.
pp 367-389. John Wiley & Sons Inc. USA. 2013.
Physical Chemistry of Macromolecules; Charles Tanford.
724 pp. John Wiley & Sons Inc, New York, USA, 1961.
Ivan de Jesús Pompa García (discusión) 15:53 27 nov 2018 (CST)
Metodo de matrices para optica geometrica
Introducción'
Cuando el sistema óptico consta de varios elementos, por ejemplo, las cuatro o cinco lentes que constituyen una lente fotográfica, necesitamos un enfoque sistemático que facilite el análisis. Si bien limitamos nuestro análisis a los rayos paraxiales, este método sistemático se maneja bien con el método de matrices. Ahora presentamos un tratamiento de imágenes que emplea matrices para describir cambios en la altura y el ángulo de un rayo a medida que progresa a través de reflexiones y refracciones sucesivas a través de un sistema óptico. Mostramos que, en el enfoque paraxial, los cambios en altura y dirección de un rayo se pueden expresar mediante ecuaciones lineales que hacen posible este enfoque de matriz. Al combinar matrices que representan refracciones individuales, reflexiones y traslaciones, un sistema óptico dado puede representarse por una matriz única, a partir de la cual se pueden deducir las propiedades esenciales del sistema óptico compuesto. El método se presta a técnicas informáticas para rastrear un rayo a través de un sistema óptico de complejidad arbitraria. La figura 4 muestra el progreso de un solo rayo a través de un sistema óptico arbitrario. El rayo se describe a una distancia de la primera superficie refractiva en términos de su altura y el ángulo de pendiente con respecto al eje óptico. Los cambios de ángulo se producen en cada refracción, como en los puntos 1 a 5, y en cada reflexión, como en el punto 6. La altura del rayo cambia durante las traslaciones entre estos puntos. Estamos buscando un procedimiento que nos permita calcular la altura y el ángulo de inclinación del rayo en cualquier punto del sistema óptico, por ejemplo, en el punto , a una distancia del espejo. En otras palabras, dados los datos de entrada en el punto , deseamos predecir valores de en el punto como datos de salida.
La traslación de matriz
Considere una traslación simple del rayo en un medio homogéneo, como en la Figura 5. Deje que el progreso axial del rayo sea , como se muestra, de modo que en el punto 1, la elevación y la dirección del rayo estén dadas por "coordenadas" entrada y , respectivamente.
y
Estas ecuaciones se pueden poner en una forma ordenada
Donde la aproximación paraxial ha sido usada. En notación matricial, se escriben las dos ecuaciones entonces:
La matriz 2 X 2 de traslación de rayo representa el efecto de la tralacion en un rayo. Los datos de entrada son modificados por la matriz de transferencia de rayos para producir datos de salida correctos
La matriz de refracción
Consideramos a continuación la refracción de un rayo en una interfaz esférica que separa los medios de los índices de refracción y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): n´ , como se muestra en la Figura 6. Necesitamos relacionar las coordenadas del rayo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): ({y´},{\alpha´ }) después de la refracción con las anteriores a la refracción, Dado que la refracción se produce en un punto, no hay cambios en la elevación, Error al representar (error de sintaxis): y=y´
El ángulo Error al representar (error de sintaxis): {\alpha´ } , por otro lado, es, mediante el uso de las aproximaciones de un angulo pequeño y observando la figura tomaron los valores siguientes:
Error al representar (error de sintaxis): { \alpha }´ =\theta´-\phi =\theta´-\frac { y }{ R }
Incorporando la forma paraxial de la ley de Snell tenemos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): n\theta =n´\theta´
Entonces tenemos:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \alpha´=\left( \frac { n }{ n´ } \right) \theta -\frac { y }{ R } =\left( \frac { n }{ n´ } \right) \left( \alpha +\frac { y }{ R } \right) -\frac { y }{ R }
Simplificando tenemos :
Error al representar (error de sintaxis): \alpha ´=\left( \frac { \\ 1 }{ R } \right) \left( \frac { n }{ n´ } -1 \right) y+\left( \frac { n }{ n´ } \right) \alpha
Las ecuaciones lineales apropiadas son:
Error al representar (error de sintaxis): y´=(1)y+(0)\alpha
Error al representar (error de sintaxis): \alpha ´=\left\lfloor \left( \frac { 1 }{ R } \right) \left( \frac { n }{ n´ } -1 \right) \right\rfloor y+\left( \frac { n }{ n´ } \right) \alpha
O, en forma de matriz:
Error al representar (error de sintaxis): \ \begin {bmatrix} y´ \\ \alpha ´ \end {bmatrix}=\ \begin {bmatrix} 1 & 0 \\ \left( \frac { 1 }{ R } \right) \left( \frac { n }{ n´ } -1 \right) & \frac { n }{ n´ } \end {bmatrix}\ \begin {bmatrix} y \\ \alpha \end {bmatrix}
Aquí, usamos una convención de signos para R, si la superficie es cóncava, es negativa y si R es positivo tendremos una superficie convexa. Además, al permitir , se obtiene la matriz de refracción adecuada para una interfaz plana (superficie plana).
La matriz de reflexión.
Finalmente, consideramos la reflexión en una superficie esférica, ilustrada en la Figura 7. En este caso consideraremos, un espejo cóncavo, R, por la explicación anterior vemos entonces que R debe tomar valores negativos. Necesitamos agregar una convención de signos para los ángulos que describen las direcciones de los rayos. Los ángulos se consideran positivos para todos los rayos que apuntan hacia arriba, ya sea antes o después de una interacción en este caso será una reflexión; Los ángulos para los rayos que apuntan hacia abajo se consideran negativos. La convención de signos se resume en el recuadro de la misma Figura. De la geometría de la figura 7, ambos Error al representar (error de sintaxis): \alpha´ y son positivos
y Error al representar (error de sintaxis): \alpha ´=\theta ´-\phi =\theta ´-\frac { y }{ -R }
Donde hemos realizado las aproximaciones de ángulos pequeños que hemos tomado anteriormente. Usando estas relaciones junto con la ley de reflexión, Error al representar (error de sintaxis): \theta =\theta ´
,
Error al representar (error de sintaxis): \alpha ´=\theta ´+\frac { y }{ -R } =\theta +\frac { y }{ R } =\alpha +\frac { 2y }{ R }
Y así, las dos ecuaciones lineales deseadas son:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): y´=\left( 1 \right) y+(0)\alpha
Error al representar (error de sintaxis): \alpha ´=\left( \frac { 2 }{ R } \right) y+(1)\alpha
En su forma de matriz es:
Error al representar (error de sintaxis): \ \begin {bmatrix} y´ \\ \alpha´ \end {bmatrix}=\ \begin {bmatrix} 1 & 0 \\ \frac { 2 }{ R } & 1 \end {bmatrix}\ \begin {bmatrix} y \\ \alpha \end {bmatrix}
Matrices de lente grueso y lente delgado.
Construimos ahora una matriz que representa la acción de una lente gruesa sobre un rayo de luz. En general, asumimos diferentes medios en lados opuestos de la lente, con índices de refracción y Error al representar (error de sintaxis): n´ , como se muestra en la Figura 8. Al atravesar la lente, el rayo sufre dos refracciones y una traslación, pasos para los cuales ya hemos derivado matrices. . Refiriéndonos a la Figura 8, donde hemos elegido por simplicidad una lente con un radio de curvatura positivo, podemos escribir, simbólicamente,
(para la primera refracción)
(para la traslación)
(para la segunda refracción)
Juntando los resultados anteriores tenemos:
Evidentemente, toda la lente gruesa se puede representar por una matriz . Recordando que la multiplicación de matrices es asociativa pero no conmutativa, se debe mantener el orden descendente. Las matrices individuales operan en el rayo de luz en el mismo orden en que las acciones ópticas correspondientes influyen en el rayo de luz cuando atraviesa el sistema. Generalizando, la ecuación matricial que representa cualquier número N de traslaciones, reflexiones y refracciones están dada por:
....................(1)
La matriz de la transferencia de rayos que representa todo el sistema óptico es:
........................(2)
Primero aplicamos este resultado a la lente gruesa de la Figura 8, cuyo índice es y cuyo grosor para los rayos paraxiales es. La aproximación correcta para una lente delgada se realiza al tener. Permitiendo que represente una matriz de refracción y represente una matriz de traslación, la matriz para la lente gruesa es, por la Ec. (2), la matriz compuesta por:
Sustituyendo tenemos:
Error al representar (error de sintaxis): M =\ \begin {bmatrix} 1 & 0 \\ \frac { { n }_{ L }-n´ }{ n´{ R }_{ 2 } } & \frac { { n }_{ L } }{ n´ } \end {bmatrix}\ \begin {bmatrix} 1 & t \\ 0 & 1 \end {bmatrix}\ \begin {bmatrix} 1 & 0 \\ \frac { { n-n }_{ L } }{ { n }_{ L }R_{ 1 } } & \frac { n }{ { n }_{ L } } \end {bmatrix}
.......................(3)
Para los casos en donde t es despreciable (t=0) y donde los lentes están rodeados por el mismo medio en cualquier lado (n=n´):
..........................(4)
Simplificando la ecuación anterior tenemos:
El elemento de matriz en la primera columna, segunda fila, puede expresarse en términos de la longitud focal de la lente, mediante las características que rigen el lente
Para que la matriz de transferencia de rayos del lente delgado sea simplemente:
se toma como positivo para una lente convexa y negativo para una lente cóncava.
A continuación, se muestra una tabla resumiendo los resultados anteriores (matrices de transferencia de rayos simples)
Sistema de matriz de rayos de transferencia
Al combinar matrices individuales apropiadas en el orden apropiado, de acuerdo con la ec. (2), es posible expresar cualquier sistema óptico mediante una sola matriz 2 x 2, que llamamos matriz del sistema.
Ejemplo:
Encuentre la matriz del sistema para la lente gruesa de la Figura 8, cuya matriz antes de la multiplicación se expresa mediante la ecuación. (3), y especifique la lente gruesa exactamente eligiendo ,, , y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): n=n´=1
Solución:
Simplificando tenemos:
Los elementos de esta matriz de rayos de transferencia compuesto, usualmente se refieren a la forma simbolica:
Describe las propiedades relevantes del sistema óptico. Teniendo en cuenta que los valores particulares de los elementos de la matriz de un sistema dependen de la ubicación del rayo en la entrada y la salida. En el caso de la lente gruesa que se acaba de calcular, el plano de entrada se eligió en la superficie izquierda de la lente y el plano de salida se eligió en la superficie derecha. Si cada uno de estos planos se mueve a cierta distancia de la lente, la matriz del sistema también incluirá una matriz de traslación inicial y una final que incorpore estas distancias. Los elementos de la matriz cambian y la matriz del sistema ahora representa este "sistema" ampliado. En cualquier caso, el determinante de la matriz del sistema tiene una propiedad muy útil:
.....................(5)
donde , y son los índices de refracción de los medios iniciales y finales del sistema óptico. La prueba de esta afirmación sigue al notar primero que el determinante de todas las matrices de transferencia de rayos individuales en la Tabla 1 tienen valores de Error al representar (error de sintaxis): n/n´
o unidad y utilizando el teorema de que el determinante de un producto de matrices es igual al producto de los determinantes. Esto quiere decir, si , entonces:
Al formar este producto, usando determinantes de matrices de transferencia de rayos, todos los índices de refracción intermedios se cancelan, y nos queda la relación , como se indica en la ecuación (5) La mayoría de las veces, como en el caso del ejemplo de lente gruesa, y se refieren al aire, y es la unidad. La condición expresada por la ec. (5) es útil para verificar la exactitud de los cálculos que producen una matriz del sistema.
Importancia de los elementos de la matriz del sistema
Examinamos ahora las implicaciones que siguen cuando cada uno de los elementos de la matriz a su vez es cero. En forma simbólica, tenemos, desde la ec. (1),
Lo que equivale a las relaciones algebraicas
1.D = 0. En este caso, , independientemente de . Como es fijo, esto significa que todos los rayos estarán en el punto en el plano de entrada y tendrán el mismo ángulo en el plano de salida, independientemente de sus ángulos en la entrada. Como se muestra en la Figura 9a, el plano de entrada coincide así con el primer plano focal del sistema óptico.
2.A = 0.Este caso es muy parecido al anterior. Aquí implica que es independiente de , de modo que todos los rayos que salen del plano de entrada en el mismo ángulo, independientemente de la altitud, llegan a la misma altitud y al plano de salida. Como se muestra en la Figura 9b, el plano de salida funciona así como el segundo plano focal.
3.B = 0. Entonces , independientemente de . Por lo tanto, todos los rayos desde un punto en altura en el plano de entrada llegan al mismo punto de altura en el plano de salida. Los puntos se relacionan con el objeto y los puntos de imagen, como se muestra en la Figura 9c, y los planes de entrada y salida correspondientes a los planos conjugados para el sistema óptico. También, como ,el elemento matriz A representa la extensión lineal.
4.C = 0. Ahora , independientemente de . Este caso es análogo al caso 3, con direcciones que reemplazan las alturas de los rayos. Los rayos entrantes, todos desde una dirección, ahora producen rayos de salida paralelos en alguna otra dirección. Además, es el aumento angular. Un sistema para el cual C=0 a veces se llama "sistema telescópico", porque un telescopio admite rayos paralelos en su objetivo y emite rayos paralelos para verlos

A continuación, mostraremos un ejemplo sencillo para esclarecer la construcción de matrices para un arreglo óptico.
Ejemplo:
Colocamos un objeto pequeño en el eje a una distancia de 16 cm del extremo izquierdo de una varilla larga de plástico con un extremo esférico pulido de radio de 4 cm, como se indica en la Figura 10, el índice de refracción del plástico es de 1,50 y el objeto está en el aire. Deje que la imagen desconocida se forme en el plano de referencia de salida, a una distancia x de la tapa esférica. Queremos determinar la distancia de la imagen x y la ampliación lateral m. La matriz del sistema que conecta el objeto y los planos de imagen consiste en el producto de tres matrices, (1) que corresponden a una traslación en el aire del objeto a la varilla, (2) una refracción en la superficie esférica, y (3 ) una traslación en plástico a la imagen.
Solución:
Recuerde tomar las matrices en orden inverso y trabajar en cm y así tenemos
Sustituyendo tenemos:
con la cantidad desconocida x incorporada en los elementos de la matriz. De acuerdo con esta discusión, cuando B = 0, el plano de salida es el plano de la imagen, de modo que la distancia de la imagen x se determina configurando
ó
Además, el aumento lineal viene expresado por el valor del elemento A:
Concluimos que la imagen ocurre 24 cm dentro de la varilla, está invertida y tiene el mismo tamaño lateral que el objeto. Esto ilustra cómo se puede usar la matriz del sistema para encontrar ubicaciones y tamaños de imágenes, aunque esto generalmente se puede hacer más rápidamente utilizando las fórmulas de imágenes gaussianas derivadas anteriormente.
Cálculo de un sistema óptico complejo
Se construirá un sistema óptico que esta conformado por tres lentes cóncavos-convexos,se encuentran a una cierta distancia uno del otro y el medio de propagación es el aire , en la siguiente tabla se muestra el arreglo del sistema óptico que queremos estudiar:
Como se explico anteriormente en el desarrollo del método de matrices, debemos de construir inicialmente una matriz total la cual representara las interacciones ópticas para una sola lente la cual es:
donde:
la matriz toda del lente
la matriz referente a la primera interacción óptica la cual es una refracción
la matriz referente a la segunda interacción óptica la cual es una traslación
la matriz referente a la tercera interacción óptica la cual es una refracción
Posteriormente, ya que se construyo una matriz que represente las interacciones ópticas de un lente podemos construir la matriz total final la cual asume todas las interacciones del sistema; tenemos entonces:
donde:
la matriz total del sistema óptico
la matriz toda del lente 3
la matriz de traslación debido al recorrido del rayo del lente 3 al 2
la matriz toda del lente 2
la matriz de traslación debido al recorrido del rayo del lente 2 al 1
la matriz toda del lente 1
Calculando la matriz total del sistema óptico tenemos:
podemos notar que el termino negativo es el inverso negativo de la distancia focal dando así una longitud focal de d=93.23 mm
Como podemos ver con ayuda de mathematicas podemos realizar el calculo de la matriz total con mucha facilidad por lo que estudiaremos la dependencia de la distancia focal para dos casos.
Primer caso:
Se dejara la distancia del lente 3 fija y se ira alejo la segunda lente de la primera. El incremento de la distancia entre las lentes se ira aumentando en 0.01mm y para cada incremento se calculara la matriz total del sistema para obtener una distancia focal.
Dando así como resultado la disminución de la distancia focal al aumentar la separación entre los lentes ,como puede comprobarse en la Fig. 1, donde se gráfica la dependencia de la distancia focal en función de la variación de la distancia entre las lentes el cual nos dice que a mayor distancia entre los lentes menor sera la distancia focal del sistema total.
Segundo caso:
En este caso disminuiremos el radio de las lentes pero solo en los planos de entrada, donde el decremento de los radios se ira disminuyendo en 0.01mm y para cada decremento se calculara la matriz total del sistema para obtener una distancia focal.
El caso de disminución de los radios de curvatura se presenta en la Fig. 2, donde se grafica la dependencia de la distancia focal de las variaciones de los radios de curvatura de las lentes. En el mismo es posible comprobar que el aumento de los radios aumenta la distancia focal.
Referencias
Óptica, Tercera Edición; Eugene Hecht.
720pp, Addison-Wesley Iberoamericana, Madrid, España, 2000.
"Introduction to Modern Optics;Grant R. Fowles,Dover Publications,1989"
"Physical optics;S. A. Akhmanov, S. Yu. Nikitin,Clarendon Press; Oxford University Press,1997"
"Principles of applied optics [1 ed.];Partha P. Banerjee, Ting-Chung PoonAksen Associates; Irwin,1991"
"Principles of optics;Max Born, Emil Wolf,Cambridge University Press,1999" Ruben Espinosa Guzman
Fenómeno de Gibbs
Fenomeno de Gibbs para funciones con saltos
Función Signo
Consideremos la función f(x)=sgn(x) para .
Que su serie de Fourier es
... (1)
Usando el siguiente teorema
Teorema 1. Sea f una función integrable en que tiene derivadas laterales en un punto en el sentido mencionado. Entonces, la serie de Fourier de f converge en a .
Que asegura que la serie de Fourier converge a la función en (definiendo el signo de 0 como 0). La convergencia no puede ser uniforme porque el limite no es una función continua, aunque si es uniforme en para cualquier .
Y que a su vez lo anterior es asegurado por el siguiente teorema
Teorema 2. Sea f continua, con derivada continua a trozos y acotada en un intervalo . Entonces la serie de Fourier de f converge a f uniformemente en para .
Por lo tanto, si tomamos , existe de modo que las sumas parciales de la serie de Fourier satisfacen , para todo y .
Por otra parte, esta claro que en las sumas parciales tienen que formar valores entre 0 y 1.
La figura 1 muestra la gráfica de la suma parcial de la serie de Fourier. Solo en la zona central de cada intervalo esta relativamente cerca de los valores de f. Con mas sumas la aproximación sera mejor
En la gráfica de (figura 2) vemos que la aproximación mejora en la zona central pero no se rebaja el ”pico” que por encima de 1 aparece para los valores de la variable cercanos a 0 (y sus correspondientes simétricos).
Aumentando el numero de sumandos de la suma parcial, la situación no cambia: la figura 3 muestra una amplificación de la gráfica para y, sin embargo, el pico se mantiene. Este hecho, que puede resultar sorprendente, no se remedia añadiendo términos a la suma parcial (en la figura 4 se muestra ). En efecto, el valor máximo de la suma parcial en no tiende a 1 cuando N tiende a infinito, sino al valor
...(2)
corresponde a tomar la suma hasta k=N-1 en la ec. (1). Los máximos de se encuentran en puntos que anulen a su derivada, que es
...(3)
(La ultima igualdad se obtiene a partir de la formula , del mismo modo que en el calculo del núcleo de Dirichlet.) Esta revidad se anula en en los ceros de que son . La segunda derivada tiene en sus puntos el signo de de modo que corresponde alternativamente a máximos y mínimos locales, comenzando en un máximo.
Como , de la expresión (3) para la derivada de la suma parcial también se deduce
Utilizando esta expresión se pueden comprobar las sumas parciales en máximos sucesivos y se comprueba que el primer máximo, que se obtiene para , es precisamente el máximo absoluto. Ahí es donde vamos a evaluar la suma parcial y calcular el limite, de modo que buscamos
...(4)
Consideramos la partición del intervalo en N intervalos iguales determinada por los puntos . Si escribimos ahora la suma de Riemann para la función asociada a esta partición, con la función evaluada en el punto medio de cada uno de los intervalos, obtenemos precisamente el valor multiplicado por . Como la función es continua, el limite de sus sumas de Riemann cuando N tiende a infinito es su integral en . Entonces el limite de vendrá dado por el expresión (2).
Un importante ejemplo: la “función” delta de Dirac
En 1926, el físico ingles P.A.M Dirac, introdujo la “función” delta de dirac, en conexión con sus estudios sobre mecánica cuántica. Realmente no se trata de una función en el sentido ordinario del temrino, sino de una distribución.
La delta de Dirac viene caracterizada por las siguientes propiedades
1.
2. no esta definida.
3. , siempre que el recinto de integración incluya x=0
4. ) es una función continua en , entonces .
En la figura 6 representamos la delta de Dirac en un sentido figurado: la delta de Dirac puede interpretarse como una función que se anula en todos los puntos salvo en x=0, donde toma el valor infinito.
Para , la función , seria la misma función o distribución pero trasladada a x=a.
El concepto de la función delta de Dirac, también llamada función impulso unitario, resulta un modelo útil en situaciones en las que, por ejemplo, tenemos un sistema mecanico sobre el cual actua una fuerza externa de gran magnitud durante un breve instante de tiempo. En el caso extremos en el que esta fuerza estuviese concentrada en un punto, vendría representada por al delta de Dirac.
La delta de dirac puede efectivamente entenderse como el limite de una sucesión de funciones que, con masa unidad, se concentran infinitamente en torno a un punto. En efecto, sea una función regular tal que
Consideremos ahora la sucesión de funciones:
Este cambio de escala no altera la masa total de la función, puesto que:
Sin embargo, a medida que tiende a 0, el soporte de la función se contrae puesto que
En el limite, cuando , las funciones , cada vez mas concentradas, convergen a la delta de Dirac, puesto que
Cuando , para toda la función continua y acotada.
Vamos a calcular las sumas parciales de Fourier para la delta de Dirac. Pero, ¿cómo puede expresarse con una serie trigonométrica una “función” tan singular como la delta de Dirac?.
En realidad, lo que se hara es calcular las sumas parciales de Fourier correspondientes a una determinada combinación lineal de deltas de Dirac.
Que se obtiene al extender de manera periódica con periodo la “función” que coincide con la delta de Dirac en y con en el punto , es decir, que la trasladada y cambiada de signo, la reflejada impar de la . Dicho de otra forma, la función que hemos llamado , esta compuesta por: impulsos unitarios positivos en los múltiplos pares de , es decir, puntos de la forma …, Error al representar (error de sintaxis): 2\pi ,\quad 0,\quad 2\pi ,\quad 4\pi… ; e impulsos unitarios negativos en los múltiplos impares de , es decir, puntos de la forma, …, Error al representar (error de sintaxis): -3\pi ,\quad -\pi ,\quad \pi ,\quad 3\pi, … ; La grafica de esta función se podria representar en la figura 7.
Aplicando las formulas para calcular los coeficientes de Fourier y teniendo en cuenta que , es una función par
Por tanto, la suma parcial de Fourier para la función queda
Que se puede expresar de la siguiente forma, dado que para los valores pares de los sumandos se anulan:
Los cálculos y graficas obtenidas requieren algunas observaciones:
En primer lugar, con toda seguridad podemos afirmar lo siguiente
Lo cual nos hace pensar que, en cierto sentido, la derivada de la función salto, debe ser la “función” .
A partir de la observación anterior; si la derivada de las sumas parciales de la función salto son las sumas parciales de la delta de Dirac, entonces la integral de las sumas parciales de la delta serán las de la función salto, es decir
Por otra parte, admite una expresión mas comoda:
Este hecho, nos proporciona la siguiente expresión para las sumas parciales de Fourier de la función salto
Mientras que
Se puede comprobar de esta forma, que los puntos críticos de las sumas parciales de la función salto son los ceros de las sumas parciales de la delta de Dirac. Es decir, que la altura que se alcanza en el primer máximo de la suma parcial de Fourier de la función salto, a la derecha de , es la mitad del área por debajo del arco central de la grafica x. Es decir
. Pasando al limite cuando , necesariamente habremos de obtener el mismo valor
En las graficas de las figuras x y Y parece observarse también algo parecido al fenómeno de Gibbs. Pero ahora es algo disinto a lo que ocurria con la función salto. En la función salto veíamos que las graficas de las sumas parciales excedían, o quedaban por debajo de la función de los alrededores de los puntos de discontinuidad. Aquí la situación es peor, porque esto ocurre no solo en las cercanías de sino a lo largo de los puntos de continuidad de la función original, por ejemplo en los puntos de intervalo . Ademas esta situación no cambian aunque aumentos la cantidad de sumandos. ¿Cuál es la razón de este comportamiento tan anómalo? Simplemente, ahora ni siquiera tenemos convergencia puntual. En efecto, si tomamos por ejemplo, un punto la función original valdrá . Sin embargo, la sucesión
No converge cuando . De hecho, lo que courre es que la grafica de oscila entre las graficas de las dos funciones , que acota superior e inferiormente a , es decir
En la figura X hemos dibujado la grafica de la suma parcial de la delta de Dirac hasta el sumando N=50, en el intervalo junto con las graficas de las funciones .
Entonces, ¿Qué tipo de representación es la que producen las sumas parciales de Fourier para la delta de Dirac en la que ni siquiera hay convergencia puntual para los puntos de la continuidad? La respuesta es que si hay convergencia, pero es una convergencia especial, una convergencia “débil”: como hemos podido ver mas arriba, en la definición de la delta de Dirac, esta función no se define de una manera clásica, dando sus valores, sino mas bien a través de sus efectos sobre otras funciones en el sentido de las distribuciones. Y en este sentido, las sumas parciales de Fourier de la delta producen sobre otras funciones los mismos efectos, puesto que las oscilaciones se cancelan a través de la integración.
Método de sumacion de Fejér.
En 1903, el matemático húngaro L. Fejér. Propuso una nueva forma de sumas los términos de la serie de Fourier. Se trata de sumar los promedios de las sumas parciales y pasar al limite. Se obtiene asi una nueva sucesión de funciones que producen convergencia incluso en algunos casos en los que la serie original no la tiene.
Veamos como se construye la suma fe Fejér a partir de las sumas parciales de Fourier se construirá una nueva sucesión con el promedio de las sumas parciales
La suma de Fejér es entonces
En cuanto a la convergencia de la sima de Fejér se tiene el siguiente teorema
Teorema de Fejér Sea definida en el intervalo . Si es acotada, supones que es integrable; si no es acotada, suponemos que la integral es absolutamente convergente. Entonces para cualquier punto del intervalo las sumas parciales de Fejér converge a .
Y como una consecuencia del Teorema de Fejér tenemos que, si es continua en , entonces la sucesión de las medias aritméticas converge uniformemente a en el interior del intervalo .
Obviamente, cuando es continua en , y por tanto, converge a .
Esta es la versión mas clásica del teorema, utilizando la integral de Riemann.
Lo primero que se observa en la nueva grafica es que ahora tenemos un tipo de convergencia distinta, de hecho ahora tenemos convergencia uniforme (según el teorema anterior) en el interior del intervalo ( y, por simetría, en ). Por otra parte se puede observar que la grafica de la suma de Fejér cae por debajo (en el , y por encima de ) de la grafica de . De hecho puede probarse que todas las sumas parciales de Fejér verifican , es decir ahora no se produce el fenómeno de Gibbs y aunque la grafica sigue teniendo las mismas oscilaciones, ahora son mucho menores.
Fourier versus Fejér
Dibujando ahora las graficas de las sumas de Fourier y las de Fejér juntas. En la figura X, se han dibujado superpuestas, las graficas de las sumas parciales de Fourier y de Fejér hasta el sumando , en el intervalo . En la figura X, se ha representado lo mismo, pero ahora en el intervalo . En ambas figuras se pueden observar como las sumas parciales de Fourier y las de Fejér parecen coincidir en algunos puntos críticos de las sumas de Fourier. En concreto en el intervalo , esto ocurre en los minimos y, debido a la simetría impar, en el intervalo , ocurre en los máximos.
Viendo que este curioso fenómeno no es solo aparente, ni debido a los errores de redondeo, sino que courre de hecho:
En primer lugar, si la N-ésima suma parcial de Fourier es
Entonces la N-ésima suma parcial de Fejér es, a partir de su expresión antes dada, se puede escribir de la forma alternativa
Donde
Para el caso particular de la función salto, estas expresiones se convierten en
Y
Los puntos en que se cortan, han de ser soluciones de la ecuación
Por otra parte, si estos puntos son máximos o minimos, es decir, puntos críticos, entonces también deben de satisfacer la ecuacion
Reescribiendo la ecuación para la suma parcial de Fourier como
Por tanto
Que se puede transformar de la siguiente manera
Ahora bien la solución de la ecuación
En el intervalo son los puntos de la forma
Y es sencillo comprobar que estos puntos son precisamente los minimos de la función , ya que sabemos que
Luego, efectivamente las graficas de las sumas parciales de Fourier y las de Fejér se cortan en los minimos de las primeras, en el intervalo y, por la simetría, en los máximos del intervalo ( (excepto en el caso , en el que no hay ningún minimo en ).
Otras funciones con saltos.
La propiedad que se ha probado para la función en , ocurre para cualquier función que tenga un salto, en el entorno de esta. Sea g una función discontinua en un punto , en el que tiene un salto . La función es continua en y, por lo tanto, el comportamiento de la serie de Fourier de g </math> en un entorno de es el mismo que el de . Es decir, la diferencia entre el limite cuando N tiende a infinito del máximo de en un entorno de y el mayor de los valores y es y lo mismo ocurre por debajo. Esta propiedad se llama fenómeno de Gibbs.
En 1898 Michelson y Stratton diseñaron un analizador armónico que permitía hacer gráficas de las sumas parciales series de Fourier. Observaron que en esas gráficas aparecía un exceso sobre el valor máximo de la función cuando estaba cerca del salto y Michelson envió una carta a la revista Nature pidiendo una explicación para el fenómeno. Durante los años 1898 y 1899 hubo varios artículos sobre el tema en la revista y finalmente fue Gibbs quien en 1899 aclaro la situación. El nombre de fenómeno de Gibbs es debido a bôcher.
Posteriormente se descubrió que ya en 1848 Wilbraham había publicado un articulo titulado On a certain periodic (Cambridge Dublin Math. J. 3, 1848) en el que había descubierto el fenómeno. Wilbraham estudiaba la serie
Que corresponde a un función que vale entre y y - en el resto del periodo y que aparece en el libro de Fourier; indica que erróneamente algunos autores dicen que las sumas parciales están comprendidas entre y , demuestra que no es así y obtiene el valor exacto del exceso.
Referencias
A source Book in Classical Analysis, Editado por G. Birkhoff (Harvard University Press, 1973).
G. Bachmann, L. Narici y E. Beckenstein, Function Fourier and wavelet analysis, Springer-Verlag, New York, 2002.
Gerald B. Folland, Fourier analysis and it's applications, Wadsworth & Brooks, California, 1992.
aproximación de ondas esféricas a planas.
Introducción.
de todas las ondas tridimencionales la onda plana es la única que puede moverse a lo largo de su dirección sin cambiar su perfil (armónica o no),aunque se ve claro que esta idea es incompleta. De la misma forma se puede definir una onda como una solucion cualquiera de la ecuación diferencial de onda. Necesitaremos una ecuación tridimensional lo cual no sera difícil de conseguir.
Onda plana.
Entraremos en la definición de onda plana. En la física de propagación de ondas (especialmente en campos y ondas electromagnéticas), una onda plana o también llamada onda monodimensional, es una onda de frecuencia constante cuyos frentes de onda (superficies con fase constante) son planos paralelos de amplitud constante normales al vector velocidad de fase. Es decir, son aquellas ondas que se propagan en una sola dirección a lo largo del espacio.
Este es el ejemplo más sencillo de onda tridimensional. Existe en un instante dado cuando todas las superficies sobre las cuales una perturbación tiene fase constante, forman un conjunto de planos, cada uno generalmente perpendicular a la dirección de propagación.
Para deducir la expresión matemática de un plano perpendicular a un vector dado k y que pasa a través de algún punto , primero se escribe el vector de posición en coordenadas cartesianas, en términos de los vectores unitarios de la base.
Comienza en algún origen arbitrario O y termina en el punto que, por el momento debe ser cualquier lugar en el espacio.
sabemos por la ecuación del plano que un vector único paralelo a un plano no basta para definir la dirección del plano, pero un vector perpendicular al plano sí la especifica. Así un plano en el espacio esta determinado por un punto en el plano y un vector kque es ortogonal al plano. Este vector ortogonal k se llama vector normal. Sea un punto arbitrario en el plano, y sean y los vectores de posición . Entonces, el vector esta representado por . El vector normal es ortogonal a cada vector en un plano determinado. En particular, es ortogonal a ver (fig 1) por lo que tenemos
Estableciendo
(1)
obligando al vector a barrer un plano perpendicular a k, al ir adquiriendo su punto extremo todos los valores permitidos.
Con
(2)
la ecuación (1) puede expresarse como
(3)
o como
(4)
donde
(5)
La forma más concisa de la ecuación de un plano perpendicular a k es entonces
El plano es el lugar de todos los puntos cuyos vectores de posición tienen cada uno la misma proyección en la dirección de .
Ahora podemos construir un conjunto de planos sobre los cuales varía de manera sinusoidal en el espacio, es decir
consideremos:
ec(6)
Por todas estas expresiones se mantiene constante sobre cada plano definido por . Como estamos analizando las funciones armónicas, deberían repetirse en el espacio después de un desplazamiento de en la dirección de k. En la figura se representa esta clase de expresión. Del infinito número de planos se han dibujado sólo unos pocos, cada uno con una diferente. Los planos deberían también haberse dibujado con una extensión espacial infinita, ya que no se han puesto límites a . La perturbación ocupa claramente todo el espacio.
La naturaleza repetitiva espacial de estas funciones armónicas se puede expresar por
(7)
Donde es la magnitud de y es un vector unitario paralelo a él.
En la forma exponencial, esto equivale a
Para que sea cierto, debemos tener
Por consiguiente
y
El vector k, cuya magnitud es el número de propagación , se llama vector de onda o de propagación. Ver ondas: vector de onda
En cualquier punto fijo del espacio donde r es constante, la fase es constante y también lo es ; en resumen, los planos están inmóviles. Para hacer que se muevan, debe hacerse variar en el tiempo, algo que puede lograrse introduciendo la dependencia del tiempo en una forma análoga a la de una onda unidimensional.
Aquí entonces
ec(8)
sin embargo, hemos examinado las ondas planas poniendo de relieve que son funciones armónicas, no obstante cualquier onda tridimensional puede expresarse como una combinación de ondas planas.
Involucraremos a la ecuación de onda tridimensional que tiene la siguiente forma:
Regresando a la onda plana, esta queda de la siguiente manera:
Son ambas soluciones de onda plana que tendrían la siguiente forma:
Donde las funciones f y g son diferenciables 2 veces son arbitrarias y no necesitan se prescisamente armonicas.
Ondas esfericas.
Hay situaciones físicas en las que podremos sacar mas provecho utilizando otro tipo de coordenadas
Considérese ahora una fuente puntual de luz, la radiación que procede de ella fluye directamente hacia afuera, se dice que es isotropa y que son esferas concentricas los frentes de onda. en términos de coordenadas esféricas polares, el operador laplaciano es:
Ahora las coordenadas(x,y,z) son:
como estamos considerando ondas que son simétricas no dependeran de ángulos solo la parte radial, por tanto: ec(9)
Entonces el laplaciano queda de la siguiente forma: , lo cual es:
También esta ecuación diferencial de onda se puede escribir como:
Al multiplicar ambos lados por r, obtenemos:
Observamos que esta expresión es ahora la ecuación de onda unidimensional, donde la variable espacial es r. la solución seria entonces: ec(10)
Esto representa una onda esférica que progresa radialmente hacia afuera, aunque también la siguiente solución es valida: , que en este caso la onda esta convergiendo hacia el origen.
Un caso especial de la solución general es la suma de las 2 soluciones con sus respectivas constantes es la onda esférica armónica:
ec(11)
Donde la constante A se denomina la intensidad de la fuente. para cualquier valor fijo del tiempo, esto representa una agrupación de esferas concentricas que abarcan todo el espacio. Cada frente de onda o superficie de fase constante esta dado por
.
nos damos cuenta que la amplitud de onda esférica depende explicitamente de r, y este termino con exponente negativo sirve como atenuación. A diferencia de la onda plana que aumenta su amplitud, esta disminuye consecuente en su propagación.
La siguiente figura muestra el siguiente hecho, cuando un frente de onda esférico se propaga hacia afuera, su radio aumenta a una distancia considerable de su fuente, una pequeña área de frente se aproximara a una porción de una onda plana.
nos damos cuenta que la ecuación de la onda plana no tiene un factor de atenuación como la ecuación de onda esférica.
si nosotros consideramos una distancia muy grande de la fuente (r muy grande)
entonces
ec(12)
que es la ecuación de una onda plana, como se había comentado esta es la única onda que no cambia mientras se propaga.
Referencias
A source Book in Classical Analysis, Editado por G. Birkhoff (Harvard University Press, 1973).
Óptica, Tercera Edición; Eugene Hecht.
720pp, Addison-Wesley Iberoamericana, Madrid, España, 2000.
Gerald B. Folland, Fourier analysis and it's applications, Wadsworth & Brooks, California, 1992.
Formulación Covariante de los campos electromagnéticos.
Introducción.
La fórmula fundamental en Mecánica Clásica, , es aproximadamente correcta, pues, no presenta los efectos que se producen al considerar grandes velocidades. Por lo cual, la Mecánica Clásica requiere de una reformulación, actualmente dada por la Teoría de la Relatividad. Con esto uno puede decir que la Mecánica Clásica obedece los principios de la relatividad. Surge la pregunta: ¿La Electrodinámica obedece los principios de la relatividad?. La respuesta es que sí y , de hecho, no requiere de una reformulación como en el caso de la Mecánica Clásica.
En la Mecánica Clásica, los conceptos de espacio y tiempo son completamente separables, esto es porque se toma al tiempo como una cantidad absoluta, independiente del sistema de referencia. Está implícito en Clásica que la "acción a distancia" debido a , ya sea, fuerzas gravitacionales o electromagnéticas, se transmite de manera instantánea. Esto deja invariante a las leyes de la Mecánica Clásica ante transformaciones Galileanas:
I.1
Siendo las variables primadas descritas en un sistema de referencia que se mueve a velocidad respecto a un sistema (comúnmente a estas traslaciones sobre un eje, en este caso el eje x, se les conoce como "boost" en x), ambos sistemas son inerciales.
De I.1, se observa que el elemento de longitud entre puntos son el mismo para ambos sistemas de referencia:
- .....I.2
En el caso de (Plano Euclidiano), la ecuación I.2 se reescribe en forma matricial como:
;
siendo
- .....I.3
la métrica en el plano Euclidiano.
También, se observa que de I.1 que .
Sin embargo, las ecuaciones de Maxwell no son invariantes ante I.1. Para visualizar dicho acervo, consideremos la ecuación de onda para un potencial:
- .....I.4
pero bajo I.1, tenemos que:
- ;
- ;
- ;
- ;
por lo que I.4 transforma como:
- .....I.5
I.5 no describe la propagación de una onda electromagnética en la manera que describe Albert Einstein en sus postulados de la teoría de la relatividad. Entonces, la electrodinámica no es consistente con la invarianza de Galileo. Sin embargo las leyes de Maxwell son invariantes ante transformaciones de Lorentz:
- .....I.6
Dicha transformación (I.6) es una transformación ortogonal en el espacio de Minkowski, con:
- .....I.7 la matriz de transformación de Lorentz y,
& ; c la velocidad de la luz.
Cuando una ecuación que expresa una relación física es transformada de un sistema de referencia a otro bajo I.6, se dice que dicha ecuación es covariante si su forma permanece sin cambio.
De lo anterior, uno puede encontrar las coordenadas espacio-tiempo de un "boost en " de un sistema que se mueve a velocidad respecto de un sistema , introduciendo la coordenada :
I.7
los índices 1,2 y 3 corresponden a las coordenadas x,y y z respectivamente.
Entonces, I.6 muestra la forma en cómo transformar de un sistema en el espacio de Minkowski, en el cual se definen 4-vectores (vectores de 4 entradas):
en otro.
I.7 se obtienen al considerar los efectos que se dan en la teoría de la relatividad especial en las ecuaciones I.1, por ejemplo, a la ecuación debe ser reemplazada por una regla que incorpore los efectos de dilatación del tiempo, la relatividad de la simultaneidad, y la no sincronización de relojes en movimiento relativo. Lo anterior implicará entonces una modificación también a la ecuación
En éste espacio, existe una analogía con el producto punto del espacio euclidiano, la única diferencia radica en que la componente de índice cero aparece un signo menos:
.....I.8
I.8 es el 4-dimensional producto escalar, de hecho, es un invariante (para el "boost en x") bajo transformaciones de Lorentz, como lo es el producto punto en el espacio euclidiano bajo transformaciones de Galileo (I.2).
Es importante aquí introducir la distinción entre un vector covariante () y un vector contravariante (), ya que, difieren sólo en el signo de la componente cero:
formalmente esto es:
- .....I.9
con la métrica de Minkowski que es un análogo a I.3.
Pero ¿qué es este espacio de Minkowski?. Bueno, si uno desea representar el movimiento de una partícula, lo normal es graficar dicho movimiento en un diagrama posición contra tiempo. En dichos diagramas la velocidad se lee como la pendiente de la recta tangente en un punto de la curva. Por esta razón, dicha técnica también se conserva en relatividad, sólo que el eje que representa al tiempo (o mejor dicho ) es el eje vertical. La velocidad será entonces el recíproco de la pendiente de la recta tangente en un punto de la curva. Una partícula en reposo está representada por una línea vertical; un fotón, viajando a la velocidad de la luz es descrito por una línea de 45 grados; y un cohete espacial viajará a una velocidad intermedia siguiendo una linea de pendiente . Llamamos a dichos diagramas diagramas de Minkowski.
Justo aquí entra el gran dilema de Albert Einstein: ¿qué hay que corregir, la Mecánica de Newton o la Electrodinámica de Maxwell?
Preliminares.
1.1 Nota.Los valores de los índices que tomaremos correrán sobre el conjunto
1.2 Acuerdo(Convención de suma). Si un índice está repetido en un término dentro de una expresión matemática, ésto indica que hay una suma sobre todos los valores de dicho índice.
1.3 Definición. Un conjunto de funciones se dice que constituyen las componentes de un campo tensorial de tipo sobre una variedad , si, bajo la transformación de coordenadas:
- ,
estas funciones transforman de acuerdo a la regla:
el rango de dicho tensor es .
En el caso especial de 1.1, tenemos los siguientes tensores:
- , vector contravariante (tensor de tipo (1,0));
- , vector covariante (tensor de tipo (0,1));
- , tensor de tipo (1,1).
De hecho, uno puede probar que la delta de Kronecker es un tensor de tipo (1,1).
Tensores de tipo (0,0) se les denomina escalares o invariantes.
1.4 Definición.Siempre es posible multiplicar tensores de tipo arbitrarios en un punto P sobre componente a componente. Más precisamente, la multiplicación de las componentes de dos tensores de tipo & en P da un tensor de tipo en P.
1.5 Definición. Considérese un tensor de orden , la contracción de dicho tensor se forma tomando la suma sobre un par de índices, uno contravariante y uno covariante. El tensor resultante de la contracción es un tensor de tipo (ordenes menor que el original).
1.6 Definición. Se dice que un tensor es simétrico si al permutar un par de sus superíndices (o un par de sus subíndices) las componentes de dicho tensor permanecen si cambio. Se dice que un tensor es anti-simétrico si al permutar un par de sus superíndices (o un par de sus subíndices) las componentes de dicho tensor se multiplican por -1.
Ecuaciones de Maxwell en forma covariante.
Nota. Las unidades que vamos a utilizar serán las unidades Gaussianas para los campos. Los índices que vamos a utilizar corren sobre siendo 0 correspondiente a la coordenada temporal y las restantes correspondientes a las coordenadas espaciales x,y,z. Buscamos escribir una acción (escalar) para el campo electromagnético covariante, es decir:
- .....3.1
siendo análoga a la lagrangiana en Mecánica Clásica, salvo que se le denomina densidad lagrangiana debido a sus unidades .
Los campos que vamos a utilizar para nuestro propósito son los auxiliares: , que satisfacen las constricciones:
- &
Construyamos el cuadripotencial y a su vez construyamos una matriz:
- ..... 3.2
A 3.2 se le conoce como tensor de intensidad de campo.
De 3.2, observamos que:
A partir de 3.2 podemos definir su dual como:
- .....3.3
Lo que se realiza en 3.3 es que cambia al campo magnético por el campo eléctrico y al campo eléctrico por el campo magnético para
Con 3.2 y 3.3 podemos construir escalares para 3.1, ya que, ésta es un escalar, sin embargo, no todas las opciones que se nos puedan presentar pueden ser utilizadas para nuestro propósito, por ejemplo, entre estas opciones tenemos:
- .....3.4
&
- .....3.5
pero 3.5 es un pseudoescalar. No hay otra opción para 3.1 que utilizar 3.4, ya que funciona perfecto para nuestro propósito( uno puede verificar realizando el producto de matrices y convencerse que 3.4 dará órdenes cuadráticos en los campos, por lo que, al hacer la variación, estos órdenes se reducirán a orden lineal en los campos, como debe ser según las ecuaciones de Maxwell),entonces:
- .....3.6
Para considerar fuentes de campo, acoplamos con un "término de interacción": . Entonces:
- .....3.7
Variando 3.7, arribamos a las ecuaciones de Euler-Lagrange(para no cargar con notación, quitemos por el momento las constantes & )
Calculemos: .Entonces:
- .
Observe que aquí bajamos los índices del tensor , para ello utilizamos la ecuación I.9 y el hecho de que es un tensor de tipo (2,0), por lo que para bajar sus índices recurrimos a la métrica de Minkowski.
Donde:
&
- .
Así:
Ahora, multiplicando por & las ecuaciones anteriores respectivamente obtenemos:
&
De lo anterior: .
Finalmente:
entonces:
- .....3.8
Nota. Retomando las constantes:
- .
con . Sin embargo 3.8 representa la Ley de Gauss & Ley de Ampere-Maxwell. Para determinar las otras leyes, debemos obtener una expresión como 3.8 para el dual de , es decir:
- .....3.9
3.9 representa la inexistencia de monopolos magnéticos & Ley de Faraday.
Las ecuaciones 3.8 & 3.9 no presentan distinción entre derivadas temporales ni espaciales, pero respetan a las variables & con igual importancia. Es por ello que las ecuaciones de Maxwell en esta forma se les conoce como ecuaciones de Maxwell en forma covariante.
Es inmediato de 3.8 que:
- , es decir:
la cual representa la ecuación de continuidad.
Conclusiones.
El campo electromagnético, como cualquier otro campo que describa fenómenos físicos, debe respetar las simetrías y leyes de conservación impuestas por la estructura del espacio y tiempo. Como Einstein y Lorentz vislumbraron, el campo electromagnético respeta las simetrías del espacio-tiempo llamado Minkowski y no el espacio (y tiempo) galileano. Sin embargo, las ecuaciones de Maxwell no están escritas en forma manifiestamente covariante (como se ha mostrado anteriormente). Esto significa que no es muy claro cómo las ecuaciones de Maxwell transforman en diversos sistemas coordenados respetando la igualdad y dominio de las variables y . Se requiere entonces un formalismo matemático para que las ecuaciones del Electromagnetismo sean independientes del sistema coordenado; que transformen bajo Lorentz de manera covariante:
Bajo la regla (donde indica la transpuesta de la matriz de transformación de Lorentz) garantizamos que, como F contiene la información de los campos:
- en un sistema de referencia inercial
&
- en un sistema de referencia inercial que se mueve respecto a S.
Referencias.
Classical Electromagnetic Radiation. Marion, J.B. and Heald, M.A. (Printed in the United States of America).
Introduction to Electrodynamics. Griffiths, D.J. (Published by Pearson Education, Inc. 2013).
Tensors, Differential Forms, and Variational Principles. Lovelock, D. and Rund, H. (Dover Publications, Inc., New York).
Láser de Cristal Líquido
Introducción
Los láseres de cristal líquido son un tema en constante desarrollo dentro de los campos de materia blanda y óptica aplicada.Dichos láseres abarcan una multitud de características extraordinarias, incluida la capacidad de ajuste de frecuencia, gran área de coherencia y, en algunos casos, emisiones multidireccionales, además tienen la capacidad de combinar grandes potencias de salida con dimensiones de cavidad muy pequeñas, dos propiedades que tradicionalmente son incompatibles.
Cristal líquido
El cristal líquido es un tipo de estado de agregación de la materia que presenta propiedades físicas tanto de la fase líquida como de la fase sólida, puesto que las moleculas de un cristal líquido pueden desplazarse unas con respecto a otras con facilidad como ocurre con los líquidos y sin embargo todas las moléculas de su estructura tienden a estar orientadas del mismo modo, como sucede en los sólidos .
Se le atribuye su descubrimiento al biólogo Frederick Reinitzer, quien realizó el hallazgo de materia que parecía tener dos puntos de fusión mientras trabajaba con derivados del colesterol en el año de 1888. Hasta entonces , sólo se conocían tres fases de la materia. Reinitzer al observar el compuesto bajo el microscopio se percató de que este fluido denso mostraba una estructura interna hasta el momento desconocida ,además el compuesto tenía dos puntos de fusión; en el primero se fundía generando un fluido denso y opaco, pero a una segunda temperatura, más alta que la primera, éste se convertía en un líquido transparente más parecido al agua.
Cabe mencionar que los cristales líquidos sólo mantienen su doble naturaleza en un determinado rango de temperaturas y presiones. A temperaturas altas o presiones bajas, el orden de la orientación da paso a las rotaciones moleculares aleatorias, con lo que deja de ser cristal líquido y se convierte en un líquido normal.
En función de la forma de las moléculas que componen al cristal este puede presentar una o más fases intermedias (mesofases) desde el estado cristalino hasta el líquido. La mesofase de nuestro interes es la : quiral nemática o fase “colestérica”( por observarse por primera ves en compuestos derivados del colesterol), además de ser una de las más comunes, es la usada en los láseres de cristal líquido. En la fase quiral nemática las moléculas tienen un ordenamiento posicional en una estructura de capas. La quiralidad (es decir, que las moléculas no tengan planos internos de simetría) induce un giro azimutal finito de una capa a la siguiente, produciendo un giro en espiral del eje molecular a lo largo de la normal de la capa . La característica clave de la importancia de este material para la óptica es que l cuenta con la existencia de un intervalo de banda fotónica para luz visible
Banda fotónica
Es ampliamente conocido que todo cristal que presente una peridiocidad en su estructura atómica, posee la característica de que los electrones inmersos en su red interna experimentan la propiedad de tener su energía restringida a un rango de valores específicos.Esta restricción se debe a la existencia de bandas de energía prohibida, para la cuál el cristal rechaza la propagación de los electrones a través del medio. Análogamente, un material que presenta una peridiocidad en su constante dieléctrica posee la propiedad de rechazar la propagación de fotónes a través del mismo. Dichas bandas prohibidas dependen de varios factores estructurales del material. Dado que las bandas prohibidas en el material dependen de la periodicidad y variación de las propiedades dieléctricas del mismo, es lógico pensar que dichas bandas varían su posición y anchura dependiendo la dirección que se considere dentro del material, con lo cual una onda de una determinada frecuencia podrá atravesar el material sin ser rechazada por el mismo, en el caso de que incida en una dirección, mientras que puede ser rechazada totalmente en el caso de incidir en otra dirección, en la cual la frecuencia de la onda esté dentro de la banda prohibida.
Elementos presentes en el láser
Elementos básicos de un láser de cistal líquido
Un láser típico, ya sea de cristal líquido o no consta de tres elementos básicos de operación :
Cavidad resonante:
También llamada cavidad laser sirve para mantener la luz circulando a través del medio activo el mayor número de veces posible, generalmente está compuesta por dos espejos, pero en este caso son remplazados por un cristal líquido, lo que permite la selección de la longitud de onda de emisión y la polarización del medio laser activo
El medio activo:
El medio láser activo es el medio material donde se produce la amplificación óptica, es dónde ocurren los procesos de excitación . En el caso de los láseres de cristal líquido el medio láser suele ser un tinte orgánico: rodamina, fluoresceína, cumarina , E- Stylbene , Umbeliferona, entre otros.
Bombeo: Para que el medio activo pueda amplificar la radiación, es necesario excitar sus niveles electrónicos o vibracionales de alguna manera. Comúnmente un haz de luz (bombeo óptico) de una lámpara de descarga u otro láser o una corriente eléctrica (bombeo eléctrico) son empleados para alimentar al medio activo con la energía necesaria. El bombeo óptico se utiliza habitualmente en láseres de estado sólido (cristales y vidrios) y láseres de colorante (líquidos y algunos polímeros) y el bombeo eléctrico es el preferido en láseres de semiconductor y de gas.
Sintonización del color
En particular, la sintonización del color del láser se puede lograr con los láseres de cristal líquido por la presencia de las antes mencionadas estructuras helicoidales de formación espontánea que provocan que el índice de refracción cambie periódicamente a lo largo del eje helicoidal del cristal y este se vuelva esencialmente un cristal fotónico.
Para lograr un ajuste continuo de la longitud de onda del láser mediante un campo eléctrico variable, es esencial la alineación de la hélice, y el campo eléctrico en el mismo plano como se muestra en la figura: Se puede elegir cualquier cualquier valor de longitud de onda en el espectro en el espectro de luz visible
Características sobresalientes
En contraste con los láseres semiconductores, se puede elegir un rango más amplio de longitud de onda mediante el ajuste de la posición de la banda fotónica . Aún son un están en desarrollo, sin embargo se espera que combinen las mejores características de los láseres de tinte, gas y diodos: Los láseres de tinte se pueden ajustar para emitir diferentes longitudes de onda, pero son muy grandes. Los láseres de gas son potentes y estables, pero no se pueden sintonizar mientras que los láseres de diodo, son mucho más pequeños pero tampoco pueden sintonizarse.
Aplicaciones
Biomédica: el tamaño pequeño, el bajo costo y el bajo consumo de energía de láseres de este tipo ofrecen una variedad de ventajas al lograr hacer dispositivos de exámenes de detección oportuna de enfermedades “de bolsillo” pues podrían brindan lecturas inmediatas sin enviar una muestra a otro laboratorio.
Médica: los láseres de cristal líquido muestran el potencial para ser utilizados en técnicas de microscopía y en terapia fotodinámica.
Tecnología: las pantallas basadas en láser de cristal líquido ofrecen la mayoría de las ventajas de las pantallas de cristal líquido estándar, un control más preciso del color. Se planea que en los años siguientes los elementos individuales sean lo suficientemente pequeños como para actuar como píxeles . Un sistema en el que cada píxel es un único dispositivo sintonizado espacialmente podría evitar los largos tiempos de relajación de la sintonización dinámica, y podría emitir cualquier color utilizando el direccionamiento espacial y la misma fuente de bombeo monocromático.
Detección ambiental: utilizando un material con un paso helicoidal altamente sensible a la temperatura, campo eléctrico, campo magnético o tensión mecánica, el cambio de color del láser de salida proporciona una medición simple y directa de las condiciones ambientales.
Referencias
S. M. Morris, A. D. Ford, C. Gillespie, M. N. Pivnenko, O. Hadeler, H. J. Coles, "The emission characteristics of liquid-crystal lasers," J. SID 14, 565-573 (2006). M. Ozaki, Y. Matsuhisa, Y. Inoue, H. Yoshida “Color-tunable liquid-crystal laser”, SPIE Newsroom. DOI: 10.1117/2.1200903.1554 . 24 April 2009 B. Maune, M. Loncar, J. Witzens, M. Hochberg, T. Baehr-Jones, D. Psaltis, Y. Qiu, and A. Scherer, "Liquid-crystal electric tuning of a photonic crystal laser", Appl. Phys. Lett. 85, 360-362 (2004).
Aurea Espin (discusión) 01:20 2 dic 2018 (CST)
Rerfracción en Metamateriales
Introducción
Victor Veselago (1968), predijo las consecuencias de la interacción de la radiación electromagnética con un material hipotético de índice de refracción negativo, el resultado sería una refracción negativa contrario a lo observado en todos los materiales existentes.
Los metamateriales son materiales construidos artificialmente que poseen propiedades electromagnéticas que no se encuentran normalmente en la naturaleza(permitividad eléctrica y permeabilidad magnética negativas). El estudio de estos materiales con propiedades electromagneticas particulares ha cobrado gran interes en los ultimos años, se utilizan en electronica para fabricación de antenas pequeñas de móviles o de satélites en los que se quieren agrupar un gran número de antenas en un espacio mínimo.
Algunas propiedades electromagnéticas interesantes son:
- Índice de refracción negativa.
- Comportamiento diferente en las ecuaciones de Fresnel.
- Comportamiento diferente en el ángulo crítico.
Propiedades de Metamateriales
Índice de refracción negativa
Cuando un haz de luz cruza la interfase entre diferentes materiales, su dirección de propagación es alterada, este cambio depende de los índices de refracción de los materiales por donde se propaga el rayo. Entre más grande sea la diferencia, mayor será la refracción del rayo. En todos los materiales conocidos a este fenómeno se le conoce como refracción positiva.
En un metamaterial el rayo de luz refractado se curva hacia el mismo lado que el rayo incidente (medido en relación a la normal a la interfaz entre el metamaterial y el material normal). Ver Figura 2.
Ecuaciones de Fresnel
Calculamos las ecuaciones de Fresnel para un metamaterial como se muestra en la figura 3
Pero $v_i=v_r$ y $\theta_i=\theta_r$ Pro lo cual la ecuación puede reescribirse como:
Y utilizando las ecuaciones
y recordado que los cosenos que aparecen son iguales entre si cuando y-0 se obtiene
combinando con la ecuación
Tenemos
Entonces la ecuacion queda como
pero como $n_t<0$ entonces
Y de manera similar se calculan las demás.
A estas ecuaciones también se les llama coeficientes de amplitud de reflexión y transmisión, en la parte inferior podemos encontar las ecuaciones de Fresnel para refracción positiva, casi no variaron con las ecuaciones para metamateriales.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): r_{\bot}=\frac{n_1 cos \theta_i - n_2 cos\theta_t}{n_1 cos \theta_i + n_2 cos\theta_t}
Las consecuencias de un índice de refracción negativo en las ecuaciones de fresnel, los coeficientes de transmisión y reflexión muestran diferencias físicas, esto es cambios de fase debido a que los valores de amplitud del campo son diferentes.
Observamos que el comportamiento de los campos incidente, reflejado y transmitido cambian con respecto a medios homogéneos, por lo que las ecuaciones de fresnel deben modificarse para un metamaterial teniendo en cuenta la condición que $n_2 < 0$, de esta manera los coeficiente de amplitud de trasmisión y reflexión quedan expresados de la siguiente forma.
Ángulo Crítico
El ángulo crítico también es conocido como el ángulo mínimo de incidencia en el cual se produce la reflexión interna total, este ángulo de incidencia se mide respecto a la normal de la separación de los medios.
Ahora de la ley de Snell donde el ángulo de refracción o transmitido es $ \theta_t =90° $, el ángulo crítico $ \theta_c $ está dado por la siguiente expresión
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \theta_c = arcsin \frac{n_1}{n_2}
Tambien sabemos que para ángulos de incidencia mayores que el ángulo crítico $\theta_i > \theta_c$ , el ángulo de refracción será mayor de $90°$, por lo cual el rayo no será refractado, ya que no pasa de un medio a otro, y por lo tanto se produce una reflexión total interna. Para metamateriales tenemos que la expresión para el ángulo crítico se modifica para obtener la siguiente forma(ver \textit{Figura 6}).
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \theta_c = arcsin \left(-\frac{n_1}{n_2} \right)
Como se hace un Metamaterial
Un metamaterial es aquel compuesto por más de dos materiales, esto implica tener un campo compuesto, como se muestra la \textit{figura 7}, esta es óptima para un metamaterial. En esta estructura veremos como al hacer incidir un haz de luz sobre una rejilla acoplada a una superficie plana, se exita un plasmon, apartir de este fenómeno es posible obtener refracción negativa (haz refractado), con plasmón se refiere a un plasma compuesto de electrones
Un plasma es un conjunto de cargas eléctricas, las cuales pueden exhibir comportamientos armónicos al ser perturbadas por un campo electromagnético.Para el caso de los metales, algunos electrones pueden moverse libremente, por lo que en estos materiales se pueden producir plasmones
Otra forma de obtener este tipo de material es realizando un conjunto de elementos ordenados periódicamente, los cuales están diseñados para responder a la acción de un campo electromagnético. El tamaño y la separación deben ser mucho menor que la longitud de onda de la radiación electromagnética de interés para el estudio. Esto permitirá que la radiación incidente interaccione con el material artificial como si éste fuera homogéneo. De esta manera se puede reemplazar el sistema compuesto por un material continuo con parámetros $\epsilon$ y $\mu$, los cuales son la permitividad eléctrica y la permeabilidad magnética, respectivamente.
Aplicaciones
Los metamateriales como subsistemas se encuentran actualmente en diversas aplicaciones: las lentes corrientes tiene un índice de refracción positivo por lo cual son curvos, como en el caso de los telescopios o de los microscopios. Los metamateriales brindan la posibilidad de que estas lentes sean planas y puedan mejorar en un grado importante su eficacia permitiendo enfocar luz en áreas muy pequeñas (más pequeña que la longitud de onda de la luz), sin preocuparnos por su forma. Revolucionarán el campo de la óptica, permitirán el desarrollo de microscopios ultrapotentes, además de importantes avances en computación cuántica y paneles solares.
Desarrollo de sistema capaz de transferir con mucha eficiencia la energía eléctrica entre dos circuitos separados, mediante el uso de metamateriales, permitiendo la deseada carga inalámbrica a distancias mayores de móviles, tabletas, etc.
Holografía
La holografía es la creación de imágenes fotográficas sin el uso de lentes. Un holograma es una estructura física que difracta la luz en una imagen, parece ser un patrón irreconocible de rayas y espirales, pero que, al iluminarlo con luz coherente, organiza la luz en una representación en tres dimensiones del objeto original. El termino "holograma" se puede referir a la película con la información codificada y también a la imagen resultante.
La palabra holografía proviene de las palabras griegas ὅλος (holos; "todo") y γραφή (graphē; "escribir" o "dibujar").
Historia
Dennis Gabor (1900-1979)
Físico británico de origen húngaro, recibió el premio nobel en 1971. Interesado en la microscopía electrónica, con la que se mejoraba el poder de resolución de los mejores microscopios ópticos hasta cien veces, mas no se tenía la suficiente resolución para las redes cristalinas de los átomos. Podía compararse con perfección óptica el mejor objetivo del microscopio con una gota de lluvia. El trabajo teórico de O. Scherzer, predecía la imposibilidad de perfeccionarlas. El límite teórico para la resolución del objetivo estaba estimado en 4 Å, casi el doble del necesario para resolver las redes cristalinas de los átomos, mientras que en la práctica era de 12 Å. Estos límites son impuestos por la necesidad de restringir la apertura de los lentes a aproximadamente $5/1000$ rad, ángulo en el cual el error de aberración esférica es casi igual que el error de difracción.
La solución
Un buen día en la Pascua de 1947, después de reflexionar sobre este problema, surgió en Dennis una solución, ¿Por qué no tomar una mala imagen, pero que contenga toda la información, y corregirla por medios ópticos? Era claro que solo con haces coherentes de electrones esto podría hacerse, con ondas de electrones que tienen una fase definida. Una fotografía ordinaria pierde la fase completamente, solo graba las intensidades. ¡No es de extrañarse que se pierda la fase, si no hay nada con que compararla! Veamos que ocurre si le agregamos un estándar, un "fondo coherente".
Las limitaciones
Como fuente de luz, se utilizaba una lampara de mercurio de alta presión, con una longitud de coherencia de $0.1 mm$. Para tener coherencia espacial, debían iluminar un agujero de $3\mu m$ de diámetro. Lo que permitía hacer hologramas de objetos con $1 cm$ de diámetro, con las que se obtenían microfotografías de $1 mm$ de diámetro, con una exposición de pocos minutos, en las emulsiones mas sensibles disponibles. Debido a la corta longitud de coherencia se limitaba a arreglar todo en un solo eje. Además del $efecto\, schlieren$, causante de perturbaciones aleatorias, había un defecto sistemático en las imágenes. La perturbación proviene del hecho que no es una sola imagen, si no dos, cada punto en el objeto emite una onda esférica secundaria, que interfiere con el fondo y produce un sistema de zonas de Fresnel circulares. Si se utiliza "holografía en línea", ambas imágenes están en línea, y se pueden separar enfocando, pero esta separación nunca es del todo perfecta, por que en general, la iluminación coherente deja una "estela". Este defecto se puede corregir utilizando el objetivo del microscopio en sentido opuesto en la reconstrucción. En los años siguientes se tuvo éxito mejorando el microscopio electrónico, pero finalmente, se tuvo que dejar el trabajo por las limitaciones de la época. Resultó que el microscopio electrónico aún estaba lejos del límite impuesto por las aberraciones ópticas, sufría de vibraciones, los campos magnéticos no se manejaban con la precisión requerida, la contaminación de la objeto y todo empeorado por las largas exposiciones requeridas en el débil haz coherente de electrones.
Idea básica de la holografía
Creación y reproducción de un holograma
Para el caso más simple donde solo hay un objeto puntual, la interferencia de la onda reflejada por el objeto y el fondo coherente u "onda de referencia" producirán franjas de interferencia, habrá máximos donde las ondas estén en fase. Registrando este patrón, e iluminándolo únicamente con el haz de referencia, la onda, en efecto, se haya en fase para la fuente de referencia A, pero como en las rendijas las fases son idénticas, también deben ser correcta para B; por lo tanto, la onda de B también de aparecer reconstruida.
La física de la holografía
Interferencia
La holografía se basa en el principio de interferencia. Un holograma captura el patrón de interferencia producido por dos o más haces de luz coherente. Se hace incidir un haz directamente en la película y este actúa como referencia para la luz dispersada por el objeto iluminado.
Debido a la superposición de dos o mas ondas, existen regiones donde se traslapan, cancelándose mutuamente parcial o totalmente, mientras que en otras regiones, las crestas y los valles resultantes son incluso mayores que las de cualquiera de las ondas constituyentes, después de la superposición, las ondas se separan y continúan sin verse afectadas.
Coherencia
Coherencia, una relación fija entre la fase de ondas en un haz de una sola frecuencia. Dos haces de luz son coherentes cuando la diferencia de fase entre sus ondas es constante; son no coherentes si hay una relación de fase aleatoria o cambiante. Los patrones de interferencia estables se forman solo por la radiación emitida por fuentes coherentes, que generalmente se producen al dividir un haz en dos o más. Un láser, a diferencia de una fuente incandescente, produce un haz en el que todos los componentes tienen una relación fija entre sí.
Fotografía y revelado
El medio de grabación debe poder resolver todas las franjas que surgen de la interferencia entre el objeto y el haz de referencia. Estas separaciones de franjas pueden variar desde decenas de micrómetros hasta menos de un micrómetro. La película fotográfica común tiene una respuesta muy baja o incluso nula en las frecuencias involucradas y no se puede usar para hacer un holograma. Si la respuesta no es plana sobre el rango de frecuencias espaciales en el patrón de interferencia, entonces la resolución de la imagen reconstruida también puede degradarse.
Difracción
El patrón de luz y franjas oscuras que se observa cuando la luz pasa un obstáculo, es un ejemplo del fenómeno de difracción. La difracción es resultado de la superposición de ondas, es un efecto de interferencia. Cuando se obstruye una onda, las partes de la onda no obstruidas interfieren entre sí en una región del espacio más allá de la obstrucción.
Las matemáticas de la holografía
El tren de ondas difundido del objeto, que penetra a un ángulo $\theta$, produce la interferencia máxima en los puntos $A, B$ y $C$ La fase relativa $\phi$ de las dos ondas, que varía a lo largo de la película, puede escribirse como función de $x$. Dado que $\phi$ se cambia por 2$\pi$, conforme $x$ avanza a lo largo de $ \overline{AB}$, $\phi/2\pi=x/\overline{AB}$. Además $\sin \theta=\lambda/\overline{AB}$.
$\therefore \phi(x)=\frac{2\pi x \sin \theta}{\lambda}$
Suponiendo que las dos ondas tienen la misma amplitud $E_0$, el campo resultante será:
$E=2E_0\cos\frac{\phi}{2} \sin{\left(\omega t-kx-\frac{\phi}{2}\right)}$
y la distribución de la irradiancia, queda como:
$I(x)=\frac{1}{2}c\varepsilon_0\left(2E_0\cos\frac{\phi}{2}\right)^2$
$I(x)=2c\varepsilon_0 E_0^2+2c\varepsilon_0 E_0^2\cos^2 \phi$
Obteniendo así una distribución de la irradiancia cosinusoidal en el plano de la película. Al emplear objetos aún más complejos, la fase relativa $\phi$ entre el objeto y las ondas de referencia variará punto por punto de manera más complicada. La diferencia de ángulo de fase $\phi$ está codificada en la configuración de las franjas, y la irradiancia de estas franjas también es alterada.
Suponiendo que el plano $xy$ es el plano del holograma $\Sigma_H$. Entonces:
$E_B(x,y)=E_{0B}\cos\left[2\pi \nu t+\phi(x,y)\right]$
describe el fondo plano u onda de referencia en $\Sigma_H$. Su amplitud $E_{0B}$, es constante, mientras que la fase depende de la posición. Si la onda estuviera orientada de tal manera que pudiera hacerse coincidir con $\Sigma_H$ por una sola rotación con un ángulo $\theta$ alrededor de $y$, la fase en cualquier punto del plano del holograma dependería de su valor de $x$. Así $\phi$ tendría otra vez la forma:
$\phi=\frac{2\pi}{\lambda}x\sin\theta=kx\sin\theta$
La onda esparcida por el objeto puede expresarse como:
$E_O(x,y)=E_{0O}(x,y)\cos\left[2\pi \nu t + \phi_O(x,y)\right]$
Se trata de una onda portadora modulada en amplitud y en fase que contiene toda la información disponible del objeto. Esta información está codificada en variaciones espaciales, y no temporales. Las dos ondas se superponen e interfieren para formar una distribución de irradiancia que se registra mediante la emulsión fotográfica.
La irradiancia resultante, salvo una constante, es $I(x)=\langle{(E_B+E_O)^2}\rangle_T$
$I(x,y)=\frac{E_{0B}^2}{2}+\frac{E_{0O}^2}{2}+E_{0B}E_{0O}\cos(\phi-\phi_O)$
La visibilidad de las franjas en el plano del holograma es:
$\mathscr{V}=\frac{2E_{0B}E_{0O}}{E_{0B}^2+E_{0O}^2}$
y contiene la información acerca de la amplitud de la onda objeto.
El perfil de la transmisión de amplitud del holograma procesado puede establecerse proporcionalmente a $I(x)$, en ese caso la onda emergente final, $E_F(x,y)$, es proporcional al producto $I(x,y)E_R(x,y)$, donde $E_R(x,y)$ es la onda de reconstrucción incidente en el holograma, entonces, si la onda de reconstrucción de frecuencia $\nu$ incide oblicuamente en $\Sigma_H$, como lo era la onda básica, se puede escribir como:
$E_R(x,y)=E_{0R}\cos\left[2\pi\nu t+ \phi(x,y)\right]$
La onda final, salvo una constante multiplicativa es:
$E_F(x,y)=\frac{1}{2}E_{0R}\left(E_{0B}^2+E_{0O}^2\right)\cos\left[2\pi\nu t+ \phi(x,y)\right]+ \frac{1}{2} E_{0R} E_{0B} E_{0O} \cos\left(2 \pi \nu t + 2\phi-\phi_0\right)+\frac{1}{2}E_{0R}E_{0B}E_{0O}\cos\left(2\pi \nu t + 2\phi-\phi_0\right)$
Tres términos describen la luz que emana del holograma; el primero se puede reescribir como:
$\frac{1}{2}\left(E_{0B}^2E_{0O}^2\right)E_{0B}E_R(x,y)$
y es una versión de amplitud modulada de la reconstrucción de la onda. Cada parte del holograma funciona como una rejilla de difracción, y este es el de orden cero, ya que no contiene información acerca de la fase de la onda objeto. Los otros términos son las ondas de banda lateral, estas son las dos ondas de primer orden difractadas por el holograma.
Holografía a gran escala
Un esquema mas ambicioso, es cinematografía en tres dimensiones, sin el uso de los lentes polarizadores.
La audiencia cubierta por zonas de visión, con el espaciamiento del ancho ocular, una
para el ojo derecho y una para el izquierdo, con un espacio en blanco entre pares. Los ojos deben ver dos imágenes diferentes; un par estereoscópico. El espectador puede mover su cabeza un poco hacia la derecha o hacia la izquierda, o incluso cuando mueve un ojo en la zona en blanco, la imagen aparecerá más oscura pero no plana, porque un ojo tiene la impresión de "estereoscopia por defecto".
Este problema es estrictamente insoluble con los medios ortodoxos de óptica, lentes, espejos, prismas. Se pueden hacer satisfactoriamente pantallas pequeñas para teatros pequeños, pero con pantallas grandes y teatros grandes, uno cae en una dilema. Si las lentes son grandes, se verán desde los asientos delanteros; si son pequeñas, no tendrán suficiente definición para los asientos traseros. La holografía puede resolver este problema, utilizando un proyector como fuente de referencia y, digamos, el sistema de zonas de visualización izquierda como objeto. La pantalla, cubierta con un emulsión, se convertirá automáticamente en un sistema óptico muy complicado, tal que cuando se proyecta una imagen desde el proyector, se verá solo desde las zonas de visión izquierda. Repitiendo el proceso con el proyector derecho, y las zonas de visualización derechas. Los hologramas muestran el fenómeno de la selectividad direccional. Si uno desplaza el iluminador de la posición original en un cierto ángulo, no habrá reflexión. Poniendo los dos proyectores en este ángulo el uno del otro, se tendrá que la imagen derecha no será vista por el ojo izquierdo y viceversa. Queda, por supuesto, una dificultad, y es que no se puede practicar holografía en la escala de un cine, y con una película tan grande como una pantalla. Pero esto también podría resolverse, haciendo la pantalla a partir de piezas pequeñas. Estas son algunas de las dificultades para realizar holografía a gran escala.
Referencias
Eugene Hecht, Óptica, 5° edición, Ed. Pearson, 2017.
Dennis Gabor – Nobel Lecture. NobelPrize.org. Nobel Media AB 2018. Mon. 3 Dec 2018. <https://www.nobelprize.org/prizes/physics/1971/gabor/lecture/>
Sesebasi (discusión) 23:01 2 dic 2018 (CST)
Óptica de cristales líquidos nemáticos
Los cristales líquidos fueron descubiertos alrededor del año 1888 por el botánico australiano Friedrich Rheinitzer al observar la composición cholesteric del benzoato, un poco después el físico alemán O. Lehmann sugiere el nombre de “cristal líquido” al observar la estructura cristalina de este. Los cristales líquidos son sustancias que presentan propiedades de sólidos y de líquidos al mismo tiempo. Existen tres tipos de cristales líquidos: liotrópicos, poliméricos y termotrópicos. Estos últimos son los más estudiados por sus propiedades ópticas y podemos clasificarlos a su vez en tres subtipos: nemáticos, colestéricos y esmécticos. Se diferencian por las distintas ordenaciones posibles de sus moléculas, que, en el caso de los nemáticos, suelen representarse por elipsoides de revolución capaces de interactuar entre sí debido a su carácter eléctrico dipolar. La fase nemática de los cristales líquidos se caracteriza por un orden orientacional de sus moléculas y por una movilidad traslacional muy semejante a la de un líquido. Las moléculas de cristal líquido nemático están orientadas en una dirección preferente, conocida como director.
El cristal líquido es una estructura molecular que posee propiedades físicas tanto de sólidos como de líquidos. El material con el que está fabricado un cristal líquido, por lo general está compuesto de un alto número de moléculas anisotrópicas birrefringentes. Sus moléculas tienen una forma elipsoidal con una orientación ordenada a través de la estructura cristalina. Pero también tienen una viscosidad comparable con la de los líquidos; ya que cuando se le aplica una fuerza eléctrica externa al cristal líquido, cada molécula puede girar o rotar con respecto a otra molécula. Los cristales líquidos son un tipo especifico de moduladores espaciales de luz en dos dimensiones. En 1963 Williams descubre la propiedad moduladora que tienen los cristales líquidos, esto al hacer pasar luz a través del cristal liquido y estimular a este con una carga eléctrica. La configuración más utilizada en pantallas de cristal líquido es la nemática. Sus moléculas poseen una orientación paralela en todo el volumen del cristal.
La estructura cristalina nemática posee propiedades ópticas importantes como lo es el giro de sus moléculas debido a una actividad óptica inducida. Que aparece cuando el cristal líquido nemático se coloca entre dos placas de vidrio pulidas con direcciones de pulidos diferentes.
El giro molecular
Es una propiedad de los cristales líquidos del tipo nemático.
Al iniciar el giro, el eje de la molécula se encuentra paralelo a la dirección de pulido del vidrio 1 y al finalizarse se encuentra paralelo a la dirección de pulido de vidrio 2. Los cristales líquidos tienes la propiedad de modificar la transmitancia al aplicarle un voltaje, con el cual creamos un campo eléctrico perpendicular a la ventana de vidrio.
Existirán entonces dipolos inducidos y la moléculas del cristal líquido experimentan pares de torsión que las llevan a alinearse con el campo a medida que aumenta el voltaje (a). Se reduce la birrefringencia
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): ∆
y la retardancia
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): ∆
La retardancia máxima se obtiene cuando el voltaje aplicado es cero. Cuando V es grande, la retardancia es un mínimo de 30 nm. Este tipo de pantallas de cristal líquido, son usados generalmente en relojes digitales y calculadoras.
Óptica relativista
introdución
La pregunta, ¿ Cómo es el aspecto de las cosas cuando se mueven a velocidades relativistas ? logró resolverse gracias a lo trabajos de un colega de Einstein, Anton Lampa, de 1924 y de Penrose y Terrell, de 1959.
La forma, posición y orientación de un objeto que se mueve a una velocidad cercana a la de la luz puede ser bastante diferente de lo que se vería a velocidades mas lentas. Estas deformaciones ópticas, conocidas como aberraciones, recuerdan a las imágenes que se producen en espejos curvos. Se debe a dos causas, compresión angular y distorsión. Por otro lado el color de los objetos puede variar debido al efecto Doppler. También la intensidad de luz que viene de objetos que se mueven a velocidades relativistas puede cambiar debido a una combinación de dilatación temporal y compresión angular. Así que la imagen del mundo que uno vería estaría afectado no solo por la contracción espacial y la dilatación temporal si no también por la velocidad finita de la luz. Las aberraciones el efecto Doppler y los cambios de intensidad son todos causados por la velocidad finita de la luz, el tema que trataremos aquí el el efecto Doppler.
Efecto Doppler relativista
El efecto Doppler se manifiesta en todo tipo de onda, incluyendo el sonido y la luz. En el caso del sonido, Por ejemplo, cuando un auto de carreras se acerca a nosotros, el ruido de su motor se escucha mas agudo, y cuando se aleja, el ruido es mas grave. Análogamente, cuando un objeto emite luz se acerca a nosotros la frecuencia de la luz aumenta, y al revés si se aleja. Con la luz, los cambios de frecuencia representan cambios de color. Un aumento de frecuencia de la luz produce un objeto azulado. Una disminución de la frecuencia hace que veamos los objetos mas rojizo. Se ha observado que la luz que llega de estrellas o galaxias lejanas es algo mas rojiza de lo que debería ser si estuvieran quietas. Del corrimiento al rojo de la luz, las observaciones de Edwin Hubble en 1920 nos permite deducir que las galaxias más lejanas se alejan de nosotros a gran velocidad. Estos resultados son una comprobación de la expansión del universo y su edad de 13.8 mil millones de años.
Ahora matemáticamente, consideremos la ecuación de onda en dos marcos de referencia
$ \Box \varphi = \Box^{\prime}\varphi\left(t^{\prime},x^{\prime}\right)=0$
donde
$\Box =\frac{1}{c^{2}\partial t^{2}}-\vec \bigtriangledown \cdot \vec \bigtriangledown$
es el operador de d' Alembert, el cual es invariante a la transformaciones de Lorentz.
Para una onda plana, la solución es
$\varphi=A\exp i[\vec k \cdot \vec x - \omega t] $,
donde $\vec k$ es el vector de onda y $\omega $ es la frecuencia angular. Como la ecuación de onda es invariante a transformaciones de Lorentz, también la fase lo es, es decir,
$-\eta_{\nu \mu}k^{\mu}x^{\mu}=\vec k \cdot \vec x - \omega t= \vec k^{\prime}\cdot \vec x^{\prime}-\omega^{\prime}t^{\prime}$.
Entonces $\vec k^{\mu}=\left(\omega/c,\vec k\right)$ se transforma igual que un cuadri-vector $x^{\\nu}=\left( ct,\vec x\right)$ de Lorentz, es decir,
$\omega^{\prime}=\gamma\left(\omega-c\vec\beta\cdot\vec k\right)$
$\vec k^{\prime}=\vec k + \frac{\gamma-1}{v^{2}}\left(\vec v \cdot \vec k\right)\vec v-\gamma\vec v\frac{\omega}{c^{2}}$.
Donde $\gamma=1/\sqrt{1-\beta^{2}}$ es el conocido factor de Lorentz. El cuatri-momento $p^{\mu}=\hbar k^{mu}$ lo obtenemos por la publicación de la constante de Planck $\hbar$ reducida. Por la ecuación de onda, la fórmula de dispersión
$\vec k\cdot\vec k=\frac{\omega^{2}}{c^{2}}$
es valida en el vacio e invariante a las transformaciones de Lorentz. Ahora, supongamos que el vector de onda $\vec k$ forma un ángulo $\theta$ con la velocidad relativa entonces el producto escalar $\vec v \cdot \vec k=vk\cos \theta$ se puede simplificar. Por lo tanto
$\omega^{\prime}= \gamma \omega \left(1-\beta\cos\theta\right)$,
que es el efecto Doppler para la frecuencia angular $\omega=2\pi f$.
Para el ángulo $\theta=0$ tenemos
$\omega^{\prime}=\gamma \omega\left(1-\beta\right)=\frac{1-\beta}{\sqrt{\left(1-\beta\right)\left(1+\beta\right)}}\omega$
$=\sqrt{\frac{1-\beta}{1+\beta}}\omega=\omega/D$ que es conocido como el efecto Doppler longitudinal, donde
$D=\sqrt{1+\beta}/\sqrt{1+\beta}$
es el factor de Doppler.
El efecto Doppler transversal $\omega=\omega^{\prime}\sqrt{1-\beta^{2}}$ se puede deducir más fácilmente de la dilatación de el tiempo. A sugerencia de Einstein, en 1938, Ives y Stilwell fueron los primeros en comprobar experimentalmente este efecto con un haz de átomos excitados de hidrógeno. Para la longitud de onda $\lambda=c/f=2\pi c/\omega$ llegamos a una relación inversa
$\lambda^{\prime}=\sqrt{\frac{1+\beta}{1-\beta}}\lambda=\sqrt{\frac{c+v}{c-v}}\lambda$.
Donde el factor $D=\sqrt{\left(c+v\right)/\left(c-v\right)}$ de Doppler es independiente de la longitud de onda. La velocidad relativa de los objetos del cosmos se obtiene mediante la relación
$1+z=\frac{\lambda^{\prime}}{\lambda}=1+\frac{\Delta\lambda}{\lambda}$
$=\sqrt{\frac{1+\beta}{1-\beta}}\simeq 1+\beta$
donde $z\equiv \Delta\lambda/\lambda$ corresponde a un corrimiento al rojo. Hay cuasares (fuentes brillantes llamados, casi estelares) tan lejos que tienen un valor $z>3$.
Bibliografía
Taylor John R., Mecánica clásica (Reverté, Barcelona, 2013)
Eckehard W. Mielke, 'Relatividad Moderna, CreateSpace, Amazon.com, ISBN-13: 9781512117820), 184 paginas.
- ↑ General Physics Java Applets, http://www.surendranath.org/Applets.html.






































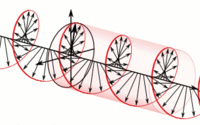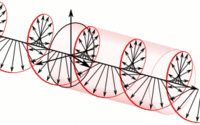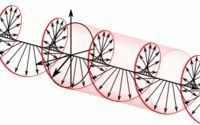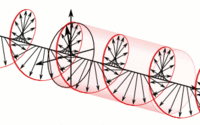









![\vec{\mathbf{E}}=E_{0}[\hat i cos(kz - \omega t) + \hat j sen(kz - \omega t)] \qquad(7)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2b7ebd505a4aae1d072c7bbba25db14717eb988a)










![\vec{\mathbf{E}}=E_{0}[\hat i cos(kz - \omega t) - \hat j sen(kz - \omega t)] \qquad(10)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8e00fc451acb2abd1eb6ad683b24010c4059589b)








![(\frac { E_{ y } }{ E_{ 0y } } )^{ 2 }+(\frac { E_{ x } }{ E_{ 0x } } )^{ 2 }\cos ^{ 2 } \epsilon -2(\frac { E_{ y } }{ E_{ 0y } } )(\frac { E_{ x } }{ E_{ 0x } } )\cos \epsilon =[1-(\frac { E_{ x } }{ E_{ 0x } } )^{ 2 }]\sin ^{ 2 } \epsilon](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/75cd688e32526b1cc9e542df30ab2e264079e546)
















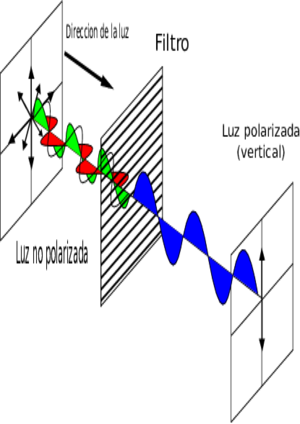


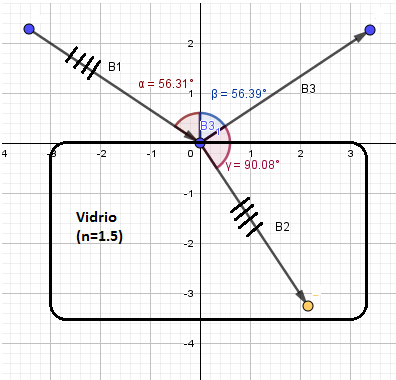
















































































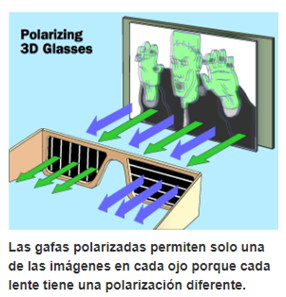


























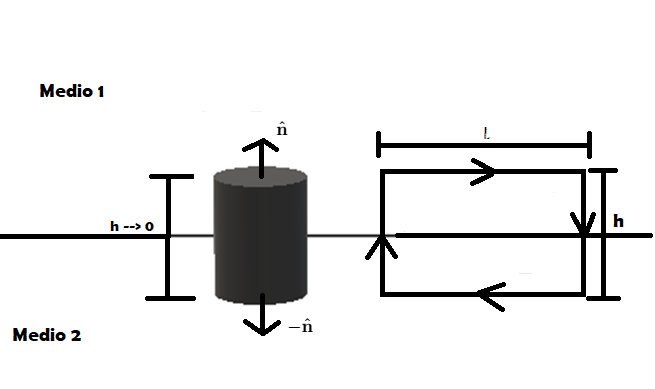



































































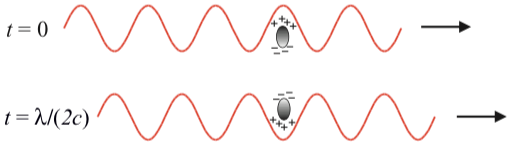



























![\qquad = \dfrac{1}{2} \epsilon_0 c \left[E_{0,1} e^{i(\omega t - \mathbf{R} \cdot \mathbf{k}_s)} + E_{0,1} e^{i(\omega t - \mathbf{R} \cdot \mathbf{k}_s) + \Delta \phi}\right] \cdot \left[E_{0,1} e^{-i(\omega t - \mathbf{R} \cdot \mathbf{k}_s)} + E_{0,1} e^{-i(\omega t - \mathbf{R} \cdot \mathbf{k}_s) + \Delta \phi}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c755998f5fd22eb87df98463c3c46386e6a2722b)
![\qquad = \dfrac{1}{2} \epsilon_0 c E_{0,1}^2 \left[1 + e^{i\Delta \phi} + e^{-i\Delta \phi} + 1\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4c50f496ecda9880b500dcc233ee072483e8ef74)
![\qquad = \dfrac{1}{2} \epsilon_0 c E_{0,1}^2 \left[2 + 2\cos \Delta \phi\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0c09f4bebc5547fc9393735badfc0a6de53ae16b)
![\qquad = \epsilon_0 c E_{0,1}^2 \left[1 + \cos \Delta \phi\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/313697ba3389477d57c4beda7b1dcacb9df9d22a)
![{\displaystyle I_T = 2 I_{s,1} \left[1 + \cos \Delta \phi\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b77bdca5a9107585f86094f6d77fad159c850be4)











![\qquad = \dfrac{1}{2}\epsilon_0 c E_{0,1}^2 \sum_{j=1}^n \sum_{k=1}^n \left[\cos(\phi_j - \phi_k) + i \sin(\phi_j - \phi_k)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/91d6524749232f91b1237b8031de0232e354590c)

































![{\displaystyle S(q) = \left[1+2 A_2 M C + 3A_3 M C^2 + \dots\right]^{-1}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/18572718c5cf8fb4b80ffbb3b80465cccd254c41)














![P(q) \approx \dfrac{1}{n^2} \sum_{j=1}^n \sum_{k=1}^n \left[1 - \dfrac{1}{6} (qr_{jk})^2\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1aa08d42d1dbb34c662c5afdcafebbb5d74e9d02)




















































































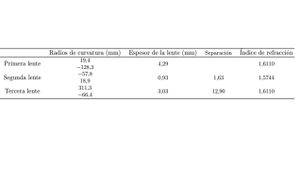












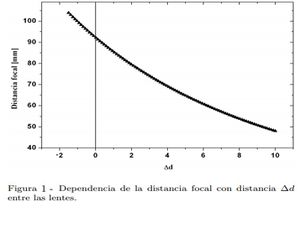





![\left[\delta,\pi-\delta\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e01541fc4ac1f94682d90c241953212c47541aff)

![\left[a,b\right]\subset\left[-\pi,\pi\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cf1ebf0739be462483d6197f4157f1470269103c)
![\left[a+\delta,b-\delta\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1ba65fcb65c22ac8c1c13fbc96d5ff055c305b07)




![x\in\left[\delta,\pi-\delta\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f991f255eb52e6df7b36f6e87bcbee6081c35d61)


























![\left[0,\pi\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a8e34615383b8ffe6f079cfd094c2b274fab51a4)












































![\frac { d }{ dx } [{ S }_{ 2n-1 }(x)]=\quad { S }_{ \Delta ,2n-1 }(x)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3009260072e10274303b272971bbdcee5675836b)




![=\frac { 2 }{ \pi sin(x) } \sum _{ r=1 }^{ n }{ [sin(2rx)-sin(2(r-1)x)] }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/dda7c0909462e5b7d9d7ead7f72f132f4091e9ea)
![=\frac { 2 }{ \pi sin(x) } \left[ \sum _{ r=1 }^{ n }{ sin(2rx)- } \sum _{ r=0 }^{ n-1 }{ sin(2rx) } \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a36fe4e385b32b6e5d05692fe93694e757644642)


![\frac { d }{ dx } [{ S }_{ 2n-1 }(x)]=\frac { 2 }{ \pi } \frac { sin(2nx) }{ sin(x) }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5683ceaa20f22ea2a15fd61b625fe0c1206062cb)










![\left[ -\frac { \pi }{ 2 } ,\frac { \pi }{ 2 } \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/54381f086ac9ffe8306d413f813abcb616e95dee)








![[a,b]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)









![[0,\pi ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
![[-\pi ,\pi ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)
![[-\pi ,0]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b78e1f27dbb353d8aa259a1ab97afe1a7e8a6cf3)

![{ S }_{ N }=\frac { { a }_{ 0 } }{ 2 } +\sum _{ k=1 }^{ N }{ [{ a }_{ k }cos(kx)+b_{ k }sin(kx)] }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ff9a29bdac8868998cda79d2524e0ab89f6a85d9)

![{ \sigma }_{ N }(x)=\frac { { a }_{ 0 } }{ 2 } +{ \beta }_{ k }\sum _{ k=1 }^{ N }{ [{ a }_{ k }cos(kx)+b_{ k }sin(kx)] }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d37fd11579da3804656ceafcbc420835d7c32948)




![\frac { d }{ dx } [{ S }_{ 2n-1 }(x)]=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9259369e5ef2241a301e74d8ecb084906c3b6625)



![=\frac { 1 }{ 2sin(x) } \sum _{ r=1 }^{ n }{ [cos(2(r-1)x-cos(2x))] }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fa1d54469ba58fd7bd2238957ca90ce9f44b3f40)
![=\frac { 1 }{ 2sin(x) } \left[ \sum _{ r=0 }^{ n-1 }{ cos(2rx)-\sum _{ r=1 }^{ n }{ (2rx) } } \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9129245191eeb9606d0bef8684486d41920ef64f)

























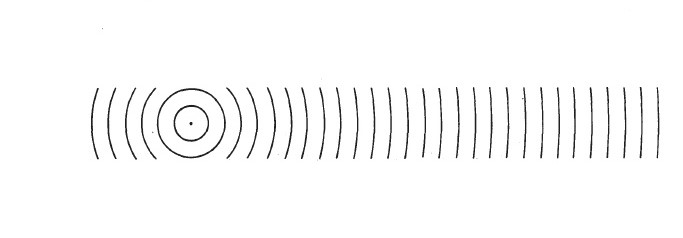
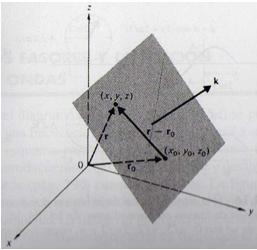

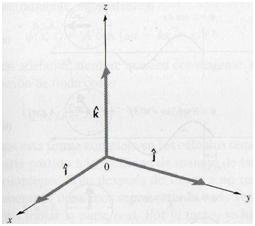























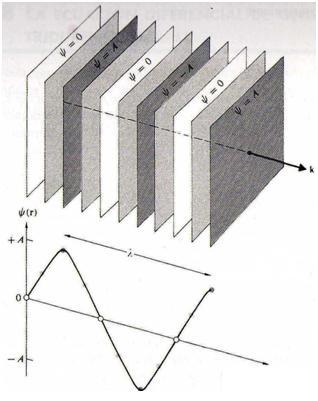


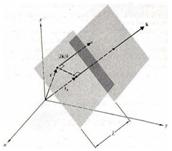











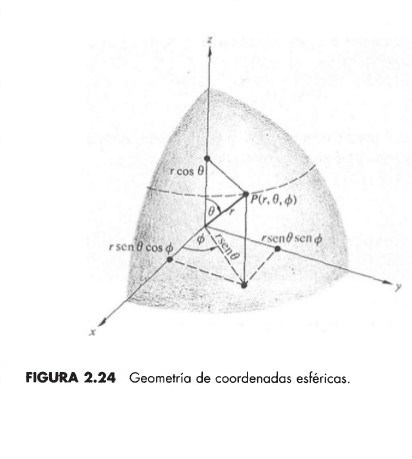














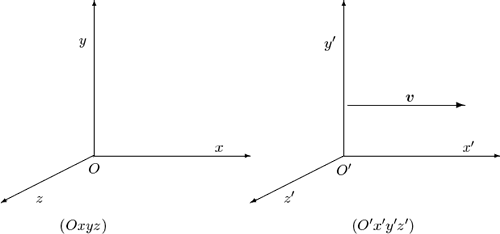






















































![[\mathcal{L}]=\frac{1}{L^{3}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5838014979eda02aa25b768fd970461e7116a1d0)





















![\frac{\partial\mathcal{L}}{\partial (\partial _{\mu}A_{\nu})}=\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}[-\frac{1}{4}g^{\alpha\rho}g^{\beta\sigma}F_{\rho\sigma}F_{\alpha\beta}]=-\frac{1}{4}g^{\alpha\rho}g^{\beta\sigma}[F_{\rho\sigma}\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}F_{\alpha\beta} + (\frac{\partial}{\partial (\partial _{\mu}A_{\nu})}F_{\rho\sigma})F_{\alpha\beta}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3dcf8ef87ae3c6c43d6a35556e6f1de55b6b7e7f)









![\frac{\partial\mathcal{L}}{\partial (\partial _{\mu}A_{\nu})}=-\frac{1}{4}[F^{\mu\nu}-F^{\nu\mu}]-\frac{1}{4}[F^{\mu\nu}-F^{\nu\mu}]=-\frac{1}{2}(F^{\mu\nu}-F^{\nu\mu})=-\frac{1}{2}(F^{\mu\nu}-(-F^{\mu\nu}))=-F^{\mu\nu}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f2a9e4df1263ca507f700a6f5f73525db67b7f5d)








![[F'^{\mu\nu}]:=F'=\Lambda F\Lambda^{t}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/23b036773dc0a35740372c55b9f0c4d2838e3c58)