Compleja:z-ej-cap1.4

La esfera de Riemann y el plano extendido

1.67. Usando la proyección estereográfica demuestre que la proyección de un círculo S en $\mathbb {S}$ corresponde a un círculo T en el plano $\mathbb {C}$. Demuestre que si S contiene al polo norte, entonces su proyección T en $\mathbb {C}$ es una recta.

Un círculo en S en $\mathbb {S}$ es la intersección de un plano con la esfera, por lo que sus puntos satisfacen una ecuación de la forma $Ax+By+Cz=D$.
Por tanto este círculo es la imagen bajo la proyección estereográfica (2), satisfaciendo

$A\left({\frac {2x}{1+|w|^{2}}}\right)+B\left({\frac {2y}{1+|w|^{2}}}\right)+c\left({\frac {|w|^{2}-1}{1+|w|^{2}}}\right)=D,$

donde $w=(x,y,0),$ por tanto $|w|^{2}=x^{2}+y^{2}$

$\Rightarrow 2Ax+2By+(x^{2}+y^{2}-1)C=D(1+x^{2}+y^{2})$

$\Rightarrow 2Ax+2By+Cx^{2}+Cy^{2}-C=Dx^{2}+Dy^{2}+D$

$\Rightarrow (C-D)x^{2}+2Ax+(C-D)y^{2}+2By-(C+D)=0$

Si $C=D$, tenemos
$2Ax+2By=2C$, i.e., $Ax+By=C$, la ecuación de una recta.

Si $C\neq D$, completando cuadrados:
$x^{2}+2{\frac {A}{C-D}}x+\left({\frac {A}{C-D}}\right)^{2}+y^{2}+2{\frac {B}{C-D}}y+\left({\frac {B}{C-D}}\right)^{2}={\frac {C+D}{C-D}}+\left({\frac {A}{C-D}}\right)^{2}+\left({\frac {B}{C-D}}\right)^{2}$.

$\Rightarrow \left(x+{\frac {A}{C-D}}\right)^{2}+\left(y+{\frac {B}{C-D}}\right)^{2}={\frac {(C+D)(C-D)+A^{2}+B^{2}}{(C-D)^{2}}}={\frac {C^{2}-D^{2}+A^{2}+B^{2}}{(C-D)^{2}}}$.

$\Rightarrow \left(x+{\frac {A}{C-D}}\right)^{2}+\left(y+{\frac {B}{C-D}}\right)^{2}={\frac {A^{2}+B^{2}+C^{2}-D^{2}}{(C-D)^{2}}}$, la ecuación de un círculo con centro en $\left(-{\frac {A}{C-D}},-{\frac {B}{C-D}}\right)$ y radio $r={\frac {\sqrt {A^{2}+B^{2}+C^{2}-D^{2}}}{C-D}}$.

---

Realizado por: Belen (discusión) 22:51 22 nov 2012 (CST)

---

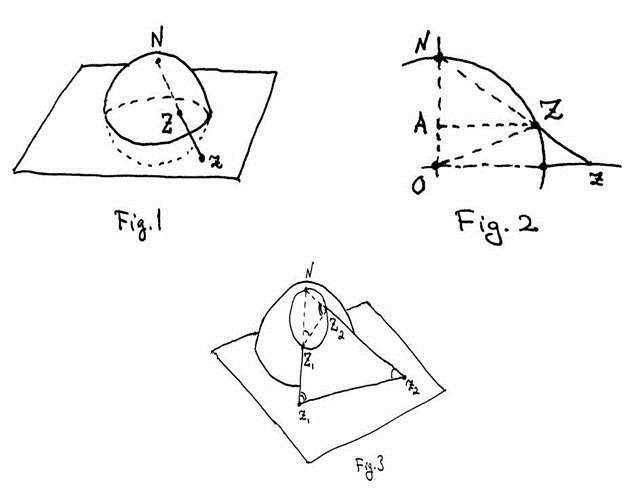
1.71.Si ${\mathcal {Z_{1}}}$,${\mathcal {Z_{2}}}$, demuestre que

$d_{c}={\frac {2\left|{\mathcal {Z_{2}}}-{\mathcal {Z_{1}}}\right|}{{\sqrt {1+\left|{\mathcal {Z_{1}}}\right|^{2}}}{\sqrt {1+\left|{\mathcal {Z_{2}}}\right|^{2}}}}}$.

Sea ${\mathcal {Z_{1}}}$,${\mathcal {Z_{2}}}\in {\mathfrak {C}}$

Por triángulos semejantes $NO{\mathcal {z}}$y$NA{\mathcal {Z}}$ $\left(figura2\right)$, implica ${\frac {\left|N-{\mathcal {z}}\right|}{1}}={\frac {\left|N-{\mathcal {Z}}\right|}{1-{\boldsymbol {\zeta }}}}$.

Pero$\left|N-{\mathcal {z}}\right|={\sqrt {\left|{\mathcal {z}}\right|^{2}+1}}$ y $1-{\boldsymbol {\zeta }}={\frac {2}{\left|{\mathcal {z}}\right|^{2}+1}}$ , entonces

$\left|N-{\mathcal {Z}}\right|={\frac {2}{\sqrt {1+\left|{\mathcal {z}}\right|^{2}}}}$ y $\left|N-{\mathcal {z}}\right|\left|N-{\mathcal {Z}}\right|=2$

El plano N_z1z2, intersecta a S en un circulo,$\left(figura3\right)$.

Vemos que$\left|N-{\mathcal {z}}_{1}\right|\left|N-{\mathcal {Z}}_{1}\right|=\left|N-{\mathcal {z}}_{2}\right|\left|N-{\mathcal {Z}}_{2}\right|$,

los triangulos N_z1z2 y N_Z1Z2, son semejantes, entonces;

${\frac {\left|{\mathcal {Z}}_{1}-{\mathcal {Z}}_{2}\right|}{\left|{\mathcal {z}}_{1}-{\mathcal {z}}_{2}\right|}}={\frac {\left|N-{\mathcal {Z}}_{2}\right|}{\left|N-{\mathcal {z}}_{1}\right|}}$

Hacemos$d_{c}\left({\mathcal {Z}}_{1},{\mathcal {Z}}_{2}\right)=\left|{\mathcal {Z}}_{1}-{\mathcal {Z}}_{2}\right|={\frac {2\left|{\mathcal {z}}_{1}-{\mathcal {z}}_{2}\right|}{{\sqrt {1+\left|{\mathcal {z}}_{1}\right|^{2}}}{\sqrt {1+\left|{\mathcal {z}}_{2}\right|^{2}}}}}$

---

Realizado por: Luis Antonio (discusión) 09:39 28 nov 2012 (CST)

---

--mfg-wiki (discusión) 17:32 15 nov 2012 (UTC)

Compleja:z-ej-cap1.1

Compleja:z-ej-cap1.2

Compleja:z-ej-cap1.3