SECCION 1.1.4
1. Demuestre que:

Se conoce como igualdad de Lagrange
Solución.
Esta demostración se hará por inducción, es decir, empezaremos suponiendo que el elemento  se encuentra en el conjunto, pues entonces el resultado implica que el elemento
se encuentra en el conjunto, pues entonces el resultado implica que el elemento  esta en el conjunto.
esta en el conjunto.
Sea 
Supongamos que  esta en
esta en  , es decir,
, es decir,

Tenemos que:

(recordemos algunas expresiones que no serán de utilidad en adelante
♠ ;
;
♣ en esta expresión se toma la suma de
en esta expresión se toma la suma de  terminos y adicionar el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): n-ésimo
para tener el lado izquierdo de la expresión)
terminos y adicionar el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): n-ésimo
para tener el lado izquierdo de la expresión)



(En la expresión  se utilizó ♣ para posteriormente en
se utilizó ♣ para posteriormente en  hacer un poco de algebra y llegar a la expresión
hacer un poco de algebra y llegar a la expresión  .)
.)
Necesitamos saber si alguno de los elementos de la expresión  tiene parecido con algo conocido ó si se anulan entre si, es por eso que se desarrolla el 3er termino de la misma.
Donde nuevamente se utiliza la idea de la expresión ♣ .
tiene parecido con algo conocido ó si se anulan entre si, es por eso que se desarrolla el 3er termino de la misma.
Donde nuevamente se utiliza la idea de la expresión ♣ .


Al comparar las expresiones  con
con  se observa que:
se observa que:

(Observese bien que el segundo termino de lado derecho de la expresión  son los
son los  términos.)
términos.)
Entonces si ahora utilizamos las expresiones  ,
,  e
e  podemos re-escribir
podemos re-escribir  de la manera siguiente:
de la manera siguiente:


![\begin{align}
\aleph=\left|\sum_{k=1}^{n}Z_{k}W_{k}\right|^2 - \overline{Z}_{n}\overline{W}_{n} \sum_{k=1}^n Z_{k}W_{k}-Z_{n}W_{n} \sum_{l=1}^n \overline{Z}_{k}\overline{W}_{k}+ \left|Z_{n}W_{n}\right|^2 - \left[\sum_{j=1}^{n-1} Z_{j}\overline{W}_{n}\overline{Z}_{j}W_{n}- \sum_{j=1}^{n-1} Z_{j}\overline{W}_{n}\overline{Z}_{n}W_{j}- \sum_{j=1}^{n-1} Z_{n}\overline{W}_{j}\overline{Z}_{j}W_{n} + \sum_{j=1}^{n-1} Z_{n}\overline{W}_{j} \overline{Z}_{n}W_{j}\right] + \left|W_{n}\right|^2 \sum_{k=1}^{n-1} \left|Z_{k}\right|^2 + \left|Z_{n}\right|^2 \sum_{l=1}^{n-1} \left|W_{l} \right|^2 + \left|Z_{n}\right|^2 \left|W_{n}\right|^2
\qquad (xi)\\
\end{align}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/58db6fac073a7e82f0f422967dcbfe5cdc665a23)
(En las expresiones  se utilizo ♠ y ♣ mas un poco de álgebra)
se utilizo ♠ y ♣ mas un poco de álgebra)


(En  recordamos que
recordamos que  , agrupamos términos y claro mas álgebra)
, agrupamos términos y claro mas álgebra)



por lo tanto si 




 .
.
--Dali 03:31 14 oct 2009 (UTC)
2.- Sean  numeros complejos, ¿Bajo que condiciones se tiene que
numeros complejos, ¿Bajo que condiciones se tiene que  ?
?
Si  , entonces
, entonces

por otro lado

y por lo tanto

--Luis Nava 02:52 5 oct 2009 (UTC)
2.- Sean  numeros complejos, ¿Bajo que condiciones se tiene que
numeros complejos, ¿Bajo que condiciones se tiene que  ?
?
Vemos que esto es realmente una igualdad cuando los puntos  son colineales.
son colineales.
Por demostrar que

Para realizar esta demostración definiremos nuestros numeros en forma polar
![z{}_{1}=r_{1}\exp\left[i\theta_{1}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8b7b3f1d69c234a74d54f14d70186f5ca86bd6f7)
![z{}_{2}=r_{2}\exp\left[i\theta_{2}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4db18bcda7bf995ff8a7fec3c366ed236215afa9)
Ahora sustuyendo esto en nuestra igualdad tenemos que:
![\left|r_{1}\exp\left[i\theta_{1}\right]+r_{2}\exp\left[i\theta_{2}\right]\right|=\left|r_{1}\exp\left[i\theta_{1}\right]\right|+\left|r_{2}\exp\left[i\theta_{2}\right]\right|](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/56fafaf6255666ab3f34d5d9a837277930b43c9b)
Tamando la norma al cuadrado
![\left|r_{1}\exp\left[i\theta_{1}\right]+r_{2}\exp\left[i\theta_{2}\right]\right|^{2}=\left(\left|r_{1}\exp\left[i\theta_{1}\right]\right|+\left|r_{2}\exp\left[i\theta_{2}\right]\right|\right)^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f83de2b8e9652280f2584e3e6d734365ecfac708)
Desarrollando temenos que
![\left(r_{1}\exp\left[i\theta_{1}\right]+r_{2}\exp\left[i\theta_{2}\right]\right)\left(r_{1}\exp\left[-i\theta_{1}\right]+r_{2}\exp\left[-i\theta_{2}\right]\right)=\left(\left|r_{1}\exp\left[i\theta_{1}\right]\right|+\left|r_{2}\exp\left[i\theta_{2}\right]\right|\right)^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cfba0cc7436409d4ee730e76550daf972d7e7557)
![r_{1}^{2}+r_{1}r_{2}\exp i\left[\theta_{1}-\theta_{2}\right]+r_{1}r_{2}\exp i\left[\theta_{2}-\theta_{1}\right]+r_{2}^{2}=r_{1}^{2}+2r_{1}r_{2}+r_{2}^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e3ea0dd81ca24c826831dc913c1ebc11780c20b2)
Simplificando un poco y factorizando  del lado izquierdo llegamos a lo siguiente
del lado izquierdo llegamos a lo siguiente
![r_{1}r_{2}\left(\exp i\left[\theta_{1}-\theta_{2}\right]+\exp i\left[\theta_{2}-\theta_{1}\right]\right)=2r_{1}r_{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0f483bce045264bc22ff558e17f2ec9cac68edf1)
![\exp i\left[\theta_{1}-\theta_{2}\right]+\exp i\left[\theta_{2}-\theta_{1}\right]=2](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/39422f6b1cf69e35fff1025499f8acab5c4f7e09)
Escribiendo estas exponenciales en terminos de senos y cosenos

Ya que la función  es impar
es impar


Despejando 

Entonces
 para
para 

Esto nos dice que esta igualdad solo se cumple cuando nuestros vectores son colineales, es decir son linealmente dependientes o uno de ellos es cero.
Generalizando esto para n, suponemos que se cumple para n-1

Donde nuestros primeros n-1 terminos lo redefinimos como  y el n-esimo como
y el n-esimo como 

Y utlizamos el mismo razonamiento
Esto es muy claro ver cuando n=2, en una grafica.
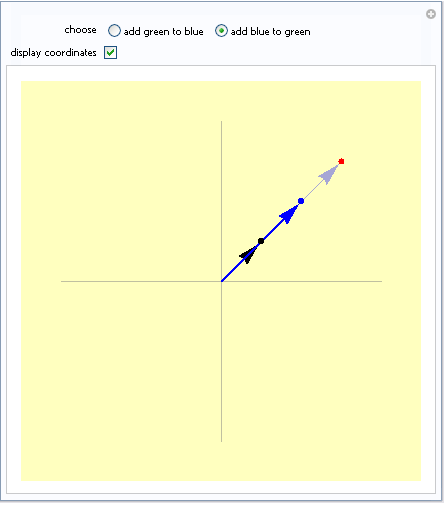
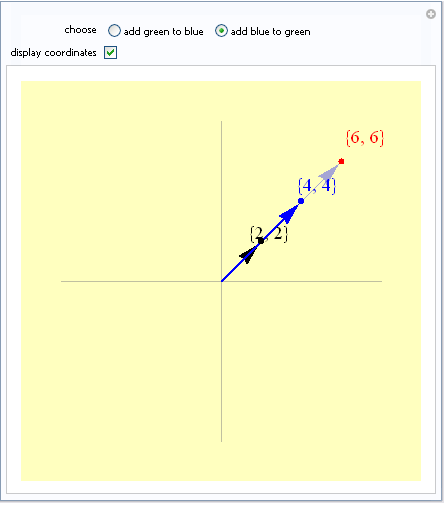
Aquí les dejo el enlace de la pagina donde consulte el código para generar las graficas para los que les interese.
Demostracion grafica
--Oscar Adrian 03:41 16 oct 2009 (UTC)
--Oscar Adrian 03:07 6 oct 2009 (UTC)
3. Encuentre el ínfimo de  en la región
en la región  , y describa en qué puntos se alcanza.
, y describa en qué puntos se alcanza.
Con una variante de la desigualdad del triángulo, tenemos que

Por tanto,

Entonces, el ínfimo de la expresión es 7.
Por otro lado, tenemos que, si 

Si tomamos la cota inferior,  , la expresión anterior es entonces:
, la expresión anterior es entonces:

Ya que la función coseno tiene su mínimo en el valor -1, tomemos una  tal que
tal que  . Para este caso, tenemos dos valores:
. Para este caso, tenemos dos valores:  y
y  ,
,
de tal forma que, con estos valores,

Con la fórmula de De Moivre, tenemos que el ínfimo de la expresión dada toma ese valor en  y
y  tales que
tales que

y

Pero, además, por le geometría de los números complejos, tenemos otros dos valores  y
y  tales que
tales que

y

Por tanto, las expresiones (2), (3), (4) y (5) nos proporcionan los valores en que el ínfimo es tomado, a saber,  y
y  .
.
--Belen 04:08 12 oct 2009 (UTC)
4. Describir la ecuación de la hipérbola en lenguaje de números complejos.(Este ejercicio no forma parte de los EJERCICICIOS 1.1.4 de CURSO BÁSICO DE VARIABLE COMPLEJA, a sido agregado a está sección porque este tema forma parte de ella
Una hipérbola en el plano complejo es el lugar geométrico
formado por un conjunto de puntos  , en el plano
, en el plano  ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias
; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias  , a dos puntos fijos llamados focos
, a dos puntos fijos llamados focos y
y  , es una costante positiva igual al doble de la distancia (osea
, es una costante positiva igual al doble de la distancia (osea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal. (vease fig. 1.1).
) que existe entre su centro y cualesquiera de sus vértices del eje focal. (vease fig. 1.1).
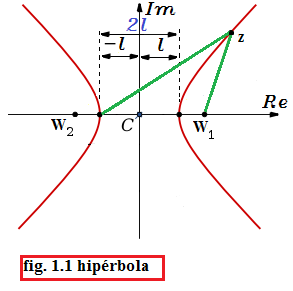
--Pedro Pablo Ramírez Martínez 23:08 17 oct 2010 (UTC)
Compleja:ej-cap1.2
Compleja:ej-cap1.3
Compleja:ej-cap1.4



























![\begin{align}
\aleph=\left|\sum_{k=1}^{n}Z_{k}W_{k}\right|^2 - \overline{Z}_{n}\overline{W}_{n} \sum_{k=1}^n Z_{k}W_{k}-Z_{n}W_{n} \sum_{l=1}^n \overline{Z}_{k}\overline{W}_{k}+ \left|Z_{n}W_{n}\right|^2 - \left[\sum_{j=1}^{n-1} Z_{j}\overline{W}_{n}\overline{Z}_{j}W_{n}- \sum_{j=1}^{n-1} Z_{j}\overline{W}_{n}\overline{Z}_{n}W_{j}- \sum_{j=1}^{n-1} Z_{n}\overline{W}_{j}\overline{Z}_{j}W_{n} + \sum_{j=1}^{n-1} Z_{n}\overline{W}_{j} \overline{Z}_{n}W_{j}\right] + \left|W_{n}\right|^2 \sum_{k=1}^{n-1} \left|Z_{k}\right|^2 + \left|Z_{n}\right|^2 \sum_{l=1}^{n-1} \left|W_{l} \right|^2 + \left|Z_{n}\right|^2 \left|W_{n}\right|^2
\qquad (xi)\\
\end{align}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/58db6fac073a7e82f0f422967dcbfe5cdc665a23)



















![z{}_{1}=r_{1}\exp\left[i\theta_{1}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8b7b3f1d69c234a74d54f14d70186f5ca86bd6f7)
![z{}_{2}=r_{2}\exp\left[i\theta_{2}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4db18bcda7bf995ff8a7fec3c366ed236215afa9)
![\left|r_{1}\exp\left[i\theta_{1}\right]+r_{2}\exp\left[i\theta_{2}\right]\right|=\left|r_{1}\exp\left[i\theta_{1}\right]\right|+\left|r_{2}\exp\left[i\theta_{2}\right]\right|](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/56fafaf6255666ab3f34d5d9a837277930b43c9b)
![\left|r_{1}\exp\left[i\theta_{1}\right]+r_{2}\exp\left[i\theta_{2}\right]\right|^{2}=\left(\left|r_{1}\exp\left[i\theta_{1}\right]\right|+\left|r_{2}\exp\left[i\theta_{2}\right]\right|\right)^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f83de2b8e9652280f2584e3e6d734365ecfac708)
![\left(r_{1}\exp\left[i\theta_{1}\right]+r_{2}\exp\left[i\theta_{2}\right]\right)\left(r_{1}\exp\left[-i\theta_{1}\right]+r_{2}\exp\left[-i\theta_{2}\right]\right)=\left(\left|r_{1}\exp\left[i\theta_{1}\right]\right|+\left|r_{2}\exp\left[i\theta_{2}\right]\right|\right)^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cfba0cc7436409d4ee730e76550daf972d7e7557)
![r_{1}^{2}+r_{1}r_{2}\exp i\left[\theta_{1}-\theta_{2}\right]+r_{1}r_{2}\exp i\left[\theta_{2}-\theta_{1}\right]+r_{2}^{2}=r_{1}^{2}+2r_{1}r_{2}+r_{2}^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e3ea0dd81ca24c826831dc913c1ebc11780c20b2)

![r_{1}r_{2}\left(\exp i\left[\theta_{1}-\theta_{2}\right]+\exp i\left[\theta_{2}-\theta_{1}\right]\right)=2r_{1}r_{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0f483bce045264bc22ff558e17f2ec9cac68edf1)
![\exp i\left[\theta_{1}-\theta_{2}\right]+\exp i\left[\theta_{2}-\theta_{1}\right]=2](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/39422f6b1cf69e35fff1025499f8acab5c4f7e09)












































