Diferencia entre revisiones de «Compleja:Zill-Cap1.5»
(Página creada con «Category:Compleja Ejercicios del capítulo 1, sección 5 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan. ---- == Sección 1.5 =...») |
|||
| (No se muestran 61 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
[[Category:Compleja]] | [[Category:Compleja]] | ||
Ejercicios del capítulo 1, sección 5 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan. | Ejercicios del capítulo 1 Números complejos y el plano complejo, sección 5 Conjuntos de puntos en el plano complejo del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan. | ||
---- | ---- | ||
| Línea 11: | Línea 12: | ||
=== Ejercicio 1 === | === Ejercicio 1 === | ||
''' | '''Trace la gráfica de la ecuación dada en el plano complejo.''' | ||
$\left|z-4+3i\right|=5$ | |||
'''Procedimiento''' | |||
Tomando a $z=x+iy$ | Tomando a $z=x+iy$ | ||
| Línea 42: | Línea 35: | ||
Que describe una circunferencia de radio $r=5$ y centro $(4,-3)$. | Que describe una circunferencia de radio $r=5$ y centro $(4,-3)$. | ||
'''Gráfica''' | |||
[[Imagen:Grafica_Zill_1.5,_Ejercicio_1.svg|400px|thumb|center| Ejercicio 1. La región descrita esta dada por la circunferencia de '''radio 5''' y centro en $(4,-3i)$ En el plano complejo]] | |||
---- | |||
Resuelto por:--[[Usuario:Luis Santos|Luis Santos]] ([[Usuario discusión:Luis Santos|discusión]]) 12:41 15 mayo 2015 (CDT) | |||
---- | |||
=== Ejercicio 2 === | |||
'''Trace la gráfica de la ecuación dada en el plano complejo.''' | |||
$\left|z+2+2i\right|=2$ | $\left|z+2+2i\right|=2$ | ||
'''Procedimiento''' | |||
Se puede escribir: | |||
$\left|x+iy+2+2i\right|=2$ | $\left|x+iy+2+2i\right|=2$ | ||
| Línea 54: | Línea 58: | ||
$\left|(x+2)+i(y+2)\right|=2$ | $\left|(x+2)+i(y+2)\right|=2$ | ||
Empleando la | Empleando la definición de norma: | ||
$(x+2)^{2}+(y+2)^{2}=4$ | $(x+2)^{2}+(y+2)^{2}=4$ | ||
| Línea 60: | Línea 64: | ||
Que describe una circunferencia de radio $r=2$ y centro en $(-2,-2)$ | Que describe una circunferencia de radio $r=2$ y centro en $(-2,-2)$ | ||
'''Gráfica''' | |||
[[Imagen:Grafica Zill 1.5, Ejercicio 2.svg|400px|thumb|center| Ejercicio 2. La región descrita esta dada por la circunferencia de '''radio 2''' y centro en $(-2,-2i)$ En el plano complejo]] | |||
---- | |||
Resuelto por:--[[Usuario:Luis Santos|Luis Santos]] ([[Usuario discusión:Luis Santos|discusión]]) 12:41 15 mayo 2015 (CDT) | |||
---- | |||
=== Ejercicio 3 === | |||
'''Trace la gráfica de la ecuación dada en el plano complejo.''' | |||
'''\[ | |||
|z+3i|=2 | |||
\]''' | |||
'''Procedimiento''' | |||
Tomando | |||
\[ | |||
z=x+iy | |||
\] | |||
\[ | |||
|x+iy+3i|=2 | |||
\] | |||
$ | de la definición de norma $|a+ib|=\sqrt{a^{2}+b^{2}}$ tenemos | ||
\[ | |||
\sqrt{\left(x\right)^{2}+\left(y+3\right)^{2}}=2 | |||
\] | |||
elecando todo al cuadrado tenemos | |||
\[ | |||
\left(x\right)^{2}+\left(y+3\right)^{2}=(2)^{2} | |||
\] | |||
Que describe una circunferencia de radio r=2 y centro $(0,-3)$. | |||
'''Gráfica''' | |||
[[Imagen:Grafica Zill 1.5, Ejercicio 3.svg|400px|thumb|center| Ejercicio 3. La región descrita esta dada por la circunferencia de '''radio 2''' y centro en $(0,-3i)$ En el plano complejo]] | |||
----- | |||
---- | |||
Resuelto por:--[[Usuario:Martin Flores Molina|Martin Flores Molina]] ([[Usuario discusión:Martin Flores Molina|discusión]]) 16:15 15 mayo 2015 (CDT) | |||
----- | |||
===Ejercicio 4=== | |||
'''Trace la gráfica de la ecuación dada en el plano complejo.''' | |||
$|2z-1|=4$ | |||
'''Procedimiento''' | |||
Definiendo a z como $z=x+yi$ del ejercicio tenemos que $|2(x+yi)-1|=4$ | |||
Entonces : | |||
$|2(x+iy)-1|=4$ | |||
$|(2x+2yi)-1|=4$ | |||
| | |||
Entonces sabiendo que $|x+yi|=\sqrt{x^{2}+y^{2}}$ | |||
Tenemos que: | |||
$\sqrt{(2x-1)^{2}+(2y)^{2}}=4$ | |||
\sqrt{ | |||
Elevando al cuadrado: | |||
$(2x-1)^{2}+(2y)^{2}=16$ | |||
Desarrollando los cuadrados: | |||
$4x^{2}-4x+1+4y^{2}=16$ | |||
Al dividir todo entre 4. | |||
$x^{2}-x+\frac{1}{4}+y^{2}=4$ | |||
Completando el cuadrado: | |||
$\left (x-\frac{1}{2} \right )^{2}+y^{2}=2^{2}$ | |||
Esta ecuación es la de un circulo centrado en $(\frac{1}{2},0)$ y de radio 2 | |||
'''Gráfica''' | |||
[[Imagen:Grafica Zill 1.5, Ejercicio 4.svg|400px|thumb|center| Ejercicio 4. La región descrita esta dada por la circunferencia de '''radio 2''' y centro en $(\frac{1}{2},0)$ En el plano complejo]] | |||
----- | |||
Realizado por: *****[[Usuario:A. Martín R. Rabelo|A. Martín R. Rabelo]] ([[Usuario discusión:A. Martín R. Rabelo|discusión]]) 17:50 15 mayo 2015 (CDT) | |||
---- | ---- | ||
| Línea 172: | Línea 174: | ||
=== Ejercicio 7 === | === Ejercicio 7 === | ||
'''Trace la gráfica de la ecuación dada en el plano complejo.''' | |||
'''Procedimiento''' | |||
$Im\left(\bar{z}+3i\right)=6$ | $Im\left(\bar{z}+3i\right)=6$ | ||
| Línea 183: | Línea 187: | ||
A continuación se muestra una gráfica de la parte imaginaria de la primera ecuación mostrada: | A continuación se muestra una gráfica de la parte imaginaria de la primera ecuación mostrada: | ||
'''Gráfica''' | |||
[[Archivo:Captura de pantalla 2015-05-19 a la(s) 18.41.46.png]] | [[Archivo:Captura de pantalla 2015-05-19 a la(s) 18.41.46.png]] | ||
'''Falta poner en svg''' | |||
----- | |||
Resuelto por: | Resuelto por: | ||
| Línea 192: | Línea 201: | ||
[[Usuario:Alejandro Juárez Toribio|Alejandro Juárez Toribio]] ([[Usuario discusión:Alejandro Juárez Toribio|discusión]]) 18:57 19 mayo 2015 (CDT) | [[Usuario:Alejandro Juárez Toribio|Alejandro Juárez Toribio]] ([[Usuario discusión:Alejandro Juárez Toribio|discusión]]) 18:57 19 mayo 2015 (CDT) | ||
----- | |||
=== Ejercicio 8 === | |||
'''Trace la gráfica de la ecuación dada en el plano complejo.''' | |||
$Im(z-i)=Re(z+4-3i)$ | |||
'''Procedimiento''' | |||
$Im(z-i)=Re(z+4-3i)$ | |||
$Im(x+(y-1)i)=Re((x+4)+(y-3)i)$ | |||
$y-1=x+4$ | |||
$x-y+4+1=0$ | |||
$x-y+5=0$ | |||
$y=x+5$ | |||
Lo cual es la ecuación de una recta. | |||
'''Gráfica''' | |||
[[Imagen:Grafica Zill 1.5, Ejercicio 8.svg|400px|thumb|center| Ejercicio 8. La región descrita esta dada por la recta que corta la parte real en $Re(z)=-5$ y en el eje imaginario $Im(z)=5$. En el plano complejo]] | |||
---- | |||
Resuelto por:--[[Usuario:Luis Santos|Luis Santos]] ([[Usuario discusión:Luis Santos|discusión]]) 12:41 15 mayo 2015 (CDT) | |||
---- | |||
=== Ejercicio 11 === | |||
'''Trace la gráfica de la ecuación dada en el plano complejo.''' | |||
$Re(z^{2})=1$ | |||
'''Procedimiento''' | |||
Sea $z=x+iy$, se tiene que $z^{2}=x^{2}-2xyi-y^{2}$ | |||
Por lo que | |||
$Re(z^{2})=Re((x+iy)^{2}=x^{2}-y^{2}$ | |||
Finalmente se tiene | |||
$x^{2}-y^{2}=1$ | |||
Una hipérbola equilátera centrada en el origen. | |||
'''Gráfica''' | |||
[[Imagen:Grafica Zill 1.5, Ejercicio 11.svg|400px|thumb|center| Ejercicio 11. La región descrita esta dada por Una hipérbola equilátera centrada en el origen. En el plano complejo]] | |||
---- | |||
Resuelto por:--[[Usuario:Luis Santos|Luis Santos]] ([[Usuario discusión:Luis Santos|discusión]]) 12:41 15 mayo 2015 (CDT) | |||
---- | ---- | ||
=== Ejercicio 33 === | === Ejercicio 33 === | ||
En la página 31 dijimos que si $\rho_{1}>0$, entonces el conjunto de puntos que satisface | |||
$\rho_{1}<|z-z_{0}|$ es el exterior del círculo de radio $\rho_{1}$ centrado en $z_0$. | |||
.En general, describe el conjunto si $\rho_{1}=0$. | |||
En particular, describa el conjunto definido por $|z+2-5i|>0$. | |||
'''Solución''' | |||
$\rho_{1}=0$ $\Rightarrow$ $|z-z_{0}|>0$ si $z=z_{0}$ $\Rightarrow|0|>0$ | $\rho_{1}=0$ $\Rightarrow$ $|z-z_{0}|>0$ si $z=z_{0}$ $\Rightarrow|0|>0$ | ||
lo cual carece sentido. | lo cual carece sentido. | ||
La | |||
La condición se cumple para cualquier par de números distintos complejos, | |||
el conjunto de puntos es todo el plano complejo salvo un punto, $z_{0}$, | el conjunto de puntos es todo el plano complejo salvo un punto, $z_{0}$, | ||
podemos acercarnos todo lo que queramos, pero no podemos llegar a | podemos acercarnos todo lo que queramos, pero no podemos llegar a | ||
tocar $z_{0}$, si | tocar $z_{0}$, si así fuera tendríamos incongruencias. | ||
Ahora bien, bajo el caso particular | Ahora bien, bajo el caso particular | ||
| Línea 215: | Línea 289: | ||
llevándolo a la forma $|z-z_{0}|>0$, tendríamos que $z_{0}=-2+5i$ | |||
De acuerdo a lo dicho anteriormente, el conjunto de puntos que cumplen | De acuerdo a lo dicho anteriormente, el conjunto de puntos que cumplen | ||
con esa | con esa condición es todo el plano complejo, salvo un punto en ese | ||
caso $z_{0}=-2+5i$, podemos acercarnos todo lo que queramos, pero | caso $z_{0}=-2+5i$, podemos acercarnos todo lo que queramos, pero | ||
no tocarlo. | no tocarlo. | ||
[[Imagen:Grafica Zill 1.5, Ejercicio 30.svg|400px|thumb|center| Ejercicio 33. La región descrita esta dada por todo el plano complejo excepto por el punto $z_0=-2+5i$]] | |||
---- | |||
[[Usuario:Jose Emmanuel Flores Calderón|Jose Emmanuel Flores Calderón]] ([[Usuario discusión:Jose Emmanuel Flores Calderón|discusión]]) 01:49 15 mayo 2015 (CDT) | [[Usuario:Jose Emmanuel Flores Calderón|Jose Emmanuel Flores Calderón]] ([[Usuario discusión:Jose Emmanuel Flores Calderón|discusión]]) 01:49 15 mayo 2015 (CDT) | ||
---- | ---- | ||
| Línea 233: | Línea 311: | ||
'''b) Hacer una lista de cinco conjuntos del plano complejo que sean no-conectados.''' | '''b) Hacer una lista de cinco conjuntos del plano complejo que sean no-conectados.''' | ||
'''Inciso a''' | |||
a) Para los conectados tenemos: | a) Para los conectados tenemos: | ||
$0<|z|<\rho$; $\rho \epsilon R$ | $0<|z|<\rho$; $\rho \epsilon R$ | ||
| Línea 250: | Línea 330: | ||
$4<Re(z)\leq 5$ | $4<Re(z)\leq 5$ | ||
'''Inciso b''' | |||
b) Para los no-conectados: | b) Para los no-conectados: | ||
| Línea 270: | Línea 350: | ||
$Im(z)>-1 \cup |z-(3-5i)|<0.1$ | $Im(z)>-1 \cup |z-(3-5i)|<0.1$ | ||
[[Usuario:Oscar Javier Gutierrez Varela|Oscar Javier Gutierrez Varela]] ([[Usuario discusión:Oscar Javier Gutierrez Varela|discusión]]) 14:35 15 mayo 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Oscar Javier Gutierrez Varela|Oscar Javier Gutierrez Varela]] ([[Usuario discusión:Oscar Javier Gutierrez Varela|discusión]]) 14:35 15 mayo 2015 (CDT) | |||
---- | ---- | ||
=== Ejercicio 40=== | === Ejercicio 40=== | ||
'''Describa el conjunto | '''Describa el conjunto sombreado en la siguiente figura:''' | ||
[[Archivo:P1.5.40.png]] | [[Archivo:P1.5.40.png]] | ||
| Línea 291: | Línea 372: | ||
\] | \] | ||
Es decir: | Es decir: | ||
'''Conclusión''' | |||
\[ | \[ | ||
\left\{z:r\leq|z|\leq R \:\: AND \:\: Re\left(z\right)\geq0 \right\} | \left\{z:r\leq|z|\leq R \:\: AND \:\: Re\left(z\right)\geq0 \right\} | ||
| Línea 298: | Línea 382: | ||
\left\{z:r\leq|z|\leq R \:\: AND \:\: 0\leq Arg\left(z\right)\leq\pi \right\} | \left\{z:r\leq|z|\leq R \:\: AND \:\: 0\leq Arg\left(z\right)\leq\pi \right\} | ||
\] | \] | ||
--[[Usuario:Tlacaelel Cruz|Tlacaelel Cruz]] ([[Usuario discusión:Tlacaelel Cruz|discusión]]) 20:31 19 mayo 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:Tlacaelel Cruz|Tlacaelel Cruz]] ([[Usuario discusión:Tlacaelel Cruz|discusión]]) 20:31 19 mayo 2015 (CDT) | |||
---- | ---- | ||
Revisión actual - 20:46 2 mar 2023
Ejercicios del capítulo 1 Números complejos y el plano complejo, sección 5 Conjuntos de puntos en el plano complejo del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 1.5
Ejercicio 1
Trace la gráfica de la ecuación dada en el plano complejo.
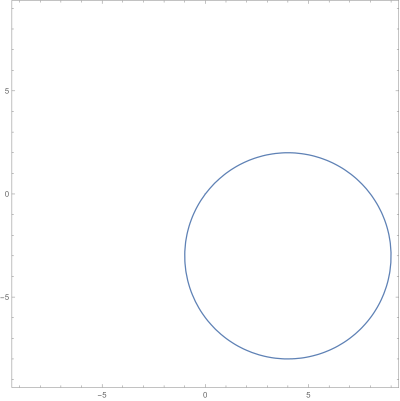
$\left|z-4+3i\right|=5$
Procedimiento
Tomando a $z=x+iy$
$\left|x+iy-4+3i\right|=5$
$\left|(x-4)+i(y+3)\right|=5$
De la definición de norma $\left|a+ib\right|=\sqrt{a^{2}+b^{2}}$, se tiene:
$\sqrt{(x-4)^{2}+(y+3)^{2}}=5$
Es decir.
$(x-4)^{2}+(y+3)^{2}=25$
Que describe una circunferencia de radio $r=5$ y centro $(4,-3)$.
Gráfica
Resuelto por:--Luis Santos (discusión) 12:41 15 mayo 2015 (CDT)
Ejercicio 2
Trace la gráfica de la ecuación dada en el plano complejo.
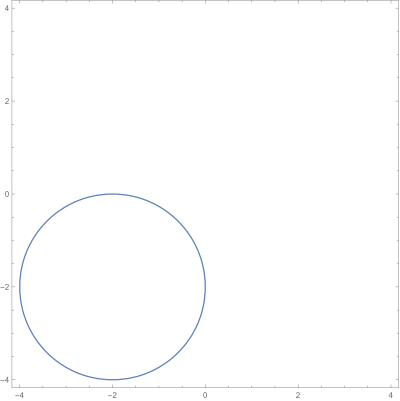
$\left|z+2+2i\right|=2$
Procedimiento
Se puede escribir:
$\left|x+iy+2+2i\right|=2$
$\left|(x+2)+i(y+2)\right|=2$
Empleando la definición de norma:
$(x+2)^{2}+(y+2)^{2}=4$
Que describe una circunferencia de radio $r=2$ y centro en $(-2,-2)$
Gráfica
Resuelto por:--Luis Santos (discusión) 12:41 15 mayo 2015 (CDT)
Ejercicio 3
Trace la gráfica de la ecuación dada en el plano complejo.
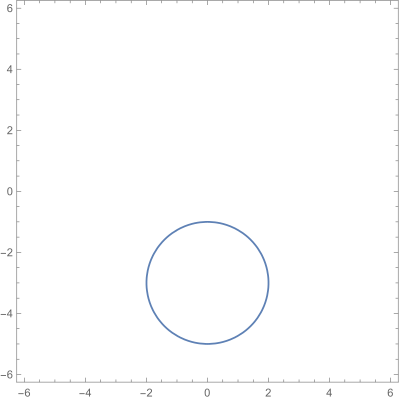
\[ |z+3i|=2 \]
Procedimiento
Tomando \[ z=x+iy \]
\[
|x+iy+3i|=2
\]
de la definición de norma $|a+ib|=\sqrt{a^{2}+b^{2}}$ tenemos
\[ \sqrt{\left(x\right)^{2}+\left(y+3\right)^{2}}=2 \]
elecando todo al cuadrado tenemos
\[ \left(x\right)^{2}+\left(y+3\right)^{2}=(2)^{2} \]
Que describe una circunferencia de radio r=2 y centro $(0,-3)$.
Gráfica
Resuelto por:--Martin Flores Molina (discusión) 16:15 15 mayo 2015 (CDT)
Ejercicio 4
Trace la gráfica de la ecuación dada en el plano complejo.
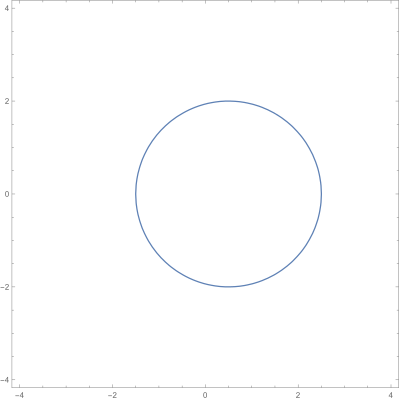
$|2z-1|=4$
Procedimiento
Definiendo a z como $z=x+yi$ del ejercicio tenemos que $|2(x+yi)-1|=4$
Entonces :
$|2(x+iy)-1|=4$
$|(2x+2yi)-1|=4$
Entonces sabiendo que $|x+yi|=\sqrt{x^{2}+y^{2}}$
Tenemos que:
$\sqrt{(2x-1)^{2}+(2y)^{2}}=4$
Elevando al cuadrado:
$(2x-1)^{2}+(2y)^{2}=16$
Desarrollando los cuadrados:
$4x^{2}-4x+1+4y^{2}=16$
Al dividir todo entre 4.
$x^{2}-x+\frac{1}{4}+y^{2}=4$
Completando el cuadrado:
$\left (x-\frac{1}{2} \right )^{2}+y^{2}=2^{2}$
Esta ecuación es la de un circulo centrado en $(\frac{1}{2},0)$ y de radio 2
Gráfica
Realizado por: *****A. Martín R. Rabelo (discusión) 17:50 15 mayo 2015 (CDT)
Ejercicio 7
Trace la gráfica de la ecuación dada en el plano complejo.
Procedimiento
$Im\left(\bar{z}+3i\right)=6$
Si $z=x+iy$ entonces:
$Im\left(\bar{z}+3i\right)=Im\left(x-iy+3i\right)=3-y=6$
Por lo que $y=-3$
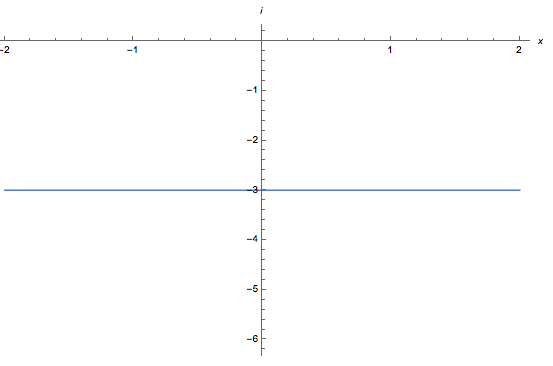
A continuación se muestra una gráfica de la parte imaginaria de la primera ecuación mostrada:
Gráfica
Falta poner en svg
Resuelto por:
Alejandro Juárez Toribio (discusión) 18:57 19 mayo 2015 (CDT)
Ejercicio 8
Trace la gráfica de la ecuación dada en el plano complejo.
$Im(z-i)=Re(z+4-3i)$
Procedimiento
$Im(z-i)=Re(z+4-3i)$
$Im(x+(y-1)i)=Re((x+4)+(y-3)i)$
$y-1=x+4$
$x-y+4+1=0$
$x-y+5=0$
$y=x+5$
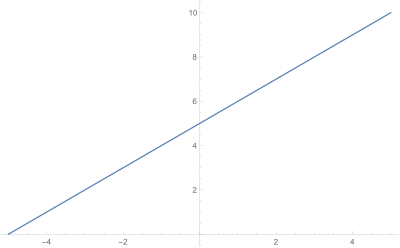
Lo cual es la ecuación de una recta.
Gráfica
Resuelto por:--Luis Santos (discusión) 12:41 15 mayo 2015 (CDT)
Ejercicio 11
Trace la gráfica de la ecuación dada en el plano complejo.
$Re(z^{2})=1$
Procedimiento
Sea $z=x+iy$, se tiene que $z^{2}=x^{2}-2xyi-y^{2}$
Por lo que
$Re(z^{2})=Re((x+iy)^{2}=x^{2}-y^{2}$
Finalmente se tiene
$x^{2}-y^{2}=1$
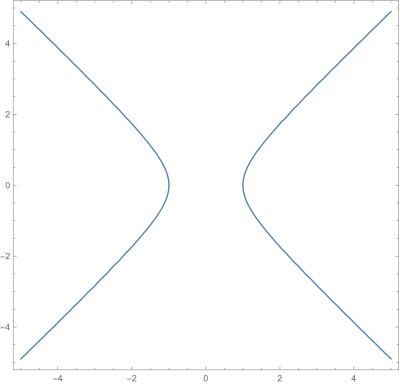
Una hipérbola equilátera centrada en el origen.
Gráfica
Resuelto por:--Luis Santos (discusión) 12:41 15 mayo 2015 (CDT)
Ejercicio 33
En la página 31 dijimos que si $\rho_{1}>0$, entonces el conjunto de puntos que satisface $\rho_{1}<|z-z_{0}|$ es el exterior del círculo de radio $\rho_{1}$ centrado en $z_0$. .En general, describe el conjunto si $\rho_{1}=0$. En particular, describa el conjunto definido por $|z+2-5i|>0$.
Solución
$\rho_{1}=0$ $\Rightarrow$ $|z-z_{0}|>0$ si $z=z_{0}$ $\Rightarrow|0|>0$ lo cual carece sentido.
La condición se cumple para cualquier par de números distintos complejos,
el conjunto de puntos es todo el plano complejo salvo un punto, $z_{0}$,
podemos acercarnos todo lo que queramos, pero no podemos llegar a
tocar $z_{0}$, si así fuera tendríamos incongruencias.
Ahora bien, bajo el caso particular \[ |z+2-5i|>0 \]
llevándolo a la forma $|z-z_{0}|>0$, tendríamos que $z_{0}=-2+5i$
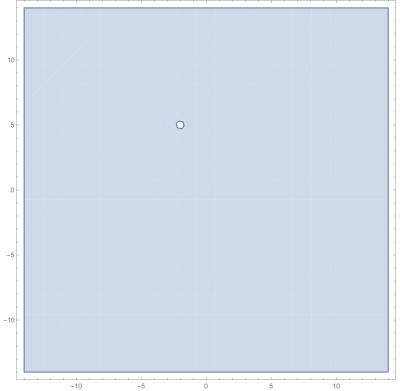
De acuerdo a lo dicho anteriormente, el conjunto de puntos que cumplen con esa condición es todo el plano complejo, salvo un punto en ese caso $z_{0}=-2+5i$, podemos acercarnos todo lo que queramos, pero no tocarlo.
Jose Emmanuel Flores Calderón (discusión) 01:49 15 mayo 2015 (CDT)
Ejercicio 35
Usando notación compleja y desigualdades en las partes a) y b):
a) Hacer una lista de cinco conjuntos del plano complejo que sean conectados.
b) Hacer una lista de cinco conjuntos del plano complejo que sean no-conectados.
Inciso a
a) Para los conectados tenemos:
$0<|z|<\rho$; $\rho \epsilon R$
$|z-z_0|\leq \rho$ con $z_0=a+ib$
$|z-z_0|>\rho$
$\beta \leq |z-z_0|<\rho$; $\beta \epsilon R$
$4<Re(z)\leq 5$
Inciso b
b) Para los no-conectados:
Para todo número $z$ que satisfaga las siguientes condiciones;
$Re(z)\neq \rho$; $\rho \epsilon R$
$Im(z)\neq \rho$
$|z-(1-2i)|\leq 5 \cup |z-(7+23i)|<1$
$Re(z)\leq 2 \cup |z-(5+i)|<0.01$
$Im(z)>-1 \cup |z-(3-5i)|<0.1$
Realizado por:Oscar Javier Gutierrez Varela (discusión) 14:35 15 mayo 2015 (CDT)
Ejercicio 40
Describa el conjunto sombreado en la siguiente figura:
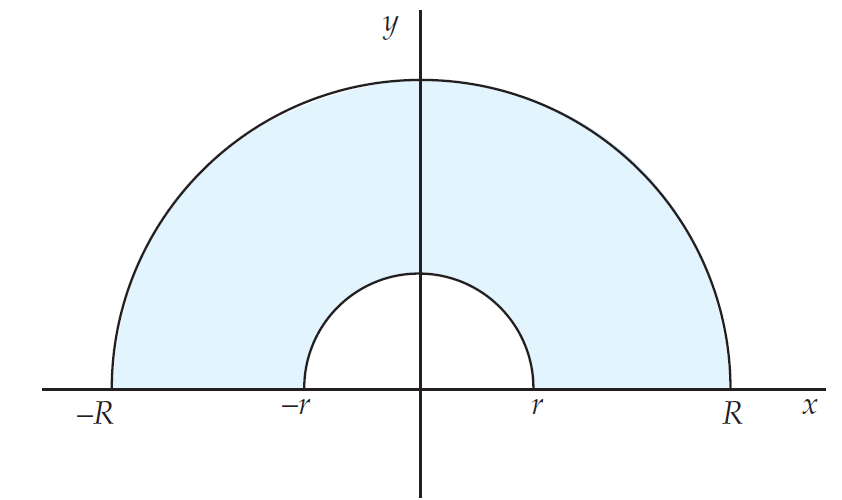
Se ve que la magnitud del número complejo esta entre r y R, es decir: \[ z:r \leq |z|\leq R \] Y que además el argumento va de 0 a $\pi$ \[ z:0\leq Arg\left(z\right)\leq\pi \] O bien la parte real es positiva \[ z:Re\left(z\right)\geq0 \] Es decir:
Conclusión
\[ \left\{z:r\leq|z|\leq R \:\: AND \:\: Re\left(z\right)\geq0 \right\} \]
\[ \left\{z:r\leq|z|\leq R \:\: AND \:\: 0\leq Arg\left(z\right)\leq\pi \right\} \]
Realizado por: Tlacaelel Cruz (discusión) 20:31 19 mayo 2015 (CDT)