Algebra de escatores
Se pueden establecer dos sistemas algebráicos, uno de escatores reales y otro de escatores imaginarios.
La interpretación geométrica de éstas álgebras es motivo de estudio y de perplejidad.
Los escatores reales
mfg-wiki 22:16 11 ene 2010 (UTC)
Escatores
Un escator o su plural escatores son elementos de un álgebra de reciente creación que puede considerarse como un sistema de números hipercomplejos.
- escatores
- son elementos de un álgebra que contienen una componente escalar y varias componentes con dirección.
- El nombre de esca-tor proviene de la contracción de esca-lar y direc-tor pues contiene componentes de ambos tipos.
- Las componentes escalares corresponden a los números reales mientras que las componentes directoras, si bien poseen dirección como los vectores no comparten las mismas reglas ni de producto ni de magnitud.
- En el Algebra de escatores pueden definirse operaciones de suma y producto.
- Pueden crearse Fractales con distintos mapeos, en particular el mapeo cuadrático.
Los escatores imaginarios en 1+2 dimensiones con magnitud constante exhiben una figura cuya proyección en dos planos es un círculo mientras que en el tercer plano es un cuadrado.
Aportación por usuarios: Manuel-tepal 22:49 9 sep 2007 (CDT) ,mfg-wiki 22:17 11 ene 2010 (UTC) mfg-wiki 16:54 24 ago 2010 (UTC)
Escatores reales: introducción (En Ingles)
A hyperbolic non distributive algebra in $1+2$ dimensions
Abstract
We introduce a non distributive algebra over the reals in dimensions 1 + 2 that in the special 1 + 1 case recovers the hyperbolic complex numbers. The algebra contains divisors of zero that can be avoided by introducing the necessary conditions. Under these conditions, the proposed addition and product operations satisfy group properties. More stringent conditions sufficient to satisfy group properties separate the algebra in two subspaces. As an example, the composition of velocities in a deformed Lorentz metric is presented. In this approach, Minkowski light cones are deformed into light pyramids.
Introduction
Systems of hypercomplex numbers, such as quaternions or the octonions are algebras over the real numbers that lack some properties for their product, either commutativity or associativity. %% The search for higher dimensional algebras retaining some of these properties is severely limited by Frobenius and Hurwitz theorems. The former theorem establishes that finite-dimensional associative division algebras over real numbers must be isomorphic to the real $\mathbb{R}$, complex $\mathbb{C}$ or quaternion $\mathbb{H}$ algebras with dimensions 1, 2, and 4, respectively. The latter theorem states that the only normed division algebras over $\mathbb{R}$ are the real $\mathbb{R}$, complex $\mathbb{C}$, quaternion $\mathbb{H}$ and the octonions $\mathbb{O}$. Of these algebras quaternions are no longer commutative and octonions are neither commutative nor associative.
These theorems require the absence of zero divisors. If distributivity and associativity are fulfilled then the algebra (except for reals and complex) is either not commutative or has divisors of zero. A theorem due to Scheffers (1893) establishes that for distributive systems with unity, the differential calculus does exist only if the systems are commutative \cite{catoni2008}. Differential calculus is crucial in order to define functions of a hypercomplex variable and to associate them with the infinite-dimensional Lie group of functional mappings. For this reason there has been renewed interest in commutative algebras such as Segre's commutative quaternions although they possess zero divisors \cite{catoni2006_1}.
Two dimensional hypercomplex numbers contain a real component and an imaginary component. Depending on the product definition of imaginary unit, these hypercomplex numbers are elliptic, parabolic or hyperbolic. Elliptic hypercomplex numbers are the complex numbers, a commutative division algebra. Hyperbolic hypercomplex two dimensional numbers or split-complex numbers form an associative and commutative algebra that is tailor made to describe Minkowski space-time special relativity in $1+1$ dimensions. Higher $N$ dimensional hyperbolic numbers have been explored using direct product rings with zero divisors as a basis \cite{fjelstad+gal1998}.
In this paper we introduce an algebra in $1+2$ dimensions that degenerates to hyperbolic $\mathbb{H}_{2}$ numbers when only one director component is present. This algebra, that we call \emph{hyperbolic scator} or \emph{real scator} algebra, and we will see that its product is commutative and associative. However, as we shall see, the product does not distribute over addition but in some special cases. Moreover, the product has zero divisors and it is defined only on a proper subset of ${\mathbb{R}}^{3}$. %% The construction can be easily generalized to any dimension, but many of its properties are straightforward generalizations of the $3$-dimensional case.
Three-dimensional scator algebra
Consider the set of all expressions of the form \[ \overset{o}{\varphi}=(f_{0};f_{1},f_{2})\in{\mathbb{R}}^{1+2}\qquad\text{with} {f_{i}\in{\mathbb{R}}}, \] with addition defined componentwise. The product of two elements $\overset{o}{\alpha}=(a_{0};a_{1},a_{2}),\overset{o}{\beta}=(b_{0};b_{1},b_{2})$ in ${\mathbb{R}}^{1+2}$, say $\overset{o}{\alpha}\cdot\overset{o}{\beta}=\overset{o}{\gamma}=(g_{0};g_{1},g_{2})\in{\mathbb{R}}^{1+2}$ is given by
$g_{0} = a_{0}b_{0}+a_{1}b_{1}+a_{2}b_{2}+\frac{a_{1}b_{1}a_{2}b_{2}}{a_{0}b_{0}}=a_{0}b_{0}\Big(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\Big)\Big(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\Big)\qquad\quad\label{eq:product def scalar}$
$g_{1} = \Big(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\Big)(a_{0}b_{1}+a_{1}b_{0})\label{eq:product def dir1}$
$g_{2} = \Big(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\Big)(a_{0}b_{2}+a_{2}b_{0}).\label{eq:product def dir2}$
In this formulation, the condition for the definition of a product is that \begin{equation} a_{0}b_{0}\neq0\quad\textrm{if}\quad a_{1}b_{1}\neq0\;\text{and}\; a_{2}b_{2}\neq0.\label{eq:condexistencia producto} \end{equation} We call the elements $\overset{o}{\varphi}=(f_{0};f_{1},f_{2})$ \textit{scators} and we will show that, with some restrictions they form a weak hypercomplex system. The scator elements are labeled with an '\textbackslash{}overset\{o\}'. This decoration is omitted when no confusion arises with the scator components.
To begin with, it is immediate that:
(1): We can identify the elements of the field ${\mathbb{R}}$ with the scators of the form $\overset{o}{\alpha}=(a_{0};0,0)$, since addition is componentwise and multiplication of two of these elements, say $\overset{o}{\alpha}$ and $\overset{o}{\beta}=(b_{0};0,0)$, assuming that $a_{0}b_{0}\neq0$, is given by \[ \overset{o}{\alpha}\cdot\overset{o}{\beta}=(a_{0};0,0)\cdot(b_{0};0,0)=(a_{0}b_{0};(1+0)(0),(1+0)(0))=(a_{0}b_{0};0,0). \] Sometimes we will use the identification $(a_{0};0,0)=a_{0}$ and call the scator $(a_{0};0,0)$ a \textit{scalar}. \medskip{}
(2): If $\overset{o}{\alpha}=(a_{0};0,0)$ is identified
with $a_{0}\in{\mathbb{R}}-\{0\}$ and if $\overset{o}{\beta}=(b_{0};b_{1},b_{2})$
is any scator (with $a_{0}b_{0}\neq0$), we have
\begin{align*} \overset{o}{\alpha}\cdot\overset{o}{\beta} & =(a_{0};0,0)\cdot(b_{0};b_{1},b_{2})\\ & =(a_{0}b_{0};(1)(a_{0}b_{1}+0\cdot b_{0}),(1)(a_{0}b_{2}+0b_{0}))\\ & =(a_{0}b_{0};a_{0}b_{1},a_{0}b_{2}). \end{align*} In other words, the product of a scalar with a scator is componentwise. \medskip{}
(3): In particular, for the scalar $(1;0,0)=1\in{\mathbb{R}}$ and for any scator $\overset{o}{\varphi}=(f_{0};f_{1},f_{1})$ we have that $1$ is neutral, i.e., $1\cdot\overset{o}{\varphi}=\overset{o}{\varphi}$. \medskip{}
(4) The product of a scalar with the sum of two scators is distributive.
(5): The product of the sum of two scalars with a scator is distributive.
(6): Whenever is defined, the product of two scators is commutative. This follows from the symmetry of the definition of product.
These remarks mean that the set of scators behaves as an algebra over the real field. However, we have the restriction for the product and, as we shall see, in general the scator product is not distributive, and there are zero divisors.
Conjugate and norm
The conjugate of $\overset{o}{\varphi}=(f_{0};f_{1},f_{2})$ is \[ \overset{o}{\varphi}^{*}=(f_{0};-f_{1},-f_{2}) \] and it is immediate that $(\overset{o}{\varphi}^{*})^{*}=\overset{o}{\varphi}$, $(\overset{o}{\alpha}+\overset{o}{\beta})^{*}=\overset{o}{\alpha}^{*}+\overset{o}{\beta}^{*}$ and $(\overset{o}{\alpha}\overset{o}{\beta})^{*}=\overset{o}{\alpha}^{*}\overset{o}{\beta}^{*}$. Moreover, $\overset{o}{\varphi}\in{\mathbb{R}}$ if and only if $\overset{o}{\varphi}^{*}=\overset{o}{\varphi}$.
The \textit{norm} or \textit{modulus} squared of $\overset{o}{\varphi}=(f_{0};f_{1},f_{2})$ is \begin{equation} \|\overset{o}{\varphi}\|^{2}=\overset{o}{\varphi}\cdot\overset{o}{\varphi}^{*}=f_{0}^{2}\left(1-\frac{f_{1}^{2}}{f_{0}^{2}}\right)\left(1-\frac{f_{2}^{2}}{f_{0}^{2}}\right).\label{eq:sca mag} \end{equation} Thus, the squared norm of a scator is a scalar, $\|\overset{o}{\varphi}\|=\|\overset{o}{\varphi}^{*}\|$ and if $\overset{o}{\varphi}=(f_{0};f_{1},f_{2})$ we have that \[ f_{0}=\frac{1}{2}\Big(\overset{o}{\varphi}+\overset{o}{\varphi}^{*}\Big). \] Moreover, a direct computation shows that the norm of a product is the product of the norms, provided that zero divisors are excluded.
Units
Given two scators $\overset{o}{\alpha}=(a_{0};a_{1},a_{2}),\overset{o}{\beta}=(b_{0};b_{1},b_{2})$ with $a_{0}b_{0}\neq0$, for its product to be $1$ we need that the first component $g_{0}=1$ and the other components $g_{1}=g_{2}=0$:
\begin{equation} g_{0}=a_{0}b_{0}+a_{1}b_{1}+a_{2}b_{2}+\frac{a_{1}b_{1}a_{2}b_{2}}{a_{0}b_{0}}=a_{0}b_{0}\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\right)=1\label{eq:product def scalar unit} \end{equation} and the director components of the product are \begin{equation} g_{1}=\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\right)\left(b_{0}a_{1}+a_{0}b_{1}\right)=0,\label{eq:product def dir1 unit} \end{equation}
\begin{equation} g_{2}=\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)\left(b_{0}a_{2}+a_{0}b_{2}\right)=0.\label{eq:product def dir2 unit} \end{equation}
Observe now that if the components of the first factor in \eqref{eq:product def dir1 unit} and \eqref{eq:product def dir2 unit} are zero, i.e., if $\left(1+\frac{a_{j}b_{j}}{a_{0}b_{0}}\right)=0$, then the scalar component is also zero, and thus this possibility is excluded. It follows that the second factors must be zero: \[ \left(b_{0}a_{1}+a_{0}b_{1}\right)=0\Rightarrow b_{1}=-\frac{b_{0}a_{1}}{a_{0}} \] and \[ \left(b_{0}a_{2}+a_{0}b_{2}\right)=0\Rightarrow b_{2}=-\frac{b_{0}a_{2}}{a_{0}}. \] The first component becomes
\[ g_{0}=a_{0}b_{0}+a_{1}b_{1}+a_{2}b_{2}+\frac{a_{1}b_{1}a_{2}b_{2}}{a_{0}b_{0}}=a_{0}b_{0}\left(1-\left(\frac{a_{1}}{a_{0}}\right)^{2}\right)\left(1-\left(\frac{a_{2}}{a_{0}}\right)^{2}\right)=1, \] from where it follows that \[ b_{0}=\frac{1}{a_{0}\left(1-\left(\frac{a_{1}}{a_{0}}\right)^{2}\right)\left(1-\left(\frac{a_{2}}{a_{0}}\right)^{2}\right)} \] and hence \[ b_{1}=-\frac{b_{0}a_{1}}{a_{0}}=-\frac{a_{1}}{a_{0}^{2}\left(1-\left(\frac{a_{1}}{a_{0}}\right)^{2}\right)\left(1-\left(\frac{a_{2}}{a_{0}}\right)^{2}\right)} \] and \[ b_{2}=-\frac{b_{0}a_{2}}{a_{0}}=-\frac{a_{2}}{a_{0}^{2}\left(1-\left(\frac{a_{1}}{a_{0}}\right)^{2}\right)\left(1-\left(\frac{a_{2}}{a_{0}}\right)^{2}\right)}. \] Now observe that we must exclude $a_{0}=0$, $\frac{a_{1}}{a_{0}}=\pm1,\frac{a_{2}}{a_{0}}=\pm1$. We have thus shown that $\overset{o}{\beta}=(b_{0};b_{1},b_{2})$ is the inverse of $\overset{o}{\alpha}=(a_{0};a_{1},a_{2})$. This can be rewritten as follows. Consider the conjugate $\overset{o}{\alpha}^{*}=(a_{0};-a_{1},-a_{2})$ of $\overset{o}{\alpha}$. Then, the product \[ \overset{o}{\alpha}\overset{o}{\alpha}^{*}=\big(a_{0}^{2}-a_{1}^{2}-a_{2}^{2}+\frac{a_{1}^{2}a_{2}^{2}}{a_{0}^{2}};0,0\big) \] and so the inverse of $\overset{o}{\alpha}$ is \[ \overset{o}{\alpha}^{-1}=\frac{1}{a_{0}^{2}\big(1-\frac{a_{1}^{2}}{a_{0}^{2}}\big)\big(1-\frac{a_{2}^{2}}{a_{0}^{2}}\big)}\overset{o}{\alpha}^{*} \] provided that $\big(1-\frac{a_{1}^{2}}{a_{0}^{2}}\big)\big(1-\frac{a_{2}^{2}}{a_{0}^{2}}\big)\neq0$. Summarizing, the scator $\overset{o}{\alpha}=(a_{0};a_{1},a_{2})$ is a unit provided that \begin{equation} a_{0}\neq\pm a_{1},a_{0}\neq\pm a_{2},\quad a_{0}\neq0\quad\text{when}\quad a_{1}a_{2}\neq0.\label{eq:excl no unidades} \end{equation} It follows that $(\overset{o}{\alpha}^{*})^{-1}=(\overset{o}{\alpha}^{-1})^{*}$.
Zero divisors
Given two non-zero scators ${\overset{o}{\alpha}}=\left(a_{0};a_{1},a_{2}\right)$ and ${\overset{o}{\beta}}=\left(b_{0};b_{1},b_{2}\right)$ such that its product ${\overset{o}{\gamma}}={\overset{o}{\alpha}}{\overset{o}{\beta}}=\left(g_{0};g_{1},g_{2}\right)=(0;0,0)$, we want to characterize these zero divisors. From the definition of the scator product \begin{equation} g_{0}=a_{0}b_{0}+a_{1}b_{1}+a_{2}b_{2}+\frac{a_{1}b_{1}a_{2}b_{2}}{a_{0}b_{0}}=a_{0}b_{0}\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\right)=0,\label{eq:product def scalar divcero} \end{equation} where the director components of the product are \begin{equation} g_{1}=\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\right)\left(b_{0}a_{1}+a_{0}b_{1}\right)=0,\label{eq:product def dir1 divcero} \end{equation}
\begin{equation} g_{2}=\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)\left(b_{0}a_{2}+a_{0}b_{2}\right)=0.\label{eq:product def dir2 divcero} \end{equation}
Condition \eqref{eq:product def scalar divcero} is fulfilled if one of the terms between parenthesis is zero: \begin{eqnarray} a_{1}b_{1} & = & -a_{0}b_{0}\label{eq:divcero 1}\\ a_{2}b_{2} & = & -a_{0}b_{0}\label{eq:divcero 2} \end{eqnarray} Now, each of the terms between parenthesis is also a factor for a $g_{2}$ and $g_{1}$ respectively. Therefore, if both terms are zero, the three components $g_{0},g_{1},g_{2}$ are zero. Thus, two factors that satisfy \begin{equation} a_{1}b_{1}=a_{2}b_{2}=-a_{0}b_{0}\label{eq:divcero} \end{equation} are zero divisors. There is another case for $g_{0}$ to be zero, namely if $a_{0}$ or $b_{0}$ is zero. If $a_{0}=0$ in a non-zero scator $\overset{o}{\alpha}$, only one of the director components is non-zero for the product to be well-defined, say $a_{0}=0,\: a_{1}\neq0,\: a_{2}=0$. In this case, from \eqref{eq:product def dir2 divcero}, the component $g_{2}=0$ and the first component of \eqref{eq:product def dir1 divcero}, must satisfy \[ g_{1}=b_{0}a_{1}=0,\Rightarrow b_{0}=0. \]
If $b_{0}=0$, the scator ${\overset{o}{\beta}}$ must have only a non-zero component, say $b_{1}$. Then the scalar component is non-zero $g_{0}=a_{1}b_{1}$. If the non-zero component is $b_{2}$ then the components of ${\overset{o}{\gamma}}$ are zero. Summarizing ${\overset{o}{\gamma}}=\left(0;0,0\right)=\left(0;a_{1},0\right)\cdot\left(0;0,b_{2}\right)$. Another possibility with these requirements is when ${\overset{o}{\alpha}}=\left(0;0,a_{2}\right)$ and ${\overset{o}{\beta}}=\left(0;b_{1},0\right)$. These two cases are included in \eqref{eq:divcero 1}, \eqref{eq:divcero 2}, because if $a_{0}=b_{0}=0$ then $a_{1}b_{1}=0$ y $a_{2}b_{2}=0$ and these are non-zero if $a_{1}=b_{2}=0$ or $a_{2}=b_{1}=0$.
So in order to avoid zero divisors we must have \begin{eqnarray} a_{1}b_{1} & \neq & -a_{0}b_{0}\label{eq:no divcero 1}\\ a_{2}b_{2} & \neq & -a_{0}b_{0}.\label{eq:no divcero 2} \end{eqnarray} A particular case of these equations is when $b_{1}=-a_{1}$, $a_{0}=b_{0}$, then from \eqref{eq:no divcero 1} $a_{1}^{2}\neq a_{0}^{2},$ which is one of the conditions for the existence of inverses. The last case for the existence of zero-divisors is when one factor $\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\right)\neq0$ and the other factor $\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)=0$. This last equality implies that $g_{0}=g_{2}=0$ and so, in order to have $g_{1}=0$, we must have that $\left(b_{0}a_{1}+a_{0}b_{1}\right)=0\Rightarrow\frac{a_{1}}{a_{0}}=-\frac{b_{1}}{b_{0}}$ since $\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)=0$, and so \[ \left(1-\frac{a_{1}^{2}}{a_{0}^{2}}\right)=0\Rightarrow a_{1}^{2}=a_{0}^{2} \] and $b_{1}^{2}=b_{0}^{2}$. Therefore, if $a_{1}^{2}=a_{0}^{2}$ y $\frac{a_{1}}{a_{0}}=-\frac{b_{1}}{b_{0}}$, then, for any $a_{0},b_{0},a_{2},b_{2}$ the product is zero. Hence, the condition \eqref{eq:divcero} becomes $a_{1}b_{1}=-a_{0}b_{0}$ but we do not have the condition $a_{2}b_{2}=-a_{0}b_{0}$, that is $a_{2}b_{2}\neq-a_{0}b_{0}$. However, in this case we have that $a_{1}b_{0}=-a_{0}b_{1}$, and dividing \[ \frac{a_{1}b_{1}}{a_{1}b_{0}}=\frac{-a_{0}b_{0}}{-a_{0}b_{1}}\Rightarrow b_{1}^{2}=b_{0}^{2} \] we obtain \[ {\overset{o}{\gamma}}=\left(0;0,0\right)=\left(a_{0};\pm a_{0},a_{2}\right)\cdot\left(b_{0};\mp b_{0},b_{2}\right) \] and \[ {\overset{o}{\gamma}}=\left(0;0,0\right)=\left(a_{0};a_{1},\pm a_{0}\right)\cdot\left(b_{0};b_{1},\mp b_{0}\right) \] and thus the corresponding zero divisor conditions are \[ a_{1}b_{1}=-a_{0}b_{0},\; a_{1}^{2}=a_{0}^{2} \] and \[ a_{2}b_{2}=-a_{0}b_{0},\; a_{2}^{2}=a_{0}^{2}. \] Notice that if only units are considered, these last two cases are excluded since \eqref{eq:excl no unidades} imposes that the scalar components should not be equal to any director component. We have thus exhausted all the possibilities for zero divisors in ${\mathbb{R}}^{1+2}$.
Associativity
Lemma: The product is associative, when divisors of zero are excluded.
proof
Evaluate ${\zeta}=\left(h_{0};h_{1},h_{2}\right)={\overset{o}{\gamma}}{\overset{o}{\varphi}}=\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}$. The scalar component from \eqref{eq:product def scalar} is \[ h_{0}=\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{0}=g_{0}f_{0}\left(1+\frac{g_{1}f_{1}}{g_{0}f_{0}}\right)\left(1+\frac{g_{2}f_{2}}{g_{0}f_{0}}\right), \] and in turn, evaluation of ${\overset{o}{\gamma}}$ in terms of the product ${\overset{o}{\alpha}}{\overset{o}{\beta}}$ gives
\begin{multline*} h_{0}=\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{0}=a_{0}b_{0}\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\right)f_{0}\\ \left(1+\frac{\left(\frac{a_{1}}{a_{0}}+\frac{b_{1}}{b_{0}}\right)f_{1}}{\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)f_{0}}\right)\left(1+\frac{\left(\frac{a_{2}}{a_{0}}+\frac{b_{2}}{b_{0}}\right)f_{2}}{\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\right)f_{0}}\right). \end{multline*} This expression may be rewritten in the nicely symmetrical form
\begin{multline*} h_{0}=\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{0}=\\ a_{0}b_{0}f_{0}\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}+\frac{a_{1}}{a_{0}}\frac{f_{1}}{f_{0}}+\frac{b_{1}}{b_{0}}\frac{f_{1}}{f_{0}}\right)\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}+\frac{a_{2}}{a_{0}}\frac{f_{2}}{f_{0}}+\frac{b_{2}}{b_{0}}\frac{f_{2}}{f_{0}}\right), \end{multline*} provided that the factors that are being canceled out in numerator and denominator are not zero, namely \begin{equation} \frac{a_{1}b_{1}}{a_{0}b_{0}}\neq-1,\quad\frac{a_{2}b_{2}}{a_{0}b_{0}}\neq-1.\label{eq:not divcero AB} \end{equation} On the other hand, evaluate ${\zeta}'=\left(h_{0}';h_{1}',h_{2}'\right)={\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)$ and to ease the notation, set $\tau={\overset{o}{\beta}}{\overset{o}{\varphi}}=(t_{0};t_{1},t_{2})$. The scalar component from \eqref{eq:product def scalar} is \[ h_{0}'=\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{0}=a_{0}t_{0}\left(1+\frac{a_{1}t_{1}}{a_{0}t_{0}}\right)\left(1+\frac{a_{2}t_{2}}{a_{0}t_{0}}\right), \] and in turn, evaluation of ${\tau}$ in terms of the product ${\overset{o}{\beta}}{\overset{o}{\varphi}}$ gives
\begin{multline*} h_{0}'=\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{0}=a_{0}b_{0}f_{0}\left(1+\frac{b_{1}f_{1}}{b_{0}f_{0}}\right)\left(1+\frac{b_{2}f_{2}}{b_{0}f_{0}}\right)\\ \left(1+\frac{\left(\frac{b_{1}}{b_{0}}+\frac{f_{1}}{f_{0}}\right)a_{1}}{\left(1+\frac{b_{1}f_{1}}{b_{0}f_{0}}\right)a_{0}}\right)\left(1+\frac{\left(\frac{b_{2}}{b_{0}}+\frac{f_{2}}{f_{0}}\right)a_{1}}{\left(1+\frac{b_{2}f_{2}}{b_{0}f_{0}}\right)a_{0}}\right). \end{multline*} This expression may be rewritten in the symmetrical form
\begin{multline*} h_{0}'=\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{0}=\\ a_{0}b_{0}f_{0}\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}+\frac{a_{1}}{a_{0}}\frac{f_{1}}{f_{0}}+\frac{b_{1}}{b_{0}}\frac{f_{1}}{f_{0}}\right)\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}+\frac{a_{2}}{a_{0}}\frac{f_{2}}{f_{0}}+\frac{b_{2}}{b_{0}}\frac{f_{2}}{f_{0}}\right), \end{multline*} provided that the terms $\frac{b_{1}f_{1}}{b_{0}f_{0}}$ and $\frac{b_{2}f_{2}}{b_{0}f_{0}}$ are different from minus one, \begin{equation} \frac{b_{1}f_{1}}{b_{0}f_{0}}\neq-1,\quad\frac{b_{2}f_{2}}{b_{0}f_{0}}\neq-1.\label{eq:not divcero BF} \end{equation} Comparison of the expressions for $h_{0}'$ and $h_{0}$, shows that they are identical, hence the scalar component of the product is associative $\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{0}=\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{0}$. Consider now the first director component from \eqref{eq:product def dir1} \[ h_{1}=\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{1}=\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{0}\frac{\left(\frac{g_{1}}{g_{0}}+\frac{f_{1}}{f_{0}}\right)}{\left(1+\frac{g_{1}f_{1}}{g_{0}f_{0}}\right)}, \] evaluation of ${\overset{o}{\gamma}}$ in terms of ${\overset{o}{\alpha}}{\overset{o}{\beta}}$ components gives \[ \frac{h_{1}}{h_{0}}=\frac{\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{1}}{\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{0}}=\frac{\left(\frac{\left(\frac{a_{1}}{a_{0}}+\frac{b_{1}}{b_{0}}\right)}{\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)}+\frac{f_{1}}{f_{0}}\right)}{\left(1+\frac{\left(\frac{a_{1}}{a_{0}}+\frac{b_{1}}{b_{0}}\right)}{\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)}\frac{f_{1}}{f_{0}}\right)}. \] This expression may also be put in a symmetrical fashion \[ \frac{h_{1}}{h_{0}}=\frac{\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{1}}{\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{0}}=\frac{\frac{a_{1}}{a_{0}}+\frac{b_{1}}{b_{0}}+\frac{f_{1}}{f_{0}}+\frac{a_{1}b_{1}f_{1}}{a_{0}b_{0}f_{0}}}{1+\frac{a_{1}b_{1}}{a_{0}b_{0}}+\frac{a_{1}f_{1}}{a_{0}f_{0}}+\frac{b_{1}f_{1}}{b_{0}f_{0}}}, \] provided that equations \eqref{eq:not divcero AB} are fulfilled. On the other hand, evaluate \[ h_{1}'=\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{1}=\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{0}\frac{\left(\frac{a_{1}}{a_{0}}+\frac{t_{1}}{t_{0}}\right)}{\left(1+\frac{a_{1}t_{1}}{a_{0}t_{0}}\right)}, \] expressing $\tau$ in terms of ${\overset{o}{\beta}}{\overset{o}{\varphi}}$ components gives \[ \frac{h_{1}'}{h_{0}'}=\frac{\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{1}}{\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{0}}=\frac{\left(\frac{a_{1}}{a_{0}}+\frac{\left(\frac{b_{1}}{b_{0}}+\frac{f_{1}}{f_{0}}\right)}{\left(1+\frac{b_{1}f_{1}}{b_{0}f_{0}}\right)}\right)}{\left(1+\frac{a_{1}}{a_{0}}\frac{\left(\frac{b_{1}}{b_{0}}+\frac{f_{1}}{f_{0}}\right)}{\left(1+\frac{b_{1}f_{1}}{b_{0}f_{0}}\right)}\right)}. \] This expression may also be put in a symmetrical fashion \[ \frac{h_{1}'}{h_{0}'}=\frac{\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{1}}{\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{0}}=\frac{\frac{a_{1}}{a_{0}}+\frac{b_{1}}{b_{0}}+\frac{f_{1}}{f_{0}}+\frac{a_{1}b_{1}f_{1}}{a_{0}b_{0}f_{0}}}{1+\frac{a_{1}b_{1}}{a_{0}b_{0}}+\frac{a_{1}f_{1}}{a_{0}f_{0}}+\frac{b_{1}f_{1}}{b_{0}f_{0}}}, \] provided that equations \eqref{eq:not divcero BF} are fulfilled. Since $h_{0}'=h_{0}$, the first component is also associative $h_{1}'=h_{1}$, $\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{1}=\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{1}$. An analogous procedure leads to the second component associativity $\left[\left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}\right]_{2}=\left[{\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right)\right]_{2}$. Since all components are associative, the product is then associative \[ \left({\overset{o}{\alpha}}{\overset{o}{\beta}}\right){\overset{o}{\varphi}}={\overset{o}{\alpha}}\left({\overset{o}{\beta}}{\overset{o}{\varphi}}\right), \] provided that conditions \ref{eq:not divcero AB} abd \ref{eq:not divcero BF} are satisfied. $\square$
The restrictions $\frac{a_{1}b_{1}}{a_{0}b_{0}}\neq-1,\:\frac{a_{2}b_{2}}{a_{0}b_{0}}\neq-1,\:\frac{b_{1}f_{1}}{b_{0}f_{0}}\neq-1,\:\frac{b_{2}f_{2}}{b_{0}f_{0}}\neq-1$ required for associativity to hold are in fact, the conditions required to avoid divisors of zero.
Restricted space
For the product of two scators to be defined we need to restrict the corresponding subspace of ${\mathbb{R}}^{1+2}$.
Lemma: The restricted space conditions $a_{0},b_{0}\neq0,$ $a_{0}^{2}>a_{1}^{2},a_{2}^{2}$ and $b_{0}^{2}>b_{1}^{2},b_{2}^{2}$ are sufficient conditions to satisfy group properties under the product operation.
proof The stronger condition $a_{0},b_{0}\neq0$, encompasses the condition required to have a well defined product \eqref{eq:condexistencia producto}. Unit and inverse existance are assured since the inequality of scalar components larger than director or versor components prevents the equalities $a_{0}^{2}=a_{1}^{2},\: a_{0}^{2}=a_{2}^{2}$. Divisors of zero are avoided because the restricted space conditions impose $\left(\frac{a_{1}}{a_{0}}\right)^{2}<1$ and $\left(\frac{b_{0}}{b_{1}}\right)^{2}>1$, hence $\frac{a_{1}}{a_{0}}\neq\pm\frac{b_{0}}{b_{1}}$ and similarly for the second components. Therefore conditions \eqref{eq:not divcero AB} and \eqref{eq:not divcero BF} are fulfilled and associativity holds. To prove closure under the restricted space domain, recall that $1>\frac{a_{j}}{a_{0}}$, thus $1-\frac{a_{j}}{a_{0}}>0$, similarly $1-\frac{b_{j}}{b_{0}}>0$. The product of these two terms gives the inequality \[ \left(1-\frac{a_{j}}{a_{0}}\right)\left(1-\frac{b_{j}}{b_{0}}\right)>0,\: j=1,2. \] The expansion of this product is $1-\frac{a_{j}}{a_{0}}-\frac{b_{j}}{b_{0}}+\frac{a_{j}}{a_{0}}\frac{b_{j}}{b_{0}}>0$, so that $1+\frac{a_{j}}{a_{0}}\frac{b_{j}}{b_{0}}>\frac{a_{j}}{a_{0}}+\frac{b_{j}}{b_{0}}$. It is possible to divide by $1+\frac{a_{j}}{a_{0}}\frac{b_{j}}{b_{0}}$ since this term is not zero, \[ 1>\frac{\frac{a_{j}}{a_{0}}+\frac{b_{j}}{b_{0}}}{1+\frac{a_{j}}{a_{0}}\frac{b_{j}}{b_{0}}}. \] Comparison with equations \eqref{eq:product def scalar}, \eqref{eq:product def dir1} and \eqref{eq:product def dir2} shows that the RHS of the inequality is the quotient $\frac{g_{j}}{g_{0}}$ of the product of two scators, thus $g_{0}>g_{j}$. The domain and the codomain of the restricted space are then equal.\end{proof}
There is a different restricted space condition, when the director components terms are larger than the scalar term $a_{0},b_{0}\neq0,$ $a_{0}^{2}<a_{1}^{2},a_{2}^{2}$ and $b_{0}^{2}<b_{1}^{2},b_{2}^{2}$, where the scator product also satisfies group properties.
Scator in terms of a basis
The scators $1,\hat{\mathbf{e}}_{1}=(0;1,0),\hat{\mathbf{e}}_{2}=(0;0,1)$ form a basis for ${\mathbb{R}}^{1+2}$ and so any scator may be written as \[ {\overset{o}{\alpha}}=\left(a_{0};a_{1},a_{2}\right)=a_{0}+a_{1}\hat{\mathbf{e}}_{1}+a_{2}\hat{\mathbf{e}}_{2}. \] The first component of the first element is necessarily a scalar as we have already proved in item (1) of remark. The product of two scators ${\overset{o}{\alpha}}{\overset{o}{\beta}}$ according to the definition \eqref{eq:product def scalar}-\eqref{eq:product def dir2} is \begin{multline} {\overset{o}{\alpha}}{\overset{o}{\beta}}=\left(a_{0}b_{0}+a_{1}b_{1}+a_{2}b_{2}+\frac{a_{1}b_{1}a_{2}b_{2}}{a_{0}b_{0}}\right)\\ +\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\right)\left(b_{0}a_{1}+a_{0}b_{1}\right)\hat{\mathbf{e}}_{1}+\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)\left(b_{0}a_{2}+a_{0}b_{2}\right)\hat{\mathbf{e}}_{2}\label{eq:product versors} \end{multline} This operation is not bilinear and therefore cannot be written in terms of the product of its addends. To wit, if the product were distributed over the scator components the following nine terms would be obtained \begin{multline*} {\overset{o}{\alpha}}{\overset{o}{\beta}}\overset{?}{=}a_{0}b_{0}+a_{0}b_{1}\hat{\mathbf{e}}_{1}+a_{0}b_{2}\hat{\mathbf{e}}_{2}+b_{0}a_{1}\hat{\mathbf{e}}_{1}+b_{0}a_{2}\hat{\mathbf{e}}_{2}\\ +b_{1}a_{1}\hat{\mathbf{e}}_{1}\hat{\mathbf{e}}_{1}+b_{2}a_{1}\hat{\mathbf{e}}_{1}\hat{\mathbf{e}}_{2}+b_{1}a_{2}\hat{\mathbf{e}}_{2}\hat{\mathbf{e}}_{1}+b_{2}a_{2}\hat{\mathbf{e}}_{2}\hat{\mathbf{e}}_{2}. \end{multline*} However, each of the director products $\hat{\mathbf{e}}_{1}\hat{\mathbf{e}}_{1},\hat{\mathbf{e}}_{1}\hat{\mathbf{e}}_{2},\hat{\mathbf{e}}_{2}\hat{\mathbf{e}}_{1},\hat{\mathbf{e}}_{2}\hat{\mathbf{e}}_{2}$ cannot be rewritten in the general form $x+y\hat{\mathbf{e}}_{1}+z\hat{\mathbf{e}}_{2}$ with $x,y,z$ independent of the scator coefficients in order to reproduce the required product terms in (\ref{eq:product versors}).
Lemma: Hyperbolic $1+1$ dimensional scators, that is with only one non-vanishing director component either $\hat{\mathbf{e}}_{1}$ or $\hat{\mathbf{e}}_{2}$, are identical to double numbers, as defined in \cite{KantorSolodovnikov:1989}.
proof
Consider the particular case of the product of two scators with only one and the same non zero director component, say $\hat{\mathbf{e}}_{2}$ (but could equally be $\hat{\mathbf{e}}_{1}$), from the scator product definition \eqref{eq:product def scalar}-\eqref{eq:product def dir2} \[ {\overset{o}{\alpha}}{\overset{o}{\beta}}=\left(a_{0}b_{0}+a_{2}b_{2};0,b_{0}a_{2}+a_{0}b_{2}\right)=a_{0}b_{0}+a_{2}b_{2}+\left(b_{0}a_{2}+a_{0}b_{2}\right)\hat{\mathbf{e}}_{2} \] The product thus becomes identical to the product of hyperbolic complex or double numbers. The product can then be distributed over the scator components \[ {\overset{o}{\alpha}}{\overset{o}{\beta}}=\left(a_{0}+a_{2}\hat{\mathbf{e}}_{2}\right)\left(b_{0}+b_{2}\hat{\mathbf{e}}_{2}\right)=a_{0}b_{0}+a_{2}b_{2}+\left(b_{0}a_{2}+a_{0}b_{2}\right)\hat{\mathbf{e}}_{2} \] provided that $\hat{\mathbf{e}}_{2}\hat{\mathbf{e}}_{2}=1$. The addition operation is the same component wise for scators and double numbers. 1+1 hyperbolic scators with either $\hat{\mathbf{e}}_{1}$ or $\hat{\mathbf{e}}_{2}$ thus form a commutative ring identical to double $\mathbb{H}_{2}$ numbers.$\square$
The equality $\hat{\mathbf{e}}_{2}\hat{\mathbf{e}}_{2}=1$ is consistent with the scator product definition (\ref{eq:product def scalar}), since the product $\left(0;0,1\right)\left(0;0,1\right)$ is equal to $\left(1;0,0\right)$. Care should be taken to make the null director component zero before the scalar component is taken to the zero limit.
On the other hand, if we consider the particular case of the product of two scators with different non-vanishing vector component from the scator product definition \[ {\overset{o}{\alpha}}{\overset{o}{\beta}}=\left(a_{0};a_{1},0\right)\left(b_{0};0,b_{2}\right)=\left(a_{0}b_{0};b_{0}a_{1},a_{0}b_{2}\right). \] In terms of the basis $1,\hat{\mathbf{e}}_{1},\hat{\mathbf{e}}_{2}$, this operation is \[ {\overset{o}{\alpha}}{\overset{o}{\beta}}=\left(a_{0}+a_{1}\hat{\mathbf{e}}_{1}\right)\left(b_{0}+b_{2}\hat{\mathbf{e}}_{2}\right)=a_{0}b_{0}+a_{1}b_{0}\hat{\mathbf{e}}_{1}+a_{0}b_{2}\hat{\mathbf{e}}_{2} \]
The product can then be distributed over the scator components provided that $\hat{\mathbf{e}}_{1}\hat{\mathbf{e}}_{2}=0$. This last equality is consistent with the scator product definition, namely the product $\left(0;1,0\right)\left(0;0,1\right)$ is equal to $\left(0;0,0\right)$. Then we can construct table \ref{tab:product-of-single} with the product of scators with a single non-vanishing component. Notice that this table does not contain all the information needed to define the product of two arbitrary scators with two non-vanishing components.
\begin{table} \noindent \begin{centering} \begin{tabular}{|c|c|c|c|} \hline & 1 & $\hat{\mathbf{e}}_{1}$ & $\hat{\mathbf{e}}_{2}$\tabularnewline \hline \hline 1 & 1 & $\hat{\mathbf{e}}_{1}$ & $\hat{\mathbf{e}}_{2}$\tabularnewline \hline $\hat{\mathbf{e}}_{1}$ & $\hat{\mathbf{e}}_{1}$ & 1 & 0\tabularnewline \hline $\hat{\mathbf{e}}_{2}$ & $\hat{\mathbf{e}}_{2}$ & 0 & 1\tabularnewline \hline \end{tabular} \par\end{centering}
\caption{\label{tab:product-of-single} Product of single director elements. This table should be read with care since it does not contain all the information needed to define the product of two arbitrary scators. } \end{table}
Recall that the characteristic matrix of a hypercomplex algebra is generated with the bi-product of all the components in the director basis. The multiplication table \ref{tab:product-of-single} describes the product of 1+2 hyperbolic scators with a single non-vanishing component. This is as close as we can get to a characteristic matrix. However, it is of limited use because the product of two 1+2 hyperbolic scators cannot be obtained from this matrix as we shall presently show due to the lack of distributivity.
Lemma: The product of two arbitrary $1+2$ hyperbolic scators cannot be represented by a matrix-matrix product.
proof
Suppose that the product of two $1+2$ hyperbolic scators can be represented by the product of two matrices $\mathcal{M}_{G}$ and $\mathcal{M}_{F}$, that is \[ \mathcal{M}_{GF}=\mathcal{M}_{G}\mathcal{M}_{F}. \] Hyperbolic scator addition can be represented by the sum of two matrices since the sum is evaluated by the sum of each component. Let the matrix $\mathcal{M}_{G}$ be the sum of two scators be represented by the sum of the matrices $\mathcal{M}_{A}$ and $\mathcal{M}_{B}$, then \[ \mathcal{M}_{GF}=\left(\mathcal{M}_{A}+\mathcal{M}_{B}\right)\mathcal{M}_{F}. \] However, matrix product is distributive over addition, thus \[ \mathcal{M}_{GF}=\mathcal{M}_{A}\mathcal{M}_{F}+\mathcal{M}_{B}\mathcal{M}_{F}. \] But we have already proved that the scator product is not distributive over addition. Therefore, the scator product cannot be isomorphic to matrix multiplication. $\square$
The concept of modulus of a complex number can be extended to hypercomplex numbers by taking the $n$-th root of the absolute value of the characteristic determinant \cite[ch.2.1.6]{catoni2008}. It is not possible to extend this procedure to this case because the characteristic matrix does not contain all the information involved in the product of two arbitrary scators.
Lack of Distributivity
The difference between the product $\left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}$ and the sum of the products ${\overset{o}{\alpha}}{\overset{o}{\gamma}}+{\overset{o}{\beta}}{\overset{o}{\gamma}}$ is a measure of the lack of distributivity. The product $\left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}$ is \begin{multline*} \left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}=\left(a_{0}+b_{0}\right)g_{0}\left(1+\frac{\left(a_{1}+b_{1}\right)g_{1}}{\left(a_{0}+b_{0}\right)g_{0}}\right)\left(1+\frac{\left(a_{2}+b_{2}\right)g_{2}}{\left(a_{0}+b_{0}\right)g_{0}}\right)\\ \left(1;\frac{\left(\frac{\left(a_{1}+b_{1}\right)}{\left(a_{0}+b_{0}\right)}+\frac{g_{1}}{g_{0}}\right)}{\left(1+\frac{\left(a_{1}+b_{1}\right)g_{1}}{\left(a_{0}+b_{0}\right)g_{0}}\right)},\frac{\left(\frac{\left(a_{2}+b_{2}\right)}{\left(a_{0}+b_{0}\right)}+\frac{g_{2}}{g_{0}}\right)}{\left(1+\frac{\left(a_{2}+b_{2}\right)g_{2}}{\left(a_{0}+b_{0}\right)g_{0}}\right)}\right), \end{multline*} while the product ${\overset{o}{\alpha}}{\overset{o}{\gamma}}$ is \[ {\overset{o}{\alpha}}{\overset{o}{\gamma}}=a_{0}g_{0}\left(1+\frac{a_{1}g_{1}}{a_{0}g_{0}}\right)\left(1+\frac{a_{2}g_{2}}{a_{0}g_{0}}\right)\left(1;\frac{\left(\frac{a_{1}}{a_{0}}+\frac{g_{1}}{g_{0}}\right)}{\left(1+\frac{a_{1}g_{1}}{a_{0}g_{0}}\right)},\frac{\left(\frac{a_{2}}{a_{0}}+\frac{g_{2}}{g_{0}}\right)}{\left(1+\frac{a_{2}g_{2}}{a_{0}g_{0}}\right)}\right), \] and the product ${\overset{o}{\beta}}{\overset{o}{\gamma}}$ is \[ {\overset{o}{\beta}}{\overset{o}{\gamma}}=b_{0}g_{0}\left(1+\frac{b_{1}g_{1}}{b_{0}g_{0}}\right)\left(1+\frac{b_{2}g_{2}}{b_{0}g_{0}}\right)\left(1;\frac{\left(\frac{b_{1}}{b_{0}}+\frac{g_{1}}{g_{0}}\right)}{\left(1+\frac{b_{1}g_{1}}{b_{0}g_{0}}\right)},\frac{\left(\frac{b_{2}}{b_{0}}+\frac{g_{2}}{g_{0}}\right)}{\left(1+\frac{b_{2}g_{2}}{b_{0}g_{0}}\right)}\right). \]
Scalar part
The difference between the product with the sum and the sum of the products $\left[\left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}-\left({\overset{o}{\alpha}}{\overset{o}{\gamma}}+{\overset{o}{\beta}}{\overset{o}{\gamma}}\right)\right]_{0}$ for the scalar part is \begin{align*} & \left(\left(a_{0}+b_{0}\right)g_{0}+\left(a_{1}+b_{1}\right)g_{1}+\left(a_{2}+b_{2}\right)g_{2}+\frac{\left(a_{1}+b_{1}\right)g_{1}\left(a_{2}+b_{2}\right)g_{2}}{\left(a_{0}+b_{0}\right)g_{0}}\right)\\ & -\left(a_{0}g_{0}+a_{1}g_{1}+a_{2}g_{2}+\frac{a_{1}g_{1}a_{2}g_{2}}{a_{0}g_{0}}\right)\\ & -\left(b_{0}g_{0}+b_{1}g_{1}+b_{2}g_{2}+\frac{b_{1}g_{1}b_{2}g_{2}}{b_{0}g_{0}}\right). \end{align*} This expression simplifies to \[ \left(\frac{\left(a_{1}+b_{1}\right)\left(a_{2}+b_{2}\right)}{\left(a_{0}+b_{0}\right)}-\frac{a_{1}a_{2}}{a_{0}}-\frac{b_{1}b_{2}}{b_{0}}\right)\frac{g_{1}g_{2}}{g_{0}}. \] The term within brackets can be factored as \[ \left(\frac{\left(b_{0}a_{1}-a_{0}b_{1}\right)\left(a_{0}b_{2}-b_{0}a_{2}\right)}{\left(a_{0}+b_{0}\right)a_{0}b_{0}}\right)\frac{g_{1}g_{2}}{g_{0}}. \]
Director component 1
The product of the sum for the first component is \[ \left[\left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}\right]_{1}=\left(a_{0}+b_{0}\right)g_{0}\left(1+\frac{\left(a_{2}+b_{2}\right)g_{2}}{\left(a_{0}+b_{0}\right)g_{0}}\right)\left(\frac{\left(a_{1}+b_{1}\right)}{\left(a_{0}+b_{0}\right)}+\frac{g_{1}}{g_{0}}\right) \] that may be expanded as \begin{multline*} \left[\left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}\right]_{1}=\\ g_{0}\left(a_{1}+b_{1}\right)+\left(a_{0}+b_{0}\right)g_{1}+\frac{\left(a_{2}+b_{2}\right)g_{1}g_{2}}{g_{0}}+\frac{\left(a_{1}+b_{1}\right)\left(a_{2}+b_{2}\right)g_{2}}{\left(a_{0}+b_{0}\right)}. \end{multline*} While the product $\left[{\overset{o}{\alpha}}{\overset{o}{\gamma}}\right]_{1}$ for the first component is \begin{eqnarray*} \left[{\overset{o}{\alpha}}{\overset{o}{\gamma}}\right]_{1} & = & a_{0}g_{0}\left(1+\frac{a_{2}g_{2}}{a_{0}g_{0}}\right)\left(\frac{a_{1}}{a_{0}}+\frac{g_{1}}{g_{0}}\right)\\ & = & a_{1}g_{0}+a_{0}g_{1}+\frac{a_{1}a_{2}g_{2}}{a_{0}}+\frac{g_{1}g_{2}a_{2}}{g_{0}} \end{eqnarray*} and a similar result holds for $\left[{\overset{o}{\beta}}{\overset{o}{\gamma}}\right]_{1}$ with the substitution $A\rightarrow B$. The difference for the first component $\left[\left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}-\left({\overset{o}{\alpha}}{\overset{o}{\gamma}}+{\overset{o}{\beta}}{\overset{o}{\gamma}}\right)\right]_{1}$ is then \begin{eqnarray*} & & \left(g_{0}\left(a_{1}+b_{1}\right)+\left(a_{0}+b_{0}\right)g_{1}+\frac{\left(a_{2}+b_{2}\right)g_{1}g_{2}}{g_{0}}+\frac{\left(a_{1}+b_{1}\right)\left(a_{2}+b_{2}\right)g_{2}}{\left(a_{0}+b_{0}\right)}\right)\\ & & -\left(a_{1}g_{0}+a_{0}g_{1}+\frac{a_{1}a_{2}g_{2}}{a_{0}}+\frac{g_{1}g_{2}a_{2}}{g_{0}}\right)\\ & & -\left(b_{1}g_{0}+b_{0}g_{1}+\frac{b_{1}b_{2}g_{2}}{b_{0}}+\frac{g_{1}g_{2}b_{2}}{g_{0}}\right). \end{eqnarray*} This expression simplifies to \[ \left(\frac{\left(a_{1}+b_{1}\right)\left(a_{2}+b_{2}\right)}{\left(a_{0}+b_{0}\right)}-\frac{a_{1}a_{2}}{a_{0}}-\frac{b_{1}b_{2}}{b_{0}}\right)g_{2} \] that may be factored as \[ \left(\frac{\left(b_{0}a_{1}-a_{0}b_{1}\right)\left(a_{0}b_{2}-b_{0}a_{2}\right)}{\left(a_{0}+b_{0}\right)a_{0}b_{0}}\right)g_{2}. \]
Director component 2
The difference $\left[\left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}-\left({\overset{o}{\alpha}}{\overset{o}{\gamma}}+{\overset{o}{\beta}}{\overset{o}{\gamma}}\right)\right]_{2}$ for the second component follows a similar procedure that gives
\[ \left(\frac{\left(b_{0}a_{1}-a_{0}b_{1}\right)\left(a_{0}b_{2}-b_{0}a_{2}\right)}{\left(a_{0}+b_{0}\right)a_{0}b_{0}}\right)g_{1}. \]
Given scators ${\overset{o}{\alpha}},{\overset{o}{\beta}},{\overset{o}{\gamma}}$ with 1+2 components the distributivity difference is
\begin{multline} \left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}-\left[\left({\overset{o}{\alpha}}{\overset{o}{\gamma}}\right)+\left({\overset{o}{\beta}}{\overset{o}{\gamma}}\right)\right]=\\ \frac{\left(b_{0}a_{1}-a_{0}b_{1}\right)\left(a_{0}b_{2}-b_{0}a_{2}\right)}{\left(a_{0}+b_{0}\right)a_{0}b_{0}}\left(\frac{g_{1}g_{2}}{g_{0}};g_{2},g_{1}\right)\label{eq: distre1+2} \end{multline}
Let us evaluate some particular cases:
(1) If the scators ${\overset{o}{\alpha}}$ and ${\overset{o}{\beta}}$ have only one and the same non-vanishing director component, say the second component, then the above expression is zero and the product is distributive over addition.
(2) If the scators ${\overset{o}{\alpha}}$ and ${\overset{o}{\beta}}$ have only one director component but not the same one, the above expression is different from zero, for example if $a_{2}=b_{1}=0$, \[ \left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}-\left[\left({\overset{o}{\alpha}}{\overset{o}{\gamma}}\right)+\left({\overset{o}{\beta}}{\overset{o}{\gamma}}\right)\right]=\frac{a_{1}b_{2}}{\left(a_{0}+b_{0}\right)}\left(\frac{g_{1}g_{2}}{g_{0}};g_{2},g_{1}\right) \]
(3) If the scator ${\overset{o}{\gamma}}=\left\{ g_{0},g_{1},0\right\} $
has only one component, then
\[
\left({\overset{o}{\alpha}}+{\overset{o}{\beta}}\right){\overset{o}{\gamma}}-\left[\left({\overset{o}{\alpha}}{\overset{o}{\gamma}}\right)+\left({\overset{o}{\beta}}{\overset{o}{\gamma}}\right)\right]=\frac{\left(b_{0}a_{1}-a_{0}b_{1}\right)\left(a_{0}b_{2}-b_{0}a_{2}\right)}{\left(a_{0}+b_{0}\right)a_{0}b_{0}}\left(0;0,g_{1}\right).
\]
Composition of velocities in a deformed Lorentz metric
We now examine one of the possible applications of real or hyperbolic scator algebra. In the canonical description of special relativity, the Lorentz transformations establish the operations required to transform time-space between inertial frames. The separation between events is chosen as the square root of a quadratic form. The signature of this form together with a Minkowskian system of coordinates completes the framework \cite{Synge72}. Einstein's theorem of addition of velocities is a consequence of this approach. Amendments to the Lorentz invariant have been proposed on different grounds, in particular regarding a fundamental length at the Planck scale \cite{AmelinoCamelia02,KowalskiGlikman04} and deformed metrics depending on the energy and nature of interactions \cite{Cardone2007}. The composition of velocities in special relativity ought to be consistent with the two fundamental postulates, the constancy of the speed of light and the equivalence of all observers in free inertial motion.
There is liberty regarding the choice of mathematical structure selected in order to model physical phenomena. Poincaré expressed this idea, according to Carnap, in the following statement: ``\ldots{} the physicist is free to ascribe to physical space any one of the mathematically possible geometrical structures, provided he makes suitable adjustments in the laws of mechanics and optics and consequently in the rules for measuring length. \cite{Reichenbach58}. In accordance with this view, it should be possible to produce a different set of rules to perform an operation, say the product. These rules cannot be arbitrarily set, but have to fulfill the constraints of the geometrical structure according to the phenomena that are being modeled or described. The procedure for measuring magnitudes should also be altered, that is, the metric modified. Physical meaning can be ascribed to this operation, in this particular proposal, the composition of velocities between inertial frames. Let us follow these guidelines. Allow for \eqref{eq:product def scalar}-\eqref{eq:product def dir2} to be the new set of product rules. Consider the quotient of the scator director components $a_{1}$ and $a_{2}$ over the scalar component $a_{0}$ represent the velocity components (divided by the real constant c) in the directions 1 and 2, that is $\beta_{a1}\equiv\frac{v_{a1}}{c},\beta_{a2}\equiv\frac{v_{a2}}{c}$. The velocity scator is then $\frac{\overset{o}{\alpha}}{a_{0}}=\left(1;\beta_{a1},\beta_{a2}\right)$. Similarly, the velocity scators $\overset{o}{\beta}$ and $\overset{o}{\gamma}$ are $\frac{\overset{o}{\beta}}{b_{0}}=\left(1;\beta_{b1},\beta_{22}\right)$ and $\frac{\overset{o}{\gamma}}{g_{0}}=\left(1;\beta_{g1},\beta_{g2}\right)$ respectively. Let the composition of velocities be represented by the product operation $\overset{o}{\gamma}=\overset{o}{\alpha}\overset{o}{\beta}=\left(g_{0};g_{1},g_{2}\right)$. The velocity component in direction 1 is \[ \beta_{g1}=\frac{g_{1}}{g_{0}}=\frac{\left(\frac{a_{1}}{a_{0}}+\frac{b_{1}}{b_{0}}\right)}{\left(1+\frac{a_{1}b_{1}}{a_{0}b_{0}}\right)}=\frac{\left(\beta_{a1}+\beta_{b1}\right)}{\left(1+\beta_{a1}\beta_{b1}\right)}. \] The composition of velocities in direction 2 is \[ \beta_{g2}=\frac{g_{2}}{g_{0}}=\frac{\left(\frac{a_{2}}{a_{0}}+\frac{b_{2}}{b_{0}}\right)}{\left(1+\frac{a_{2}b_{2}}{a_{0}b_{0}}\right)}=\frac{\left(\beta_{a2}+\beta_{b2}\right)}{\left(1+\beta_{a2}\beta_{b2}\right)}. \] From these results, we have recently established the generalization for the composition of velocities to three dimensions \cite{fernandez-guasti2011_2}. The constraints imposed on the mathematical structure are that the product operation forms a commutative group. These constraints are established on the following grounds:
- Closure - the composition of velocities should be an admissible velocity.
- Neutral - a relative velocity frame should exist that does not alter
the velocity of the object.
- Inverse - there should exist a frame for any event where the object
is at rest.
- Associativity - the composition of velocities should fulfill the reciprocity
principle \cite{Berzi1968}. + Commutativity - the composition of velocities should fulfill the reciprocity principle.
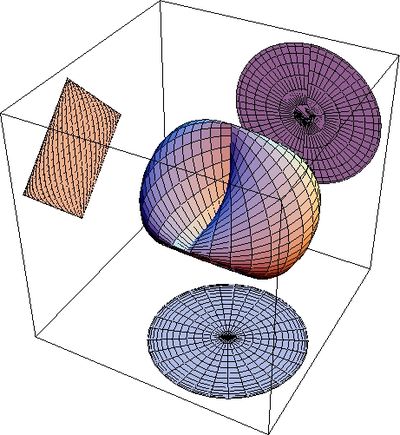
In one dimension, the group-theoretic differentiable functions are isomorphic to the sum of the reals \cite{zaldivar2011}. In higher dimensions \ldots{} Let the definition of magnitude be given by \eqref{eq:sca mag}. This magnitude definition is identical to the Lorentz metric $\sqrt{c^{2}t^{2}-x^{2}-y^{2}-z^{2}}$ in 1+1 dimensions (one spatial dimension). It also approaches the Lorentz metric in the paraxial regime. Departures arise in two or more spatial dimensions, that is, when the Thomas precession comes into play \cite{fernandez-guasti2011_2}. The equation for constant metric $m$ is given by $\sqrt{c^{2}t^{2}-x^{2}-y^{2}+\frac{x^{2}y^{2}}{c^{2}t^{2}}}=m$; In polynomial form with $c=1$, \[ t^{4}-\left(m^{2}+x^{2}+y^{2}\right)t^{2}+x^{2}y^{2}=0 \] For a light-like event, the constant $m$ is zero. The light curves for constant time $t$ are squares with side equal to $2t$ \cite{Fernandezguasti92}. The light events surface is composed by two tetragonal pyramids joined by their vertices at the origin. A plot of the light pyramid as well as the light cone in Minkowski space is shown in figure \ref{fig:cono mink-1}. \begin{figure}[ht] \begin{centering} \includegraphics[scale=0.6]{scator-metric-1-sxy-mink-cono0} \includegraphics[scale=0.65]{scator-metric-1-f012-1} \par\end{centering}
\caption{\label{fig:cono mink-1}Minkowski's light cone (left) and light pyramid (right) obtained with the scator metric. The vertical axis represents the time axis and the two orthogonal axes represent two spatial dimensions. The velocity at any point of the pyramid surface is always c as may be seen from the scator metric definition. } \end{figure}
The restricted space condition establishes the function domain, which,
in the special relativity terminology, corresponds to the admissible
velocity. For director components larger than the scalar components,
spatial-like events are described. Hypothetical particles within this
realm have been named tachyons. For director components smaller than
the scalar components, time-like events are described. These are the
events within the light pyramid accessible to an observer located
at the vertex of the dipyramid. The proposed framework is in accordance
with the constancy of the speed of light limit regardless of the motion
of the source. An important feature of the present proposal is that
the composition of velocities forms a commutative group. The velocity
reciprocity principle is then immediately fulfilled.
Conclusions
We have presented an algebra structured in $\mathbb{R}^{3}$ with componetwise addition and a novel product operation that has zero divisors. If these divisors are excluded, both the addition and product operations satisfy commutative group properties. However, the product does not distribute over addition. Note that in the two dimensonal case, distributivity holds and the algebra is iso to hyperbolic complex numbers.
The first scator component comports like a real scalar whereas the two remaining components are symmetrical and exhibit a behaviour similar to quantities with direction. The construction can be generalized to any dimension. \foreignlanguage{spanish}{The product of two scators $\overset{o}{\alpha}=\left(a_{0};a_{1},a_{2},\ldots,a_{n}\right)$ y $\overset{o}{\beta}=\left(b_{0};b_{1},b_{2},\ldots,b_{n}\right)$ with arbitrary dimension $n$ is then defined by $\overset{o}{\gamma}=\overset{o}{\alpha}\overset{o}{\beta}=\left(g_{0};g_{1},g_{2},\ldots,g_{n}\right)$, where the scalar component of the product is \begin{equation} g_{0}=a_{0}b_{0}\prod_{k=1}^{n}\left(1+\frac{a_{k}b_{k}}{a_{0}b_{0}}\right)\label{eq:product def scalar n-dim} \end{equation} and the j$^{\text{th}}$ director component is \begin{equation} g_{j}=a_{0}b_{0}\prod_{k\neq j}^{n}\left(1+\frac{a_{k}b_{k}}{a_{0}b_{0}}\right)\left(\frac{a_{j}}{a_{0}}+\frac{b_{j}}{b_{0}}\right).\label{eq:product def director j n-dim} \end{equation} }The identity between the norm of a product and the product of the norms described in \eqref{Conjugate-and-norm.} extended to $n$ dimensions gives rise to Lagrange's and higher order identities\cite{Fernandezguasti12}.
Complex numbers are to Euclidean geometry as hyperbolic numbers are to Minkowski space-time special relativity \cite{catoni2008}. However, just as it occurs in Euclidean space, a \{differentiable\} system of hypercomplex numbers extended beyond the $1+1$ dimensional framework has been elusive. It is thus natural to extend the 1+2 dimensional hypercomplex system presented here to a deformed Lorentz - Minkowski time-space.