Diferencia entre revisiones de «Vibra: probs Finn»
Sin resumen de edición |
|||
| Línea 63: | Línea 63: | ||
[[Usuario:LeonardoFR|LeonardoFR]] ([[Usuario discusión:LeonardoFR|discusión]]) 18:50 25 jun 2020 (CDT) | [[Usuario:LeonardoFR|LeonardoFR]] ([[Usuario discusión:LeonardoFR|discusión]]) 18:50 25 jun 2020 (CDT) | ||
| Línea 132: | Línea 133: | ||
Aceleración | Aceleración | ||
\[ | \[ | ||
a(0)=-0.04Sen(0.5)=-19. | a(0)=-0.04Sen(0.5)=-19.17X10^{-3} \frac{m}{s^{2}} | ||
\] | \] | ||
| Línea 147: | Línea 148: | ||
Aceleración | Aceleración | ||
\[ | \[ | ||
a(5)=-0.04Sen(1)=-3. | a(5)=-0.04Sen(1)=-3.37X10^{-2} \frac{m}{s^{2}} | ||
\] | \] | ||
[[Usuario:LeonardoFR|LeonardoFR]] ([[Usuario discusión:LeonardoFR|discusión]]) 00: | d)graficar las funciones de desplazamiento, velocidad y aceleración | ||
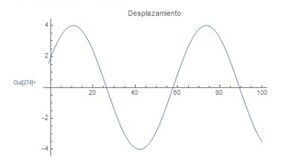
[[Archivo:Desplazamiento.jpg|miniaturadeimagen|centro]] | |||
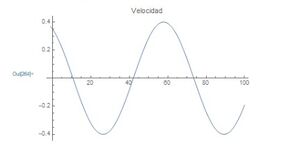
[[Archivo:Velocidad.jpg|miniaturadeimagen|centro]] | |||
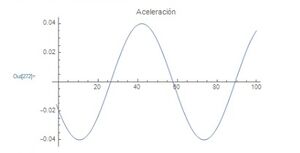
[[Archivo:Aceleración.jpg|miniaturadeimagen|centro]] | |||
[[Usuario:LeonardoFR|LeonardoFR]] ([[Usuario discusión:LeonardoFR|discusión]]) 00:18 26 jun 2020 (CDT) | |||
== EJERCICIO 12.4 == | == EJERCICIO 12.4 == | ||
Una partícula está situada en el extremo de un vibrador que pasa por su posición de equilibrio con una velocidad de 2$\frac{m}{s}$ la amplitud es de $10^{-3}$ m. ¿Cuál es la frecuencia y el periodo del vibrador? | Una partícula está situada en el extremo de un vibrador que pasa por su posición de equilibrio con una velocidad de 2$\frac{m}{s}$ la amplitud es de $10^{-3}$ m. ¿Cuál es la frecuencia y el periodo del vibrador? | ||
Revisión del 00:18 26 jun 2020
Introducción
Este es un apartado con algunos ejercicios extraídos del libro de Alonso y Finn, 'Física Volumen I: Mecánica'. Mautona97 (discusión) 16:46 16 jun 2020 (CDT)
EJERCICIO 12.1
Una rueda de 30 cm de radio tiene una manguera a su borde. La rueda gira a $0.5 \frac{rev}{seg}$ con su eje de posición horizontal, suponiendo que los rayos de sol incidan verticalmente sobre la Tierra, la manigueta está teniendo un movimiento armónico simple, encontrar: a)Periodo de oscilación de la sombra b)La frecuencia c)Amplitud d)Escribir las ecuaciones que expresan su desplazamiento en función del tiempo, suponer la fase inicial cero.
Solución: Datos: $ ω=0.5 \frac{rev}{seg}$, Radio= 30 cm
a) Para encontrar la frecuencia tenemos \[ T=\frac{2\pi}{ω} \]
Tenemos que sustituir pero al momento de convertir $\frac{rev}{seg}$ a $\frac{rad}{seg}$ multiplicarmos por $2\pi$
\[ T=\frac{2\pi}{0.5*2\pi\frac{rad}{seg}} \]
\[ T=2s \]
b) Para la frecuencia tenemos que \[ T=\frac{1}{f} \] Por lo tanto \[ f=\frac{1}{T} \] Sustituyendo \[ f=\frac{1}{2s} \]
\[ f=0.5 Hz \]
c) Aquí simplemente tenemos que entender que podemos ver el radio como la Amplitud de la onda por lo tanto
A=30cm
d) Para las ecuaciones de movimiento sabemos \[ x(t)= Asen(ωt+\varphi) \] Sustituyendo los valores que ya conocemos donde $\omega$=$ \pi \frac{rad}{s}$ Finalmente obtenemos \[ x(t)= 0.3sen(\pi*t) \] Donde la fase inicial es cero ($\varphi$=0)
LeonardoFR (discusión) 18:50 25 jun 2020 (CDT)
EJERCICIO 12.3
Un oscilador armónico simple está descrito por la ecuación: \[ x(t)= 4Sen(0.1t+0.5) \]
Donde todas las cantidades se expresan en MKS Encuentre: a. Amplitud, periodo, frecuencia y la fase inicial del movimiento b. Velocidad y aceleración del movimiento c. Condiciones iniciales d. La posición, la velocidad y la aceleración para t=5s e. Hacer el gráfico de la posición, velocidad, y aceleración en función del tiempo
Solución: a) Sabemos que la ecuación para un oscilador armónico es: \[ x(t)= ASen(\omega*t+\varphi) \]
Al compararla con la ecuación que nos da el problema podemos obtener:
Amplitud: A=4 Velocidad angular: $\omega$= 0.1 $\frac{rad}{s}$ Fase inicial: $\varphi$= 0.5 Periodo: (Para este sabemos que) \[ T= \frac{2\pi}{w} \] Entonces obtenemos \[ T= \frac{2\pi}{0.1} seg = 20\pi seg \]
Y para la frecuencia sabemos que \[ f= \frac{1}{T} \] Sustituyendo T \[ f= \frac{1}{20\pi} seg = 0.05\pi seg \]
b) Para la velocidad tenemos que derivar la ecuación de posición que se nos dio \[ v(t)=\frac{dx}{dt}= 0.4Cos(0.1t+0.5) \] Y para la aceleración es la doble derivada de la ecuación de posición o la primera derivada de la velocidad \[ a(t)=\frac{d^{2}x}{d^{2}t}=\frac{dv}{dt}=-0.04Sen(0.1t+0.5) \]
c) Ecuaciones con condiciones iniciales cuando t=0 Desplazamiento o posición \[ x(0)=4Sen(0.5)=1.92m \] Velocidad \[ v(0)=0.4Cos(0.5)=0.351 \frac{m}{s} \] Aceleración \[ a(0)=-0.04Sen(0.5)=-19.17X10^{-3} \frac{m}{s^{2}} \]
d) Ecuaciones cuando t=5s
\[ x(5)=4Sen(1)=3.37m \] Velocidad \[ v(5)=0.4Cos(1)=0.216 \frac{m}{s} \] Aceleración \[ a(5)=-0.04Sen(1)=-3.37X10^{-2} \frac{m}{s^{2}} \]
d)graficar las funciones de desplazamiento, velocidad y aceleración
LeonardoFR (discusión) 00:18 26 jun 2020 (CDT)
EJERCICIO 12.4
Una partícula está situada en el extremo de un vibrador que pasa por su posición de equilibrio con una velocidad de 2$\frac{m}{s}$ la amplitud es de $10^{-3}$ m. ¿Cuál es la frecuencia y el periodo del vibrador? Escribir la ecuación que exprese su desplazamiento en función del tiempo
Para este caso necesitamos encontrar primero la velocidad angular, que sale de la igualdad de la energía cinética y la energía cinética rotacional las cuales son:
\[ E_k=\frac{1}{2} m v^2 \]
\[ E_kr=\frac{1}{2} m \omega^2(A^2-x^2) \]
Al igualarlas obtenemos
\[ \frac{1}{2} m v^2= \frac{1}{2} m \omega^2(A^2-x^2) \]
Pero esta pasa por el punto de equilibro por lo tanto x=0 \[ \frac{1}{2} m v^2= \frac{1}{2} m \omega^2(A^2) \] Donde al despejar $\omega$
\[ \omega=\sqrt{\frac{v^2}{A^2}}=\frac{v}{A} \]
Sustituyendo \[ \omega=\frac{2\frac{m}{s}}{10^{-3}m} \] Entonces obtenemos la velocidad angular \[ \omega=2000\frac{rad}{s} \] Una vez sabiendo esto podemos calcular el periodo
\[ T=\frac{2\pi}{\omega} \] Sustituyendo \[ T=\frac{2\pi}{2000\frac{rad}{s}} = \pi*10^{-3} segundos \]
Y obtenemos la frecuencia \[ f=\frac{1}{T} \] \[ f=\frac{10^{3}}{\pi}= 318.3 s \]
Y para obtener la ecuación en función del tiempo, conocemos la función característica x(t)=Asen($\omega$ t + $\varphi$)
Sustituyendo con los valores proporcionados tenemos
\[ x(t)=10^{-3}sen(2000t+\varphi) \]
LeonardoFR (discusión) 19:24 25 jun 2020 (CDT)
EJERCICIO 12.5
Una partícula cuya masa es de 1 gramo vibra con movimiento armónico simple de 2mm de aplitud. Su aceleración en el extremo de su recorrido es de $8*10^{3}ms^{-2}$. Calcula la frecuencia del movimiento y la velocidad de la partícula cuando pasa por la posición de equilibrio y cuando la elongación es de 1.2 mm. Escribir la ecuación que describe la fuerza en función de la posición y el tiempo.
Solución.
i) Para calcular la frecuencia, se tiene que
\[ m\frac{d^{2}x}{dt^{2}}=-kx, \] podemos despejar a k para obtener posteriormente la frecuencia a partir de la frecuencia angular y la masa. Por lo tanto:
\[ k=-\frac{ma}{x}\Rightarrow\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{-\frac{ma}{x}}{m}}=\sqrt{-\frac{a}{x}}=\sqrt{\frac{8*10^{3}\frac{m}{s^{2}}}{2*10^{-3}m}}=2*10^{3}\,{rad}*{s} ^{-1}. \]
Así la frecuencia está dada por
\[ f=\frac{\omega}{2\pi}\Rightarrow f=\frac{1}{\pi}*10^{3}\,{s}^{-1}. \]
ii) La velocidad de la partícula cuando pasa por la posición de equilibrio puede ser calculada a partir de la energía potencial inicial, dado que
\[ E_{P}=\frac{1}{2}kx^{2} \]
y en la posición de equilibrio
\[ E_{P}=E_{k}\Rightarrow\frac{1}{2}kx^{2}=\frac{1}{2}mv_{f}^{2}, \]
por lo tanto
\[ v_{f}=\sqrt{\frac{kx^{2}}{m}}\Rightarrow v_{f}=\sqrt{\frac{(4*10^{3}\frac{kg}{s^{2}})(2*10^{-3}{m})^{2}}{1*10^{-3}{kg}}}=4\frac{m}{s}. \]
Ahora bien, en la posición cuando la elongación es de 1.2 mm, la velocidad se puede observar como:
\[ \frac{1}{2}m(v_{f}^{2}-v_{0}^{2})=-\frac{1}{2}kx_{f}^{2}, \]
se tiene entonces
\[ v_{f}=\sqrt{v_{0}^{2}-\frac{k}{m}x^{2}}=\sqrt{v_{0}^{2}-\omega^{2}x^{2}}=\sqrt{(16\frac{m}{s})^{2}-(2*10^{3}{s^{-1}})^{2}(1.2*10^{-3}{m})^{2}}=3.2\,\frac{m}{s}. \]
iii) Para la ecuación de la fuerza, simplemente se tiene que, dada la función de posición
\[ x=A\sin(\omega t+\alpha)\Rightarrow a=-\omega^{2}A\sin(\omega t+\alpha), \]
por la ecuación de Newton
\[ F=m\frac{d^{2}x}{dt^{2}}=m(-\omega^{2}A\sin(\omega t+\alpha))=-kA\sin(\omega t+\alpha). \]
Sustituyendo todos los valores conocidos, concluimos que
\[ F=-8\sin((2*10^{3}{s^{-1}})t+\alpha)\,N. \] Mautona97 (discusión) 16:46 16 jun 2020 (CDT)
EJERCICIO 12.15
Un bloque de madera cuya densidad con respecto al agua es $\rho$ tiene dimensiones a,b y c. Mientras está flotando en el agua con el lado a en la posición vertical, se empuja hacia abajo y se suelta. Encontrar el periodo de oscilación resultante.
Solución.
Sabemos que la frecuencia del movimiento está dada por
\[ f=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}, \]
por lo tanto, el periodo estará dado por
\begin{equation} P=2\pi\sqrt{\frac{m}{k}}. \end{equation}
De hidrostática se sabe que la magnitud de la fuerza de empuje de un fluido está dada por
\[ B=\rho_{f}gV_{d}, \]
donde $\rho_{f}$ es la densidad del fluido en cuestión, g es la aceleración de la gravedad y $V_{d}$ es el volumen desplazado por el cuerpo. Si igualamos dicha fuerza a la que produce un resorte, se tendría que
\[ \rho_{f}gV_{d}=-kx\Rightarrow k=-\frac{\rho_{f}gV_{d}}{x}. \]
Sustituyendo en la ecuación (1) se tiene que:
\begin{equation} P=2\pi\sqrt{\frac{m}{-\frac{\rho_{f}gV_{d}}{x}}}=2\pi\sqrt{\frac{\rho\rho_{f}V_{d}}{-\frac{\rho_{f}gV_{d}}{x}}}=2\pi\sqrt{-\frac{\rho x}{g}}, \end{equation}
dado que el desplazamiento x es en realidad -a, podemos sustituir en (2) como
\[ P=2\pi\sqrt{-\rho\frac{-a}{g}}=2\pi\sqrt{\rho\frac{a}{g}}. \] Por lo tanto el periodo está dado por \[ P=2\pi\sqrt{\rho\frac{a}{g}}. \]
Mautona97 (discusión) 17:54 16 jun 2020 (CDT)
EJERCICIO 12.57
Escribir la ecuación del movimiento de un oscilador armónico simple sin amoritguamiento al cual se la aplica la fuerza $F=F_{0}\cos(\omega_{f}t)$. Verificar que su solución es
\[ x=[\frac{F_{0}}{m(\omega_{0}^{2}-\omega_{f}^{2})}]\cos(\omega_{f}t). \]
Solución.
Escribimos la ecuación diferencial para los movimientos armónicos simples (sin amortiguamiento) con una fuerza oscilatoria es
\[ F_{T}=m\frac{d^{2}x}{dt^{2}}=F_{0}\cos(\omega_{f}t)-kx\Rightarrow m\frac{d^{2}x}{dt^{2}}+kx=F_{0}\cos(\omega_{f}t); \]
la cual podemos reescribir como
\[ \frac{d^{2}x}{dt^{2}}+\frac{k}{m}x=\frac{F_{0}}{m}\cos(\omega_{f}t)\Rightarrow\frac{d^{2}x}{dt^{2}}+\omega_{0}^{2}x=\frac{F_{0}}{m}\cos(\omega_{f}t) \]
una vez definida, calculamos la segunda derivada respecto del tiempo de la función de posición como
\[ \frac{d^{2}}{dt^{2}}[\frac{F_{0}}{m(\omega_{0}^{2}-\omega_{f}^{2})}]\cos(\omega_{f}t)=-\omega_{f}^{2}[\frac{F_{0}}{m(\omega_{0}^{2}-\omega_{f}^{2})}]\cos(\omega_{f}t)=-\omega_{f}^{2}x. \]
Por lo tanto
\[ \frac{d^{2}x}{dt^{2}}+\omega_{0}^{2}x=\frac{F_{0}}{m}\cos(\omega_{f}t)\Rightarrow-\omega_{f}^{2}x+\omega_{0}^{2}x=\frac{F_{0}}{m}\cos(\omega_{f}t), \]
factorizando se tiene
\[ x(\omega_{0}^{2}-\omega_{f}^{2})=\frac{F_{0}}{m}\cos(\omega_{f}t)\Rightarrow[\frac{F_{0}}{m(\omega_{0}^{2}-\omega_{f}^{2})}]\cos(\omega_{f}t)*(\omega_{0}^{2}-\omega_{f}^{2})=\frac{F_{0}}{m}\cos(\omega_{f}t), \]
lo que comprueba que la solución dada es correcta. Mautona97 (discusión) 17:20 16 jun 2020 (CDT)