Diferencia entre revisiones de «Vibra: oscilador forzado»
m (Mfgwi trasladó la página Solucion oscilador forzado no amortiguado con fuerza senoidal y amortiguado con fuerza de un pulso a Vibra: oscilador forzado sin dejar una redirección) |
|||
| (No se muestran 27 ediciones intermedias de 2 usuarios) | |||
| Línea 1: | Línea 1: | ||
=Solución del oscilador forzado no amortiguado con fuerza motriz senoidal = | |||
''' | =Antecedentes= | ||
En la naturaleza ocurren movimientos que se repiten en intervalos iguales de tiempo,estos movimientos se les llaman movimientos periódicos, el tiempo mínimo necesario para que se repita el movimiento se le llama periodo, en consecuencia , al número de veces que se repite el movimiento por unidad de tiempo se le llama frecuencia<ref name="Serway2008"> Serway A.R.,Jewett W.J.,(2008)''Física para ciencias e ingeniería'', 7a. Edicion,CENGAGE Learning.</ref>, ejemplos: El movimiento del planeta alrededor del sol, un péndulo que cuelga libremente y lo empuja y luego lo suelta se mece libremente de un lado hacia otro y regresa a su posición inicial,Las moléculas y sus átomos oscilan alrededor de sus posiciones de equilibrio, las ondas electromagnéticas son vectores de campos eléctricos y magnéticos que oscilan con el tiempo, el caso de estudio típico es el resorte que se fija en un extremo y en el otro extremo se le añade una masa, luego se estira o se comprime este resorte una cierta distancia respecto de su posición relajada de equilibrio, por la rigidez propia del resorte aparece una fuerza en sentido contrario al desplazamiento que tiende a regresar al resorte a su posición de equilibrio, frecuentemente ocurre que el sistema masa-resorte regresa a su posición de equilibrio y continúa desplazándose más allá de esta posición hasta alcanzar otra posición extrema máxima opuesta a la anterior, se detiene y se regresa , así se genera un movimiento oscilatorio, si la fuerza recuperadora es proporcional al desplazamiento de la masa y se dirige siempre a la posición de equilibrio se tiene lo que se llama un movimiento armónico simple. Por otra parte,si este sistema oscila inmerso en un medio viscoso que afecta y altera frenando el libre movimiento de la masa se dice que se tiene un oscilador amortiguado,sin embargo cuando es despreciable el efecto de amortiguamiento se tiene un oscilador libre; en el sistema amortiguado aparece otra fuerza que se opone al movimiento pero esta es proporcional a la rapidez con que se mueve la masa, o sea, es proporcional a la derivada del desplazamiento respecto al tiempo,esta fuerza terminaría por detener el movimiento de la masa por completo y para evitar eso se hace necesario aplicar una fuerza motriz externa que puede ser de distintos tipos, armónica o pulsante o no armónica, en ese caso se tiene un oscilador amortiguado forzado.En particular ,en el caso del oscilador amortiguado forzado con una fuerza motriz externa armónica con una frecuencia propia independiente de la frecuencia de oscilación merece mención aparte el caso cuando ambas frecuencias: la frecuencia natural del oscilador y la frecuencia de la fuerza externa son iguales porque en este caso conforme transcurre el tiempo se generan cada vez desplazamientos más grandes que alcanzarán valores más allá de los límites permisibles físicamente llegando a destruir el sistema. | |||
=Caso de frecuencias diferentes= | |||
A continuación, en esta sección,se resuelve el oscilador forzado sin amortiguación sometido a una fuerza motriz senoidal. | A continuación, en esta sección,se resuelve el oscilador forzado sin amortiguación sometido a una fuerza motriz senoidal. | ||
la ecuación es: | la ecuación es<ref name="Main1993"> Main G.I.,(1993)''Vibrations and Waves in Physics'', 3rd Edition,Cambridge University Press.</ref>: | ||
\begin{equation} | \begin{equation} | ||
y^{"}+\omega_{0} | y^{"}+\omega_{0}^2y=F_{0}\sin (\omega t) | ||
\label{ec1} | |||
\end{equation} | \end{equation} | ||
y las condiciones iniciales son: | y las condiciones iniciales son: | ||
$y(0)=0$ y $y^{'}(0)=0$. | $y(0)=0$ y $y^{'}(0)=0$. | ||
en la primera parte se resuelve para cuando las frecuencias de oscilación de la fuerza motriz y del oscilador no son iguales, para ello se emplea el método de la transformada de Laplace. | en la primera parte se resuelve para cuando las frecuencias de oscilación de la fuerza motriz y del oscilador no son iguales, para ello se emplea el método de la transformada de Laplace <ref name="Zill 2015">Zill G. D.,Wright S.W.,(2015)''Ecuaciones Diferenciales con problemas con valores en la frontera'',8ava. edición, CENGAGE Learning.</ref>. | ||
Aplicando la transformada de | Aplicando la transformada de Laplace a ambos lados de (\ref{ec1}): | ||
\begin{equation} | \begin{equation} | ||
s^2Y(s)-sy(0)-y^{'}(0)+\omega_{0}Y(s)=F_{0}\frac{\omega}{s^2+\omega^2} | s^2Y(s)-sy(0)-y^{'}(0)+\omega_{0}Y(s)=F_{0}\frac{\omega}{s^2+\omega^2} | ||
\label{ec2} | |||
\end{equation} | \end{equation} | ||
| Línea 21: | Línea 27: | ||
\begin{equation} | \begin{equation} | ||
Y(s)=\frac{F_{0}}{(s^2+\omega_{0}^{2})}\frac{\omega}{(\omega^{2}+s^{2})} | Y(s)=\frac{F_{0}}{(s^2+\omega_{0}^{2})}\frac{\omega}{(\omega^{2}+s^{2})} | ||
\label{ec3} | |||
\end{equation} | \end{equation} | ||
y aplicando el método de fracciones parciales a la ecuación ( | y aplicando el método de fracciones parciales a la ecuación (\ref{ec3}): | ||
\begin{equation} | \begin{equation} | ||
\frac{F_{0}}{(s^2+\omega_{0}^{2})}\frac{\omega}{(\omega^{2}+s^{2})}=\frac{As+B}{s^{2}+\omega^{2}}+\frac{Cs+D}{s^{2}+\omega_{0}^{2}} | \frac{F_{0}}{(s^2+\omega_{0}^{2})}\frac{\omega}{(\omega^{2}+s^{2})}=\frac{As+B}{s^{2}+\omega^{2}}+\frac{Cs+D}{s^{2}+\omega_{0}^{2}} | ||
\label{ec4} | |||
\end{equation} | \end{equation} | ||
continuando con el desarrollo del método de fracciones parciales: | continuando con el desarrollo del método de fracciones parciales: | ||
\begin{equation} | \begin{equation} | ||
(As+B)(s^{2}+\omega_{0}^{2})+(Cs+D)(s^{2}+\ | (As+B)(s^{2}+\omega_{0}^{2})+(Cs+D)(s^{2}+\omega^{2})=F_{0}\omega | ||
\label{ec5} | |||
\end{equation} | \end{equation} | ||
se rescribe asi: | se rescribe asi: | ||
\begin{equation} | \begin{equation} | ||
s^3(A+C)+s^2(B+D)+s(A\omega_{0}^{2}+C\omega^{2})+B\omega_{0}^{2}+D\omega^{2}=F_{0}\omega | s^3(A+C)+s^2(B+D)+s(A\omega_{0}^{2}+C\omega^{2})+B\omega_{0}^{2}+D\omega^{2}=F_{0}\omega | ||
\label{ec6} | |||
\end{equation} | \end{equation} | ||
Resulta el siguiente sistema de ecuaciones simultaneas: | Resulta el siguiente sistema de ecuaciones simultaneas: | ||
\begin{equation} | \begin{equation} | ||
A+C=0 | A+C=0 | ||
\label{ec7} | |||
\end{equation} | \end{equation} | ||
\begin{equation} | \begin{equation} | ||
B+D=0 | B+D=0 | ||
\label{ec8} | |||
\end{equation} | \end{equation} | ||
\begin{equation} | \begin{equation} | ||
A\omega_{0}^{2}+C\omega^{2}=0 | A\omega_{0}^{2}+C\omega^{2}=0 | ||
\label{ec9} | |||
\end{equation} | \end{equation} | ||
\begin{equation} | \begin{equation} | ||
B\omega_{0}^{2}+D\omega^{2}=0 | B\omega_{0}^{2}+D\omega^{2}=0 | ||
\label{ec10} | |||
\end{equation} | \end{equation} | ||
resolviendo simultáneamente para A,B,C,D: | resolviendo simultáneamente para A,B,C,D: | ||
$A=0$,$B=-\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}$,$C=0$ y $D=\frac{F_{0}\omega}{{\omega^{2}-\omega_{0}^{2}}}$. | $A=0$,$B=-\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}$,$C=0$ y $D=\frac{F_{0}\omega}{{\omega^{2}-\omega_{0}^{2}}}$. | ||
Sustituyendo A,B,C,D en ( | Sustituyendo A,B,C,D en (\ref{ec4}) y luego en (\ref{ec3}): | ||
\begin{equation} | \begin{equation} | ||
Y(s)=-\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}\frac{1}{s^{2}+\omega^{2}}+\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}(\frac{\omega_{0}}{\omega_{0}})\frac{1}{s^{2}+\omega_{o}^{2}} | Y(s)=-\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}\frac{1}{s^{2}+\omega^{2}}+\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}(\frac{\omega_{0}}{\omega_{0}})\frac{1}{s^{2}+\omega_{o}^{2}} | ||
\label{ec11} | |||
\end{equation} | \end{equation} | ||
Aplicando ahora la transformada inversa de Laplace: | Aplicando ahora la transformada inversa de Laplace: | ||
$y(t)=\mathcal{L}^{-1}{Y(s)}$, entonces se obtiene: | $y(t)=\mathcal{L}^{-1}{Y(s)}$, entonces se obtiene: | ||
\begin{equation} | \begin{equation} | ||
y(t)==-\frac{F_{0} | y(t)==-\frac{F_{0}}{\omega^{2}-\omega_{0}^{2}}\sin \omega t+\frac{F_{0}\omega}{(\omega^{2}-\omega_{0}^{2})\omega_{0}}\sin \omega_{0} | ||
t | t | ||
\label{ec12} | |||
\end{equation} | \end{equation} | ||
se puede rescribir asi: | se puede rescribir asi: | ||
\begin{equation} | \begin{equation} | ||
y(t)=\frac{\omega F_{0}}{\omega^{2}-\omega_{0}^{2}} (\frac{\sin \omega_{0} t }{\omega_{0}}-\frac{\sin \omega t }{\omega}) | y(t)=\frac{\omega F_{0}}{\omega^{2}-\omega_{0}^{2}} (\frac{\sin \omega_{0} t }{\omega_{0}}-\frac{\sin \omega t }{\omega}) | ||
\label{ec13} | |||
\end{equation} | \end{equation} | ||
esto fue para el caso de frecuencias | esto fue para el caso de frecuencias del oscilador y de la fuerza externa diferentes. | ||
=Caso de frecuencias iguales= | |||
Partiendo de la ec ( | Partiendo de la ec (\ref{ec3}) pero haciendo $\omega=\omega_{0}$: | ||
\begin{equation} | \begin{equation} | ||
Y(s)=\frac{\omega_{0} F_{0}} {(s^{2}+\omega_{0}^{2})(s^{2}+\omega_{0}^{2})} | Y(s)=\frac{\omega_{0} F_{0}} {(s^{2}+\omega_{0}^{2})(s^{2}+\omega_{0}^{2})} | ||
\label{ec14} | |||
\end{equation} | \end{equation} | ||
por fracciones parciales: | por fracciones parciales: | ||
\begin{equation} | \begin{equation} | ||
\frac{\omega_{0} F_{0}} {(s^{2}+\omega_{0}^{2})(s^{2}+\omega_{0}^{2})}=\frac{As+B}{s^{2}+\omega_{0}^{2}}+\frac{Cs+D}{(s^{2}+\omega_{0}^{2})^{2}} | \frac{\omega_{0} F_{0}} {(s^{2}+\omega_{0}^{2})(s^{2}+\omega_{0}^{2})}=\frac{As+B}{s^{2}+\omega_{0}^{2}}+\frac{Cs+D}{(s^{2}+\omega_{0}^{2})^{2}} | ||
\label{ec15} | |||
\end{equation} | \end{equation} | ||
se puede rescribir asi: | se puede rescribir asi: | ||
\begin{equation} | \begin{equation} | ||
(As+B)(s^{2}+\omega_{0}^{2})+{(Cs+D)}=F_{0} \omega_{0} | (As+B)(s^{2}+\omega_{0}^{2})+{(Cs+D)}=F_{0} \omega_{0} | ||
\label{ec16} | |||
\end{equation} | \end{equation} | ||
Efectuando operaciones,desarrollando y factorizando términos: | Efectuando operaciones,desarrollando y factorizando términos: | ||
\begin{equation} | \begin{equation} | ||
s^{3}A+s^{2}B+s(A\omega_{0}^{2}+C)+(B \omega_{0}^{2}+D)=\omega_{0} F_{0} | s^{3}A+s^{2}B+s(A\omega_{0}^{2}+C)+(B \omega_{0}^{2}+D)=\omega_{0} F_{0} | ||
\label{ec17} | |||
\end{equation} | \end{equation} | ||
Despejando las incógnitas A,B,C,D: | Despejando las incógnitas A,B,C,D: | ||
| Línea 88: | Línea 109: | ||
\begin{equation} | \begin{equation} | ||
Y(s)=\frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})^{2}} | Y(s)=\frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})^{2}} | ||
\label{ec18} | |||
\end{equation} | \end{equation} | ||
pero rescribiendo: | pero rescribiendo: | ||
\begin{equation} | \begin{equation} | ||
\frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})^{2}}=\frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})} \frac{\omega_{0}}{\omega_{0}(s^{2}+\omega_{0}^{2})} | \frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})^{2}}=\frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})} \frac{\omega_{0}}{\omega_{0}(s^{2}+\omega_{0}^{2})} | ||
\label{ec19} | |||
\end{equation} | \end{equation} | ||
Aplicando ahora la transformada inversa de Laplace: | Aplicando ahora la transformada inversa de Laplace: | ||
| Línea 97: | Línea 120: | ||
\begin{equation} | \begin{equation} | ||
Y(s)=\frac{F_{0}}{\omega_{0}}\sin (\omega_{0} t) \sin (\omega_{0} t ) | Y(s)=\frac{F_{0}}{\omega_{0}}\sin (\omega_{0} t) \sin (\omega_{0} t ) | ||
\label{ec20} | |||
\end{equation} | \end{equation} | ||
Aplicando el teorema de la convolución: | Aplicando el teorema de la convolución: | ||
\begin{equation} | \begin{equation} | ||
\frac{F_{0}}{\omega_{0}}\int_0^t \sin \omega\tau\sin(t-\tau)d\tau=\frac{F_{0}}{2\omega_{0}}(\sin \omega_{0}t-\omega_{0} t \cos \omega_{0} t) | \frac{F_{0}}{\omega_{0}}\int_0^t \sin \omega\tau\sin(t-\tau)d\tau=\frac{F_{0}}{2\omega_{0}}(\sin \omega_{0}t-\omega_{0} t \cos \omega_{0} t) | ||
\label{ec21} | |||
\end{equation} | \end{equation} | ||
| Línea 106: | Línea 131: | ||
\begin{equation} | \begin{equation} | ||
y(t)=\frac{F_{0}}{2\omega_{0}}(\sin \omega_{0}t-\omega_{0} t \cos \omega_{0} t) | y(t)=\frac{F_{0}}{2\omega_{0}}(\sin \omega_{0}t-\omega_{0} t \cos \omega_{0} t) | ||
\label{ec22} | |||
\end{equation} | \end{equation} | ||
=Solución del Oscilador forzado amortiguado con fuerza motriz puntual= | |||
A continuación se resuelve el caso de un Oscilador Amortiguado sometido a una fuerza de un pulso empleando la transformada de Laplace, para ello se hace uso del delta de | A continuación se resuelve el caso de un Oscilador Amortiguado sometido a una fuerza de un pulso empleando la transformada de Laplace, para ello se hace uso del delta de Dirac para modelar la fuerza de un pulso en este caso unitario, posteriormente en el desarrollo del método de Laplace se hace uso del teorema de traslación para pasar del dominio de la frecuencia al dominio del tiempo. | ||
La ecuación general del oscilador amortiguado sometido a la fuerza de un pulso (golpe) unitario es: | La ecuación general del oscilador amortiguado sometido a la fuerza de un pulso (golpe) unitario es: | ||
\begin{equation} | \begin{equation} | ||
y"(t)+by'(t)+\omega_{0}^{2}y(t)=\delta(t-a) | y"(t)+by'(t)+\omega_{0}^{2}y(t)=\delta(t-a) | ||
\label{ec23} | |||
\end{equation} | \end{equation} | ||
con las siguientes condiciones iniciales: | con las siguientes condiciones iniciales: | ||
| Línea 120: | Línea 147: | ||
\begin{equation} | \begin{equation} | ||
\mathcal{L}(y"(t))=s^{2}Y(s)-sy(0)-y'(0) | \mathcal{L}(y"(t))=s^{2}Y(s)-sy(0)-y'(0) | ||
\label{ec24} | |||
\end{equation} | \end{equation} | ||
y | y | ||
\begin{equation} | \begin{equation} | ||
\mathcal{L}(y'(t))=Y(s)-y(0) | \mathcal{L}(y'(t))=Y(s)-y(0) | ||
\label{ec25} | |||
\end{equation} | \end{equation} | ||
y aplicando la transformada de laplace al delta de dirac: | y aplicando la transformada de laplace al delta de dirac: | ||
\begin{equation} | \begin{equation} | ||
\mathcal{L}(\delta(t-a)=e^{-sa} | \mathcal{L}(\delta(t-a)=e^{-sa} | ||
\label{ec26} | |||
\end{equation} | \end{equation} | ||
Aplicando ( | Aplicando (\ref{ec24}) y (\ref{ec25}) y (\ref{ec26}) a (\ref{ec23}) simplificando y reescribiendo: | ||
\begin{equation} | \begin{equation} | ||
Y(s)=\frac{e^{-sa}}{(s^2+bs+\omega_{0}^{2})} | Y(s)=\frac{e^{-sa}}{(s^2+bs+\omega_{0}^{2})} | ||
\label{ec27} | |||
\end{equation} | \end{equation} | ||
Acompletando el binomio cuadrado en el denominador y rescribiendo: | Acompletando el binomio cuadrado en el denominador y rescribiendo: | ||
\begin{equation} | \begin{equation} | ||
Y(s)=\frac{e^{-sa}}{(s+b/2)^{2}+(\sqrt{\omega_{0}^{2}-b^{2}/4})^{2}} | Y(s)=\frac{e^{-sa}}{(s+b/2)^{2}+(\sqrt{\omega_{0}^{2}-b^{2}/4})^{2}} | ||
\label{ec28} | |||
\end{equation} | \end{equation} | ||
Por inspección y aplicando el teorema de la traslación de Laplace a ( | Por inspección y aplicando el teorema de la traslación de Laplace a (\ref{ec28}): | ||
\begin{equation} | \begin{equation} | ||
y(t)=H(t-a)\frac{\sin{((\sqrt{\omega_{0}^{2}-b^2/4})(t-a))} }{\sqrt{\omega_{0}^{2}-b^2/4}}e^{-b(t-a)/2} | y(t)=H(t-a)\frac{\sin{((\sqrt{\omega_{0}^{2}-b^2/4})(t-a))} }{\sqrt{\omega_{0}^{2}-b^2/4}}e^{-b(t-a)/2} | ||
\label{ec29} | |||
\end{equation} | \end{equation} | ||
donde $H(t-a)$ es la función de Heaviside. | donde $H(t-a)$ es la función de Heaviside. | ||
| Línea 149: | Línea 182: | ||
La letra $\omega_{0}$ se refiere a la frecuencia angular natural propia del oscilador y que en el caso de un resorte oscilador depende del cociente de su constante de rigidez entre su masa. | La letra $\omega_{0}$ se refiere a la frecuencia angular natural propia del oscilador y que en el caso de un resorte oscilador depende del cociente de su constante de rigidez entre su masa. | ||
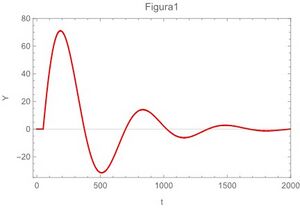
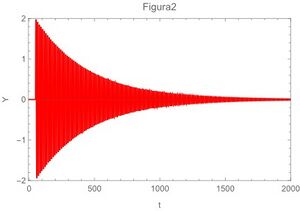
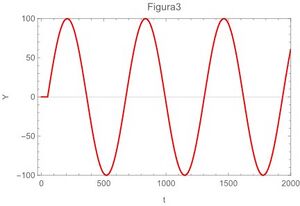
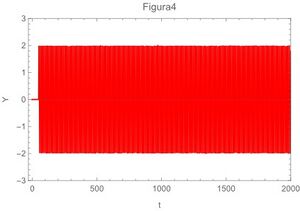
A continuación las gráficas de la ecuación ( | A continuación las gráficas <ref name="MathGraf2020"> Software Wolfram (2020).''Mathematica''.</ref> de la ecuación (\ref{ec29}) para los 4 casos extremos,también se grafican la ecuación (\ref{ec22}) en la fig 5 y en la fig 6 se gráfica la ecuación (\ref{ec13}) | ||
[[Archivo:Imagen1.jpg|miniaturadeimagen|izquierda|Muy amortiguado y oscilación lenta]] | [[Archivo:Imagen1.jpg|miniaturadeimagen|izquierda|Muy amortiguado y oscilación lenta]] | ||
[[Archivo:Imagen2.jpg|miniaturadeimagen|derecha|Muy amortiguado y oscilación rápida]] | [[Archivo:Imagen2.jpg|miniaturadeimagen|derecha|Muy amortiguado y oscilación rápida]] | ||
[[Archivo:Imagen3.jpg|miniaturadeimagen|izquierda|Poco amortiguado y oscilación lenta]] | [[Archivo:Imagen3.jpg|miniaturadeimagen|izquierda|Poco amortiguado y oscilación lenta]] | ||
[[Archivo:Imagenn4.jpg|miniaturadeimagen|derecha|Poco amortiguado y oscilación rápida]] | [[Archivo:Imagenn4.jpg|miniaturadeimagen|derecha|Poco amortiguado y oscilación rápida]] | ||
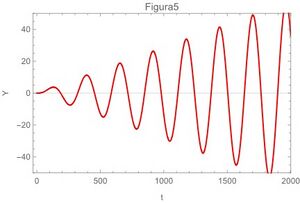
[[Archivo:Imagenn5.jpg|miniaturadeimagen|izquierda|Frecuencia natural del oscilador y de la fuerza motriz iguales]] | |||
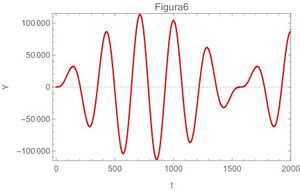
. | [[Archivo:Imagen6.jpg|miniaturadeimagen|derecha|Frecuencia natural del oscilador y de la fuerza motriz diferentes]] | ||
<br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | |||
<br><br><br><br><br><br><br><br><br><br><br><br><br><br> | |||
=Referencias= | |||
| Línea 167: | Línea 199: | ||
[[Categoría: Vibra]] | |||
. | . | ||
Revisión actual - 05:58 13 nov 2023
Solución del oscilador forzado no amortiguado con fuerza motriz senoidal
Antecedentes
En la naturaleza ocurren movimientos que se repiten en intervalos iguales de tiempo,estos movimientos se les llaman movimientos periódicos, el tiempo mínimo necesario para que se repita el movimiento se le llama periodo, en consecuencia , al número de veces que se repite el movimiento por unidad de tiempo se le llama frecuencia[1], ejemplos: El movimiento del planeta alrededor del sol, un péndulo que cuelga libremente y lo empuja y luego lo suelta se mece libremente de un lado hacia otro y regresa a su posición inicial,Las moléculas y sus átomos oscilan alrededor de sus posiciones de equilibrio, las ondas electromagnéticas son vectores de campos eléctricos y magnéticos que oscilan con el tiempo, el caso de estudio típico es el resorte que se fija en un extremo y en el otro extremo se le añade una masa, luego se estira o se comprime este resorte una cierta distancia respecto de su posición relajada de equilibrio, por la rigidez propia del resorte aparece una fuerza en sentido contrario al desplazamiento que tiende a regresar al resorte a su posición de equilibrio, frecuentemente ocurre que el sistema masa-resorte regresa a su posición de equilibrio y continúa desplazándose más allá de esta posición hasta alcanzar otra posición extrema máxima opuesta a la anterior, se detiene y se regresa , así se genera un movimiento oscilatorio, si la fuerza recuperadora es proporcional al desplazamiento de la masa y se dirige siempre a la posición de equilibrio se tiene lo que se llama un movimiento armónico simple. Por otra parte,si este sistema oscila inmerso en un medio viscoso que afecta y altera frenando el libre movimiento de la masa se dice que se tiene un oscilador amortiguado,sin embargo cuando es despreciable el efecto de amortiguamiento se tiene un oscilador libre; en el sistema amortiguado aparece otra fuerza que se opone al movimiento pero esta es proporcional a la rapidez con que se mueve la masa, o sea, es proporcional a la derivada del desplazamiento respecto al tiempo,esta fuerza terminaría por detener el movimiento de la masa por completo y para evitar eso se hace necesario aplicar una fuerza motriz externa que puede ser de distintos tipos, armónica o pulsante o no armónica, en ese caso se tiene un oscilador amortiguado forzado.En particular ,en el caso del oscilador amortiguado forzado con una fuerza motriz externa armónica con una frecuencia propia independiente de la frecuencia de oscilación merece mención aparte el caso cuando ambas frecuencias: la frecuencia natural del oscilador y la frecuencia de la fuerza externa son iguales porque en este caso conforme transcurre el tiempo se generan cada vez desplazamientos más grandes que alcanzarán valores más allá de los límites permisibles físicamente llegando a destruir el sistema.
Caso de frecuencias diferentes
A continuación, en esta sección,se resuelve el oscilador forzado sin amortiguación sometido a una fuerza motriz senoidal. la ecuación es[2]: \begin{equation} y^{"}+\omega_{0}^2y=F_{0}\sin (\omega t) \label{ec1} \end{equation} y las condiciones iniciales son: $y(0)=0$ y $y^{'}(0)=0$. en la primera parte se resuelve para cuando las frecuencias de oscilación de la fuerza motriz y del oscilador no son iguales, para ello se emplea el método de la transformada de Laplace [3].
Aplicando la transformada de Laplace a ambos lados de (\ref{ec1}):
\begin{equation} s^2Y(s)-sy(0)-y^{'}(0)+\omega_{0}Y(s)=F_{0}\frac{\omega}{s^2+\omega^2} \label{ec2} \end{equation}
sustituyendo condiciones iniciales , simplificando y despejando $Y(s)$ \begin{equation} Y(s)=\frac{F_{0}}{(s^2+\omega_{0}^{2})}\frac{\omega}{(\omega^{2}+s^{2})} \label{ec3} \end{equation} y aplicando el método de fracciones parciales a la ecuación (\ref{ec3}): \begin{equation} \frac{F_{0}}{(s^2+\omega_{0}^{2})}\frac{\omega}{(\omega^{2}+s^{2})}=\frac{As+B}{s^{2}+\omega^{2}}+\frac{Cs+D}{s^{2}+\omega_{0}^{2}} \label{ec4} \end{equation} continuando con el desarrollo del método de fracciones parciales: \begin{equation} (As+B)(s^{2}+\omega_{0}^{2})+(Cs+D)(s^{2}+\omega^{2})=F_{0}\omega \label{ec5} \end{equation} se rescribe asi: \begin{equation} s^3(A+C)+s^2(B+D)+s(A\omega_{0}^{2}+C\omega^{2})+B\omega_{0}^{2}+D\omega^{2}=F_{0}\omega \label{ec6} \end{equation} Resulta el siguiente sistema de ecuaciones simultaneas: \begin{equation} A+C=0 \label{ec7} \end{equation} \begin{equation} B+D=0 \label{ec8} \end{equation} \begin{equation} A\omega_{0}^{2}+C\omega^{2}=0 \label{ec9} \end{equation} \begin{equation} B\omega_{0}^{2}+D\omega^{2}=0 \label{ec10} \end{equation} resolviendo simultáneamente para A,B,C,D: $A=0$,$B=-\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}$,$C=0$ y $D=\frac{F_{0}\omega}{{\omega^{2}-\omega_{0}^{2}}}$. Sustituyendo A,B,C,D en (\ref{ec4}) y luego en (\ref{ec3}): \begin{equation} Y(s)=-\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}\frac{1}{s^{2}+\omega^{2}}+\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}(\frac{\omega_{0}}{\omega_{0}})\frac{1}{s^{2}+\omega_{o}^{2}} \label{ec11} \end{equation} Aplicando ahora la transformada inversa de Laplace: $y(t)=\mathcal{L}^{-1}{Y(s)}$, entonces se obtiene: \begin{equation} y(t)==-\frac{F_{0}}{\omega^{2}-\omega_{0}^{2}}\sin \omega t+\frac{F_{0}\omega}{(\omega^{2}-\omega_{0}^{2})\omega_{0}}\sin \omega_{0} t \label{ec12} \end{equation} se puede rescribir asi: \begin{equation} y(t)=\frac{\omega F_{0}}{\omega^{2}-\omega_{0}^{2}} (\frac{\sin \omega_{0} t }{\omega_{0}}-\frac{\sin \omega t }{\omega}) \label{ec13} \end{equation} esto fue para el caso de frecuencias del oscilador y de la fuerza externa diferentes.
Caso de frecuencias iguales
Partiendo de la ec (\ref{ec3}) pero haciendo $\omega=\omega_{0}$: \begin{equation} Y(s)=\frac{\omega_{0} F_{0}} {(s^{2}+\omega_{0}^{2})(s^{2}+\omega_{0}^{2})} \label{ec14} \end{equation} por fracciones parciales: \begin{equation} \frac{\omega_{0} F_{0}} {(s^{2}+\omega_{0}^{2})(s^{2}+\omega_{0}^{2})}=\frac{As+B}{s^{2}+\omega_{0}^{2}}+\frac{Cs+D}{(s^{2}+\omega_{0}^{2})^{2}} \label{ec15} \end{equation} se puede rescribir asi: \begin{equation} (As+B)(s^{2}+\omega_{0}^{2})+{(Cs+D)}=F_{0} \omega_{0} \label{ec16} \end{equation} Efectuando operaciones,desarrollando y factorizando términos: \begin{equation} s^{3}A+s^{2}B+s(A\omega_{0}^{2}+C)+(B \omega_{0}^{2}+D)=\omega_{0} F_{0} \label{ec17} \end{equation} Despejando las incógnitas A,B,C,D: $A=B=C=0$, $D=F_{0 } \omega_{0}$ por lo tanto: \begin{equation} Y(s)=\frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})^{2}} \label{ec18} \end{equation} pero rescribiendo: \begin{equation} \frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})^{2}}=\frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})} \frac{\omega_{0}}{\omega_{0}(s^{2}+\omega_{0}^{2})} \label{ec19} \end{equation} Aplicando ahora la transformada inversa de Laplace: , entonces se obtiene: \begin{equation} Y(s)=\frac{F_{0}}{\omega_{0}}\sin (\omega_{0} t) \sin (\omega_{0} t ) \label{ec20} \end{equation} Aplicando el teorema de la convolución: \begin{equation} \frac{F_{0}}{\omega_{0}}\int_0^t \sin \omega\tau\sin(t-\tau)d\tau=\frac{F_{0}}{2\omega_{0}}(\sin \omega_{0}t-\omega_{0} t \cos \omega_{0} t) \label{ec21} \end{equation}
o sea: \begin{equation} y(t)=\frac{F_{0}}{2\omega_{0}}(\sin \omega_{0}t-\omega_{0} t \cos \omega_{0} t) \label{ec22} \end{equation}
Solución del Oscilador forzado amortiguado con fuerza motriz puntual
A continuación se resuelve el caso de un Oscilador Amortiguado sometido a una fuerza de un pulso empleando la transformada de Laplace, para ello se hace uso del delta de Dirac para modelar la fuerza de un pulso en este caso unitario, posteriormente en el desarrollo del método de Laplace se hace uso del teorema de traslación para pasar del dominio de la frecuencia al dominio del tiempo. La ecuación general del oscilador amortiguado sometido a la fuerza de un pulso (golpe) unitario es: \begin{equation} y"(t)+by'(t)+\omega_{0}^{2}y(t)=\delta(t-a) \label{ec23} \end{equation} con las siguientes condiciones iniciales: $y'(0)=0$, es decir con velocidad inicial cero, y $y(0)=0$, o sea parte de la posición de equilibrio. Aplicando la transformada de Laplace para la primera y segunda derivada que dice: \begin{equation} \mathcal{L}(y"(t))=s^{2}Y(s)-sy(0)-y'(0) \label{ec24} \end{equation} y \begin{equation} \mathcal{L}(y'(t))=Y(s)-y(0) \label{ec25} \end{equation} y aplicando la transformada de laplace al delta de dirac: \begin{equation} \mathcal{L}(\delta(t-a)=e^{-sa} \label{ec26} \end{equation} Aplicando (\ref{ec24}) y (\ref{ec25}) y (\ref{ec26}) a (\ref{ec23}) simplificando y reescribiendo: \begin{equation} Y(s)=\frac{e^{-sa}}{(s^2+bs+\omega_{0}^{2})} \label{ec27} \end{equation} Acompletando el binomio cuadrado en el denominador y rescribiendo: \begin{equation} Y(s)=\frac{e^{-sa}}{(s+b/2)^{2}+(\sqrt{\omega_{0}^{2}-b^{2}/4})^{2}} \label{ec28} \end{equation} Por inspección y aplicando el teorema de la traslación de Laplace a (\ref{ec28}): \begin{equation} y(t)=H(t-a)\frac{\sin{((\sqrt{\omega_{0}^{2}-b^2/4})(t-a))} }{\sqrt{\omega_{0}^{2}-b^2/4}}e^{-b(t-a)/2} \label{ec29} \end{equation} donde $H(t-a)$ es la función de Heaviside.
En términos físicos,la letra $a$ se refiere a el momento en que se propina el golpe o pulso, a partir de este momento se inicia la perturbación y dado que es un movimiento amortiguado con frecuencia propia de oscilación en algún momento se detendrá el movimiento después de varias oscilaciones.
La letra $b$ se refiere a el coeficiente de fricción en el que está inmerso el oscilador, cuando este numero es cero se trata de un oscilador que oscila libremente por tiempo indefinido.
La letra $\omega_{0}$ se refiere a la frecuencia angular natural propia del oscilador y que en el caso de un resorte oscilador depende del cociente de su constante de rigidez entre su masa.
A continuación las gráficas [4] de la ecuación (\ref{ec29}) para los 4 casos extremos,también se grafican la ecuación (\ref{ec22}) en la fig 5 y en la fig 6 se gráfica la ecuación (\ref{ec13})
Referencias
.
- ↑ Serway A.R.,Jewett W.J.,(2008)Física para ciencias e ingeniería, 7a. Edicion,CENGAGE Learning.
- ↑ Main G.I.,(1993)Vibrations and Waves in Physics, 3rd Edition,Cambridge University Press.
- ↑ Zill G. D.,Wright S.W.,(2015)Ecuaciones Diferenciales con problemas con valores en la frontera,8ava. edición, CENGAGE Learning.
- ↑ Software Wolfram (2020).Mathematica.