Vibra: amortiguamiento
En física, cuando nos referimos al amortiguamiento, hablamos de la pérdida de energía que un sistema físico puede tener. Esto generalmente es debido a la disipación de la energía en forma de calor.
El amortiguamiento es una característica fundamental de los sistemas mecánicos, ya que estos, con su uso progresivo disipan la energía en forma de calor. Esta es una de las razones por las que no existe una máquina perfecta que sea cien por cien eficiente, ya que parte de la energía que le proporcionemos al sistema, terminará perdiéndose en calor.
Generalmente, cuando describimos un sistema físico, tendemos a sobresimplificarlo despreciando términos como la fricción; si bien esto ofrece una aproximación que en muchos casos es útil, la naturaleza tiende a comportarse de un modo más intrincado y sutil. Hacer aproximaciones despreciando la fricción conlleva consigo los siguientes 4 problemas:
- Al no tener fuerzas disipativas, el sistema puede moverse indefinidamente, cosa que en los fenómenos mecánicos ondulatorios no sucede, ya que siempre existe una fricción en el interior del muelle, cuerda u objeto con el que se esté trabajando.
- Despreciar la fricción implica negar la interacción que se produce cuando dos cuerpos están en contacto; en el caso de los osciladores, ya sea la cuerda o el muelle, tendrán una fricción interna que disipará la energía.
- Despreciar la fricción implica tener resultados (según el problema) poco fieles a la realidad, cosa que puede implicar errores de cálculo en problemas que requieran de la conservación de la energía, como construcciones de obras, la producción de maquinarias industriales, etcétera.
- La fricción implica una pérdida de energía (ya que es una fuerza no conservativa); esta energía se pierde en forma de calor y el calor dilata los materiales, cosa que puede afectar el resultado de algún procedimiento ingenieril.
De esta manera, es evidente que, hacer los cálculos despreciando la fricción, conlleva un sesgo que puede ser arriesgado según el problema que se trate. Por eso mismo, aquí se desarrollan algunas ideas básicas del amortiguamiento.
Osciladores amortiguados
El ejemplo mas común para referirnos al amortiguamiento, es el oscilador amortiguado, que consiste en un sistema oscilatorio, que va perdiendo energía por la fricción del cuerpo con el medio en el que éste se encuentra.
Los osciladores amortiguados tienen tres peculiaridades que los describen como tal:
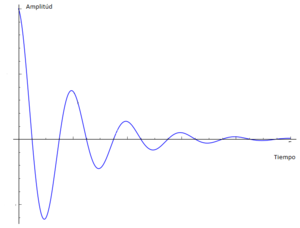
$\bullet$ La amplitud de oscilación disminuye con el tiempo.
$\bullet$ La energía disminuye con el tiempo.
$\bullet$ En el espacio fase el movimiento es descrito por espirales que convergen en el origen.
Estas tres peculiaridades son producto de la pérdida de energía por la fricción que existe con el medio.
Existen varios tipos de osciladores amortiguados, dentro de los que cabe mencionar:
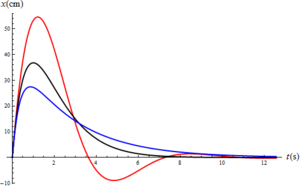
$1)$ El oscilador fuertemente amortiguado, consiste en un cuerpo en un medio con constante de amortiguamiento grande. En otras palabras, el medio por el que se desplaza el cuerpo disipa con facilidad la energía, dando como resultado oscilaciones de amplitud cada vez menor. Este comportamiento generalmente se observa en medios con densidades altas.
$2)$ El oscilador críticamente amortiguado tiene como condición que $\frac{b}{2m}=\sqrt{\frac{k}{m}}$, donde $b$ es la constante de amortiguamiento del medio, $m$ es la masa y k la constante de restitución del resorte.
$3)$ El oscilador levemente amortiguado (línea roja de la imagen de la derecha), donde la constante de amortiguamiento del medio es pequeña, y por ende tendremos soluciones complejas.
A continuación se expone una demostración formal del oscilador levemente amortiguado. Este mismo procedimiento puede utilizarse para dar solución al caso fuertemente amortiguado y al caso críticamente amortiguado.
Solución del oscilador levemente amortiguado
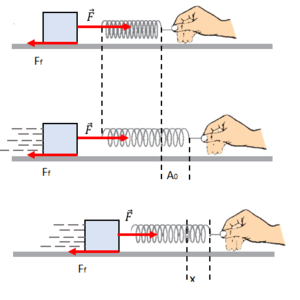
El oscilador amortiguado, es un modelo físico que nos permite estudiar fenómenos oscilatorios cuando existe una fuerza de fricción. Dicha fuerza de fricción, generalmente es debida al paso del objeto por un fluido, y tiene un comportamiento de tipo Stokes, es decir,
$F_f=-bv$
Donde $F_f$ es la fuerza de fricción, $b$ es la constante de amortiguamiento del fluido y $v$ es la velocidad del objeto de estudio. Nótese que el signo de $b$ es negativo, ya que la fuerza de fricción va en dirección contraria al movimiento.
Nosotros, para el caso, estudiaremos una masa $m$ con un solo grado de libertad, la cual estará acoplada a un resorte con constante restitutiva $k$; el sistema se encontrará en un fluido con constante de amortiguamiento $b$. Por la segunda relación de Newton, sabemos que la suma de fuerzas será,
$m\ddot{x}=-kx-b\dot{x}$, donde $\dot{x}=\frac{dx}{dt}$
De donde se deduce,
Que es la ecuación canónica del oscilador amortiguado.
A continuación se obtendrá la solución de la ecuación diferencial lineal homogenea de segundo orden. Sea $r$ elevado a la potencia del grado de cada una de las derivadas. Sustituimos en la ecuación diferencial anterior: $m r^2+br+k=0$; esto implica...
$r=(\frac{-b\pm \sqrt{b^2-4mk} }{2m})$.
Dado que el amortiguamiento es leve se puede observar que $b^2 - 4mk < 0$, lo que implica que la solución de $r$ será compleja. Para este tipo de casos, podemos proponer la siguiente solución para la ecuación diferencial,
$x(t)=(e^\frac{-b\cdot t}{2m})[C_1 \cos(\frac{-b\pm \sqrt{(b^2)-4mk} }{2m} t)+C_2 \sin(\frac{-b\pm \sqrt{b^2-4mk} }{2m} t)] $
Ahora hacemos el siguiente cambio de variable
$\omega=(\frac{-b\pm \sqrt{b^2-4mk} }{2m})$; de esta manera tenemos...
$x(t)=(e^\frac{-b\cdot t}{2m})[C_1\cos(\omega t)+C_2\sin(\omega t)]$
donde $C_1$ y $C_2$ son constantes de integración.
A continuación procedemos a aplicar las condiciones iniciales. Como primera condición inicial, sabemos que, al tiempo $t=0$, el resorte se encuentra estirado con una amplitud máxima $A_0$, es decir, $x(0)=A_0$. Igualmente como segunda condición inicial, supondremos que el resorte es soltado desde el reposo cuando éste se encuentra en la amplitud máxima; en otras palabras: $\dot{x}(0)=0$. Aplicando la primer condición inicial tenemos,
$A_0=C_1\cos(0)+C_2\sin(0)$; Por lo tanto $C_1=A_0$;
Para aplicar la segunda condición inicial, es necesario derivar a $x(t)$, como se muestra a continuación
$\dot{x}=\frac{-b}{2m}e^\frac{-b\cdot t}{2m}[A_0\cos(\omega t)+C_2\sin(\omega t)]-\omega A_0\sin(\omega t)+\omega C_2\cos(\omega t)$
Aplicando la segunda condición inicial tenemos,
$0=\frac{-b}{2m}[A_0\cos(0)+C_2\sin(0)]-\omega A_0\sin(0)+\omega C_2\cos(0)$. Simplifico,
$=\frac{-b}{2m}(A_0)+\omega C_2$; Despejamos $C_2$:
$C_2=\frac{b}{2\omega m}A_0$
Sustituimos, finalmente, los valores de $C_1$ y $C_2$ en la ecuación de $x(t)$
Siendo esta la solución al problema del oscilador levemente amortiguado.
Cabe mencionar que existen otras formas de obtener la solución al problema del oscilador levemente amortiguado, una de ellas es proponer como solución el Ansatz en la ecuación diferencial canónica del oscilador amortiguado.
Aarón patrick murphy lorea (discusión) 21:37 29 jun 2020 (CDT)