Usuario:Wendy

WENDY CAROLINA GONZALEZ OLIVARES

VARIABLE COMPLEJA

E-MAIL: shelylgk@hotmail.com

TEL:5522200631

--Wendy 01:53 22 sep 2009 (UTC) Demostración

---

EJERCICIOS

1.- Hallar Z tales que:

A) $\displaystyle {e^{z}=-2}$

SOLUCION

Escribimos $\displaystyle {e^{z}}$ como $\displaystyle {e^{x}}{e^{iy}}$

$\displaystyle {e^{x}}{e^{iy}=\rho {e^{i\phi }}}$

$\displaystyle {\rho =e^{x}=|e^{z}|=2}$, por lo que $\displaystyle {x=\ln 2}$

Ahora para $\displaystyle {y}$

$\displaystyle {e^{iy}=e^{i\phi }=-1}$; para que esto se cumpla $\displaystyle {\phi =\pi +2n\pi }$

Finalmente

$\displaystyle {z=\ln 2+{{(2n+1)}\pi }i}$

B) $\displaystyle {e^{2z-1}=1}$

SOLUCION

Escribimos

$\displaystyle {e^{2x+2iy-1}=1}$

$\displaystyle {e^{2x-1}}{e^{2iy}=\rho {e^{i\phi }}}$

donde $\displaystyle {\rho =1}$

y para que esto se cumpla $\displaystyle {e^{2x-1}=1}$

entonces $\displaystyle {2x-1=0}$; por lo tanto $\displaystyle {x={\frac {1}{2}}}$

Ahora para $\displaystyle {y}$

$\displaystyle {e^{2iy}=e^{i\phi }=1}$; esto es $\displaystyle {2y=0+(2n\pi )}$

Finalmente

$\displaystyle {z={\frac {1}{2}}+{n\pi }i}$

2.-Evaluar la siguiente integral $\int _{\,0}^{\,{\frac {\pi }{6}}}\,{{e}^{2i\,t}}\,dt$

SOLUCION

Denotemos la integral anterior con $\displaystyle {Int}$; entonces

$Int={\frac {{e}^{2i\,t}}{2i}}{\biggr |}_{0}^{\frac {\pi }{6}}$

$Int=\displaystyle {{\frac {e^{2i{\frac {\pi }{6}}}}{2i}}-{\frac {1}{2i}}}$

$Int=\displaystyle {\frac {1}{2i}}[{{\cos({\frac {\pi }{3}})+{i}\sin({\frac {\pi }{3}})-1}]}$

$Int=\displaystyle {{\frac {\sqrt {3}}{4}}+{\frac {i}{4}}}$

3.-Muestre que $\int _{\,0}^{\,2\pi }\,{{e}^{im\,\theta }}\,{{e}^{-in\,\theta }}\,d\theta$ es 0 si m=n y vale $\displaystyle {2\pi }$ si m es diferente de n

SOLUCION

$\int _{\,0}^{\,2\pi }\,{{e}^{im\,\theta }}\,{{e}^{-in\,\theta }}\,d\theta =\int _{\,0}^{\,2\pi }\,{{e}^{i(m-n)\,\theta }}\,d\theta$

Denotemos el resultado anterior como $\displaystyle {Int}$; entonces

$Int={\frac {{e}^{i(m-n)\,\theta }}{i(m-n)}}{\biggr |}_{0}^{2\pi }$

$Int=\displaystyle {{\frac {1}{i(m-n)}}-{\frac {1}{i(m-n)}}}$

$Int=\displaystyle {0}$

pero cuando m=n

$Int=\int _{\,0}^{\,2\pi }\,d\theta =2\pi$

4.-Encuentre el valor de la integral $\displaystyle {g(z)={\frac {1}{(z^{2}+4)^{2}}}}$ de alrededor del círculo $\displaystyle {|z-i|=2}$

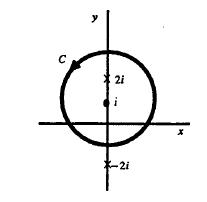
SOLUCION

Podemos escribir la integral de $\displaystyle {g(z)}$ como:

$Int=\displaystyle {\int _{\,C}\,{\frac {\frac {1}{(z+2i)^{2}}}{(z-2i)^{2}}}dz}$

si ${\displaystyle f^{k}\left(z\right)={\displaystyle {\dfrac {k!}{2\Pi i}}\int _{\gamma }{\dfrac {f\left(w\right)}{\left(w-z\right)^{k+1}}}}dw}$

con $\displaystyle k=1$

entonces

$Int=\displaystyle {{\frac {2i\pi }{1!}}{\frac {d}{dz}}{\frac {1}{(z+2i)^{2}}}{\biggr |}_{z=2i}}$

$Int=\displaystyle {2i\pi {\frac {-2}{(z+2i)^{3}}}{\biggr |}_{z=2i}}$

$Int=\displaystyle {\frac {-4i\pi }{(4i)^{3}}}$

$Int=\displaystyle {\frac {\pi }{16}}$