Radiacion: antenas

Introducción

En esencia, una antena es un sistema conductor metálico capaz de radiar y recibir ondas electromagnéticas, y una guía de onda es un tubo metálico conductor por medio del cual se propaga energía electromagnética de alta frecuencia, por lo general entre una antena y un transmisor, un receptor, o ambos.

---

Electromagnetismo en las antenas

El comportamiento de las ondas electromagnéticas y de cómo se desplazan en el medio queda expresado analíticamente por medio de las ecuaciones de Maxwell[1], que se transcriben a continuación:

$\nabla \times {\vec {H}}=\varepsilon {\vec {E}}+{\vec {J}}...\left(1\right)$ $\nabla \times {\vec {E}}=-\mu {\vec {H}}...\left(2\right)$ $\nabla \cdot {\vec {E}}={\frac {\rho }{\varepsilon }}...\left(3\right)$ $\nabla \cdot {\vec {B}}=0...\left(4\right)$

Para nuestro caso, las ondas electromagnéticas se propagan en el espacio libre y se tiene ${\vec {J}}=0$ y la ecuación (1) se reduce a:

$\nabla \times {\vec {H}}=\varepsilon {\vec {E}}...\left(5\right)$

Por lo tanto, la ec (4) se cumple si el campo magnético se expresa como el rotacional de un potencial, al cual se le asigna el nombre de potencial vectorial ${\vec {A}}$.

Como la divergencia de un rotacional es cero, se puede establecer entonces:

${\vec {H}}={\frac {1}{\mu }}\nabla \times {\vec {A}}...\left(6\right)$

donde $\mu$ es la permeabilidad magnética.

De la misma manera, se establece una relación entre el campo eléctrico y el potencial escalar V. En este caso se tiene sustituyendo la ecuación (5) en la ecuación (2),

$\nabla \times {\vec {E}}=-\mu {\frac {\partial {\vec {H}}}{\partial t}}=-\mu \left({\frac {1}{\mu }}\nabla \times {\frac {\partial {\vec {A}}}{\partial t}}\right)$

Factorizando los rotacionales:

$\nabla \times \left({\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}\right)$

Esta ecuación indica que el campo ${\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}$ es conservativo, ya que su rotacional es cero, y en este caso se puede expresar como menos el gradiente de un potencial escalar $-\nabla V$, donde el signo menos indica que la fuerza decrece con la distancia.

Tenemos entonces:

${\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}=-\nabla V$

O sea,

${\vec {E}}=-\nabla V-{\frac {\partial {\vec {A}}}{\partial t}}...\left(7\right)$

El campo eléctrico se expresa a través de un potencial vectorial ${\vec {A}}$ y otro escalar V.

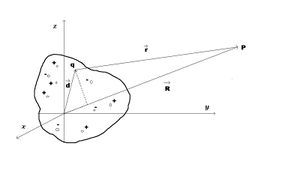
Campos y radiación de una fuente oscilante localizada

Si consideramos que los potenciales, los campos y la radiación debidos a un sistema de cargas y corrientes varían sinusoidalmente con el tiempo

$\left\{{\begin{matrix}\rho (x,t)=\rho (x)\mathbf {e} ^{-i\omega t}\\{\vec {J}}(x,t)={\vec {J}}(x)\mathbf {e} ^{-i\omega t}\end{matrix}}\right...\left(8\right)$

La solución para el potencial vectorial es:

${\vec {A}}={\frac {\mu _{0}}{4\pi }}\int {\vec {J}}(x')d^{3}x'...\left(9\right)$

La integral puede ponerse en forma más familiar si se integra por partes:

$\int {\vec {J}}d^{3}x'={\vec {J}}x'-\int x'(\nabla \cdot {\vec {J}})d^{3}x'...\left(10\right)$

Donde el primer término es $\int _{S}{\vec {J}}x_{3}'\cdot da$ (por el teorema de divergencia), y como ${\vec {J}}$ esta dentro del volumen V, es cero en la superficie. Por lo tanto $\int {\vec {J}}d^{3}x'=-\int _{V}J_{d^{3}x'}d^{3}x'$. Ahora haciendo uso de la ecuación de continuidad.

Tomando la divergencia de la ec (1)

$\nabla \cdot (\nabla \times {\vec {H}})=\nabla \cdot (\varepsilon {\vec {E}}+{\vec {J}})$

$0=\nabla \cdot (\varepsilon {\vec {E}}+{\vec {J}})$

$\nabla \cdot {\vec {J}}=-\varepsilon {\frac {\partial (\nabla \cdot {\vec {E}})}{\partial t}}=-{\frac {\partial \rho }{\partial t}}=i\rho ...\left(11\right)$

Sustituyendo este resultado en la ecuación (10), nos queda:

$\int {\vec {J}}d^{3}x'=-i\int x'\rho (x')d^{3}x'...\left(12\right)$

Así que el vector potencial se puede escribir como:

${\vec {A}}={\frac {\mu _{0}}{4\pi }}i{\vec {p}}{\frac {\mathbf {e} ^{i\kappa r}}{\vec {r}}}...\left(13\right)$

en donde ${\vec {p}}=\int x'\rho (x')d^{3}x'$ es el momento dipolar eléctrico.

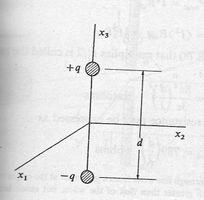
Dipolo Corto

La primera derivada del momento dipolar de un sistema de cargas $q_{\alpha }$

Sistema de cargas $q_{\alpha }$

${\dot {p}}(t')={\frac {d}{dt'}}\sum _{\alpha }q_{\alpha }{\vec {r'_{\alpha }}}(t')=\sum _{\alpha }(q_{\alpha }{\dot {\vec {r'}}}+{\vec {r'_{\alpha }}}q_{\alpha })...\left(14\right)$

Haciendo ahora los vectores ${\vec {r'_{\alpha }}}$ fijos y haciendo cambiar las cargas $q_{\alpha }$ con respecto al tiempo. Un ejemplo sencillo de esta situación se muestra en la fig (2) donde podemos considerar la variación temporal de las cargas como equivalentes al flujo de corrientes entre $x_{3}=+{\frac {d}{2}}$ y $x_{3}=-{\frac {d}{2}}$. Así,

${\dot {\vec {p}}}=\sum _{\alpha }{\dot {\vec {r}}}{\dot {q_{\alpha }}}={\vec {I}}(t')d{\vec {e_{3}}}...\left(15\right)$

En cada una de las dos mitades de la antena la corriente tiene la misma dirección, su valor es ${\vec {I}}$ en el punto de en el punto de excitación y disminuye de forma aproximadamente lineal hasta anularse en los extremos.

${\vec {I}}(x_{3})={\vec {I}}(1-{\frac {2\left|x_{3}\right|}{d}})...\left(16\right)$

Fig 2