Radiacion: antenas

Introducción

En esencia, una antena es un sistema conductor metálico capaz de radiar y recibir ondas electromagnéticas, y una guía de onda es un tubo metálico conductor por medio del cual se propaga energía electromagnética de alta frecuencia, por lo general entre una antena y un transmisor, un receptor, o ambos.

---

Electromagnetismo en las antenas

El comportamiento de las ondas electromagnéticas y de cómo se desplazan en el medio queda expresado analíticamente por medio de las ecuaciones de Maxwell[1], que se transcriben a continuación:

$\nabla \times {\vec {H}}=\varepsilon {\vec {E}}+{\vec {J}}...\left(1\right)$ $\nabla \times {\vec {E}}=-\mu {\vec {H}}...\left(2\right)$ $\nabla \cdot {\vec {E}}={\frac {\rho }{\varepsilon }}...\left(3\right)$ $\nabla \cdot {\vec {B}}=0...\left(4\right)$

Para nuestro caso, las ondas electromagnéticas se propagan en el espacio libre y se tiene ${\vec {J}}=0$ y la ecuación (1) se reduce a:

$\nabla \times {\vec {H}}=\varepsilon {\vec {E}}...\left(5\right)$

Por lo tanto, la ec (4) se cumple si el campo magnético se expresa como el rotacional de un potencial, al cual se le asigna el nombre de potencial vectorial ${\vec {A}}$.

Como la divergencia de un rotacional es cero, se puede establecer entonces:

${\vec {H}}={\frac {1}{\mu }}\nabla \times {\vec {A}}...\left(6\right)$

donde $\mu$ es la permeabilidad magnética.

De la misma manera, se establece una relación entre el campo eléctrico y el potencial escalar V. En este caso se tiene sustituyendo la ecuación (5) en la ecuación (2),

$\nabla \times {\vec {E}}=-\mu {\frac {\partial {\vec {H}}}{\partial t}}=-\mu \left({\frac {1}{\mu }}\nabla \times {\frac {\partial {\vec {A}}}{\partial t}}\right)$

Factorizando los rotacionales:

$\nabla \times \left({\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}\right)$

Esta ecuación indica que el campo ${\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}$ es conservativo, ya que su rotacional es cero, y en este caso se puede expresar como menos el gradiente de un potencial escalar $-\nabla V$, donde el signo menos indica que la fuerza decrece con la distancia.

Tenemos entonces:

${\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}=-\nabla V$

O sea,

${\vec {E}}=-\nabla V-{\frac {\partial {\vec {A}}}{\partial t}}...\left(7\right)$

El campo eléctrico se expresa a través de un potencial vectorial ${\vec {A}}$ y otro escalar V.

Campos y radiación de una fuente oscilante localizada

Si consideramos que los potenciales, los campos y la radiación debidos a un sistema de cargas y corrientes varían sinusoidalmente con el tiempo

$\left\{{\begin{matrix}\rho (x,t)=\rho (x)\mathbf {e} ^{-i\omega t}\\{\vec {J}}(x,t)={\vec {J}}(x)\mathbf {e} ^{-i\omega t}\end{matrix}}\right...\left(8\right)$

La solución para el potencial vectorial es:

${\vec {A}}={\frac {\mu _{0}}{4\pi }}\int {\vec {J}}(x')d^{3}x'...\left(9\right)$

La integral puede ponerse en forma más familiar si se integra por partes:

$\int {\vec {J}}d^{3}x'={\vec {J}}x'-\int x'(\nabla \cdot {\vec {J}})d^{3}x'...\left(10\right)$

Donde el primer término es $\int _{S}{\vec {J}}x_{3}'\cdot da$ (por el teorema de divergencia), y como ${\vec {J}}$ esta dentro del volumen V, es cero en la superficie. Por lo tanto $\int {\vec {J}}d^{3}x'=-\int _{V}J_{d^{3}x'}d^{3}x'$. Ahora haciendo uso de la ecuación de continuidad.

Tomando la divergencia de la ec (1)

$\nabla \cdot (\nabla \times {\vec {H}})=\nabla \cdot (\varepsilon {\vec {E}}+{\vec {J}})$

$0=\nabla \cdot (\varepsilon {\vec {E}}+{\vec {J}})$

$\nabla \cdot {\vec {J}}=-\varepsilon {\frac {\partial (\nabla \cdot {\vec {E}})}{\partial t}}=-{\frac {\partial \rho }{\partial t}}=i\rho ...\left(11\right)$

Sustituyendo este resultado en la ecuación (10), nos queda:

$\int {\vec {J}}d^{3}x'=-i\int x'\rho (x')d^{3}x'...\left(12\right)$

Así que el vector potencial se puede escribir como:

${\vec {A}}={\frac {\mu _{0}}{4\pi }}i{\vec {p}}{\frac {\mathbf {e} ^{i\kappa r}}{\vec {r}}}$

en donde ${\vec {p}}=\int x'\rho (x')d^{3}x'$ es el momento dipolar eléctrico.

Dipolo Corto

La primera derivada del momento dipolar de un sistema de cargas $q_{\alpha }$

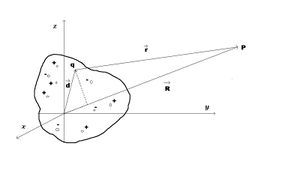
Sistema de cargas $q_{\alpha }$

${\dot {p}}(t')={\frac {d}{dt'}}\sum _{\alpha }q_{\alpha }{\vec {r'_{\alpha }}}(t')=\sum _{\alpha }(q_{\alpha }{\dot {\vec {r'}}}+{\vec {r'_{\alpha }}}q_{\alpha })$