Radiacion: antenas

Introducción

En esencia, una antena es un sistema conductor metálico capaz de radiar y recibir ondas electromagnéticas, y una guía de onda es un tubo metálico conductor por medio del cual se propaga energía electromagnética de alta frecuencia, por lo general entre una antena y un transmisor, un receptor, o ambos.

---

Electromagnetismo en las antenas

El comportamiento de las ondas electromagnéticas y de cómo se desplazan en el medio queda expresado analíticamente por medio de las ecuaciones de Maxwell[1], que se transcriben a continuación:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla\times\vec{H}=\varepsilon\vec{E}+\vec{J}...\left(1\right) Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla\times\vec{E}=-\mu\vec{H}...\left(2\right) Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla\cdot\vec{E}=\frac{\rho}{\varepsilon}...\left(3\right) Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla\cdot\vec{B}=0...\left(4\right)

Para nuestro caso, las ondas electromagnéticas se propagan en el espacio libre y se tiene Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{J}=0 y la ecuación (1) se reduce a:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla\times\vec{H}=\varepsilon\vec{E}...\left(5\right)

El signo superior corresponde a los valores positivos de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): x_3 y el inferior a los negativos. El momento dipolar es paralelo al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): x_3 y tiene el valor:

Por lo tanto, la ec (4) se cumple si el campo magnético se expresa como el rotacional de un potencial, al cual se le asigna el nombre de potencial vectorial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{A} .

Como la divergencia de un rotacional es cero, se puede establecer entonces:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{H}=\frac{1}{\mu}\nabla\times\vec{A}...\left(6\right)

donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \mu es la permeabilidad magnética.

De la misma manera, se establece una relación entre el campo eléctrico y el potencial escalar V. En este caso se tiene sustituyendo la ecuación (5) en la ecuación (2),

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla\times\vec{E}=-\mu\frac{\partial \vec{H}}{\partial t}=-\mu\left(\frac{1}{\mu}\nabla\times\frac{\partial \vec{A}}{\partial t}\right)

Factorizando los rotacionales:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla\times\left(\vec{E}+\frac{\partial \vec{A}}{\partial t}\right)

Esta ecuación indica que el campo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{E}+\frac{\partial \vec{A}}{\partial t} es conservativo, ya que su rotacional es cero, y en este caso se puede expresar como menos el gradiente de un potencial escalar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): -\nabla V , donde el signo menos indica que la fuerza decrece con la distancia.

Tenemos entonces:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{E}+\frac{\partial \vec{A}}{\partial t}=-\nabla V

O sea,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{E}=-\nabla V-\frac{\partial \vec{A}}{\partial t}...\left(7\right)

El campo eléctrico se expresa a través de un potencial vectorial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{A} y otro escalar V.

Campos y radiación de una fuente oscilante localizada

Si consideramos que los potenciales, los campos y la radiación debidos a un sistema de cargas y corrientes varían sinusoidalmente con el tiempo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left \{\begin{matrix}\rho(x,t)=\rho(x)\mathbf{e}^{-i\omega t}\\\vec{J}(x,t)=\vec{J}(x)\mathbf{e}^{-i\omega t}\end{matrix}\right ...\left(8\right)

La solución para el potencial vectorial es:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{A}=\frac{\mu_{0}}{4\pi}\int \vec{J}(x')d^3 x'...\left(9\right)

La integral puede ponerse en forma más familiar si se integra por partes:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \int \vec{J}d^3 x'=\vec{J} x'-\int x'(\nabla\cdot\vec{J})d^3 x' ...\left(10\right)

Donde el primer término es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \int_S \vec{J} x_3'\cdot da (por el teorema de divergencia), y como Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{J} esta dentro del volumen V, es cero en la superficie. Por lo tanto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \int \vec{J}d^3 x'=-\int_V J_{d^{3}x'} d^{3}x' . Ahora haciendo uso de la ecuación de continuidad.

Tomando la divergencia de la ec (1)

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla\cdot(\nabla\times\vec{H})=\nabla\cdot(\varepsilon\vec{E}+\vec{J})

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 0=\nabla\cdot(\varepsilon\vec{E}+\vec{J})

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla\cdot\vec{J}=-\varepsilon\frac{\partial (\nabla\cdot\vec{E})}{\partial t}=-\frac{\partial \rho}{\partial t} =i \rho ...\left(11\right)

Sustituyendo este resultado en la ecuación (10), nos queda:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \int \vec{J}d^3 x'=-i\int x'\rho(x')d^3 x'...\left(12\right)

Así que el vector potencial se puede escribir como:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{A}=\frac{\mu_{0}}{4\pi} i \vec{p} \frac{\mathbf{e}^{i\kappa r}}{\vec{r}}...\left(13\right)

en donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{p}=\int x'\rho(x')d^3x' es el momento dipolar eléctrico.

Dipolo Corto

La primera derivada del momento dipolar de un sistema de cargas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): q_{\alpha}

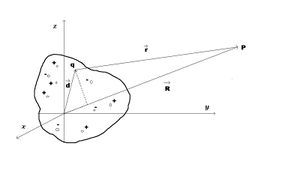
Sistema de cargas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): q_{\alpha}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \dot{p}(t')=\frac{d}{dt'}\sum_\alpha q_\alpha \vec{r'_\alpha}(t')=\sum_\alpha (q_\alpha \dot{\vec{r'}}+\vec{r'_\alpha} q_\alpha)...\left(14\right)

Haciendo ahora los vectores Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{r'_\alpha} fijos y haciendo cambiar las cargas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): q_\alpha 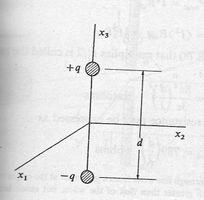con respecto al tiempo. Un ejemplo sencillo de esta situación se muestra en la fig (2) donde podemos considerar la variación temporal de las cargas como equivalentes al flujo de corrientes entre Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): x_3=+\frac{d}{2} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): x_3=-\frac{d}{2} . Así,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \dot{\vec{p}}=\sum_\alpha \dot{\vec{r}}\dot{q_\alpha}=\vec{I}(t') d\vec{e_3}...\left(15\right)

En cada una de las dos mitades de la antena la corriente tiene la misma dirección, su valor es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{I} en el punto de en el punto de excitación y disminuye de forma aproximadamente lineal hasta anularse en los extremos.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{I}(x_3)=\vec{I} (1-\frac{2 \left|x_{3}\right|}{d})...\left(16\right)

Fig 2

Según la ecuación de continuidad [11], la densidad lineal de carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \rho es constante a lo largo de cada brazo de la antena, y tiene el valor:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \rho(x_3)=\pm\frac{2I}{\omega d}...\left(17\right)

El signo superior corresponde a los valores positivos de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): x_3 y el inferior a los negativos. El momento dipolar es paralelo al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): x_3 y tiene el valor:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \int_{-\frac{d}{2}}^{\frac{d}{2}} x_3 \rho(z)\,dx_3= \frac{\vec{I} d}{2 \omega}...\left(18\right)

La distribución angular de potencia radiada es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{dP}{d\Omega}=\frac{I_{0}^{2}}{128\pi^{2}\epsilon_{0}c}...\left(19\right)

mientras que la potencia radiada total es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): P=\frac{I^{2}(kd)^{2}}{48\pi\epsilon_{0}c}...\left(20\right)

Vemos que para una corriente de excitación, la potencia radiada aumenta con el cuadrado de la frecuencia.

Antena Lineal

Consideremos una antena como se muestra en la Fig (2). Esta antena consta de dos cables, cada uno con longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{d}{2} con una pequeña separación entre ellos con el fin de aplicar una señal sinusoidal. La corriente se anula en los extremos de la antena; por lo tanto, la densidad de corriente puede escribirse:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{J}(\vec{r},t)dv=e_3 \vec{I}\mathbf{e}^{-i\omega t}\sin(\frac{kd}{2}-k|x_3|)dx_3...\left(21\right)

Archivo:ANTENA LINEAL.jpg

Fig (2) Antena Lineal

donde la señal de entrada es:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \vec{I}(t)=\vec{I}\mathbf{e}^{-i\omega t}\sin(\frac{kd}{2})

y la densidad de corriente puede escribirse:

${\vec {J}}(x)=I\sin({\frac {kd}{2}}-k|x_{3}|)\delta (x_{1})\delta (x_{2})e_{3}...\left(22\right)$

para $|x_{3}|<d_{2}$. Las funciones delta nos garantizan que la corriente fluye solamente a lo largo del eje $x_{3}$, ${\vec {I}}$ es el valor máximo de la corriente si $kd\geq \pi$. El valor de la corriente en el centro es, por tanto, ${\vec {I}}={\vec {I}}=\sin({\frac {kd}{2}})$

De modo que

${\vec {J}}({\vec {r}},t')={\vec {J}}({\vec {r'}})\mathbf {e} ^{-i\omega t}=e_{3}{\vec {J}}(x'_{3})\mathbf {e} ^{-i\omega t}...\left(23\right)$

Para calcular las propiedades del campo de radiación producido por esa antena, iniciaremos con la expresión general para el vector potencial:

${\vec {A}}({\vec {r}},t)={\frac {1}{c}}\int _{V}{\frac {{\vec {J}}({\vec {r}},t)}{{\vec {r}}-{\vec {r'}}}}...\left(24\right)$

El vector de inducción magnética esta dado por la expresión:

${\vec {B}}={\frac {1}{c}}\nabla \times \left\{{\frac {1}{r}}\int _{V}{\vec {J}}({\vec {r}},t)\right\}dv...\left(25\right)$

Expandiendo el rotacional y despreciando el término grad(1/r) ya que no contribuye a la radiación, obtenemos

${\vec {B}}_{rad}={\frac {1}{cr}}\nabla \times \left\{\int _{V}{\vec {J}}({\vec {r}},t)\right\}dv={\frac {1}{cr}}\nabla \times {\vec {f}}(t)...\left(26\right)$

donde

${\vec {f}}(t)\equiv \int _{V}{\vec {J}}(r,t)dv...\left(27\right)$

Ahora escribimos

$\nabla \times {\vec {f}}(t)\sum _{i,j,k}\epsilon _{i,j,k}{\vec {e}}_{i}{\frac {\partial f_{k}}{\partial x_{j}}}=\sum _{i,j,k}\epsilon _{i,j,k}{\vec {e}}_{i}{\frac {\partial f_{k}}{\partial t'}}{\frac {\partial t'}{\partial x_{j}}}=-{\frac {1}{c}}\sum _{i,j,k}\epsilon _{i,j,k}{\vec {e}}_{i}n_{j}{\frac {\partial f_{k}}{\partial t'}}...\left(28\right)$

Por lo tanto,

$\nabla \times {\vec {f}}(t')=-{\frac {1}{c}}{\hat {n}}\times {\frac {\partial {\vec {f}}}{\partial t'}}...\left(29\right)$

de lo cual obtenemos

${\vec {B}}_{rad}=-{\frac {1}{c^{2}r}}{\hat {n}}\times {\frac {\partial }{\partial t}}\int _{V}{\vec {J}}({\vec {r'}},t')dv'...\left(30\right)$

haciendo la sustitución de ${\frac {\partial }{\partial t}}$ por ${\frac {\partial }{\partial t'}}$ es permitible en una aproximación de $t'=t-{\frac {r}{c}}$, donde r es una constante. Así

${\vec {B}}_{rad}=-{\frac {1}{c}}{\hat {n}}\times {\frac {\partial {\vec {A}}}{\partial t}}...\left(31\right)$

Este resultado solo depende de la suposición de que en el punto el el que ${\vec {B}}$ se mide esta lejos de la fuente.

Regresando a la ecuación (24) y escribiendo explícitamente la dependencia del tiempo, obtenemos

${\vec {A}}({\vec {r}},t)={\vec {A}}({\vec {r}})\mathbf {e} ^{-i\omega t}={\frac {1}{c}}\int _{V}{\frac {{\vec {J}}({\vec {r'}})\mathbf {e} ^{-i\omega t}\mathbf {e} ^{-ik|{\vec {r}}-{\vec {r'}}|}}{|{\vec {r}}-{\vec {r'}}|}}...\left(32\right)$.

Ahora por la ley de los cosenos.

$|{\vec {r}}-{\vec {r'}}|=(r^{2}-2{\vec {r}}\cdot {\vec {r'}}+r'^{2})^{\frac {1}{2}}...\left(33\right)$

Donde asumimos $r'\ll r$, expandiendo esta expresión obtenemos

$|{\vec {r}}-{\vec {r'}}|=r\left[1-{\frac {{\hat {n}}\cdot {\vec {r'}}}{r}}+{\frac {r'^{2}}{2r^{2}}}-{\frac {1}{8}}\left({\frac {2{\hat {n}}\cdot {\vec {r'}}}{r}}\right)^{2}+...\right]=r-{\hat {n}}\cdot {\vec {r'}}+{\frac {r'^{2}}{2r}}\sin ^{2}\theta +...\left(34\right)$

Archivo:LEY DE LOS COSENOS.jpg

Fig (3) LEY DE LOS COSENOS

El denominador de la ecuación (33) se puede aproximar simplemente por $r$

Ahora la ecuación (24) se reduce a

${\vec {A}}\left({\vec {r}}\right)={\frac {\mathbf {e} ^{ikr}}{cr}}\int _{V}{\vec {J}}\left({\vec {r'}}\right)\mathbf {e} ^{ikr'}\cos \theta dv'...\left(35\right)$

Ahora la cantidad $|{\vec {r}}-{\vec {r'}}|$ en el denominador de la ecuación (32) se puede aproximar simplemente por r.

${\vec {A}}\left({\vec {r}}\right)={\frac {\mathbf {e} ^{ikr}}{cr}}\int _{-{\frac {d}{2}}}^{\frac {d}{2}}\sin \left({\frac {kd}{2}}-k|x_{3}'|\right)\mathbf {e} ^{-ik|x_{3}'|\cos \theta }dx'_{3}...\left(36\right)$

por lo que

${\vec {A}}\left({\vec {r}}\right)=e_{3}{\frac {2{\vec {I}}\mathbf {e} ^{ikr}}{ckr}}\left({\frac {\cos \left({\frac {kd}{2}}\cos \theta \right)-\cos {\frac {kd}{2}}}{\sin ^{2}\theta }}\right)...\left(37\right)$

puesto que tiene una sola componente, en la dirección $x_{3}$, $|{\hat {n}}\times {\vec {A}}|=A_{3}\sin \theta$. Por lo tanto, para la ecuación ${\vec {B}}_{rad}$, obtenemos

$|{\vec {B}}_{rad}|=kA_{3}\sin \theta ...\left(38\right)$

Ahora ${\vec {B}}_{rad}$ tiene una dependencia sinusoidal respecto al tiempo, de modo que el promedio al cuadrado de ${\vec {B}}_{rad}$ es

$<|{\vec {B}}_{rad}|^{2}>={\frac {1}{2}}k^{2}A_{3}^{2}\sin ^{2}\theta ={\frac {2{\vec {I}}^{2}}{c^{2}r^{2}}}\left({\frac {\cos \left({\frac {kd}{2}}\cos \theta \right)-\cos {\frac {kd}{2}}}{\sin \theta }}\right)^{2}...\left(39\right)$

El tiempo promedio en que el vector de Poyting contribuye a la radiación es

$<{\vec {S}}_{rad}>={\frac {c}{4\pi }}<|{\vec {B}}_{rad}|^{2}>{\hat {n}}...\left(40\right)$

y el promedio de energía radiada por unidad de ángulo sólido es

$<{\frac {d{\vec {P}}}{d\Omega }}>=r^{2}<{\vec {S}}_{rad}>\cdot {\hat {n}}={\frac {{\vec {I}}^{2}}{2\pi c}}\left({\frac {\cos \left({\frac {kd}{2}}\cos \theta \right)-\cos {\frac {kd}{2}}}{\sin \theta }}\right)^{2}...\left(41\right)$

a distribución angular depende del valor de $kd$. En el límite de las longitudes de onda larga (kd«1), se reduce al caso del dipolo. Para los valores particulares $kd=\pi$, $2\pi$, que corresponden a una (dos) semilongitudes de onda, de oscilación de la corriente a lo largo de la antena, las distribuciones angulares son

${\frac {d{\vec {P}}}{d\Omega }}={\frac {1}{4\pi \epsilon _{0}}}{\frac {I^{2}}{2\pi c}}\left\{{\begin{matrix}{\frac {\cos ^{2}\left({\frac {\pi }{2}}\cos \theta \right)}{\sin ^{2}\theta }},kd=\pi \\{\frac {4\cos ^{4}\left({\frac {\pi }{2}}\cos \theta \right)}{\sin ^{2}\theta }},kd=2\pi \end{matrix}}\right...\left(42\right)$