Optica: optica fisica

coherencia temporal y espacial

Figura 1.El experimento de Young, en la figura (a) tenemos la fuente luminosa que ilumina dos rendijas que se difractan al pasar por ellas. En la fifura (b) la fuente es puntual y por los orificios

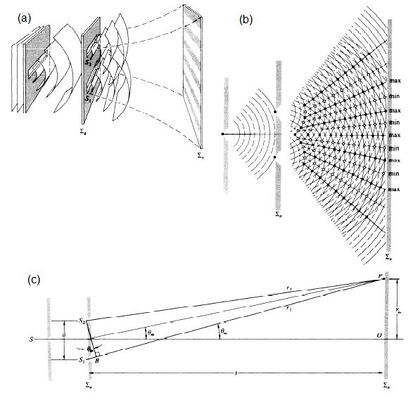
Si en la figura (a) la fuente primaria que llamamos S, si se encoge hasta convertirse en una fuente puntual sobre el eje central que tiene un ancho de banda de frecuencia finito (b), los efectos de coherencia temporal predominarán.

Las perturbaciones ópticas en ${S}_{1}$ y ${S}_{2}$ son entonces idénticas, donde ${S}_{1}$ y ${S}_{2}$ son las ventanas que muestra la figura (b) en el plano intermedio. La coherencia mutua ${\tilde {\Gamma }}_{12}(\tau )=\left\langle \mathbf {V} _{1}(t)\mathbf {V} _{2}^{*}(t+\tau )\right\rangle$ entre los dos puntos donde las perturbaciones son idénticas es en este caso la autocoherencia del campo.

De aquí que podamos escribirla como

${\tilde {\Gamma }}(S_{1},S_{2},\tau )={\tilde {\Gamma }}_{12}(\tau )={\tilde {\Gamma }}_{11}(\tau )$ o´ ${\tilde {\gamma }}_{12}(\tau )={\tilde {\gamma }}_{11}(\tau ).$

lo mismo obtenemos cuando ${S}_{1}$ y ${S}_{2}$ se fusionan y ${\tilde {\gamma }}_{11}(\tau )$ se denomina grado de coherencia temporal complejo donde $\tau$ es el intervalo de tiempo que se separan.

Esta interpretación es un poco diferente para un interferómetro de división de amplitud (Michelson), donde $\tau$ es igual a la diferencia de recorrido dividida por c. La expresión para la irradiancia I $I=I_{1}+I_{2}+2(I_{1}I_{2})^{\frac {1}{2}}Re{\tilde {\gamma }}_{12}(\tau ),$ contendra entonces a ${\tilde {\gamma }}_{11}(\tau )$ en lugar de ${\tilde {\gamma }}_{12}(\tau )$.

Ahora si una onda luminosa con el interferómetro se divide en dos perturbaciones del campo idénticas de la forma ${\tilde {\mathbf {V} }}(t)=\mathbf {V} _{0}e^{i\phi (t)}$;y este después las vuelve a combinar para generar una distribución de franjas, entonces

${\tilde {\gamma }}_{11}(\tau )={\frac {\left\langle {\tilde {\mathbf {V} }}(t+\tau ){\tilde {\mathbf {V} }}^{*}(t)\right\rangle }{{\tilde {|\mathbf {V} |}}^{2}}}={\frac {\left\langle e^{i\phi (t+\tau )}e^{-i\phi (t)}\right\rangle }{{\tilde {|\mathbf {V} |}}^{2}}}{\tilde {|\mathbf {V} |}}^{2}=\left\langle e^{i\phi (t+\tau )}e^{-i\phi (t)}\right\rangle$

Para saber que tipo de resultados nos generara la ecuación anterior y como varia veamos primero que pasa con una onda plana monocromatica de longitud de coherencia infinita Error al representar (error de sintaxis): \phi(t)= \mathbf{k • r}-\omega t

donde Error al representar (error de sintaxis): \Delta\phi=\mathbf{k•r}-\omega(t+\tau)-\mathbf{k•r}+\omega t=-\omega\tau que nos lleva a

${\tilde {\gamma }}_{11}(\tau )=e^{i\omega \tau }=\cos \omega \tau -i\sin \omega \tau$

de tal modo que $|{\tilde {\gamma }}_{11}|=1$, llamada coherencia completa.

Pasemos al caso opuesto, con una onda monocromatica con $\tau >$ longitud de coherencia de tal modo que $\Delta \phi$ sera al azar, variando entre 0 y $2\pi$ de tal manera que la integral se promedia a cero, $|{\tilde {\gamma }}_{11}(\tau )|=0$, llamada incoherencia completa.

Para tener una buena visibilidad $\tau <\Delta t_{c}$.

Es importante entender que la transformada de Fourier de la función de autocoherencia es el espectro energético que describe la distribución de la energía espectral de la luz, esto lo veremos más adelante cuando trabajemos con las aplicaciones del teorema que nos muestra la relación entre el grado de coherencia complejo en una región del espacio y la distribución de la irradiancia correspondiente en la fuente extensa que da lugar a los campos luminosos, este teorema es el Teorema de Van Cittert Zernike,

Teorema de Cittert-Zernike

Archivo:Opti1.jpg

Figura 2.

Se presenta una fuente incoherente extensa cuasimonocromática, S, situada en el plano $\sigma$ y con una irradiancia proporcionada por I(y,z). También se muestra en una pantalla de observación en la que se hallan dos puntos, $P_{1}$ y $P_{2}$ a una distancia $R_{1}$ y $R_{2},$ respectivamente, desde un elemento diminuto de S.

Vamos a determinar la intensidad mutua $J_{12}$ y el grado de coherencia complejo $j_{12}$ para los puntos de $P_{1}$ y $P_{2}$ en la pantalla A iluminada por un haz de luz proviniente de $\sigma$.

Por simplicidad $\sigma$ sera tomada como un plano paralelo al plano de A y vamos a suponer que el medio entre la fuente y la pantalla es homogéneo. También suponemos que las dimensiones lineales de $\sigma$ son pequeñas en comparación con la distancia $00^{\prime }$ entre los planos de la fuente y la pantalla, y que el ángulo entre las líneas que unen un punto de la fuente S a $P_{1}$ y $P_{2}$ son pequeños.

Imaginemos entonces que la fuente se divide en elementos $d\sigma _{1},d\sigma _{2},...$ centrado en los puntos $S_{1},S_{2},...$ de dimensiones lineales pequeñas comparadas con la longitud de onda ${\tilde {\lambda }}$. Es decir, si $v_{m1}(t)$ y $v_{m2}(t)$ son los trastornos del campo complejos en $P_{1}$ y $P_{2}$, debido al elemento $d\sigma _{1}$, el total de las alteraciones en estos puntos son ahora las vibraciones de luz que surgen de los diferentes elementos de la fuente, y puede ser asumida como estadísticamente independientes (incoherentes entre sí), de modo que

$J(P_{1},P_{2})=\left\langle \mathbf {v} _{1}(t)\mathbf {v} _{2}^{*}(t)\right\rangle =\sum _{m}\left\langle \mathbf {v} _{m1}(t)\mathbf {v} _{m2}^{*}(t)\right\rangle +\sum \sum _{nm}\left\langle \mathbf {v} _{m1}(t)\mathbf {v} _{n2}^{*}(t)\right\rangle$

$J(P_{1},P_{2})=\sum _{m}\left\langle \mathbf {v} _{m1}(t)\mathbf {v} _{m2}^{*}(t)\right\rangle +\sum \sum _{nm}0$

Si $R_{m1}$ y $R_{m2}$ son las distancias de $P_{1}$ y $P_{2}$ del elemento de origen $d\sigma _{m}$ las perturbaciones del campo las podemos escribir como

$V_{m1}(t)=A_{m}\left(t-{\frac {R_{m1}}{v}}\right){\frac {e^{-2i{\tilde {\nu }}\pi (t-{\frac {R_{m1}}{v}})}}{R_{m1}}}$

;

$V_{m2}(t)=A_{m}\left(t-{\frac {R_{m2}}{v}}\right){\frac {e^{-2i{\tilde {\nu }}\pi (t-{\frac {R_{m2}}{v}})}}{R_{m2}}}$

Donde $|A_{m}|$ caracteriza a la intensidad y el argumento $A_{m}$ la fase de la de la radiación del elemento m-esimo, v es la velocidad de la luz en el medio entre la fuente y la pantalla.

Por lo tanto

$\left\langle \mathbf {v} _{m1}(t)\mathbf {v} _{m2}^{*}(t)\right\rangle =\left\langle A_{m}\left(t-{\frac {R_{m1}}{v}}\right)A_{m}^{*}\left(t-{\frac {R_{m1}}{v}}\right)\right\rangle {\frac {e^{2i\pi {\tilde {\nu }}{\frac {(R_{m1}-R_{m2})}{v}}}}{R_{m1}R_{m2}}}=\left\langle A_{m}\left(t\right)A_{m}^{*}\left(t-{\frac {R_{m2}-R_{m1}}{v}}\right)\right\rangle {\frac {e^{2i\pi {\tilde {\nu }}{\frac {(R_{m1}-R_{m2})}{v}}}}{R_{m1}R_{m2}}}$

si la diferencia de caminos $(R_{m1}-R_{m2})$ es pequeña comparada con la longitud de coherencia de la Luz podemos despreciar el termino ${\frac {(R_{m1}-R_{m2})}{v}}$ en el argumento de $A_{m}^{*}$ y se obtiene

$J(P_{1},P_{2})=\sum _{m}\left\langle A_{m}\left(t\right)A_{m}^{*}\left(t\right)\right\rangle {\frac {e^{2i\pi {\tilde {\nu }}{\frac {(R_{m1}-R_{m2})}{v}}}}{R_{m1}R_{m2}}}$

Como mencionamos $\left\langle A_{m}\left(t\right)A_{m}^{*}\left(t\right)\right\rangle$ caracteriza la intensidad de radiación de los elementos de la fuente $d\sigma$asi que con I(S), la intensidad por unidad de área de la fuente, dejándonos así

$J(P_{1},P_{2})=\int _{\sigma }I(S){\frac {e^{i{\tilde {k}}(R_{1}-R_{2})}}{R_{1}R_{2}}}dS$

Regresando a la notación de $R_{1}$ y $R_{2}$ que ya definimos y el numero de onda en el medio $k={\frac {2\pi {\tilde {\nu }}}{v}}={\frac {2\pi }{\tilde {\lambda }}}$

El grado complejo de coherencia queda entonces

$j(P_{1},P_{2})={\frac {J(P_{1},P_{2})}{\sqrt {I(P_{1})I(P_{2})}}}={\frac {1}{\sqrt {I(P_{1})I(P_{2})}}}\int _{\sigma }I(S){\frac {e^{ik(R_{1}-R_{2})}}{R_{1}R_{2}}}dS...(1)$

Con las intensidades de $P_{1}$ y $P_{2}$

$I(P_{1})=J(P_{1},P_{1})=\int _{\sigma }{\frac {I(S)}{{R_{1}}^{2}}}dS$

$I(P_{2})=J(P_{2},P_{2})=\int _{\sigma }{\frac {I(S)}{{R_{2}}^{2}}}dS$

La aumento en la cantidad de coherencia supone una caída importante de la velocidad de conteo, dado que la señal decrece cuadráticamente con la distancia a la fuente y linealmente con el tamaño de la rendija.

El cálculo da como resultado una integral con una estructura conocida cuya forma y cuyos resultados son iguales a los de una integral de difracción, con tal que cada término se vuelva a interpretar correctamente. Notemos que esta integral (1), en una conexión diferente, esto es en el cálculo, sobre la base del principio de Fresnel, de la alteración compleja en el patrón de difracción derivado de la difracción de una onda esférica en una apertura en una pantalla opaca. Más precisamente, la integral (1) implica que la igualdad de grado de coherencia complejo, que describe la correlación de las vibraciones en un punto fijo $P_{2}$ y el punto variable $P_{1}$ en un plano iluminado por una fuente primaria extensa cuasimonocromática (incoherente), es igual a la normalización de la amplitud compleja en el punto correspondiente $P_{1}$ en un cierto patrón de difracción, centrado en $P_{2}$. Este patrón se obtendría en la sustitución de la fuente por una abertura de difracción de la misma forma y tamaño de la fuente, y llenado con una onda esférica convergente para $P_{2}$, la apertura es proporcional a la distribución de intensidad a través de la fuente.

Aplicaciones.

En la mayoría de las aplicaciones de la intensidad I(S) que puede suponerse como independiente de la posición de S en la superficie (la intensidad es uniforme). El problema de difracción correspondiente es entonces el de la difracción de una onda esférica de amplitud de uniforme por una abertura de la misma forma y tamaño de la fuente.

Sean $(x,y)$ las coordenadas de un punto de fuente típico S, en el plano sigma con el origen en 0, y $(X_{1},Y_{1})$ y $(X_{2},Y_{2})$ las coordenadas de $P_{1}$ y $P_{2}$, en el plano paralelo A y con origenel 0´. Entonces, si R representa la distancia de 0 a 0´

${R_{1}}^{2}=({X_{1}-x})^{2}+({Y_{1}-y})^{2}+R^{2}$

$\psi ={\frac {{\tilde {k}}[(X_{1}^{2}+Y_{1}^{2})-({X_{2}}^{2}-{Y_{2}}^{2})]}{R2}}$

Entonces, si las dimensiones lineales de una fuente y la distancia entre $P_{1}$ y $P_{2}$ son pequeñas comparadas con la distancia de esos puntos a la fuente, el grado de coherencia $j_{12}$ es igual al valor absoluto de la transformada de FOURIER normalizada de la función intensidad de la fuente.

$j(P_{1},P_{2})={\frac {e^{i\psi }\int \int _{\sigma }I(x,y)e^{ik({\frac {(X_{1}-X_{2})x}{r}}+{\frac {(Y_{1}-Y_{2})y}{r}}}dxdy}{\int \int _{\sigma }I(x,y)dxdy}}...(2)$

Para una fuente circular uniforme de radio $\rho$ con centro en O, la expresión anterior la podemos reescribir entonces

$j(P_{1},P_{2})=({\frac {2J_{1}(v)}{v}})e^{i\psi }$

donde

$v={\frac {{\tilde {k}}\rho }{R}}{\sqrt {(X_{1}-X_{2})^{2}+(Y_{1}-Y_{2})^{2}}}$

$J_{1}$ es la función de Bessel primer orden. Donde $|{\frac {2J_{1}(v)}{v}}|$ decrece constantemente desde el valor uno cuando $v=0$, al valor cero cuando $v=3.83$; así como los puntos $P_{1}$ y $P_{2}$ son separados mas y mas, el grado de coherencia decrece constantemente y hay una completa incoherencia cuando $P_{1}$ y $P_{2}$ son separados por una distancia

$P_{1}P_{2}={\sqrt {(X_{1}-X_{2})^{2}+(Y_{1}-Y_{2})^{2}}}={\frac {0.61R{\tilde {\lambda }}}{\rho }}$

Un incremento adicional en v reintroduce una cantidad pequeña de coherencia, pero el grado de coherencia permanece menor a 0.14, y hay una completa incoherencia para $v=7.02$. Puesto que $J_{1}(v)$ cambia de signo cada vez que v pasa a través de cada cero de $J_{1}(v)$ la fase $B_{12}=argj_{12}$ cambia por $\pi$, en consecuencia la posición de las franjas oscuras y brillantes son intercambiadas después de cada desaparición de las franjas.

$P_{1}P_{2}={\frac {0.16R{\tilde {\lambda }}}{\rho }}$

entonces ${\tilde {\Gamma }}_{12}(0)$ es sencillamente una función sinc cuando la fuente es una rendija y una función Bessel cuando es circular. Obsérvese en la figura la función sinc.

$\beta ={\frac {kb}{2}}sen\theta$

y

$\theta \thickapprox sen\theta .$

Por lo tanto, si $P_{1}$ está a una distancia y desde $P_{2},$

$\beta ={\frac {kb\theta }{2}}$

y

$\theta ={\frac {y}{l}},$

por lo tanto

$\left|{\tilde {\gamma }}_{12}(0)\right|=\left|sinc({\frac {\pi by}{l\lambda }})\right|.$

Mas sobre el teorema: [[1]] [[2]] [[3]]

Sobre Fourier Optica: Optica de Fourier

REFERENCIAS.

1. Óptica, autor: Eugene Hecht, Tercera edición, Addison Wesley Iberoamericana, Madrid, 2000.

2. Principles of optica, autores: Max Born y Emil Wolf, Quinta edición 1975, Pergamon Press.