Optica: Principio de Huygens-Fresnel

Principio de Huygens-Fesnel

El Principio de Huygens indica que cada punto en un frente de onda puede ser considerado como centro de una perturbación secundaria que da lugar a ondas esféricas, y el frente de onda en cualquier instante puede ser considerado como la envolvente de esas ondas. Fresnel pudo darse cuenta de la difracción complementando la Construcción de Huygens con el postulado de que las ondas secundarias interfieren mutuamente.

Desarrollo matemático

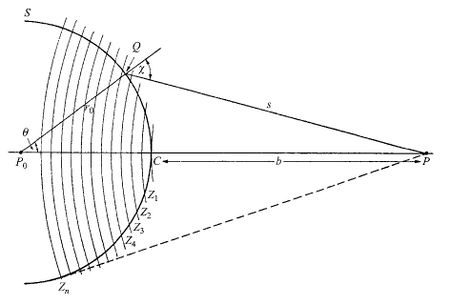
Figura 1. Posición instantánea de una onda monocromática con radio $r_{o}$. Construcción de las zonas de Fresnel

Consideremos $S$ la posición instantánea de una onda esférica monocromática con radio $r_{o}$ y centro en $P_{o}$. $P$ es el punto donde queremos ver la perturbación. El punto $Q$ está en la superficie de la espera teniendo un angulo $\theta$ respecto a la linea entre $P_{o}$ y $P$. Ahí existe una perturbación dada por $Q=A{\frac {e^{ikr_{o}}}{r_{o}}}$. Donde $A$ es la amplitud por unidad de tiempo.

Según el Principio de Huygens-Fresnel consideramos cada elemento del frente de onda como centro de una perturbación secundaria la cual se propaga en la forma de ondas esféricas. Tomemos un elemento de perturbación $dU$ debida al elemento S en Q:

$dU(P)=K(\chi ){\frac {Ae^{ikr_{o}}}{r_{o}}}{\frac {e^{iks}}{s}}dS$ (1)

Donde $s=QP$ y $K(\chi )$ es el factor de inclinación que describe la variación con dirección de la amplitud de las ondas secundarias y $\chi$ es el ángulo entre la normal en el punto $Q$ y la línea $s$.

$K(\chi )$ es máximo cuando $\chi =0$ y empieza a decrecer cuando $\chi$ va aumentando. $K(\chi )$ es cero cuando $\chi ={\frac {\pi }{2}}$.

Integrando la ecuación (1) obtenemos la pertubación total en $P$:

$U(P)={\frac {Ae^{ikr_{o}}}{r_{o}}}\iint \limits _{S}{\frac {e^{iks}}{s}}K(\chi )\,dS$ (2)

Para evaluar esa ecuación es necesario construir las zonas de Fresnel.

Construcción de zonas de Fresnel

Tomemos varios círculos con centro en $P$ y diferentes radios:

$b,b+{\frac {\lambda }{2}},b+{\frac {2\lambda }{2}},...$

Donde $b=CP$ y $C$ es el punto de intersección de $PP_{o}$ con el frende de onda $S$.

Las esfércas dividen a $S$ en varias zonas: $Z_{1},Z_{2},Z_{3},...,Z_{j},...$

Suponemos que $r_{o}$ y $b$ son mucho mayores que $\lambda$. Por lo tanto $K(\chi )$ debe tener el mismo valor $K_{j}$ en diferentes zonas (pues las $Z_{j}$ están muy pegadas).

Regresando al problema

De la Figura 1 vemos:

$s^{2}=r_{o}^{2}+(r_{o}+b)^{2}-2r_{o}(r_{o}+b)cos\theta$

Si derivamos respecto a $s$ tenemos:

$sds=r_{o}(r_{o}+b)sin\theta d\theta$

Por otro lado, tenemos el diferencial de la superficie $S$:

$dS=r_{o}^{2}sin\theta d\theta d\varphi ={\frac {r_{o}}{r_{o}+b}}sdsd\varphi$

Donde $\phi$ es el ángulo azimutal.

De la ecuación (2) vemos que es una doble integral. Por un lado integramos respecto a $\phi$ y nos da $2\pi$. Entonces nos queda una ecuación con una sola integral que descibre la j-ésima contribución (de cada zona de Fresnel):

$U_{j}(P)=2\pi {\frac {Ae^{ikr_{o}}}{r_{o}+b}}K_{j}\int _{b+(j-1){\frac {\lambda }{2}}}^{b+j{\frac {\lambda }{2}}}e^{iks}ds$

Resolviendo la integral y como $k\lambda =2\pi$:

$U_{j}(P)=2i\lambda (-1)^{j+1}K_{j}{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}$ (3)

Reacomodando tenemos que el efecto total en P es la suma de todas las contribuciones:

$U(P)=2i\lambda {\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}\sum _{j=1}^{n}(-1)^{j+1}K_{j}$(4)

Algo sobre series

En la ecuación (4) tenemos esta serie:

$\sum =\sum _{j=1}^{n}(-1)^{j+1}K_{j}=K_{1}-K_{2}+K_{3}-...+(-1)^{n+1}K_{n}$ (5)

La cual podemos desarrollar usando el método de Schuster, el cual consiste en separar elementos de la serie en dos partes y formar grupos:

$\sum ={\frac {K_{1}}{2}}+[{\frac {K_{1}}{2}}-K_{2}+{\frac {K_{3}}{2}}]+[{\frac {K_{3}}{2}}-K_{4}+{\frac {K_{5}}{2}}]+...$

Donde el último término puede ser ${\frac {1}{2}}K_{n-1}-K_{n}$ o ${\frac {1}{2}}K_{n}$ si es impar o par, respectivamente.

Ahora, supongamos que $K_{j}$ es mayor que el promedio de sus vecinos $K_{j-1}$ y $K_{j+1}$. Entonces cada uno de los términos en los paréntesis de la ecuación aterior son negativos y resultaría (6):

$\sum <{\frac {K_{1}}{2}}+{\frac {K_{n}}{2}}$ para $n$ par $\sum <{\frac {K_{1}}{2}}+{\frac {K_{n-1}}{2}}-K_{n}$ para $n$ impar

Por otro lado, también la ecuación (5) podemos escribirla de la siguiente manera:

$\sum =K_{1}-{\frac {K_{2}}{2}}-[{\frac {K_{2}}{2}}-K_{3}+{\frac {K_{4}}{2}}]-[{\frac {K_{4}}{2}}-K_{5}+{\frac {K_{6}}{2}}]+...$

Con el último termino siendo $-{\frac {1}{2}}K_{n-1}+K_{n}$ o $-{\frac {1}{2}}K_{n}$ según si $n$ es par o impar.

De forma similar al método de Schuster, la ecuación anterior resulta (7):

$\sum >K_{1}-{\frac {K_{2}}{2}}-{\frac {K_{n-1}}{2}}+K_{n}$ para $n$ par $\sum >K_{1}-{\frac {K_{2}}{2}}-{\frac {K_{n}}{2}}$ para $n$ impar

$K_{j}$ difiere muy poco de los valores de sus vecinos $K_{j-1}$ y $K_{j+1}$ por ello el lado derecho de las ecuaciones (6) y (7) son casi iguales, es decir (8):

$\sum ={\frac {K_{1}}{2}}+{\frac {K_{n}}{2}}$ si $n$ es par $\sum ={\frac {K_{1}}{2}}-{\frac {K_{n}}{2}}$ si $n$ es impar

Solución del problema

Tomando la ecuación (4) y sustituyendo las ecuaciones (8), tenemos (9):

$U(P)=i\lambda (K_{1}\pm K_{n}){\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}$

Donde el signo $\pm$ es positivo o negativo si $n$ es par o impar.

De esta ecuación y la ecuación (3) para $U_{j}$:

$U(P)={\frac {1}{2}}[U_{1}(P)+U_{n}(P)]$

De aquí notamos que la perturbación total $U(P)$ depende sólamente de la perturbación debida a la primera zona $U_{1}$ y la última $U_{n}$. Pero veamos qué pasa con la perturbación $U_{n}$.

Si tomamos la última zona de Fresnel $Z_{n}$, vemos que el la recta $s$ es tangente a la superfice $S$. Es decir, el ángulo $\chi ={\frac {\pi }{2}}$ y por lo tanto $K_{n}(\chi )=0$.

Entonces la ecuación (9) resultaría:

$U(P)=i\lambda K_{1}{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}={\frac {1}{2}}U_{1}(P)$ (10)

Esto quiere decir que la perturbación total $U(P)$ es igual a la mitad de la perturbación debida a la primera zona.

Si tomamos la ecuación (10) para $U(P)$ y la ecuación (3) para $U_{1}(P)$ tendríamos que:

$i\lambda K_{1}=1\Rightarrow K_{1}=-{\frac {i}{\lambda }}={\frac {e^{-i{\frac {\pi }{2}}}}{\lambda }}$ (11)

Es decir, la ecuación (10) resultaría:

$U(P)=i\lambda K_{1}{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}={\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}$ (12)

Obstrucción de un plano

Supongamos que tenemos un plano con una abertura muy pequeña circular perpendicular a $CP$ (ver Figura 1) y además que cubra todas las zonas salvo la mitad de la primera. Usando las ecuaciones (3) y (11), asumiendo que $j=1$ y multiplicando por ${\frac {1}{2}}$:

$U(P)=i\lambda K_{1}{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}={\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}$

Que es el mismo resultado de la ecuación (12), es decir, da el mismo resultado si no tuvieramos el plano.

Ahora supongamos que tenemos un plano pero que cubre todas las zonas de Fresnel salvo la primera. Usando de nueva cuenta la ecuación (3), tenemos:

$U(P)=2i\lambda K_{1}{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}=2{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}$

Que es 4 veces mayor a que si el plano no estuviera (Comparado con la ecuación 10).

Con esto podemos ver que usando el plano, podemos aumentar o disminuir la perturbación sobre algún punto. Eso tiene gran aplicación en la ingeniería, por ejemplo en la constucción de lentes.

Referencia y links

Marx Born & Emil Wolf Principles of Optics 6th Edition

Sobre los lentes de Fresnel: http://teleformacion.edu.aytolacoruna.es/FISICA/document/fisicaInteractiva/OptGeometrica/Instrumentos/fresnel/fresnel.htm