Diferencia entre revisiones de «Optica: Interferencia de haces multiples»
Sin resumen de edición |
|||
| (No se muestran 97 ediciones intermedias de 4 usuarios) | |||
| Línea 1: | Línea 1: | ||
=Interferencia De Haces Múltiples= | |||
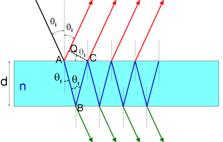
[[Archivo:001_diagrama2.1.jpg|430x330px|thumb|right|Figura 1 Interferencia de haces múltiples de una película paralela. ]] | |||
La interferencia de haces múltiples se da cuando un número muy grande de ondas mutuamente coherentes se hacen interferir. | |||
El método más común de producir este número de ondas mutuamente coherentes es por división de amplitud. Esta división ocurre por reflexión múltiple entre dos superficies paralelas parcialmente reflectoras. | |||
El primer rayo es parcialmente reflejado y parcialmente transmitido en la primer superficie. La parte transmitida es subsecuente-mente reflejada hacia atrás y hacia adelante entre las dos superficies. | |||
<math>\ | Comencemos el análisis matemático calculando la diferencia de fase entre las dos ondas que interfieren, para ello basta con determinar la diferencia de camino óptico <math>\Lambda</math> entre los rayos que representan esas ondas. | ||
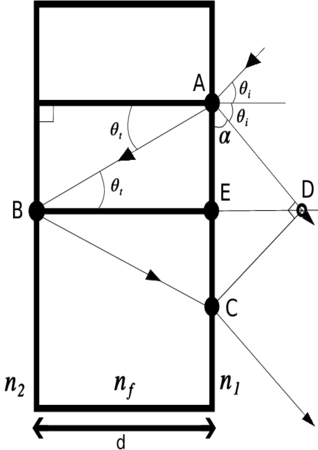
Iniciamos haciendo el cálculo de la diferencia de camino óptico para los dos primeros rayos reflejados. Observemos la Figura 1.1 | |||
[[Archivo:Division.svg|430x450px|thumb|right|Figura 1.1 Diagrama de la diferencia de camino óptico <math>\Lambda</math> entre dos rayos sucesivos]] | |||
Sabemos que la diferencia de camino óptico viene dada por | |||
\begin{equation}\Lambda ={ n }_{ f }(\overline { AB } +\overline { BC } )-{ n }_{ i }(\overline { AD } ).\end{equation} | |||
Como <math>\overline { AB } \equiv \overline { BC } =\frac { d }{ \cos { { \theta }_{ t } } } </math> y tambien del triangulo <math>\Delta \overline { ACD } </math> podemos observar por ángulos complementarios que <math>\cos { \alpha } =\sin { { \theta }_{ i } } </math> | |||
lo | Por lo tanto \begin{equation}\cos { \alpha } \equiv \frac { \overline { AD } }{ \overline { AC } } \equiv \sin { { \theta }_{ i } },\end{equation} | ||
Entonces \begin{equation}\overline { AD } =\overline { AC } \sin { { \theta }_{ i } },\end{equation} | |||
Así \begin{equation}\Lambda ={ 2n }_{ f }\frac { d }{ \cos { { \theta }_{ t } } } -{ n }_{ 1 }\overline { AC } \sin { { \theta }_{ i } }.\end{equation} | |||
De la relación de Snell sabemos que \begin{equation}{ n }_{ 1 }\sin { { \theta }_{ i } } ={ n }_{ f }\sin { { \theta }_{ t } },\end{equation} | |||
Entonces \begin{equation}\Lambda ={ 2n }_{ f }\frac { d }{ \cos { { \theta }_{ t } } } -{ n }_{ 1 }\overline { AC } \frac { { n }_{ f } }{ { n }_{ 1 } } \sin { { \theta }_{ t } }.\end{equation} | |||
De \begin{equation}\tan { { \theta }_{ t } } \equiv \frac { \overline { AE } }{ d } =\frac { \frac { 1 }{ 2 } \overline { AC } }{ d },\end{equation} | |||
Tenemos que \begin{equation}\overline { AC } =2d\tan { { \theta }_{ t } },\end{equation} | |||
Asi \begin{equation}\Lambda ={ 2n }_{ f }\frac { d }{ \cos { { \theta }_{ t } } } -{ n }_{ f }2d\tan { { \theta }_{ t } } \sin { { \theta }_{ i } },\end{equation} | |||
\begin{equation}\Lambda ={ 2n }_{ f }\frac { d }{ \cos { { \theta }_{ t } } } -{ n }_{ f }2d \frac { \sin ^{ 2 }{ { \theta }_{ t } } }{ \cos { { \theta }_{ t } } } ,\end{equation} | |||
Factorizando | |||
\begin{equation}\Lambda =\frac { 2{ n }_{ f }d }{ \cos { { \theta }_{ t } } } (1-\sin ^{ 2 }{ { \theta }_{ t }) },\end{equation} | |||
\begin{equation}\Lambda =\frac { 2{ n }_{ f }d }{ \cos { { \theta }_{ t } } } \cos ^{ 2 }{ { \theta }_{ t } },\end{equation} | |||
Por lo tanto \begin{equation}\Lambda =2{ n }_{ f }d\cos { { \theta }_{ t } }.\end{equation} | |||
Que es la diferencia de camino óptico entre dos rayos (dos ondas planas) consecutivos, que es la misma para cualquier tipo de rayos (ondas) consecutivos tanto transmitidos como reflejados, que no es otra cosa más que la distancia recorrida, a la velocidad de la luz en el vacío, en un tiempo <math>t</math> en un medio con índice de refracción <math>n</math>. | |||
Donde <math>d</math> es la separación entre las dos superficies reflectoras y <math>\theta</math> es el ángulo entre cualquier rayo interno reflejado y la superficie normal. | |||
El desfase o diferencia de fase correspondiente y asociado con la diferencia de camino óptico es precisamente el producto del módulo del vector de onda en el espacio libre y <math>\Lambda</math>, es decir, <math> k_{0}\Lambda</math>. Si la película está sumergida en un solo medio, el índice de refracción podrá escribirse como \begin{equation}n_{1}=n_{2}=n_{f}.\end{equation} | |||
La diferencia de fase correspondiente entre dos rayos sucesivos es entonces | |||
\begin{equation}\delta=\frac{2\pi}{\lambda_{0}}\Lambda=\frac{4\pi}{\lambda_{0}}n_{f}d\cos\theta.\end{equation} | |||
Donde <math>\lambda</math> es la longitud de onda en el medio y <math>n_{f}</math> es el índice de refracción del medio entre las superficies reflectoras. | |||
=Amplitud Total Reflejada= | |||
Ahora definamos las variables. | Ahora definamos las variables. | ||
r es el coeficiente de reflexión de las amplitudes desde el interior del | <math> | ||
r</math> | |||
es el coeficiente de reflexión de las amplitudes desde el interior del interferómetro. | |||
<math> | |||
t</math> | |||
es el coeficiente de transmisión de las amplitudes para un rayo que viene del exterior. | |||
<math> | |||
t'</math> | |||
es el coeficiente de transmisión para las amplitudes para un rayo que sale de la cavidad del interferómetro. | |||
<math> | |||
\delta</math> | |||
es la diferencia de fase entre dos reflexiones consecutivas. | |||
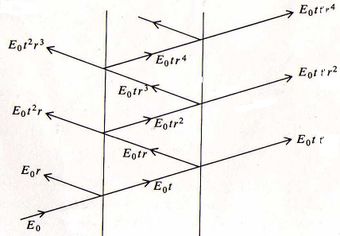
[[Archivo:interferencia HM.jpg|340x240px|thumb|right|Figura 2. Múltiples reflexiones entre dos superficies paralelas. ]] | |||
Tomando la diferencia de fase anterior y sumando las amplitudes de los rayos transmitidos | Tomando la diferencia de fase anterior y sumando las amplitudes de los rayos transmitidos | ||
tenemos entonces | tenemos entonces | ||
\begin{equation}\tilde{E}_{1r}=E_{0}re^{i\omega t},\end{equation} | |||
\begin{equation}\tilde{E}_{1r}=E_{0}tt'r'e^{i\left(\omega t-\delta\right)},\end{equation} | |||
\begin{equation}\tilde{E}_{1r}=E_{0}tt'r'^{3}e^{i\left(\omega t-2\delta\right)},\end{equation} | |||
\begin{equation}\tilde{E}_{1r}=E_{0}tt'r'^{(2N-3)}e^{i\left(\omega t-\left(N-1\right)\delta\right)}.\end{equation} | |||
donde <math>E_{0}e^{i\omega t}</math> es la onda incidente. | donde <math>E_{0}e^{i\omega t}</math> es la onda incidente. | ||
Los términos <math>\delta,2\delta,...,(N-1)\delta</math> son las contribuciones a la fase procedentes de una diferencia de longitud de camino óptico entre rayos adyacentes. | Los términos <math>\delta,2\delta,...,(N-1)\delta</math> son las contribuciones a la fase procedentes de una diferencia de longitud de camino óptico entre rayos adyacentes. | ||
[[Archivo:66666.jpg|340x240px|thumb|right|Figura 2.1 Caminos de los rayos de luz de múltiples reflexiones entre dos superficies paralelas. ]] | |||
\begin{equation}\tilde{E}_{rT}=\sum E_{ir}=E_{0}re^{i\omega t}+\sum_{j=2}^{N}E_{0}tr'^{(2j-3)}t'e^{i\left(\omega t-\left(j-1\right)\delta\right)},\end{equation} | |||
Arreglando la expresión | |||
\begin{equation}\tilde{E}_{rT}=E_{0}e^{i\omega t}\left[r+\left\{ \sum_{j=2}^{N}\left(r'^{2}e^{i\delta}\right)^{j-2}\right\} r'tt'e^{-i\delta}\right].\end{equation} | |||
Si <math>[r'^{2}e^{i\delta}]<1</math>, y si el número de términos en la serie se aproxima al infinito, la serie converge. La onda resultante se transforma en: | Si <math>[r'^{2}e^{i\delta}]<1</math>, y si el número de términos en la serie se aproxima al infinito, la serie converge. La onda resultante se transforma en: | ||
<math> | <math>\tilde{E}_{r}=E_{0}e^{i\omega t}\left[r+\frac{r'tt'e^{-i\delta}}{1-r'^{2}e^{-i\delta}}\right].</math> | ||
En el caso de absorción cero, cuando no se extrae energía de las | En el caso de absorción cero, cuando no se extrae energía de las ondas, se pueden utilizar las relaciones <math>tt'=1-r^{2}, y r=-r' </math> para volver a escribir la ecuación como | ||
\begin{equation}\tilde{E}_{r}=E_{0}e^{i\omega t}\left[\frac{r\left(1-e^{-i\delta}\right)}{1-r^{2}e^{-i\delta}}\right].\end{equation} | |||
La irradiancia se obtiene tomando el cuadrado complejo de esta amplitud quedando | La irradiancia se obtiene tomando el cuadrado complejo de esta amplitud quedando | ||
\begin{equation}I_{r}=\tilde{E}_{r}\tilde{E}_{r}^{*}=E_{0}^{2}\left[\frac{r\left(1-e^{i\delta}\right)}{1-r^{2}e^{i\delta}}\right]\left[\frac{r\left(1-e^{i\delta}\right)}{1-r^{2}e^{i\delta}}\right],\end{equation} | |||
Realizando el producto y simplificando se obtiene que la irradiancia es | |||
\begin{equation}I_{r}=E_{0}^{2}\frac{2r^{2}\left(1-\cos\theta\right)}{\left(1+r^{4}\right)-2r^{2}\cos\delta}.\end{equation} | |||
=Amplitud Total Transmitida= | |||
De forma parecida, las amplitudes de las ondas transmitidas proporcionadas por | De forma parecida, las amplitudes de las ondas transmitidas proporcionadas por | ||
\begin{equation}\tilde{E}_{1t}=E_{0}tt'e^{i\omega t},\end{equation} | |||
\begin{equation}\tilde{E}_{2t}=E_{0}tt'r'^{2}e^{i\left(\omega t-\delta\right)},\end{equation} | |||
\begin{equation}\tilde{E}_{3t}=E_{0}tt'r'^{4}e^{i\left(\omega t-2\delta\right)},\end{equation} | |||
\begin{equation}\tilde{E}_{Nr}=E_{0}tt'r'^{2\left(N-1\right)}e^{i\left(\omega t-\left(N-1\right)\delta\right)},\end{equation} | |||
\begin{equation}\tilde{E}_{tT}=E_{0}e^{i\omega t}\left[tt'\sum_{j=1}^{N}r'^{(j-1)}e^{-i\left(j-1\right)\delta}\right],\end{equation} | |||
Pueden sumarse para dar como resultado | Pueden sumarse para dar como resultado | ||
\begin{equation}\tilde{E}_{t}=E_{0}e^{i\omega t}\frac{tt'}{1-r^{2}e^{-i\delta}}.\end{equation} | |||
Multiplicando también por su complejo conjugado | Multiplicando también por su complejo conjugado | ||
\begin{equation}I_{t}=I_{i}\left(tt'\right)^{2}\frac{1}{1-r^{2}e^{-i\delta}}\frac{1}{1-r^{2}e^{i\delta}},\end{equation} | |||
se obtiene la irradiancia del haz transmitido | se obtiene la irradiancia del haz transmitido | ||
\begin{equation}I_{t}=I_{i}\left(tt'\right)^{2}\frac{1}{\left(1+r^{4}\right)-2r^{2}\cos\delta}......(*) | |||
\end{equation} | |||
o bien | o bien | ||
\begin{equation}I_{t}=I_{i}\frac{\left(1-r^{2}\right)^{2}}{\left(1+r^{4}\right)-2r^{2}\cos\delta}.\end{equation} | |||
Notemos que para dieléctricos | Notemos que para dieléctricos | ||
\begin{equation}I_{r}+I_{t}=\frac{\left(1-r^{2}\right)^{2}+2r^{2}\left(1-\cos\delta\right)}{\left(1+r^{4}\right)-2r^{2}\cos\delta}I_{i},\end{equation} | |||
expandiendo la ecuación y despejando | expandiendo la ecuación y despejando | ||
\begin{equation}I_{r}+I_{t}=\frac{1+r^{4}-2r^{2}-2r^{2}\cos\delta+2r^{2}}{\left(1+r^{4}\right)-2r^{2}\cos\delta}I_{i}=I_{i}.\end{equation} | |||
si no se absorbe nada de la energía incidente, la densidad de flujo de la onda incidente será exactamente igual a la suma de la densidad de flujo reflejada por la película más la densidad de flujo total transmitida al salir de la película, es decir | si no se absorbe nada de la energía incidente, la densidad de flujo de la onda incidente será exactamente igual a la suma de la densidad de flujo reflejada por la película más la densidad de flujo total transmitida al salir de la película, es decir | ||
\begin{equation}I_{i}=I_{i}=I_{r}+I_{t}.\end{equation} | |||
si <math>\delta=2\pi m</math> Existirá un máximo | |||
\begin{equation}I_{tmax}=I_{i}\frac{\left(1-r^{2}\right)^{2}}{1+r^{4}-2r^{2}}=I_{i},\end{equation} | |||
\begin{equation}I_{rmin}=0.\end{equation}Por conservación de energía. | |||
Ahora si <math>\delta=\left(2m+1\right)\pi</math> se producirá un mínimo en la densidad del flujo transmitido | |||
\begin{equation}I_{tmin}=I_{i}\frac{\left(1-r^{2}\right)^{2}}{(1+r^{2})^{2}}.\end{equation} | |||
El máximo correspondiente en la densidad de flujo reflejado es | El máximo correspondiente en la densidad de flujo reflejado es | ||
\begin{equation}I_{rmax}=I_{i}\frac{4r^{2}}{(1+r^{2})^{2}}.\end{equation} | |||
Si escribimos | Si escribimos | ||
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{(1-r^{2})^{2}}{1+r^{4}-2r^{2}\left(\cos^{2}\frac{\delta}{2}-\sin^{2}\frac{\delta}{2}\right)},\end{equation} | |||
Mediante la identidad trigonométrica \begin{equation}\sin^{2}\theta+\cos^{2}\theta=1,\end{equation} | |||
Entonces | |||
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{(1-r^{2})^{2}}{1+r^{4}-2r^{2}\left(1-2\sin^{2}\frac{\delta}{2}\right)},\end{equation} | |||
desarrollando el | desarrollando el álgebra y agrupando términos | ||
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{\left(1-r^{2}\right)^{2}}{\left(1-r^{2}\right)^{2}+4r^{2}\sin^{2}\frac{\delta}{2}},\end{equation} | |||
Simplificando se obtiene | |||
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{1}{1+\left[\frac{2r}{1-r^{2}}\sin\frac{\delta}{2}\right]^{2}},\end{equation} | |||
que es llamado coeficiente de fineza | que es llamado coeficiente de fineza | ||
\begin{equation}\mathcal{F}=\left(\frac{2r}{1-r^{2}}\right)^{2}=\frac{4R}{(1-R)^{2}},\end{equation} | |||
con lo cual estas ecuaciones se | con lo cual estas ecuaciones se podrán escribir como | ||
\begin{equation}\frac{I_{r}}{I_{t}}=\frac{\mathcal{F}\sin^{2}\frac{\delta}{2}}{1+\mathcal{F}\sin^{2}\frac{\delta}{2}},\end{equation} | |||
y | |||
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{1}{1+\mathcal{F}\sin^{2}\frac{\delta}{2}}\equiv A\left(\delta\right).\end{equation} | |||
En donde el término <math>\frac{1}{1+\ | En donde el término <math>\frac{1}{1+\mathcal{F}\sin^{2}\frac{\delta}{2}}\equiv A\left(\delta\right)</math> se denomina función de Airy y representa la distribución de la densidad de flujo transmitida | ||
=Función de Airy= | |||
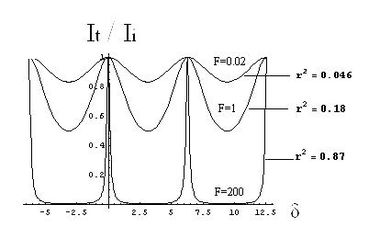
[[Archivo:inter.jpg|380x250px|thumb|right|Figura 4. Función de Airy]] | |||
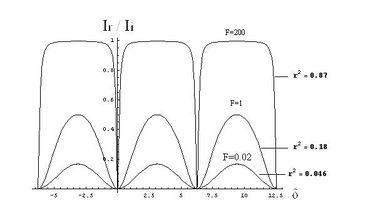
[[Archivo:funcion A.jpg|380x250px|thumb|right|Figura 4.1 Uno menos la Función de Airy ]] | |||
las | La funcion de Airy representa la distribución de la densidad de flujo transmitida ( Figura 4). La función complementaria <math>[1-A\left(\theta\right)]</math>, se observa en la Figura 4.1 Cuando <math>\frac{\delta}{2}=\pi m</math> la función de Airy es igual a la unidad para todos los valores de <math>F</math> y por lo tanto de <math>r</math>. Al aproximarse esta a uno, la densidad de flujo transmitido es muy pequeño, excepto dentro de máximos agudos centrados en los puntos <math>\frac{\delta}{2}=\pi m</math>. La interferencia de haces múltiples conduce a una redistribución de la densidad de energía en comparación con la distribución sinusoidal de dos haces. | ||
La función de Airy es una función de <math>\theta_{t}</math> o <math>\theta_{i}</math> debido a su dependencia de <math>\delta</math>. Cada máximo de la curva de densidad de flujo corresponde a un determinado <math>\delta</math> y a una <math>\theta_{i}</math> particular. En el caso de una placa plana paralela,las franjas, en luz transmitida, consistirán de una serie de anillos brillantes delgados sobre un fondo casi completamente oscuro. En luz reflejada, las franjas serán estrechas y oscuras sobre un fondo casi uniformemente brillante. | |||
Las franjas de espesor constante pueden también hacerse agudas y estrechas por medio de un recubrimiento ligero de plata sobre las superficies reflectoras a fin de producir interferencia de haces múltiples. | |||
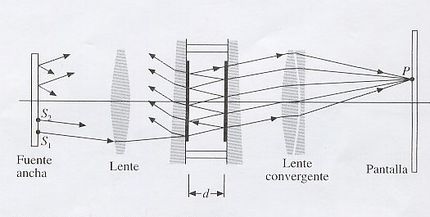
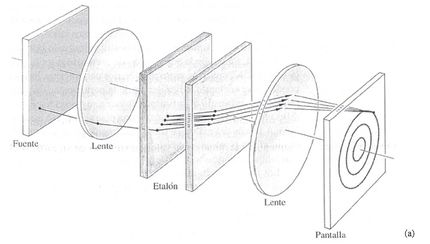
=Interferómetro de Fabry-Perot= | |||
Este tipo de interferómetro forma las franjas con base en múltiples reflexiones en dos superficies planas y paralelas, por lo tanto la interferencia no es solo entre 2 frentes de onda, sino entre un número muy grande de ellas. A fin de lograr estas reflexiones múltiples, las superficies se recubren con una capa reflectora ya sea metálica o dieléctrica, separadas una distancia <math>d</math> . Con este tipo de interferencia múltiple las franjas ya no tienen perfil senoidal como cuando son solo 2 frentes de onda sino que tienen un perfil muy angosto, aumentando así la precisión con que se puede medir su forma y posición. En este interferómetro las franjas son de igual inclinación usando una fuente extendida. | |||
El espacio de aire contenido generalmente varia de algunos milímetros a varios centímetros cuando el aparato se usa para interferometría, y a menudo para mayores distancias cuando se emplea como cavidad resonante de láser. Si el espacio puede variarse mecánicamente con el movimiento de uno de los espejos, se llama interferómetro. Cuando los espejos se mantienen fijos y se ajustan en paralelo fijando con un tornillo algún tipo de espaciador (invar o cuarzo), suele llamársela ''Etalon'' (Figura 5.) | |||
Todos los rayos incidentes en el espacio separador con un determinado ángulo resultaran en una sola franja circular de irradiancia uniforme (Figura 5.1). Con una fuente difusa ancha, las bandas de interferencia serán anillos concéntricos estrechos (Figura 5.2), correspondientes a la distribución de transmisión de haces múltiples. | |||
Las películas de metal parcialmente transparentes que se emplean frecuentemente para aumentar la reflectancia <math>(R=r^{2})</math> absorberan una fracción A de la densidad de flujo, esta fracción se denomina absortancia. [[Archivo:001_diagrama2.3.jpg|430x330px|thumb|right|Figura 5. Interferómetro de Fabry-Perot ]] | |||
[[Archivo:001_diagrama2.4.jpg|430x330px|thumb|right|Figura 5.1 Franja Circular ]] | |||
[[Archivo:001_diagrama2.5.jpg|430x330px|thumb|right|Figura 5.2 Anillos Concéntricos ]] | |||
La expresión | La expresión | ||
\begin{equation}T+R=1,\end{equation} | |||
donde T es la transmitancia, se reescribe como | donde T es la transmitancia, se reescribe como | ||
\begin{equation}T+R+A=1 ..............(**)\end{equation} | |||
Las películas | Las películas metálicas presentan un desplazamiento adicional de fase <math>\phi(\theta_{i})</math>, que puede diferir de cero o <math>\pi</math>. El desfase entre dos ondas transmitidas sucesivamente es entonces | ||
\begin{equation}\delta=\frac{4\pi}{\lambda}n_{t}d\cos\theta+2\delta_{r}.\end{equation} | |||
Para las condiciones que estan siendo consideradas, | Para las condiciones que estan siendo consideradas, <math>\theta_{i}</math> es pequeño y <math>\phi</math> puede considerarse constante. Por lo general, d es tan grande y <math>\lambda_{0}</math> tan pequeño que <math>\phi</math> puede omitirse. entonces la ecuación (*) puede expresarse como | ||
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{T^{2}}{1+R^{2}-2R\cos\delta},\end{equation} | |||
o de manera equivalente | o de manera equivalente | ||
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{T^{2}}{(1-R^{2})}A(\delta),\end{equation} | |||
Utilizando la ecuación (*) y la definición de la función de Airy, obtenemos | Utilizando la ecuación (**) y la definición de la función de Airy, obtenemos | ||
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{\left(1-R-A\right)^{2}}{\left(1-R\right)^{2}}A\left(\delta\right),\end{equation} | |||
simplificando | simplificando | ||
\begin{equation}\frac{I_{t}}{I_{i}}=\left(1-\frac{A}{1-R}\right)^{2}A\left(\delta\right).\end{equation} | |||
Dado que la parte absorbida A no es nunca cero, los máximos de la densidad de flujo transmitido siempre serán algo menor que . Por lo tanto, el máximo de transmisión se define como | Dado que la parte absorbida A no es nunca cero, los máximos de la densidad de flujo transmitido <math>(I_{tmax)}</math> | ||
siempre serán algo menor que <math>I_{i}</math>. Por lo tanto, el máximo de transmisión se define como | |||
\begin{equation}I_{i}\left(1-\frac{A}{1-R}\right)^{2}\equiv I_{tmax}.\end{equation} | |||
La irradiancia relativa de la distribución de franjas estará determinada por la función de Airy, ya que | La irradiancia relativa de la distribución de franjas estará determinada por la función de Airy, ya que | ||
\begin{equation}\frac{I_{t}}{I_{tmax}}=A\left(\theta\right)=\frac{1}{1+\F\sin^{2}\frac{\delta}{2}}.\end{equation} | |||
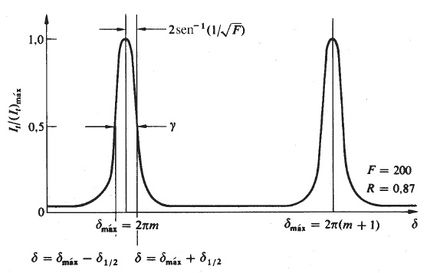
Los máximos en la transmisión se dan para valores especificos del desfase (Figura 5.3) | |||
[[Archivo:001_diagrama2.6.jpg|430x330px|thumb|right|Figura 5.3 Interferómetro de Fabry-Perot ]] | |||
\begin{equation}\delta_{max}=2\pi m.\end{equation} | |||
<math>\delta_{max} | Por tanto, la irradiancia disminuirá a la mitad su valor máximo cada vez que <math>\delta=\delta_{max}\pm\delta_{\frac{1}{2}}</math> dado que | ||
\begin{equation}\gamma=2\frac{\delta_{i}}{2},\end{equation} | |||
\begin{equation}\frac{1}{2}=\frac{1}{1+\F\sin\left(\frac{\frac{\delta}{2}+\delta_{max}}{2}\right)},\end{equation} | |||
de donde se ve que | de donde se ve que | ||
\begin{equation}\sin\left(\frac{\delta_{\frac{1}{2}}}{2}+m\pi\right)=\pm sin\left(\frac{\delta_{\frac{1}{2}}}{2}\right),\end{equation} | |||
elevando al cuadrado ambos lados de la ecuación | elevando al cuadrado ambos lados de la ecuación | ||
\begin{equation}\sin^{2}\left(\frac{\delta_{\frac{1}{2}}}{2}+m\pi\right)=\sin^{2}\left(\frac{\delta_{\frac{1}{2}}}{2}\right),\end{equation} | |||
entonces | entonces | ||
\begin{equation}\sin^{2}\left(\frac{\delta_{\frac{1}{2}}}{2}\right)=\frac{1}{\mathcal{F}},\end{equation} | |||
Eliminando el término cuadrado de la ecuación de lado derecho y despejando obtenemos | |||
\begin{equation}\delta_{\frac{1}{2}}=2\arcsin\left(\sqrt{\frac{1}{\mathcal{F}}}\right),\end{equation} | |||
<math>\gamma=4\arcsin\left(\frac{1}{\sqrt{\ | Sustituyendo el valor de <math>\gamma</math> | ||
\begin{equation}\gamma=4\arcsin\left(\frac{1}{\sqrt{\mathcal{F}}}\right),\end{equation} | |||
Dado que F es, por lo general muy grande, | Dado que <math>\mathcal{F}</math> es, por lo general muy grande, | ||
\begin{equation}\arcsin\left(\sqrt{\frac{1}{\mathcal{F}}}\right)\approxeq\left(\sqrt{\frac{1}{\mathcal{F}}}\right),\end{equation} | |||
entonces se obtiene | entonces se obtiene | ||
\begin{equation}\frac{\delta_{\frac{1}{2}}}{2}=\frac{1}{\sqrt{\mathcal{F}}},\end{equation} | |||
y por lo tanto el ancho medio <math>\gamma=2\frac{\delta_{i}}{2}</math> es igual a | y por lo tanto el ancho medio <math>\gamma=2\frac{\delta_{i}}{2}</math> es igual a | ||
\begin{equation}\gamma\approxeq\left(\frac{4}{\sqrt{\mathcal{F}}}\right).\end{equation} | |||
Otro valor interesante es la relación de la separación de los máximos adyacentes con respecto al ancho medio. Denominada fineza | |||
\begin{equation}\Upsilon\equiv\frac{2\pi}{\gamma}=\frac{\pi}{2}\sqrt{\mathcal{F}}.\end{equation} | |||
[https://youtu.be/Aqftqp29aWE Video: Construyendo Un Interferometro Fabry-Perot] | |||
=Referencias= | |||
<references/>Hecht E. Óptica, Addisson Wesley Iberoamericana, 2000 [Cap.9] | |||
[[Category:optica]] | |||
Revisión actual - 04:21 19 sep 2023
Interferencia De Haces Múltiples
La interferencia de haces múltiples se da cuando un número muy grande de ondas mutuamente coherentes se hacen interferir.
El método más común de producir este número de ondas mutuamente coherentes es por división de amplitud. Esta división ocurre por reflexión múltiple entre dos superficies paralelas parcialmente reflectoras.
El primer rayo es parcialmente reflejado y parcialmente transmitido en la primer superficie. La parte transmitida es subsecuente-mente reflejada hacia atrás y hacia adelante entre las dos superficies.
Comencemos el análisis matemático calculando la diferencia de fase entre las dos ondas que interfieren, para ello basta con determinar la diferencia de camino óptico entre los rayos que representan esas ondas.
Iniciamos haciendo el cálculo de la diferencia de camino óptico para los dos primeros rayos reflejados. Observemos la Figura 1.1
Sabemos que la diferencia de camino óptico viene dada por \begin{equation}\Lambda ={ n }_{ f }(\overline { AB } +\overline { BC } )-{ n }_{ i }(\overline { AD } ).\end{equation}
Como Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline { AB } \equiv \overline { BC } =\frac { d }{ \cos { { \theta }_{ t } } } y tambien del triangulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \Delta \overline { ACD } podemos observar por ángulos complementarios que
Por lo tanto \begin{equation}\cos { \alpha } \equiv \frac { \overline { AD } }{ \overline { AC } } \equiv \sin { { \theta }_{ i } },\end{equation}
Entonces \begin{equation}\overline { AD } =\overline { AC } \sin { { \theta }_{ i } },\end{equation}
Así \begin{equation}\Lambda ={ 2n }_{ f }\frac { d }{ \cos { { \theta }_{ t } } } -{ n }_{ 1 }\overline { AC } \sin { { \theta }_{ i } }.\end{equation}
De la relación de Snell sabemos que \begin{equation}{ n }_{ 1 }\sin { { \theta }_{ i } } ={ n }_{ f }\sin { { \theta }_{ t } },\end{equation}
Entonces \begin{equation}\Lambda ={ 2n }_{ f }\frac { d }{ \cos { { \theta }_{ t } } } -{ n }_{ 1 }\overline { AC } \frac { { n }_{ f } }{ { n }_{ 1 } } \sin { { \theta }_{ t } }.\end{equation}
De \begin{equation}\tan { { \theta }_{ t } } \equiv \frac { \overline { AE } }{ d } =\frac { \frac { 1 }{ 2 } \overline { AC } }{ d },\end{equation}
Tenemos que \begin{equation}\overline { AC } =2d\tan { { \theta }_{ t } },\end{equation}
Asi \begin{equation}\Lambda ={ 2n }_{ f }\frac { d }{ \cos { { \theta }_{ t } } } -{ n }_{ f }2d\tan { { \theta }_{ t } } \sin { { \theta }_{ i } },\end{equation}
\begin{equation}\Lambda ={ 2n }_{ f }\frac { d }{ \cos { { \theta }_{ t } } } -{ n }_{ f }2d \frac { \sin ^{ 2 }{ { \theta }_{ t } } }{ \cos { { \theta }_{ t } } } ,\end{equation}
Factorizando
\begin{equation}\Lambda =\frac { 2{ n }_{ f }d }{ \cos { { \theta }_{ t } } } (1-\sin ^{ 2 }{ { \theta }_{ t }) },\end{equation}
\begin{equation}\Lambda =\frac { 2{ n }_{ f }d }{ \cos { { \theta }_{ t } } } \cos ^{ 2 }{ { \theta }_{ t } },\end{equation}
Por lo tanto \begin{equation}\Lambda =2{ n }_{ f }d\cos { { \theta }_{ t } }.\end{equation}
Que es la diferencia de camino óptico entre dos rayos (dos ondas planas) consecutivos, que es la misma para cualquier tipo de rayos (ondas) consecutivos tanto transmitidos como reflejados, que no es otra cosa más que la distancia recorrida, a la velocidad de la luz en el vacío, en un tiempo en un medio con índice de refracción Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): n .
Donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): d
es la separación entre las dos superficies reflectoras y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \theta
es el ángulo entre cualquier rayo interno reflejado y la superficie normal.
El desfase o diferencia de fase correspondiente y asociado con la diferencia de camino óptico es precisamente el producto del módulo del vector de onda en el espacio libre y , es decir, . Si la película está sumergida en un solo medio, el índice de refracción podrá escribirse como \begin{equation}n_{1}=n_{2}=n_{f}.\end{equation}
La diferencia de fase correspondiente entre dos rayos sucesivos es entonces
\begin{equation}\delta=\frac{2\pi}{\lambda_{0}}\Lambda=\frac{4\pi}{\lambda_{0}}n_{f}d\cos\theta.\end{equation}
Donde es la longitud de onda en el medio y es el índice de refracción del medio entre las superficies reflectoras.
Amplitud Total Reflejada
Ahora definamos las variables.
es el coeficiente de reflexión de las amplitudes desde el interior del interferómetro.
es el coeficiente de transmisión de las amplitudes para un rayo que viene del exterior.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): t' es el coeficiente de transmisión para las amplitudes para un rayo que sale de la cavidad del interferómetro.
es la diferencia de fase entre dos reflexiones consecutivas.
Tomando la diferencia de fase anterior y sumando las amplitudes de los rayos transmitidos tenemos entonces
\begin{equation}\tilde{E}_{1r}=E_{0}re^{i\omega t},\end{equation}
\begin{equation}\tilde{E}_{1r}=E_{0}tt'r'e^{i\left(\omega t-\delta\right)},\end{equation}
\begin{equation}\tilde{E}_{1r}=E_{0}tt'r'^{3}e^{i\left(\omega t-2\delta\right)},\end{equation}
\begin{equation}\tilde{E}_{1r}=E_{0}tt'r'^{(2N-3)}e^{i\left(\omega t-\left(N-1\right)\delta\right)}.\end{equation}
donde es la onda incidente.
Los términos son las contribuciones a la fase procedentes de una diferencia de longitud de camino óptico entre rayos adyacentes.
\begin{equation}\tilde{E}_{rT}=\sum E_{ir}=E_{0}re^{i\omega t}+\sum_{j=2}^{N}E_{0}tr'^{(2j-3)}t'e^{i\left(\omega t-\left(j-1\right)\delta\right)},\end{equation}
Arreglando la expresión
\begin{equation}\tilde{E}_{rT}=E_{0}e^{i\omega t}\left[r+\left\{ \sum_{j=2}^{N}\left(r'^{2}e^{i\delta}\right)^{j-2}\right\} r'tt'e^{-i\delta}\right].\end{equation}
Si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): [r'^{2}e^{i\delta}]<1 , y si el número de términos en la serie se aproxima al infinito, la serie converge. La onda resultante se transforma en:
En el caso de absorción cero, cuando no se extrae energía de las ondas, se pueden utilizar las relaciones para volver a escribir la ecuación como
\begin{equation}\tilde{E}_{r}=E_{0}e^{i\omega t}\left[\frac{r\left(1-e^{-i\delta}\right)}{1-r^{2}e^{-i\delta}}\right].\end{equation}
La irradiancia se obtiene tomando el cuadrado complejo de esta amplitud quedando
\begin{equation}I_{r}=\tilde{E}_{r}\tilde{E}_{r}^{*}=E_{0}^{2}\left[\frac{r\left(1-e^{i\delta}\right)}{1-r^{2}e^{i\delta}}\right]\left[\frac{r\left(1-e^{i\delta}\right)}{1-r^{2}e^{i\delta}}\right],\end{equation}
Realizando el producto y simplificando se obtiene que la irradiancia es
\begin{equation}I_{r}=E_{0}^{2}\frac{2r^{2}\left(1-\cos\theta\right)}{\left(1+r^{4}\right)-2r^{2}\cos\delta}.\end{equation}
Amplitud Total Transmitida
De forma parecida, las amplitudes de las ondas transmitidas proporcionadas por
\begin{equation}\tilde{E}_{1t}=E_{0}tt'e^{i\omega t},\end{equation}
\begin{equation}\tilde{E}_{2t}=E_{0}tt'r'^{2}e^{i\left(\omega t-\delta\right)},\end{equation}
\begin{equation}\tilde{E}_{3t}=E_{0}tt'r'^{4}e^{i\left(\omega t-2\delta\right)},\end{equation}
\begin{equation}\tilde{E}_{Nr}=E_{0}tt'r'^{2\left(N-1\right)}e^{i\left(\omega t-\left(N-1\right)\delta\right)},\end{equation}
\begin{equation}\tilde{E}_{tT}=E_{0}e^{i\omega t}\left[tt'\sum_{j=1}^{N}r'^{(j-1)}e^{-i\left(j-1\right)\delta}\right],\end{equation}
Pueden sumarse para dar como resultado
\begin{equation}\tilde{E}_{t}=E_{0}e^{i\omega t}\frac{tt'}{1-r^{2}e^{-i\delta}}.\end{equation}
Multiplicando también por su complejo conjugado
\begin{equation}I_{t}=I_{i}\left(tt'\right)^{2}\frac{1}{1-r^{2}e^{-i\delta}}\frac{1}{1-r^{2}e^{i\delta}},\end{equation}
se obtiene la irradiancia del haz transmitido
\begin{equation}I_{t}=I_{i}\left(tt'\right)^{2}\frac{1}{\left(1+r^{4}\right)-2r^{2}\cos\delta}......(*) \end{equation}
o bien
\begin{equation}I_{t}=I_{i}\frac{\left(1-r^{2}\right)^{2}}{\left(1+r^{4}\right)-2r^{2}\cos\delta}.\end{equation}
Notemos que para dieléctricos
\begin{equation}I_{r}+I_{t}=\frac{\left(1-r^{2}\right)^{2}+2r^{2}\left(1-\cos\delta\right)}{\left(1+r^{4}\right)-2r^{2}\cos\delta}I_{i},\end{equation}
expandiendo la ecuación y despejando
\begin{equation}I_{r}+I_{t}=\frac{1+r^{4}-2r^{2}-2r^{2}\cos\delta+2r^{2}}{\left(1+r^{4}\right)-2r^{2}\cos\delta}I_{i}=I_{i}.\end{equation}
si no se absorbe nada de la energía incidente, la densidad de flujo de la onda incidente será exactamente igual a la suma de la densidad de flujo reflejada por la película más la densidad de flujo total transmitida al salir de la película, es decir
\begin{equation}I_{i}=I_{i}=I_{r}+I_{t}.\end{equation}
si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \delta=2\pi m Existirá un máximo
\begin{equation}I_{tmax}=I_{i}\frac{\left(1-r^{2}\right)^{2}}{1+r^{4}-2r^{2}}=I_{i},\end{equation}
\begin{equation}I_{rmin}=0.\end{equation}Por conservación de energía.
Ahora si se producirá un mínimo en la densidad del flujo transmitido
\begin{equation}I_{tmin}=I_{i}\frac{\left(1-r^{2}\right)^{2}}{(1+r^{2})^{2}}.\end{equation}
El máximo correspondiente en la densidad de flujo reflejado es
\begin{equation}I_{rmax}=I_{i}\frac{4r^{2}}{(1+r^{2})^{2}}.\end{equation}
Si escribimos
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{(1-r^{2})^{2}}{1+r^{4}-2r^{2}\left(\cos^{2}\frac{\delta}{2}-\sin^{2}\frac{\delta}{2}\right)},\end{equation}
Mediante la identidad trigonométrica \begin{equation}\sin^{2}\theta+\cos^{2}\theta=1,\end{equation}
Entonces
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{(1-r^{2})^{2}}{1+r^{4}-2r^{2}\left(1-2\sin^{2}\frac{\delta}{2}\right)},\end{equation}
desarrollando el álgebra y agrupando términos
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{\left(1-r^{2}\right)^{2}}{\left(1-r^{2}\right)^{2}+4r^{2}\sin^{2}\frac{\delta}{2}},\end{equation}
Simplificando se obtiene
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{1}{1+\left[\frac{2r}{1-r^{2}}\sin\frac{\delta}{2}\right]^{2}},\end{equation}
que es llamado coeficiente de fineza
\begin{equation}\mathcal{F}=\left(\frac{2r}{1-r^{2}}\right)^{2}=\frac{4R}{(1-R)^{2}},\end{equation}
con lo cual estas ecuaciones se podrán escribir como
\begin{equation}\frac{I_{r}}{I_{t}}=\frac{\mathcal{F}\sin^{2}\frac{\delta}{2}}{1+\mathcal{F}\sin^{2}\frac{\delta}{2}},\end{equation}
y
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{1}{1+\mathcal{F}\sin^{2}\frac{\delta}{2}}\equiv A\left(\delta\right).\end{equation}
En donde el término se denomina función de Airy y representa la distribución de la densidad de flujo transmitida
Función de Airy
La funcion de Airy representa la distribución de la densidad de flujo transmitida ( Figura 4). La función complementaria Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): [1-A\left(\theta\right)]
, se observa en la Figura 4.1 Cuando la función de Airy es igual a la unidad para todos los valores de y por lo tanto de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): r
. Al aproximarse esta a uno, la densidad de flujo transmitido es muy pequeño, excepto dentro de máximos agudos centrados en los puntos . La interferencia de haces múltiples conduce a una redistribución de la densidad de energía en comparación con la distribución sinusoidal de dos haces.
La función de Airy es una función de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \theta_{t}
o debido a su dependencia de . Cada máximo de la curva de densidad de flujo corresponde a un determinado y a una Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \theta_{i}
particular. En el caso de una placa plana paralela,las franjas, en luz transmitida, consistirán de una serie de anillos brillantes delgados sobre un fondo casi completamente oscuro. En luz reflejada, las franjas serán estrechas y oscuras sobre un fondo casi uniformemente brillante.
Las franjas de espesor constante pueden también hacerse agudas y estrechas por medio de un recubrimiento ligero de plata sobre las superficies reflectoras a fin de producir interferencia de haces múltiples.
Interferómetro de Fabry-Perot
Este tipo de interferómetro forma las franjas con base en múltiples reflexiones en dos superficies planas y paralelas, por lo tanto la interferencia no es solo entre 2 frentes de onda, sino entre un número muy grande de ellas. A fin de lograr estas reflexiones múltiples, las superficies se recubren con una capa reflectora ya sea metálica o dieléctrica, separadas una distancia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): d . Con este tipo de interferencia múltiple las franjas ya no tienen perfil senoidal como cuando son solo 2 frentes de onda sino que tienen un perfil muy angosto, aumentando así la precisión con que se puede medir su forma y posición. En este interferómetro las franjas son de igual inclinación usando una fuente extendida.
El espacio de aire contenido generalmente varia de algunos milímetros a varios centímetros cuando el aparato se usa para interferometría, y a menudo para mayores distancias cuando se emplea como cavidad resonante de láser. Si el espacio puede variarse mecánicamente con el movimiento de uno de los espejos, se llama interferómetro. Cuando los espejos se mantienen fijos y se ajustan en paralelo fijando con un tornillo algún tipo de espaciador (invar o cuarzo), suele llamársela Etalon (Figura 5.)
Todos los rayos incidentes en el espacio separador con un determinado ángulo resultaran en una sola franja circular de irradiancia uniforme (Figura 5.1). Con una fuente difusa ancha, las bandas de interferencia serán anillos concéntricos estrechos (Figura 5.2), correspondientes a la distribución de transmisión de haces múltiples.
Las películas de metal parcialmente transparentes que se emplean frecuentemente para aumentar la reflectancia absorberan una fracción A de la densidad de flujo, esta fracción se denomina absortancia.
La expresión
\begin{equation}T+R=1,\end{equation} donde T es la transmitancia, se reescribe como
\begin{equation}T+R+A=1 ..............(**)\end{equation}
Las películas metálicas presentan un desplazamiento adicional de fase , que puede diferir de cero o . El desfase entre dos ondas transmitidas sucesivamente es entonces
\begin{equation}\delta=\frac{4\pi}{\lambda}n_{t}d\cos\theta+2\delta_{r}.\end{equation}
Para las condiciones que estan siendo consideradas, es pequeño y puede considerarse constante. Por lo general, d es tan grande y tan pequeño que puede omitirse. entonces la ecuación (*) puede expresarse como
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{T^{2}}{1+R^{2}-2R\cos\delta},\end{equation}
o de manera equivalente
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{T^{2}}{(1-R^{2})}A(\delta),\end{equation}
Utilizando la ecuación (**) y la definición de la función de Airy, obtenemos
\begin{equation}\frac{I_{t}}{I_{i}}=\frac{\left(1-R-A\right)^{2}}{\left(1-R\right)^{2}}A\left(\delta\right),\end{equation}
simplificando
\begin{equation}\frac{I_{t}}{I_{i}}=\left(1-\frac{A}{1-R}\right)^{2}A\left(\delta\right).\end{equation}
Dado que la parte absorbida A no es nunca cero, los máximos de la densidad de flujo transmitido siempre serán algo menor que . Por lo tanto, el máximo de transmisión se define como
\begin{equation}I_{i}\left(1-\frac{A}{1-R}\right)^{2}\equiv I_{tmax}.\end{equation}
La irradiancia relativa de la distribución de franjas estará determinada por la función de Airy, ya que
\begin{equation}\frac{I_{t}}{I_{tmax}}=A\left(\theta\right)=\frac{1}{1+\F\sin^{2}\frac{\delta}{2}}.\end{equation}
Los máximos en la transmisión se dan para valores especificos del desfase (Figura 5.3)
\begin{equation}\delta_{max}=2\pi m.\end{equation}
Por tanto, la irradiancia disminuirá a la mitad su valor máximo cada vez que dado que
\begin{equation}\gamma=2\frac{\delta_{i}}{2},\end{equation}
\begin{equation}\frac{1}{2}=\frac{1}{1+\F\sin\left(\frac{\frac{\delta}{2}+\delta_{max}}{2}\right)},\end{equation}
de donde se ve que
\begin{equation}\sin\left(\frac{\delta_{\frac{1}{2}}}{2}+m\pi\right)=\pm sin\left(\frac{\delta_{\frac{1}{2}}}{2}\right),\end{equation}
elevando al cuadrado ambos lados de la ecuación
\begin{equation}\sin^{2}\left(\frac{\delta_{\frac{1}{2}}}{2}+m\pi\right)=\sin^{2}\left(\frac{\delta_{\frac{1}{2}}}{2}\right),\end{equation}
entonces
\begin{equation}\sin^{2}\left(\frac{\delta_{\frac{1}{2}}}{2}\right)=\frac{1}{\mathcal{F}},\end{equation}
Eliminando el término cuadrado de la ecuación de lado derecho y despejando obtenemos
\begin{equation}\delta_{\frac{1}{2}}=2\arcsin\left(\sqrt{\frac{1}{\mathcal{F}}}\right),\end{equation}
Sustituyendo el valor de \begin{equation}\gamma=4\arcsin\left(\frac{1}{\sqrt{\mathcal{F}}}\right),\end{equation}
Dado que es, por lo general muy grande,
\begin{equation}\arcsin\left(\sqrt{\frac{1}{\mathcal{F}}}\right)\approxeq\left(\sqrt{\frac{1}{\mathcal{F}}}\right),\end{equation}
entonces se obtiene
\begin{equation}\frac{\delta_{\frac{1}{2}}}{2}=\frac{1}{\sqrt{\mathcal{F}}},\end{equation}
y por lo tanto el ancho medio es igual a
\begin{equation}\gamma\approxeq\left(\frac{4}{\sqrt{\mathcal{F}}}\right).\end{equation}
Otro valor interesante es la relación de la separación de los máximos adyacentes con respecto al ancho medio. Denominada fineza \begin{equation}\Upsilon\equiv\frac{2\pi}{\gamma}=\frac{\pi}{2}\sqrt{\mathcal{F}}.\end{equation} Video: Construyendo Un Interferometro Fabry-Perot
Referencias
Hecht E. Óptica, Addisson Wesley Iberoamericana, 2000 [Cap.9]











![\tilde{E}_{r}=E_{0}e^{i\omega t}\left[r+\frac{r'tt'e^{-i\delta}}{1-r'^{2}e^{-i\delta}}\right].](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c3138b97dd1a2f8a1dfedf72dd9cc4a4ec36b962)