Diferencia entre revisiones de «Optica: Capitulo8-problemas»
| (No se muestran 63 ediciones intermedias de 8 usuarios) | |||
| Línea 1: | Línea 1: | ||
Problemas capítulo 8 Óptica Hecht, Polarizacion. | |||
Ejercicios resueltos sobre Polarizacion. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema. | |||
Algunas ediciones del Hecht, tienen distintas numeraciones para problemas idénticos. | |||
[[categoría:Optica]] | [[categoría:Optica]] | ||
[[categoría:Cursos]] | [[categoría:Cursos]] | ||
---- | |||
= 3ra Edición en Español= | |||
== Ejercicio 8.1 3ra Edición en Español == | |||
Describa detalladamente el estado de polarización de cada una de las siguientes ondas. | |||
(a) $\textbf{E}= \hat{\imath} E_{0}\cos\left(kz-\omega t\right)-\hat{\jmath} E_{0}\cos\left(kz-\omega t\right) $ | |||
(b) $\textbf{E}= \hat{\imath} E_{0}\sin 2\pi\left(\frac{z}{\lambda}-\nu t\right)-\hat{\jmath} E_{0}\sin 2\pi \left(\frac{z}{\lambda | |||
}-\nu t\right) $ | |||
(c) $\textbf{E}= \hat{\imath} E_{0}\sin \left(\omega t-kz\right)+\hat{\jmath} E_{0}\sin \left(\omega t-kz-\pi /4\right) $ | |||
(d) $\textbf{E}= \hat{\imath} E_{0}\cos\left(\omega t-kz\right)+\hat{\jmath} E_{0}\cos\left(\omega t-kz+\pi/2\right) $ | |||
Solución | |||
(a) La ecuación dada por | |||
$\textbf{E}= \hat{\imath} E_{0}\cos\left(kz-\omega t\right)-\hat{\jmath} E_{0}\cos\left(kz-\omega t\right) \Rightarrow$ | |||
$\textbf{E}=\left(\hat{\imath}-\hat{\jmath}\right)E_{0}\cos\left(kz-\omega t\right) $ | |||
De la forma de la ecuación deducimos que su estado es polarizada linealmente a 135 grados respecto al plano $xy$ y en cada componente tiene la misma magnitud $E_{0}$. | |||
(b) La ecuación esta dada por | |||
$\textbf{E}= \hat{\imath} E_{0}\sin 2\pi\left(\frac{z}{\lambda}-\nu t\right)-\hat{\jmath} E_{0}\sin 2\pi \left(\frac{z}{\lambda | |||
}-\nu t\right) \Rightarrow$ | |||
$\textbf{E}=\left(\hat{\imath}-\hat{\jmath}\right)E_{0}\sin\left(\frac{2\pi}{\lambda} z-2\pi \nu t\right)\Rightarrow $ | |||
$\textbf{E}=\left(\hat{\imath}-\hat{\jmath}\right)E_{0}\sin\left(kz-\omega t\right)$ | |||
Donde empleamos el echo que $k=\frac{2\pi}{\lambda}$ y $\omega=2\pi \nu$ | |||
De la forma de la ecuación deducimos que su estado es polarizada linealmente a 135 grados respecto al plano $xy$ y en cada componente tiene la misma magnitud $E_{0}$. Notemos que esta onda es la misma que la de el inciso (a), desfasada $\frac{\pi}{2}$ | |||
(c) El componente $E_{x}$ le lleva ventaja de $\frac{\pi}{4}$ a la componente $E_{y}$, por tanto su estado es polarizada elíptica de mano izquierda y su forma es como en la siguiente figura. | |||
[[Archivo:elipse.jpg]] | |||
(d) El componente $E_{y}$ le lleva ventaja de $\frac{\pi}{2}$ a la componente $E_{x}$, por tanto su estado es polarizada circular a la derecha y su forma es como en la siguiente figura. | |||
[[Archivo:circulo.jpg]] | |||
---- | ---- | ||
=== Ejercicio 8.30 === | Realizado por: Usuario [[Usuario:Jesús|Jesús Flores Ortega]] | ||
---- | |||
== Ejercicio 8.3 3ra Edición en Español == | |||
Demuestre analíticamente que la superposición de un estado R y L que tienen diferentes amplitudes,llevaría a un estado ${\epsilon}$, como se muestra en la figura 8.8 .¿ Cual debería ser el valor de ${\epsilon}$? | |||
${E_R}= i{E_0}cos{(kz-wt)}+j{E_0}sen{(kz-wt)}$ | |||
${E_L}=i{E´_0}cos{(kz-wt)}-j{E´_0}sen{(kz-wt)}$ | |||
$E={E_R}+{E_L}= i({E_0}+{E´_0})cos{(kz-wt)}+j({E_0}-{E´_0})sen{(kz-wt)}$ | |||
dejando | |||
$({E_0}+{E´_0})={E´´_0x}$ y $({E_0}-{E´_0})={E´´_0y}$ | |||
por lo que : | |||
$E=i{E´´_0x}cos{(kz-wt)} + j{E´´_0y}sen{(kz-wt)}$ | |||
---- | |||
Aportación de: Usuario [[Usuario:Luisa Alejandra Vega Sanchez]] | |||
---- | |||
== Ejercicio 8.6 3ra Edición en Español == | |||
''''' Escriba una expresión para un estado <math>\Re</math> de onda lumínica de frecuencia <math>\omega</math> propagándose en la dirección positiva x tal que a <math>t=0</math> y <math>x=0</math>, el campo <math>\vec{E}</math> a punta en la dirección z negativa. ''''' | |||
''' Solución ''' | |||
Consideremos la onda electromagnética <math> \vec{E}(\vec{r},t)=\tilde{E}_{0}(\vec{r},t)\hat{n} </math> cuyo vector de onda es <math> \vec{k}</math> y su vector de polarización es <math> \hat{n}</math>. Sea W un frente de onda, entonces, <math> \exists</math> <math> \beta =\{\hat{r}_{1},\hat{r}_{2}\}\subseteq W </math> tal que: | |||
:<math> \hat{n}=a_{1}\hat{r}_{1} + a_{2}\hat{r}_{2} </math>. | |||
siendo <math> \beta </math> una base para <math> W </math> y, <math> W </math> el espacio afín del subespacio vectorial P que pasa por el origen. (W es una traslación de P)Entonces: | |||
<math> \vec{E}(\vec{r},t)=\tilde{E}_{01}(\vec{r},t)\hat{r}_{1} + \tilde{E}_{02}(\vec{r},t)\hat{r}_{2}</math>. | |||
Por supuesto que la dependencia del campo <math>\vec{E}</math> y de sus componentes <math>\tilde{E}_{01}</math>, <math> \tilde{E}_{02}</math> es sinusoidal, es decir: | |||
<math>\vec{E}(\vec{r},t)=E_{01}\cos(\vec{k}\cdot\vec{r}-\omega t+\delta)\hat{r}_{1} + E_{02}\cos(\vec{k}\cdot\vec{r}-\omega t+\epsilon)\hat{r}_{2}</math> | |||
Ahora, en un estado <math>\Re</math> se deben de cumplir las siguientes condiciones: | |||
:i)<math> \epsilon = \delta + (-\frac{\pi}{2} + 2m\pi) </math> donde <math> m=\{...,-2,-1,0,1,2,...\} </math>; | |||
:ii)<math>\hat{r}_{1}\cdot\hat{r}_{2} = 0 </math> & | |||
:iii)<math>E_{01}=E_{02}=E_{0}</math> | |||
''a priori'', <math> \vec{E}(\vec{r},t)=E_{0}[\cos(\vec{k}\cdot\vec{r}-\omega t+\delta)\hat{r}_{1} + \sin(\vec{k}\cdot\vec{r}-\omega t+\delta)\hat{r}_{2}]</math> | |||
Sea que <math> \vec{k}=k\hat{x}</math>, no hay más para <math>\hat{r}_{1},\hat{r}_{2}</math> que <math>\hat{r}_{1}=\hat{y}</math> & <math>\hat{r}_{2}=\hat{z}</math>. Por lo que | |||
:<math>\vec{E}(\vec{x},t)=E_{0}[\cos(kx-\omega t +\delta)\hat{y} + \sin(kx-\omega t +\delta)\hat{z}]</math> | |||
Sin embargo, se desea que a <math>t=0</math> y <math>x=0</math>, el campo <math>\vec{E}</math> apunte en la dirección z negativa, es decir: | |||
<math> E_{0}[\cos(\delta)\hat{y} + \sin(\delta)\hat{z}]=0\hat{y}-E_{0}\hat{z} </math> | |||
Lo cual es cierto si, y sólo si: | |||
<math> \cos(\delta) = 0</math> & <math> \sin(\delta)=-1 </math>. Por tanto, hagamos <math> \delta=\frac{3}{2}\pi </math>, entonces: | |||
<math>\vec{E}(x,t)=E_{0}[\cos(kx-\omega t + \frac{3}{2}\pi)\hat{y} + \sin(kx-\omega t + \frac{3}{2}\pi)\hat{z}]</math>, que es lo mismo que: | |||
:<math>\vec{E}(x,t)=E_{0}[\sin(kx-\omega t )\hat{y} - \cos(kx-\omega t)\hat{z}]</math> | |||
que es una de las expresiones de la onda que se piden en el problema. | |||
---- | |||
Realizado por: Usuario [[Usuario:diegophy17|Diego de la Cruz López]] | |||
---- | |||
= 5ta Edición en Ingles = | |||
== Ejercicio 8.4 5ta Edición en Ingles == | |||
Describa detalladamente el estado de la polarización de cada una de las siguientes ondas: | |||
'''a)'''<math>\vec{E}=\hat{i}E_0 cos(kz-\omega t)+\hat{j}E_0 cos(kz-\omega t)</math> | |||
'''b)'''<math>\vec{E}=\hat{i}E_0 sen[2\pi(z/\lambda-\omega t)]-\hat{j}E_0 sen[2\pi (z/\lambda-\omega t)]</math> | |||
'''c)'''<math>\vec{E}=\hat{i}E_0 sen(\omega t-kz)-\hat{j}E_0 sen(\omega t-kz-\pi /4)</math> | |||
'''d)'''<math>\vec{E}=\hat{i}E_0 cos(kz- \omega t)+\hat{j}E_0 cos(kz-\omega t+\pi /2)</math> | |||
'''Solución:''' | |||
Analicemos los máximos de los valores extremos por componentes. | |||
'''Inciso a''' | |||
Para la expresión '''a)''' vemos que cuando: | |||
Si <math>kz-\omega t=0</math>; <math>\vec{E}=E_0[\hat{i}1-\hat{j}1</math>] | |||
Si <math>kz-\omega t=\pi /2</math>; <math>\vec{E}=E_0[\hat{i}0-\hat{j}0</math>] | |||
Si <math>kz-\omega t=3\pi /2</math>; <math>\vec{E}=E_0[\hat{i}-1-\hat{j}-1</math>] | |||
Con esto podemos darnos cuenta fácilmente que el campo '''E''' de '''a)''' es una recta con pendiente 1. | |||
'''Inciso b''' | |||
Para la expresión '''b)''' tenemos: | |||
Si <math>z/\lambda-\omega t=0</math>; <math>\vec{E}=E_0[\hat{i}0\hat{j}0</math>] | |||
Si <math>z/\lambda-\omega t=\pi /2</math>; <math>\vec{E}=E_0[\hat{i}1-\hat{j}1</math>] | |||
Si <math>z/\lambda-\omega t=\pi </math>; <math>\vec{E}=E_0[\hat{i}0+\hat{j}0</math>] | |||
Si <math>z/\lambda-\omega t=3\pi /2</math>; <math>\vec{E}=E_0[-\hat{i}1+\hat{j}1</math>] | |||
Concluimos que el campo '''E''' de '''b)''' es una recta con pendiente -1 | |||
'''Inciso c''' | |||
Para la expresión '''c)''' tenemos: | |||
Si <math>kz-\omega t=0</math>; <math>\vec{E}=E_0\hat{i}0[-\hat{j}\sqrt{2}/2</math>] | |||
Si <math>kz-\omega t=\pi /2</math>; <math>\vec{E}=E_0[\hat{i}1+\hat{j}\sqrt{2}/2</math>] | |||
Si <math>kz-\omega t=\pi </math>; <math>\vec{E}=E_0[\hat{i}1+\hat{j}\sqrt{2}/2</math>] | |||
Si <math>kz-\omega t=3\pi /2</math>; <math>\vec{E}=E_0[-\hat{i}1-\hat{j}\sqrt{2}/2</math>] | |||
Es un poco más complicado de visualizar la forma, pero si se unen los puntos que conocemos, podemos interpretar que es una elipse para '''E''' de '''c)''' | |||
'''Inciso d''' | |||
Finalmente, para '''d)''' | |||
Si <math>kz-\omega t=0</math>; <math>\vec{E}=E_0[\hat{i}1+\hat{j}0</math>] | |||
Si <math>kz-\omega t=\pi /2</math>; <math>\vec{E}=E_0[\hat{i}0-\hat{j}1</math>] | |||
Si <math>kz-\omega t=3\pi /2</math>; <math>\vec{E}=E_0[-\hat{i}1+\hat{j}0</math>] | |||
Si <math>kz-\omega t=2\pi</math>; <math>\vec{E}=E_0[\hat{i}1+\hat{j}0</math>] | |||
Claramente, '''E''' de '''d)''' es un circulo de radio E | |||
---- | |||
Realizado por: Usuario [[Usuario:Onáfeder|Fernando Valencia Hernández]] | |||
---- | |||
== Ejercicio 8.28 5ta Edición en Ingles == | |||
Dado <math>200\frac { W }{ { m }^{ 2 } } </math> de luz polarizada incide aleatoria mente en una pila de polarizadores lineales ideales que se colocan uno detrás de otro con el eje de transmisión de la primera vertical, el segundo a 30 grados, el tercero a 60 y el cuarto a 90. cuanta luz emerge? | |||
'''Solución''' | |||
Irradianza de luz polarizada aleatoriamente (luz natural) | |||
<math>{ I }_{ 0 }=200\frac { W }{ { m }^{ 2 } } </math> | |||
El angulo de transmisión son 0, 30, 60, y 90 grados respectivamente | |||
cuando la luz natural de irradianza incide en un polarizador lineal, la luz proveniente del polarizador lineal se convierte en la mitad | |||
entonces del 1er polarizador <math>{ I }_{ (0) }=\frac { 200 }{ 2 } </math> = <math>{ I }_{ 0 }=100\frac { w }{ { m }^{ 2 } } </math> | |||
la diferencia de angulo entre el 1er y 2do | |||
<math>\theta =30-0=30\ </math> | |||
De la ley de Malus, la irradiación de la luz emerge del 2do polarizador lineal | |||
<math>{ I }_{ \theta }=I(0){ cos }^{ 2 }30</math> | |||
<math>(100){ (\frac { \sqrt { 3 } }{ 2 } })^{ 2 }</math> | |||
<math>75\frac { w }{ { m }^{ 2 } } </math> | |||
angulo entre los polarizadores 2do y 3ro | |||
<math>90-30=30\ </math> | |||
aplicando de nuevo la ley de Malus para el tercer polarizador | |||
<math>I(\theta )=I(30){ cos }^{ 2 }30</math> | |||
<math>(75){ (\frac { \sqrt { 3 } }{ 2 } ) }^{ 2 }</math> | |||
<math>\frac { 225 }{ 4 } \frac { w }{ { m }^{ 2 } } </math> | |||
<math>I(\theta )=56.25\frac { w }{ { m }^{ 2 } } </math> '''...(1)''' | |||
Esto es incidente en el cuarto polarizador | |||
Angulo entre los polarizadores 3ro y 4to | |||
<math>I({ \theta }_{ 1 })=I(\theta ){ cos }^{ 2 }30</math> | |||
<math>(56.25){ (\frac { \sqrt { 3 } }{ 2 } ) }^{ 2 }=56.25(\frac { 3 }{ 4 } )</math> | |||
esto nos da: <math>42.1875\frac { W }{ { m }^{ 2 } } </math> | |||
Esta ultima cantidad es la irradiacion de luz que emerge después de pasar por cuatro polarizadores | |||
---- | |||
Realizado por: Usuario [[Usuario:salvadormorales|Salvador Morales Carranza]] | |||
---- | |||
== Ejercicio 8.30 5ta Edición en Ingles == | |||
Un polarizador ideal rota con una velocidad angular <math>\omega</math> entre un par de polarizadores similares cruzados y estacionarios. Muestre que la densidad de flujo emergente estará modulada por cuatro veces la frecuencia de rotación. En otras palabras, muestre que | Un polarizador ideal rota con una velocidad angular <math>\omega</math> entre un par de polarizadores similares cruzados y estacionarios. Muestre que la densidad de flujo emergente estará modulada por cuatro veces la frecuencia de rotación. En otras palabras, muestre que | ||
| Línea 14: | Línea 303: | ||
donde <math>I_1</math> es la densidad de flujo emergente del primer polarizador e <math>I</math> es la densidad de flujo final. | donde <math>I_1</math> es la densidad de flujo emergente del primer polarizador e <math>I</math> es la densidad de flujo final. | ||
'''Solución:''' | |||
El ángulo que hay entre el primer polarizador y el segundo que está girando es <math>\theta</math>. Si la amplitud de la luz que sale del primer polarizador es $E_{01}$, entonces la que emerge del polarizador en rotación debe ser | El ángulo que hay entre el primer polarizador y el segundo que está girando es <math>\theta</math>. Si la amplitud de la luz que sale del primer polarizador es $E_{01}$, entonces la que emerge del polarizador en rotación debe ser | ||
| Línea 39: | Línea 329: | ||
</math> | </math> | ||
Entonces | '''Entonces''' | ||
<math> | <math> | ||
| Línea 50: | Línea 340: | ||
I = \dfrac{I_1}{8} \left[1 - \cos^4(4\omega t)\right] | I = \dfrac{I_1}{8} \left[1 - \cos^4(4\omega t)\right] | ||
</math> | </math> | ||
---- | ---- | ||
Realizado por: [[Usuario:Ivan de Jesús Pompa García|Ivan de Jesús Pompa García]] ([[Usuario discusión:Ivan de Jesús Pompa García|discusión]]) 22:02 5 nov 2018 (CST) | |||
---- | ---- | ||
==Ejercicio 8.47 5ta Edición en Ingles== | |||
'''''Un haz de luz natural incide en una interfaz aire-vidrio <math>{ n }_{ ti }</math> a 40°,Calcular el grado de polarización de la luz reflejada.''''' | '''''Un haz de luz natural incide en una interfaz aire-vidrio <math>{ n }_{ ti }</math> a 40°,Calcular el grado de polarización de la luz reflejada.''''' | ||
'''Solución:''' | |||
: | : | ||
:Ocupando la expresión 8.33 del libro, para el grado de polarización de la luz reflejada es: | :Ocupando la expresión 8.33 del libro, para el grado de polarización de la luz reflejada es: | ||
| Línea 151: | Línea 387: | ||
:Sustituyendo los valores numéricos: | :Sustituyendo los valores numéricos: | ||
: | : | ||
:<math>{ \theta }_{ t }={ sin }^{ -1 }\left( \frac { (1) | :<math>{ \theta }_{ t }={ sin }^{ -1 }\left( \frac { (1)sin40^{\circ} }{ 1.5 } \right) </math> | ||
: | : | ||
:<math>{ \theta }_{ t }=25. | :<math>{ \theta }_{ t }=25.4^{\circ}</math> | ||
: | : | ||
:Sustituyendo el anterior resultado en (3): | :Sustituyendo el anterior resultado en (3): | ||
: | : | ||
:<math>{ R }_{ \parallel }=\frac { { Tan }^{ 2 }({ | :<math>{ R }_{ \parallel }=\frac { { Tan }^{ 2 }({ 40^{\circ}-25.4^{\circ}) } }{ { Tan }^{ 2 }({ 40^{\circ}+25.4^{\circ}) } } </math> | ||
: | : | ||
:<math>{ R }_{ \parallel }=0.0143</math> ....(5) | :<math>{ R }_{ \parallel }=0.0143</math> ....(5) | ||
| Línea 163: | Línea 399: | ||
:Similar para (4): | :Similar para (4): | ||
: | : | ||
:<math>{ R }_{ \bot }=\frac { { Sin }^{ 2 }({ | :<math>{ R }_{ \bot }=\frac { { Sin }^{ 2 }({ 40^{\circ}-25.4^{\circ}) } }{ { Sin }^{ 2 }({ 40^{\circ}+25.4^{\circ}) } } </math> | ||
: | : | ||
:<math>{ R }_{ \bot }=0.0768</math>.......(6) | :<math>{ R }_{ \bot }=0.0768</math>.......(6) | ||
| Línea 181: | Línea 417: | ||
:<math>V=\frac { { R }_{ \bot }-{ R }_{ \parallel } }{ { { R }_{ \bot }{ +R }_{ \parallel } } } </math>...(10) | :<math>V=\frac { { R }_{ \bot }-{ R }_{ \parallel } }{ { { R }_{ \bot }{ +R }_{ \parallel } } } </math>...(10) | ||
: | : | ||
'''Conclusión:''' | |||
:finalmente sustituyendo (5) y (6) en (10): | :finalmente sustituyendo (5) y (6) en (10): | ||
: | : | ||
| Línea 189: | Línea 427: | ||
:Por lo tanto el grado de polarización es del 69% | :Por lo tanto el grado de polarización es del 69% | ||
: | : | ||
---- | |||
Realizado por: Usuario[[Usuario:Luis Chávez |Luis Manuel Chávez Antonio]] | |||
---- | ---- | ||
== Ejercicio 8.48 5ta Edición en Ingles == | |||
Demuestre que el grado de polarización de $(V_r)$ de la luz reflejada puede expresarse como: | |||
:::: $V_r= \frac{R_{\perp} - R_{ \parallel}}{R_{\perp} + R_{ \parallel}}$ | |||
'''Solución:''' | |||
: | Partimos de la definición de grado de polarización: | ||
:::: $V= \frac{I_p}{I_p + I_n}$ | |||
Donde $I_p$ e $I_n$ son las densidades de flujo constitutivas de la luz polarizada y no polarizada o luz natural . | |||
Estas cantidades son función de la Reflectancia: | |||
$R_{ \parallel}= \frac{I_{ \parallel }}{I_0}$ | |||
$R_{ \perp} = \frac{I_{ \perp }}{I_0}$ | |||
Despejando $I_{ \perp }$ y $I_{ \parallel}$ obtenemos: | |||
$I_{0} R_{ \parallel}= I_{ \parallel }$ | |||
$I_0 R_{ \perp} = I_{ \perp } $ | |||
Recordemos que para la luz reflejada no polarizada : $I_{\parallel}= I_{ \perp }$ | |||
Mientras que en luz reflejada polarizada : $I_p =I_{r \perp } - I_{r \parallel }$ | |||
Con esto en mente , hacemos la sustitución en la definición de grado de polarización: | |||
$V= \frac{I_p}{I_p + I_n} =\frac{ I_{r \perp } - I_{r \parallel }}{ I_{r \perp } - I_{r \parallel } + 2 I_{r \parallel }}$ | |||
$V= \frac {I_0 R_{ \perp} - I_0 R_{ \parallel }}{ I_0 R_{ \perp} - I_0 R_{ \parallel} + 2 I_0 R_{ \parallel}}$ | |||
$V=\frac {I_0 R_{ \perp} - I_0 R_{ \parallel}}{ I_0 R_{ \perp} + I_0 R_{ \parallel} }$ | |||
Factorizamos $I_0$: | |||
$V=\frac {I_0( R_{ \perp} - R_{ \parallel})}{ I_0( R_{ \perp} + R_{ \parallel}) }$ | |||
El factor $\frac {I_0}{I_0}=1$ y obtenemos la expresión para el grado de polarización $V_r$ de la luz reflejada : | |||
$V_r= \frac{R_{\perp} - R_{ \parallel}}{R_{\perp} + R_{ \parallel}}$ | |||
---- | |||
Realizado por: Usuario [[Usuario:Aurea Espin|Aurea Espin]] ([[Usuario discusión:Aurea Espin|discusión]]) 10:59 11 nov 2018 (CST) | |||
---- | |||
== Ejercicio 8.49 5ta Edición en Ingles == | |||
<math> | '''''Un haz de luz natural que incide en el aire en un interfaz de vidrio <math>(n=1.5)</math> a 70° se refleja parcialmente. Calcular la reflectancia general. ¿Como se compararía esto con el caso de incidencia en, digamos ,56.3 °?''''' | ||
'''Solución:''' | |||
Los datos que tenemos son: | |||
Angulo de incidencia del haz de luz en el interfaz de aire-vidrio. <math>\theta _{i}=70</math> | |||
<math> | Indice de refracción de medio. <math>(n=1.5)</math> | ||
Partiendo de la ley de Snell: | |||
<math>{ \theta | <math>n_{i}sen \theta _{i}=n_{r}sen \theta _{r}</math> | ||
<math>\frac{n_{r}}{n_{i}}=\frac{sen \theta _{i}}{sen \theta _{r}}</math> | |||
<math>\ | <math>\frac{1.5}{1}=\frac{sen (70) }{sen \theta _{r}}</math> | ||
<math> | <math>{sen \theta _{r}}=\frac{sen(70)}{1.5}</math> | ||
<math> | <math>{sen \theta _{r}}=\frac{0.93969}{1.5}</math> | ||
<math>{sen \theta _{r}}=0.6264</math> | |||
- | <math>\theta _{r}=sen^{-1}(0.6264)</math> | ||
<math> \theta _{r}=38.78</math> | |||
Por lo tanto en angulo de transmisión es <math> \theta _{r}=38.78</math> | |||
De las ecuaciones de Fresnel | |||
Componente paralelo de reflectancia: | |||
<math>R_{||}=\frac{tan^{2}(\theta _{i}-\theta _{r})}{tan^{2}(\theta _{i}+\theta _{r})}</math> | |||
sustituimos los valores de <math>\theta _{i}</math> y <math>\theta _{r}</math> | |||
<math>R_{||}=\frac{tan^{2}(70-38.78)}{tan^{2}(70+38.78)}</math> | |||
<math>R_{||}=\left [\frac{tan(31.22)}{tan(108.78)} \right ]^{2}</math> | |||
<math>R_{||}=\left [\frac{0.606}{-2.94} \right ]^{2}</math> | |||
<math>R_{||}=0.04246</math> | |||
<math>R_{ \perp}=\frac{sen^{2}(\theta _{i}-\theta _{r})}{sen^{2}(\theta _{i}+\theta _{r})}</math> | |||
<math>R_{ \perp}=\frac{sen^{2}(70-38.78)}{sen^{2}(70+38.78)}</math> | |||
<math>R_{ \perp}=\left [\frac{sen(31.22)}{sen(108.78)} \right ]^{2}</math> | |||
<math>R_{ \perp}=\left [\frac{0.5183}{0.9467} \right ]^{2}</math> | |||
<math>R_{ \perp}=\left [0.5474 \right ]^{2}</math> | |||
<math>R_{ \perp}=0.2996</math> | |||
Sobre toda la reflectancia <math>R=\frac{1}{2}(R_{ \parallel}+ R_{ \perp})</math> | |||
<math>R=\frac{1}{2}(0.04246+0.2996)</math> | |||
Sobre toda la reflectancia <math>R=0.17107</math> | |||
Es decir 17.107 % de la luz se refleja o también se puede decir 17.107 % de la luz incidente se refleja | |||
Cuando el angulo de incidencia <math>\theta _{i}=56.3</math> | |||
De la ley de Snell: | |||
<math>\frac{n_{r}}{n_{i}}=\frac{sen \theta _{i}}{sen \theta _{r}}</math> | |||
<math>\frac{1.5}{1}=\frac{sen (56.3)}{sen (\theta _{r})}</math> | |||
<math>{sen (\theta _{r})}=\frac{0.831}{1.5}</math> | |||
<math>{sen (\theta _{r})}=0.5546</math> | |||
<math>\theta _{r}=sen^{-1}(0.5546)</math> | |||
<math>\theta _{r}=33.68</math> | |||
<math> | En angulo de transmisión es: <math>\theta _{r}=33.68</math> | ||
<math>\frac{ | Nuevamente usamos la ecuación: <math>R_{||}=\frac{tan^{2}(\theta _{i}-\theta _{r})}{tan^{2}(\theta _{i}+\theta _{r})}</math> | ||
<math> | <math>R_{||}=\frac{tan^{2}(56.3-33.68)}{tan^{2}(56.3+33.68)}</math> | ||
<math>{ | <math>R_{||}=\left [\frac{tan(22.62)}{tan(89.98)} \right ]^{2}</math> | ||
<math>{ | <math>R_{||}= \left [\frac{0.4166}{3993.46} \right ]^{2}</math> | ||
<math>{ | <math>R_{||}= 1.0886 \times10^{-8} </math> | ||
<math>\theta _{r} | <math>R_{ \perp}=\frac{sen^{2}(\theta _{i}-\theta _{r})}{sen^{2}(\theta _{i}+\theta _{r})}</math> | ||
<math> \ | <math>R_{ \perp}=\frac{sen^{2}(56.3-33.68)}{sen^{2}(56.3+33.68)}</math> | ||
<math>R_{ \perp}=\left [\frac{sen(22.62)}{sen(89.68)} \right ]^{2}</math> | |||
<math>R_{ \perp}=\left [\frac{0.3846}{0.9999} \right ]^{2}</math> | |||
<math>R_{ | <math>R_{ \perp}=0.14791</math> | ||
Sobre toda la reflectancia <math>R=\frac{1}{2}(R_{ \parallel}+ R_{ \perp})</math> | |||
<math> | <math>R=\frac{1}{2}(1.0886\times 10^{-8}+0.14791)</math> | ||
<math> | <math>R=0.07395</math> | ||
Porcentaje de reflectancia = 7.395 % | |||
En este caso, la incidencia del angulo de 56.3° es igual al angulo de polarización. Así la luz reflejada esta totalmente polarizada. Pero en el primer caso la luz reflejada esta parcialmente polarizada. En el primer caso 17.107 % de la luz incidente se refleja y se polariza parcialmente. Pero en el caso posterior 7.395 % se refleja la luz incidente y se polariza totalmente. | |||
----- | |||
Realizado por: Usuario [[Usuario:Enrique Ortiz Martinez |Enrique Ortiz Martinez]] | |||
---- | |||
== Ejercicio 8.52 5ta Edición en Ingles == | |||
'''''Un rayo de luz amarilla incide sobre una placa de calcita a <math>{ 50 }^{ \circ }</math>.La placa se corta de modo que el eje óptico sea paralelo a la cara frontal y perpendicular al plano de incidencia.Encuentra la separación angular entre los dos rayos emergentes ''''' | |||
'''Solución:''' | |||
<math> | Sabemos que: | ||
El indice de refracción <math>({ n }_{ 0 })</math> del rayo ordinario en la placa de cuarzo = 1.6584 | |||
El indice de refracción <math>({ n }_{ e })</math> de rayos extraordinarios en la placa de cuarzo =1.4864 | |||
<math> | Angulo <math>{ \theta }_{ i }</math> de incidencia de la luz amarilla en el cristal de calcita =<math>{ 50 }^{ \circ }</math> | ||
Sabemos que la ley de Snell es: | |||
<math> | <math>\frac { sen{ (\theta }_{ i }) }{ sen{ (\theta }_{ t }) } =n</math> | ||
Para el rayo ordinario tenemos : | |||
<math>sen{ \theta }_{ i }={ n }_{ o }sen{ \theta }_{ to }</math> | |||
<math>sen{ \theta }_{ to }=\frac { sen{ \theta }_{ i } }{ { n }_{ o } } </math> | |||
<math>sen{ \theta }_{ to }=\frac { sen{ 50 }^{ \circ } }{ 1.6584 } </math> | |||
<math>sen{ \theta }_{ to }=\frac { 0.766 }{ 1.6584 } </math> | |||
<math>sen{ \theta }_{ to }=0.4619</math> | |||
<math>{ \theta }_{ to }={ sen }^{ -1 }0.4619</math> | |||
<math>{ \theta }_{ to }={ 27 }^{ \circ }35'</math> | |||
Para rayos extraordinarios tenemos análogamente de la ley de Snell | |||
<math>{ | <math>sen{ \theta }_{ te }=\frac { sen{ \theta }_{ i } }{ { n }_{ e } } </math> | ||
<math>{ | <math>sen{ \theta }_{ te }=\frac { sen{ 50 }^{ \circ } }{ 1.4864 } </math> | ||
<math>\theta _{ | <math>sen{ \theta }_{ te }=\frac { 0.766 }{ 1.4864 } </math> | ||
<math>\theta _{ | <math>sen{ \theta }_{ te }=0.515</math> | ||
<math>{ \theta }_{ te }={ sen }^{ -1 }0.515</math> | |||
<math>{ \theta }_{ te }={ 31 }^{ \circ }4'</math> | |||
<math> | Por lo tanto la separación angular <math>\Delta \theta </math> entre los dos rayos emergentes es: | ||
<math> | <math>\Delta \theta ={ \theta }_{ te }-{ \theta }_{ to }</math> | ||
<math> | <math>\Delta \theta ={ 31 }^{ \circ }4'-{ 27 }^{ \circ }35'</math> | ||
<math> | <math>\Delta \theta ={ 3 }^{ \circ }29'</math> | ||
---- | |||
Realizado por: [[Usuario:Ruben Espinosa|Ruben Espinosa Guzman]] | |||
---- | |||
== Ejercicio 8.69 5ta Edición en Ingles == | |||
Un compensador de Babinet se coloca 45° entre polarizadores lineales cruzados y se elimina con luz de sodio. Al colocar una lámina fina de mica (índices 1.599 y 1.594) en el compensador, todas las bandas negras se desplazan una cuarta parte del espacio que las separa. Calcule la retardancia de la lámina y su espesor. | |||
'''Solución:''' | |||
La retardancia está dada por: | |||
:$\Delta φ=\frac{2π}{λ_0} dΔn$ | |||
:Donde $\Delta φ=\frac{(14)}{(2π)}=\frac{π}{2}$ | |||
:Despejando d | |||
:$\frac{\pi}{2}=\frac{2\pi\ d(0.005)}{589.3\times{10}^{-9}}$ | |||
:$d=\frac{589.3\times{10}^{-9}}{4(0.005)}=2.94\times{10}^{-5}m$ | |||
---- | |||
Realizado por: [[Usuario:Verenisse|Verenisse]] | |||
---- | |||
== Ejercicio 8.73 5ta Edición en Ingles== | |||
'''''Considere una celda de kerr cuyas placas están separadas por una distancia d. Sea l la longitud efectiva de esas placas (ligeramente diferente de la longitud real debido a la franja del campo). Muestra que | |||
<math>\Delta \varphi =2\pi Kl{ { V }^{ 2 } }/{ { d }^{ 2 } }</math>.''''' | |||
'''Solución:''' | |||
Donde: | |||
<math>d</math>: Separacion de las placas en celdas de Kerr | |||
: | <math>l</math>: Longitud efectiva de las placas en celdas de Kerr | ||
La diferencia entre los indices <math>{ n }_{ \parallel }</math> y <math>{ n }_{ \bot }</math> asociada con las dos orientaciones del plano de vibracion de la onda (es decir, paralela y perpendicular al campo eléctrico aplicado), es | |||
<math>\Delta n=\lambda \cdot K\cdot { E }^{ 2 }</math> | |||
Donde: | |||
<math>K</math>: Kerr constante | |||
<math>E</math>: Intensidad de campo eléctrico. | |||
<math>\Delta n=\lambda \cdot K\cdot { \left( \frac { V }{ d } \right) }^{ 2 }</math> | |||
<math> | Porque <math>Campo\quad electrico\quad (E)=\frac { Potencia\quad (V) }{ Distancia\quad (d) } </math> | ||
<math>\Delta n=\lambda \cdot K\cdot \frac { { V }^{ 2 } }{ { d }^{ 2 } } \quad ...(1)</math> | |||
<math>({ n }_{ \parallel }-{ n }_{ \bot })=\left[ \left( \frac { \lambda }{ { \lambda }_{ \parallel } } \right) -\left( \frac { \lambda }{ { \lambda }_{ \bot } } \right) \right] </math> | |||
Donde: | |||
<math>{ \lambda }_{ \parallel }</math>: Longitud de onda de las ondas en un dice de refracción <math>({ n }_{ \parallel })</math> | |||
<math>{ \lambda }_{ \bot }</math>: Longitud de onda de las ondas en un indice de refracción <math>{ (n }_{ \bot })</math> | |||
<math>\ | <math>({ n }_{ \parallel }-{ n }_{ \bot })=\lambda \left[ \frac { 1 }{ { \lambda }_{ \parallel } } -\frac { 1 }{ { \lambda }_{ \bot } } \right] </math> | ||
<math>({ n }_{ \parallel }-{ n }_{ \bot })=\lambda \left[ \frac { { \phi }_{ \parallel } }{ { 2\pi l }_{ \parallel } } -\frac { { \phi }_{ \bot } }{ { 2\pi l }_{ \bot } } \right] </math> | |||
<math>{ | Porque: <math>Fase\quad de\quad diferencia=\frac { 2\pi }{ \lambda } (camino\quad de\quad diferencia)</math> | ||
<math>( | <math>({ n }_{ \parallel }-{ n }_{ \bot })=\frac { \lambda }{ { 2\pi }l } \left[ { \phi }_{ \parallel }-{ \phi }_{ \bot } \right] </math> | ||
<math> | Porque <math>{ l }_{ \parallel }={ l }_{ \bot }=l</math> | ||
<math>\Delta n=\frac { \lambda }{ { 2\pi }l } \Delta \phi \quad ...(2)</math> | |||
De la Ec. (1) y (2) | |||
<math>\frac { \lambda }{ { 2\pi }l } \Delta \phi =\lambda \cdot K\cdot \frac { { V }^{ 2 } }{ { d }^{ 2 } } </math> | |||
<math> | <math>\frac { 1 }{ { 2\pi }l } \Delta \phi =K\cdot \frac { { V }^{ 2 } }{ { d }^{ 2 } } </math> | ||
<math> | <math>\Delta \phi ={ 2\pi }lK\cdot \frac { { V }^{ 2 } }{ { d }^{ 2 } } </math> | ||
---- | |||
Realizado por: [[Usuario:Luis Gutierrez|Luis Gutiérrez Melgarejo]] | |||
---- | |||
=4ta Edición en Ingles= | |||
== Ejercicio 8.17 4ta Edición en Ingles == | |||
Imagine un par de polarizadores cruzados con ejes de transmisión vertical y horizontal. El rayo que sale del primer polarizador tiene una densidad de flujo $I_1$, y por supuesto la luz no atraviesa el analizador por lo que $I_2=0$. Ahora se inserta un polarizador lineal perfecto con su eje de transmisión a $45^\text{o}$ de la vertical entre los otros polarizadores. Calcule $I_2$. | |||
'''Solución''' | |||
Ya que el ángulo entre el analizador y el polarizador es $45^\text{o}$ podemos utilizar la ley de Malus para la máxima irradianza (Ecuación 8.24 Óptica, Hecht, 4a ed.) | |||
$ | $I_f=I_0\text{cos}^2\theta$ | ||
$ | Llamemos a la densidad de flujo que sale por el tercer polarizador que se encuentra en medio $I_m$ y apliquemos la ley de Malus | ||
$ | $I_m=I_1\text{cos}^2 45^\text{o}= \frac{I_1}{2}$ | ||
Recordemos que el polarizador del extremo final también se encuentra a $45^\text{o}$ del polarizador del centro así que aplicamos la misma formula intercambiando el valor de la densidad inicial por la que acabamos de calcular | |||
$I_2=I_m\text{cos}^2 45^\text{o}= \frac{I_m}{2}=\frac{I_1}{4}$ | |||
Por lo tanto | |||
$ | $I_2=\frac{I_1}{4}$ | ||
---- | |||
Realizado por: Usuario [[Usuario:Flor|Flor Ivon Vivar]] | |||
---- | |||
== Ejercicio 8.45 4ta Edición en Ingles == | |||
Un compensador de Babinet esta puesto a $45°$ en medio de polarizadores cruzados y esta siendo iluminado con luz de sodio (589.6 nm). Cuando una delgada hoja de mica (índices 1.599 y 1.594) es puesta en el compensador, las bandas negras, todas cambian por $1/4$ del espacio reparándolas. calcular el retardo de fase de la hoja y el grueso de ésta. | |||
'''Solución''' | |||
Cuando la mica es puesta las bandas negras cambian su separación de fase de $\Delta\varphi$ a $1/4\Delta\varphi$. Entonces si antes de que se pusiera la mica, las ondas tenían una fase completa de $\Delta\varphi=2\pi$, la nueva fase será $\Delta\varphi´= (1/4)(\Delta\varphi)= (1/4)(2\pi)=\frac{\pi}{2}$, por lo que la hoja hace un retardo de fase de $\pi/2$. | |||
Para obtener el grosor de la mica podemos ocupar la siguiente relación: | |||
$\Delta\varphi´=\frac{2\pi|n_{o}-n_{e}|d}{\lambda_0}$ | |||
Con d el grosor de la mica, $n_{o}$ y $n_{e}$ los índices de los medios en los que las ondas ordinarias y extraordinarias atraviesan, respectivamente. | |||
Así el grosor de la hoja de mica es: | |||
$d=\frac{\Delta\varphi´\lambda_0}{2\pi\Delta{n}}$ con $\Delta{n}= |n_{o}-n_{e}|$. | |||
$d= \frac{\Delta\varphi´\lambda_0}{2\pi\Delta{n}}= \pi/2[\frac{589.6 \times 10^{-9}}{2\pi(5 \times 10^{-3})}]= 2.94 \times 10^-5 m$ | |||
[[Usuario: | ---- | ||
Realizado por: Usuario [[Usuario: Pedro J. Julián]] | |||
---- | |||
Revisión actual - 03:59 19 sep 2023
Problemas capítulo 8 Óptica Hecht, Polarizacion.
Ejercicios resueltos sobre Polarizacion. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema.
Algunas ediciones del Hecht, tienen distintas numeraciones para problemas idénticos.
3ra Edición en Español
Ejercicio 8.1 3ra Edición en Español
Describa detalladamente el estado de polarización de cada una de las siguientes ondas.
(a) $\textbf{E}= \hat{\imath} E_{0}\cos\left(kz-\omega t\right)-\hat{\jmath} E_{0}\cos\left(kz-\omega t\right) $
(b) $\textbf{E}= \hat{\imath} E_{0}\sin 2\pi\left(\frac{z}{\lambda}-\nu t\right)-\hat{\jmath} E_{0}\sin 2\pi \left(\frac{z}{\lambda }-\nu t\right) $
(c) $\textbf{E}= \hat{\imath} E_{0}\sin \left(\omega t-kz\right)+\hat{\jmath} E_{0}\sin \left(\omega t-kz-\pi /4\right) $
(d) $\textbf{E}= \hat{\imath} E_{0}\cos\left(\omega t-kz\right)+\hat{\jmath} E_{0}\cos\left(\omega t-kz+\pi/2\right) $
Solución
(a) La ecuación dada por
$\textbf{E}= \hat{\imath} E_{0}\cos\left(kz-\omega t\right)-\hat{\jmath} E_{0}\cos\left(kz-\omega t\right) \Rightarrow$
$\textbf{E}=\left(\hat{\imath}-\hat{\jmath}\right)E_{0}\cos\left(kz-\omega t\right) $
De la forma de la ecuación deducimos que su estado es polarizada linealmente a 135 grados respecto al plano $xy$ y en cada componente tiene la misma magnitud $E_{0}$.
(b) La ecuación esta dada por
$\textbf{E}= \hat{\imath} E_{0}\sin 2\pi\left(\frac{z}{\lambda}-\nu t\right)-\hat{\jmath} E_{0}\sin 2\pi \left(\frac{z}{\lambda }-\nu t\right) \Rightarrow$
$\textbf{E}=\left(\hat{\imath}-\hat{\jmath}\right)E_{0}\sin\left(\frac{2\pi}{\lambda} z-2\pi \nu t\right)\Rightarrow $
$\textbf{E}=\left(\hat{\imath}-\hat{\jmath}\right)E_{0}\sin\left(kz-\omega t\right)$
Donde empleamos el echo que $k=\frac{2\pi}{\lambda}$ y $\omega=2\pi \nu$
De la forma de la ecuación deducimos que su estado es polarizada linealmente a 135 grados respecto al plano $xy$ y en cada componente tiene la misma magnitud $E_{0}$. Notemos que esta onda es la misma que la de el inciso (a), desfasada $\frac{\pi}{2}$
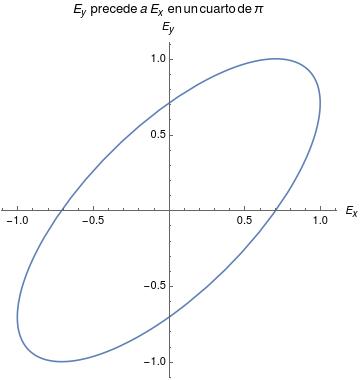
(c) El componente $E_{x}$ le lleva ventaja de $\frac{\pi}{4}$ a la componente $E_{y}$, por tanto su estado es polarizada elíptica de mano izquierda y su forma es como en la siguiente figura.
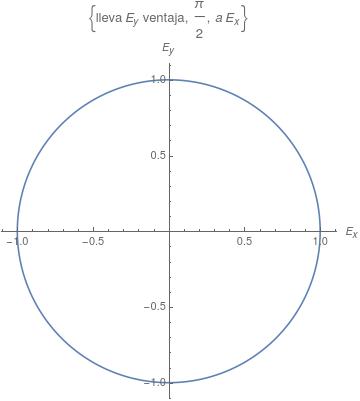
(d) El componente $E_{y}$ le lleva ventaja de $\frac{\pi}{2}$ a la componente $E_{x}$, por tanto su estado es polarizada circular a la derecha y su forma es como en la siguiente figura.
Realizado por: Usuario Jesús Flores Ortega
Ejercicio 8.3 3ra Edición en Español
Demuestre analíticamente que la superposición de un estado R y L que tienen diferentes amplitudes,llevaría a un estado ${\epsilon}$, como se muestra en la figura 8.8 .¿ Cual debería ser el valor de ${\epsilon}$?
${E_R}= i{E_0}cos{(kz-wt)}+j{E_0}sen{(kz-wt)}$
${E_L}=i{E´_0}cos{(kz-wt)}-j{E´_0}sen{(kz-wt)}$
$E={E_R}+{E_L}= i({E_0}+{E´_0})cos{(kz-wt)}+j({E_0}-{E´_0})sen{(kz-wt)}$
dejando
$({E_0}+{E´_0})={E´´_0x}$ y $({E_0}-{E´_0})={E´´_0y}$
por lo que :
$E=i{E´´_0x}cos{(kz-wt)} + j{E´´_0y}sen{(kz-wt)}$
Aportación de: Usuario Usuario:Luisa Alejandra Vega Sanchez
Ejercicio 8.6 3ra Edición en Español
Escriba una expresión para un estado de onda lumínica de frecuencia propagándose en la dirección positiva x tal que a y , el campo a punta en la dirección z negativa.
Solución
Consideremos la onda electromagnética cuyo vector de onda es y su vector de polarización es . Sea W un frente de onda, entonces, tal que:
- .
siendo una base para y, el espacio afín del subespacio vectorial P que pasa por el origen. (W es una traslación de P)Entonces:
.
Por supuesto que la dependencia del campo y de sus componentes , es sinusoidal, es decir:
Ahora, en un estado se deben de cumplir las siguientes condiciones:
- i) donde ;
- ii) &
- iii)
a priori,
Sea que , no hay más para que & . Por lo que
Sin embargo, se desea que a y , el campo apunte en la dirección z negativa, es decir:
Lo cual es cierto si, y sólo si:
& . Por tanto, hagamos , entonces:
, que es lo mismo que:
que es una de las expresiones de la onda que se piden en el problema.
Realizado por: Usuario Diego de la Cruz López
5ta Edición en Ingles
Ejercicio 8.4 5ta Edición en Ingles
Describa detalladamente el estado de la polarización de cada una de las siguientes ondas:
a)
b)
c)
d)
Solución:
Analicemos los máximos de los valores extremos por componentes.
Inciso a
Para la expresión a) vemos que cuando:
Si ; ]
Si ; ]
Si ; ]
Con esto podemos darnos cuenta fácilmente que el campo E de a) es una recta con pendiente 1.
Inciso b
Para la expresión b) tenemos:
Si ; ]
Si ; ]
Si ; ]
Si ; ]
Concluimos que el campo E de b) es una recta con pendiente -1
Inciso c
Para la expresión c) tenemos:
Si ; ]
Si ; ]
Si ; ]
Si ; ]
Es un poco más complicado de visualizar la forma, pero si se unen los puntos que conocemos, podemos interpretar que es una elipse para E de c)
Inciso d
Finalmente, para d)
Si ; ]
Si ; ]
Si ; ]
Si ; ]
Claramente, E de d) es un circulo de radio E
Realizado por: Usuario Fernando Valencia Hernández
Ejercicio 8.28 5ta Edición en Ingles
Dado de luz polarizada incide aleatoria mente en una pila de polarizadores lineales ideales que se colocan uno detrás de otro con el eje de transmisión de la primera vertical, el segundo a 30 grados, el tercero a 60 y el cuarto a 90. cuanta luz emerge?
Solución
Irradianza de luz polarizada aleatoriamente (luz natural)
El angulo de transmisión son 0, 30, 60, y 90 grados respectivamente
cuando la luz natural de irradianza incide en un polarizador lineal, la luz proveniente del polarizador lineal se convierte en la mitad
entonces del 1er polarizador =
la diferencia de angulo entre el 1er y 2do
De la ley de Malus, la irradiación de la luz emerge del 2do polarizador lineal
angulo entre los polarizadores 2do y 3ro
aplicando de nuevo la ley de Malus para el tercer polarizador
...(1)
Esto es incidente en el cuarto polarizador
Angulo entre los polarizadores 3ro y 4to
esto nos da:
Esta ultima cantidad es la irradiacion de luz que emerge después de pasar por cuatro polarizadores
Realizado por: Usuario Salvador Morales Carranza
Ejercicio 8.30 5ta Edición en Ingles
Un polarizador ideal rota con una velocidad angular entre un par de polarizadores similares cruzados y estacionarios. Muestre que la densidad de flujo emergente estará modulada por cuatro veces la frecuencia de rotación. En otras palabras, muestre que
donde es la densidad de flujo emergente del primer polarizador e es la densidad de flujo final.
Solución:
El ángulo que hay entre el primer polarizador y el segundo que está girando es . Si la amplitud de la luz que sale del primer polarizador es $E_{01}$, entonces la que emerge del polarizador en rotación debe ser
Ahora bien, el último polarizador tiene un ángulo de respecto del primero, lo que significa que el ángulo de salida será , entonces la amplitud resultante será
Además, sabemos que
Entonces
Entonces
Y como llegamos a
Realizado por: Ivan de Jesús Pompa García (discusión) 22:02 5 nov 2018 (CST)
Ejercicio 8.47 5ta Edición en Ingles
Un haz de luz natural incide en una interfaz aire-vidrio a 40°,Calcular el grado de polarización de la luz reflejada.
Solución:
- Ocupando la expresión 8.33 del libro, para el grado de polarización de la luz reflejada es:
- .....(A)
- Donde es la densidad de flujo constituyente de la luz polarizada y es la densidad de flujo constituyente de la luz no polarizada.
- La densidad de flujo constituyente de la luz polarizada esta dada por:
- ....(1)
- La onda total reflejada tiene una irradiancia dada:
- ....(2)
- Aquí y son la irradiancia y estan dadas por las ecuaciones de Fresnel:
- .....(3)
- Y
- ........(4)
- Aquí es el ángulo incidente y es el ángulo transmitido:
- Tenemos por ley de Snell:
- Despejando
- Sustituyendo los valores numéricos:
- Sustituyendo el anterior resultado en (3):
- ....(5)
- Similar para (4):
- .......(6)
- Sustituyendo (1) y (2) en (A) tenemos:
- ......(7)
- Ahora tomando .....(8)
- Reemplazando, (7) tiene la forma:
- ....(9)
- Reduciendo la expresión anterior:
- ...(10)
Conclusión:
- finalmente sustituyendo (5) y (6) en (10):
- Por lo tanto el grado de polarización es del 69%
Realizado por: UsuarioLuis Manuel Chávez Antonio
Ejercicio 8.48 5ta Edición en Ingles
Demuestre que el grado de polarización de $(V_r)$ de la luz reflejada puede expresarse como:
- $V_r= \frac{R_{\perp} - R_{ \parallel}}{R_{\perp} + R_{ \parallel}}$
Solución:
Partimos de la definición de grado de polarización:
- $V= \frac{I_p}{I_p + I_n}$
Donde $I_p$ e $I_n$ son las densidades de flujo constitutivas de la luz polarizada y no polarizada o luz natural .
Estas cantidades son función de la Reflectancia:
$R_{ \parallel}= \frac{I_{ \parallel }}{I_0}$
$R_{ \perp} = \frac{I_{ \perp }}{I_0}$
Despejando $I_{ \perp }$ y $I_{ \parallel}$ obtenemos:
$I_{0} R_{ \parallel}= I_{ \parallel }$
$I_0 R_{ \perp} = I_{ \perp } $
Recordemos que para la luz reflejada no polarizada : $I_{\parallel}= I_{ \perp }$
Mientras que en luz reflejada polarizada : $I_p =I_{r \perp } - I_{r \parallel }$
Con esto en mente , hacemos la sustitución en la definición de grado de polarización:
$V= \frac{I_p}{I_p + I_n} =\frac{ I_{r \perp } - I_{r \parallel }}{ I_{r \perp } - I_{r \parallel } + 2 I_{r \parallel }}$
$V= \frac {I_0 R_{ \perp} - I_0 R_{ \parallel }}{ I_0 R_{ \perp} - I_0 R_{ \parallel} + 2 I_0 R_{ \parallel}}$
$V=\frac {I_0 R_{ \perp} - I_0 R_{ \parallel}}{ I_0 R_{ \perp} + I_0 R_{ \parallel} }$
Factorizamos $I_0$:
$V=\frac {I_0( R_{ \perp} - R_{ \parallel})}{ I_0( R_{ \perp} + R_{ \parallel}) }$
El factor $\frac {I_0}{I_0}=1$ y obtenemos la expresión para el grado de polarización $V_r$ de la luz reflejada :
$V_r= \frac{R_{\perp} - R_{ \parallel}}{R_{\perp} + R_{ \parallel}}$
Realizado por: Usuario Aurea Espin (discusión) 10:59 11 nov 2018 (CST)
Ejercicio 8.49 5ta Edición en Ingles
Un haz de luz natural que incide en el aire en un interfaz de vidrio a 70° se refleja parcialmente. Calcular la reflectancia general. ¿Como se compararía esto con el caso de incidencia en, digamos ,56.3 °?
Solución:
Los datos que tenemos son:
Angulo de incidencia del haz de luz en el interfaz de aire-vidrio.
Indice de refracción de medio.
Partiendo de la ley de Snell:
Por lo tanto en angulo de transmisión es
De las ecuaciones de Fresnel
Componente paralelo de reflectancia:
sustituimos los valores de y
Sobre toda la reflectancia
Sobre toda la reflectancia
Es decir 17.107 % de la luz se refleja o también se puede decir 17.107 % de la luz incidente se refleja
Cuando el angulo de incidencia
De la ley de Snell:
En angulo de transmisión es:
Nuevamente usamos la ecuación:
Sobre toda la reflectancia
Porcentaje de reflectancia = 7.395 %
En este caso, la incidencia del angulo de 56.3° es igual al angulo de polarización. Así la luz reflejada esta totalmente polarizada. Pero en el primer caso la luz reflejada esta parcialmente polarizada. En el primer caso 17.107 % de la luz incidente se refleja y se polariza parcialmente. Pero en el caso posterior 7.395 % se refleja la luz incidente y se polariza totalmente.
Realizado por: Usuario Enrique Ortiz Martinez
Ejercicio 8.52 5ta Edición en Ingles
Un rayo de luz amarilla incide sobre una placa de calcita a .La placa se corta de modo que el eje óptico sea paralelo a la cara frontal y perpendicular al plano de incidencia.Encuentra la separación angular entre los dos rayos emergentes
Solución:
Sabemos que: El indice de refracción del rayo ordinario en la placa de cuarzo = 1.6584
El indice de refracción de rayos extraordinarios en la placa de cuarzo =1.4864
Angulo de incidencia de la luz amarilla en el cristal de calcita =
Sabemos que la ley de Snell es:
Para el rayo ordinario tenemos :
Para rayos extraordinarios tenemos análogamente de la ley de Snell
Por lo tanto la separación angular entre los dos rayos emergentes es:
Realizado por: Ruben Espinosa Guzman
Ejercicio 8.69 5ta Edición en Ingles
Un compensador de Babinet se coloca 45° entre polarizadores lineales cruzados y se elimina con luz de sodio. Al colocar una lámina fina de mica (índices 1.599 y 1.594) en el compensador, todas las bandas negras se desplazan una cuarta parte del espacio que las separa. Calcule la retardancia de la lámina y su espesor.
Solución:
La retardancia está dada por:
- $\Delta φ=\frac{2π}{λ_0} dΔn$
- Donde $\Delta φ=\frac{(14)}{(2π)}=\frac{π}{2}$
- Despejando d
- $\frac{\pi}{2}=\frac{2\pi\ d(0.005)}{589.3\times{10}^{-9}}$
- $d=\frac{589.3\times{10}^{-9}}{4(0.005)}=2.94\times{10}^{-5}m$
Realizado por: Verenisse
Ejercicio 8.73 5ta Edición en Ingles
Considere una celda de kerr cuyas placas están separadas por una distancia d. Sea l la longitud efectiva de esas placas (ligeramente diferente de la longitud real debido a la franja del campo). Muestra que
.
Solución:
Donde: : Separacion de las placas en celdas de Kerr
: Longitud efectiva de las placas en celdas de Kerr
La diferencia entre los indices y asociada con las dos orientaciones del plano de vibracion de la onda (es decir, paralela y perpendicular al campo eléctrico aplicado), es
Donde: : Kerr constante : Intensidad de campo eléctrico.
Porque
Donde: : Longitud de onda de las ondas en un dice de refracción
: Longitud de onda de las ondas en un indice de refracción
Porque:
Porque
De la Ec. (1) y (2)
Realizado por: Luis Gutiérrez Melgarejo
4ta Edición en Ingles
Ejercicio 8.17 4ta Edición en Ingles
Imagine un par de polarizadores cruzados con ejes de transmisión vertical y horizontal. El rayo que sale del primer polarizador tiene una densidad de flujo $I_1$, y por supuesto la luz no atraviesa el analizador por lo que $I_2=0$. Ahora se inserta un polarizador lineal perfecto con su eje de transmisión a $45^\text{o}$ de la vertical entre los otros polarizadores. Calcule $I_2$.
Solución
Ya que el ángulo entre el analizador y el polarizador es $45^\text{o}$ podemos utilizar la ley de Malus para la máxima irradianza (Ecuación 8.24 Óptica, Hecht, 4a ed.)
$I_f=I_0\text{cos}^2\theta$
Llamemos a la densidad de flujo que sale por el tercer polarizador que se encuentra en medio $I_m$ y apliquemos la ley de Malus
$I_m=I_1\text{cos}^2 45^\text{o}= \frac{I_1}{2}$
Recordemos que el polarizador del extremo final también se encuentra a $45^\text{o}$ del polarizador del centro así que aplicamos la misma formula intercambiando el valor de la densidad inicial por la que acabamos de calcular
$I_2=I_m\text{cos}^2 45^\text{o}= \frac{I_m}{2}=\frac{I_1}{4}$
Por lo tanto
$I_2=\frac{I_1}{4}$
Realizado por: Usuario Flor Ivon Vivar
Ejercicio 8.45 4ta Edición en Ingles
Un compensador de Babinet esta puesto a $45°$ en medio de polarizadores cruzados y esta siendo iluminado con luz de sodio (589.6 nm). Cuando una delgada hoja de mica (índices 1.599 y 1.594) es puesta en el compensador, las bandas negras, todas cambian por $1/4$ del espacio reparándolas. calcular el retardo de fase de la hoja y el grueso de ésta.
Solución
Cuando la mica es puesta las bandas negras cambian su separación de fase de $\Delta\varphi$ a $1/4\Delta\varphi$. Entonces si antes de que se pusiera la mica, las ondas tenían una fase completa de $\Delta\varphi=2\pi$, la nueva fase será $\Delta\varphi´= (1/4)(\Delta\varphi)= (1/4)(2\pi)=\frac{\pi}{2}$, por lo que la hoja hace un retardo de fase de $\pi/2$. Para obtener el grosor de la mica podemos ocupar la siguiente relación:
$\Delta\varphi´=\frac{2\pi|n_{o}-n_{e}|d}{\lambda_0}$
Con d el grosor de la mica, $n_{o}$ y $n_{e}$ los índices de los medios en los que las ondas ordinarias y extraordinarias atraviesan, respectivamente.
Así el grosor de la hoja de mica es:
$d=\frac{\Delta\varphi´\lambda_0}{2\pi\Delta{n}}$ con $\Delta{n}= |n_{o}-n_{e}|$.
$d= \frac{\Delta\varphi´\lambda_0}{2\pi\Delta{n}}= \pi/2[\frac{589.6 \times 10^{-9}}{2\pi(5 \times 10^{-3})}]= 2.94 \times 10^-5 m$
Realizado por: Usuario Usuario: Pedro J. Julián





















![\vec{E}(\vec{r},t)=E_{0}[\cos(\vec{k}\cdot\vec{r}-\omega t+\delta)\hat{r}_{1} + \sin(\vec{k}\cdot\vec{r}-\omega t+\delta)\hat{r}_{2}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a06287fd67091708acbb3d9d3bdd45725d3c0f13)




![\vec{E}(\vec{x},t)=E_{0}[\cos(kx-\omega t +\delta)\hat{y} + \sin(kx-\omega t +\delta)\hat{z}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6abef0f0bd42cd78d2af44e24b119787bcc0cd7e)
![E_{0}[\cos(\delta)\hat{y} + \sin(\delta)\hat{z}]=0\hat{y}-E_{0}\hat{z}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5a97a895605d4e6ef92ccd2bba8b8758b81ac136)



![\vec{E}(x,t)=E_{0}[\cos(kx-\omega t + \frac{3}{2}\pi)\hat{y} + \sin(kx-\omega t + \frac{3}{2}\pi)\hat{z}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/885fb1bafcc09ba0d68ac2e186c1c9514c97debc)
![\vec{E}(x,t)=E_{0}[\sin(kx-\omega t )\hat{y} - \cos(kx-\omega t)\hat{z}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/463fd13c63d21ed8eb13bb945462648790517874)

![{\displaystyle {\vec {E}}={\hat {i}}E_{0}sen[2\pi (z/\lambda -\omega t)]-{\hat {j}}E_{0}sen[2\pi (z/\lambda -\omega t)]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c69eb932f6cd8dd59841bc657aef3ed6da929f60)







































![I = \dfrac{I_1}{8} \left[1-\cos(4\omega t)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f70563a3b07791743bf0f6bcaa39fe068bbc5b7b)








![I = \dfrac{1}{2} E_{01}^2 \cos^2 \theta \sin^2 \theta = \dfrac{1}{2} E_{01}^2 \dfrac{1}{2} \left(1 + \cos(2\theta)\right) \dfrac{1}{2} \left(1 - \cos(2\theta)\right) = \dfrac{E_{01}^2}{2} \dfrac{1}{4} \left(1 - \cos^2(2\theta)\right) = \dfrac{E_{01}^2}{2} \dfrac{1}{4} \left\{1 - \dfrac{1}{2}\left[1 + \cos^4(4\theta)\right]\right\}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e0056ba24e1ca55fa63a42ecf0531000730ab210)
![I=\dfrac{E_{01}^2}{2} \dfrac{1}{8} \left[1 - \cos^4(4\theta)\right] = \dfrac{E_{01}^2}{2} \dfrac{1}{8} \left[1 - \cos^4(4\omega t)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d2a18c6737fa527b7c7e64eabf273e848338fe3d)

![I = \dfrac{I_1}{8} \left[1 - \cos^4(4\omega t)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0b58cc4f4b75a8201be4ebaed7419a18a5b48a16)








































![R_{||}=\left [\frac{tan(31.22)}{tan(108.78)} \right ]^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/02de5b45ce0f49685dee9ed90167248f48666af2)
![R_{||}=\left [\frac{0.606}{-2.94} \right ]^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2ed8474f016c7711a6ea15a389e0837bcdbcec56)



![R_{ \perp}=\left [\frac{sen(31.22)}{sen(108.78)} \right ]^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/251832ee9919352745e73f9b466d48655ecd57fc)
![R_{ \perp}=\left [\frac{0.5183}{0.9467} \right ]^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/41cafc1e7883ca83c629259173944a88d92096f8)
![R_{ \perp}=\left [0.5474 \right ]^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e5f846e7dc5a37852e6ab8edd5e4223e41023743)











![R_{||}=\left [\frac{tan(22.62)}{tan(89.98)} \right ]^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f2c4a54d0203a7cb9e37845eeae69e598394f154)
![R_{||}= \left [\frac{0.4166}{3993.46} \right ]^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0b07627351a243e4a55f22ab77925aedab6bea26)


![R_{ \perp}=\left [\frac{sen(22.62)}{sen(89.68)} \right ]^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3aeab79aadee8df8a342494775f1089e1d518378)
![R_{ \perp}=\left [\frac{0.3846}{0.9999} \right ]^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/54c2268404fa9cda2e1853a34b335a2852fc37ab)



































![({ n }_{ \parallel }-{ n }_{ \bot })=\left[ \left( \frac { \lambda }{ { \lambda }_{ \parallel } } \right) -\left( \frac { \lambda }{ { \lambda }_{ \bot } } \right) \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/37ec4b7a9db5593dd52e7bb0467a184ce3627431)




![({ n }_{ \parallel }-{ n }_{ \bot })=\lambda \left[ \frac { 1 }{ { \lambda }_{ \parallel } } -\frac { 1 }{ { \lambda }_{ \bot } } \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f5ed01f710e9b4a6d1a97d2f8eb0e6fe8d2c2160)
![({ n }_{ \parallel }-{ n }_{ \bot })=\lambda \left[ \frac { { \phi }_{ \parallel } }{ { 2\pi l }_{ \parallel } } -\frac { { \phi }_{ \bot } }{ { 2\pi l }_{ \bot } } \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e5cce6d61e3fa534836535b90ae3eab63a08c296)

![({ n }_{ \parallel }-{ n }_{ \bot })=\frac { \lambda }{ { 2\pi }l } \left[ { \phi }_{ \parallel }-{ \phi }_{ \bot } \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ea7a1377cd3ad0b7ed64fe0a3026f20dda822d42)




