Optica: Capitulo2-problemas

Bienvenidos. En esta página pueden dejar las soluciones a sus problemas del Hecht- Capítulo 2, con el siguiente formato:

Problema 1

Planteamiento del problema

Solución

y su respectiva firma

--Gael

---

Problema 2

Planteamiento del problema

Solución

y su respectiva firma

---

Etcétera.

---

Ejercicio 2.32

---

Indique cuales de las siguientes ecuaciones representan a una onda viajera:

• $\psi (y,t) = exp\left[-\left(a^2 y^2 + b^2 t^2 -2abty\right)\right]$

Solución: Para tener una onda viajera se debe tener una dependencia funcional de la forma:

$\psi = f(y \mp vt)$

donde $y$ será la dirección de propagación si el signo de $vt$ es negativo y $-y$ si el signo de $vt$ es positivo. Además

$v = \dfrac{\omega}{k}$

Notamos que dentro de la exponencial se tiene un trinomio cuadrado perfecto, por lo que

$\left(a^2 y^2 + b^2 t^2 -2abty\right) = \left(ay - bt\right)^2 = a^2 \left(y - bt/a\right)^2$

de donde concluimos que

* La onda es viajera con dirección de propagación $+y$

* La onda tiene una velocidad $v = \omega / k = b / a$

• $\psi (z,t) = A \sin \left(az^2 - bt^2\right)$

Solución: En este caso el argumento de la función seno tiene una dependencia funcional cuadrática en las coordenadas espaciales y temporales, por ello no tiene una dependencia funcional de la forma $f(z \mp vt)$ y no se trata de una onda viajera.

• $\psi (x,t) = A \sin 2\pi \left(\dfrac{x}{a} + \dfrac{t}{b} \right)^2$

Solución: Tenemos dentro de la función seno los términos $\left(\dfrac{x}{a} + \dfrac{t}{b}\right)^2 = \dfrac{1}{a^2} \left(x + \dfrac{at}{b}\right)^2$ y por ello

* La onda es viajera con dirección de propagación $-x$

* La onda tiene una velocidad $v = \omega / k = a / b$

• $\psi (x,t) = A \cos^2 2\pi \left(t-x\right)$

Solución: En este caso resulta simple ver que $(t-x) = - (x - t)$ y por ello

* La onda es viajera con dirección de propagación $+x$

* La onda tiene una velocidad $v = \omega / k = 1$

Ivan de Jesús Pompa García (discusión) 13:31 14 oct 2018 (CDT)

---

Ejercicio 2.21

---

Empezando por el siguiente teorema: Si $z=f(x,y)$ y $x=g(t), y=h(t)$, entonces

$\frac{dz}{dt}=\frac{\partial z}{\partial x} \frac{dx}{dt}+ \frac{\partial z}{\partial y} \frac{dy}{dt}$

Derive la ecuación (2.34)

$\pm v=- \left(\frac{\partial \psi}{\partial t}\right)_x /\left(\frac{\partial \psi}{\partial x}\right)_t$

Solución:

Para una onda que se propaga con fase constante:

$\psi(x,t)=A \sin k(x\pm vt)$

con $\phi(x,t)=k(x\pm vt)=constante$

Cualquier punto de onda armónica con magnitud fija, se mueve de tal manera que $\phi(x,t)$ sea constante en el tiempo, i.e.,

$\frac{d}{dt}\phi(x,t)=0$ o de otra forma, $\frac{d}{dt}\psi(x,t)=0$.

Esto es cierto para toda clase de onda, periódica o no.

Así:

$\frac{d\psi}{dt}=\frac{\partial \psi}{\partial x} \frac{dx}{dt}+ \frac{\partial \psi}{\partial t} \frac{dt}{dt}$

$\frac{d\psi}{dt}=\frac{\partial \psi}{\partial x} (\pm v)+ \frac{\partial \psi}{\partial t} =0$

Despejando $\pm v$ se obtiene la expersión requerida:

$\pm v=- \left(\frac{\partial \psi}{\partial t}\right)_x /\left(\frac{\partial \psi}{\partial x}\right)_t$

donde el signo de $v$ depende del sentido de propagación de la onda.

--Sergio

---

Ejercicio 2.49

---

Demuestre que las ecuaciones (2.64) y (2.65) las cuales son ondas planas de forma arbitraria, satisfacen la ecuación de onda de tres dimensiones diferencial.

Solución:

Las siguientes dos ecuaciones:

$\psi (x,y,z,t)=f(\alpha x+\beta y+\gamma z-vt)$......................(2.64)

$\psi (x,y,z,t)=g(\alpha x+\beta y+\gamma z+vt)$......................(2.65)

Son funciones, en las cuales f y g son dos veces diferenciables consideremos una función de la forma:

$\psi (x,y,z,t)={e}^{ik(\alpha x+\beta y+\gamma z\pm vt)}$........(1)

Calculando las derivadas parciales de la ecuación (1) obtenemos:

${\frac {\partial ^{2}\psi }{\partial x^{2}}}=-\alpha ^{2}k^{2}\psi$

${\frac {\partial ^{2}\psi }{\partial y^{2}}}=-\beta ^{2}k^{2}\psi$

${\frac {\partial ^{2}\psi }{\partial z^{2}}}=-\gamma ^{2}k^{2}\psi$

${\frac {\partial ^{2}\psi }{\partial t^{2}}}=-k^{2}v^{2}\psi$...............(2)

Agregando las tres derivadas espaciales y utilizando el echo que $\alpha ^{2}+\beta ^{2}+\gamma ^{2}=1$ obtenemos:

${\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}=-k^{2}(\alpha ^{2}+\beta ^{2}+\gamma ^{2})\psi$

Por la consideración anterior tenemos entonces que :

${\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}=-k^{2}\psi$.......(3)

De la ecuación (2) notamos que se puede reescribir como :

${\frac {1}{v^{2}}}{\frac {\partial ^{2}\psi }{\partial t^{2}}}=-k^{2}\psi$..........(4)

Ahora combinando la parte temporal ecuación (4) y la parte espacial ecuación (3) por transitividad tenemos:

${\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}={\frac {1}{v^{2}}}{\frac {\partial ^{2}\psi }{\partial t^{2}}}$

Por lo tanto cumple con la ecuación de onda en tres dimensiones

Ruben Espinosa Guzman 21:22 15 oct 2018

---

Ejercicio 2.45

---

Demostrar que la parte imaginaria de un número complejo ${\tilde {z}}$ está dada por $({\tilde {z}}-{\tilde {z}}^{*})/2i$.

Solución:

El numero complejo z, tiene la siguiente forma: ${\tilde {z}}=x+iy$ Donde $x$, es la parte real y $y$ es la parte imaginaria del numero complejo $z$ Se tiene tambien que el complejo conjugado del numero ${\tilde {z}}$ es ${\tilde {z}}^{*}=x-iy$ Restando el complejo conjugado a el numero complejo ${\tilde {z}}$ antes definido se tiene:

${\tilde {z}}-{\tilde {z}}^{*}=(x+iy)-(x-iy)$

$=x+iy-x+iy$

$=2iy$

Reorganizando la ecuación anterior para la parte imaginaria $y$, se tiene:

$y={\frac {{\tilde {z}}-{\tilde {z}}^{*}}{2i}}$

Por lo tanto la parte imaginaria de una numero complejo es:

${\frac {{\tilde {z}}-{\tilde {z}}^{*}}{2i}}$

Luis Gutiérrez Melgarejo 22:13 15 oct 2018

---

Ejercicio 2.48

---

Empezando por la ecuación (2.51), compruebe que

$\psi (x,y,z,t)=Ae^{i[k(\alpha x+\beta y+\gamma z)\mp \omega t]}$

y que

$\alpha ^{2}+\beta ^{2}+\gamma ^{2}=1$

Solución:

La onda armónica plana en coordenadas cartesianas se expresa como:

$\psi (x,y,z,t)=Ae^{i(k_{x}x+k_{y}y+k_{z}z\pm \omega t)}$..........(2.51)

Si $\alpha$, $\beta$ y $\gamma$ son los cosenos de dirección de ${\vec {k}}$ en las direcciones $x$, $y$ y $z$ respectivamente, entonces:

$k_{x}=k\alpha$

$k_{y}=k\beta$

$k_{z}=k\gamma$

así, la ecuación (2.51) puede expresarse como:

$\psi (x,y,z,t)=Ae^{i[k\alpha x+k\beta y+k\gamma z\pm \omega t]}$

$\psi (x,y,z,t)=Ae^{i[k(\alpha x+\beta y+\gamma z)\pm \omega t]}$

La magnitud del vector de propagación ${\vec {k}}$ es:

$|{\vec {k}}|=k$..........(1)

en términos de componentes, magnitud de ${\vec {k}}$, $|{\vec {k}}|$

$=(k_{x}^{2}+k_{y}^{2}+k_{z}^{2})^{\frac {1}{2}}$

$=[(k\alpha )^{2}+(k\beta )^{2}+(k\gamma )^{2}]^{\frac {1}{2}}$

$=k[(\alpha )^{2}+(\beta )^{2}+(\gamma )^{2}]^{\frac {1}{2}}$

$=k(\alpha ^{2}+\beta ^{2}+\gamma ^{2})^{\frac {1}{2}}$..........(2)

de la ecuación (1) y (2):

$k(\alpha ^{2}+\beta ^{2}+\gamma ^{2})^{\frac {1}{2}}=k$

$(\alpha ^{2}+\beta ^{2}+\gamma ^{2})^{\frac {1}{2}}=1$

$\alpha ^{2}+\beta ^{2}+\gamma ^{2}=1$

Enrique Ortiz Martinez 23:08 15 oct 2018

---

Ejercicio 2.56

---

Mostrar explícitamente, que la función: $\Psi \left({\overrightarrow {r}},t\right)=Aexp\left\lceil i\left({\overrightarrow {k}}\bullet {\overrightarrow {r}}+\varpi t+\epsilon \right)\right\rceil$ describe una onda siempre que $v={\frac {\varpi }{k}}$

Solución:

Empecemos escribiendo el vector k y el vector r, en coordenadas cartesianas:

${\overrightarrow {k}}={k}_{x}+{k}_{y}+{k}_{z}$:

${\overrightarrow {r}}={x}+{y}+{z}$

Haciendo el producto punto de K con r.

${\overrightarrow {k}}\bullet {\overrightarrow {r}}={k}_{x}{x}+{k}_{y}{y}+{k}_{z}{z}$

Sustituyendo en la función de onda:

$\Psi =Aexp\left[i\left({k}_{x}x+{k}_{y}y+{k}_{z}z+\varpi t+\varepsilon \right)\right]$

Tenemos que la ecuación de onda es:

${\triangledown }^{2}\Psi ={\frac {1}{{v}^{2}}}{\frac {{\partial }^{2}\Psi }{\partial {t}^{2}}}$

sustituyendo la función de onda en la ecuación anterior, obtenemos primero del laplaciano:

${\triangledown }^{2}\Psi =-({{k}_{x}^{2}+{k}_{y}^{2}+{k}_{z}^{2})Aexp\left[i\left({\overrightarrow {k}}\bullet {\overrightarrow {r}}+\varpi t+\varepsilon \right)\right]}$

El signo menos proviene del hecho de que $i^{2}=-1$

Ahora calculando las parciales con respecto a t:

${\frac {{\partial }^{2}\Psi }{\partial {t}^{2}}}=-{\varpi }^{2}Aexp\left[i\left({\overrightarrow {k}}\bullet {\overrightarrow {r}}+\varpi t+\varepsilon \right)\right]$

Donde la magnitud de k es:

$\left|k\right|={\sqrt {{k}_{x}^{2}+{k}_{y}^{2}+{k}_{z}^{2}}}$

${k}^{2}={k}_{x}^{2}+{k}_{y}^{2}+{k}_{z}^{2}$

Tenemos que la función de onda es:

${\nabla }^{2}\Psi ={-k}^{2}Aexp\left[i\left({k}_{x}x+{k}_{y}y+{k}_{z}z+\varpi t+\varepsilon \right)\right]$

Ahora comparando con la segunda parcial del tiempo, tenemos que la función de onda es solución si se cumple lo siguiente:

$-{k}^{2}Aexp\left[i\left({k}_{x}x+{k}_{y}y+{k}_{z}z+\varpi t+\varepsilon \right)\right]=-{\varpi }^{2}Aexp\left[i\left({k}_{x}x+{k}_{y}y+{k}_{z}z+\varpi t+\varepsilon \right)\right]$

La última igualdad se cumple solo si:

${v}^{2}={\frac {{\varpi }^{2}}{{k}^{2}}}$

Finalmente la función de onda $\Psi$ es solución si:

$v={\frac {\varpi }{k}}$

Luis Manuel chávez Antonio

---

Ejercicio 2.40

---

Dada la onda $\psi (x,t)=5.0exp(-ax^{2}-bt^{2}-2(ab)^{(}1/2)xt)$, calcule su dirección de propagación. Determine algunos valores de $\psi$ y realice un boceto del perfil de onda en t=0 para a=25m^-2 y b=9.0s^2. ¿Cuál es la velocidad de la onda?.

Solución:

Para siplificar los calculos, podemos ver que $-ax^{2}-bt^{2}-2(ab)^{(}1/2)xt=-[a^{(}1/2)x+b^{(}1/2)t]^{2})$ Por tanto:

$\psi (x,t)=5.0exp(-[a^{(}1/2)x-b^{(}1/2)t]^{2})$

Claramente, como se vio en cursos de cálculo básico. Una función de la forma

$''f''=f(x-B)$

Siendo A y B valores positivos, la función f se desplazará hacía el eje positivo de las x. Por lo tanto la dirección de la propagación de dicha onda, será hacia el eje positivo de x.

Para encontrar explicitamente el valor de la velocidad, se sabe que la ecucaión dada, el argumento de la exponencial es de la forma:

$\psi =kx-wt$

Y se sabe que:

$''v''=w/t$

Asi que

$v=[b/a]^{(}1/2)=[9.0/25]^{(}1/2)=3/5$m/s.

A tiempo t=0 la ecuación de onda queda como:

$\psi (x,t)=5.0exp(-[a^{(}1/2)x]^{2})=5.0exp(-ax^{2})$.

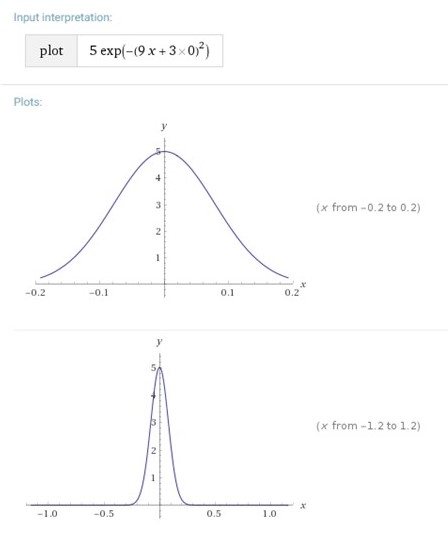
Que claramente es una función Gausseana. Es facil ver que cuando x=0. Implica que $\psi (x,t)=5.0$ Por otro lado, cuando x^2>>>1, $\psi$ tiende a 0.

Se anexa la gráfica de dicha función para apreciar el comportamiento de la Gausseana.

José Fernando Valencia Hernández

---

Ejercicio 2.25

Muestra que $\Psi (x,t)=Acos(kx-\omega t)$ es solución de la ecuación de onda diferencial.

solución:

ecuación de onda diferencial unidimensional es:

${\frac {{\partial }^{2}\Psi }{\partial {x}^{2}}}={\frac {1}{{v}^{2}}}{\frac {{\partial }^{2}\Psi }{{\partial t}^{2}}}$ aquí $\Psi$es la función de onda, v es la velocidad de onda, t es el tiempo y x representa la distancia

La relación entre velocidad angular, número de onda y velocidad de onda es:

$\omega =kv$ aqui $\omega$ es la velocidad angular y $k$ es el numero de onda

por la relacion, $\Psi (x,t)=Acos(kx-\omega t)$...(1)

sacamos su diferencial con respecto a x

${\frac {\partial \Psi }{\partial x}}=-Aksen(kx\quad -\omega t)$ de nuevo diferenciar con respeto a x

${\frac {{\partial }^{2}\Psi }{\partial {x}^{2}}}=-A{k}^{2}cos(kx-\omega t)$....(2)

y sustituyendo en (2) a ${\frac {{\omega }^{2}}{{v}^{2}}}={k}^{2}$

${\frac {{\partial }^{2}\Psi }{\partial {x}^{2}}}=-A{\frac {\omega }{{v}^{2}}}^{2}cos(kx-\omega t)$

diferenciar la ecuación (1) con respecto a una t

${\frac {\partial \Psi }{\partial t}}=-A(-\omega )sen(kx\quad -\omega t)$ y diferenciando de nuevo con respecto a t

${\frac {{\partial }^{2}\Psi }{\partial {t}^{2}}}=-A{\omega }^{2}cos(kx\quad -\omega t)$

multiplicando por ${\frac {1}{{v}^{2}}}$

${\frac {1}{{v}^{2}}}{\frac {{\partial }^{2}\Psi }{\partial {t}^{2}}}=-{\frac {1}{{v}^{2}}}A{\omega }^{2}cos(kx\quad -\omega t)$

arreglando de nuevo:

${\frac {1}{{v}^{2}}}{\frac {{\partial }^{2}\Psi }{\partial {t}^{2}}}=-A{\frac {{\omega }^{2}}{{v}^{2}}}cos(kx\quad -\omega t)$...(3)

por ecuación (2) y (3)

${\frac {{\partial }^{2}\Psi }{\partial {x}^{2}}}=-{\frac {1}{{v}^{2}}}{\frac {{\partial }^{2}\Psi }{\partial {t}^{2}}}$.

queda demostrado que la ecuación diferencial dada es solución.

Salvador morales carranza

---

Ejercicio 2.38

---

¿Cuáles de las siguientes expresiones corresponden a ondas en desplazamiento? ¿Cuál es la velocidad de cada una? Las cantidades a,b y c son constantes positivas.

(a) $\psi (z,t) = \left(az-bt\right)^2$

(b)$\psi (x,t) = \left(ax+bt+c\right)^2$

(c)$\psi (x,t) = \frac{1}{\left(ax^2+b\right)}$

Solución: La forma de las ecuaciones que describen las ondas en desplazamiento es :

$\psi = f (x \pm vt )$

Y debe satisfacer la ecuación diferencial de onda :

$\frac{\partial^2 \psi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$

Para el inciso (a)

$\psi (z,t) = \left(z-\frac{b}{a}t\right)^2$

Calculamos sus derivadas parciales a primer orden:

$\frac{\partial \psi}{\partial z}= 2\left(z-\frac{b}{a}t\right)$

$\frac{\partial \psi}{\partial t}= -2 \frac{b}{a}\left(z-\frac{b}{a}t\right)$

Sus derivadas a segundo orden :

$\frac{\partial^2 \psi}{\partial z^2}= 2$

$\frac{\partial^2 \psi}{\partial t^2}= 2 \frac{b^2}{a^2}$

Con :$\frac{1}{v^2}= \frac{a^2}{b^2}$

Se cumple que:

$\frac{\partial^2 \psi}{\partial x^2}=2=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$

$\frac{\partial^2 \psi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$

• Se satisface la ecuación de onda
• Su velocidad es $|v|=\frac{b}{a}$
• Al ser de la forma $\psi = f (x -vt )$ sabemos que la velocidad va en el sentido negativo del eje z

Para el inciso (b)

$\psi (x,t) = \left(x+\frac{b}{a}t+\frac{c}{a}\right)^2$

Al igual que en el inciso anterior, para comprobar si se cumple la ecuación de onda , obtenemos las primeras derivadas:

$\frac{\partial \psi}{\partial x}= 2\left(x+\frac{b}{a}t+\frac{c}{a}\right)$

$\frac{\partial \psi}{\partial t}= 2 \frac{b}{a}\left(x+\frac{b}{a}t+\frac{c}{a}\right) $

Las segundas derivadas son:

$\frac{\partial^2 \psi}{\partial z^2}= 2$

$\frac{\partial^2 \psi}{\partial t^2}= 2 \frac{b^2}{a^2}$

Con :$\frac{1}{v^2}= \frac{a^2}{b^2}$

$\frac{\partial^2 \psi}{\partial x^2}=2=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$

$\frac{\partial^2 \psi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$

• Se satisface la ecuación de onda
• Su velocidad es $|v|=\frac{b}{a}$
• Como es de la forma $\psi = f (x + vt )$ su velocidad es positiva

Para el inciso (c)

$\psi (x,t) = \frac{1}{\left(ax^2+b\right)}$

• No tiene una dependencia en t

$\psi = f (x \pm vt )$

• No cumple con la ecuación de onda
• Por lo tanto, no describe una onda.

Aurea Espin (discusión) 18:26 20 oct 2018 (CDT)