Diferencia entre revisiones de «Optica: Capitulo2-problemas»
Sin resumen de edición |
|||
| (No se muestran 33 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
Problemas capítulo 2 Óptica Hecht, El movimiento ondulatorio. | |||
Ejercicios resueltos sobre el movimiento ondulatorio. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema. | |||
Algunas ediciones del Hecht, tienen distintas numeraciones para problemas idénticos. | |||
===Ejercicio 2.39=== | ===Ejercicio 2.39=== | ||
Indique cuales de las siguientes ecuaciones representan a una onda viajera: | Indique cuales de las siguientes ecuaciones representan a una onda viajera: | ||
| Línea 83: | Línea 87: | ||
---- | ---- | ||
== Ejercicio 2.22 3ra Edición en español == | |||
Utilizando los resultados del ejercicio anterior (ejercicio 2.21) demuestre que para una onda armónica con fase: | |||
<center><math>\varphi (x,t)=k(x-vt) ~~~~~~~~~~~(1)</math></center> | |||
podemos calcular la velocidad estableciendo $\frac{d\varphi}{dt}=0$. Aplique la técnica a la función de onda: | |||
<center><math>\psi ( | <center><math>\psi (y,t)= A \mathrm{cos} \pi (3*10^{6}y+9*10^{14}t)~~~~~~~~~~~(2)</math></center> | ||
'''Solución''' | |||
Del ejercicio anterior obtenemos que: | |||
<center> | <center>$\frac{d \varphi}{d t}=\frac{\partial \varphi}{\partial x}\frac{dx}{dt}+\frac{\partial \varphi}{\partial t}\frac{dt}{dt} $</center> | ||
Ahora derivamos nuestra ecuación (1) respecto del tiempo y obtenemos: | |||
<center> | <center>$\frac{d \varphi}{d t}=k\frac{dx}{dt}-kv=0 \Rightarrow$ | ||
$\frac{dx}{dt}=\pm v$</center> | |||
<center> | donde: | ||
<center>$\frac{\partial \varphi}{\partial x}=k$ y $\frac{\partial \varphi}{\partial t}=-kv$</center> | |||
Ahora, aplicamos esta técnica a la fase de la ecuación (2) $\varphi(y,t)=\pi (3*10^{6}y+9*10^{14}t)$ y obtenemos: | |||
<center>$\frac{d \varphi}{d t}=3*10^{6}\pi v+9*10^{14}\Rightarrow$$ 3*10^{6}\pi v+9*10^{14}=0 \Rightarrow$$v=-3*10^{8} \mathrm{m/s}$</center> | |||
---- | ---- | ||
Realizado por: [[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23: | Realizado por: [[Usuario:Jesus|Jesús Flores Ortega]],[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:26 27 oct 2020 (CDT) | ||
---- | ---- | ||
= | = 4ta Edición en Ingles = | ||
==Ejercicio 2.20 4ta Edición en Ingles== | |||
Muestre que | |||
$\psi\left({x},t\right)=A \text{cos}\left(kx-\omega t-\frac{\pi}{2}\right)$ | |||
es quivalente a | |||
$\psi\left({x},t\right)=A \text{sen}\left(kx-\omega t\right).$ | |||
'''Solución:''' | |||
Usemos la formula para el coseno de la suma de ángulos | |||
$ \text{cos}(x \pm y) = \text{cos}(x) \text{cos}(y) \mp \text{sen}(x) \text{sen}(y), $ | |||
con la cual la función | |||
$\psi\left({x},t\right)=A \text{cos}\left(kx-\omega t-\frac{\pi}{2}\right)$ | |||
toma la forma | |||
$\psi\left({x},t\right)=A \left[\text{cos}\left(kx-\omega t\right)\text{cos}\left(\frac{\pi}{2}\right)+\text{sen}\left(kx-\omega t\right)\text{sen}\left(\frac{\pi}{2}\right)\right].$ | |||
Recordemos ahora que | |||
$\text{cos}\left(\frac{\pi}{2}\right)=0$ y $\text{sen}\left(\frac{\pi}{2}\right)=1,$ | |||
''' | '''Conclusión''' | ||
Sustituyendo obtenemos | |||
$\psi\left({x},t\right)=A\text{sen}\left(kx-\omega t\right),$ | |||
por lo tanto | |||
$A \text{cos}\left(kx-\omega t-\frac{\pi}{2}\right)=A\text{sen}\left(kx-\omega t\right).$ | |||
---- | |||
Realizado por: [[Usuario:Flor|Flor Ivon Vivar]] | |||
---- | |||
== Ejercicio 2.35 4ta Edición en Ingles == | |||
:Considerar una onda de luz que tiene una velocidad de fase de $3 \times 10^8 m/s$ y una frecuencia de $6 \times 10^{14} Hz$. a) ¿ Cuál es la distancia mas corta entre dos puntos de la onda los cuales tienen una diferencia de fase de 30° ?, b)¿Qué cambio de fase ocurre en un punto dado en un $\Delta{t}= 10^{-6}s$?, y c) ¿ Cuántas ondas han pasado en ese intervalo de tiempo? | |||
<center> | '''''Solución''''': | ||
:a) La longitud de onda $\lambda$ se define como la distancia que recorre la onda en un determinado tiempo llamado periodo. Si la longitud de onda realiza un ciclo de 360° ó $2\pi rad$ cada periodo y $30°$ son $\frac{2\pi}{12}$, entonces basta con dividir a la longitud de onda entre 12 para obtener la respuesta: | |||
:<center>$v=\lambda\nu$; $\lambda=\frac{v}{\nu}$ --> $\frac{\lambda}{12}= \frac{v}{12\nu}$</center> | |||
:<center>$\frac{\lambda}{12}= 4.16 \times 10^{-8} m $</center> | |||
:b)$\Delta{t} \Rightarrow \Delta{\varphi} $ (en el mismo punto); $\Delta{\varphi}= \varphi_2 - \varphi_1$, $\Delta{t}= 10^{-6} s$; | |||
<center> | <center>$\varphi_1= \omega{t_1} - Kx_1$</center> | ||
:<center>$\varphi_2= \omega{t_2} - Kx_1$</center> | |||
:<center>$\Delta{\varphi}= \varphi_2 - \varphi_1= \omega(t_2 - t_1)= \omega\Delta{t}$</center> | |||
:Con $\omega$ y K la frecuencia angular y el número de onda, respectivamente. | |||
:<center>$\Delta{\varphi}= \omega\Delta{t}$</center> | |||
:<center>$\Delta{\varphi}= 2\pi(6 \times 10^{14})(1 \times 10^{-6})$</center> | |||
:Esto quiere decir que un número entero multiplica a $2\pi rad$ lo que equivale a dar una vuelta, entonces no habrá cambio de fase ya que el punto de la primera fase siempre va a llegar al mismo punto de donde empezó. $\Delta{\varphi}$=0. | |||
:c) Si la frecuencia $\nu$ es el número de ciclos que da cada segundo, entonces: | |||
:$\nu{t}$= Número de ondas que pasan en ese intervalo de tiempo | |||
<center> | :<center>$\nu{t}= 6 \times 10^{14}(1 \times 10^{-6})= 6 \times 10^8 ondas$</center> | ||
---- | |||
Realizado por: [[Pedro J. Julian Salgado]], [[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:28 27 oct 2020 (CDT) | |||
---- | |||
== Ejercicio 2.44 4ta Edición en Ingles == | |||
Muestre que $\psi\left(\vec{k}\cdot\vec{r},t\right)$ puede representar una onda plana donde $\vec{k}$ es normal al frente de onda. | |||
''Sugerencia''. Sean $\vec{r}_{1}$, $\vec{r}_2$ dos vectores posición del origen a cualesquiera dos puntos del plano, pruebe que | |||
<center>$\psi\left(\vec{r}_{1},t\right)=\psi\left(\vec{r}_{2},t\right)$.</center> | |||
'''Solución:''' | |||
Una función vectorial ''viajera'', tiene la siguiente expresión: | |||
<center> | <center>$\psi\left(\vec{r},t\right)\equiv \psi\left(\vec{r}-\vec{v}t\right)$</center> | ||
En particular una ''onda plana'' tiene como argumento: | |||
<center>$\psi\left(\vec{r},t\right)=\psi\left(\vec{k}\cdot\vec{r}-\omega t\right)$</center> | |||
Si el vector $\vec{r}_{1}$ y $\vec{r}_{2}$ son vectores dirigidos hacia el frente de onda, entonces satisfacen: | |||
<center>$\left(\vec{r}_{2}-\vec{r}_{1}\right)\cdot\vec{k}=0$</center> | |||
'''Conclusión''' | |||
Observamos que: | |||
$\psi\left(\vec{r}_{1},t\right)=\psi\left(\vec{k}\cdot\vec{r}_{1}-\omega t\right) =\psi\left(\vec{k}\cdot\vec{r}_{2}-\left(\vec{k}\cdot\vec{r}_{2}-\vec{k}\cdot\vec{r}_{1}\right)-\omega t\right)=\psi\left(\vec{k}\cdot\vec{r}_{2}-\vec{k}\cdot\left(\vec{r}_{2}-\vec{r}_{1}\right)-\omega t\right)=\psi\left(\vec{k}\cdot\vec{r}_{2}-\omega t\right)=\psi\left(\vec{r}_{2},t\right)$ | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:diegophy17|Diego de la Cruz]],[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:13 27 oct 2020 (CDT) | ||
[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23: | |||
---- | ---- | ||
= 5ta Edición en Ingles = | |||
== Ejercicio 2.25 5ta Edición en Ingles == | |||
Muestra que <math>\Psi (x,t)=Acos(kx-\omega t)</math> es solución de la ecuación de onda diferencial. | Muestra que <math>\Psi (x,t)=Acos(kx-\omega t)</math> es solución de la ecuación de onda diferencial. | ||
''' | '''Solución:''' | ||
ecuación de onda | ecuación de onda Diferencial unidimensional es:: | ||
<math>\frac { { \partial }^{ 2 }\Psi }{ \partial { x }^{ 2 } } =\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 }\Psi }{ { \partial t }^{ 2 } } </math> aquí <math>\Psi </math>es la función de onda, '''v''' es la velocidad de onda, '''t''' es el tiempo y '''x''' representa la distancia | <math>\frac { { \partial }^{ 2 }\Psi }{ \partial { x }^{ 2 } } =\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 }\Psi }{ { \partial t }^{ 2 } } </math> aquí <math>\Psi </math>es la función de onda, '''v''' es la velocidad de onda, '''t''' es el tiempo y '''x''' representa la distancia | ||
| Línea 334: | Línea 259: | ||
La relación entre velocidad angular, número de onda y velocidad de onda es: | La relación entre velocidad angular, número de onda y velocidad de onda es: | ||
<math>\omega =kv</math> aqui <math>\omega </math> es la velocidad angular y <math>k</math> es el numero de onda por la | <math>\omega =kv</math> aqui <math>\omega </math> es la velocidad angular y <math>k</math> es el numero de onda por la relación: | ||
<center><math>\Psi (x,t)=Acos(kx-\omega t) ~~~~~~~~~~~(1)</math></center> | <center><math>\Psi (x,t)=Acos(kx-\omega t) ~~~~~~~~~~~(1)</math></center> | ||
| Línea 352: | Línea 277: | ||
<center><math>\frac { { \partial }^{ 2 }\Psi }{ \partial { x }^{ 2 } } =-A{ \frac { \omega }{ { v }^{ 2 } } }^{ 2 }cos(kx-\omega t)</math></center> | <center><math>\frac { { \partial }^{ 2 }\Psi }{ \partial { x }^{ 2 } } =-A{ \frac { \omega }{ { v }^{ 2 } } }^{ 2 }cos(kx-\omega t)</math></center> | ||
Diferenciar la ecuación (1) con respecto a <math>t</math>: | |||
<math>\frac { \partial \Psi }{ \partial t } =-A(-\omega )sen(kx\quad -\omega t)</math> | <math>\frac { \partial \Psi }{ \partial t } =-A(-\omega )sen(kx\quad -\omega t)</math> | ||
| Línea 367: | Línea 292: | ||
<center><math>\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } =-A\frac { { \omega }^{ 2 } }{ { v }^{ 2 } } cos(kx\quad-\omega t)~~~~~~~~~~~(3)</math></center> | <center><math>\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } =-A\frac { { \omega }^{ 2 } }{ { v }^{ 2 } } cos(kx\quad-\omega t)~~~~~~~~~~~(3)</math></center> | ||
'''Conclusión''' | |||
De acuerdo con las ecuaciones (2) y (3) | |||
<center><math>\frac { { \partial }^{ 2 }\Psi }{ \partial { x }^{ 2 } } =-\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } </math></center> | <center><math>\frac { { \partial }^{ 2 }\Psi }{ \partial { x }^{ 2 } } =-\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } </math></center> | ||
Queda demostrado que la ecuación diferencial dada es solución. | |||
[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:24 27 oct 2020 (CDT) | ---- | ||
Realizado por: [[Usuario:salvadormorales|Salvador morales carranza]], [[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:24 27 oct 2020 (CDT) | |||
---- | ---- | ||
== Ejercicio 2.38 5ta Edición en Ingles == | |||
¿Cuáles de las siguientes expresiones corresponden a ondas en desplazamiento? ¿Cuál es la velocidad de cada una? Las cantidades a,b y c son constantes positivas. | ¿Cuáles de las siguientes expresiones corresponden a ondas en desplazamiento? ¿Cuál es la velocidad de cada una? Las cantidades a,b y c son constantes positivas. | ||
<center>(a) $\psi (z,t) = \left(az-bt\right)^2$</center> | <center>(a) $\psi (z,t) = \left(az-bt\right)^2$</center> | ||
| Línea 385: | Línea 315: | ||
<center>(c)$\psi (x,t) = \frac{1}{\left(ax^2+b\right)}$</center> | <center>(c)$\psi (x,t) = \frac{1}{\left(ax^2+b\right)}$</center> | ||
'''''Solución''''' | '''''Solución''''' | ||
La forma de las ecuaciones que describen las ondas en desplazamiento es : | |||
:<center>$\psi = f (x \pm vt )$</center> | :<center>$\psi = f (x \pm vt )$</center> | ||
| Línea 455: | Línea 387: | ||
*Por lo tanto, no describe una onda. | *Por lo tanto, no describe una onda. | ||
[[Usuario:Aurea Espin|Aurea Espin]] ([[Usuario discusión:Aurea Espin|discusión]]) 18:26 20 oct 2018 (CDT) | ---- | ||
Realizado por: [[Usuario:Aurea Espin|Aurea Espin]] ([[Usuario discusión:Aurea Espin|discusión]]) 18:26 20 oct 2018 (CDT), | |||
[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:25 27 oct 2020 (CDT) | |||
---- | |||
[ | == Ejercicio 2.40 5ta Edición en Ingles == | ||
-- | |||
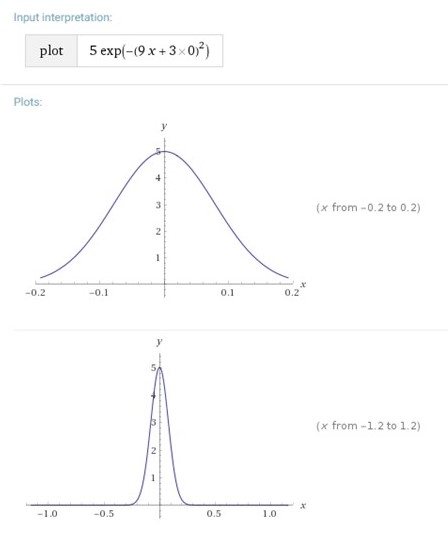
Dada la onda <math> \psi (x,t)=5.0exp(-ax^2-bt^2-2(ab)^\frac12xt)</math>, calcule su dirección de propagación. Determine algunos valores de <math>\psi</math> y realice un boceto del perfil de onda en <math>t=0</math> para <math>a=25m^-2</math> y <math>b=9.0s^2</math>. ¿Cuál es la velocidad de la onda? | |||
'''Solución:''' | |||
Para simplificar los cálculos, podemos ver que <math>-ax^2-bt^2-2(ab)^\frac12xt=-[a^\frac12 x+b^\frac12t]^2)</math> | |||
Por tanto: | |||
:<math>\psi (x,t)=5.0exp(-[a^\frac12x-b^\frac12t]^2)</math> | |||
:Claramente, como se vio en cursos de cálculo básico. Una función de la forma: | |||
:<math>''f''=f(x-B)</math> | |||
:Siendo A y B valores positivos, la función f se desplazará hacía el eje positivo de las x. Por lo tanto la dirección de la propagación de dicha onda, será hacia el eje positivo de x. | |||
:Para encontrar explícitamente el valor de la velocidad, se sabe que la ecuación dado el argumento de la exponencial es de la forma: | |||
:<math>\psi=kx-wt</math> | |||
:Y se sabe que: | |||
:<math>''v''=\frac wt</math> | |||
:Asi que | |||
:<math>v=(\frac ba)^\frac12=(\frac{9.0}{25})^\frac12=(\frac35) \frac ms</math>. | |||
:A tiempo t=0 la ecuación de onda queda como: | |||
:<math>\psi (x,t)=5.0exp(-[a^\frac12x]^2)=5.0exp(-ax^2)</math>. | |||
:Que claramente es una función Gaussiana. Es fácil ver que cuando x=0. Implica que <math>\psi (x,t)=5.0</math> Por otro lado, cuando x^2>>>1, <math>\psi</math> tiende a 0. | |||
:Se anexa la gráfica de dicha función para apreciar el comportamiento de la Gaussiana. | |||
'''Gráfica''' | |||
[[Archivo:grafica problema 2.40.jpeg]] | |||
---- | |||
Realizado por: [[Usuario:Onáfeder|José Fernando Valencia Hernández]], [[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:23 27 oct 2020 (CDT) | |||
---- | |||
== Ejercicio 2.45 5ta Edición en Ingles == | |||
Demostrar que la parte imaginaria de un número complejo <math>\tilde { z } </math> está dada por <math>(\tilde { z } -\tilde { z }^{*})/2i</math>. | |||
'''Solución''' | |||
< | El numero complejo z, tiene la siguiente forma: | ||
<math>\tilde { z }=x+iy</math> | |||
Donde <math>x</math>, es la parte real y <math>y</math> es la parte imaginaria del numero complejo <math>z</math> | |||
también se tiene que el complejo conjugado del numero <math>\tilde { z } </math> es | |||
<math>{ \tilde { z } }^{ * }=x-iy</math> | |||
restando el complejo conjugado a el numero complejo <math>\tilde { z }</math> antes definido se obtiene: | |||
<center><math>\tilde { z } -{ \tilde { z } }^{ * }=(x+iy)-(x-iy)=x+iy-x+iy=2iy</math></center> | |||
Reorganizando la ecuación anterior para la parte imaginaria <math>y</math>, se tiene: | |||
<math>y=\frac { \tilde { z } -{ \tilde { z } }^{ * } }{ 2i } </math> | |||
Por lo tanto la parte imaginaria de una numero complejo es: | |||
<math>\frac { \tilde { z } -{ \tilde { z } }^{ * } }{ 2i } </math> | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Luis Gutierrez|Luis Gutiérrez Melgarejo]] 22:13 15 oct 2018 | ||
[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:16 27 oct 2020 (CDT) | |||
---- | ---- | ||
== Ejercicio 2.48 5ta Edición en Ingles == | |||
'''Empezando por la ecuación (2.51), compruebe que:''' | |||
<center><math>\psi (x,y,z,t)=Ae^{i[k(\alpha x+\beta y+\gamma z)\mp \omega t]}~~~</math> y que <math>~~~\alpha ^{2}+ \beta ^{2}+\gamma ^{2}=1</math></center> | |||
'''Solución''' | |||
La onda armónica plana en coordenadas cartesianas se expresa como:: | |||
<math>\psi (x,y,z,t)=Ae^{i(k_{x}x+k_{y}y+k_{z}z\pm \omega t)}~~~~~~~~~~~(2.51)</math> | |||
Si <math>\alpha </math>, <math>\beta </math> y <math>\gamma</math> son los cosenos de dirección de <math>\vec{k}</math> en las direcciones <math>x</math>, <math>y</math> y <math>z</math> respectivamente, entonces: | |||
<center><math>k_{x}=k\alpha </math></center> | |||
<center><math>k_{y}=k\beta </math></center> | |||
<center><math>k_{z}=k\gamma </math></center> | |||
Así, la ecuación (2.51) puede expresarse como: | |||
<center><math>\psi (x,y,z,t)=Ae^{i[k\alpha x+k\beta y+k\gamma z\pm \omega t]}</math></center> | |||
<center><math>\psi (x,y,z,t)=Ae^{i[k(\alpha x+\beta y+\gamma z)\pm \omega t]}</math></center> | |||
La magnitud del vector de propagación <math>\vec{k}</math> es: | |||
<center><math>|\vec{k}|=k~~~~~~~~~~~(1)</math></center> | |||
En términos de componentes, la magnitud de <math>\vec{k}</math>, es <math>|\vec{k}|</math></center> | |||
<center><math>=(k_{x}^{2}+k_{y}^{2}+k_{z}^{2})^{\frac{1}{2}}~~~~~~~~~~~~~~</math></center> | |||
<center><math>=[(k\alpha)^{2}+(k\beta )^{2} +(k\gamma )^{2}]^{\frac{1}{2}}</math></center> | |||
<center><math>=k[(\alpha)^{2}+(\beta )^{2} +(\gamma )^{2}]^{\frac{1}{2}}~~~~~</math></center> | |||
<center><math>=k(\alpha^{2}+\beta ^{2} +\gamma ^{2})^{\frac{1}{2}}~~~~~~~(2)</math></center> | |||
De la ecuación (1) y (2): | |||
<center><math>k(\alpha^{2}+\beta ^{2} +\gamma ^{2})^{\frac{1}{2}}=k</math></center> | |||
<center><math>(\alpha^{2}+\beta ^{2} +\gamma ^{2})^{\frac{1}{2}}=1</math></center> | |||
<center><math>\alpha^{2}+\beta ^{2} +\gamma ^{2}=1</math></center> | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Enrique Ortiz|Enrique Ortiz Martinez]] 23:08 15 oct 2018 | ||
[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:20 27 oct 2020 (CDT) | |||
---- | ---- | ||
== Ejercicio 2.49 5ta Edición en Ingles == | |||
Demuestre que las ecuaciones (2.64) y (2.65) las cuales son ondas planas de forma arbitraria, satisfacen la ecuación de onda de tres dimensiones diferencial. | |||
'''''Solución''''' | |||
Las siguientes dos ecuaciones: | |||
<center><math>\psi (x,y,z,t)=f(\alpha x+\beta y+\gamma z-vt)~~~~~~~~~~~ (2.64)</math></center> | |||
<center><math>\psi (x,y,z,t)=g(\alpha x+\beta y+\gamma z+vt) ~~~~~~~~~~~ (2.65)</math></center> | |||
Son funciones, en las cuales f y g son dos veces diferenciables consideremos una función de la forma: | |||
<center><math>\psi (x,y,z,t)={ e }^{ ik(\alpha x+\beta y+\gamma z\pm vt) }~~~~~~~~~~~(1) | |||
</math></center> | |||
Calculando las derivadas parciales de la ecuación (1) obtenemos: | |||
<center><math>\frac{\partial^2 \psi }{\partial x^2}=-\alpha ^{2}k^{2}\psi </math></center> | |||
<center><math>\frac{\partial^2 \psi }{\partial y^2}=-\beta ^{2}k^{2}\psi </math></center> | |||
<center><math>\frac{\partial^2 \psi }{\partial z^2}=-\gamma^{2}k^{2}\psi </math></center> | |||
<center><math>\frac{\partial^2 \psi }{\partial t^2}=-k^{2}v^{2}\psi ~~~~~~~~~~~(2)</math></center> | |||
Agregando las tres derivadas espaciales y utilizando el echo que <math>\alpha ^{2}+\beta ^{2}+\gamma ^{2}=1</math> obtenemos: | |||
<center><math>\frac{\partial^2 \psi }{\partial x^2}+\frac{\partial^2 \psi }{\partial y^2}+\frac{\partial^2 \psi }{\partial z^2}=-k^{2}(\alpha ^{2}+\beta ^{2}+\gamma ^{2})\psi</math></center> | |||
Por la consideración anterior tenemos entonces que : | |||
<center><math>\frac{\partial^2 \psi }{\partial x^2}+\frac{\partial^2 \psi }{\partial y^2}+\frac{\partial^2 \psi }{\partial z^2}=-k^{2}\psi~~~~~~~~~~~(3) | |||
</math></center> | |||
De la ecuación (2) notamos que se puede reescribir como : | |||
<center><math>\frac{1}{v^{2}}\frac{\partial^2 \psi }{\partial t^2}=-k^{2}\psi ~~~~~~~~~~~(4)</math></center> | |||
Ahora combinando la parte temporal ecuación (4) y la parte espacial ecuación (3) por transitividad tenemos: | |||
: | |||
<center><math>\frac{\partial^2 \psi }{\partial x^2}+\frac{\partial^2 \psi }{\partial y^2}+\frac{\partial^2 \psi }{\partial z^2}=\frac{1}{v^{2}}\frac{\partial^2 \psi }{\partial t^2}</math></center> | |||
Por lo tanto cumple con la ecuación de onda en tres dimensiones | |||
---- | ---- | ||
Realizado por: | Realizado por: [[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:15 27 oct 2020 (CDT) | ||
---- | ---- | ||
== Ejercicio 2.56 5ta Edición en Ingles == | |||
'' | |||
< | '''''Mostrar explícitamente, que la función:: | ||
<math>\Psi \left( \overrightarrow { r } ,t \right) =Aexp\left\lceil i\left( \overrightarrow { k } \bullet \overrightarrow { r } +\varpi t+\epsilon \right) \right\rceil </math>''''' | |||
'''''describe una onda siempre que: <math>v=\frac { \varpi }{ k } </math>''''' | |||
'''''Solución''''' | |||
Empecemos escribiendo el vector k y el vector r, en coordenadas cartesianas: | |||
:<math>\overrightarrow { k } ={ k }_{ x }+{ k }_{ y }+{ k }_{ z }</math>: | |||
<math>\overrightarrow { r } ={ x }+{ y }+{ z }</math> | |||
:Haciendo el producto punto de K con r. | |||
:<math>\overrightarrow { k } \bullet \overrightarrow { r } ={ k }_{ x }{ x }+{ k }_{ y }{ y }+{ k }_{ z }{ z }</math> | |||
:Sustituyendo en la función de onda: | |||
:<math>\Psi =Aexp\left[ i\left( { k }_{ x }x+{ k }_{ y }y+{ k }_{ z }z+\varpi t+\varepsilon \right) \right] </math> | |||
:Tenemos que la ecuación de onda es: | |||
:<math>{ \triangledown }^{ 2 }\Psi =\frac { 1 }{ { v }^{ 2 } } \frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } </math> | |||
:Sustituyendo la función de onda en la ecuación anterior, obtenemos primero el laplaciano: | |||
:<math>{ \triangledown }^{ 2 }\Psi =-({ { k }_{ x }^{ 2 }+{ k }_{ y }^{ 2 }+{ k }_{ z }^{ 2 })Aexp\left[ i\left( \overrightarrow { k } \bullet \overrightarrow { r } +\varpi t+\varepsilon \right) \right] }</math> | |||
:El signo menos proviene del hecho de que <math>i^{ 2 }=-1</math> | |||
:Ahora calculando las parciales con respecto a <math>t</math> | |||
:<math>\frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } =-{ \varpi }^{ 2 }Aexp\left[ i\left( \overrightarrow { k } \bullet \overrightarrow { r } +\varpi t+\varepsilon \right) \right] </math> | |||
:Donde la magnitud de k es: | |||
:<math>\left| k \right| =\sqrt { { k }_{ x }^{ 2 }+{ k }_{ y }^{ 2 }+{ k }_{ z }^{ 2 } } </math> | |||
:<math>{ k }^{ 2 }={ k }_{ x }^{ 2 }+{ k }_{ y }^{ 2 }+{ k }_{ z }^{ 2 }</math> | |||
:Tenemos que la función de onda es:: | |||
<math>{ \nabla }^{ 2 }\Psi ={ -k }^{ 2 }Aexp\left[ i\left( { k }_{ x }x+{ k }_{ y }y+{ k }_{ z }z+\varpi t+\varepsilon \right) \right]</math> | |||
:Ahora comparando con la segunda parcial del tiempo, tenemos que la función de onda es solución si se cumple lo siguiente: | |||
:<math>-{ k }^{ 2 }Aexp\left[ i\left( { k }_{ x }x+{ k }_{ y }y+{ k }_{ z }z+\varpi t+\varepsilon \right) \right]=-{ \varpi }^{ 2 }Aexp\left[ i\left( { k }_{ x }x+{ k }_{ y }y+{ k }_{ z }z+\varpi t+\varepsilon \right) \right]</math> | |||
:La última igualdad se cumple solo si: | |||
:<math>{ v }^{ 2 }=\frac { { \varpi }^{ 2 } }{ { k }^{ 2 } }</math> | |||
Finalmente la función de onda <math>\Psi </math> es solución si: | |||
:<math>v=\frac { \varpi }{ k } </math> | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Luis Chávez|Luis Manuel chávez Antonio]], [[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:21 27 oct 2020 (CDT) | ||
---- | ---- | ||
= Otras Ediciones = | |||
== Ejercicio 2.6 Otras Ediciones== | |||
¿Cuántas ondas de luz amarilla $(\lambda=580\ nm)$ caben en una distancia en el espacio igual al espesor de un trozo de papel $(0.0076 cm)$? ¿Hasta dónde se extenderá el mismo número de microondas $(\nu={10}^{10}\ Hz,\ es\ decir,\ 10GHz\ \ y\ \upsilon=3\times{10}^8\ m/s)$? | |||
'''Solución''' | |||
:Sea '''k''' el número de onda, que esta dada por: | :Sea '''k''' el número de onda, que esta dada por: | ||
:<center>$k=\frac{1}{\lambda}m$</center> | :<center>$k=\frac{1}{\lambda}m$</center> | ||
| Línea 631: | Línea 671: | ||
:Por lo tanto las ondas se extienden '''3.9 m'''. | :Por lo tanto las ondas se extienden '''3.9 m'''. | ||
--[[Verenisse]] | ---- | ||
Realizado por: [[Verenisse]], [[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:29 27 oct 2020 (CDT) | |||
---- | |||
== Ejercicio 2.13 Otras Ediciones == | |||
Calcular: la frecuencia,la longitud de onda, el periodo,la amplitud, la velocidad de fase, la dirección de movimiento. | |||
<center><math>(a) :\psi=4sen(2\pi(0.2X-3t))~~~~~~~~~~~(1)</math></center> | <center><math>(a) :\psi=4sen(2\pi(0.2X-3t))~~~~~~~~~~~(1)</math></center> | ||
<center><math>(b) :\psi=\frac{1}{2.5} * sen(7X+3.5t)~~~~~~~~~~~(2)</math></center> | <center><math>(b) :\psi=\frac{1}{2.5} * sen(7X+3.5t)~~~~~~~~~~~(2)</math></center> | ||
| Línea 655: | Línea 695: | ||
:<center><math>v=\frac{\omega}{k}=\frac{2\pi}{2\pi}=1\frac ms</math></center> | :<center><math>v=\frac{\omega}{k}=\frac{2\pi}{2\pi}=1\frac ms</math></center> | ||
Para la dirección de movimiento de las funciones de onda armónica la ecuación (3) el argumento completo de la función es la fase de la onda: | |||
:<center><math>\phi=kx-\omega*t</math></center> | :<center><math>\phi=kx-\omega*t</math></center> | ||
| Línea 662: | Línea 702: | ||
:<center><math>\phi=2\pi*0,2=1,256m</math></center> | :<center><math>\phi=2\pi*0,2=1,256m</math></center> | ||
Para (b) | |||
:<center><math>\psi=\frac{1}{2.5}*sen(7X+3.5t) ~~~~~~~~~~~(2)</math></center> | :<center><math>\psi=\frac{1}{2.5}*sen(7X+3.5t) ~~~~~~~~~~~(2)</math></center> | ||
| Línea 691: | Línea 731: | ||
Realizado por: [[luisa alejandra vega sanchez]],[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:29 27 oct 2020 (CDT) | Realizado por: [[luisa alejandra vega sanchez]],[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 23:29 27 oct 2020 (CDT) | ||
---- | ---- | ||
[[Category:optica]] | |||
Revisión actual - 08:06 5 oct 2023
Problemas capítulo 2 Óptica Hecht, El movimiento ondulatorio.
Ejercicios resueltos sobre el movimiento ondulatorio. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema.
Algunas ediciones del Hecht, tienen distintas numeraciones para problemas idénticos.
Ejercicio 2.39
Indique cuales de las siguientes ecuaciones representan a una onda viajera:
- $\psi (y,t) = exp\left[-\left(a^2 y^2 + b^2 t^2 -2abty\right)\right]$
- Solución: Para tener una onda viajera se debe tener una dependencia funcional de la forma:
- $\psi = f(y \mp vt)$
- donde $y$ será la dirección de propagación si el signo de $vt$ es negativo y $-y$ si el signo de $vt$ es positivo. Además
- $v = \dfrac{\omega}{k}$
- Notamos que dentro de la exponencial se tiene un trinomio cuadrado perfecto, por lo que
- $\left(a^2 y^2 + b^2 t^2 -2abty\right) = \left(ay - bt\right)^2 = a^2 \left(y - bt/a\right)^2$
- de donde concluimos que
- * La onda es viajera con dirección de propagación $+y$
- * La onda tiene una velocidad $v = \omega / k = b / a$
- $\psi (z,t) = A \sin \left(az^2 - bt^2\right)$
- Solución: En este caso el argumento de la función seno tiene una dependencia funcional cuadrática en las coordenadas espaciales y temporales, por ello no tiene una dependencia funcional de la forma $f(z \mp vt)$ y no se trata de una onda viajera.
- $\psi (x,t) = A \sin 2\pi \left(\dfrac{x}{a} + \dfrac{t}{b} \right)^2$
- Solución: Tenemos dentro de la función seno los términos $\left(\dfrac{x}{a} + \dfrac{t}{b}\right)^2 = \dfrac{1}{a^2} \left(x + \dfrac{at}{b}\right)^2$ y por ello
- * La onda es viajera con dirección de propagación $-x$
- * La onda tiene una velocidad $v = \omega / k = a / b$
- $\psi (x,t) = A \cos^2 2\pi \left(t-x\right)$
- Solución: En este caso resulta simple ver que $(t-x) = - (x - t)$ y por ello
- * La onda es viajera con dirección de propagación $+x$
- * La onda tiene una velocidad $v = \omega / k = 1$
Ivan de Jesús Pompa García (discusión) 13:31 14 oct 2018 (CDT)
3ra Edición en español
Ejercicio 2.21 3ra Edición en español
Empezando por el siguiente teorema: Si $z=f(x,y)$ y $x=g(t), y=h(t)$, entonces
- $\frac{dz}{dt}=\frac{\partial z}{\partial x} \frac{dx}{dt}+ \frac{\partial z}{\partial y} \frac{dy}{dt}$
- Derive la ecuación (2.34)
- $\pm v=- \left(\frac{\partial \psi}{\partial t}\right)_x /\left(\frac{\partial \psi}{\partial x}\right)_t$
Solución
Para una onda que se propaga con fase constante:
- $\psi(x,t)=A \sin k(x\pm vt)$
- con $\phi(x,t)=k(x\pm vt)=constante$
- Cualquier punto de onda armónica con magnitud fija, se mueve de tal manera que $\phi(x,t)$ sea constante en el tiempo, i.e.,
- $\frac{d}{dt}\phi(x,t)=0$ o de otra forma, $\frac{d}{dt}\psi(x,t)=0$.
- Esto es cierto para toda clase de onda, periódica o no.
Así:
- $\frac{d\psi}{dt}=\frac{\partial \psi}{\partial x} \frac{dx}{dt}+ \frac{\partial \psi}{\partial t} \frac{dt}{dt}$
- $\frac{d\psi}{dt}=\frac{\partial \psi}{\partial x} (\pm v)+ \frac{\partial \psi}{\partial t} =0$
Conclusión
- Despejando $\pm v$ se obtiene la expresión requerida:
$\pm v=- \left(\frac{\partial \psi}{\partial t}\right)_x /\left(\frac{\partial \psi}{\partial x}\right)_t$
- donde el signo de $v$ depende del sentido de propagación de la onda.
Realizado por: Sergio
Ejercicio 2.22 3ra Edición en español
Utilizando los resultados del ejercicio anterior (ejercicio 2.21) demuestre que para una onda armónica con fase:
podemos calcular la velocidad estableciendo $\frac{d\varphi}{dt}=0$. Aplique la técnica a la función de onda:
Solución
Del ejercicio anterior obtenemos que:
Ahora derivamos nuestra ecuación (1) respecto del tiempo y obtenemos:
donde:
Ahora, aplicamos esta técnica a la fase de la ecuación (2) $\varphi(y,t)=\pi (3*10^{6}y+9*10^{14}t)$ y obtenemos:
Realizado por: Jesús Flores Ortega,Carlosmiranda (discusión) 23:26 27 oct 2020 (CDT)
4ta Edición en Ingles
Ejercicio 2.20 4ta Edición en Ingles
Muestre que
$\psi\left({x},t\right)=A \text{cos}\left(kx-\omega t-\frac{\pi}{2}\right)$
es quivalente a
$\psi\left({x},t\right)=A \text{sen}\left(kx-\omega t\right).$
Solución:
Usemos la formula para el coseno de la suma de ángulos
$ \text{cos}(x \pm y) = \text{cos}(x) \text{cos}(y) \mp \text{sen}(x) \text{sen}(y), $
con la cual la función
$\psi\left({x},t\right)=A \text{cos}\left(kx-\omega t-\frac{\pi}{2}\right)$
toma la forma
$\psi\left({x},t\right)=A \left[\text{cos}\left(kx-\omega t\right)\text{cos}\left(\frac{\pi}{2}\right)+\text{sen}\left(kx-\omega t\right)\text{sen}\left(\frac{\pi}{2}\right)\right].$
Recordemos ahora que
$\text{cos}\left(\frac{\pi}{2}\right)=0$ y $\text{sen}\left(\frac{\pi}{2}\right)=1,$
Conclusión
Sustituyendo obtenemos
$\psi\left({x},t\right)=A\text{sen}\left(kx-\omega t\right),$
por lo tanto
$A \text{cos}\left(kx-\omega t-\frac{\pi}{2}\right)=A\text{sen}\left(kx-\omega t\right).$
Realizado por: Flor Ivon Vivar
Ejercicio 2.35 4ta Edición en Ingles
- Considerar una onda de luz que tiene una velocidad de fase de $3 \times 10^8 m/s$ y una frecuencia de $6 \times 10^{14} Hz$. a) ¿ Cuál es la distancia mas corta entre dos puntos de la onda los cuales tienen una diferencia de fase de 30° ?, b)¿Qué cambio de fase ocurre en un punto dado en un $\Delta{t}= 10^{-6}s$?, y c) ¿ Cuántas ondas han pasado en ese intervalo de tiempo?
Solución:
- a) La longitud de onda $\lambda$ se define como la distancia que recorre la onda en un determinado tiempo llamado periodo. Si la longitud de onda realiza un ciclo de 360° ó $2\pi rad$ cada periodo y $30°$ son $\frac{2\pi}{12}$, entonces basta con dividir a la longitud de onda entre 12 para obtener la respuesta:
$v=\lambda\nu$; $\lambda=\frac{v}{\nu}$ --> $\frac{\lambda}{12}= \frac{v}{12\nu}$ $\frac{\lambda}{12}= 4.16 \times 10^{-8} m $
- b)$\Delta{t} \Rightarrow \Delta{\varphi} $ (en el mismo punto); $\Delta{\varphi}= \varphi_2 - \varphi_1$, $\Delta{t}= 10^{-6} s$;
$\varphi_2= \omega{t_2} - Kx_1$
$\Delta{\varphi}= \varphi_2 - \varphi_1= \omega(t_2 - t_1)= \omega\Delta{t}$ - Con $\omega$ y K la frecuencia angular y el número de onda, respectivamente.
$\Delta{\varphi}= \omega\Delta{t}$ $\Delta{\varphi}= 2\pi(6 \times 10^{14})(1 \times 10^{-6})$
- Esto quiere decir que un número entero multiplica a $2\pi rad$ lo que equivale a dar una vuelta, entonces no habrá cambio de fase ya que el punto de la primera fase siempre va a llegar al mismo punto de donde empezó. $\Delta{\varphi}$=0.
- c) Si la frecuencia $\nu$ es el número de ciclos que da cada segundo, entonces:
- $\nu{t}$= Número de ondas que pasan en ese intervalo de tiempo
$\nu{t}= 6 \times 10^{14}(1 \times 10^{-6})= 6 \times 10^8 ondas$
Realizado por: Pedro J. Julian Salgado, Carlosmiranda (discusión) 23:28 27 oct 2020 (CDT)
Ejercicio 2.44 4ta Edición en Ingles
Muestre que $\psi\left(\vec{k}\cdot\vec{r},t\right)$ puede representar una onda plana donde $\vec{k}$ es normal al frente de onda. Sugerencia. Sean $\vec{r}_{1}$, $\vec{r}_2$ dos vectores posición del origen a cualesquiera dos puntos del plano, pruebe que
Solución:
Una función vectorial viajera, tiene la siguiente expresión:
En particular una onda plana tiene como argumento:
Si el vector $\vec{r}_{1}$ y $\vec{r}_{2}$ son vectores dirigidos hacia el frente de onda, entonces satisfacen:
Conclusión
Observamos que:
$\psi\left(\vec{r}_{1},t\right)=\psi\left(\vec{k}\cdot\vec{r}_{1}-\omega t\right) =\psi\left(\vec{k}\cdot\vec{r}_{2}-\left(\vec{k}\cdot\vec{r}_{2}-\vec{k}\cdot\vec{r}_{1}\right)-\omega t\right)=\psi\left(\vec{k}\cdot\vec{r}_{2}-\vec{k}\cdot\left(\vec{r}_{2}-\vec{r}_{1}\right)-\omega t\right)=\psi\left(\vec{k}\cdot\vec{r}_{2}-\omega t\right)=\psi\left(\vec{r}_{2},t\right)$
Realizado por: Diego de la Cruz,Carlosmiranda (discusión) 23:13 27 oct 2020 (CDT)
5ta Edición en Ingles
Ejercicio 2.25 5ta Edición en Ingles
Muestra que es solución de la ecuación de onda diferencial.
Solución:
ecuación de onda Diferencial unidimensional es::
aquí es la función de onda, v es la velocidad de onda, t es el tiempo y x representa la distancia
La relación entre velocidad angular, número de onda y velocidad de onda es:
aqui es la velocidad angular y es el numero de onda por la relación:
sacamos su diferencial con respecto a :
de nuevo diferenciar con respeto a :
y sustituyendo en (2) :
Diferenciar la ecuación (1) con respecto a :
y diferenciando de nuevo con respecto a t:
multiplicando por
arreglando de nuevo:
Conclusión
De acuerdo con las ecuaciones (2) y (3)
Queda demostrado que la ecuación diferencial dada es solución.
Realizado por: Salvador morales carranza, Carlosmiranda (discusión) 23:24 27 oct 2020 (CDT)
Ejercicio 2.38 5ta Edición en Ingles
¿Cuáles de las siguientes expresiones corresponden a ondas en desplazamiento? ¿Cuál es la velocidad de cada una? Las cantidades a,b y c son constantes positivas.
Solución
La forma de las ecuaciones que describen las ondas en desplazamiento es :
$\psi = f (x \pm vt )$
Y debe satisfacer la ecuación diferencial de onda :
$\frac{\partial^2 \psi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$
Para el inciso (a)
$\psi (z,t) = \left(z-\frac{b}{a}t\right)^2$
Calculamos sus derivadas parciales a primer orden:
$\frac{\partial \psi}{\partial z}= 2\left(z-\frac{b}{a}t\right)$
$\frac{\partial \psi}{\partial t}= -2 \frac{b}{a}\left(z-\frac{b}{a}t\right)$
Sus derivadas a segundo orden :
$\frac{\partial^2 \psi}{\partial z^2}= 2$
$\frac{\partial^2 \psi}{\partial t^2}= 2 \frac{b^2}{a^2}$
Con :$\frac{1}{v^2}= \frac{a^2}{b^2}$
Se cumple que:
$\frac{\partial^2 \psi}{\partial x^2}=2=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$
$\frac{\partial^2 \psi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$
- Se satisface la ecuación de onda
- Su velocidad es $|v|=\frac{b}{a}$
- Al ser de la forma $\psi = f (x -vt )$ sabemos que la velocidad va en el sentido positivo del eje z
Para el inciso (b)
$\psi (x,t) = \left(x+\frac{b}{a}t+\frac{c}{a}\right)^2$
Al igual que en el inciso anterior, para comprobar si se cumple la ecuación de onda , obtenemos las primeras derivadas:
$\frac{\partial \psi}{\partial x}= 2\left(x+\frac{b}{a}t+\frac{c}{a}\right)$
$\frac{\partial \psi}{\partial t}= 2 \frac{b}{a}\left(x+\frac{b}{a}t+\frac{c}{a}\right) $
Las segundas derivadas son:
$\frac{\partial^2 \psi}{\partial z^2}= 2$
$\frac{\partial^2 \psi}{\partial t^2}= 2 \frac{b^2}{a^2}$
Con :$\frac{1}{v^2}= \frac{a^2}{b^2}$
$\frac{\partial^2 \psi}{\partial x^2}=2=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$
$\frac{\partial^2 \psi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \psi}{\partial t^2}$
- Se satisface la ecuación de onda
- Su velocidad es $|v|=\frac{b}{a}$
- Como es de la forma $\psi = f (x + vt )$ su velocidad va en el sentido negativo del eje z
Para el inciso (c)
$\psi (x,t) = \frac{1}{\left(ax^2+b\right)}$
- No tiene una dependencia en t
$\psi = f (x \pm vt )$
- No cumple con la ecuación de onda
- Por lo tanto, no describe una onda.
Realizado por: Aurea Espin (discusión) 18:26 20 oct 2018 (CDT), Carlosmiranda (discusión) 23:25 27 oct 2020 (CDT)
Ejercicio 2.40 5ta Edición en Ingles
Dada la onda , calcule su dirección de propagación. Determine algunos valores de y realice un boceto del perfil de onda en para y . ¿Cuál es la velocidad de la onda?
Solución:
Para simplificar los cálculos, podemos ver que Por tanto:
- Claramente, como se vio en cursos de cálculo básico. Una función de la forma:
- Siendo A y B valores positivos, la función f se desplazará hacía el eje positivo de las x. Por lo tanto la dirección de la propagación de dicha onda, será hacia el eje positivo de x.
- Para encontrar explícitamente el valor de la velocidad, se sabe que la ecuación dado el argumento de la exponencial es de la forma:
- Y se sabe que:
- Asi que
- .
- A tiempo t=0 la ecuación de onda queda como:
- .
- Que claramente es una función Gaussiana. Es fácil ver que cuando x=0. Implica que Por otro lado, cuando x^2>>>1, tiende a 0.
- Se anexa la gráfica de dicha función para apreciar el comportamiento de la Gaussiana.
Gráfica
Realizado por: José Fernando Valencia Hernández, Carlosmiranda (discusión) 23:23 27 oct 2020 (CDT)
Ejercicio 2.45 5ta Edición en Ingles
Demostrar que la parte imaginaria de un número complejo está dada por .
Solución
El numero complejo z, tiene la siguiente forma: Donde , es la parte real y es la parte imaginaria del numero complejo también se tiene que el complejo conjugado del numero es restando el complejo conjugado a el numero complejo antes definido se obtiene:
Reorganizando la ecuación anterior para la parte imaginaria , se tiene:
Por lo tanto la parte imaginaria de una numero complejo es:
Realizado por: Luis Gutiérrez Melgarejo 22:13 15 oct 2018 Carlosmiranda (discusión) 23:16 27 oct 2020 (CDT)
Ejercicio 2.48 5ta Edición en Ingles
Empezando por la ecuación (2.51), compruebe que:
Solución
La onda armónica plana en coordenadas cartesianas se expresa como::
Si , y son los cosenos de dirección de en las direcciones , y respectivamente, entonces:
Así, la ecuación (2.51) puede expresarse como:
La magnitud del vector de propagación es:
En términos de componentes, la magnitud de , es
De la ecuación (1) y (2):
Realizado por: Enrique Ortiz Martinez 23:08 15 oct 2018 Carlosmiranda (discusión) 23:20 27 oct 2020 (CDT)
Ejercicio 2.49 5ta Edición en Ingles
Demuestre que las ecuaciones (2.64) y (2.65) las cuales son ondas planas de forma arbitraria, satisfacen la ecuación de onda de tres dimensiones diferencial.
Solución
Las siguientes dos ecuaciones:
Son funciones, en las cuales f y g son dos veces diferenciables consideremos una función de la forma:
Calculando las derivadas parciales de la ecuación (1) obtenemos:
Agregando las tres derivadas espaciales y utilizando el echo que obtenemos:
Por la consideración anterior tenemos entonces que :
De la ecuación (2) notamos que se puede reescribir como :
Ahora combinando la parte temporal ecuación (4) y la parte espacial ecuación (3) por transitividad tenemos:
Por lo tanto cumple con la ecuación de onda en tres dimensiones
Realizado por: Carlosmiranda (discusión) 23:15 27 oct 2020 (CDT)
Ejercicio 2.56 5ta Edición en Ingles
Mostrar explícitamente, que la función:: describe una onda siempre que:
Solución
Empecemos escribiendo el vector k y el vector r, en coordenadas cartesianas:
- :
- Haciendo el producto punto de K con r.
- Sustituyendo en la función de onda:
- Tenemos que la ecuación de onda es:
- Sustituyendo la función de onda en la ecuación anterior, obtenemos primero el laplaciano:
- El signo menos proviene del hecho de que
- Ahora calculando las parciales con respecto a
- Donde la magnitud de k es:
- Tenemos que la función de onda es::
- Ahora comparando con la segunda parcial del tiempo, tenemos que la función de onda es solución si se cumple lo siguiente:
- La última igualdad se cumple solo si:
Finalmente la función de onda es solución si:
Realizado por: Luis Manuel chávez Antonio, Carlosmiranda (discusión) 23:21 27 oct 2020 (CDT)
Otras Ediciones
Ejercicio 2.6 Otras Ediciones
¿Cuántas ondas de luz amarilla $(\lambda=580\ nm)$ caben en una distancia en el espacio igual al espesor de un trozo de papel $(0.0076 cm)$? ¿Hasta dónde se extenderá el mismo número de microondas $(\nu={10}^{10}\ Hz,\ es\ decir,\ 10GHz\ \ y\ \upsilon=3\times{10}^8\ m/s)$?
Solución
- Sea k el número de onda, que esta dada por:
$k=\frac{1}{\lambda}m$ - sustituyendo los datos:
$k=\frac{7.6\times{10}^{-5}m}{580\times{10}^{-9}m}=131$ - caben 131 ondas de luz amarilla en 0.0076 cm.
- Para calcular hasta donde se extiende el mismo número de microondas, calculamos la longitud de onda:
$\lambda=\frac{c}{\nu}=\frac{3\times{10}^8\ m/s}{{10}^{10}\ 1/s}=0.03\ m$ $(0.03m)*(131)=3.9 m$ - Por lo tanto las ondas se extienden 3.9 m.
Realizado por: Verenisse, Carlosmiranda (discusión) 23:29 27 oct 2020 (CDT)
Ejercicio 2.13 Otras Ediciones
Calcular: la frecuencia,la longitud de onda, el periodo,la amplitud, la velocidad de fase, la dirección de movimiento.
- Teniendo :$\psi=A senK(x-vt)$...(3) y compararla con 1, se puede tener que .
- Entonces para la frecuencia:
sustituyendo el valor de v:
- Para la longitud de onda.
- Para el periodo:
- para la amplitud se tiene de la ecuación (1), que A=4.
- Para la velocidad de fase:
Para la dirección de movimiento de las funciones de onda armónica la ecuación (3) el argumento completo de la función es la fase de la onda:
sustituyendo los valores a t=0.
Para (b)
- Teniendo:
y compararla con 1 se puede tener que A=1/2,5 K=1 v=3,5.
- Entonces para la frecuencia:
- sustituyendo el valor de v:
- Para la longitud de onda:
- Para el periodo:
- para la amplitud se tiene de la ecuación (1) que
- Para la velocidad de fase:
para la dirección de movimiento de las funciones de onda armónica la ecu (3) el argumento completo de la función es la fase de la onda:
sustituyendo los valores a t=0.
Realizado por: luisa alejandra vega sanchez,Carlosmiranda (discusión) 23:29 27 oct 2020 (CDT)


























![{\displaystyle -ax^{2}-bt^{2}-2(ab)^{\frac {1}{2}}xt=-[a^{\frac {1}{2}}x+b^{\frac {1}{2}}t]^{2})}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c16f9c4d71de912c8685ebcff5210eb674fa7e6b)
![{\displaystyle \psi (x,t)=5.0exp(-[a^{\frac {1}{2}}x-b^{\frac {1}{2}}t]^{2})}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/792d9d56c32045f2035bbc1d8bd7a6bc651212c2)




![{\displaystyle \psi (x,t)=5.0exp(-[a^{\frac {1}{2}}x]^{2})=5.0exp(-ax^{2})}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/95ce5819afd9c1c613d997369df96528612a872d)










![{\displaystyle \psi (x,y,z,t)=Ae^{i[k(\alpha x+\beta y+\gamma z)\mp \omega t]}~~~}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d4ac3f31645bfbff92f6d661cc14e9cb6fbdb6d7)









![\psi (x,y,z,t)=Ae^{i[k\alpha x+k\beta y+k\gamma z\pm \omega t]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d3dfd53456aad6a0107d5302996bf832f7e9d140)
![\psi (x,y,z,t)=Ae^{i[k(\alpha x+\beta y+\gamma z)\pm \omega t]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3b400ce785a36481bfaa53bde2ce872a04b6f4d8)



![=[(k\alpha)^{2}+(k\beta )^{2} +(k\gamma )^{2}]^{\frac{1}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3c923c4bfb1b3479494168ebd5dd63abada154bc)
![{\displaystyle =k[(\alpha )^{2}+(\beta )^{2}+(\gamma )^{2}]^{\frac {1}{2}}~~~~~}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/72388bcb1417a21553155972ca6928fa2515ba7a)




















![\Psi =Aexp\left[ i\left( { k }_{ x }x+{ k }_{ y }y+{ k }_{ z }z+\varpi t+\varepsilon \right) \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/33d0eda2df6a0ce172513841e10334b9a2e803f3)

![{ \triangledown }^{ 2 }\Psi =-({ { k }_{ x }^{ 2 }+{ k }_{ y }^{ 2 }+{ k }_{ z }^{ 2 })Aexp\left[ i\left( \overrightarrow { k } \bullet \overrightarrow { r } +\varpi t+\varepsilon \right) \right] }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a8563d3fc67e86101fa37bee5bdf724c59f5cf92)

![\frac { { \partial }^{ 2 }\Psi }{ \partial { t }^{ 2 } } =-{ \varpi }^{ 2 }Aexp\left[ i\left( \overrightarrow { k } \bullet \overrightarrow { r } +\varpi t+\varepsilon \right) \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c9da81da90fdc4f6970971990ccee6ad97791ae3)


![{ \nabla }^{ 2 }\Psi ={ -k }^{ 2 }Aexp\left[ i\left( { k }_{ x }x+{ k }_{ y }y+{ k }_{ z }z+\varpi t+\varepsilon \right) \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3a0eb4c7271fc988f4daf4c14c3542f798bfdd7b)
![-{ k }^{ 2 }Aexp\left[ i\left( { k }_{ x }x+{ k }_{ y }y+{ k }_{ z }z+\varpi t+\varepsilon \right) \right]=-{ \varpi }^{ 2 }Aexp\left[ i\left( { k }_{ x }x+{ k }_{ y }y+{ k }_{ z }z+\varpi t+\varepsilon \right) \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/dab8ecde0257b8a8dee938e2318576f7974c22f1)



















