Diferencia entre revisiones de «Optica: Capitulo12-problemas»
Sin resumen de edición |
Sin resumen de edición |
||
| (No se muestran 41 ediciones intermedias del mismo usuario) | |||
| Línea 3: | Línea 3: | ||
Ejercicios resueltos sobre las bases de la teoría de la Coherencia de luz. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema. | Ejercicios resueltos sobre las bases de la teoría de la Coherencia de luz. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema. | ||
Algunas ediciones del | Algunas ediciones del Hecht, tienen distintas numeraciones para problemas idénticos. | ||
| Línea 13: | Línea 14: | ||
---- | ---- | ||
=== Ejercicio 12.6 == | = 3ra Edición en español = | ||
== Ejercicio 12.1 3ra Edición en español == | |||
Suponga que formamos una distribución de franjas con el interferómetro de Michelson. Utilizando como fuente una lampara de vapor de mercurio.Encienda la lámpara en su imaginación y analice lo que les pasara a las franjas según la presión del vapor de mercurio vaya aumentando hasta lograr su valor de estado estacionario | |||
'''Solución''' | |||
A presiones bajas, la intensidad emitida por la lámpara es baja, el ancho de banda es estrecho y la longitud de coherencia es grande. | |||
Las franjas mostrarán inicialmente un alto contraste, disminuirán, el contraste disminuirá y las franjas podrían incluso desaparecer por completo. | |||
---- | |||
Realizado por: [[Usuario: luisa vega ]] | |||
---- | |||
== Ejercicio 12.6 3ra Edición en español== | |||
'''Refiriéndose a la fuente de hendidura y la disposición de la pantalla con orificios de la figura P.12.6, muestre por integración sobre la fuente que: | '''Refiriéndose a la fuente de hendidura y la disposición de la pantalla con orificios de la figura P.12.6, muestre por integración sobre la fuente que: | ||
$ I(Y)\propto b + \frac{\sin(\frac{\pi ab}{\lambda l})}{\frac{\pi a}{\lambda l}}\cos(\frac{2\pi aY}{\lambda s}) $''' | |||
'''Solución''' | |||
En el caso especial de dos fuentes con ''misma amplitud'' que inciden en un punto Q, la contribución a la irradiancia por estas fuentes es: | En el caso especial de dos fuentes con ''misma amplitud'' que inciden en un punto Q, la contribución a la irradiancia por estas fuentes es: | ||
$ I=2I_{0}(1+\cos\delta)=4I_{0}\cos^{2}(\frac{\delta}{2}) $ (ver capítulo 9, ecuación 9.17). | |||
Siendo, por su puesto <math> I_{0}=I_{1}=I_{2}=\langle |\vec{E}_{1}|^{2}\rangle_{T}=\langle |\vec{E}_{2}|^{2}\rangle_{T} </math> & <math> \delta</math> la diferencia entre las fases de dichas fuentes. | Siendo, por su puesto <math> I_{0}=I_{1}=I_{2}=\langle |\vec{E}_{1}|^{2}\rangle_{T}=\langle |\vec{E}_{2}|^{2}\rangle_{T} </math> & <math> \delta</math> la diferencia entre las fases de dichas fuentes. | ||
| Línea 37: | Línea 62: | ||
:<math> dI\propto (1+\cos(k\Lambda)dy </math>, siendo, por su puesto, <math> k\equiv\frac{2\pi}{\lambda} </math>. | :<math> dI\propto (1+\cos(k\Lambda)dy </math>, siendo, por su puesto, <math> k\equiv\frac{2\pi}{\lambda} </math>. | ||
'''Conclusión''' | |||
Por tanto: | Por tanto: | ||
| Línea 50: | Línea 79: | ||
---- | |||
Realizado por: [[Usuario:diegophy17|Diego de la Cruz López]] | |||
---- | ---- | ||
== Ejercicio 12.10 3ra Edición en español == | |||
Tomando el diámetro angular del sol visto desde la tierra como alrededor de $\frac{1}{2}^{\text{o}}$, determine el diámetro correspondiente del área de coherencia despreciando variaciones en el brillo sobre la superficie. | |||
'''Solución:''' | |||
Ya que nuestra fuente podemos considerarla como un disco por lo lejano del sol y ya que podemos despreciar variaciones de brillo, ocuparemos la ecuación 12.30 del libro de Hecht 4a ed: | |||
$h=0.32\frac{\bar{\lambda}_0}{\theta},$ | |||
donde $h$ es el radio del área de coherencia $\bar{\lambda}_0$ es la longitud de onda de la luz y | |||
$\theta$ el diámetro angular. | |||
Ahora convertimos el ángulo a radianes | |||
$\theta=\frac{1}{2}^{\text{o}}=\frac{\pi}{360}=0.00872664625$ | |||
Para la longitud de onda consideremos la figura | |||
[[Archivo:Luz_sol.jpg]] | |||
en el espectro visible un promedio aproximado se encuentra cerca de los $550\text{nm}$ así que usaremos | |||
$\bar{\lambda}_0=550\text{nm}.$ | |||
Sustituyendo en la formula | |||
$h=0.32\frac{550\text{nm}}{0.00872664625}=20168\text{nm},$ | |||
'''Conclusión.''' | |||
con el radio calculamos entonces el diámetro | |||
$d=2h=40336\text{nm}.$ | |||
---- | ---- | ||
=== Ejercicio 12.14 | Realizado por: [[Usuario:Flor|Flor Ivon Vivar]] | ||
---- | |||
== Ejercicio 12.15 3ra Edición en español == | |||
Deseamos construir un arreglo de dos orificios iluminados por una fuente de rendija uniforme , cuasicromática e incoherente de longitud de onda promedio de 500 nm y ancho b, a una distancia de 1.5 metros de la pantalla. si los orificios están separados por 0.50 mm , ¿Qué tan ancho puede ser la fuente si la visibilidad de las franjas en el plano de observación no debe ser menos del 85 por ciento? | |||
Solución | |||
:Esto se puede obtener del grado de coherencia $\mid\gamma_{12}(\tau)\mid$ ya que éste solo varía entre 0 y 1, y así en la región de la franja central ($\tau= 0$), el grado de coherencia sólo se hace una función sinc(x), y de esta al igualarla con 0.85 (85 por ciento de visibilidad), observamos que debemos buscar un valor para "x" tal que evaluado en la función sinc(x) nos devuelva el valor de 0.85: | |||
:$\mid\frac{senx}{x}\mid= 0.85$ | |||
:Por lo que al buscar en las tablas de sinc(x) se encuentra que $sinc(0.95)\thickapprox 0.85$, por lo tanto: | |||
:$\mid\gamma_{12}(0)\mid= \mid sinc(x)\mid= \mid sinc(\frac{\pi by}{l \lambda})\mid$. | |||
:Con b el ancho de la rendija, (y) la distancia de separación entre los orificios y "l" la distancia entre la rendija y la pantalla con los orificios. | |||
:De aquí que $0.97 = \frac{\pi by}{l\lambda}$, despejando "b": | |||
:$b= \frac{l \lambda(0.95)}{y \pi}$ ó $b= \frac{(1.5 [m])(500 \times 10^{-9} [m])(0.95)}{\pi (0.50 \times 10^{-3}[m])}\thickapprox 4.6 [cm]$ | |||
---- | |||
Realizado por: [[Usuario: Pedro J. Julián]] | |||
---- | |||
=5ta Edición en Ingles.= | |||
== Ejercicio 12.3 5ta Edición en Ingles== | |||
considerando el ejercicio 12.2,imagine ahora que las cosas se extienden, en el espacio en un momento determinado, cada onda daría como un resultado una distribución de irradiancia $I_1$ e $I_2$ | |||
Que le ocurre a la irradiación neta al añadir más ondas de frecuencia diferentes. Explíquelo en términos de longitud de coherencia. Hipotéticamente que le ocurre a la distribución según el ancho de la banda de la frecuencia se va aproximando al infinito. | |||
'''Solución.''' | |||
La irradiancia neta se vuelve más uniforme a medida que se agregan más ondas. Habrá un patrón menos distinguido, que corresponde a una longitud de coherencia menor. | |||
la irradiancia se hará constante a medida que el ancho de banda se vaya hasta el infinito | |||
---- | |||
Realizado por: [[Usuario: luisa vega ]] | |||
---- | |||
== Ejercicio 12.8 5ta Edición en Ingles== | |||
Suponga que formamos una distribución de franjas con el interferómetro de Michelson, y que utiliza como fuente una lámpara de vapor de mercurio. Encienda la lámpara en su imaginación y analice lo que les pasará a las franjas según aumente la presión del vapor de mercurio hasta lograr su valor de estado estacionario. | |||
'''Solución:''' | |||
A bajas presiones, la intensidad emitida desde la lámpara es baja, el ancho de banda es estrecho y la longitud de coherencia es grande. Las franjas inicialmente mostrarán un alto contraste, aunque serán bastante débiles. | |||
A medida que aumenta la presión, la longitud de coherencia disminuirá, el contraste caerá, y las franjas podrían incluso desaparecer por completo. | |||
---- | |||
Realizado por: [[Usuario:Sesebasi|Sesebasi]] ([[Usuario discusión:Sesebasi|discusión]]) 23:16 2 dic 2018 (CST) | |||
---- | |||
== Ejercicio 12.14 5ta Edición en Ingles== | |||
Elabore los detalles que nos llevan a la expresión de la visibilidad dada por la ecuación 12.22. | Elabore los detalles que nos llevan a la expresión de la visibilidad dada por la ecuación 12.22. | ||
'''Solución''' | |||
Las intensidades máximas y mínimas son | Las intensidades máximas y mínimas son: | ||
<math> | <math> | ||
| Línea 78: | Línea 206: | ||
</math> | </math> | ||
Sustituimos para obtener | |||
<math> | <math> | ||
| Línea 85: | Línea 213: | ||
</math> | </math> | ||
'''Conclusión''' | |||
Obteniendo finalmente que | |||
<math> | <math> | ||
| Línea 93: | Línea 225: | ||
que es la ecuación 12.22. | que es la ecuación 12.22. | ||
[[Usuario:Ivan de Jesús Pompa García|Ivan de Jesús Pompa García]] ([[Usuario discusión:Ivan de Jesús Pompa García|discusión]]) 20:46 28 nov 2018 (CST) | |||
---- | |||
Realizado por: [[Usuario:Ivan de Jesús Pompa García|Ivan de Jesús Pompa García]] ([[Usuario discusión:Ivan de Jesús Pompa García|discusión]]) 20:46 28 nov 2018 (CST) | |||
---- | ---- | ||
== Ejercicio 12.15 5ta Edición en Ingles== | |||
¿Bajo que circunstancias la irradiancia en <math>\sum o</math> en la figura P.12.15 sera igual a <math>4l_{0}</math> donde <math>l_{0}</math> es la irradiancia debida a una fuente puntual incoherente sola? | ¿Bajo que circunstancias la irradiancia en <math>\sum o</math> en la figura P.12.15 sera igual a <math>4l_{0}</math> donde <math>l_{0}</math> es la irradiancia debida a una fuente puntual incoherente sola? | ||
[[Archivo:P.12.15.png|marco|centro|Figura P.12.15]] | |||
'''Solución''' | |||
| Línea 175: | Línea 313: | ||
[[Usuario:Enrique Ortiz Martinez|Enrique Ortiz Martinez]] | ---- | ||
Realizado por: [[Usuario:Enrique Ortiz Martinez|Enrique Ortiz Martinez]] | |||
---- | ---- | ||
== Ejercicio 12.16 5ta Edición en Ingles== | |||
Supongamos que llevamos a cabo el experimento de Young con un agujero circular pequeño con un diámetro de 0.1 mm. enfrente de una lámpara de sodio $(\lambda = 589.3 nm)$ que actúa como fuente. Si la distancia desde la fuente hasta las rendijas es de 1 m ¿A qué distancia entre sí se hallarán las rendijas cuando el patrón de franjas desaparezca? | |||
'''Solución:''' | |||
Suponemos, como se hace a menudo, que "buena coherencia" significa una visibilidad de 0.88 o mejor. Para una fuente en forma de disco, esto se da cuando $\frac{ \pi h \theta }{ \bar{\lambda_0}}$ de la ecuación $\mathscr{V} = 2\frac{J_1( \pi h \theta_s \setminus \bar{\lambda_0 })}{ \pi h \theta_s \setminus \bar{\lambda_0}} $ es igual a uno, es decir si: | |||
$h= 0.32 \frac{\bar{\lambda_0}}{\theta_s}$ | |||
Para una fuente de anchura de banda estrecha de diámetro $D$ puesta a una distancia $R$, existe un área de coherencia igual a $\pi \left( \frac{h}{2} \right) ^2$ en la que $\mid \bar{ \gamma_{12} } \mid \geq 0.88 $ . Ya que $\frac{D}{R}= \theta_s$ : | |||
$h=0.32 \frac{R \bar{\lambda_0}}{D}$ | |||
Con esta expresión podemos estimar los parámetros físicos requeridos en un experimento de interferencia o difracción. | |||
En este caso para el experimento de Young: | |||
$h=0.32 \frac{R \bar{\lambda_0}}{D} = 0.32 \frac{1 \times (589.3 \times 10^{-9} ) }{0.1 \times 10^{-3} }$ $ = 1.885 \times 10^{-3} m $ | |||
Esto indica que una serie de aberturas colocadas a una distancia de $1.9$ $ mm$ producirá franjas buenas . | |||
Por otro lado, se obtiene que | |||
$h= 1.22 \frac{ \bar{\lambda_0} }{ \theta_s}$ $ =1.22 \frac{R \bar{\lambda_0}}{D} $ $=1.22 \frac{589.3 \times 10^{-9} }{0.1 \times 10^{-3}} $ $= 7.189 \times 10^{-3} m $ | |||
Las franjas desaparecerán cuando la distancia entre rendijas sea de $7.2 $ $mm$ | |||
---- | ---- | ||
Realizado por: [[Usuario:Aurea Espin|Aurea Espin]] ([[Usuario discusión:Aurea Espin|discusión]]) 02:37 2 dic 2018 (CST) | |||
[[Usuario: | |||
---- | ---- | ||
== Ejercicio 12.18 5ta Edición en Ingles== | |||
'''Mostrar que las ecuaciones (12.34) y (12.35) siguen de las ecuaciones (12.32) y (12.33) (consultar libro)''' | |||
'''Solución:''' | |||
Sabemos que: | |||
${ I }_{ 1 }(t)=\Delta { I }_{ 1 }(t)+\left< { I }_{ 1 } \right> $ | |||
$ | Así que : | ||
${ I }_{ 1 }(t+\tau )=\Delta { I }_{ 1 }(t+\tau )+\left< { I }_{ 1 } \right> $ | |||
Y ${ I }_{ 2 }(t)=\Delta { I }_{ 2 }(t)+\left< { I }_{ 2 } \right> $ | |||
Por lo tanto: | |||
$\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< \left\lfloor \left< { I }_{ 1 } \right> +\Delta { I }_{ 1 }(t+\tau ) \right\rfloor \left\lfloor \left< { I }_{ 2 } \right> +\Delta { I }_{ 2 }(t) \right\rfloor \right> $ | |||
$\ | $\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< \left< { I }_{ 1 } \right> \left< { I }_{ 2 } \right> +\left< { I }_{ 1 } \right> \Delta { I }_{ 2 }(t)+\left< { I }_{ 2 } \right> \Delta { I }_{ 1 }(t+\tau )+\left< \Delta { I }_{ 1 }(t+\tau )\Delta { I }_{ 2 }(t) \right> \right> $.............(1) | ||
Pero | |||
${ \left< \Delta { I }_{ 1 }(t) \right> }_{ T }=0$ y ${ \left< \Delta { I }_{ 2 }(t) \right> }_{ T }=0$ | |||
Sustituyendo estos valores en la ecuación (1) obtenemos: | |||
$\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< { I }_{ 1 } \right> \left< { I }_{ 2 } \right> +\left< \Delta { I }_{ 1 }(t+\tau )\Delta { I }_{ 2 }(t) \right> $ ...................(2) | |||
Ya que $\left< { I }_{ 1 } \right> $ es independiente del tiempo. | |||
Comparando la ecuación (2) con : | |||
$\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< { I }_{ 1 } \right> \left< { I }_{ 2 } \right> +{ \left| \tilde { { \Gamma }_{ 12 }(\tau ) } \right| }^{ 2 }$ | |||
Entonces: | |||
$\left< { { \Delta I }_{ 1 }(t+\tau )\Delta I }_{ 2 }(t) \right> ={ \left| \tilde { { \Gamma }_{ 12 }(\tau ) } \right| }^{ 2 }$ | |||
Por lo tanto se demuestra el enunciado del problema. | |||
Ahora comparando la ecuación (2) con: | |||
$\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< { I }_{ 1 } \right> \left< { I }_{ 2 } \right> \left[ 1+{ \left| \tilde { \gamma _{ 12 }(\tau ) } \right| }^{ 2 } \right] $ | |||
Obtenemos entonces : | |||
'''Conclusión''' | |||
$\left< { { \Delta I }_{ 1 }(t+\tau )\Delta I }_{ 2 }(t) \right> =1+{ \left| \tilde { \gamma _{ 12 }(\tau ) } \right| }^{ 2 }$ | |||
Por lo tanto se demuestra el enunciado del problema. | |||
== Ejercicio 12.20 5ta Edición en Ingles== | |||
Imagina que tenemos el aparato del experimento de Young, donde uno de los dos orificios está cubierto por un filtro de densidad neutra que corta la irradiancia en un factor de 12 y el otro agujero está cubierto por una lámina transparente de vidrio, por lo que hay ningún cambio de fase relativo introducido. Calcular la visibilidad en el hipotético caso de iluminación completamente coherente. | |||
'''Solución''' | |||
Tenemos que la visibilidad esta dada por: | |||
<math>V=\frac { 2\sqrt { { I }_{ 1 } } \sqrt { { I }_{ 2 } } }{ { I }_{ 1 }+{ I }_{ 2 } } |{ \gamma }_{ 12 }(r)|</math> ....(1) | |||
El valor de <math>|{ \gamma }_{ 12 }(r)|</math> sera igual a 1 para todos los valores de <math>r</math> | |||
Esto es <math>|{ \gamma }_{ 12 }(r)|=1</math> | |||
Entonces la ecuación 1 se convierte en: | |||
<math>V=\frac { 2\sqrt { { I }_{ 1 } } \sqrt { { I }_{ 2 } } }{ { I }_{ 1 }+{ I }_{ 2 } } </math> ........(2) | |||
Sabemos que un orificio esta cubierto con un filtro neutro que corta la irradiancia en un factor de 12, y otro cubierto por una lamina transparente de vidrio. Por lo tanto, no hay cambio en la irradiancia de lo que emitió ese orificio. | |||
Las irradiancias son: | |||
<math>{ I }_{ 1 }=I</math> | |||
<math>{ I }_{ 2 }=12I</math> | |||
Sustituyendo las expresiones anteriores en la ecuacion (2): | |||
<math>V=\frac { 2\sqrt { I } \sqrt { 12I } }{ { I }+{ 12I } } </math> | |||
Simplificando: | |||
<math>V=\frac { 2\sqrt { 12 } }{ { 13 } } </math> | |||
Finalmente: | |||
<math>V=0.5329</math> | |||
---- | |||
Realizado por: [[Usuario:Luis Chávez|Luis Manuel Chávez Antonio]] | |||
---- | |||
== Ejercicio 12.25 5ta Edición en Ingles== | |||
Supongamos que tenemos una fuente de hendidura incoherente, cuasimonocromatica uniforme como una lampara de descarga con una mascara y un instalador en frente de ella. deseamos iluminar una región de una pantalla de apertura a 10 metros de distancia de modo que el modulo de grado complejo de coherencia en todas las partes dentro de una región de 1mm de ancho sea igual o mayor que 90% cuando su longitud de onda es d 500 nm. que tan ancha puede ser la rendija? | |||
'''Solución''' | |||
dada la distancia de la pantalla <math>{ 10 }^{ 4 }mm</math> | |||
longitud de onda es de <math>\lambda </math> 500nm que es <math>5\times { 10 }^{ -4 }mm</math> | |||
separación de hendiduras ´a´ es <math>1mm</math> | |||
ancho de cada rendija w=? | |||
dada la visibilidad de 90%=v | |||
Sabemos que | |||
<math>V=\quad \left| sen\left( \frac { a\pi w }{ \lambda S } \right) \right| </math> | |||
== | <math>0.9=\quad \left| sen\left( \frac { 1.mm(\pi w) }{ { 10 }^{ 4 }mm\times 5{ 10 }^{ -4 }mm } \right) \right| ={ sen }^{ -1 }\left( 0.9 \right) =\frac { \pi w }{ 5 } </math> | ||
<math>w=\frac { 5 }{ \pi } { sen }^{ -1 }(0.9)</math> | |||
'''Conclusión''' | |||
<math>w=1.782mm</math> | |||
Debe ser el ancho de cada rendija. | |||
---- | |||
Realizado por: [[Usuario:salvadormorales|Salvador Morales]] | |||
---- | |||
== Ejercicio 12.24 5ta Edición en Ingles == | |||
Deseamos construir una configuración de doble orificio iluminada por una fuente de hendidura incoherente, cuasimonuchromal uniforme, de longitud de onda media de 500nm y ancho b, a una distancia de 1.5m de la pantalla de apertura. Si los orificios esta separados por 0.5mm, ¿Que ancho puede tener la fuente si la visibilidad de las franjas en el plano de | Deseamos construir una configuración de doble orificio iluminada por una fuente de hendidura incoherente, cuasimonuchromal uniforme, de longitud de onda media de 500nm y ancho b, a una distancia de 1.5m de la pantalla de apertura. Si los orificios esta separados por 0.5mm, ¿Que ancho puede tener la fuente si la visibilidad de las franjas en el plano de observación no deben ser inferiores a 85%? | ||
:'''solución''' | :'''solución''' | ||
Si un patrón de | Si un patrón de difracción centrado en el punto P. Esta distribución de campo difractada, normalizada a la unidad en P, es en todas partes igual al valor de <math>{ \gamma }_{ 12 }(0)</math> en este punto. Este es el teorema de Van Cittert-Zernike | ||
Del teorema antes mencionado, la visibilidad en el plano de observación | Del teorema antes mencionado, la visibilidad en el plano de observación | ||
| Línea 435: | Línea 537: | ||
<math>b=0.46mm</math> | <math>b=0.46mm</math> | ||
---- | ---- | ||
Realizado por: [[Usuario:Luis Gutierrez|Luis Gutiérrez Melgarejo]] | |||
---- | |||
---- | |||
Realizado por: [[Usuario:Ruben Espinosa|Ruben Espinosa Guzman]] | |||
---- | |||
==Ejercicio 12.21 5ta Edición en Ingles== | |||
:Suponga que el dispositivo de doble rendija de Young está iluminado por luz solar con una longitud de onda media de 550 nm. Calcule la separación entre las rendijas a las que las franjas desaparecerían. | :Suponga que el dispositivo de doble rendija de Young está iluminado por luz solar con una longitud de onda media de 550 nm. Calcule la separación entre las rendijas a las que las franjas desaparecerían. | ||
'''Solución:''' | '''Solución:''' | ||
Las franjas desparecen cuando | Las franjas desparecen cuando | ||
| Línea 514: | Línea 574: | ||
<math>\therefore\ a=5.93\times{10}^{-5}m</math> | <math>\therefore\ a=5.93\times{10}^{-5}m</math> | ||
---- | ---- | ||
Realizado por: [[Usuario: Verenisse|Verenisse]] | |||
---- | ---- | ||
Revisión actual - 13:09 5 sep 2023
Problemas capítulo 12 Óptica Hecht, Las bases de la teoría de la Coherencia.
Ejercicios resueltos sobre las bases de la teoría de la Coherencia de luz. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema.
Algunas ediciones del Hecht, tienen distintas numeraciones para problemas idénticos.
3ra Edición en español
Ejercicio 12.1 3ra Edición en español
Suponga que formamos una distribución de franjas con el interferómetro de Michelson. Utilizando como fuente una lampara de vapor de mercurio.Encienda la lámpara en su imaginación y analice lo que les pasara a las franjas según la presión del vapor de mercurio vaya aumentando hasta lograr su valor de estado estacionario
Solución
A presiones bajas, la intensidad emitida por la lámpara es baja, el ancho de banda es estrecho y la longitud de coherencia es grande. Las franjas mostrarán inicialmente un alto contraste, disminuirán, el contraste disminuirá y las franjas podrían incluso desaparecer por completo.
Realizado por: Usuario: luisa vega
Ejercicio 12.6 3ra Edición en español
Refiriéndose a la fuente de hendidura y la disposición de la pantalla con orificios de la figura P.12.6, muestre por integración sobre la fuente que:
$ I(Y)\propto b + \frac{\sin(\frac{\pi ab}{\lambda l})}{\frac{\pi a}{\lambda l}}\cos(\frac{2\pi aY}{\lambda s}) $
Solución
En el caso especial de dos fuentes con misma amplitud que inciden en un punto Q, la contribución a la irradiancia por estas fuentes es:
$ I=2I_{0}(1+\cos\delta)=4I_{0}\cos^{2}(\frac{\delta}{2}) $ (ver capítulo 9, ecuación 9.17).
Siendo, por su puesto & la diferencia entre las fases de dichas fuentes.
Para un elemento diferencial de la fuente de ancho en el punto S', la optical path difference length ,denotado por , de P en Y vía las dos rendijas es:
ya que, recordando que para dos fuentes que inciden sobre un mismo punto Q, la optical path difference length está dada por (bajo la aproximación de ángulos pequeños):
(ver capítulo 9, ecuación 9.23,9.24). De la ecuación 12.2 del capítulo 12, podemos observar que:
& que por la ecuación 12.3 de capítulo 12, podemos escribir la contribución a la irradiancia de un elemento como:
- , siendo, por su puesto, .
Conclusión
Por tanto:
- .
- .
Por tanto, usando las identidades trigonométricas: & , obtenemos:
- .
Realizado por: Diego de la Cruz López
Ejercicio 12.10 3ra Edición en español
Tomando el diámetro angular del sol visto desde la tierra como alrededor de $\frac{1}{2}^{\text{o}}$, determine el diámetro correspondiente del área de coherencia despreciando variaciones en el brillo sobre la superficie.
Solución:
Ya que nuestra fuente podemos considerarla como un disco por lo lejano del sol y ya que podemos despreciar variaciones de brillo, ocuparemos la ecuación 12.30 del libro de Hecht 4a ed:
$h=0.32\frac{\bar{\lambda}_0}{\theta},$
donde $h$ es el radio del área de coherencia $\bar{\lambda}_0$ es la longitud de onda de la luz y $\theta$ el diámetro angular.
Ahora convertimos el ángulo a radianes
$\theta=\frac{1}{2}^{\text{o}}=\frac{\pi}{360}=0.00872664625$
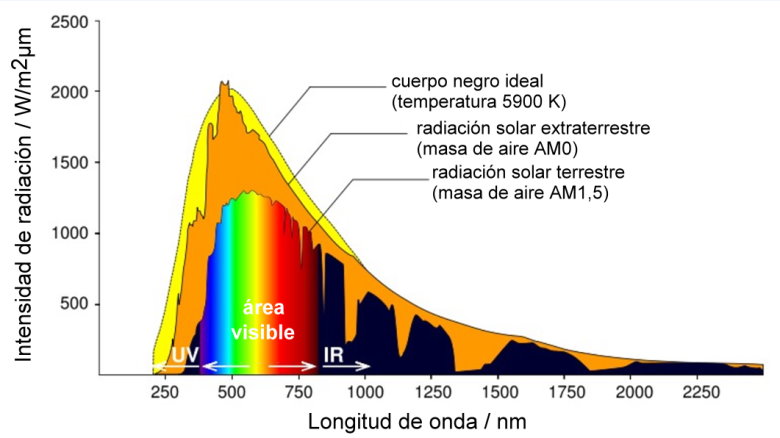
Para la longitud de onda consideremos la figura
en el espectro visible un promedio aproximado se encuentra cerca de los $550\text{nm}$ así que usaremos
$\bar{\lambda}_0=550\text{nm}.$
Sustituyendo en la formula
$h=0.32\frac{550\text{nm}}{0.00872664625}=20168\text{nm},$
Conclusión.
con el radio calculamos entonces el diámetro
$d=2h=40336\text{nm}.$
Realizado por: Flor Ivon Vivar
Ejercicio 12.15 3ra Edición en español
Deseamos construir un arreglo de dos orificios iluminados por una fuente de rendija uniforme , cuasicromática e incoherente de longitud de onda promedio de 500 nm y ancho b, a una distancia de 1.5 metros de la pantalla. si los orificios están separados por 0.50 mm , ¿Qué tan ancho puede ser la fuente si la visibilidad de las franjas en el plano de observación no debe ser menos del 85 por ciento?
Solución
- Esto se puede obtener del grado de coherencia $\mid\gamma_{12}(\tau)\mid$ ya que éste solo varía entre 0 y 1, y así en la región de la franja central ($\tau= 0$), el grado de coherencia sólo se hace una función sinc(x), y de esta al igualarla con 0.85 (85 por ciento de visibilidad), observamos que debemos buscar un valor para "x" tal que evaluado en la función sinc(x) nos devuelva el valor de 0.85:
- $\mid\frac{senx}{x}\mid= 0.85$
- Por lo que al buscar en las tablas de sinc(x) se encuentra que $sinc(0.95)\thickapprox 0.85$, por lo tanto:
- $\mid\gamma_{12}(0)\mid= \mid sinc(x)\mid= \mid sinc(\frac{\pi by}{l \lambda})\mid$.
- Con b el ancho de la rendija, (y) la distancia de separación entre los orificios y "l" la distancia entre la rendija y la pantalla con los orificios.
- De aquí que $0.97 = \frac{\pi by}{l\lambda}$, despejando "b":
- $b= \frac{l \lambda(0.95)}{y \pi}$ ó $b= \frac{(1.5 [m])(500 \times 10^{-9} [m])(0.95)}{\pi (0.50 \times 10^{-3}[m])}\thickapprox 4.6 [cm]$
Realizado por: Usuario: Pedro J. Julián
5ta Edición en Ingles.
Ejercicio 12.3 5ta Edición en Ingles
considerando el ejercicio 12.2,imagine ahora que las cosas se extienden, en el espacio en un momento determinado, cada onda daría como un resultado una distribución de irradiancia $I_1$ e $I_2$ Que le ocurre a la irradiación neta al añadir más ondas de frecuencia diferentes. Explíquelo en términos de longitud de coherencia. Hipotéticamente que le ocurre a la distribución según el ancho de la banda de la frecuencia se va aproximando al infinito.
Solución.
La irradiancia neta se vuelve más uniforme a medida que se agregan más ondas. Habrá un patrón menos distinguido, que corresponde a una longitud de coherencia menor. la irradiancia se hará constante a medida que el ancho de banda se vaya hasta el infinito
Realizado por: Usuario: luisa vega
Ejercicio 12.8 5ta Edición en Ingles
Suponga que formamos una distribución de franjas con el interferómetro de Michelson, y que utiliza como fuente una lámpara de vapor de mercurio. Encienda la lámpara en su imaginación y analice lo que les pasará a las franjas según aumente la presión del vapor de mercurio hasta lograr su valor de estado estacionario.
Solución:
A bajas presiones, la intensidad emitida desde la lámpara es baja, el ancho de banda es estrecho y la longitud de coherencia es grande. Las franjas inicialmente mostrarán un alto contraste, aunque serán bastante débiles. A medida que aumenta la presión, la longitud de coherencia disminuirá, el contraste caerá, y las franjas podrían incluso desaparecer por completo.
Realizado por: Sesebasi (discusión) 23:16 2 dic 2018 (CST)
Ejercicio 12.14 5ta Edición en Ingles
Elabore los detalles que nos llevan a la expresión de la visibilidad dada por la ecuación 12.22.
Solución
Las intensidades máximas y mínimas son:
y
Y sabiendo que la visibilidad está dada por
Sustituimos para obtener
Conclusión
Obteniendo finalmente que
que es la ecuación 12.22.
Realizado por: Ivan de Jesús Pompa García (discusión) 20:46 28 nov 2018 (CST)
Ejercicio 12.15 5ta Edición en Ingles
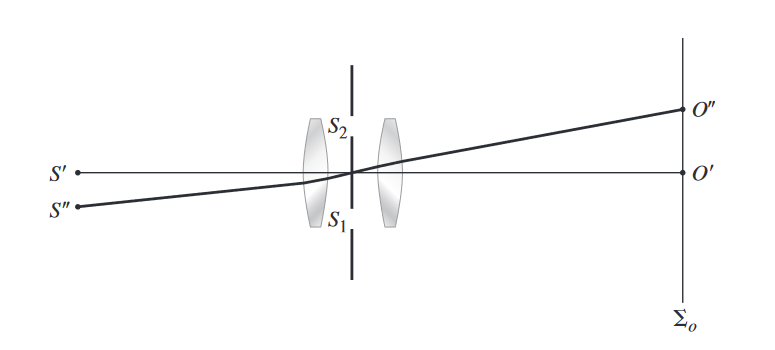
¿Bajo que circunstancias la irradiancia en en la figura P.12.15 sera igual a donde es la irradiancia debida a una fuente puntual incoherente sola?
Solución
La irradiancia debido a a es :
-----(1)
La irradiancia debido a a es :
-----(2)
La irradiancia debido a y a es
Sustituimos la ecuación (1) y (2) en la anterior y obtenemos:
Desde arriba
Por lo tanto, en el punto en que la irradiancia debe ser la diferencia de fase y debe ser :
Realizado por: Enrique Ortiz Martinez
Ejercicio 12.16 5ta Edición en Ingles
Supongamos que llevamos a cabo el experimento de Young con un agujero circular pequeño con un diámetro de 0.1 mm. enfrente de una lámpara de sodio $(\lambda = 589.3 nm)$ que actúa como fuente. Si la distancia desde la fuente hasta las rendijas es de 1 m ¿A qué distancia entre sí se hallarán las rendijas cuando el patrón de franjas desaparezca?
Solución:
Suponemos, como se hace a menudo, que "buena coherencia" significa una visibilidad de 0.88 o mejor. Para una fuente en forma de disco, esto se da cuando $\frac{ \pi h \theta }{ \bar{\lambda_0}}$ de la ecuación $\mathscr{V} = 2\frac{J_1( \pi h \theta_s \setminus \bar{\lambda_0 })}{ \pi h \theta_s \setminus \bar{\lambda_0}} $ es igual a uno, es decir si:
$h= 0.32 \frac{\bar{\lambda_0}}{\theta_s}$
Para una fuente de anchura de banda estrecha de diámetro $D$ puesta a una distancia $R$, existe un área de coherencia igual a $\pi \left( \frac{h}{2} \right) ^2$ en la que $\mid \bar{ \gamma_{12} } \mid \geq 0.88 $ . Ya que $\frac{D}{R}= \theta_s$ : $h=0.32 \frac{R \bar{\lambda_0}}{D}$
Con esta expresión podemos estimar los parámetros físicos requeridos en un experimento de interferencia o difracción. En este caso para el experimento de Young: $h=0.32 \frac{R \bar{\lambda_0}}{D} = 0.32 \frac{1 \times (589.3 \times 10^{-9} ) }{0.1 \times 10^{-3} }$ $ = 1.885 \times 10^{-3} m $
Esto indica que una serie de aberturas colocadas a una distancia de $1.9$ $ mm$ producirá franjas buenas .
Por otro lado, se obtiene que $h= 1.22 \frac{ \bar{\lambda_0} }{ \theta_s}$ $ =1.22 \frac{R \bar{\lambda_0}}{D} $ $=1.22 \frac{589.3 \times 10^{-9} }{0.1 \times 10^{-3}} $ $= 7.189 \times 10^{-3} m $
Las franjas desaparecerán cuando la distancia entre rendijas sea de $7.2 $ $mm$
Realizado por: Aurea Espin (discusión) 02:37 2 dic 2018 (CST)
Ejercicio 12.18 5ta Edición en Ingles
Mostrar que las ecuaciones (12.34) y (12.35) siguen de las ecuaciones (12.32) y (12.33) (consultar libro)
Solución:
Sabemos que:
${ I }_{ 1 }(t)=\Delta { I }_{ 1 }(t)+\left< { I }_{ 1 } \right> $
Así que : ${ I }_{ 1 }(t+\tau )=\Delta { I }_{ 1 }(t+\tau )+\left< { I }_{ 1 } \right> $
Y ${ I }_{ 2 }(t)=\Delta { I }_{ 2 }(t)+\left< { I }_{ 2 } \right> $
Por lo tanto: $\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< \left\lfloor \left< { I }_{ 1 } \right> +\Delta { I }_{ 1 }(t+\tau ) \right\rfloor \left\lfloor \left< { I }_{ 2 } \right> +\Delta { I }_{ 2 }(t) \right\rfloor \right> $
$\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< \left< { I }_{ 1 } \right> \left< { I }_{ 2 } \right> +\left< { I }_{ 1 } \right> \Delta { I }_{ 2 }(t)+\left< { I }_{ 2 } \right> \Delta { I }_{ 1 }(t+\tau )+\left< \Delta { I }_{ 1 }(t+\tau )\Delta { I }_{ 2 }(t) \right> \right> $.............(1)
Pero
${ \left< \Delta { I }_{ 1 }(t) \right> }_{ T }=0$ y ${ \left< \Delta { I }_{ 2 }(t) \right> }_{ T }=0$
Sustituyendo estos valores en la ecuación (1) obtenemos:
$\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< { I }_{ 1 } \right> \left< { I }_{ 2 } \right> +\left< \Delta { I }_{ 1 }(t+\tau )\Delta { I }_{ 2 }(t) \right> $ ...................(2)
Ya que $\left< { I }_{ 1 } \right> $ es independiente del tiempo.
Comparando la ecuación (2) con :
$\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< { I }_{ 1 } \right> \left< { I }_{ 2 } \right> +{ \left| \tilde { { \Gamma }_{ 12 }(\tau ) } \right| }^{ 2 }$
Entonces:
$\left< { { \Delta I }_{ 1 }(t+\tau )\Delta I }_{ 2 }(t) \right> ={ \left| \tilde { { \Gamma }_{ 12 }(\tau ) } \right| }^{ 2 }$
Por lo tanto se demuestra el enunciado del problema.
Ahora comparando la ecuación (2) con:
$\left< { { I }_{ 1 }(t+\tau )I }_{ 2 }(t) \right> =\left< { I }_{ 1 } \right> \left< { I }_{ 2 } \right> \left[ 1+{ \left| \tilde { \gamma _{ 12 }(\tau ) } \right| }^{ 2 } \right] $
Obtenemos entonces :
Conclusión
$\left< { { \Delta I }_{ 1 }(t+\tau )\Delta I }_{ 2 }(t) \right> =1+{ \left| \tilde { \gamma _{ 12 }(\tau ) } \right| }^{ 2 }$ Por lo tanto se demuestra el enunciado del problema.
Ejercicio 12.20 5ta Edición en Ingles
Imagina que tenemos el aparato del experimento de Young, donde uno de los dos orificios está cubierto por un filtro de densidad neutra que corta la irradiancia en un factor de 12 y el otro agujero está cubierto por una lámina transparente de vidrio, por lo que hay ningún cambio de fase relativo introducido. Calcular la visibilidad en el hipotético caso de iluminación completamente coherente.
Solución
Tenemos que la visibilidad esta dada por:
....(1)
El valor de sera igual a 1 para todos los valores de
Esto es
Entonces la ecuación 1 se convierte en:
........(2)
Sabemos que un orificio esta cubierto con un filtro neutro que corta la irradiancia en un factor de 12, y otro cubierto por una lamina transparente de vidrio. Por lo tanto, no hay cambio en la irradiancia de lo que emitió ese orificio.
Las irradiancias son:
Sustituyendo las expresiones anteriores en la ecuacion (2):
Simplificando:
Finalmente:
Realizado por: Luis Manuel Chávez Antonio
Ejercicio 12.25 5ta Edición en Ingles
Supongamos que tenemos una fuente de hendidura incoherente, cuasimonocromatica uniforme como una lampara de descarga con una mascara y un instalador en frente de ella. deseamos iluminar una región de una pantalla de apertura a 10 metros de distancia de modo que el modulo de grado complejo de coherencia en todas las partes dentro de una región de 1mm de ancho sea igual o mayor que 90% cuando su longitud de onda es d 500 nm. que tan ancha puede ser la rendija?
Solución
dada la distancia de la pantalla
longitud de onda es de 500nm que es
separación de hendiduras ´a´ es
ancho de cada rendija w=?
dada la visibilidad de 90%=v
Sabemos que
Conclusión
Debe ser el ancho de cada rendija.
Realizado por: Salvador Morales
Ejercicio 12.24 5ta Edición en Ingles
Deseamos construir una configuración de doble orificio iluminada por una fuente de hendidura incoherente, cuasimonuchromal uniforme, de longitud de onda media de 500nm y ancho b, a una distancia de 1.5m de la pantalla de apertura. Si los orificios esta separados por 0.5mm, ¿Que ancho puede tener la fuente si la visibilidad de las franjas en el plano de observación no deben ser inferiores a 85%?
- solución
Si un patrón de difracción centrado en el punto P. Esta distribución de campo difractada, normalizada a la unidad en P, es en todas partes igual al valor de en este punto. Este es el teorema de Van Cittert-Zernike
Del teorema antes mencionado, la visibilidad en el plano de observación
Donde que para angulos pequeños
Asi que,
y y
Sustituyendo estos valores en lo anterior, obtenemos
Por lo tanto la visibilidad
Sabemos que
Entonces, la visibilidad
Sea entonces la visibilidad ... (1)
Ademas la visibilidad de las franjas en el plano de observacion no debe ser inferior al 85%, siente este el valor minimo de la visibilidad V=85%=0.85
Sustituyendo el valor de V en la ec. (1) obtenemos
Esto es posible cuando
...(2)
Donde:
= longitud de onda=500nm =
y= Orificio de separación=0.5mm=
l= Distancia de la pantalla a la apertura=1.5m
Sustituyendo estos valores en al ec. (2) obtenemos
Realizado por: Luis Gutiérrez Melgarejo
Realizado por: Ruben Espinosa Guzman
Ejercicio 12.21 5ta Edición en Ingles
- Suponga que el dispositivo de doble rendija de Young está iluminado por luz solar con una longitud de onda media de 550 nm. Calcule la separación entre las rendijas a las que las franjas desaparecerían.
Solución:
Las franjas desparecen cuando
despejando (donde es la separación de las rendijas).
para
donde = distancia del sol y = diámetro del sol
Sustituyendo valores
Realizado por: Verenisse










![I\propto b+ \frac{\lambda l}{2\pi a}[\sin(\frac{ab\pi}{\lambda l} +\frac{2\pi aY}{\lambda s})-\sin(-\frac{\pi ab}{\lambda l}+\frac{2\pi aY}{\lambda s})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a4a35a62bc3d1f64aa3ec646f114b102a7aadc4d)














![{I}'=2l_{0}\left [2cos^{2}\left ( \frac{{\delta }'}{2} \right ) \right ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/574f6208699b5a3c90d8b2ccbd86e81f3c83a536)



![{I}''=2l_{0}\left [2cos^{2}\left ( \frac{{\delta }''}{2} \right ) \right ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0b95c6cf9b9254ce1fb00d0d1033f6ace098b3bb)



![2l_{0}\left [(1+cos({\delta }'))+(1+cos({\delta }'')) \right ]=4l_{0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bc077085c13db767199b41b422a1824e6fe52d0b)
![\left [ 2+cos({\delta }')+cos({\delta }'') \right ] =2](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6ab154806ceebe07bbcc0edf225dcdaf43069145)



















































![a=\lambda\frac{l}{b}\ =\frac{\left[(5.50\times{10}^{-7}m)(1.50\times{10}^{11}m)\right]}{2(6.96\times{10}^8m)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0082faf4f05396d76ca0c5cade2b89da1921306c)
