Ondas: Velocidad de grupo
Antecedentes Históricos
El concepto de velocidad de grupo se debe a W. R. Hamilton en 1839[1]
, pero la distinción entre las velocidades de fase y de grupo fue puesta en claro por Lord Rayleigh en 1877[2]
en su "Teoria del sonido".
Definición de onda
Podemos definir a una onda como una perturbación o protuberancia que se propaga con una determinada dependencia espacio-temporal, acarreando energía. De manera general, una onda necesita de dos componentes principales para desarrollarse como tal. El primer componente es la fuente de perturbación, es decir un componente físico que actúe de tal forma que pueda crear a la onda.
La perturbación de una onda, se propaga con una determinada dependencia espacio-temporal. La perturbación de una magnitud física consiste a menudo en una variación periódica y sobre todo oscilatoria (repetición entre valores extremos opuestos) por lo que, en particular, la onda se considera como la propagación de una vibración originada en un punto.
Análisis Matemático
Si la forma de pulso de la onda no cambia con el tiempo, podemos representar el desplazamiento para todos los tiempos posteriores con respecto a un marco de referencia estacionario con un origen en 0, tomando la siguiente forma:
...(1)
Esta función representa una onda viajera, es decir, una onda que se mueve hacia la derecha a una velocidad .
Si el pulso viaja hacia la izquierda el desplazamiento es de la forma:
...(2)
Por lo que, una expresión matemática del desplazamiento es:
...(3)
Supongamos que existen dos ondas que se propagan en una cuerda con diferentes frecuencias y longitudes de onda en el mismo sentido. A la primera onda le asignaremos una función y a la segunda onda le asignaremos otra función diferente denominada . Tal como se muestra en las figuras 1 y 2.
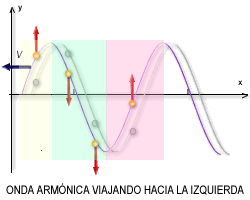
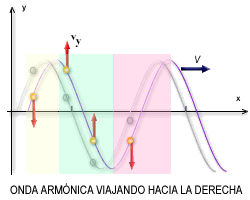
Todas las ondas de una clase determinada se desplazan con la misma velocidad de fase en un medio no dispersivo mientras que en un medio dispersivo, la velocidad de propagación depende de su frecuencia. Cuando varias ondas se combinan para formar una perturbación compuesta, la envolvente de modulación se desplazara a una velocidad distinta de la de las ondas constitutivas.
Supongamos que tenemos dos soluciones particulares. Podemos suponer, por tanto, que tenemos dos soluciones casi iguales a la ecuación diferencial de onda representadas por las funciones de onda y , cada una de las cuales tiene la misma aplitud.
...(4)
...(5)
Donde es la frecuencia angular y representa el número de longitudes de onda en un período de radianes y se denomina número de onda.
El principio de superposición de ondas señala que: "La elongación resultante de la interacción de dos ondas es la suma algebraica de las elongaciones correspondientes a las ondas individuales". Es decir, para obtener la onda resultante, tenemos que sumar las funciones de onda y , quedando una expresión de la siguiente manera:
...(6)
Usando la ley de los cosenos, obtenemos:
Si las dos ondas combinadas son de casi la misma longitud de onda podemos simplificar nuestra descripción para una perturbación combinada poniendo
Y ahora utilizando estas expresiones en obtenemos
...(7)
...(8)
Este resultado puede interpretarse como una onda armónica de frecuencia y número de onda propagándose en el eje x. La amplitud de esta onda , sin embargo, no es constante sino que varía con el tiempo.
Para graficar la suma de y , primero graficamos la onda sinusoidal de gran longitud de onda. La solución se encuentra entre esta onda larga y se reflejada en el eje de abcisas, y tiene una longitud de onda relativamente pequeña. Las ondas de oscilación rápida varían muy lentamente su amplitud.
En la figura 3 podemos observar que la velocidad total del envolvente se mueve a una velocidad de fase:
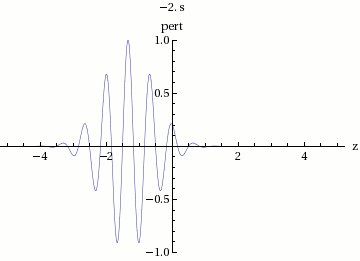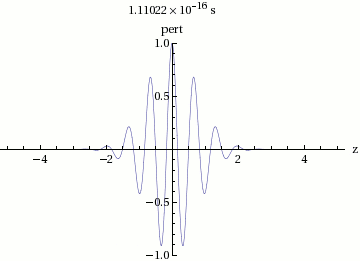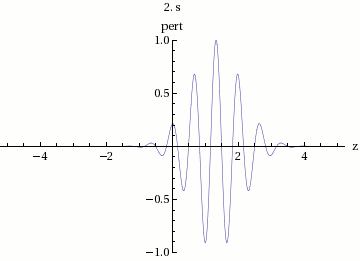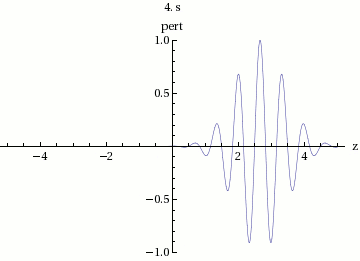
Dicha velocidad de fase de la amplitud de la onda, contiene un grupo de ondas internas, es decir, la suma de todas ellas. Por lo cual, esta velocidad es la llamada velocidad de grupo .
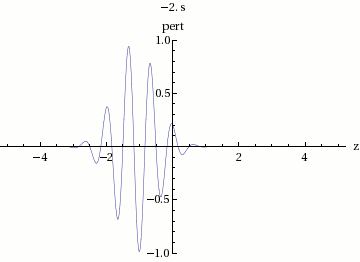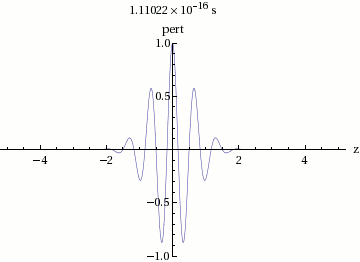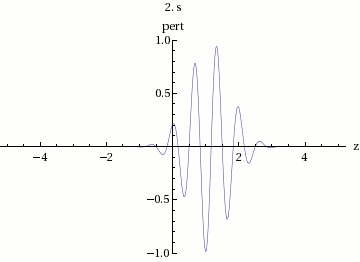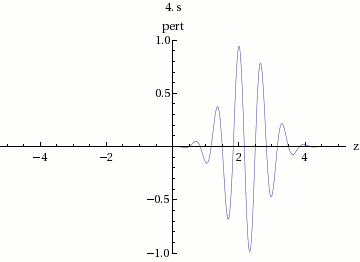
La pendiente de la curva de dispersión es siempre menos marcada que ; es decir, mientras que en la dispersión anómala . Ya que , la ecuación (10) da
Pos consiguiente, en medios no dispersos donde es independiente de , y . Concretamente en el vacío , y . En medios dispersivos , donde n es conocida, , siendo útil volver a escribir como
Utilizando Variable compleja
Otra formade encontrar la velocidad de grupo, es usar números complejos.
Supongamos que tenemos dos soluciones particulares. Podemos suponer, por tanto, que tenemos dos soluciones casi iguales a la ecuación de onda representadas por las funciones de onda y , cada una de las cuales tiene la misma amplitud,
...(13)
...(14)
pero cuyas pulsaciones y números de onda difieren sólo en pequeñas cantidades:
Si formamos la solución compuesta por la suma de y , tendremos
...(15)
El segundo corchete es precisamente el doble del coseno del argumento de la exponencial y la parte real del primer corchete es también un coseno. Entonces la parte real de la función de onda será
...(16)
donde encontramos una amplitud lentamente variable, correspondiente al término
el cual modula a la función de onda. La oscilación principal tiene lugar a una frecuencia , que según nuestra hipótesis de que Δω es pequeño, difiere poco de ω. Tal como se muestra en la figura.
La velocidad U llamada velocidad de grupo a la que se propagan los grupos de ondas vendrá dada por la condición de que la fase en términos de amplitud sea constante. Así
Referencias
Dinámica Clásica de las Partículas y Sistemas, Jerry B. Marion, Ed. Reverté, S. A., 1992, pp. 570-573
Ecuaciones en Derivadas Parciales con Series de Fourier y Problemas de Contorno, Richard Haberman, Ed. Prentice Hall
Vibraciones y Ondas, A. P. French, Ed. Reverté, S. A., 2000, pp. 259-262
Optics, Hecht, Ed. Addison Wesley, Segunda Edición, 1990, pp. 252-253








![\Psi _1(\textbf {z},t)=A \cos[\kappa_1 z -t \omega_1]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9079dcaf9ce122317498f9ddf5a54740d54f416b)
![\Psi _2(\textbf {z},t)=A \cos[\kappa_2 z -t \omega_2]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2dd6d5a8a949a0d086dea470a5bb5e53e5a095dc)



![\Psi (\textbf {z},t)=A \cos[(\kappa-\Delta \kappa) z-(\omega-\Delta \omega)t]+ A \cos[(\kappa+\Delta \kappa)z-(\omega+\Delta \omega)t]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/54c320a55dbae668792e63a00dfe2064ae536d84)






![\textstyle \Psi (\textbf {z},t)=2 A \cos[\frac{1}{2} z (\kappa-\Delta\kappa)+\frac{1}{2} z (\kappa+\Delta \kappa)-\frac{1}{2} t (\omega-\Delta \omega)-\frac{1}{2} t (\omega+\Delta \omega)] \cos[\frac{1}{2} z (\kappa-\Delta \kappa)-\frac{1}{2} z (\kappa+\Delta \kappa)- \frac{1}{2} t (\omega-\Delta \omega)+\frac{1}{2} t (\omega+\Delta \omega)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/78f9af69b773e3ab43def48bc63a9b798861703b)



![2 A \cos [(\Delta \kappa) z- (\Delta \omega) t]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c3f2afbf33dc02f27f2fb40985294756b063fcd9)


























![\Psi (\textbf {z},t)=\Psi_1+\Psi_2=A[{e}^{i\omega t} \cdot {e}^{-i\kappa z} + {e}^{i(\omega + \Delta \omega) t}\cdot {e}^{-i(\kappa+\Delta\kappa)}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/324bf3ed0c17b5ea16252b30c1f07cbe0a18dc14)
![= A[{e}^{i(\omega+\frac{\Delta\omega}{2})t}\cdot {e}^{-i(\kappa+\frac{\Delta\kappa}{2})z}]\cdot[{e}^{-i(\frac{(\Delta \omega) t-(\Delta \kappa)z}{2})}+ {e}^{i(\frac{(\Delta \omega) t-(\Delta \kappa)z}{2})}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/41e43224967ef6620b4228af1364ab414feda847)
![\Psi (\textbf {z},t)=2A \cos(\frac{\Delta\omega t-\Delta \kappa z}{2})\cos[(\omega+\frac{\Delta \omega}{2})t-(\kappa\frac{\Delta\kappa}{2})z]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9eba9454208e943b40924a7ab0d911e907191fe4)
![2A\cos[\frac{(\Delta\omega)t-(\Delta\kappa)z}{2}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/11439e127a58ad576eaf34bc66ea2dd56b0ffefb)