Ondas: Polarizacion
Introducción
El estudio acerca del comportamiento y naturaleza de la luz incluye nombres de grandes maestros a traves de la historia, además de ser un tema bastante amplio.
El siguiente articulo se limita unicamente a tratar el tema de polarización de la luz(lineal, circular y elíptica) aunque otro tipo de ondas también presenta el fenómeno, como es el caso de las ondas sísmicas. Cabe aclarar que hacer al uso del termino “luz polarizada” es hacer referencia a que la luz tiene una orientación. La luz puede ser tratada como una onda electromagnética transversal. Conviene recordar que una onda tansversal es aquella donde la perturbación o vibración ocurre en los planos perpendiculares a la dirección del movimento.
Sabemos que los campos eléctrico y magnetico guardan una cierta relación entre si, por lo que una vez conocido el campo elécrico trasnversal entonces podremos determinar el campo magnético transversal, esto es:
Polarización lineal.
En general, la magnitud y dirección del vector campo eléctrico en cualquier punto a lo largo de la trayectoria es una función del tiempo y del espacio. En el caso de las ondas transversales si el desplazamiento es una oscilacion hacia atras y adelante de una linea transversal z fija, se dice que las ondas estan linealmente polarizadas.La luz está linealmente polarizada si el vector eléctrico conserva constante su dirección, cambiando unicamente de forma senoidal con el tiempo y el espacio su magnitud y sentido.
Imaginemos dos ondas de luz linealmente polarizadas de la misma frecuencia, moviendose a traves de la misma región del espacio, en la misma dirección, siendo sus vectores campo elélctrico colineales, las perturbaciones superpuestas se combinarán simplemente para formar una onda resultante linealmente polarizada.
Representemos estas dos ondas de luz de la manera siguiente:
donde ɛ es la diferencia de fase relativa entre las ondas, ambas viajando en la dirección z, es la magnitud del campo eléctrico.
Tal perturbación puede escribirse siempre como una superposicion de las dos perturbaciones independientes linealmente polarizadas, la que podemos escribir como sigue:
si ɛ es cero o un multiplo entero de ±2π se dice que las ondas estan en fase, para este caso se tiene que:
Las magnitudes relativas de las componentes determinarán la orientación de la polarización, es decir:
Recordar que la amplitud en la luz linealmente polarizada no es constante sin embargo las dos ondas consideradas estan en fase.
Polarización circular.
Si el desplazamiento en una onda transversal es un movimiento en círculo , se dice que las ondas están circularmente polarizadas.
Supongamos que se van propagando a lo largo de la misma trayectoria z dos ondas linelmente polarizadas las cuales conservan su amplitud constante pero existe una diferencia de fase relativa entre ellas.
Consideremos para la ecuacion (1) el punto z=0 y ωt=-φ, la amplitud como dijimos sera constante (E) y apunta a lo largo del eje de las y, un tiempo corto despues la componente en y es un poco mas pequeña y la componente en x es un poco mas grande, la magnitud del vector sigue siendo la misma y gira en el sentido de las manecillas del reloj, este movimiento continua en el tiempo hasta que por ejemplo ωt=90º-φ entonces el vector apuntará en la dirección del eje de las x, dicho de otro modo estan fuera de fase.
Este tipo de movimento se le llama circular polarizada a derechas.
Alternativamente para el caso cuando el movimiento sea circular polarizada a izquierdas
Polarización elíptica.
Por lo que a la descripción matemática se refiere tanto la luz lineal como circular se pueden considerar como casos especiales de la luz elipticamente polarizada o mas simplemente luz elíptica.Esto significa que, en general, el vector de campo eléctrico girará cambiando también su magnitud.
Para tratar esto de manera analítica tomemos las representaciones siguientes:
al tomar haciendo uso de las siguientes relaciones:
despejando y sustituyendola adecuadamente podemos llegar a la
siguiente relación:
ordenando terminos y tomando asi la expresión:
podemos transformarla de la siguiente manera:
Es posible mostrar que esta es la ecuación de una elipse, para ello rotamos esta ecuación a un nuevo sistema de coordenadas (η,ξ) giradas un ángulo Ψ con respecto al sistema de coordenas (x,y) como se muestra en la figura.
Si para la ecuacion 2 Ψ=0 o δ= ±π , ± ,,,, podemos obtener la ecuación ya conocida:
Además si sabemos que:
lo cual es un círculo. Si Ψ es un multiplo par de π encontramos en la ecuación 2 que:
de manera similar si Ψ es un multiplo impar de π:
Ambas son lineas rectas con pendiente:
Podemos llevar a cabo la rotación a un nuevo sistema de coordenadas por medio de las siguientes ecuaciones de transformación:
que al ser empleadas para transformar 2 nos dan:
el ángulo Ψ se escoge de tal manera que los semiejes de la elipse coincidan con los ejes η,ξ. Esto se logra haciendo que el coeficiente de de la ecuacion 3 sea igual a cero, por tanto:
que al utilizar las identidades:
podemos obtener una orientación de la elipse dada por:
al escribir la ecuación 2 sin el termino del coeficiente que igualamos con cero anteriormente tendriamos una ecuación la cual puede ser reescrita, para finalmente obtener la forma general siguiente:
en donde las constantes a.b son los semiejes mayor y menor respectivamente.
Es posible demostrar que:
Parámetros de Stokes
Para determinar la forma completa del estado de polarización de un haz de luz (bien sea natural o parcialmente polarizado) son necesarios tres parámetros independientes, por ejemplo, los semiejes a y b y la orientacion Ψ de la elipse.
A estos parámetros se les llama parámetros de Stokes. G.Stokes con el proposito de poder describir en forma matematica la luz parcialemente polarizada introdujo cuatro parámetros, que determinan por completo la elipse de polarización.
Estos parámetros estan definidos en terminos de , Ψ y son:
Donde representa la irradiancia del haz. Solamente tres de estos parametros son independientes, ya que ellos se relacionan entre si por:
Si definimos ahora una cantidad χ mediante :
entonces:
pero usando 4 y 5 se pueden escribir como:
y substituyendo aqui los valores de tenemos:
por otro lado podemos ver que:
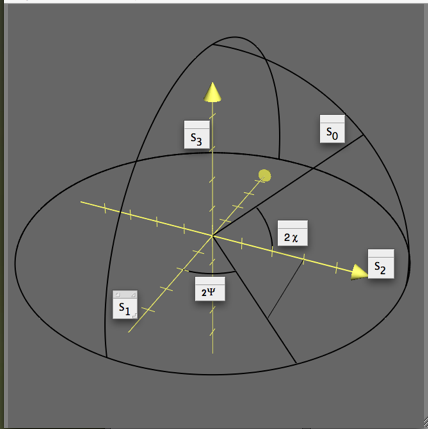
La relacion dada por la ecuación 6 sugiere que se pueden representar los parámetros por puntos en una esfera con radio .
Los parámetros de Stokes se pueden representar con base a la esfera de Poincaré de la manera siguiente:
Hemos visto en general que un haz completamente polarizado tiene en general polarizacion eliptica, la cual puede tomar las formas particulares circular o lineal.
La luz esta completamente polarizada sólo si las componentes son coherentes entre si, es decir si tienen una diferencia de fase δ constante.
Podemos pensar en una onda no polarizada como una en la cual el estado de polarización cambia al azar en forma sumamente rápida . Una onda tal tiene la caracteristica de que su irradiancia es la misma en cualquier plano de polarización que se mida.
Para representar en forma completa el estado de polarización, incluyendo los de luz parcialmente polarizada, es necesario especificar cuatro parámetros independiente.
Los parametros son los siguientes:
Estos parámetros (que estan definidos como los promedios temporales de los parametros de Stokes para luz completamente polarizada) representan fisicamente lo siguiente:
I representa la irradiancia total del haz.
M indica el predominio de la componente horizontal o vertical, segun sea positivo o negativo.
C representa la tendencia del angulo χ para la orientacion de la elipse, hacia -45º o +45º segun sea positivo o negativo.
S indica si la polarización es derecha o izquierda, según sea positivo o negativo. Este parámetro es cero si la polarización es lineal.
Bibliografía
Daniel Malacara. Optica básica. Fondo de la cultura económica, 1989
David S. Kliger, James W. Lewis y Cora E. Randall. Polarized light in optics and spectroscopy. Academic Press,Inc. 1990
Frank S.Crawford, Jr. Ondas. (Berkeley physics course - volumen 3) . Edit Reverté 1994
Eugene Hetch. Optica. Pearson Education 2003
![B\left(z,t\right)=\mathbf{\hat{e}_{z}}\times\left[E^{+}\left(z,t)-E^{-}\left(z,t\right)\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3f8be4b48e3c5d4d879616fe52488963ec4dfd0a)






![E_{\text{cpd}}=E^{}\left\{\sin[wt-kz+\phi]\mathbf{\hat{e}_{\text{x}}}+\sin[wt-kz+\phi+\frac{\pi}{2}]\mathbf{\hat{e}_{\text{y}}}\right\}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4d930bd9d3f25f66659eb315e475cdc0a1bfa088)
![E_{\text{cpd}}=E^{}\left\{\sin[wt-kz+\phi]\mathbf{\hat{e}_{\text{x}}}+\cos[wt-kz+\phi]\mathbf{\hat{e}_{\text{y}}}\right\}
\qquad(1)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f71e57cbfea9b97a7d03f9087d8fbd7bfe65345d)
![E_{\text{cpd}}=E^{}\left\{\sin[wt-kz+\phi]\mathbf{\hat{e}_{\text{x}}}+\sin[wt-kz+\phi-\frac{\pi}{2}]\mathbf{\hat{e}_{\text{y}}}\right\}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/de6f1a30f66aa972cc6d76f756be0c9bbd9e0e91)
![E_{\text{cpd}}=E^{}\left\{\sin[wt-kz+\phi]\mathbf{\hat{e}_{\text{x}}}-\cos[wt-kz+\phi]\mathbf{\hat{e}_{\text{y}}}\right\}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f55182910182f0bcd74fe6c7dc023b2b1cf58e33)




![\sin(\omega t-kz)=\left[1-cos^{2}(kz-\omega t)\right]^{\frac{1}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f0995e75214cc574c46e6aaee126b026992fbc25)

![E_{y}=a_{2}\frac{E_{x}}{a_{1}}E_{x}\cos\delta-a_{2}\left[1-\left(\frac{E_{x}}{a_{1}^{2}}\right)^{2}\right]\sin\delta](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9229958b5172421356201d140dcb8b604a1a8b54)
![\left(\frac{E_{y}}{a_{2}}-\frac{E_{x}}{a_{1}}\cos\delta\right)^{2}=\left[1-\left(\frac{E_{x}}{a_{1}^{2}}\right)^{2}\right]\sin^{2}\delta](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3acaa4e48fe92042db2fe0aa615060a645708e00)










![\left[a_{2}^{2}\cos^{2}\psi+a_{1}^{2}\sin^{2}\psi-2a_{1}a_{2}\sin\psi \cos\psi \cos\delta\right]E_{\eta}^{2}+\left[a_{2}^{2}\sin\psi+a_{1}^{2}\cos^{2}\psi+2a_{1}a_{2}\sin\psi \cos\psi \cos\delta\right]E_{\xi}^{2}-2\left[\left(a_{2}^{2}-a_{1}^{2}\right)\sin\psi \cos\psi+a_{1}a_{2}(\cos^{2}\psi-\sin^{2}\psi)\cos\delta\right]E_{\eta}E_{\xi}=a_{2}^{2}a_{1}^{2}\sin^{2}\delta\qquad(3)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d79a71114f0b88dc5a7b354b5ab596a186b63b00)