Ondas: Membrana

Ecuación de onda para membranas

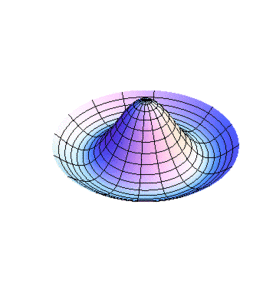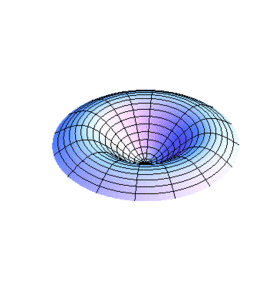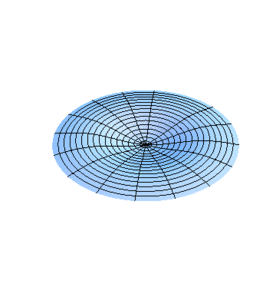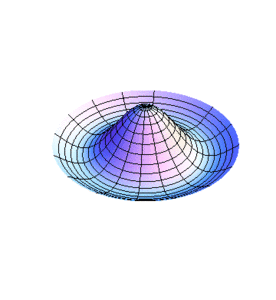
En la sección Ondas: Cuerdas y Corrientes- Transversalesse mencionan algunos casos de ondas en una dimensión. Para el caso de dos dimensiones se considera una membrana estirada y flexible siendo esta la contraparte en dos dimensiones de la cuerda estirada y flexible.

Se considera que la membrana se encuentra en un principio en reposo en el plano xy con una tensión superficial ($\tau$) a lo largo de cualquier línea recta que cruce la membrana, el análogo bidimensional de la tensión del a cuerda, y que la membrana posee una densidad por unidad de área ($\sigma$).

Supongamos que tenemos un elemento rectangular $\Delta x$,$\Delta y$ de la membrana, cuando la membrana sufre un desplazamiento surge una fuerza neta en dirección del eje z por cada pareja de fuerzas de tensión $\tau \Delta x$ y $\tau \Delta y$ que actúan en las cuatro orillas del elemento rectangular. Cada par puede considerarse el equivalente a la tensión en una cuerda hipotética que consiste de una tira de la membrana donde su ancho mide $\Delta x$ y se extiendo a lo largo del eje y, o de ancho $\Delta y$ y se extiende a lo largo del eje x. Para la primera tira la fuerza neta en la dirección del eje z es:

$\tau \Delta x\left({\frac {\partial \Psi }{\partial y}}_{y+\Delta y}-{\frac {\partial \Psi }{\partial y}}_{y}\right)=\tau \Delta x{\frac {\partial ^{2}\Psi }{\partial y^{2}}}\Delta y$

Para la segunda tira, la fuerza neta es:

$\tau \Delta y\left({\frac {\partial \Psi }{\partial x}}_{x+\Delta x}-{\frac {\partial \Psi }{\partial x}}_{x}\right)=\tau \Delta y{\frac {\partial ^{2}\Psi }{\partial x^{2}}}\Delta x$

La suma de estas fuerzas debe de ser igual a la masa de la membrana $\sigma \Delta x\Delta y$ por su aceleración, eso es,

$\Delta x\Delta y\tau \left({\frac {\partial ^{2}\Psi }{\partial x^{2}}}+{\frac {\partial ^{2}\Psi }{\partial y^{2}}}\right)=\Delta x\Delta y\sigma {\frac {\partial ^{2}\Psi }{\partial t^{2}}}$

Dividiendo la ecuación entre $\Delta x\Delta y$ se obtiene la ecuación de onda tal que,

${\frac {\partial ^{2}\Psi }{\partial x^{2}}}+{\frac {\partial ^{2}\Psi }{\partial y^{2}}}={\frac {1}{C_{m}}}{\frac {\partial ^{2}\Psi }{\partial t^{2}}}$

Donde,

$C_{m}=\left({\frac {\tau }{\sigma }}\right)^{1/2}$

Es la velocidad de propagación para una onda transversal en la membrana.

Dado que se encuentra en un plano la ecuación de onda puede convertirse de coordenadas cartesianas a coordenadas polares quedando de la siguiente manera

--Alejandro Angel Galvan Garcia 21:50 26 mar 2012 (UTC)

---

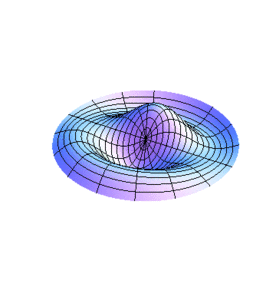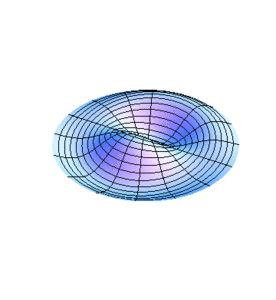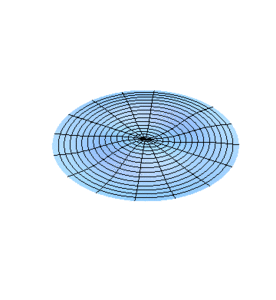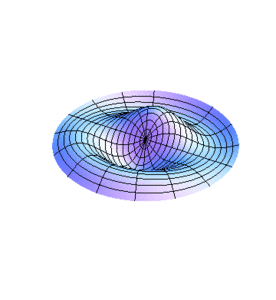
Modos normales de una membrana circular

Vamos a estudiar ahora los modos normales de vibración de una membrana con límite fijo circular, por lo que resulta conveniente transformar a coordenadas polares la ecuación de onda obtenida en la sección anterior para simplificar el tratamiento que a continuación se hace.

Usando las relaciones $x=r\cos(\theta )$, $y=r\mathrm {sen} (\theta )$, y por la regla de la cadena obtenemos

${\frac {\partial ^{2}\Psi }{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial \Psi }{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}\Psi }{\partial \theta ^{2}}}={\frac {1}{C_{m}^{2}}}{\frac {\partial ^{2}\Psi }{\partial t^{2}}}$

Ahora, por el método de separación de variables trataremos de encontrar una solución de la forma producto a la ecuación anterior que satisfaga la condición de no desplazamiento en la frontera de la membrana. Como veremos en seguida, las variables de la ecuación de onda son separables en el sistema coordenado que estamos usando. Sea

$\Psi (r,\theta ,t)=R(r)\Theta (\theta )T(t)$

Figura 1.

Figura 2.

Figura 3.

Figura 4.