Ondas: Membrana

Ecuación de onda para membranas

En la sección Ondas: Cuerdas y Corrientes- Transversales se mencionan algunos casos de ondas en una dimensión. Para el caso de dos dimensiones se considera una membrana estirada y flexible siendo esta la contraparte en dos dimensiones de la cuerda estirada y flexible.

Se considera que la membrana se encuentra en un principio en reposo en el plano xy con una tensión superficial ($\tau$) a lo largo de cualquier línea recta que cruce la membrana, el análogo bidimensional de la tensión de la cuerda, y que la membrana posee una densidad por unidad de área ($\sigma$).

Supongamos que tenemos un elemento rectangular $\Delta x$,$\Delta y$ de la membrana, cuando la membrana sufre un desplazamiento surge una fuerza neta en dirección del eje z por cada pareja de fuerzas de tensión $\tau \Delta x$ y $\tau \Delta y$ que actúan en las cuatro orillas del elemento rectangular. Cada par puede considerarse el equivalente a la tensión en una cuerda hipotética que consiste de una tira de la membrana donde su ancho mide $\Delta x$ y se extiende a lo largo del eje y, o de ancho $\Delta y$ y se extiende a lo largo del eje x. Para la primera tira la fuerza neta en la dirección del eje z es:

\begin{equation} \qquad \tau\Delta x\left(\left(\frac{\partial\Psi}{\partial y}\right)_{y+\Delta y}-\left(\frac{\partial\Psi}{\partial y}\right)_y\right)=\tau\Delta x\frac{\partial^2\Psi}{\partial y^2}\Delta y \label{primera} \end{equation}

Para la segunda tira, la fuerza neta es:

\begin{equation} \qquad \tau\Delta y\left(\left(\frac{\partial\Psi}{\partial x}\right)_{x+\Delta x}-\left(\frac{\partial\Psi}{\partial x}\right)_x\right)=\tau\Delta y\frac{\partial^2\Psi}{\partial x^2}\Delta x \label{segunda} \end{equation}

La suma de estas fuerzas debe de ser igual a la masa de la membrana $\sigma \Delta x\Delta y$ por su aceleración, eso es,

\begin{equation} \qquad \Delta x\Delta y\tau\left(\frac{\partial^2\Psi}{\partial x^2}+\frac{\partial^2\Psi}{\partial y^2}\right)=\Delta x\Delta y\sigma\frac{\partial^2\Psi}{\partial t^2} \label{tercera} \end{equation}

Dividiendo la ecuación entre $\Delta x\Delta y$ se obtiene la ecuación de onda tal que,

\begin{equation} \qquad \frac{\partial^2\Psi}{\partial x^2}+\frac{\partial^2\Psi}{\partial y^2}=\frac{1}{C_m^2}\frac{\partial^2\Psi}{\partial t^2} \label{cuarta} \end{equation}

Donde:

\begin{equation} \qquad C_m=\left(\frac{\tau}{\sigma}\right)^{1/2} \label{quinta} \end{equation}

Es la velocidad de propagación para una onda transversal en la membrana.

---

Aportación de: Alejandro Angel Galvan Garcia 21:50 26 mar 2012 (UTC)

---

Modos normales de una membrana circular

Vamos a estudiar ahora los modos normales de vibración de una membrana con límites circulares fijos, por lo que resulta conveniente transformar a coordenadas polares la ecuación (\ref{cuarta}) para simplificar el tratamiento que a continuación se hace.

Usando las relaciones $x=r\cos(\theta )$, $y=r\mathrm {sen} (\theta )$, y por la regla de la cadena obtenemos

\begin{equation} \qquad C_m^2\left (\frac{\partial^2\Psi}{\partial r^2}+\frac{1}{r}\frac{\partial\Psi}{\partial r}+\frac{1}{r^2}\frac{\partial^2\Psi}{\partial\theta^2} \right )=\frac{\partial^2\Psi}{\partial t^2} \label{sexta} \end{equation}

Ahora, por el método de separación de variables trataremos de encontrar una solución de la forma producto a la ecuación anterior que satisfaga la condición de no desplazamiento en la frontera de la membrana. Como veremos en seguida, las variables de la ecuación (\ref{sexta}) son separables en el sistema coordenado que estamos usando. Sea

\begin{equation} \qquad \Psi(r,\theta,t)=R(r)\Theta(\theta)T(t) \label{septima} \end{equation}

Derivando y sustituyendo en la ecuación (\ref{sexta}), obtenemos:

\begin{equation} \qquad R \Theta T''=C_m^2\left (R'' \Theta T + \frac{1}{r}R'\Theta T + \frac{1}{r^2 }R \Theta'' T \right ) \label{octava} \end{equation}

Donde las primas denotan la diferenciación ordinaria. Dividiendo por $R\Theta T$ en ambos lados de la ecuación anterior nos queda

\begin{equation} \qquad \frac{C_m^2}{R}(R''+\frac{1}{r}R') +\frac{C_m^2}{r^2\Theta}\Theta''=\frac{1}{T}T'' \label{novena} \end{equation}

Como el lado izquierdo no depende de la variable $t$ así como el derecho no depende de las variables $r$ y $\theta$, podemos concluir que para que sea cierta la igualdad ambas partes de la ecuación deben de ser iguales a una constante, que llamaremos de separación, por ejemplo $-\omega ^{2}$. Introduciendo esta constante en la ecuación anterior obtenemos las dos siguientes

\begin{equation} \qquad T''+ \omega^2 T=0 \label{decima} \end{equation}

\begin{equation} \frac{C_m^2}{R}(R''+\frac{1}{r}R')+\omega^2=-\frac{C_m^2}{r^2\Theta}\Theta'' \label{onceava} \end{equation}

La segunda ecuación podemos a su vez separarla en dos ecuaciones diferenciales ordinarias introduciendo una segunda variable de separación $n^{2}$. Después de multiplicar por $r^{2}/C_{m}^{2}$ a (\ref{onceava}), obtenemos

\begin{equation} \qquad \Theta''+ n^2 \Theta=0 \label{doceava} \end{equation}

\begin{equation} \qquad R''+\frac{1}{r}R'+ [\frac{\omega^2}{C_m^2}- \frac{n^2}{r^2}]R=0 \label{treceava} \end{equation}

Con el cambio de variable $u=\omega r/C_{m}^{2}$ en (\ref{treceava}), obtenemos la ecuación de Bessel

\begin{equation} \qquad R''+\frac{1}{u}R'+ (1-\frac{n^2}{u^2})R=0 \label{catorceavo} \end{equation}

En este caso las primas representan la diferenciación con respecto a la variable $u$. Siendo esta ecuación de segundo orden, tiene dos soluciones linealmente independientes para cada valor del parámetro m. Las dos soluciones de la ecuación (\ref{catorceavo}) normalmente se presentan como $J_{n}(u)$ y $N_{n}(u)$. La solución $J_{n}(u)$ es conocida como función de Bessel de primer tipo de orden n. La otra solución $N_{n}(u)$, es conocida como función de Neumann ( o función de Bessel de segundo tipo). Como la función de Neumann no puede representar el desplazamiento de una membrana circular , solo se utiliza la función de Bessel de primer tipo, y esta función puede ser expresada en una serie infinita de la manera:

\begin{equation} \qquad J_n(u)=\frac{u^n}{2^nn!}\left[1-\frac{u^2}{1!2^2(n+1)}+\frac{u^4}{2!2^4(n+1)(n+2)}-...\right] \label{15} \end{equation}

El coeficiente numérico $1/2^{n}n!$ es puramente convencional. Todas las funciones de Bessel a excepción de $J_{0}$ se desvanecen en el origen y $J_{0}(0)=1$. La gráfica de la función de Bessel obedece un comportamiento similar al de una onda sinusoidal amortiguada.

Las funciones de Bessel obedecen las siguientes relaciones de recursión:

\begin{equation} \qquad J_{n+1}(u)=\frac{2n}{u}J_n(u)-J_{n-1}(u) \label{16} \end{equation}

\begin{equation} \qquad \frac{dJ_n(u)}{du}=-\frac{n}{u}J_n(u)+J_{n-1}(u) \label{17} \end{equation}

Estas relaciones pueden establecerse directamente de la serie infinita dada en (\ref{15}). Muestran que solo es necesario tener los valores numéricos de $J_{0}$ y $J_{1}$ para conocer los valores de las funciones de Bessel de orden mayor, así como las primeras derivadas.

Por otra parte, las soluciones generales de (\ref{decima}) y (\ref{onceava}) son, respectivamente:

\begin{equation} \qquad T(t)= b_1\cos(\omega t)+ b_2\mathrm{sen}(\omega t) \label{18} \end{equation}

\begin{equation} \qquad \Theta(\theta)= c_1\cos(n \theta)+ c_2\mathrm{sen}(n \theta) \label{19} \end{equation}

Consideremos ahora algunos ejemplos de los modos normales de la membrana que estamos tratando. Cuando $n=0$, podemos escribir a (\ref{septima}) como

\begin{equation} \qquad \Psi(r,t)= A J_0(\frac{\omega}{C_m} r)\cos(\omega t) \label{20} \end{equation}

Nótese que se uso también la condición inicial ${\frac {\partial \Psi }{\partial t}}=0$, es decir la membrana parte del reposo, de donde la constante $b_{2}=0$ en (\ref{18}). Sea a el radio de las membranas, para satisfacer ahora la condición de frontera

\begin{equation} \qquad \Psi(a,\theta,t)=0 \label{21} \end{equation}

Es decir, que los límites estén fijos, tiene que cumplirse

\begin{equation} \qquad J_0(\frac{\omega}{C_m} a)=0 \Rightarrow \frac{\omega_{0l} a}{C_m}= u_{0l} \\ \mathrm{l=1,2,...} \label{22} \end{equation}

Donde las $u_{0l}$ son las raíces de $J_{0}(u)=0$. Una extensa lista de los ceros de las funciones de Bessel puede encontrarse en la literatura, veáse por ejemplo la tabla con los primeros 700 ceros de estas funciones de C. L. Beattie. Las frecuencias en las cuales se excitan los modos normales de vibración son

\begin{equation} \qquad \omega_{0l} =\frac{C_m u_{0l}}{a}, l=1,2,... \label{23} \end{equation}

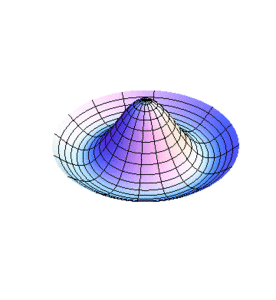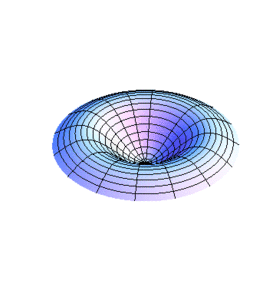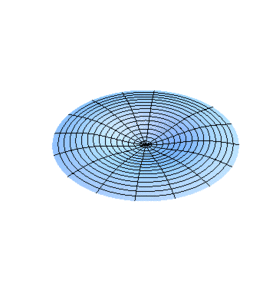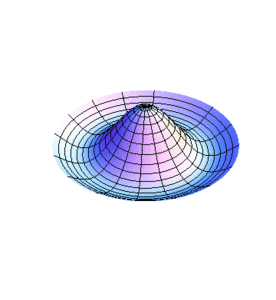
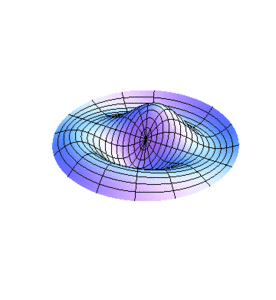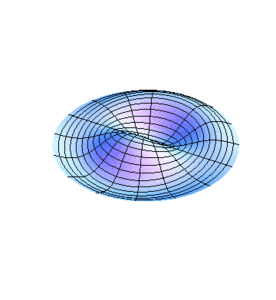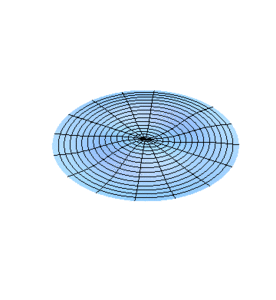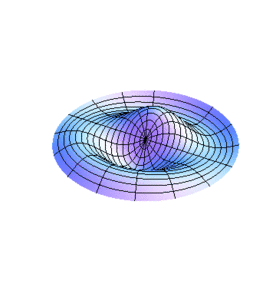
En la figura 1 se muestra la vibración de una membrana circular cuando se tienen la raíz $u_{02}$ de la función Bessel de orden 0. La figura 2 corresponde al caso de tener la raíz $u_{03}$ de esta función.

Figura 1. Modo normal de vibración con $n=0,l=2$

Figura 2. Modo normal de vibración con $n=0,l=3$

De manera similar pueden analizarse otros casos. No es de extrañar que siendo los límites fijos de las membranas círculos, los modos normales de vibración expresen dicha geometría con círculos concéntricos y líneas diametrales. De hecho, al momento de excitar una de las frecuencias $\omega _{nl}$ en las membranas habrá n diámetros nodales y l-1 círculos nodales en los radios $r=u_{nl}a/u_{np},\ p=1,2,...n-1$, además de la frontera $r=a$. En las figuras 3 y 4 se muestra la vibración de una membrana para el caso $n=1$ teniendo un diámetro nodal en la fig. 3 ($n=1,l=1$) y tanto un diámetro como un círculo nodal en la fig. 4 ($n=1,l=2$).

Figura 3. Modo normal de vibración con $n=1,l=1$

Figura 4. Modo normal de vibración con $n=1,l=2$

---

Aportación de: Alejandro Angel Galvan Garcia 19:29 29 mar 2012 (UTC) y Roberto Verdel Aranda 05:03 28 mar 2012 (UTC)

---