Diferencia entre revisiones de «Ondas: Atenuacion suave»
Sin resumen de edición |
Sin resumen de edición |
||
| (No se muestran 16 ediciones intermedias de 2 usuarios) | |||
| Línea 1: | Línea 1: | ||
La palabra atenuación se refiere al decaimiento de la amplitud y de la energía en un movimiento oscilatorio, debido a la existencia de fuerzas de amortiguación que afectan al movimiento. Nuestro propósito principal es el estudio de este fenómeno en una onda que se propaga a través de un medio, sin embargo comenzaremos con el análisis de lo que ocurre en el caso de un movimiento oscilatorio sin propagación, tomando como ejemplo más sencillo el de un oscilador armónico. Esto lo haremos con la intención de facilitar la comprensión de la atenuación en ondas viajeras, además de para observar las semejanzas y diferencias que existen en ambos casos de movimiento (sin y con propagación). | La palabra '''atenuación''' se refiere al decaimiento de la amplitud y de la energía en un movimiento oscilatorio, debido a la existencia de fuerzas de amortiguación que afectan al movimiento. Nuestro propósito principal es el estudio de este fenómeno en una onda que se propaga a través de un medio, sin embargo comenzaremos con el análisis de lo que ocurre en el caso de un movimiento oscilatorio sin propagación, tomando como ejemplo más sencillo el de un [http://es.wikipedia.org/wiki/Oscilador_arm%C3%B3nico oscilador armónico]. Esto lo haremos con la intención de facilitar la comprensión de la atenuación en ondas viajeras, además de para observar las semejanzas y diferencias que existen en ambos casos de movimiento (sin y con propagación). | ||
Además, como se verá más adelante, las características del movimiento oscilatorio varían de forma considerable dependiendo el grado de atenuación en el sistema. Nosotros estudiaremos el caso que se conoce como '''atenuación suave'''. | |||
== Atenuación (sin propagación) == | == Atenuación (sin propagación) == | ||
Supongamos que en un oscilador armónico no actúan fuerzas de fricción. Si esta suposición fuese cierta, un péndulo o un peso suspendido en un resorte oscilarían indefinidamente. En realidad, la amplitud de la oscilación disminuye poco a poco hasta cero como resultado de la fricción. En este caso se dice que el movimiento está amortiguado y se le conoce como '''movimiento armónico amortiguado'''. | Supongamos que en un oscilador armónico no actúan fuerzas de fricción. Si esta suposición fuese cierta, un péndulo o un peso suspendido en un resorte oscilarían indefinidamente. En realidad, la amplitud de la oscilación disminuye poco a poco hasta cero como resultado de la fricción y otras fuerzas amortiguadoras. En este caso se dice que el movimiento está amortiguado y se le conoce como '''movimiento armónico amortiguado'''. | ||
Para describir cómo las fuerzas que actúan sobre el oscilador afectan la vibración, tomemos un sistema de resorte-masa con una fuerza de amortiguación o atenuación debida a que la masa se mueve dentro de un cilindro lubricado ('''Figura 1'''). | |||
[[Imagen:Resorte-masa.jpg|thumb|300px|Figura 1|center]] | |||
[[Imagen:Resorte-masa.jpg|thumb|300px| | |||
En este sistema, asumimos que la masa experimenta una fuerza de fricción o de amortiguación <math>F_a\,\!</math> opuesta siempre al movimiento, y cuya magnitud es proporcional a la velocidad instantánea. Entonces se tiene: | En este sistema, asumimos que la masa experimenta una fuerza de fricción o de amortiguación <math>F_a\,\!</math> opuesta siempre al movimiento, y cuya magnitud es proporcional a la velocidad instantánea. Entonces se tiene: | ||
<center><math>F_a = - b \left ( \frac{dx}{dt} \right )</math></center> | <center><math>F_a = - b \left ( \frac{dx}{dt} \right )</math></center> | ||
Donde <math>b\,\!</math> es una constante positiva llamada resistencia que puede ser ajustada dependiendo del grado de lubricación del cilindro. Sus unidades son <math>Kgs^{-1}</math>. | |||
Donde <math>b\,\!</math> es una constante llamada resistencia que puede ser ajustada dependiendo del grado de lubricación del cilindro. Sus unidades son <math>Kgs^{-1}</math>. | |||
Escribimos la segunda ley de Newton: | Escribimos la segunda ley de Newton: | ||
<center><math>ma = F\,\!</math></center> | <center><math>ma = F\,\!</math></center> | ||
Pero <math>F\,\!</math> es la suma de la fuerza del resorte <math>\left ( F_R=-k_Rx \right )</math> (Ver [http://es.wikipedia.org/wiki/Ley_de_elasticidad_de_Hooke Ley de Hooke]) y la fuerza de amortiguación. Sustituyendo esto en la segunda ley de Newton tenemos: | |||
Pero <math>F\,\!</math> es la suma de la fuerza del resorte <math>\left ( F_R=-k_Rx \right )</math> y la fuerza de amortiguación. Sustituyendo esto en la segunda ley de Newton tenemos: | |||
<center><math>ma = F_R+F_a\,\!</math></center> | <center><math>ma = F_R+F_a\,\!</math></center> | ||
En términos de derivadas: | En términos de derivadas: | ||
<center><math>m\frac{d^2x}{dt^2} = -k_Rx-b\frac{dx}{dt}\,\!</math></center> | <center><math>m\frac{d^2x}{dt^2} = -k_Rx-b\frac{dx}{dt}\,\!</math></center> | ||
Dividimos entre m y el término de la derecha lo pasamos al lado izquierdo de la ecuación: | Dividimos entre m y el término de la derecha lo pasamos al lado izquierdo de la ecuación: | ||
<center><math>\frac{d^2x}{dt^2} + \gamma\frac{dx}{dt} + \omega_o^2x = 0\,\!</math></center> | <center><math>\frac{d^2x}{dt^2} + \gamma\frac{dx}{dt} + \omega_o^2x = 0\,\!</math></center> | ||
Donde: | Donde: | ||
<math>\gamma \equiv \frac{b}{m}\,\!</math> se le cococe como la anchura o el ancho. | <math>\gamma \equiv \frac{b}{m}\,\!</math> se le cococe como la anchura o el ancho. | ||
<math>\omega_o \equiv \left ( \frac{k_R}{m} \right )^\frac{1}{2}\,\!</math> es la frecuencia angular. | <math>\omega_o \equiv \left ( \frac{k_R}{m} \right )^\frac{1}{2}\,\!</math> es la frecuencia angular. | ||
Esta es una [http://es.wikipedia.org/wiki/Ecuaci%C3%B3n_diferencial_ordinaria#Ecuaciones_diferenciales_ordinarias_de_segundo_orden ecuación diferencial de segundo orden] homogénea de coeficientes constantes. Entonces damos una solución de la forma: | |||
Esta es una ecuación diferencial | |||
<center><math>x = e^{rt}\,\!</math></center> | <center><math>x = e^{rt}\,\!</math></center> | ||
Esto lleva a que la ecuación característica de la ecuación diferencial es: | Esto lleva a que la ecuación característica de la ecuación diferencial es: | ||
<center><math>r^2 + \gamma r + \omega_o^2 = 0\,\!</math></center> | <center><math>r^2 + \gamma r + \omega_o^2 = 0\,\!</math></center> | ||
Entonces: | Entonces: | ||
<center><math>r = - \frac{1}{2} \gamma \pm \left ( \frac{1}{4} \gamma^2 - \omega_o^2 \right )^\frac{1}{2}\,\!</math></center> | <center><math>r = - \frac{1}{2} \gamma \pm \left ( \frac{1}{4} \gamma^2 - \omega_o^2 \right )^\frac{1}{2}\,\!</math></center> | ||
Dependiendo el tamaño relativo de <math>\gamma\,\!</math> y <math>\omega_o\,\!</math>, la expresión entre paréntesis puede ser positiva, negativa ó cero, que tendrá una gran influencia en la naturaleza del movimiento. La siguiente tabla muestra la clasificación de la atenuación dependiendo de la relación entre <math>\omega_o\,\!</math> y <math>\gamma\,\!</math>: | |||
{| border="1" cellpadding="5" cellspacing="0" align="center" | |||
|- | |||
! style="background:red; color:white" |Tipo de Atenuación | |||
! style="background:red; color:white" |Expresión característica | |||
|- | |||
! Suave | |||
| align="center" |<math>\left ( \gamma < 2 \omega_o \right )</math> | |||
|- | |||
! Severa | |||
| align="center" |<math>\left ( \gamma > 2 \omega_o \right )</math> | |||
|- | |||
! Crítica | |||
| align="center" |<math>\left ( \gamma = 2 \omega_o \right )</math> | |||
|} | |||
Nosotros nos enfocaremos al estudio del primer caso. | |||
=== Atenuación suave === | === Atenuación suave === | ||
En la '''atenuación suave ''' se tiene la raíz cuadrada de una cantidad negativa, llevándonos a un exponente complejo. Escribimos: | En la '''atenuación suave ''' se tiene la raíz cuadrada de una cantidad negativa, llevándonos a un exponente complejo. Escribimos: | ||
<center><math>r = -\frac{1}{2} \gamma \pm i \omega_f\,\!</math></center> | <center><math>r = -\frac{1}{2} \gamma \pm i \omega_f\,\!</math></center> | ||
Donde: | Donde: | ||
<center><math>\omega_f \equiv \left ( \omega_o^2 -\frac{1}{4} \gamma^2 \right )^\frac{1}{2}\,\!</math></center> | <center><math>\omega_f \equiv \left ( \omega_o^2 -\frac{1}{4} \gamma^2 \right )^\frac{1}{2}\,\!</math></center> | ||
La solución de la ecuación diferencial es: | |||
<center><math>x(t) = e^{-\frac{1}{2} \gamma t} \left ( C_1 \cos \omega_f t + C_2 \sin \omega_f t \right )\,\!</math></center> | |||
En la cual <math>C_1\,\!</math> y <math>C_2\,\!</math> son constantes. Esta ecuación se puede escribir en forma alternativa de la siguiente manera <ref>Dennis G. Zill. '''Ecuaciones Diferenciales con aplicaciones de modelado'''. (International Thomson editores). pp. 200, pp. 206</ref> : | |||
<center><math>x(t) = Ae^{-\frac{1}{2} \gamma t} \cos \left ( \omega_f t + \phi \right )...(1)</math></center> | <center><math>x(t) = Ae^{-\frac{1}{2} \gamma t} \cos \left ( \omega_f t + \phi \right )...(1)</math></center> | ||
Tenemos dos constantes arbitrarias <math>A\,\!</math> y <math>\phi\,\!</math> que podemos ajustar utilizando las condiciones iniciales del movimiento. Entonces supongamos que se toma la masa que está unida al resorte y se aleja una distancia <math>A_1\,\!</math> respecto a su posición de equilibrio. Además la velocidad inicial, es decir, la velocidad del sistema al momento de soltar la masa es igual a cero. Así tenemos lo siguiente: | Tenemos dos constantes arbitrarias <math>A\,\!</math> y <math>\phi\,\!</math> que podemos ajustar utilizando las condiciones iniciales del movimiento. Entonces supongamos que se toma la masa que está unida al resorte y se aleja una distancia <math>A_1\,\!</math> respecto a su posición de equilibrio. Además la velocidad inicial, es decir, la velocidad del sistema al momento de soltar la masa es igual a cero. Así tenemos lo siguiente: | ||
<center><math>x(0) = A\cos \phi = A_1\,\!</math></center> | <center><math>x(0) = A\cos \phi = A_1\,\!</math></center> | ||
| Línea 100: | Línea 92: | ||
<center><math>x'(0) = - \frac{1}{2}\gamma A \cos \phi - \omega_f A \sin \phi = 0\,\!</math></center> | <center><math>x'(0) = - \frac{1}{2}\gamma A \cos \phi - \omega_f A \sin \phi = 0\,\!</math></center> | ||
Dividendo la segunda ecuación entre la primera: | Dividendo la segunda ecuación entre la primera: | ||
<center><math>\tan \phi = -\frac{\gamma}{2\omega_f}\,\!</math></center> | <center><math>\tan \phi = -\frac{\gamma}{2\omega_f}\,\!</math></center> | ||
Esto lleva a que la amplitud inicial es: | Esto lleva a que la amplitud inicial es: | ||
<center><math>A = A_1 \sec \phi = \left ( \frac{\omega_o}{\omega_f} \right ) A_1</math></center> | <center><math>A = A_1 \sec \phi = \left ( \frac{\omega_o}{\omega_f} \right ) A_1</math></center> | ||
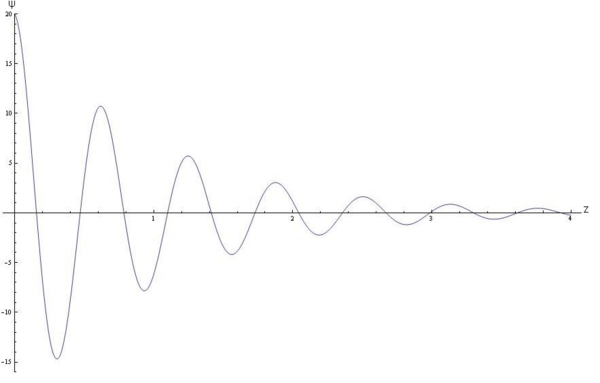
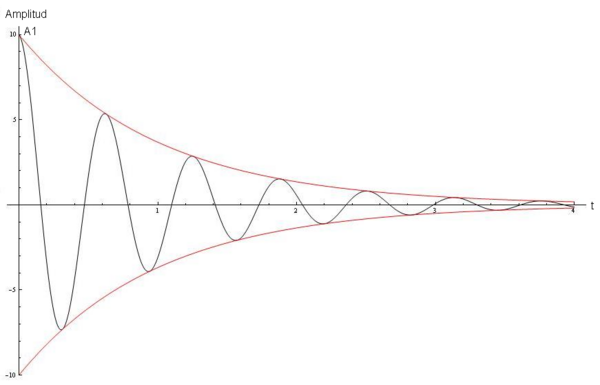
Lo que tenemos aquí es una vibración amortiguada suave o '''atenuación suave ''' ('''Figura 2'''). Cuando existe fricción, la frecuencia es menor y el período mayor en el movimiento. La fricción hace más lento al movimiento. Si no hubiera fricción, <math>b=0\,\!</math>, entonces <math>\gamma=0\,\!</math> y <math>\omega_f=\omega_o\,\!</math>, que es la frecuencia angular del movimiento sin amortiguación. Cuando hay fricción, <math>\omega_f\,\!</math> es menor que <math>\omega_o\,\!</math>. | |||
Lo que tenemos aquí es una vibración amortiguada suave o '''atenuación suave ''' (''' | |||
| Línea 128: | Línea 115: | ||
Particularmente, cuando <math>\gamma \ll \omega_o\,\!</math>, a esta condición de movimiento se le llama '''atenuación muy suave''', donde <math>\omega_f \approx \omega_o\,\!</math>. | Particularmente, cuando <math>\gamma \ll \omega_o\,\!</math>, a esta condición de movimiento se le llama '''atenuación muy suave''', donde <math>\omega_f \approx \omega_o\,\!</math>. | ||
[[Imagen:Onda_osc.PNG|thumb| | [[Imagen:Onda_osc.PNG|thumb|600px|center|Figura 2. Sistema con atenuación suave. La masa unida al resorte es llevada a una posición inicial <math>A1</math> respecto a su posición de equilibrio y es soltada con una velocidad inicial igual a cero. Las gráficas rojas remarcan el decaimiento exponencial de las oscilaciones del sistema.]] | ||
=== Energía en el movimiento amortiguado === | === Energía en el movimiento amortiguado === | ||
Como la fuerza de fricción o amortiguación siempre se opone al movimiento, continuamente remueve energía del sistema, por lo que la energía ya no es constante como ocurre en el oscilador armónico sin fricción. | Como la fuerza de fricción o amortiguación siempre se opone al movimiento, continuamente remueve energía del sistema, por lo que la energía ya no es constante como ocurre en el oscilador armónico sin fricción. | ||
La energía total del sistema es la suma de la energía cinética del sistema y la energía potencial del resorte: | La energía total del sistema es la suma de la energía cinética del sistema y la energía potencial del resorte: | ||
<center><math>E = K + U = \frac{1}{2}m\left ( \frac{dx}{dt} \right )^2 + \frac{1}{2}kx^2...(2)\,\!</math></center> | <center><math>E = K + U = \frac{1}{2}m\left ( \frac{dx}{dt} \right )^2 + \frac{1}{2}kx^2...(2)\,\!</math></center> | ||
Para observar cómo varía la energía con el tiempo derivamos la ecuación anterior respecto al tiempo y utilizamos la regla de la cadena: | Para observar cómo varía la energía con el tiempo derivamos la ecuación anterior respecto al tiempo y utilizamos la regla de la cadena: | ||
<center><math>\frac{dE}{dt} = \frac{dE}{dv} \cdot \frac{dv}{dt} + \frac{dE}{dx} \cdot \frac{dx}{dt} = \left ( m \frac{d^2x}{dt^2} + kx \right ) \frac{dx}{dt}\,\!</math></center> | <center><math>\frac{dE}{dt} = \frac{dE}{dv} \cdot \frac{dv}{dt} + \frac{dE}{dx} \cdot \frac{dx}{dt} = \left ( m \frac{d^2x}{dt^2} + kx \right ) \frac{dx}{dt}\,\!</math></center> | ||
Así, encontramos de la segunda ley de Newton: | Así, encontramos de la segunda ley de Newton: | ||
<center><math>\frac{dE}{dt} = - b \left ( \frac{dx}{dt} \right )^2...(3)\,\!</math></center> | <center><math>\frac{dE}{dt} = - b \left ( \frac{dx}{dt} \right )^2...(3)\,\!</math></center> | ||
La energía disminuye conforme pasa el tiempo, lo cual es porque las vibraciones van disminuyendo gradualmente, a diferencia de un movimiento oscilatorio sin atenuación, en el que [[Usuario: Eduardo Nava |la energía se conserva]]. | |||
La energía disminuye conforme pasa el tiempo, lo cual es porque las vibraciones van disminuyendo gradualmente | |||
La ecuación '''(3)''' es válida para cualquier tipo de atenuación: suave, severa o crítica. | La ecuación '''(3)''' es válida para cualquier tipo de atenuación: suave, severa o crítica. | ||
Una fórmula explícita para <math>E\,\!</math> bajo las condiciones de atenuación resulta de sustituir '''(1)''' en '''(2)''': | Una fórmula explícita para <math>E\,\!</math> bajo las condiciones de atenuación resulta de sustituir '''(1)''' en '''(2)''': | ||
<center><math>E = \frac{1}{2} mA^2e^{-\gamma t} \left \{ \omega_o^2 + \frac{1}{2} \gamma \omega_f \sin \left [2 \left (\omega_f t + \phi \right ) \right ] + \frac{1}{4} \gamma^2 \cos \left [2 \left ( \omega_f t + \phi \right ) \right ] \right \}\,\!</math></center> | <center><math>E = \frac{1}{2} mA^2e^{-\gamma t} \left \{ \omega_o^2 + \frac{1}{2} \gamma \omega_f \sin \left [2 \left (\omega_f t + \phi \right ) \right ] + \frac{1}{4} \gamma^2 \cos \left [2 \left ( \omega_f t + \phi \right ) \right ] \right \}\,\!</math></center> | ||
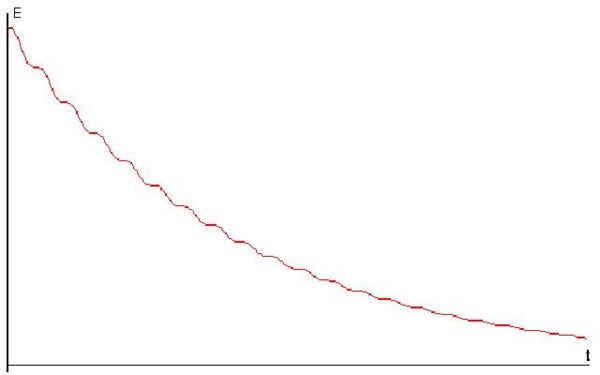
El segundo y el tercer término de la derecha en la ecuación anterior describen pequeñas oscilaciones de <math>E\,\!</math> dentro de cada ciclo, como se observa en la '''Figura 3''', pero no contribuyen casi nada para un promedio de varios ciclos completos. Entonces podemos escribir a la energía promedio: | |||
El segundo y el tercer término de la derecha en la ecuación anterior describen pequeñas oscilaciones de <math>E\,\!</math> dentro de cada ciclo, como se observa en la ''' | |||
<center><math>\left \langle E \right \rangle \approx \frac{1}{2} m \omega_o^2 A^2 e^{- \gamma t}\,\!</math></center> | <center><math>\left \langle E \right \rangle \approx \frac{1}{2} m \omega_o^2 A^2 e^{- \gamma t}\,\!</math></center> | ||
Donde <math>\left \langle E \right \rangle\,\!</math> cae un factor <math>e^{-1}\,\!</math> cuando el tiempo se incrementa <math>1/\gamma\,\!</math>. | Donde <math>\left \langle E \right \rangle\,\!</math> cae un factor <math>e^{-1}\,\!</math> cuando el tiempo se incrementa <math>1/\gamma\,\!</math>. | ||
[[Imagen:Energia_con_amortiguacion.jpg|thumb| | [[Imagen:Energia_con_amortiguacion.jpg|thumb|600px|center|Figura 3. Energía del sistema amortiguado en función del tiempo.]] | ||
Un parámetro equivalente para describir la ligereza o suavidad de una amortiguación es el '''factor-Q''' o factor de calidad, dado por: | Un parámetro equivalente para describir la ligereza o suavidad de una amortiguación es el '''factor-Q''' o factor de calidad, dado por: | ||
<center><math>Q \equiv \frac{\omega_o}{\gamma}\,\!</math></center> | <center><math>Q \equiv \frac{\omega_o}{\gamma}\,\!</math></center> | ||
Un sistema con '''atenuación suave ''' tiene <math>Q>1/2\,\!</math>, y un sistema con '''atenuación muy suave ''' tiene <math>Q \approx \omega_f / \gamma \gg 1</math>. | Un sistema con '''atenuación suave ''' tiene <math>Q>1/2\,\!</math>, y un sistema con '''atenuación muy suave ''' tiene <math>Q \approx \omega_f / \gamma \gg 1</math>. | ||
Un sistema con '''atenuación suave ''' completa muchos ciclos antes de que la amplitud caiga un factor <math>e^{-1}\,\!</math>. El '''factor-Q''' también es la medida de este número de ciclos (n) <ref>F. G. Smith, J. H. Thomson. '''Optics'''. (Ed. Wiley, 1971). pp. 26</ref>, por lo que el '''factor-Q''' también puede ser definido como: | |||
Un sistema con '''atenuación suave ''' completa muchos ciclos antes de que la amplitud caiga un factor <math>e^{-1}\,\!</math>. El '''factor-Q''' también es la medida de este número de ciclos (n), por lo que el '''factor-Q''' también puede ser definido como: | |||
<center><math>Q = \pi n\,\!</math></center> | <center><math>Q = \pi n\,\!</math></center> | ||
== Atenuación en ondas viajeras == | == Atenuación en ondas viajeras == | ||
La mayoría de los sistemas de ondas reales son afectados por fuerzas de atenuación las cuales causan que una onda viajera pierda su energía mientras se propaga a través del medio. Entonces aparece una nueva fuerza de atenuación <math>-\beta \left ( \partial \psi / \partial | La mayoría de los sistemas de ondas reales son afectados por fuerzas de atenuación las cuales causan que una onda viajera pierda su energía mientras se propaga a través del medio. Entonces aparece una nueva fuerza de atenuación <math>-\beta \left ( \partial \psi / \partial z \right ) \Delta z\,\!</math> actuando sobre un segmento de longitud <math>\Delta z\,\!</math>, <math>\beta\,\!</math> es la resistencia por unidad de longitud. Esta fuerza agrega un nuevo término en la [[Ondas: ecuación de onda|ecuación de onda]], que ahora se lee: | ||
<center><math>\frac{\partial^2 \psi}{\partial t^2} = v^2 \left ( \frac{\partial^2 \psi}{\partial z^2} \right ) - \frac{\beta}{\mu} \left ( \frac{\partial \psi}{\partial z} \right )\,\!</math></center> | |||
Donde <math>\mu\,\!</math> es la masa por unidad de longitud <ref>Iain G. Main. '''Vibrations and Waves in Physics'''. (Cambridge University Press). Cap. 9, pp. 141-142</ref>. Esta ecuación se puede expresar como: | |||
<center><math>\frac{\partial^2 \psi}{\partial t^2} + \Gamma \left ( \frac{\partial \psi}{\partial z} \right ) = v^2 \left ( \frac{\partial^2 \psi}{\partial z^2} \right ) </math></center> | |||
Con <math>\Gamma \equiv \beta / \mu \,\!</math>. | Con <math>\Gamma \equiv \beta / \mu \,\!</math>. | ||
Esta ecuación se satisface con la siguiente solución: | Esta ecuación se satisface con la siguiente solución: | ||
<center><math>\psi = A \cos \left ( \omega t - kz + \phi \right )\,\!</math></center> | <center><math>\psi = A \cos \left ( \omega t - kz + \phi \right )\,\!</math></center> | ||
También se puede escribir así <ref>Iain G. Main. '''Vibrations and Waves in Physics'''. (Cambridge University Press). pp. 10-14, pp. 143</ref>: | |||
También se puede escribir | |||
<center><math>\psi = Re \left \{ D \exp \left [ i \left ( \omega t - kz \right ) \right ] \right \}</math></center> | <center><math>\psi = Re \left \{ D \exp \left [ i \left ( \omega t - kz \right ) \right ] \right \}</math></center> | ||
Donde <math>D = A e^{i \phi}\,\!</math> | Donde <math>D = A e^{i \phi}\,\!</math> | ||
| Línea 226: | Línea 183: | ||
Para que sea cierto que esta ecuación es solución de la ecuación de onda, la nueva relación entre la frecuencia angular <math>\omega\,\!</math> y el [[Número de onda|número de onda]] <math>k\,\!</math> debido a la atenuación es: | |||
<center><math>\omega^2 - i \Gamma \omega = v^2 k^2...(4)\,\!</math></center> | <center><math>\omega^2 - i \Gamma \omega = v^2 k^2...(4)\,\!</math></center> | ||
Como <math>\omega\,\!</math> y <math>\Gamma\,\!</math> son reales, <math>k\,\!</math> debe ser complejo, que se puede reescribir como: | Como <math>\omega\,\!</math> y <math>\Gamma\,\!</math> son reales, <math>k\,\!</math> debe ser complejo, que se puede reescribir como: | ||
<center><math>k = K -i \kappa ...(5)\,\!</math></center> | <center><math>k = K -i \kappa ...(5)\,\!</math></center> | ||
Donde <math>K\,\!</math> y <math>\kappa\,\!</math> son reales. Entonces una onda viajera senoidal es descrita por la ecuación: | Donde <math>K\,\!</math> y <math>\kappa\,\!</math> son reales. Entonces una onda viajera senoidal es descrita por la ecuación: | ||
<center><math>\psi = Re \left \{ D \exp \left [ i \left ( \omega t - Kz + i \kappa z \right ) \right] \right \} = \exp \left ( - \kappa z \right ) Re \left \{ D \exp \left [ i \left ( \omega t - Kz \right ) \right ] \right \} ...(6)\,\!</math></center> | <center><math>\psi = Re \left \{ D \exp \left [ i \left ( \omega t - Kz + i \kappa z \right ) \right] \right \} = \exp \left ( - \kappa z \right ) Re \left \{ D \exp \left [ i \left ( \omega t - Kz \right ) \right ] \right \} ...(6)\,\!</math></center> | ||
Que es la ecuación de una onda viajera con atenuación. | Que es la ecuación de una onda viajera con atenuación. | ||
La onda dada por '''(6)''' difiere de una onda viajera sin atenuación por un factor <math>e^{-\kappa z}\,\!</math>. Cada punto vibra armónicamente, y puntos separados por una distancia <math>2\pi v/ \gamma\,\!</math> vibran en fase entre sí, sin embargo estos puntos que se encuentran en fase no tienen la misma amplitud. | |||
La onda dada por '''(6)''' difiere de una onda viajera | |||
En este caso la amplitud decae exponencialmente a lo largo de la vibración por un factor <math>e^{-1}\,\!</math> cuando recorre una distancia <math>2v/ \Gamma\,\!</math>. | En este caso la amplitud decae exponencialmente a lo largo de la vibración por un factor <math>e^{-1}\,\!</math> cuando recorre una distancia <math>2v/ \Gamma\,\!</math>. | ||
Observemos que el decrecimiento exponencial de la amplitud de la onda viajera en función de la distancia que recorre es similar al decrecimiento exponencial de la amplitud en una vibración amortiguada en función del tiempo. | Observemos que el decrecimiento exponencial de la amplitud de la onda viajera en función de la distancia que recorre es similar al decrecimiento exponencial de la amplitud en una vibración amortiguada en función del tiempo. | ||
Reescribiendo '''(4)''' tenemos: | Reescribiendo '''(4)''' tenemos: | ||
<center><math>\omega^2 \left ( 1 - i \frac{\Gamma}{\omega} \right ) = v^2 k^2\,\!</math></center> | <center><math>\omega^2 \left ( 1 - i \frac{\Gamma}{\omega} \right ) = v^2 k^2\,\!</math></center> | ||
El factor <math>\Gamma / \omega\,\!</math> mide el grado de atenuación en una onda de la misma manera que <math>\gamma / \omega_o\,\!</math> lo hace para el oscilador amortiguado. | El factor <math>\Gamma / \omega\,\!</math> mide el grado de atenuación en una onda de la misma manera que <math>\gamma / \omega_o\,\!</math> lo hace para el oscilador amortiguado. | ||
Cuando <math>\Gamma / \omega \ll 1\,\!</math>, es decir, cuando <math>\Gamma\,\!</math> es mucho menor que <math>\omega\,\!</math> tenemos una atenuación muy suave: | Cuando <math>\Gamma / \omega \ll 1\,\!</math>, es decir, cuando <math>\Gamma\,\!</math> es mucho menor que <math>\omega\,\!</math> tenemos una atenuación muy suave: | ||
| Línea 272: | Línea 216: | ||
<center><math>\omega \left ( 1 - i \frac{\Gamma}{2 \omega} \right ) \approx \pm v \left ( K - i \kappa \right )\,\!</math></center> | <center><math>\omega \left ( 1 - i \frac{\Gamma}{2 \omega} \right ) \approx \pm v \left ( K - i \kappa \right )\,\!</math></center> | ||
Separando las partes real e imaginaria: | Separando las partes real e imaginaria: | ||
<center><math>K \approx \pm \frac{\omega}{v}\,\!</math></center> | <center><math>K \approx \pm \frac{\omega}{v}\,\!</math></center> | ||
| Línea 282: | Línea 224: | ||
<center><math>\kappa \approx \frac{\Gamma}{2v}\,\!</math></center> | <center><math>\kappa \approx \frac{\Gamma}{2v}\,\!</math></center> | ||
[[Imagen:Onda_ate.PNG|thumb| | |||
[[Imagen:Onda_ate.PNG|thumb|600px|center|Figura 4. Propagación de una onda viajera con atenuación en función de la distancia que recorre.]] | |||
== Referencias == | |||
<references/> | |||
== Bibliografía == | == Bibliografía == | ||
*Iain G. Main. '''Vibrations and Waves in Physics'''. 3a edición. Cambridge University Press. | |||
*F. G. Smith, J. H. Thomson. '''Optics'''. Ed. Wiley. 1971. | |||
*Robert Resnick, David Halliday. '''Física. Parte 1'''. Ed. C.E.C.S.A. 1982 | |||
*Dennis G. Zill. '''Ecuaciones diferenciales con aplicaciones de modelado'''. 6a edición. International Thomson editores. | |||
---- | |||
Aportación de: Rojas Calderón Rafael Alejandro--[[Usuario:Kanon1106|Kanon1106]] 22:35 4 abr 2009 (CDT) | |||
---- | |||
[[Categoría: Ondas]] | [[Categoría: Ondas]] | ||
Revisión actual - 17:44 22 may 2023
La palabra atenuación se refiere al decaimiento de la amplitud y de la energía en un movimiento oscilatorio, debido a la existencia de fuerzas de amortiguación que afectan al movimiento. Nuestro propósito principal es el estudio de este fenómeno en una onda que se propaga a través de un medio, sin embargo comenzaremos con el análisis de lo que ocurre en el caso de un movimiento oscilatorio sin propagación, tomando como ejemplo más sencillo el de un oscilador armónico. Esto lo haremos con la intención de facilitar la comprensión de la atenuación en ondas viajeras, además de para observar las semejanzas y diferencias que existen en ambos casos de movimiento (sin y con propagación).
Además, como se verá más adelante, las características del movimiento oscilatorio varían de forma considerable dependiendo el grado de atenuación en el sistema. Nosotros estudiaremos el caso que se conoce como atenuación suave.
Atenuación (sin propagación)
Supongamos que en un oscilador armónico no actúan fuerzas de fricción. Si esta suposición fuese cierta, un péndulo o un peso suspendido en un resorte oscilarían indefinidamente. En realidad, la amplitud de la oscilación disminuye poco a poco hasta cero como resultado de la fricción y otras fuerzas amortiguadoras. En este caso se dice que el movimiento está amortiguado y se le conoce como movimiento armónico amortiguado.
Para describir cómo las fuerzas que actúan sobre el oscilador afectan la vibración, tomemos un sistema de resorte-masa con una fuerza de amortiguación o atenuación debida a que la masa se mueve dentro de un cilindro lubricado (Figura 1).
En este sistema, asumimos que la masa experimenta una fuerza de fricción o de amortiguación opuesta siempre al movimiento, y cuya magnitud es proporcional a la velocidad instantánea. Entonces se tiene:
Donde es una constante positiva llamada resistencia que puede ser ajustada dependiendo del grado de lubricación del cilindro. Sus unidades son .
Escribimos la segunda ley de Newton:
Pero es la suma de la fuerza del resorte (Ver Ley de Hooke) y la fuerza de amortiguación. Sustituyendo esto en la segunda ley de Newton tenemos:
En términos de derivadas:
Dividimos entre m y el término de la derecha lo pasamos al lado izquierdo de la ecuación:
Donde:
se le cococe como la anchura o el ancho.
es la frecuencia angular.
Esta es una ecuación diferencial de segundo orden homogénea de coeficientes constantes. Entonces damos una solución de la forma:
Esto lleva a que la ecuación característica de la ecuación diferencial es:
Entonces:
Dependiendo el tamaño relativo de y , la expresión entre paréntesis puede ser positiva, negativa ó cero, que tendrá una gran influencia en la naturaleza del movimiento. La siguiente tabla muestra la clasificación de la atenuación dependiendo de la relación entre y :
| Tipo de Atenuación | Expresión característica |
|---|---|
| Suave | |
| Severa | |
| Crítica |
Nosotros nos enfocaremos al estudio del primer caso.
Atenuación suave
En la atenuación suave se tiene la raíz cuadrada de una cantidad negativa, llevándonos a un exponente complejo. Escribimos:
Donde:
La solución de la ecuación diferencial es:
En la cual y son constantes. Esta ecuación se puede escribir en forma alternativa de la siguiente manera [1] :
Tenemos dos constantes arbitrarias y que podemos ajustar utilizando las condiciones iniciales del movimiento. Entonces supongamos que se toma la masa que está unida al resorte y se aleja una distancia respecto a su posición de equilibrio. Además la velocidad inicial, es decir, la velocidad del sistema al momento de soltar la masa es igual a cero. Así tenemos lo siguiente:
Dividendo la segunda ecuación entre la primera:
Esto lleva a que la amplitud inicial es:
Lo que tenemos aquí es una vibración amortiguada suave o atenuación suave (Figura 2). Cuando existe fricción, la frecuencia es menor y el período mayor en el movimiento. La fricción hace más lento al movimiento. Si no hubiera fricción, , entonces y , que es la frecuencia angular del movimiento sin amortiguación. Cuando hay fricción, es menor que .
En la vibración amortiguada, la amplitud decae exponencialmente con el tiempo . Es decir, cae por un factor cuando el tiempo se incrementa por .
Obsérvese que la amplitud del movimiento disminuye gradualmente a cero. El intervalo de tiempo durante el cual la amplitud disminuye una fracción su valor inicial recibe el nombre de tiempo de vida promedio de la oscilación. El factor de amplitud es así que . Si no hubiera fricción,, así y la amplitud tendría un valor constante conforme transcurriese el tiempo, y el tiempo de vida medio sería infinito.
Si la fuerza de fricción es bastante grande, se hace tan grande que la ecuación (1) ya no es solución de la ecuación diferencial del movimiento. Entonces el movimiento no tiene periodicidad. El cuerpo simplemente regresa a su posición de equilibrio al soltarlo desde su punto inicial.
Particularmente, cuando , a esta condición de movimiento se le llama atenuación muy suave, donde .
Energía en el movimiento amortiguado
Como la fuerza de fricción o amortiguación siempre se opone al movimiento, continuamente remueve energía del sistema, por lo que la energía ya no es constante como ocurre en el oscilador armónico sin fricción.
La energía total del sistema es la suma de la energía cinética del sistema y la energía potencial del resorte:
Para observar cómo varía la energía con el tiempo derivamos la ecuación anterior respecto al tiempo y utilizamos la regla de la cadena:
Así, encontramos de la segunda ley de Newton:
La energía disminuye conforme pasa el tiempo, lo cual es porque las vibraciones van disminuyendo gradualmente, a diferencia de un movimiento oscilatorio sin atenuación, en el que la energía se conserva.
La ecuación (3) es válida para cualquier tipo de atenuación: suave, severa o crítica.
Una fórmula explícita para bajo las condiciones de atenuación resulta de sustituir (1) en (2):
El segundo y el tercer término de la derecha en la ecuación anterior describen pequeñas oscilaciones de dentro de cada ciclo, como se observa en la Figura 3, pero no contribuyen casi nada para un promedio de varios ciclos completos. Entonces podemos escribir a la energía promedio:
Donde cae un factor cuando el tiempo se incrementa .
Un parámetro equivalente para describir la ligereza o suavidad de una amortiguación es el factor-Q o factor de calidad, dado por:
Un sistema con atenuación suave tiene , y un sistema con atenuación muy suave tiene .
Un sistema con atenuación suave completa muchos ciclos antes de que la amplitud caiga un factor . El factor-Q también es la medida de este número de ciclos (n) [2], por lo que el factor-Q también puede ser definido como:
Atenuación en ondas viajeras
La mayoría de los sistemas de ondas reales son afectados por fuerzas de atenuación las cuales causan que una onda viajera pierda su energía mientras se propaga a través del medio. Entonces aparece una nueva fuerza de atenuación actuando sobre un segmento de longitud , es la resistencia por unidad de longitud. Esta fuerza agrega un nuevo término en la ecuación de onda, que ahora se lee:
Donde es la masa por unidad de longitud [3]. Esta ecuación se puede expresar como:
Con .
Esta ecuación se satisface con la siguiente solución:
También se puede escribir así [4]:
Donde
significa que sólo tomaremos la parte real del complejo entre llaves.
Para que sea cierto que esta ecuación es solución de la ecuación de onda, la nueva relación entre la frecuencia angular y el número de onda debido a la atenuación es:
Como y son reales, debe ser complejo, que se puede reescribir como:
Donde y son reales. Entonces una onda viajera senoidal es descrita por la ecuación:
Que es la ecuación de una onda viajera con atenuación.
La onda dada por (6) difiere de una onda viajera sin atenuación por un factor . Cada punto vibra armónicamente, y puntos separados por una distancia vibran en fase entre sí, sin embargo estos puntos que se encuentran en fase no tienen la misma amplitud.
En este caso la amplitud decae exponencialmente a lo largo de la vibración por un factor cuando recorre una distancia .
Observemos que el decrecimiento exponencial de la amplitud de la onda viajera en función de la distancia que recorre es similar al decrecimiento exponencial de la amplitud en una vibración amortiguada en función del tiempo.
Reescribiendo (4) tenemos:
El factor mide el grado de atenuación en una onda de la misma manera que lo hace para el oscilador amortiguado.
Cuando , es decir, cuando es mucho menor que tenemos una atenuación muy suave:
Separando las partes real e imaginaria:
Referencias
- ↑ Dennis G. Zill. Ecuaciones Diferenciales con aplicaciones de modelado. (International Thomson editores). pp. 200, pp. 206
- ↑ F. G. Smith, J. H. Thomson. Optics. (Ed. Wiley, 1971). pp. 26
- ↑ Iain G. Main. Vibrations and Waves in Physics. (Cambridge University Press). Cap. 9, pp. 141-142
- ↑ Iain G. Main. Vibrations and Waves in Physics. (Cambridge University Press). pp. 10-14, pp. 143
Bibliografía
- Iain G. Main. Vibrations and Waves in Physics. 3a edición. Cambridge University Press.
- F. G. Smith, J. H. Thomson. Optics. Ed. Wiley. 1971.
- Robert Resnick, David Halliday. Física. Parte 1. Ed. C.E.C.S.A. 1982
- Dennis G. Zill. Ecuaciones diferenciales con aplicaciones de modelado. 6a edición. International Thomson editores.
Aportación de: Rojas Calderón Rafael Alejandro--Kanon1106 22:35 4 abr 2009 (CDT)




















































![E = \frac{1}{2} mA^2e^{-\gamma t} \left \{ \omega_o^2 + \frac{1}{2} \gamma \omega_f \sin \left [2 \left (\omega_f t + \phi \right ) \right ] + \frac{1}{4} \gamma^2 \cos \left [2 \left ( \omega_f t + \phi \right ) \right ] \right \}\,\!](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/98686a033f1b3ad6bb9818e2f76cfa7d94245bc2)















![\psi = Re \left \{ D \exp \left [ i \left ( \omega t - kz \right ) \right ] \right \}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0b6436c5a3d7e6ee043dd25ed56ea6f86cabc4d0)









![\psi = Re \left \{ D \exp \left [ i \left ( \omega t - Kz + i \kappa z \right ) \right] \right \} = \exp \left ( - \kappa z \right ) Re \left \{ D \exp \left [ i \left ( \omega t - Kz \right ) \right ] \right \} ...(6)\,\!](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/37acb8094fe1cc8df848717994c0fbef71d415c8)