Usuario:Eduardo Nava
Introducción
En esta pagina se discutirán dos distintos análisis que nos conducen a la conservación de la energía en una onda. En el primer análisis, se ocuparán conceptos de mecánica clásica; mientras que en el segundo, se ocuparán conceptos puramente matemáticos.
Para introducir el concepto de energía en una onda, en la sección 3.1, se discutirá el caso de la energía cinética y potencial de una masa acoplada a un resorte. Posteriormente, en la sección 3.2, se deducirá la energía cinética y potencial en cualquier punto de una cuerda que se encuentre en movimiento ondulatorio, esto se hará ocupando conocimientos de mecánica clásica. Al final, en la sección 4, ocupando la ecuación de continuidad, se deducirá la energía cinética y potencial.
Energía
El concepto de energía en sus variadas formas ocupa una posición clave en la teoría física. Dicha importancia es primordialmente por el hecho de que la energía se conserva de una u otra forma, se presume que la energía contenida del universo es constante. [1]
La energía puede cambiar de forma fácilmente, como por ejemplo; movimiento en el espacio, se hace irreversible perdiéndose en el entorno en forma de calor, etc.
Derivación de energía cinética y potencial
Derivación de energía cinética y potencial de una masa acoplada a un resorte
En un tiempo dado, las partículas de un medio que transporta una onda están en diversos estados de movimiento. Evidentemente, el medio está dotado de una energía en su estado de reposo natural, es decir, existen contribuciones de energía potencial de la deformación y energía cinética del movimiento. De esta manera, asi como en los sistemas mecánicos se presentan dos tipos de energías[2].
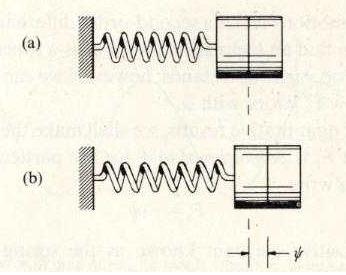
En esta sección se analizará el movimiento de una masa acoplada a un resorte.
Cuando la masa se mueve con rapidez (ver Figura 1) en cualquier dirección, su energía cinética es:
Cuando el resorte es extendido o comprimido por una distancia , almacena energía potencial:
Donde "s" es el coeficiente de elasticidad del resorte.
Por tanto la energía total es:
Recordando que la energía total es constante durante la vibración, pues las fuerzas de disipación como la fricción y viscosidad no son tomadas en cuenta. Por tanto:
Usando la ecuación (3) se obtiene que:
La ecuación (4) es la ecuación del movimiento armónico.
Para descubrir como varia la energía cinética y la energía potencial con respecto al tiempo, se usa la ecuación para un movimiento armónico:
Derivando (5)
Donde
Sustituyendo (5) en (2) y (6) en (1) respectivamente, se llega a
Por tanto la ecuación (3) se reescribe como
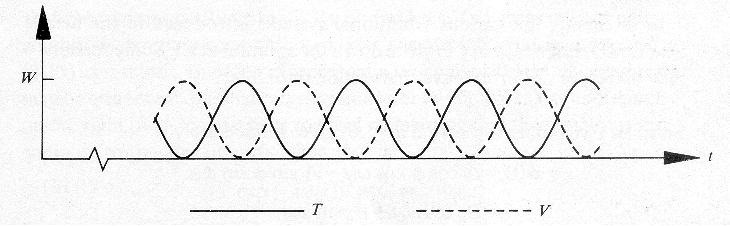
Para una masa y resorte dado, la energía total es proporcional al cuadrado de su amplitud, pero no depende de una fase constante.
Cuando el resorte está extendido o comprimido en su máxima distancia la masa llega momentáneamente al reposo y la energía cinética desaparece. En ese momento toda la energía del sistema se almacena en el resorte como energía potencial. Cuando la masa pasa por tiene un máximo y contiene el total de energía del sistema. En otros puntos del ciclo, hay una variable mezclada de energía potencia y cinética, pero la suma de dichas energías nunca cambia, así pues, en este sistema se presenta una continua transferencia de energía de la masa hacia el resorte y viceversa. (Figura 2)
Propagación de energía en una cuerda con movimiento ondulatorio
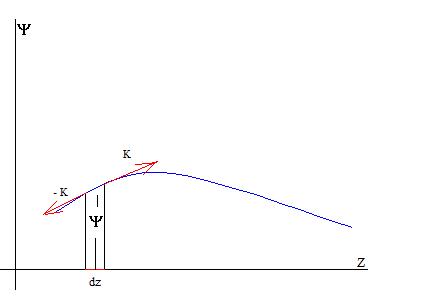
Un segmento de una cuerda elástica puede almacenar tanto energía cinética como energía potencial[3] . Para poder entender mejor este problema, se alaniza un pequeño segmento de cuerda, tan pequeño que se considera como recto como recto, que está comprendido entre z y z+dz, como se muestra en la figura 3.
Se supondrán cierto que los desplazamientos de las partículas de la cuerda son estrictamente transversales y que el valor de la tensión "K" no varía por la deformación de la cuerda.
La masa del segmento pequeño es y su velocidad transversal . De esta manera:
De esta forma se definirá la energía cinética por unidad de longitud, que se denomina densidad de energía cinética, para dicho segmento:
La densidad de energía potencial en un punto depende del desplazamiento . La energía potencial puede calcularse hallando el incremento de longitud de la cuerda cuando se deforma. Este alargamiento, multiplicado por la tensión constante "K", es igual al trabajo realizado en la deformación. Es decir
Por el teorema Trabajo-Energía se tiene que
como
Por tanto
De esta forma:
en donde
Dada la hipótesis de desplazamientos pequeños , la ecuación anterior se puede aproximar utilizando el desarrollo del binomio, obteniéndose:
por tanto
De esta manera la densidad de energía potencial quedaría
Como cualquier movimiento de la cuerda satisface la ecuación , por tanto , y utilizando las ecuaciones (7) y (8) se tiene que la energía total es:
Esta expresión se utiliza para cualquier perturbación, pero si la ecuación de onda viajera es también satisfecha, los dos términos de la derecha de la ecuación (9) podrán ser iguales en cualquier lugar, y se pueda decir que la energía cinética y potencial son iguales en todo punto sobre una cuerda llevada por una onda viajera.
Flujo de energía
Ahora se desea calcular la velocidad con que la energía pasa por un punto z de la cuerda, de izquierda a derecha. Se sabe que la cuerda del lado derecho experimenta una fuerza externa debido a la cuerda de la izquierda, dicha fuerza es aproximadamente igual a [4]. Esta fuerza pudría ejercer trabajo si el punto z se mueve fuera de : esto es, si es positivo en ese instante. La velocidad con la que trabaja es
Esta es la potencia derivada de izquierda a derecha que paso por el punto z.
La ecuación (10) es nuevamente una ecuación es bastante general. Al aplicar esta ecuación a una onda viajera, se obtiene que
Hay que recordar que como en este caso se trata de una onda viajera, los terminos de la derecha son iguales, por tanto la ecuación (11) se puede rescribir como
La potencia P es positiva para la onda viajera de la derecha y negativa para la onda viajera de la izquierda, por tanto la energía viaja en la misma dirección de la onda.
Explicación geométrica
Para explicará mejor lo que sucede con la energía se explicara de forma geométrica, para esto, se ocupará la ecuación de onda viajera siguiente
Con esta ecuación se puede llegar a que la densidad de energía total es
En la figura 4 se observa la distribución de la energía total a lo largo de una cuerda. Los máximos de la densidad de energía ocurren cuando los puntos de la cuerda estan en el desplazamiento igual a cero. Como lo sugiere la ecuación (12), la energía se mueve con el perfil de onda cuando se mueve a través de la cuerda de izquierda a derecha.
Ecuación identidad de energía
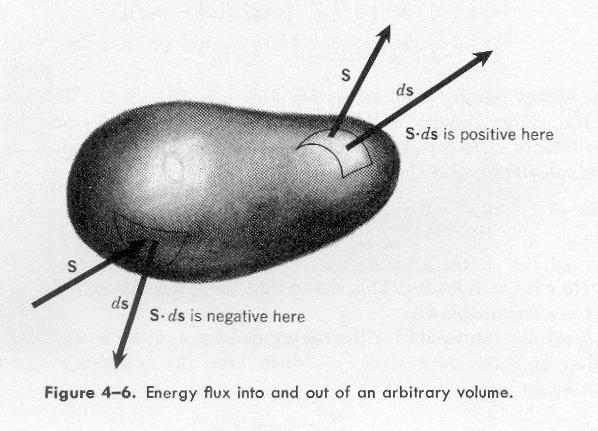
Para poder discutir sobre la energía de una onda, es necesario definir una cantidad asociada con la onda que tenga las dimesiones de energía, y que dicha cantidad se conserve [5]. La ley de conservación de energía implica que en ausencia de fuentes o sumideros en una región finita del espacio, la cantidad de energía acumulada o disipada debe de ser calculada considerando la cantidad de energía que entra y sale a través de la frontera de dicha región.
Matemáticamente, este balance de energía, o conservación, está expresada en términos de una relación llamada ecuación de continuidad. Esta ecuación, es una ecuación relativa a la conservación de una magnitud que caracteriza a un objeto (masa, carga eléctrica, energía, etc) y su correspondiente densidad.
La expresión de la ecuación de continuidad es la siguiente:
El primer término es la variación temporal de la densidad, representada por la derivada parcial de con respecto al tiempo. El segundo término es la divergencia de la densidad de corriente, que nos da el balance de flujo que entra o que sale del volumen que consideramos.
En conjunto, nos está diciendo que la variación de la densidad con el tiempo es igual al balance entre la incorporación y el abandono de masa (o carga eléctrica, etc) del sistema por el hecho de llevar una determinada velocidad. Físicamente la ecuación de continuidad nos habla de la conservación de la magnitud asociada a la densidad (masa por unidad de volumen, carga por unidad de volumen, etc). Si un sistema no tiene ni pérdidas ni ganancias de materia, la densidad del mismo será constante.
En nuestro caso, para demostrar la conservación de la energía en una onda, debemos definir una densidad de energía y una cantidad de flujo ,que satisfaga la misma condición de la ecuación de continuidad. Dichas cantidades pueden ser obtenidas analizando el modelo de una onda propagándose a traves de un medio particular. Para esto se ocupa la ecuación de onda:
Al multiplicar la ecuación de onda por un factor , se obtiene que
Sin embargo,
y además
.
De manera que el primer término de la ecuación diferencial puede escribirse como
Por otro lado el segundo término que involucra segundas derivadas temporales puede reescribirse como
Sustituyendo (14) y (15) en (13), se llega a
Si se reagrupan las derivadas temporales y espaciales, se obtiene que
Al comparar la ecuación (12) y (16) se llega a la conclusión que la ecuación (16) es una ecuación de continuidad,por tanto, se pueden definir una densidad
y un flujo
Así, y no tienen dimensiones de energía por unidad de longitud o flujo de energía, de hecho estas cantidades son adimensionales. Pero estas pueden convertirse en una densidad de energía y en un flujo de energía multiplicando por , donde es la masa por unidad de longitud y la velocidad de la onda. Por tanto, una definición apropiada de densidad de energía y de flujo de energía es
El primer término de la ecuación (17) nos recuerda la energía cinética y el segundo término la energía potencial. De hecho, si se aplicara la ecuación (17) para calcular la densidad de energía de una onda plana , el resultado sería
La ecuación (19) dice que la densidad de energía es una función que oscila con respecto al tiempo. El máximo de la densidad de energía es el mismo que el de la densidad de energía de un oscilador armónico de densidad de masa (la mitad es energía cinética y la otra mitad es potencial).
El cálculo de muestra que
Donde v es la velocidad. Esto muestra que la interpretación de como flujo de energía es razonable.
Se puede encontrar una expresión similar para la densidad de energía y también para el flujo de energía en tres dimensiones, en donde la ecuación de continuidad se escribe
La conservación de energía se expresa integrado la ecuación (20) sobre un volumen V
En el último paso de la ecuación (21) se ocupó el teorema de Gauss con elemento del volumen que rodea a la superficie. La dirección de es a lo largo de la normal de superficie (figura 5).
La derivación de la expresión para la densidad de energía es exactamente igual que antes. Se comienza multiplicando la ecuación de onda por y donde es la masa por unidad de volumen
por tanto
Referencias
- ↑ Crawford Frank S., Waves , Ed. Reverté 1994
- ↑ Main Lain G., Vibrations and Waves in physics, Cambridge University Press 1993
- ↑ French A.P. (Athony Philip), Vibrations and Waves, Reverté 1974
- ↑ Main Lain G., Vibrations and Waves in physics, Cambridge University Press 1993
- ↑ S. Borowitz, Fundamentals of Quantum Mechanics, W.A. Benjamin, NY (1967)
--jaguar bebé 23:07 5 abr 2009 (CDT)





























![ds=dz \left[1+ \left( \frac{\partial \psi}{\partial z} \right) \right]^\frac{1}{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1b44a7a1844d7706b6e0dd6dd93f310440c7bcb7)






![W= \frac{1}{2} \mu \left(\frac{\partial \psi}{\partial t} \right)^2+\frac{1}{2} K \left(\frac{\partial \psi}{\partial z} \right)^2=\frac {Z}{2v}\left[\left( \frac{\partial \psi}{\partial t}\right)^2+ v^2 \left( \frac{\partial \psi}{\partial z} \right)^2 \right] \qquad(9)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b08214db1aef52ae58e54bdc7c162a077db0c8d1)



















![\frac{\partial }{\partial t} {1 \over 2}\left[ {\left(
{\frac{\partial \psi }{\partial z}} \right)^2+\frac{1}{v^2}\dot {\psi }^2}
\right]-\frac{\partial }{\partial z}\left( {\dot {\psi }\frac{\partial \psi
}{\partial z}} \right)=0 \qquad(16)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b50fade243fc4140d989b0e848fe41dec7f4b19a)
![\psi_\rho '= {1 \over
2}\left[ {\left( {\frac{\partial \psi }{\partial z}}
\right)^2+\frac{1}{v^2}\dot {\psi }^2} \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2bc4b846aa29e9aeebf7168d16b1284d8c866882)





![\psi_\rho = {\sigma \over
2}\left[ {\left( {\frac{\partial \psi }{\partial z}}
\right)^2+\frac{1}{v^2}\dot {\psi }^2} \right]\qquad(17)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1974c1075614f2bfdd18dd223e0bfbc67b5597e2)

![\left( A \exp\left[ \mathbf{i} \left( \omega t - kz \right) \right] \right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ba0801a19be0114851e76947dfc5dfe8a786891d)
![\psi_\rho= {\sigma \over 2} \left[ \frac{1}{v^2} \left(- \omega^2 \right) + k^2 \right] A^2 \exp\left[ 2 \mathbf{i} \left( \omega t - kz \right) \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c813c18d8ffdfb91b9a5d80d5b98885243c6bce8)
![\psi_\rho= - \frac{1}{2} \rho v^2 \left( 2 \frac{A^2 \omega^2}{v^2} \right) \exp\left[ 2 \mathbf{i} \left( \omega t - kz \right) \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/395ed2564a199bd53c4fb71033411a7c04354a8e)
![\psi_\rho= - \rho A^2 \omega^2 \exp\left[ 2 \mathbf{i} \left( \omega t - kz \right) \right] \qquad(19)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2f412da003929811123f92eb0a298fe94ec71b18)
![\triangleright \psi_\rho = - \sigma A^2 \omega k \exp\left[ 2 \mathbf{i} \left( \omega t - kz \right) \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/dcc08f66b94ceb36944626e163051f624b13ef42)






![\sigma \left[ \frac{1}{2} \frac{\partial}{\partial t} \left( \frac{\dot{\psi}^2}{v^2} + \left( \nabla \psi \cdot \nabla \psi \right) \right) \right] - \sigma \nabla \cdot \left( \dot{\psi} \nabla \psi \right)=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2d020738bbf392e84fc0b809745502b9de70c021)
![\psi_\rho= \frac{\sigma}{2} \left[ \frac{ \dot{\psi}^2 }{v^2} + \left( \nabla \psi \cdot \nabla \psi \right) \right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8f8d6458f90f600dd9f63bed6a87ebe7ab88bc5b)