Diferencia entre revisiones de «Ondas: 3 dimensiones»
m (→Referencias) |
|||
| Línea 70: | Línea 70: | ||
\end{equation} | \end{equation} | ||
La cual es independiente de $y$ y $z$, y es una onda desplazándose positivamente en $x$. | La cual es independiente de $y$ y $z$, y es una onda desplazándose positivamente en $x$. | ||
Ahora veamos su solución general ya dependiente de las 4 variables, para ello redefinimos las siguientes ecuaciones: | Ahora veamos su solución general ya dependiente de las 4 variables: | ||
\begin{equation} | |||
\psi(\vec{r},t)=Ae^{i(\vec{k}\cdot\vec{r}-wt)};\thinspace con \thinspace \vec{r}=(x,y,z) | |||
\end{equation} | |||
Se puede ver que tiene la misma forma que la ecuación de onda en una dimensión. | |||
Ahora vamos a encontrar $w$ y $k$ y para ello redefinimos las siguientes ecuaciones: | |||
\[ | \[ | ||
| Línea 106: | Línea 113: | ||
w^2=v^2(k_x^2+k_y^2+k_z^2) | w^2=v^2(k_x^2+k_y^2+k_z^2) | ||
\] | \] | ||
\begin{equation} | \begin{equation} | ||
w=v\sqrt{(k_x^2+k_y^2+k_z^2)} | w=v\sqrt{(k_x^2+k_y^2+k_z^2)} | ||
| Línea 115: | Línea 122: | ||
\begin{equation} | \begin{equation} | ||
w=v|\vec{k}| | w=v|\vec{k}| | ||
\end{equation} | \end{equation} | ||
| Línea 128: | Línea 129: | ||
\psi(x,y,z,t)=Ae^{i(k_xx+k_yy+k_zz-wt)} | \psi(x,y,z,t)=Ae^{i(k_xx+k_yy+k_zz-wt)} | ||
\end{equation} | \end{equation} | ||
Como es habitual, se pueden obtener soluciones reales tomando las partes reales o imaginarias. Verificar | |||
que (6) satisface la ecuación de onda, puede simplemente sustituir (6) en (9.7) y verificar que el | |||
se cumple la ecuación de onda. La relación de dispersión (9.10) hace que eso suceda | |||
=Referencias= | =Referencias= | ||
Revisión del 09:26 9 nov 2020
Ondas en 3 dimensiones
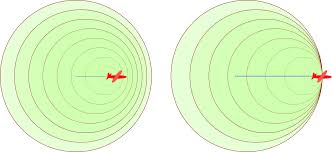
Las ondas tridimensionales son ondas que se propagan en tres dimensiones, se conocen también como ondas esféricas, porque sus frentes de ondas son esferas concéntricas que salen de la fuente de perturbación expandiéndose en todas direcciones (3D). Ejemplos de ondas tridimensionales son: las ondas sonoras y las ondas electromagnéticas
Cuando se propaga una onda en un espacio de tres dimensiones, la fase Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \phi es una función continua de x,y,z,t. en un instante dado cualquiera Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): t_{0} , la fase tiene el mismo valor en todos los puntos de ciertas superficies a las que se da el nombre de superficie de onda. Vienen definidas por la relación.
Donde es una función de las coordenadas espaciales y es el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \phi correspondiente a una superficie particular en el instante
En general, las superficies de onda constituyen una familia de superficies en la que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \Phi es el parámetro variable que selecciona a un miembro particular de la familia. Lassuperficies de onda pueden constituir una familia de esféras concéntricas o una familia de planos paralelos y también puede adoptar otras formas. Las ondas se denominan ondas esféricas,ondas planas, etc., segun sea la forma de las superficies de onda. Cuando avanzan las ondas por una región que hasta entonces no había sido perturbada, la superficie correspondiente a la primera cresta de denomina frente de onda.
Ecuación de onda en tres dimensiones
La función de onda dada por la ecuación (14) en el tema Ondas: planas es una solución partícular de de la ecuación diferencial en tres dimensiones, calculamos entonces las derivadas parciales de la ecuación (14) antes mencionada
\begin{equation}
\frac{\partial^{2}\psi}{\partial{x^{2}}}=-\alpha^{2}k^{2}\psi
\end{equation}
\begin{equation} \frac{\partial^{2}\psi}{\partial{y^{2}}}=-\beta^{2}k^{2}\psi \end{equation}
\begin{equation} \frac{\partial^{2}\psi}{\partial{z^{2}}}=-\gamma^{2}k^{2}\psi \end{equation}
\begin{equation} \frac{\partial^{2}\psi}{\partial{t^{2}}}=-\omega^{2}\psi \end{equation}
Sumando las tres derivadas parciales y usando el hecho de que , obtenemos
\begin{equation} \frac{\partial^{2}\psi}{\partial{x^{2}}}+\frac{\partial^{2}\psi}{\partial{y^{2}}}+\frac{\partial^{2}\psi}{\partial{z^{2}}}=-k^{2}\psi \end{equation}
Combinando esto con la derivada del tiempo, ecuación 4 y recordando que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): v=\omega/k , llegamos a
\begin{equation} \frac{\partial^{2}\psi}{\partial{x^{2}}}+\frac{\partial^{2}\psi}{\partial{y^{2}}}+\frac{\partial^{2}\psi}{\partial{z^{2}}}=\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial{t^{2}}} \end{equation}
que es la ecuación diferencial de onda tridimencional. Obsérvese que x, y, y z aparecen simétricamente y que la forma es precisamente la que uno esperaría de la generalización de la ecuación unidimensional que se puede ver en Ondas: ecuación de onda
La ecuación 6 se escribe,por lo general, de una forma más concisa introduciendo el operador Laplaciano
\begin{equation} \nabla^{2}=\frac{\partial^{2}}{\partial{x^{2}}}+\frac{\partial^{2}}{\partial{y^{2}}}+\frac{\partial^{2}}{\partial{z^{2}}} \end{equation}
Por tanto, la ecuación de onda se puede escribir de forma compacta en términos del laplaciano como:
\begin{equation} \nabla^{2}\psi=\frac{1}{v^{2}}\frac{\partial^{2}{\psi}}{\partial{t^{2}}} \end{equation}
Soluciones a la ecuación de onda tridimensional
Las soluciones de la ecuación de onda tridimensional (ecuación 8) no son más difíciles de conseguir que los de la ecuación de onda unidimensional. De hecho, si buscamos soluciones que sean independientes de $y$ y $z$, recuperamos las soluciones obtenidas para la ecuación unidimensional. Entonces, por ejemplo, la solución (compleja) de onda
\begin{equation} \psi(x,y=0,z=0,t)= Ae^{ik(x-vt)} \end{equation} La cual es independiente de $y$ y $z$, y es una onda desplazándose positivamente en $x$. Ahora veamos su solución general ya dependiente de las 4 variables:
\begin{equation} \psi(\vec{r},t)=Ae^{i(\vec{k}\cdot\vec{r}-wt)};\thinspace con \thinspace \vec{r}=(x,y,z) \end{equation}
Se puede ver que tiene la misma forma que la ecuación de onda en una dimensión. Ahora vamos a encontrar $w$ y $k$ y para ello redefinimos las siguientes ecuaciones:
\[ \frac{\partial^{2}\psi}{\partial{x^{2}}}=-\alpha^{2}k^{2}\psi=-k_x^2\psi \]
\[ \frac{\partial^{2}\psi}{\partial{y^{2}}}=-\beta^{2}k^{2}\psi=-k_y^2\psi \]
\[ \frac{\partial^{2}\psi}{\partial{z^{2}}}=-\gamma^{2}k^{2}\psi=-k_z^2\psi \]
\[ \frac{\partial^{2}\psi}{\partial{t^{2}}}=-\omega^{2}\psi \]
Entonces la ecuación de onda es:
\[ \nabla^{2}\psi=\frac{1}{v^{2}}\frac{\partial^{2}{\psi}}{\partial{t^{2}}} \] \begin{equation} -(k_x^2+k_y^2+k_z^2)\psi(\vec{r},t)=-\frac{w^2}{v^2}\psi(\vec{r},t) \end{equation}
despejando $w$
\[ -(k_x^2+k_y^2+k_z^2)=-\frac{w^2}{v^2} \]
\[ w^2=v^2(k_x^2+k_y^2+k_z^2) \]
\begin{equation} w=v\sqrt{(k_x^2+k_y^2+k_z^2)} \end{equation}
y definiendo $k$ como $\vec{k}=(k_x,k_y,k_z)$, entonces $w$ es:
\begin{equation} w=v|\vec{k}| \end{equation}
Por lo tanto su solución es:
\begin{equation} \psi(x,y,z,t)=Ae^{i(k_xx+k_yy+k_zz-wt)} \end{equation}
Como es habitual, se pueden obtener soluciones reales tomando las partes reales o imaginarias. Verificar que (6) satisface la ecuación de onda, puede simplemente sustituir (6) en (9.7) y verificar que el se cumple la ecuación de onda. La relación de dispersión (9.10) hace que eso suceda