Diferencia entre revisiones de «Numeros complejos»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 8: | Línea 8: | ||
<center><math>(x_1+iy_1)+(x_2+iy_2)=(x_1+x_2)+(y_1+y_2)i</math></center> | <center><math>(x_1+iy_1)+(x_2+iy_2)=(x_1+x_2)+(y_1+y_2)i</math></center> | ||
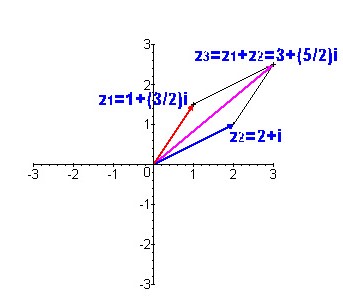
[[Imagen:ma3.jpg|center|thumb|400x300px|Figura 2.]] | [[Imagen:ma3.jpg|center|thumb|400x300px|Figura 2.Suma de complejos]] | ||
El producto de los números complejos se define de la siguiente manera: | El producto de los números complejos se define de la siguiente manera: | ||
| Línea 17: | Línea 17: | ||
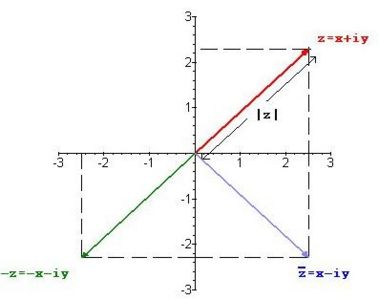
El complejo conjugado del numero complejo <math>\tilde{z}=x+iy</math>, se define como <math>\tilde{z}^*=x-iy</math>. | El complejo conjugado del numero complejo <math>\tilde{z}=x+iy</math>, se define como <math>\tilde{z}^*=x-iy</math>. | ||
[[Imagen:ma1.jpg|center|thumb|400x300px|Figura 3.]] | [[Imagen:ma1.jpg|center|thumb|400x300px|Figura 3.Módulo, Conjugado de un número complejo]] | ||
Para determinar el cociente de dos números complejos, multiplicamos numerador y denominador por el complejo conjugado del denominador. | Para determinar el cociente de dos números complejos, multiplicamos numerador y denominador por el complejo conjugado del denominador. | ||
| Línea 30: | Línea 30: | ||
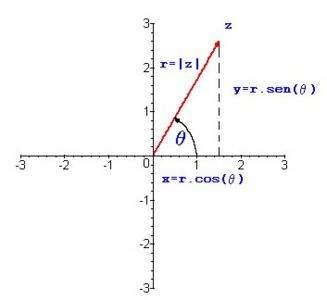
<center><math>\tilde{z}=x+iy=r(cos\theta+i\, sen\theta)</math></center> | <center><math>\tilde{z}=x+iy=r(cos\theta+i\, sen\theta)</math></center> | ||
Donde <math>r=|z|=\sqrt{x^2+y^2}</math> | Donde <math>r=|z|=\sqrt{x^2+y^2}</math> | ||
[[Imagen:ma5.jpg|center|thumb|400x300px|Figura 4.]] | [[Imagen:ma5.jpg|center|thumb|400x300px|Figura 4.Forma polar de un número complejo]] | ||
La forma polar de los números complejos proporciona una perspectiva de la multiplicación y la división, Sean | La forma polar de los números complejos proporciona una perspectiva de la multiplicación y la división, Sean | ||
| Línea 39: | Línea 39: | ||
Con las formulas adición de angulos para coseno y seno, llegamos a | Con las formulas adición de angulos para coseno y seno, llegamos a | ||
<center><math>\tilde{z_1}\tilde{z_2}=r_1r_2[(cos\theta_1+\theta_2)+i(sen\theta_1+\theta_2)]</math></center> | <center><math>\tilde{z_1}\tilde{z_2}=r_1r_2[(cos\theta_1+\theta_2)+i(sen\theta_1+\theta_2)]</math></center> | ||
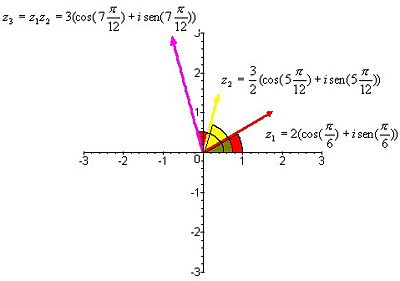
[[Imagen:ma4.jpg|center|thumb|400x450px|Figura 5.]] | [[Imagen:ma4.jpg|center|thumb|400x450px|Figura 5.Producto de complejos en forma polar]] | ||
Entonces al multiplicar dos números complejos se multiplican sus módulos y se suman sus argumentos:<ref> James Stewart,Cálculo,Ed.Thomson,México 2006, pp.A79-A85</ref> | Entonces al multiplicar dos números complejos se multiplican sus módulos y se suman sus argumentos:<ref> James Stewart,Cálculo,Ed.Thomson,México 2006, pp.A79-A85</ref> | ||
Revisión del 16:33 16 dic 2007
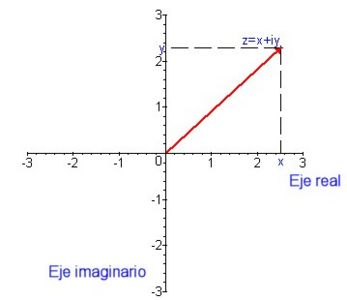
Un número complejo se puede representar mediante una expresión de la forma , donde y son números reales, e es un símbolo con la propiedad de que . El número complejo también se puede denotar por medio del par ordenado y graficar como un punto en un plano llamado (plano de Argand), donde el eje es el eje real y el eje , el eje imaginario, como en la figura 1.
La parte real del número complejo es el número real la parte imaginaria, el número real .
La suma de dos números complejos se define sumando sus partes reales e imaginarias, respectivamente:
El producto de los números complejos se define de la siguiente manera:
Ya que , lo anterior se transforma en
El complejo conjugado del numero complejo , se define como .
Para determinar el cociente de dos números complejos, multiplicamos numerador y denominador por el complejo conjugado del denominador.
Forma polar
Si consideramos todo número complejo
como un punto en el plano de Argand (figura 1)este puede representarse en términos de coordenadas polares.[1] .Tenemos
Donde
La forma polar de los números complejos proporciona una perspectiva de la multiplicación y la división, Sean y expresados en forma polar.Entonces
Con las formulas adición de angulos para coseno y seno, llegamos a
Entonces al multiplicar dos números complejos se multiplican sus módulos y se suman sus argumentos:[2] ,(figura 3). Un análisis similar muestra que para dividir dos números complejos, se dividen los módulos y se restan los argumentos.
La multiplicación y la divisiónen en forma polar es muy simple y se expresan de la iguiente manera:
En donde utilizamos la fórmula de Euler para expresarlas así.
LA fórmula de Euler es:
por lo anterior
debido a que por ser una función par y por ser una función impar
tenemos que
sumando y substrayendo la ecuación(1)y (2) llegamos a
,
Esta misma formula nos permite escribir
Cualquier número complejo se puede representar como la suma de una parte real y una parte imaginaria tal como se menciono anteriormente.
En la forma polar donde
y
En el caso particular, como es el de describir una onda armónica en su representación compleja , tenemos la libertad de escoger cualquier parte.[3]






















![\tilde{z_1}\tilde{z_2}=r_1r_2[(cos\theta_1+\theta_2)+i(sen\theta_1+\theta_2)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/33b05baa906930d5f6d7a16b0fd7afd330ad513b)
![\frac{\tilde{z_1}}{\tilde{z_2}}=\frac{r_1}{r_2}[cos(\theta_1-\theta_2)+isen(\theta_1-\theta_2)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b94c8dd844193d7117bf836b07efc0929b841d8a)













