Diferencia entre revisiones de «Numeros complejos»
Sin resumen de edición |
|||
| (No se muestran 34 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
Un número complejo se puede representar mediante una expresión de la forma <math> | Numeros complejos, propiedades y operaciones con numeros complejos. | ||
[[Imagen: | |||
== Introducción == | |||
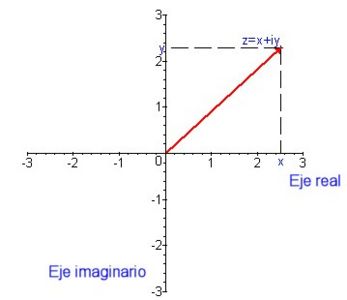
Un número complejo se puede representar mediante una expresión de la forma <math>z=x+iy</math>, donde <math>x</math> y <math>y</math>son números reales, e <math>i</math> es un símbolo con la propiedad de que <math>i^2=-1</math>. El número complejo <math>x+iy</math> también se puede denotar por medio del par ordenado <math>(x,y)</math>y graficar como un punto en un plano llamado (plano de Argand), donde el eje <math>x</math> es el eje real y el eje <math>y</math>, el eje imaginario, tal como se muestra en la figura 1. | |||
== Operaciones básicas de números complejos == | |||
[[Imagen:ma2.jpg|center|thumb|400x300px|Figura 1. Números complejos como puntos en el plano de Argand]] | |||
La parte real del número complejo <math>x+iy</math>es el número real <math>x</math>la parte imaginaria, el número real <math>y</math>. | La parte real del número complejo <math>x+iy</math>es el número real <math>x</math>la parte imaginaria, el número real <math>y</math>. | ||
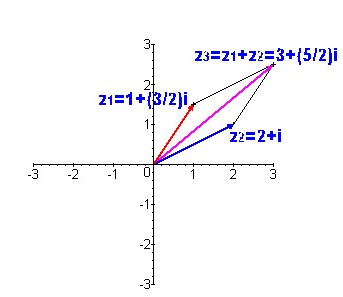
La suma | La suma de dos números complejos se define sumando sus partes reales e imaginarias, respectivamente: | ||
<center><math>(x_1+iy_1)+(x_2+iy_2)=(x_1+x_2)+(y_1+y_2)i</math></center> | <center><math>(x_1+iy_1)+(x_2+iy_2)=(x_1+x_2)+(y_1+y_2)i</math></center> | ||
[[Imagen: | [[Imagen:ma3.jpg|center|thumb|400x300px|Figura 2. Suma de complejos]] | ||
El producto de los números complejos se define de la siguiente manera: | El producto de los números complejos se define de la siguiente manera: | ||
<center><math>(x_1+iy_1)(x_2+iy_2)=(x_1)(x_2+iy_2)+(iy_1)(x_2+iy_2)</math></center> | <center><math>(x_1+iy_1)(x_2+iy_2)=(x_1)(x_2+iy_2)+(iy_1)(x_2+iy_2)</math></center> | ||
<center><math>x_1x_2+x_1y_2i+y_1x_2i+(y_1y_2)i^2</math></center> | <center><math>=x_1x_2+x_1y_2i+y_1x_2i+(y_1y_2)i^2</math></center> | ||
Ya que <math> i^2=-1</math>, lo anterior se transforma en <center><math>(x_1+iy_1)(x_2+iy_2)=(x_1x_2-y_1y_2)+(x_1y_2+y_1x_2)i</math></center> | Ya que <math> i^2=-1</math>, lo anterior se transforma en <center><math>(x_1+iy_1)(x_2+iy_2)=(x_1x_2-y_1y_2)+(x_1y_2+y_1x_2)i</math></center> | ||
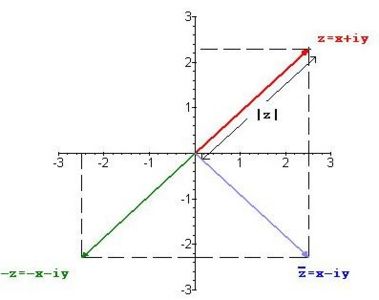
El complejo conjugado del número complejo <math>z=x+iy</math>, se define como <math>\tilde{z}=x-iy</math>. | |||
Para determinar el cociente de dos números complejos, multiplicamos numerador y denominador por el complejo conjugado del denominador. | Para determinar el cociente de dos números complejos, multiplicamos numerador y denominador por el complejo conjugado del denominador. | ||
<math>\frac{x_1+iy_1}{x_2+iy_2}=\frac{x_1+iy_1}{x_2+iy_2}\,\frac{x_2-iy_2}{x_2-iy_2}</math> | <math>\frac{x_1+iy_1}{x_2+iy_2}=\frac{x_1+iy_1}{x_2+iy_2}\,\frac{x_2-iy_2}{x_2-iy_2}</math> | ||
El módulo, o valor absoluto <math>|z|</math> de un número complejo <math>z=x+iy</math> es su distancia al origen. | |||
En la figura 3 vemos que si <math>z=x+iy</math>, entonces | |||
<math>|z|=\sqrt{x^2+y^2}</math> | |||
Observe que | |||
<center><math>z\tilde{z}=(x+iy)(x-iy)=x^2+xyi-xyi-y^2i^2=x^2+y^2</math></center> | |||
de modo que <center><math>z\tilde{z}=|z|^2</math></center> | |||
[[Imagen:ma1.jpg|center|thumb|400x300px|Figura 3. Módulo, Conjugado y opuesto de un número complejo]] | |||
Esto explica por qué funciona, en general, el procedimiento de división. | |||
<math>\frac{z}{w}=\frac{z}{w}\frac{\tilde{w}}{\tilde{w}}=\frac{z\tilde{w}}{|w|^2}</math> | |||
==Forma polar== | ==Forma polar== | ||
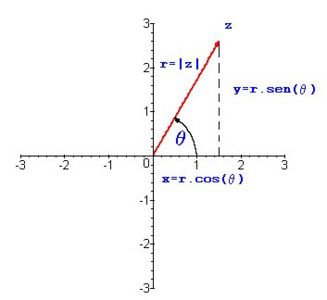
Si consideramos todo número complejo <center><math>\tilde{z}=x+iy</math></center>como un punto <math>(x,y)</math> en el plano de Argand (figura 1)este puede representarse en términos de coordenadas polares.<ref> Ruel V.Churchill,Variable compleja y aplicaciones,Ed. | Si consideramos todo número complejo <center><math>\tilde{z}=x+iy</math></center>como un punto <math>(x,y)</math> en el plano de Argand (figura 1)este puede representarse en términos de coordenadas polares. | ||
<ref> Ruel V.Churchill,Variable compleja y aplicaciones,Ed.y McGraw-Hill,1 ed, 1988 pp.14-19</ref> | |||
<math>(r,\theta)</math>.Tenemos | |||
<center><math>x=rcos\theta</math>, <math>y=rsen\theta</math></center> | <center><math>x=rcos\theta</math>, <math>y=rsen\theta</math></center> | ||
| Línea 31: | Línea 53: | ||
<center><math>\tilde{z}=x+iy=r(cos\theta+i\, sen\theta)</math></center> | <center><math>\tilde{z}=x+iy=r(cos\theta+i\, sen\theta)</math></center> | ||
Donde <math>r=|z|=\sqrt{x^2+y^2}</math> | Donde <math>r=|z|=\sqrt{x^2+y^2}</math> | ||
[[Imagen: | [[Imagen:ma5.jpg|center|thumb|400x300px|Figura 4. Forma polar de un número complejo]] | ||
La forma polar de los números complejos proporciona una perspectiva de la multiplicación y la división, Sean | La forma polar de los números complejos proporciona una perspectiva de la multiplicación y la división, Sean | ||
| Línea 40: | Línea 62: | ||
Con las formulas adición de angulos para coseno y seno, llegamos a | Con las formulas adición de angulos para coseno y seno, llegamos a | ||
<center><math>\tilde{z_1}\tilde{z_2}=r_1r_2[(cos\theta_1+\theta_2)+i(sen\theta_1+\theta_2)]</math></center> | <center><math>\tilde{z_1}\tilde{z_2}=r_1r_2[(cos\theta_1+\theta_2)+i(sen\theta_1+\theta_2)]</math></center> | ||
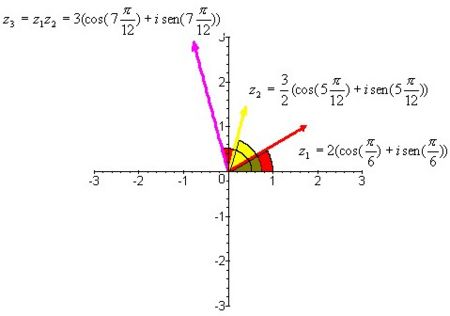
[[Imagen: | [[Imagen:ma4.jpg|center|thumb|450x450px|Figura 5. Producto de complejos en forma polar]] | ||
Entonces al multiplicar dos números complejos se multiplican sus módulos y se suman sus argumentos:<ref> James Stewart,Cálculo,Ed.Thomson,México 2006, pp.A79-A85</ref> | Entonces al multiplicar dos números complejos se multiplican sus módulos y se suman sus argumentos:<ref> James Stewart,Cálculo,Ed.Thomson,México 2006, pp.A79-A85</ref> | ||
| Línea 49: | Línea 71: | ||
La multiplicación y la | La multiplicación y la división en en forma polar es muy simple y se expresan de la siguiente manera: | ||
<math>\tilde{z_1}\, \tilde{z_2}=r_1 r_2e^{i(\theta_1+\theta_2)}</math> | <math>\tilde{z_1}\, \tilde{z_2}=r_1 r_2e^{i(\theta_1+\theta_2)}</math> | ||
| Línea 55: | Línea 77: | ||
La fórmula de Euler es: | |||
<center><math>\mathbf{e}^{i\theta}=cos\theta+isen\theta\qquad (1)</math></center> | <center><math>\mathbf{e}^{i\theta}=cos\theta+isen\theta\qquad (1)</math></center> | ||
| Línea 65: | Línea 87: | ||
sumando y substrayendo la ecuación(1)y (2) llegamos a | sumando y substrayendo la ecuación (1) y (2) llegamos a | ||
<math>cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}</math>, | <math>cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}</math>, | ||
| Línea 72: | Línea 94: | ||
Esta misma formula nos permite escribir <center><math>\tilde{z}=re^{i\theta}=rcos\theta+irsen\theta</math></center> | Esta misma formula nos permite escribir <center><math>\tilde{z}=re^{i\theta}=rcos\theta+irsen\theta</math></center> | ||
Cualquier número complejo se puede representar como la suma de una parte real <math>Re(\tilde{z})</math> y una parte imaginaria <math>Im(\tilde{z})</math> | Cualquier número complejo se puede representar como la suma de una parte real <math>Re(\tilde{z})</math> y una parte imaginaria <math>Im(\tilde{z})</math> tal como se menciono anteriormente. | ||
<center><math>\tilde{z}=Re(\tilde{z})+Im(\tilde{z})</math></center> | <center><math>\tilde{z}=Re(\tilde{z})+Im(\tilde{z})</math></center> | ||
| Línea 79: | Línea 100: | ||
En la forma polar donde | En la forma polar donde | ||
<center><math>Re(\tilde{z})=rcos\theta</math></center> y <center><math>Im(\tilde{z})=rsen\theta</math></center> | <center><math>Re(\tilde{z})=rcos\theta</math></center> y <center><math>Im(\tilde{z})=rsen\theta</math></center> | ||
En el caso particular, como es el de describir una onda armónica en su representación compleja, tenemos la libertad de escoger cualquier parte. | En el caso particular, como es el de describir una [[Superposición de ondas#El método complejo| onda armónica en su representación compleja ]], tenemos la libertad de escoger cualquier parte.<ref> Hecht, Óptica, Ed.Pearson, 3ra ed 2006, pp.23-24</ref> | ||
=Referencias= | ==Referencias== | ||
{|class=wikitable | {|class=wikitable | ||
| Línea 87: | Línea 108: | ||
<references/> | <references/> | ||
|} | |} | ||
[[categoría: | [[categoría:Matematicas]] | ||
---- | |||
Aportación por usuario: Usuario: Isela [[Usuario:Isela|Isela]] | |||
---- | |||
= Números complejos y algunas propiedades = | |||
Los número complejos surgen por la necesidad de realizar y/o resolver | |||
ecuaciones cuadráticas en los reales donde tenemos que: | |||
$x^{2}+1=0\Rightarrow x^{2}=-1$ por lo cual la respuesta es: | |||
$x=\sqrt{-1}$ este es imposibles en los reales y por este motivo | |||
se dio la necesidad de tener un nuevo conjunto de números llamados | |||
complejos. Naturalmente tenemos que: $\mathbb{R\epsilon\mathbb{C}}$ | |||
Y para nuestra comodidad en los complejos tenemos que a la raíz de | |||
menos uno le denominamos una letra llamada i, así de nuestro ejemplo | |||
tenemos que: | |||
$x=i$ | |||
Comúnmente los complejos se denominan con la letra z y tienen una | |||
parte real y una imaginaria: | |||
$z=x+iy$ o también $z=a+ib$ donde x ó a se denotan por reales también | |||
y y ó b son los imaginarios del número complejo z. | |||
También existen su conjugado en complejos la cual es: | |||
$\overline{z}=a-bi$ | |||
Tenemos algunas propiedades de la suma para estos números que son | |||
similares a la de los reales: | |||
*1 Es cerrada bajo la suma | |||
*2 Es asociativa | |||
*3 Existe un neutro o idéntico aditivo | |||
*4 Existe un inverso aditivo | |||
*5 Pueden conmutar | |||
Para demostrar estas 5 propiedades tenemos que: | |||
$z=a+bi$ , $w=c+di$ y $v=e+fi$ | |||
*1.- $z+w=\left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i$ | |||
Por lo tanto $\left[z+w\right]\epsilon\mathbb{C}$ | |||
*2.- $\left(z+w\right)+v=z+\left(w+v\right)$ | |||
$\left(z+w\right)+v=\left[\left(a+bi\right)+c+di\right]+\left(e+fi\right)=\left[\left(a+c\right)+\left(b+d\right)i\right]+\left(e+fi\right)=\left[\left(\left(a+c\right)+e\right)+\left(\left(b+d\right)+f\right)i\right]=$ | |||
$=\left[a+\left(c+e\right)\right]+\left[b+\left(d+f\right)\right]i=\left(a+bi\right)+\left[\left(c+e\right)+\left(b+f\right)i\right]=z+\left(w+v\right)$ | |||
*3.- $0+z=\left(0+0i\right)+\left(a+bi\right)=\left(0+a\right)+\left(0+b\right)i=a+bi=z$ | |||
*4.-$z+\left(-z\right)=\left(a+bi\right)+\left(-a-bi\right)=\left(a-a\right)+\left(b-b\right)i=0+0i=0$ | |||
Además análogamente: | |||
$-z+z=\left(-a-bi\right)+\left(a+bi\right)=0+0i=0$ | |||
*5.-$z+w=w+z$ | |||
$z+w=\left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i=\left(c+a\right)+\left(d+b\right)i=\left(c+di\right)+\left(a+bi\right)=w+z$ | |||
Análogamente también existen propiedades de la multiplicación para | |||
los complejos como en los reales: | |||
* 1.-Es cerrada | |||
* 2.-Es asociativa | |||
* 3.-Existe un neutro multiplicativo | |||
* 4.-Existe un inverso multiplicativo | |||
Sean $z=a+bi$ y $w=c+di$ y $v=e+fi$ | |||
*1.- $zw=\left(a+bi\right)\left(c+di\right)=\left(ac-bd\right)+\left(bc+ad\right)i$ | |||
*2.-$\left(zw\right)v=z\left(wv\right)$ | |||
*3.-$1\cdotp z=z=z\cdotp1$ | |||
*4.-$z\cdotp z^{-1}=1$ | |||
Además existen propiedades para los complejos de la forma $a+bi$ tales | |||
como | |||
*1) \[\overline{z\pm w}=\overline{z}\pm\overline{w}\] | |||
*2) \[\overline{z\cdotp w}=\overline{z}\overline{w}\] | |||
*3) \[\frac{\overline{z}}{w}=\frac{\overline{z}}{\overline{w}}\] | |||
*4) \[\overline{\overline{z}}=z\] | |||
*5) \[\overline{z}=z\] solo si z es real | |||
*6) \[z\overline{z}=\left|z\right|^{2}\] | |||
*7) \[\frac{1}{z}=\frac{\overline{z}}{\left|z\right|^{2}}\] | |||
*8) \[\left|z\right|\geq0\] para todo z en los complejos | |||
*9) \[\left|z\right|=0\Longleftrightarrow z=0\] | |||
*10) \[\left|zw\right|=\left|z\right|\left|w\right|\] | |||
*11) \[\left|\frac{z}{w}\right|\frac{\left|z\right|}{\left|w\right|}\] | |||
*12) \[\left|z+w\right|\leq\left|z\right|+\left|w\right|\] | |||
Potencias de i | |||
$i=\sqrt{-1}$ | |||
$i^{2}=-1$ | |||
$i^{3}=-i=-\sqrt{-1}$ | |||
$i^{4}=i^{2}i^{2}=\left(-1\right)\left(-1\right)=1$ | |||
$i^{5}=i^{4}i=1\sqrt{-1}=i$ | |||
---- | |||
Realizado por: [[Usuario:Luis Enrique Martínez Valverde|Luis Enrique Martínez Valverde]] ([[Usuario discusión:Luis Enrique Martínez Valverde|discusión]]) 15:49 5 jul 2015 (CDT) | |||
---- | |||
= Operadores diferenciales complejos. = | |||
Definimos a los operadores como $\nabla$ (delta) y $\nabla^{*}$ (delta trazo) por | |||
$\nabla \equiv \frac{\partial}{\partial x} + i \frac{\partial}{\partial y} = 2 \frac{\partial}{\partial z^{*}}$ | |||
$\nabla^{*} \equiv \frac{\partial}{\partial x} - i \frac{\partial}{\partial y} = 2 \frac{\partial}{\partial}$ | |||
Donde $z^{*} $ es el conjugado de $z$ | |||
El operador $\nabla$ nos lleva a definir las siguientes operaciones. En todos los casos consideramos $F(x, y)$ como una función real continuamente diferenciable de $x$ y $y$ (escalar), mientras $A(x, y) = P(x, y) + iQ(x. y)$ es una función compleja continuamente diferenciable de $x$ y (vectorial). | |||
En términos de las coordenadas conjugadas, $F(x, y) = F(\frac{z + z^{*}}{2}, \frac{z + z^{*}}{2i}) = G(z, z^{*})$ y $A(x, y) = B(z, z^{*})$ . | |||
== Gradiente == | |||
Definimos el gradiente de una función real $F$ (escalar) por | |||
$grad F = \nabla F = \frac{\partial F}{\partial x} + i \frac{\partial F}{\partial y} = 2 \frac{\partial G}{\partial z^{*}}$ | |||
Geométricamente, esto representa un vector normal a la curva $F(x, y) = c$ donde $c$ es una constante. | |||
Similarmente, el gradiente de una función compleja $A = P + iQ$ (vectorial) esta definida por | |||
$grad A = \nabla A = (\frac{\partial}{\partial x} + i \frac{\partial}{\partial y}) (P + iQ) = \frac{\partial P}{\partial x} - \frac{\partial Q}{\partial y} + i(\frac{\partial P}{\partial y} + \frac{\partial Q}{\partial x}) = 2\frac{\partial B}{\partial z^{*}}$ | |||
En particular si $B$ es una función analítica de $z$ entonces $\frac{\partial B}{\partial z^{*}} = 0$ y así el gradiente es cero; es decir, $\frac{\partial P}{\partial x} = \frac{\partial Q}{\partial y}, \frac{\partial P}{\partial y} = - \frac{\partial Q}{\partial x}$, lo cual muestra que las ecuaciones de Cauchy - Riemann son satisfechas en este caso. | |||
== Divergencia == | |||
Usando la definición de producto interior de dos números complejos para extenderla al caso de operadores, definimos la divergencia de una función compleja (vectorial) por | |||
$div A = \nabla \cdot A = Re {\nabla^{*} A} = Re \{(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}) (P + iQ)\} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} = 2 Re \{\frac{\partial B}{\partial z}\}$ | |||
Similarmente podemos definir la divergencia de una función real. Nótese que la divergencia de una función real o compleja (escalar o vectorial) es siempre una función real (escalar). | |||
== Rotor == | |||
Utilizando la definición del producto vectorial de dos números complejos definimos el rotor de una función real o compleja por medio de | |||
$Rot A = \nabla \times A = Im \{\nabla^{*} A\} = Im \{(\frac{\partial}{\partial x} - i \frac{\partial}{\partial y})(P + iQ) \} = \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 2 Im \{\frac{\partial B}{\partial z} \}$ | |||
Similarmente podemos definir el rotor de una función real. | |||
== Laplaciano == | |||
El operador laplaciano esta definido como el producto escalar de $\nabla$ consigo mismo, es decir. | |||
$\nabla \cdot \nabla \equiv \nabla^2 \equiv Re \{\nabla^{*} \nabla\} = Re \{(\frac{\partial}{\partial x} - i \frac{\partial}{\partial y}) (\frac{\partial}{\partial x} + i \frac{\partial}{\partial y})\} = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} = 4 \frac{\partial^2}{\partial z \partial z^{*}}$ | |||
Notemos que si $A$ es analítica, $\nabla^2 A = 0$ así que $\nabla^2 P = 0$ y $\nabla^2 Q = 0$ , es decir, $P$ y $Q$ son armónicas. | |||
---- | |||
Aportación de: [[Usuario:Angelina Nohemi Mendoza Tavera|Angelina Nohemi Mendoza Tavera]] ([[Usuario discusión:Angelina Nohemi Mendoza Tavera|discusión]]) 18:47 5 jul 2015 (CDT) | |||
---- | |||
[[Category:Compleja]] | |||
Revisión actual - 05:31 9 oct 2023
Numeros complejos, propiedades y operaciones con numeros complejos.
Introducción
Un número complejo se puede representar mediante una expresión de la forma , donde y son números reales, e es un símbolo con la propiedad de que . El número complejo también se puede denotar por medio del par ordenado y graficar como un punto en un plano llamado (plano de Argand), donde el eje es el eje real y el eje , el eje imaginario, tal como se muestra en la figura 1.
Operaciones básicas de números complejos
La parte real del número complejo es el número real la parte imaginaria, el número real .
La suma de dos números complejos se define sumando sus partes reales e imaginarias, respectivamente:
El producto de los números complejos se define de la siguiente manera:
Ya que , lo anterior se transforma en
El complejo conjugado del número complejo , se define como .
Para determinar el cociente de dos números complejos, multiplicamos numerador y denominador por el complejo conjugado del denominador.
El módulo, o valor absoluto de un número complejo es su distancia al origen. En la figura 3 vemos que si , entonces
Observe que
de modo que
Esto explica por qué funciona, en general, el procedimiento de división.
Forma polar
Si consideramos todo número complejo
como un punto en el plano de Argand (figura 1)este puede representarse en términos de coordenadas polares.
[1] .Tenemos
Donde
La forma polar de los números complejos proporciona una perspectiva de la multiplicación y la división, Sean y expresados en forma polar.Entonces
Con las formulas adición de angulos para coseno y seno, llegamos a
Entonces al multiplicar dos números complejos se multiplican sus módulos y se suman sus argumentos:[2] ,(figura 3). Un análisis similar muestra que para dividir dos números complejos, se dividen los módulos y se restan los argumentos.
La multiplicación y la división en en forma polar es muy simple y se expresan de la siguiente manera:
En donde utilizamos la fórmula de Euler para expresarlas así.
La fórmula de Euler es:
por lo anterior
debido a que por ser una función par y por ser una función impar
tenemos que
sumando y substrayendo la ecuación (1) y (2) llegamos a
,
Esta misma formula nos permite escribir
Cualquier número complejo se puede representar como la suma de una parte real y una parte imaginaria tal como se menciono anteriormente.
En la forma polar donde
y
En el caso particular, como es el de describir una onda armónica en su representación compleja , tenemos la libertad de escoger cualquier parte.[3]
Referencias
Aportación por usuario: Usuario: Isela Isela
Números complejos y algunas propiedades
Los número complejos surgen por la necesidad de realizar y/o resolver ecuaciones cuadráticas en los reales donde tenemos que:
$x^{2}+1=0\Rightarrow x^{2}=-1$ por lo cual la respuesta es:
$x=\sqrt{-1}$ este es imposibles en los reales y por este motivo se dio la necesidad de tener un nuevo conjunto de números llamados complejos. Naturalmente tenemos que: $\mathbb{R\epsilon\mathbb{C}}$
Y para nuestra comodidad en los complejos tenemos que a la raíz de menos uno le denominamos una letra llamada i, así de nuestro ejemplo tenemos que:
$x=i$
Comúnmente los complejos se denominan con la letra z y tienen una parte real y una imaginaria:
$z=x+iy$ o también $z=a+ib$ donde x ó a se denotan por reales también y y ó b son los imaginarios del número complejo z.
También existen su conjugado en complejos la cual es:
$\overline{z}=a-bi$
Tenemos algunas propiedades de la suma para estos números que son similares a la de los reales:
- 1 Es cerrada bajo la suma
- 2 Es asociativa
- 3 Existe un neutro o idéntico aditivo
- 4 Existe un inverso aditivo
- 5 Pueden conmutar
Para demostrar estas 5 propiedades tenemos que:
$z=a+bi$ , $w=c+di$ y $v=e+fi$
- 1.- $z+w=\left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i$
Por lo tanto $\left[z+w\right]\epsilon\mathbb{C}$
- 2.- $\left(z+w\right)+v=z+\left(w+v\right)$
$\left(z+w\right)+v=\left[\left(a+bi\right)+c+di\right]+\left(e+fi\right)=\left[\left(a+c\right)+\left(b+d\right)i\right]+\left(e+fi\right)=\left[\left(\left(a+c\right)+e\right)+\left(\left(b+d\right)+f\right)i\right]=$
$=\left[a+\left(c+e\right)\right]+\left[b+\left(d+f\right)\right]i=\left(a+bi\right)+\left[\left(c+e\right)+\left(b+f\right)i\right]=z+\left(w+v\right)$
- 3.- $0+z=\left(0+0i\right)+\left(a+bi\right)=\left(0+a\right)+\left(0+b\right)i=a+bi=z$
- 4.-$z+\left(-z\right)=\left(a+bi\right)+\left(-a-bi\right)=\left(a-a\right)+\left(b-b\right)i=0+0i=0$
Además análogamente:
$-z+z=\left(-a-bi\right)+\left(a+bi\right)=0+0i=0$
- 5.-$z+w=w+z$
$z+w=\left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i=\left(c+a\right)+\left(d+b\right)i=\left(c+di\right)+\left(a+bi\right)=w+z$
Análogamente también existen propiedades de la multiplicación para los complejos como en los reales:
- 1.-Es cerrada
- 2.-Es asociativa
- 3.-Existe un neutro multiplicativo
- 4.-Existe un inverso multiplicativo
Sean $z=a+bi$ y $w=c+di$ y $v=e+fi$
- 1.- $zw=\left(a+bi\right)\left(c+di\right)=\left(ac-bd\right)+\left(bc+ad\right)i$
- 2.-$\left(zw\right)v=z\left(wv\right)$
- 3.-$1\cdotp z=z=z\cdotp1$
- 4.-$z\cdotp z^{-1}=1$
Además existen propiedades para los complejos de la forma $a+bi$ tales como
- 1) \[\overline{z\pm w}=\overline{z}\pm\overline{w}\]
- 2) \[\overline{z\cdotp w}=\overline{z}\overline{w}\]
- 3) \[\frac{\overline{z}}{w}=\frac{\overline{z}}{\overline{w}}\]
- 4) \[\overline{\overline{z}}=z\]
- 5) \[\overline{z}=z\] solo si z es real
- 6) \[z\overline{z}=\left|z\right|^{2}\]
- 7) \[\frac{1}{z}=\frac{\overline{z}}{\left|z\right|^{2}}\]
- 8) \[\left|z\right|\geq0\] para todo z en los complejos
- 9) \[\left|z\right|=0\Longleftrightarrow z=0\]
- 10) \[\left|zw\right|=\left|z\right|\left|w\right|\]
- 11) \[\left|\frac{z}{w}\right|\frac{\left|z\right|}{\left|w\right|}\]
- 12) \[\left|z+w\right|\leq\left|z\right|+\left|w\right|\]
Potencias de i
$i=\sqrt{-1}$
$i^{2}=-1$
$i^{3}=-i=-\sqrt{-1}$
$i^{4}=i^{2}i^{2}=\left(-1\right)\left(-1\right)=1$
$i^{5}=i^{4}i=1\sqrt{-1}=i$
Realizado por: Luis Enrique Martínez Valverde (discusión) 15:49 5 jul 2015 (CDT)
Operadores diferenciales complejos.
Definimos a los operadores como $\nabla$ (delta) y $\nabla^{*}$ (delta trazo) por
$\nabla \equiv \frac{\partial}{\partial x} + i \frac{\partial}{\partial y} = 2 \frac{\partial}{\partial z^{*}}$
$\nabla^{*} \equiv \frac{\partial}{\partial x} - i \frac{\partial}{\partial y} = 2 \frac{\partial}{\partial}$
Donde $z^{*} $ es el conjugado de $z$
El operador $\nabla$ nos lleva a definir las siguientes operaciones. En todos los casos consideramos $F(x, y)$ como una función real continuamente diferenciable de $x$ y $y$ (escalar), mientras $A(x, y) = P(x, y) + iQ(x. y)$ es una función compleja continuamente diferenciable de $x$ y (vectorial).
En términos de las coordenadas conjugadas, $F(x, y) = F(\frac{z + z^{*}}{2}, \frac{z + z^{*}}{2i}) = G(z, z^{*})$ y $A(x, y) = B(z, z^{*})$ .
Gradiente
Definimos el gradiente de una función real $F$ (escalar) por
$grad F = \nabla F = \frac{\partial F}{\partial x} + i \frac{\partial F}{\partial y} = 2 \frac{\partial G}{\partial z^{*}}$
Geométricamente, esto representa un vector normal a la curva $F(x, y) = c$ donde $c$ es una constante.
Similarmente, el gradiente de una función compleja $A = P + iQ$ (vectorial) esta definida por
$grad A = \nabla A = (\frac{\partial}{\partial x} + i \frac{\partial}{\partial y}) (P + iQ) = \frac{\partial P}{\partial x} - \frac{\partial Q}{\partial y} + i(\frac{\partial P}{\partial y} + \frac{\partial Q}{\partial x}) = 2\frac{\partial B}{\partial z^{*}}$
En particular si $B$ es una función analítica de $z$ entonces $\frac{\partial B}{\partial z^{*}} = 0$ y así el gradiente es cero; es decir, $\frac{\partial P}{\partial x} = \frac{\partial Q}{\partial y}, \frac{\partial P}{\partial y} = - \frac{\partial Q}{\partial x}$, lo cual muestra que las ecuaciones de Cauchy - Riemann son satisfechas en este caso.
Divergencia
Usando la definición de producto interior de dos números complejos para extenderla al caso de operadores, definimos la divergencia de una función compleja (vectorial) por
$div A = \nabla \cdot A = Re {\nabla^{*} A} = Re \{(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}) (P + iQ)\} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} = 2 Re \{\frac{\partial B}{\partial z}\}$
Similarmente podemos definir la divergencia de una función real. Nótese que la divergencia de una función real o compleja (escalar o vectorial) es siempre una función real (escalar).
Rotor
Utilizando la definición del producto vectorial de dos números complejos definimos el rotor de una función real o compleja por medio de
$Rot A = \nabla \times A = Im \{\nabla^{*} A\} = Im \{(\frac{\partial}{\partial x} - i \frac{\partial}{\partial y})(P + iQ) \} = \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 2 Im \{\frac{\partial B}{\partial z} \}$
Similarmente podemos definir el rotor de una función real.
Laplaciano
El operador laplaciano esta definido como el producto escalar de $\nabla$ consigo mismo, es decir.
$\nabla \cdot \nabla \equiv \nabla^2 \equiv Re \{\nabla^{*} \nabla\} = Re \{(\frac{\partial}{\partial x} - i \frac{\partial}{\partial y}) (\frac{\partial}{\partial x} + i \frac{\partial}{\partial y})\} = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} = 4 \frac{\partial^2}{\partial z \partial z^{*}}$
Notemos que si $A$ es analítica, $\nabla^2 A = 0$ así que $\nabla^2 P = 0$ y $\nabla^2 Q = 0$ , es decir, $P$ y $Q$ son armónicas.
Aportación de: Angelina Nohemi Mendoza Tavera (discusión) 18:47 5 jul 2015 (CDT)




























![\tilde{z_1}\tilde{z_2}=r_1r_2[(cos\theta_1+\theta_2)+i(sen\theta_1+\theta_2)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/33b05baa906930d5f6d7a16b0fd7afd330ad513b)
![\frac{\tilde{z_1}}{\tilde{z_2}}=\frac{r_1}{r_2}[cos(\theta_1-\theta_2)+isen(\theta_1-\theta_2)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b94c8dd844193d7117bf836b07efc0929b841d8a)













