Diferencia entre revisiones de «Determinacion de frecuencias y modos naturales»
Sin resumen de edición |
|||
| (No se muestran 34 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
= Introducción= | |||
Existen diversos métodos numéricos y analíticos que han sido desarrollados para determinar las frecuencias naturales y los modos de sistemas con múltiples grados de libertad. | |||
Es muy favorable determinar frecuencias y modos naturales para predecir o analizar fenómenos. Algunos ejemplos son: | |||
frecuencias naturales | |||
$\circ$ Frecuencia fundamental de vigas y flechas. | |||
$\circ$ Frecuencia fundamental de un sistema de tres grados de libertad, como un sistema masa resorte o péndulos. | |||
$\circ$ Frecuencia fundamental de una flecha con rotores. | |||
$\circ$ Frecuencias naturales de un sistema torsional. | |||
== | ==Breve contexto histórico== | ||
Obtendremos el valor aproximado de la $\textbf{frecuencia fundamental}$ de un sistema | Matemáticos y científicos como Taylor, Bernoulli. D´Alembert, Euler, Lagrange o Fourier contribuyeron al desarrollo de la teoría de vibraciones. | ||
compuesto en función de las frecuencias naturales de sus partes componentes. | |||
Wallis y Sauveur observaron independientemente el fenómeno de los modos de vibración en cuerdas. Ellos demostraron que la frecuencia del segundo modo de vibración era $\textbf{el doble que la del primer modo y que la del tercer modo era el triple}.$ | |||
Se le atribuye a Sauveur como el primero en asignar la denominación de “fundamental” a la frecuencia natural más baja y “armónicas” a las demás. <ref name = "Análisis dimensional de los modos de vibración de un eje ferroviario, Miguel Pérez Rodríguez ">Miguel Pérez Rodríguez ,Análisis dimensional de los modos de vibración de un eje ferroviario, Universidad Carlos III de Madrid,Leganés,2012. </ref> | |||
En 1877 Rayleigh publicó el libro Teoría del sonido. Entre sus contribuciones esta el método de la conservación de la energía para el cálculo de las frecuencias. | |||
Después de que se sentaran estos descubrimientos iniciales, empezó a existir un interés practico al aplicar los conocimientos en necesidades humanas. | |||
[[Archivo:Rayl.jpg|350px|thumb|right|'''Fig. 0''' John Rayleigh ]] | |||
En tiempos más "recientes" son destacables las contribuciones a la teoría de vibraciones de Stodola, Timoshenko y Mindlin; | |||
Stodola desarrolló un método de análisis de vibraciones en vigas que se aplicó al estudio de vibraciones el los álabes de turbinas. | |||
Los trabajos de Timoshenko y Mindlin ampliaron las teorías de de vibraciones de vigas y placas. | |||
Durante buena parte del siglo XX los estudios de vibraciones que abordaban problemas de ingeniería complejos, utilizaban modelos muy simplificados con unos pocos grados de libertad. Gracias al desarrollo de los ordenadores digitales en la década de los cincuenta, se hizo posible el uso de modelos cada vez más complejos. | |||
El desarrollo posterior de los métodos de elementos finitos, permitió a los ingenieros utilizar ordenador para analizar sistemas complejos de miles de grados de libertad en campos como la dinámica vehicular y estructuras. | |||
Actualmente la aplicación de la teoría de vibraciones, así como determinar frecuencias y modos naturales se aplica en diferentes áreas como biológicas y de la salud, entre otras. | |||
<ref name = "Análisis dimensional de los modos de vibración de un eje ferroviario, Miguel Pérez Rodríguez "/> | |||
==Tabla Comparativa== | |||
{| class="wikitable" | |||
!Método | |||
!¿Qué nos ayuda a encontrar? | |||
|- | |||
|Fórmula de Dunkerley | |||
| El valor aproximado de la frecuencia fundamental de un sistema compuesto. | |||
|- | |||
|Método de Rayleigh | |||
| El valor aproximado de la frecuencia fundamental de un sistema que siempre es mayor que el valor verdadero. | |||
|- | |||
|Método de Holzer | |||
|Las frecuencias y modos naturales del sistema, uno a la vez, por medio de varios valores de prueba de cada frecuencia. | |||
|- | |||
|Método de iteración matricial | |||
|Todas las frecuencias naturales utilizando vectores de prueba y el procedimiento de deflación matricial. | |||
|- | |||
|Método de Jacobi | |||
|Todos los valores y vectores característicos al mismo tiempo sin utilizar vectores de prueba. | |||
|} | |||
=Fórmula de Dunkerley= | |||
Obtendremos el valor aproximado de la $\textbf{frecuencia fundamental}$ de un sistema compuesto en función de las frecuencias naturales de sus partes componentes. | |||
Derivaremos abusando de que las altas frecuencias naturales de la mayoría de los sistemas vibratorios son grandes comparadas con sus frecuencias fundamentales.<ref name = "Generalization of Dunkerley’s equation for the undamped linear positive semidefinite system, Jianhua Zheng, Ji Wang">Jianhua Zheng, Ji Wang, Generalization of Dunkerley’s equation for the undamped linear positive semidefinite system, International Conference on Advances in Computational Modeling and Simulation, 2012.</ref> | |||
Para derivar la fórmula de Dunkerley, considere un sistema general de n grados de libertad cuyos valores eigen se pueden determinar resolviendo la ecuación de frecuencia: | Para derivar la fórmula de Dunkerley, considere un sistema general de n grados de libertad cuyos valores eigen se pueden determinar resolviendo la ecuación de frecuencia: | ||
| Línea 33: | Línea 79: | ||
\end{equation} | \end{equation} | ||
En un sistema de masa concentrada con una matriz diagonal, la ecuación $\ref{fre2}$ se escribe como | En un sistema de masa concentrada con una matriz diagonal, la ecuación ($\ref{fre2}$) se escribe como: | ||
\begin{equation} \label{matsum} | \begin{equation} \label{matsum} | ||
| Línea 59: | Línea 105: | ||
\end{equation} | \end{equation} | ||
es decir | es decir: | ||
\begin{equation}\label{matsum2} | \begin{equation}\label{matsum2} | ||
| Línea 71: | Línea 117: | ||
\end{equation} | \end{equation} | ||
Realizando la expansión de la ecuación $\ref{matsum2}$ | Realizando la expansión de la ecuación ($\ref{matsum2}$): | ||
\begin{multline} \label{exp} | \begin{multline} \label{exp} | ||
| Línea 79: | Línea 125: | ||
\end{multline} | \end{multline} | ||
Una ecuación polinomial de grado enésimo en $\frac{1}{\omega^2}$. Si las raíces de la ecuación $\ref{exp}$ se indica como $\frac{1}{\omega_{1}^{2}}$ , $\frac{1}{\omega_{2}^{2}}$, $\cdots$, $\frac{1}{\omega_{n}^{2}}$. Por lo tanto | Una ecuación polinomial de grado enésimo en $\frac{1}{\omega^2}$. Si las raíces de la ecuación ($\ref{exp}$) se indica como $\frac{1}{\omega_{1}^{2}}$ , $\frac{1}{\omega_{2}^{2}}$, $\cdots$, $\frac{1}{\omega_{n}^{2}}$. Por lo tanto: | ||
\begin{ | \begin{equation} \label{exp2} | ||
\left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{1}^{2}} \right) \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{2}^{2}} \right) \cdots \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{n}^{2}} \right)\\ | \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{1}^{2}} \right) \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{2}^{2}} \right) \cdots \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{n}^{2}} \right)\\ | ||
= \left(\frac{1}{\omega^{2}}\right)^n - \left(\frac{1}{\omega_{1}^{2}} + \frac{1}{\omega_{2}^{2}} + \cdots + \frac{1}{\omega_{n}^{2}}\right) \left(\frac{1}{\omega^{2}} \right)^{n-1} - \cdots = 0 | = \left(\frac{1}{\omega^{2}}\right)^n - \left(\frac{1}{\omega_{1}^{2}} + \frac{1}{\omega_{2}^{2}} + \cdots + \frac{1}{\omega_{n}^{2}}\right) \left(\frac{1}{\omega^{2}} \right)^{n-1} - \cdots = 0 | ||
\end{ | \end{equation} | ||
Igualando el coeficiente de $\left(\frac{1}{\omega^{2}} \right)^{n-1}$ en las ecuaciones $\ref{exp2}$ y $\ref{exp}$ se obtiene | Igualando el coeficiente de $\left(\frac{1}{\omega^{2}} \right)^{n-1}$ en las ecuaciones ($\ref{exp2}$) y ($\ref{exp}$) se obtiene: | ||
\begin{equation}\label{igual} | \begin{equation}\label{igual} | ||
| Línea 92: | Línea 138: | ||
\end{equation} | \end{equation} | ||
En la mayoría de los casos las frecuancias altas $\omega_2 , \omega_3, \cdots , \omega_n$ son considerablemente más grandes que la frecuencia fundamental $\omega_1$ | En la mayoría de los casos las frecuancias altas $\omega_2 , \omega_3, \cdots , \omega_n$ son considerablemente más grandes que la frecuencia fundamental $\omega_1$. | ||
\begin{equation*} | \begin{equation*} | ||
| Línea 98: | Línea 144: | ||
\end{equation*} | \end{equation*} | ||
Por lo tanto la ecuación $\ref{igual}$ se puede escribir aproximadamente como | Por lo tanto la ecuación ($\ref{igual}$) se puede escribir aproximadamente como: | ||
\begin{equation}\label{igual2} | \begin{equation}\label{igual2} | ||
| Línea 104: | Línea 150: | ||
\end{equation} | \end{equation} | ||
Esta ecuación se conoce como ''fórmula de Dunkerley''. La frecuencia fundamental que se da en la ecuación $\ref{igual2}$ siempre será menor que el valor exacto. En algunos casos convendrá más volver a escribir la ecuación $\ref{igual2}$ como: | Esta ecuación se conoce como ''fórmula de Dunkerley''. La frecuencia fundamental que se da en la ecuación ($\ref{igual2}$) siempre será menor que el valor exacto. En algunos casos convendrá más volver a escribir la ecuación ($\ref{igual2}$) como: | ||
\begin{equation} | \begin{equation} | ||
| Línea 111: | Línea 157: | ||
donde $\omega_{in} = ( {1}/{a_{ii}m_i} )^{1/2} = ({k_{ii}}/{m_i})^{1/2} $ indica la frecuencia natural de un sistema de un solo grado de libertad compuesto de la masa $m_i$ y el resorte de rigidez $k_ii, i =1,2, \cdots, n$. | donde $\omega_{in} = ( {1}/{a_{ii}m_i} )^{1/2} = ({k_{ii}}/{m_i})^{1/2} $ indica la frecuencia natural de un sistema de un solo grado de libertad compuesto de la masa $m_i$ y el resorte de rigidez $k_ii, i =1,2, \cdots, n$. <ref name = "Vibraciones Mecánicas Rao">Rao, Singiresu S. Vibraciones Mecánicas, Quinta Edición, Edit. Pearson Educación, México, 2012.</ref> | ||
=Método de Rayleigh= | |||
Este método se puede ampliar para encontrar el valor aproximado de la frecuencia natural fundamental de un sistema discreto (cualquier cuerpo se compone de una estructura discreta o una distribución continua de materia). El método está basado en el principio de Rayleigh, el cual se puede citar como sigue: | Este método se puede ampliar para encontrar el valor aproximado de la frecuencia natural fundamental de un sistema discreto (cualquier cuerpo se compone de una estructura discreta o una distribución continua de materia). El método está basado en el principio de Rayleigh, el cual se puede citar como sigue: | ||
| Línea 126: | Línea 172: | ||
Derivaremos una expresión para el valor apropiado de la primera frecuencia natural de | Derivaremos una expresión para el valor apropiado de la primera frecuencia natural de | ||
un sistema de varios grados de libertad de acuerdo con el método de Rayleigh (Ver ecuación $\ref{MetRay}$). | un sistema de varios grados de libertad de acuerdo con el método de Rayleigh (Ver ecuación ($\ref{MetRay}$)). | ||
Las energías cinéticas y potencial de un sistema de $n$ grados de libertad se expresan como: | |||
\begin{equation} \label{T} | \begin{equation} \label{T} | ||
| Línea 139: | Línea 184: | ||
\end{equation} | \end{equation} | ||
Para enconttrar las frecuencias naturales, suponga que el movimiento armónico es | Para enconttrar las frecuencias naturales, suponga que el movimiento armónico es: | ||
\begin{equation} \label{x} | \begin{equation} \label{x} | ||
| Línea 151: | Línea 196: | ||
\end{equation} | \end{equation} | ||
Sustituyendo la ecuación $\ref{x}$ en las ecuaciones $\ref{T}$ y $\ref{V}$ | Sustituyendo la ecuación ($\ref{x}$) en las ecuaciones ($\ref{T}$) y ($\ref{V}$). | ||
\begin{equation} \label{Tmax} | \begin{equation} \label{Tmax} | ||
| Línea 161: | Línea 206: | ||
\end{equation} | \end{equation} | ||
Igualando $T_{máx}=V_{máx}$, obtenemos | Igualando $T_{máx}=V_{máx}$, obtenemos: | ||
\begin{equation} \label{w} | \begin{equation} \label{w} | ||
| Línea 168: | Línea 213: | ||
Y es el lado derecho de la ecuación que se conoce como cociente de ''Rayleigh'' y se indica como $R(\vec{X})$. | Y es el lado derecho de la ecuación que se conoce como cociente de ''Rayleigh'' y se indica como $R(\vec{X})$. | ||
La ecuación ($\ref{w}$) tambien se puede obtener a partir de la relación ${k} \vec{X} = \omega^2 {m} \vec{X}$. Premultiplicando esta ecuación por $\vec{X}^T$ y resolviendo la ecuación resultante se obtiene la ecuación ($\ref{w}$). | |||
$\textbf{Propiedades del cociente de Rayleigh }$ | $\textbf{Propiedades del cociente de Rayleigh }$ | ||
Como ya antes se expresó, $R(\vec{X})$ tiene un valor estacionario cuando el vector arbitrario $\vec{X}$ se acerca a cualquier vector característico $\vec{X}^{(r)}$. | |||
El método de Holzer es en esencia un esquema de prueba y error para determinar las frecuencias | Para comprobarlo, expresamos el vector arbitrario $\vec{X}$ en función de los modos normales del sistema, $\vec{X}^{(i)}$, como: | ||
naturales de sistemas $\textbf{subamortiguados}$, $\textbf{amortiguados}$, $\textbf{semidefinidos}$, fijos, o sistemas vibratorios ramificados que implican desplazamientos lineales y angulares. El método también proporciona los modos. | |||
\begin{equation} \label{Xvec} | |||
\vec{X} = c_1 \vec{X}^{1} + c_2 \vec{X}^{2} + c_3 \vec{X}^{3} + \cdots | |||
\end{equation} | |||
Entonces: | |||
\begin{equation} \label{XTk} | |||
\vec{X}^T [k] \vec{X} = c_1^2 \vec{X}^{(1)^T} [k] \vec{X}^{(1)} + c_2^2 \vec{X}^{(2)^T} [k] \vec{X}^{(2)} + c_3^2 \vec{X}^{(3)^T} [k] \vec{X}^{(3)} + \cdots | |||
\end{equation} | |||
Y | |||
\begin{equation} \label{XTm} | |||
\vec{X}^T [m] \vec{X} = c_1^2 \vec{X}^{(1)^T} [m] \vec{X}^{(1)} + c_2^2 \vec{X}^{(2)^T} [m] \vec{X}^{(2)} + c_3^2 \vec{X}^{(3)^T} [m] \vec{X}^{(3)} + \cdots | |||
\end{equation} | |||
Sabiendo que los términos cruzados de la forma $c_i c_j \vec{X}^{(i)^T} [k] \vec{X}^{(j)}$ y $c_i c_j \vec{X}^{(i)^T} [m] \vec{X}^{(j)}$, $i \neq j$, son cero de acuerdo con la propiedad de ortogonalidad. Utilizando las ecuaciones ($\ref{XTk}$) y ($\ref{XTm}$) y la relación: | |||
\begin{equation} \label{rel} | |||
\vec{X}^{(i)^T} [k] \vec{X}^{(i)} = \omega^2 \vec{X}^{(i)^T} [m] \vec{X}^{(i)} | |||
\end{equation} | |||
el cociente de Rayleight de la ecuación ($\ref{w}$) se expresa como: | |||
\begin{equation} \label{w2} | |||
\omega^2 = R(\vec{X}) = \frac{c_1^2 \omega_1^2 \vec{X}^{(1)^T} [m] \vec{X}^{(1)} + c_2^2 \omega_2^2 \vec{X}^{(2)^T} [m] \vec{X}^{(2)} + \cdots}{c_1^2 \vec{X}^{(1)^T} [m] \vec{X}^{(1)} + c_2^2 \vec{X}^{(2)^T} [m] \vec{X}^{(2)} + \cdots} | |||
\end{equation} | |||
Si los modos normales, se normalizan, la ecuación ($\ref{w2}$) se escribe como: | |||
\begin{equation} \label{w3} | |||
\omega^2 = R(\vec{X}) = \frac{c_1^2 \omega_1^2 + c_2^2 \omega_2^2 + \cdots}{c_1^2 + c_2^2 + \cdots} | |||
\end{equation} | |||
Si $\vec{X}$ difiere poco del vector característico $\vec{X}^{(r)}$, el coeficiente $c_r$ será mucho mayor que los coeficientes restantes $c_i (i \neq r)$ y la ecuación ($\ref{w3}$) se escribe como: | |||
\begin{equation} \label{w4} | |||
R(\vec{X}) = \frac{c_r^2 \omega_r^2 + c_2^2 \sum_{i=1,2,\cdots} \left( \frac{c_i}{c_r} \right)^2 \omega_i^2 }{c_1^2 + c_2^2 \sum_{i=1,2,\cdots} \left( \frac{c_i}{c_r} \right)^2} | |||
\end{equation} | |||
Dado que $|c_i/c_r| = \varepsilon_i \ll 1$, donde $\varepsilon_i$ es un número pequeño para todas las $i r$, la ecuación ($\ref{w4}$) nos proporciona: | |||
\begin{equation} \label{Rx} | |||
R(\vec{X}) = \omega_r^2 [1 + 0(\varepsilon ^2)] | |||
\end{equation} | |||
donde $ 0(\varepsilon ^2)$ representa una expresión en e del segundo orden o mayor. La ecuación ($\ref{Rx}$) indica que si el vector arbitrario $\vec{X}$ difiere del vector característico $\vec{X}^{(r)}$ en una pequeña cantidad del primer orden, $R \vec{X}$ difiere del valor característico $\omega_r^2$ en una pequeña cantidad del segundo orden. | |||
El valor "estacionario" (recordando que no es un estado en reposo) es en realidad un valor mínimo cerca del modo fundamental $\vec{X}^{(1)}$. Para ver esto, sea $r=1$ en la ecuación ($\ref{w4}$) y escribimos: | |||
\begin{equation*} \ | |||
R(\vec{X}) = \frac{\omega_1^2 + \sum_{i=2,3, \cdots} \left( \frac{c_i}{c_1} \right)^2 \omega_i^2 }{ \left\lbrace 1 + \sum_{i=1,2,\cdots} \left( \frac{c_i}{c_r} \right)^2 \right\rbrace} | |||
\end{equation*} | |||
\begin{equation*} | |||
\simeq \omega_1^2 + \sum_{i=2,3, \cdots} \varepsilon_i^2 \omega_i^2 - \omega_1^2 \sum_{i=2,3, \cdots} \varepsilon_i^2 | |||
\end{equation*} | |||
\begin{equation} \label{aprox} | |||
\simeq \omega_1^2 + \sum_{i=2,3, \cdots} (\omega_i^2 - \omega_1^2) \varepsilon_i^2 | |||
\end{equation} | |||
Puesto que, por lo general, $\omega_i^2 > \omega_1^2 $ con $i = 2, 3, ...,$ la ecuación ($\ref{aprox}$) conduce a: | |||
\begin{equation} \label{R>} | |||
R(\vec{X}) \geq \omega_1^2 | |||
\end{equation} | |||
la cual muestra que el cociente de Rayleigh nunca es menor que el primer valor característico. | |||
Análogamente de la misma manera, podemos mostrar que: | |||
\begin{equation} \label{R<} | |||
R(\vec{X}) \leq \omega_n^2 | |||
\end{equation} | |||
Concluyendo que el cociente de Rayleigh nunca es más alto que el valor característico más alto. | |||
Así que el cociente de Rayleigh constituye un límite superior para $\omega_1^2$ y un límite inferior para $\omega_n^2$. | |||
=Método de Holzer = | |||
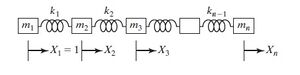
El método de Holzer es en esencia un esquema de prueba y error para determinar las frecuencias naturales de sistemas $\textbf{subamortiguados}$, $\textbf{amortiguados}$, $\textbf{semidefinidos}$, fijos, o sistemas vibratorios ramificados que implican desplazamientos lineales y angulares. El método también proporciona los modos. | |||
[[Archivo:SistemaMR.jpg|miniaturadeimagen]250px|thumb|cent|'''Fig. 1''' Sistema masa resorte con ambos extremos libres ]] | [[Archivo:SistemaMR.jpg|miniaturadeimagen]250px|thumb|cent|'''Fig. 1''' Sistema masa resorte con ambos extremos libres ]] | ||
Empezando por el análisis de vibración de sistemas de resorte-masa. Las ecuaciones de | Empezando por el análisis de vibración de sistemas de resorte-masa. Las ecuaciones de movimiento de un sistema de resorte-masa (vea la figura $\textbf{Fig. 1}$) se expresan como: | ||
movimiento de un sistema de resorte-masa (vea la figura $\textbf{Fig. 1}$) se expresan como | |||
\begin{equation} \label{m1} | \begin{equation} \label{m1} | ||
| Línea 193: | Línea 323: | ||
Para movimiento armónico, $x_i(t) = X_i \cos \omega t$ , donde $X_i$ es la amplitud de la masa m_i y las ecuaciones $\ref{m1}$ y $\ref{m2}$ se escriben como | Para movimiento armónico, $x_i(t) = X_i \cos \omega t$ , donde $X_i$ es la amplitud de la masa m_i y las ecuaciones ($\ref{m1}$) y ($\ref{m2}$) se escriben como: | ||
\begin{equation} \label{wm1} | \begin{equation} \label{wm1} | ||
| Línea 208: | Línea 338: | ||
El procedimiento para el método de Holzer se inicia con una frecuencia de prueba \omega y la amplitud de la masa $m_i$ como $X_1=1$. Las ecuaciones $\ref{wm2}$ y $\ref{wm1}$ se pueden utilizar entonces para obtener las amplitudes de las masas $m_2, m_3, \cdots, m_i :$ | El procedimiento para el método de Holzer se inicia con una frecuencia de prueba \omega y la amplitud de la masa $m_i$ como $X_1=1$. Las ecuaciones ($\ref{wm2}$) y ($\ref{wm1}$) se pueden utilizar entonces para obtener las amplitudes de las masas $m_2, m_3, \cdots, m_i :$ | ||
\begin{equation} \label{X2} | \begin{equation} \label{X2} | ||
| Línea 233: | Línea 363: | ||
\end{equation} | \end{equation} | ||
Los cálculos se repiten con otras frecuencias más de prueba $\omega$. Las frecuencias naturales se identifican como aquellos valores de $\omega$ que proporcionan $F=0$ para un sistema con ambos extremos | Los cálculos se repiten con otras frecuencias más de prueba $\omega$. Las frecuencias naturales se identifican como aquellos valores de $\omega$ que proporcionan $F=0$ para un sistema con ambos extremos libres. Para ello, es conveniente trazar una gráfica entre $F$ y $\omega$, utilizando el mismo procedimiento para sistemas de resorte-masa que para sistemas $\textbf{torsionales}$. | ||
libres. Para ello, es conveniente trazar una gráfica entre $F$ y $\omega$, utilizando el mismo procedimiento | <ref name = "Vibraciones Mecánicas Rao">Rao, Singiresu S. Vibraciones Mecánicas, Quinta Edición, Edit. Pearson Educación, México, 2012.</ref> | ||
para sistemas de resorte-masa que para sistemas $\textbf{torsionales}$. | |||
= | |||
=Método de iteración matricial= | |||
La | Otro método existente es el de iteración maticial, el cuál no se tocará a detalle ya que la única intención es darlo a conocer. | ||
Este método asume que las frecuencias naturales son distintas y también separadas de modo que $\omega_1 < \omega_2 < , \cdots , \omega_n$. La iteración se inicia seleccionando un vector de prueba $\vec X_1$, el que luego se premultiplica por la matriz dinámica [D]. | |||
Utilizando la convergencia del proceso se explica como sigue: | |||
De acuerdo con el teorema de expansión, cualquier vector arbitrario de $n$ dimensiones $\vec{X}$ 1 se puede expresar como una combinación lineal de $n$ vectores característicos ortogonales del sistema $\vec{x}(i), i = 1,2, \cdots , n$ | |||
=Método de Jacobi= | |||
El método de Jacobi también es un método iterativo pero produce todos los valores y vectores característicos de $[D]$ al mismo tiempo, donde $[D] = [d_ij]$ es una matriz simétrica real de orden $n \times n$. | |||
El método está basado en un teorema de álgebra lineal que establece que una matriz | El método está basado en un teorema de álgebra lineal que establece que una matriz simétrica real [D] tiene sólo valores característicos reales y que en ella existe una matriz ortogonal real $[R]$ de modo que $[R]^T[D][R]$ es diagonal. <ref name = "Vibraciones Mecánicas Rao">Rao, Singiresu S. Vibraciones Mecánicas, Quinta Edición, Edit. Pearson Educación, México, 2012.</ref> | ||
simétrica real [D] tiene sólo valores característicos reales y que en ella existe una matriz ortogonal real $[R]$ de modo que $[R]^T[D][R]$ es diagonal. | |||
Los elementos diagonales son los valores característicos, y las columnas de la matriz $[R]$ son los vectores característicos. De acuerdo con el método de Jacobi, la matriz $[R]$ se genera como un producto de varias matrices de rotación de la forma | Los elementos diagonales son los valores característicos, y las columnas de la matriz $[R]$ son los vectores característicos. De acuerdo con el método de Jacobi, la matriz $[R]$ se genera como un producto de varias matrices de rotación de la forma: | ||
\begin{equation} | \begin{equation} | ||
[R_1]_{n \times n} | [R_1]_{n \times n} = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
& & & i & & j & & &\\ | & & & i & & j & & &\\ | ||
| Línea 277: | Línea 398: | ||
\end{equation} | \end{equation} | ||
donde todos los elementos aparte de los que aparecen en las columnas y filas $i$ y $j$ son idénticos a los | donde todos los elementos aparte de los que aparecen en las columnas y filas $i$ y $j$ son idénticos a los de la matriz identidad $[I]$. | ||
de la matriz identidad $[I]$. | Si las entradas seno y coseno aparecen en las posiciones $(i, i), (i, j), (j, i)$ y $(j, j)$, entonces los elementos correspondientes de $[R1]^T[D][R1]$ se calculan como sigue: | ||
Si las entradas seno y coseno aparecen en las posiciones $(i, i), (i, j), (j, i)$ | |||
y $(j, j)$, entonces los elementos correspondientes de $[R1]^T[D][R1]$ se calculan como sigue: | |||
\begin{equation} | \begin{equation} | ||
| Línea 294: | Línea 413: | ||
\end{equation} | \end{equation} | ||
Es conveniente elegir a $\theta$ como sigue, para hacer $\underline{d_{ij}} = \underline{d_{ji}} = 0 $ | Es conveniente elegir a $\theta$ como sigue, para hacer $\underline{d_{ij}} = \underline{d_{ji}} = 0 $. | ||
\begin{equation} | \begin{equation} | ||
| Línea 302: | Línea 421: | ||
Así, cada paso del método de Jacobi reduce un par de elementos fuera de la diagonal a cero. | Así, cada paso del método de Jacobi reduce un par de elementos fuera de la diagonal a cero. | ||
Notar que en el siguiente paso, al mismo tiempo que el método reduce un nuevo par de cero, introduce contribuciones no cero en posiciones que antes eran cero. Sin embargo, las matrices sucesivas de la forma | Notar que en el siguiente paso, al mismo tiempo que el método reduce un nuevo par de cero, introduce contribuciones no cero en posiciones que antes eran cero. Sin embargo, las matrices sucesivas de la forma: | ||
\begin{equation*} | \begin{equation*} | ||
| Línea 308: | Línea 427: | ||
\end{equation*} | \end{equation*} | ||
Convergen a la forma diagonal requerida; la matriz final [R], cuyas columnas da los vectores eigen | |||
se escriben entonces como | se escriben entonces como: | ||
\begin{equation} | \begin{equation} | ||
[R] = [R_1][R_2][R_3] \cdots | [R] = [R_1][R_2][R_3] \cdots | ||
\end{equation} | \end{equation} | ||
=Bibliografía complementaria= | |||
*https://www.institucional.frc.utn.edu.ar/sistemas/Noticias/INV/Seminarios/ast_2007_presentacion_giro.pdf | |||
*https://www.academia.utp.ac.pa/sites/default/files/docente/72/clase_8_determinacion_de_frecuencias_naturales_y_formas_modales.pdf | |||
[[Usuario:Carlosmiranda|Carlosmiranda]] ([[Usuario discusión:Carlosmiranda|discusión]]) 16:24 22 nov 2020 (CST) | |||
[[Categoría: Vibra]] | |||
Revisión actual - 04:43 5 oct 2023
Introducción
Existen diversos métodos numéricos y analíticos que han sido desarrollados para determinar las frecuencias naturales y los modos de sistemas con múltiples grados de libertad.
Es muy favorable determinar frecuencias y modos naturales para predecir o analizar fenómenos. Algunos ejemplos son:
$\circ$ Frecuencia fundamental de vigas y flechas.
$\circ$ Frecuencia fundamental de un sistema de tres grados de libertad, como un sistema masa resorte o péndulos.
$\circ$ Frecuencia fundamental de una flecha con rotores.
$\circ$ Frecuencias naturales de un sistema torsional.
Breve contexto histórico
Matemáticos y científicos como Taylor, Bernoulli. D´Alembert, Euler, Lagrange o Fourier contribuyeron al desarrollo de la teoría de vibraciones.
Wallis y Sauveur observaron independientemente el fenómeno de los modos de vibración en cuerdas. Ellos demostraron que la frecuencia del segundo modo de vibración era $\textbf{el doble que la del primer modo y que la del tercer modo era el triple}.$
Se le atribuye a Sauveur como el primero en asignar la denominación de “fundamental” a la frecuencia natural más baja y “armónicas” a las demás. [1]
En 1877 Rayleigh publicó el libro Teoría del sonido. Entre sus contribuciones esta el método de la conservación de la energía para el cálculo de las frecuencias.
Después de que se sentaran estos descubrimientos iniciales, empezó a existir un interés practico al aplicar los conocimientos en necesidades humanas.
En tiempos más "recientes" son destacables las contribuciones a la teoría de vibraciones de Stodola, Timoshenko y Mindlin; Stodola desarrolló un método de análisis de vibraciones en vigas que se aplicó al estudio de vibraciones el los álabes de turbinas. Los trabajos de Timoshenko y Mindlin ampliaron las teorías de de vibraciones de vigas y placas.
Durante buena parte del siglo XX los estudios de vibraciones que abordaban problemas de ingeniería complejos, utilizaban modelos muy simplificados con unos pocos grados de libertad. Gracias al desarrollo de los ordenadores digitales en la década de los cincuenta, se hizo posible el uso de modelos cada vez más complejos.
El desarrollo posterior de los métodos de elementos finitos, permitió a los ingenieros utilizar ordenador para analizar sistemas complejos de miles de grados de libertad en campos como la dinámica vehicular y estructuras.
Actualmente la aplicación de la teoría de vibraciones, así como determinar frecuencias y modos naturales se aplica en diferentes áreas como biológicas y de la salud, entre otras.
Tabla Comparativa
| Método | ¿Qué nos ayuda a encontrar? |
|---|---|
| Fórmula de Dunkerley | El valor aproximado de la frecuencia fundamental de un sistema compuesto. |
| Método de Rayleigh | El valor aproximado de la frecuencia fundamental de un sistema que siempre es mayor que el valor verdadero. |
| Método de Holzer | Las frecuencias y modos naturales del sistema, uno a la vez, por medio de varios valores de prueba de cada frecuencia. |
| Método de iteración matricial | Todas las frecuencias naturales utilizando vectores de prueba y el procedimiento de deflación matricial. |
| Método de Jacobi | Todos los valores y vectores característicos al mismo tiempo sin utilizar vectores de prueba. |
Fórmula de Dunkerley
Obtendremos el valor aproximado de la $\textbf{frecuencia fundamental}$ de un sistema compuesto en función de las frecuencias naturales de sus partes componentes.
Derivaremos abusando de que las altas frecuencias naturales de la mayoría de los sistemas vibratorios son grandes comparadas con sus frecuencias fundamentales.[2]
Para derivar la fórmula de Dunkerley, considere un sistema general de n grados de libertad cuyos valores eigen se pueden determinar resolviendo la ecuación de frecuencia:
\begin{equation} \label{fre} |-[k]+ \omega^2 [m]|= 0 \end{equation}
o
\begin{equation}\label{fre2} \left|-\frac{1}{\omega^2}[I]+[a][m] \right|=0 \end{equation}
En un sistema de masa concentrada con una matriz diagonal, la ecuación ($\ref{fre2}$) se escribe como:
\begin{equation} \label{matsum} \left|-\frac{1}{\omega^2} \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix} + \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} \begin{bmatrix} m_{1} & 0 & \cdots & 0 \\ 0 & m_{2} & \cdots & 0 \\ \vdots \\ 0 & 0 & \cdots & m_{n} \end{bmatrix} \right| =0 \end{equation}
es decir:
\begin{equation}\label{matsum2} \begin{vmatrix} \left(- \frac{1}{\omega^2} + a_{11}m_{1} \right) & a_{12}m_2 & \cdots & a_{1n}m_n \\ a_{21}m_1 & \left(- \frac{1}{\omega^2} + a_{22}m_{2} \right) & \cdots & a_{2n}m_n\\ \vdots \\ a_{n1}m_1 & a_{n2}m_2 & \cdots & \left(- \frac{1}{\omega^2} + a_{nn}m_{n} \right) \end{vmatrix} =0 \end{equation}
Realizando la expansión de la ecuación ($\ref{matsum2}$):
\begin{multline} \label{exp} \left(\frac{1}{\omega^2} \right)^n - (a_{11}m_1 + a_{22}m_2 + \cdots + a_{nn} m_n) \left(\frac{1}{\omega^2} \right)^{n-1}\\ + (a_{11} a_{33}m_1 m_3 + \cdots + a_{n-1,n-1} a_{nn}m_{n-1}m_n\\ - a_{12}a_{21}m_1m_2 - \cdots - a_{n-1,n} a_{n,n-1} m_{n-1}m_n) \left(\frac{1}{\omega^2} \right)^{n-2}- \cdots = 0 \end{multline}
Una ecuación polinomial de grado enésimo en $\frac{1}{\omega^2}$. Si las raíces de la ecuación ($\ref{exp}$) se indica como $\frac{1}{\omega_{1}^{2}}$ , $\frac{1}{\omega_{2}^{2}}$, $\cdots$, $\frac{1}{\omega_{n}^{2}}$. Por lo tanto:
\begin{equation} \label{exp2} \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{1}^{2}} \right) \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{2}^{2}} \right) \cdots \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{n}^{2}} \right)\\ = \left(\frac{1}{\omega^{2}}\right)^n - \left(\frac{1}{\omega_{1}^{2}} + \frac{1}{\omega_{2}^{2}} + \cdots + \frac{1}{\omega_{n}^{2}}\right) \left(\frac{1}{\omega^{2}} \right)^{n-1} - \cdots = 0 \end{equation}
Igualando el coeficiente de $\left(\frac{1}{\omega^{2}} \right)^{n-1}$ en las ecuaciones ($\ref{exp2}$) y ($\ref{exp}$) se obtiene:
\begin{equation}\label{igual} \frac{1}{\omega_{1}^{2}} + \frac{1}{\omega_{2}^{2}} + \cdots + \frac{1}{\omega_{n}^{2}} = a_{11}m_1 + a_{22}m_2 + \cdots + a_{nn} m_n \end{equation}
En la mayoría de los casos las frecuancias altas $\omega_2 , \omega_3, \cdots , \omega_n$ son considerablemente más grandes que la frecuencia fundamental $\omega_1$.
\begin{equation*} \frac{1}{\omega_{i}^{2}} \ll \frac{1}{\omega_{1}^{2}}, i= 2,3, \cdots, n \end{equation*}
Por lo tanto la ecuación ($\ref{igual}$) se puede escribir aproximadamente como:
\begin{equation}\label{igual2} \frac{1}{\omega_{1}^{2}} \simeq a_{11}m_1 + a_{22}m_2 + \cdots + a_{nn} m_n \end{equation}
Esta ecuación se conoce como fórmula de Dunkerley. La frecuencia fundamental que se da en la ecuación ($\ref{igual2}$) siempre será menor que el valor exacto. En algunos casos convendrá más volver a escribir la ecuación ($\ref{igual2}$) como:
\begin{equation} \frac{1}{\omega_{1}^{2}} \simeq \frac{1}{\omega_{1n}^{2}} + \frac{1}{\omega_{2n}^{2}}+ \cdots + \frac{1}{\omega_{nn}^{2}} \end{equation}
donde $\omega_{in} = ( {1}/{a_{ii}m_i} )^{1/2} = ({k_{ii}}/{m_i})^{1/2} $ indica la frecuencia natural de un sistema de un solo grado de libertad compuesto de la masa $m_i$ y el resorte de rigidez $k_ii, i =1,2, \cdots, n$. [3]
Método de Rayleigh
Este método se puede ampliar para encontrar el valor aproximado de la frecuencia natural fundamental de un sistema discreto (cualquier cuerpo se compone de una estructura discreta o una distribución continua de materia). El método está basado en el principio de Rayleigh, el cual se puede citar como sigue:
"La frecuencia de vibración de un sistema conservador vibratorio respecto a una posición de equilibrio tiene en valor estacionario de un modo natural. Este valor estacionario, de hecho, es un valor mínimo en la proximidad del modo natural fundamental."
Resaltando que estacionario no refiere a un estado de reposo, sino a un modo resonante de un objeto extendido vibrante.
\begin{equation} \label{MetRay} T = \frac{1}{2} \int_0^l w^2 dm= \frac{1}{2} w^2 \rho A(x) dx \end{equation}
Derivaremos una expresión para el valor apropiado de la primera frecuencia natural de un sistema de varios grados de libertad de acuerdo con el método de Rayleigh (Ver ecuación ($\ref{MetRay}$)).
Las energías cinéticas y potencial de un sistema de $n$ grados de libertad se expresan como:
\begin{equation} \label{T} T= \frac{1}{2} \dot{x}^T [M] \dot{x} \end{equation}
\begin{equation} \label{V} V= \frac{1}{2} \vec{x}^T [k] \vec{x} \end{equation}
Para enconttrar las frecuencias naturales, suponga que el movimiento armónico es:
\begin{equation} \label{x} \vec{x} = \vec{X} \cos \omega t \end{equation}
donde $\vec{X}$ indica el vector de amplitudes (modo de forma) y $\omega$ representa la frecuencia natural de vibración. Si el sistema es conservador, la energía cinética máxima es igual a la energía potencial máxima:
\begin{equation} \label{T-T} T_{máx}= V_{máx} \end{equation}
Sustituyendo la ecuación ($\ref{x}$) en las ecuaciones ($\ref{T}$) y ($\ref{V}$).
\begin{equation} \label{Tmax} T_{máx}= \frac{1}{2} \vec{X}^T [m] \vec{X} \omega^2 \end{equation}
\begin{equation} \label{Vmax} V_{máx}= \frac{1}{2} \vec{X}^T [k] \vec{X} \end{equation}
Igualando $T_{máx}=V_{máx}$, obtenemos:
\begin{equation} \label{w} \omega^2 = \frac{ \vec{X}^T [k] \vec{X} }{ \vec{X}^T [m] \vec{X}} \end{equation}
Y es el lado derecho de la ecuación que se conoce como cociente de Rayleigh y se indica como $R(\vec{X})$.
La ecuación ($\ref{w}$) tambien se puede obtener a partir de la relación ${k} \vec{X} = \omega^2 {m} \vec{X}$. Premultiplicando esta ecuación por $\vec{X}^T$ y resolviendo la ecuación resultante se obtiene la ecuación ($\ref{w}$).
$\textbf{Propiedades del cociente de Rayleigh }$
Como ya antes se expresó, $R(\vec{X})$ tiene un valor estacionario cuando el vector arbitrario $\vec{X}$ se acerca a cualquier vector característico $\vec{X}^{(r)}$.
Para comprobarlo, expresamos el vector arbitrario $\vec{X}$ en función de los modos normales del sistema, $\vec{X}^{(i)}$, como:
\begin{equation} \label{Xvec} \vec{X} = c_1 \vec{X}^{1} + c_2 \vec{X}^{2} + c_3 \vec{X}^{3} + \cdots \end{equation}
Entonces:
\begin{equation} \label{XTk} \vec{X}^T [k] \vec{X} = c_1^2 \vec{X}^{(1)^T} [k] \vec{X}^{(1)} + c_2^2 \vec{X}^{(2)^T} [k] \vec{X}^{(2)} + c_3^2 \vec{X}^{(3)^T} [k] \vec{X}^{(3)} + \cdots \end{equation}
Y
\begin{equation} \label{XTm} \vec{X}^T [m] \vec{X} = c_1^2 \vec{X}^{(1)^T} [m] \vec{X}^{(1)} + c_2^2 \vec{X}^{(2)^T} [m] \vec{X}^{(2)} + c_3^2 \vec{X}^{(3)^T} [m] \vec{X}^{(3)} + \cdots \end{equation}
Sabiendo que los términos cruzados de la forma $c_i c_j \vec{X}^{(i)^T} [k] \vec{X}^{(j)}$ y $c_i c_j \vec{X}^{(i)^T} [m] \vec{X}^{(j)}$, $i \neq j$, son cero de acuerdo con la propiedad de ortogonalidad. Utilizando las ecuaciones ($\ref{XTk}$) y ($\ref{XTm}$) y la relación:
\begin{equation} \label{rel} \vec{X}^{(i)^T} [k] \vec{X}^{(i)} = \omega^2 \vec{X}^{(i)^T} [m] \vec{X}^{(i)} \end{equation}
el cociente de Rayleight de la ecuación ($\ref{w}$) se expresa como:
\begin{equation} \label{w2} \omega^2 = R(\vec{X}) = \frac{c_1^2 \omega_1^2 \vec{X}^{(1)^T} [m] \vec{X}^{(1)} + c_2^2 \omega_2^2 \vec{X}^{(2)^T} [m] \vec{X}^{(2)} + \cdots}{c_1^2 \vec{X}^{(1)^T} [m] \vec{X}^{(1)} + c_2^2 \vec{X}^{(2)^T} [m] \vec{X}^{(2)} + \cdots} \end{equation}
Si los modos normales, se normalizan, la ecuación ($\ref{w2}$) se escribe como:
\begin{equation} \label{w3} \omega^2 = R(\vec{X}) = \frac{c_1^2 \omega_1^2 + c_2^2 \omega_2^2 + \cdots}{c_1^2 + c_2^2 + \cdots} \end{equation}
Si $\vec{X}$ difiere poco del vector característico $\vec{X}^{(r)}$, el coeficiente $c_r$ será mucho mayor que los coeficientes restantes $c_i (i \neq r)$ y la ecuación ($\ref{w3}$) se escribe como:
\begin{equation} \label{w4} R(\vec{X}) = \frac{c_r^2 \omega_r^2 + c_2^2 \sum_{i=1,2,\cdots} \left( \frac{c_i}{c_r} \right)^2 \omega_i^2 }{c_1^2 + c_2^2 \sum_{i=1,2,\cdots} \left( \frac{c_i}{c_r} \right)^2} \end{equation}
Dado que $|c_i/c_r| = \varepsilon_i \ll 1$, donde $\varepsilon_i$ es un número pequeño para todas las $i r$, la ecuación ($\ref{w4}$) nos proporciona:
\begin{equation} \label{Rx} R(\vec{X}) = \omega_r^2 [1 + 0(\varepsilon ^2)] \end{equation}
donde $ 0(\varepsilon ^2)$ representa una expresión en e del segundo orden o mayor. La ecuación ($\ref{Rx}$) indica que si el vector arbitrario $\vec{X}$ difiere del vector característico $\vec{X}^{(r)}$ en una pequeña cantidad del primer orden, $R \vec{X}$ difiere del valor característico $\omega_r^2$ en una pequeña cantidad del segundo orden.
El valor "estacionario" (recordando que no es un estado en reposo) es en realidad un valor mínimo cerca del modo fundamental $\vec{X}^{(1)}$. Para ver esto, sea $r=1$ en la ecuación ($\ref{w4}$) y escribimos:
\begin{equation*} \ R(\vec{X}) = \frac{\omega_1^2 + \sum_{i=2,3, \cdots} \left( \frac{c_i}{c_1} \right)^2 \omega_i^2 }{ \left\lbrace 1 + \sum_{i=1,2,\cdots} \left( \frac{c_i}{c_r} \right)^2 \right\rbrace} \end{equation*}
\begin{equation*} \simeq \omega_1^2 + \sum_{i=2,3, \cdots} \varepsilon_i^2 \omega_i^2 - \omega_1^2 \sum_{i=2,3, \cdots} \varepsilon_i^2 \end{equation*}
\begin{equation} \label{aprox} \simeq \omega_1^2 + \sum_{i=2,3, \cdots} (\omega_i^2 - \omega_1^2) \varepsilon_i^2 \end{equation}
Puesto que, por lo general, $\omega_i^2 > \omega_1^2 $ con $i = 2, 3, ...,$ la ecuación ($\ref{aprox}$) conduce a:
\begin{equation} \label{R>}
R(\vec{X}) \geq \omega_1^2
\end{equation}
la cual muestra que el cociente de Rayleigh nunca es menor que el primer valor característico.
Análogamente de la misma manera, podemos mostrar que:
\begin{equation} \label{R<} R(\vec{X}) \leq \omega_n^2 \end{equation}
Concluyendo que el cociente de Rayleigh nunca es más alto que el valor característico más alto.
Así que el cociente de Rayleigh constituye un límite superior para $\omega_1^2$ y un límite inferior para $\omega_n^2$.
Método de Holzer
El método de Holzer es en esencia un esquema de prueba y error para determinar las frecuencias naturales de sistemas $\textbf{subamortiguados}$, $\textbf{amortiguados}$, $\textbf{semidefinidos}$, fijos, o sistemas vibratorios ramificados que implican desplazamientos lineales y angulares. El método también proporciona los modos.
Empezando por el análisis de vibración de sistemas de resorte-masa. Las ecuaciones de movimiento de un sistema de resorte-masa (vea la figura $\textbf{Fig. 1}$) se expresan como:
\begin{equation} \label{m1} m_1 \ddot{x_1} + k_1 (x_1 - x_2) = 0 \end{equation}
\begin{equation} \label{m2}
m_2 \ddot{x_2} + k_1 (x_2 - x_1) + k_2(x_2 - x_3) = 0
\end{equation}
Para movimiento armónico, $x_i(t) = X_i \cos \omega t$ , donde $X_i$ es la amplitud de la masa m_i y las ecuaciones ($\ref{m1}$) y ($\ref{m2}$) se escriben como:
\begin{equation} \label{wm1} \omega^2 m_1 X_1 = k_1 (x_1 - x_2) \end{equation}
\begin{equation*} \omega^2 m_2 X_2 = k_1 (x_2 - x_1) + k_2(x_2 - x_3) \end{equation*}
\begin{equation} \label{wm2} = - \omega^2 m_1 X_1 + k_2 (X_2 - X_3) \end{equation}
El procedimiento para el método de Holzer se inicia con una frecuencia de prueba \omega y la amplitud de la masa $m_i$ como $X_1=1$. Las ecuaciones ($\ref{wm2}$) y ($\ref{wm1}$) se pueden utilizar entonces para obtener las amplitudes de las masas $m_2, m_3, \cdots, m_i :$
\begin{equation} \label{X2} X_2 = X_1 - \frac{\omega^2 m_1 X_1}{k_1} \end{equation}
\begin{equation} \label{X3} X_3 = X_2 - \frac{\omega^2}{k^2} (m_1 X_1 + m_2 X_2) \end{equation}
\begin{equation} \label{Xi} X_i = X_{i-1} - \frac{\omega^2}{k_{i-1}} (\sum_{k=1}^{i-1} m_k X_k) \end{equation}
\begin{equation*} i= 2,3, \cdots, n \end{equation*}
La fuerza resultante aplicada a la última masa ($\textit{enésima}$) se calcula como sigue:
\begin{equation} \label{F} F= \sum_{i=1}^{n} \omega^2 m_i X_i \end{equation}
Los cálculos se repiten con otras frecuencias más de prueba $\omega$. Las frecuencias naturales se identifican como aquellos valores de $\omega$ que proporcionan $F=0$ para un sistema con ambos extremos libres. Para ello, es conveniente trazar una gráfica entre $F$ y $\omega$, utilizando el mismo procedimiento para sistemas de resorte-masa que para sistemas $\textbf{torsionales}$. [3]
Método de iteración matricial
Otro método existente es el de iteración maticial, el cuál no se tocará a detalle ya que la única intención es darlo a conocer.
Este método asume que las frecuencias naturales son distintas y también separadas de modo que $\omega_1 < \omega_2 < , \cdots , \omega_n$. La iteración se inicia seleccionando un vector de prueba $\vec X_1$, el que luego se premultiplica por la matriz dinámica [D].
Utilizando la convergencia del proceso se explica como sigue:
De acuerdo con el teorema de expansión, cualquier vector arbitrario de $n$ dimensiones $\vec{X}$ 1 se puede expresar como una combinación lineal de $n$ vectores característicos ortogonales del sistema $\vec{x}(i), i = 1,2, \cdots , n$
Método de Jacobi
El método de Jacobi también es un método iterativo pero produce todos los valores y vectores característicos de $[D]$ al mismo tiempo, donde $[D] = [d_ij]$ es una matriz simétrica real de orden $n \times n$.
El método está basado en un teorema de álgebra lineal que establece que una matriz simétrica real [D] tiene sólo valores característicos reales y que en ella existe una matriz ortogonal real $[R]$ de modo que $[R]^T[D][R]$ es diagonal. [3]
Los elementos diagonales son los valores característicos, y las columnas de la matriz $[R]$ son los vectores característicos. De acuerdo con el método de Jacobi, la matriz $[R]$ se genera como un producto de varias matrices de rotación de la forma:
\begin{equation} [R_1]_{n \times n} = \begin{bmatrix} & & & i & & j & & &\\ 1 & 0 & & & & & & &\\ 0 & 1 & & & & & & & \\ & & \ddots & & & & & & \\ & & & \cos{\theta} & & \sin{\theta} & & & \\ & & & & \ddots & & & & \\ & & & \sin{\theta} & & \cos{\theta} & & & \\ & & & & & & \ddots & & \\ & & & & & & & 1 & \end{bmatrix} \end{equation}
donde todos los elementos aparte de los que aparecen en las columnas y filas $i$ y $j$ son idénticos a los de la matriz identidad $[I]$. Si las entradas seno y coseno aparecen en las posiciones $(i, i), (i, j), (j, i)$ y $(j, j)$, entonces los elementos correspondientes de $[R1]^T[D][R1]$ se calculan como sigue:
\begin{equation} \underline{d_{ii}} = d_{ii} \cos^2\theta + 2d_{ij} \sin{\theta} \cos{\theta} + d_{jj} \sin^2 {\theta} \end{equation}
\begin{equation} \underline{d_{ij}} = d_{ji} = (d_{jj} - d_{ii}) \sin{\theta} \cos{\theta} + d_{ij} (\cos^2{\theta} - \sin^2 {\theta}) \end{equation}
\begin{equation} \underline{d_{jj}} = d_{ii} \sin^2\theta - 2d_{ij} \sin{\theta} \cos{\theta} + d_{jj} \cos^2 {\theta} \end{equation}
Es conveniente elegir a $\theta$ como sigue, para hacer $\underline{d_{ij}} = \underline{d_{ji}} = 0 $.
\begin{equation} \tan{2\theta} = \left( \frac {2d_{ij}}{d_{ii}- d{jj}} \right) \end{equation}
Así, cada paso del método de Jacobi reduce un par de elementos fuera de la diagonal a cero.
Notar que en el siguiente paso, al mismo tiempo que el método reduce un nuevo par de cero, introduce contribuciones no cero en posiciones que antes eran cero. Sin embargo, las matrices sucesivas de la forma:
\begin{equation*} [R_2]^T[R_1]^T[D][R_1][R_2], [R_3]^T[R_2]^T[R_1]^T[D][R_1][R_2][R_3], \cdots \end{equation*}
Convergen a la forma diagonal requerida; la matriz final [R], cuyas columnas da los vectores eigen se escriben entonces como:
\begin{equation} [R] = [R_1][R_2][R_3] \cdots \end{equation}
Bibliografía complementaria
- https://www.institucional.frc.utn.edu.ar/sistemas/Noticias/INV/Seminarios/ast_2007_presentacion_giro.pdf
- https://www.academia.utp.ac.pa/sites/default/files/docente/72/clase_8_determinacion_de_frecuencias_naturales_y_formas_modales.pdf
Carlosmiranda (discusión) 16:24 22 nov 2020 (CST)
- ↑ 1,0 1,1 Miguel Pérez Rodríguez ,Análisis dimensional de los modos de vibración de un eje ferroviario, Universidad Carlos III de Madrid,Leganés,2012.
- ↑ Jianhua Zheng, Ji Wang, Generalization of Dunkerley’s equation for the undamped linear positive semidefinite system, International Conference on Advances in Computational Modeling and Simulation, 2012.
- ↑ 3,0 3,1 3,2 Rao, Singiresu S. Vibraciones Mecánicas, Quinta Edición, Edit. Pearson Educación, México, 2012.