Compleja:ej-cap1.4

EJERCICIOS 1.4.1

1.-Demuestre la identidad $\left(f.g\right)'\left(z\right)=f'\left(z\right)g\left(z\right)+f\left(z\right)g'\left(z\right)$.

Sean $f$ y $g$, dos funciones definidas y derivables en un mismo punto $z$.

${\frac {\left(f.g\right)\left(z+h\right)-\left(f.g\right)\left(z\right)}{h}}={\frac {f\left(z+h\right).g\left(z+h\right)-f\left(z\right)g\left(z\right)}{h}}$

Si se suma y se resta en el numerador $f\left(z\right).g\left(z+h\right)$, la fracción anterior no varía.

$={\frac {f\left(z+h\right).g\left(z+h\right)-f\left(z\right).g\left(z+h\right)+f\left(z\right).g\left(z+h\right)-f\left(z\right)g\left(z\right)}{h}}$

Sacando $g\left(z+h\right)$ factor comun en los dos primeros sumandos, y $f\left(z\right)$, en los otros dos.

$={\frac {g\left(z+h\right)\left[f\left(z+h\right)-f\left(z\right)\right]+f\left(z\right)\left[g\left(z+h\right)-g\left(z\right)\right]}{h}}$

$=g\left(z+h\right).{\frac {f\left(z+h\right)-f\left(z\right)}{h}}+f\left(z\right).{\frac {g\left(z+h\right)-g\left(z\right)}{h}}$.

Si ahora se toman limites cuando $h$ tiende a cero.

$\lim _{h\rightarrow 0}g\left(z+h\right)=g\left(z\right)$, pues $g$ es continua en $z$ ya que es derivable en $z$.

$\lim _{h\rightarrow 0}{\frac {f\left(z+h\right)-f\left(z\right)}{h}}=f'\left(z\right)$, por definición de derivada.

$\lim _{h\rightarrow 0}f\left(z\right)=f\left(z\right)$, al no depender $f\left(z\right)$ de $h$.

$\lim _{h\rightarrow 0}{\frac {g\left(z+h\right)-g\left(z\right)}{h}}=g'\left(z\right)$, por definición.

por tanto, $\left(f.g\right)'\left(z\right)=\lim _{h\rightarrow 0}{\frac {\left(f.g\right)\left(z+h\right)-\left(f.g\right)\left(z\right)}{h}}$

$\left(f.g\right)'\left(z\right)=f'\left(z\right)g\left(z\right)+f\left(z\right)g'\left(z\right)$

--Josua Da Vinci 20:36 17 nov 2009 (UTC)

---

2.- Encuentre una región donde ${\frac {3z^{4}-2z^{2}+i}{z^{3}-27i}}$ sea holomorfa, calcule la derivada.

Solución

Utilizando la regla de derivación para cocientes

$f\left(z\right)={\frac {u}{g}}$

$f'\left(z\right)={\frac {u'g-g'u}{g^{2}}}$

Se tiene lo siguiente

$f\left(z\right)={\frac {3z^{4}-2z^{2}+i}{z^{3}-27i}}$

$f'\left(z\right)={\frac {\left(12z^{3}-4z\right)\left(z^{3}-27i\right)-\left(3z^{2}\right)\left(3z^{4}-2z^{2}+i\right)}{\left(z^{3}-27i\right)^{2}}}$

$f'\left(z\right)={\frac {3z^{6}+5z^{4}-324z^{3}-3iz+96z}{\left(z^{3}-27i\right)^{2}}}$

$f\left(z\right)$ es holomorfa en $\mathbb {C-\left\{\pm \right\}}$

--Dali 01:56 15 nov 2009 (UTC)

---

3 Sea f la funcion de$\mathbb {R} ^{2}$ en $\mathbb {R} ^{2}$ en definida por ${\begin{array}{lcr}f(x,y)&=(x^{2}+y^{2},0)\end{array}}$(en notación compleja $z\Rightarrow \ |z|^{2}$),calcule su matriz jacobiana.

Por definición la matriz jacobiana es

${\begin{vmatrix}{\frac {df_{1}}{dx}}&{\frac {df_{1}}{dy}}\\{\frac {df_{2}}{dx}}&{\frac {df_{2}}{dy}}\end{vmatrix}}$

Para números que pertenecen al campo de los reales.

partiendo de ${\begin{array}{lcr}f(x,y)&=(x^{2}+y^{2},0)\end{array}}$

donde $f_{1}=x^{2}+y^{2}$ y $f_{2}=0$

Usando las definiciones obtenemos su matriz jacobiana, obteniendo sus parciales.

${\frac {df_{1}}{dx}}=2x$, ${\frac {df_{1}}{dy}}=2y$, ${\frac {df_{2}}{dx}}=0$, ${\frac {df_{2}}{dy}}=0$,

Construyendo su matriz jacobiana tenemos finalmente.

${\begin{vmatrix}2x&2y\\0&0\end{vmatrix}}$

--Karla 22:08 15 nov 2009 (UTC)Karla

4. Sea $f(z)=$

EJERCICIOS 1.4.2

1.Verifique directamente que se cumplen las ecuaciones de Cauchy-Riemann para la función $z\longmapsto \ 3z^{3}+2z$.

Sean $A$ abierto en $\mathbb {C}$, y $f:A\longmapsto \mathbb {C}$,una funcion holomorfa en $z_{0}\in A$, entonces si $f\left(z\right)=u\left(z\right)+iv\left(z\right),$ se tiene.

(Ecuaciones de Cauchy-Riemann).

${\frac {\partial u}{\partial x\,}}(z_{0})={\frac {\partial v}{\partial y\,}}(z_{0})$

${\frac {\partial u}{\partial y\,}}(z_{0})=-{\frac {\partial v}{\partial x\,}}(z_{0})$

$\delta \left(z\right)=3z^{3}+2z$ y $Z=X+iY$.

$\delta \left(z\right)=3x^{3}-9xy^{2}+2x+i\left(9x^{2}y-3y^{3}+2y\right)$

Donde:

$u\left(z_{0}\right)=3x^{3}-9xy^{2}+2x$ y $v\left(z_{0}\right)=9x^{2}y-3y^{3}+2y$

${\frac {\partial u}{\partial x\,}}(z_{0})=9x^{2}-9y^{2}+2$

${\frac {\partial v}{\partial y\,}}(z_{0})=9x^{2}-9y^{2}+2$

Y

${\frac {\partial u}{\partial y\,}}(z_{0})=-18xy$

$-{\frac {\partial v}{\partial x\,}}(z_{0})=-\left(18xy\right)$

Por tanto se cumplen las ecuaciones de Cauchy-Riemann.

--Josua Da Vinci 23:40 3 dic 2009 (UTC)

---

4.- Demuestre que la función $z\rightarrow \sin {\overline {z}}$ no es holomorfa en ningún punto del plano.

Primero desarrollando $\sin {\overline {z}}$ como $\sin \left(x-iy\right)$ tenemos lo siguiente:

$f\left(z\right)=\sin {\overline {z}}=\sin x\cosh y-i\sinh y\cos x=u+iv$

$\therefore u=\sin x\cosh y;v=-\sinh y\cos x$

Ahora para mostrar que nuestra función no es holomorfa basta con probar que no se cumplen las Ecuaciones de Cauchy-Riemann

${\frac {\partial u}{\partial x}}={\frac {\partial v}{\partial y}}$ y ${\frac {\partial u}{\partial y}}=-{\frac {\partial v}{\partial x}}$

Calculando estas parciales tenemos que:

${\frac {\partial u}{\partial x}}=\cos x\cosh y$

${\frac {\partial v}{\partial y}}=-\cos x\cosh y$

Donde es fácil ver que

${\frac {\partial u}{\partial x}}=\cos x\cosh y\neq -\cos x\cosh y={\frac {\partial v}{\partial y}}$

Para la otra igualdad calculamos las parciales

${\frac {\partial u}{\partial y}}=\sin x\sinh y$

${\frac {\partial v}{\partial x}}=\sin x\sinh y$

Y hacemos la comparación de la misma forma

${\frac {\partial u}{\partial y}}=\sin x\sinh y\neq -\sin x\sinh y=-{\frac {\partial v}{\partial x}}$

Como se puede ver son distintas.

$\therefore$ La función $\sin {\overline {z}}$ no es holomorfa en ningun punto del plano.

--Oscar Adrian 06:23 4 dic 2009 (UTC)

---

5. Encuentre un dominio de analiticidad para la funcion${z}\rightarrow log(z-7+i)$ y calcule la derivada, donde log denota la rama de logaritmo con valores en $({\frac {\pi }{2}},{\frac {5\pi }{2}})$ .

Solución:

sea $z\in \mathbb {C} ,z=x+iy$

$\ f(z)=log(z-7+i)=log(x+iy-7+i)=log\left((x-7)+i(y+1)\right)$

con rama en $({\frac {\pi }{2}},{\frac {5\pi }{2}})$

esto es $\ x-7=0\quad \ y\geq -1$

$\therefore$ el dominio de analiticidad es $A=\mathbb {C} -\lbrace z\in \mathbb {C} /x=7,y\geq -1\rbrace$

la derivada de $\ f(z)=log(z-7+i)$ es:

$\ f'(z)={\frac {1}{z-7+i}}$

--Luis Antelmo 21:57 5 dic 2009 (UTC)

6. Encuentre un dominio de analiticidad para la funciòn$z\rightarrow \log(e^{z}+1)$ y encuentre la derivada, donde log denota la rama $(0,2\pi )$ de logaritmo

Para encontrar los puntos de analiticidad, localizamos aquellos donde la función no es analítica; es decir donde la función es real positiva, por tanto los puntos localizados se excluirán del dominio.

Condiciòn:

$e^{z}+1\ >0$

Donde $e^{z}=e^{x}e^{iy}$

$e^{iy}=0$

$e^{z}>-1$

$e^{x}>-1$ se cumple excepto en $k\pi$

CASO 1 k=0

$cos\pi k$=1 obteniendo el logaritmo $log1=0$ y por lo tanto la condicion $e^{x}>-1$ no se cumple

CASO 2 k= Número impar, por ejemplo k=1

$cos\pi k$=-1 , $log(-1)=\mathbb {C}$ por lo tanto $e^{x}>-1$ no se cumple

CASO 3 k=Número par, por ejemplo k=2

$cos\pi k$=1 , $log1=0$ en k=2 no se cumple

Entonces en estos puntos la función es no analítica; por lo tanto en todos los demás puntos la función será analítica. En estos puntos de no analiticidad no tiene sentido hablar de derivada.

Por tanto solo tiene sentido hablar de la derivada en el dominio que hemos definido, la derivada de la función:

$f(z)=log(e^{z}+1)$

$z^{\prime }={\frac {e^{z}}{e^{z}+1}}$ donde $z=x+iy$

El dominio de la funcion $z\rightarrow \log(e^{z}+1)$ son todos los puntos tales que cumplan la condición.

$e^{z}>-1$ excepto donde $\pi k$ donde k es un número real, tomamos k entre 0 y 2 para satisfacer la rama $(0,2\pi )$ excepto los puntos que localizamos con la condición $k\pi$ donde k pertenece al campo de los números reales.

Gráficamente lo podemos ver:

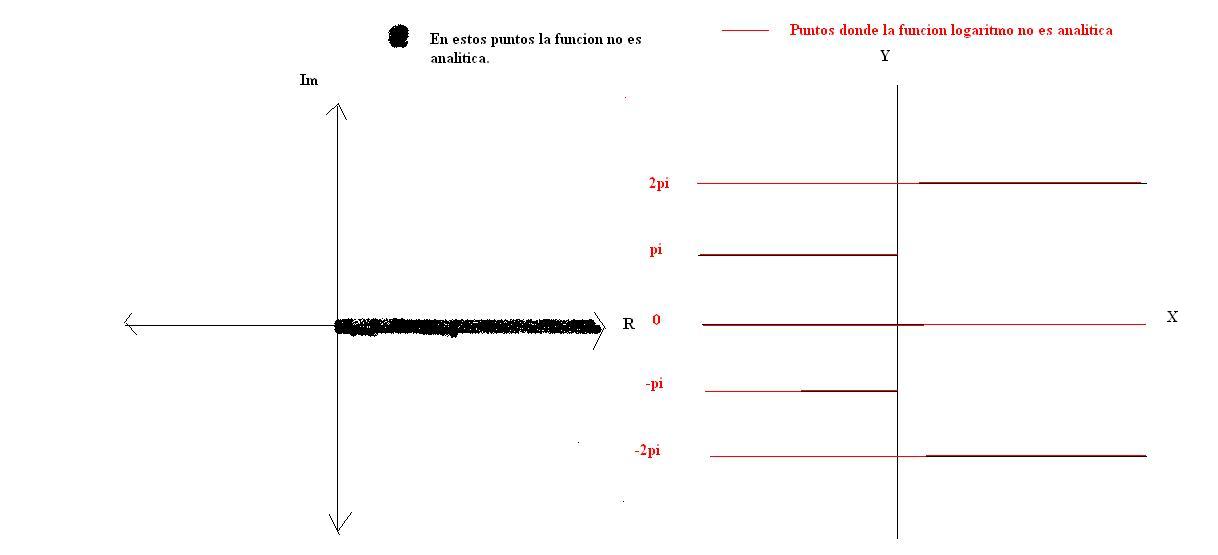
El dominio de la función todo los puntos restantes.

--Karla 16:56 4 dic 2009 (UTC)karla

EJERCICIOS 1.4.3

1. Interprete geométricamente la no con formalidad de la función $\quad z\rightarrow \ z^{4}\quad$ en el origen.

Definición de con formalidad. Si aplicamos transformaciones el ángulo se conserva. Por lo anterior buscamos en el origen los puntos donde los ángulos, después de la rotación no se conservan.

En la función $\quad z\rightarrow \ z^{4}\quad$

Tomamos $\phi =\pi$ es el ángulo que forman los vectores $(-1,0)$ Y$(1,0)$ En ángulo después de aplicar la transformación de la función $\quad z\rightarrow \ z^{4}\quad$ serà $\theta =0$ los vectores son paralelos.

Gráficamente

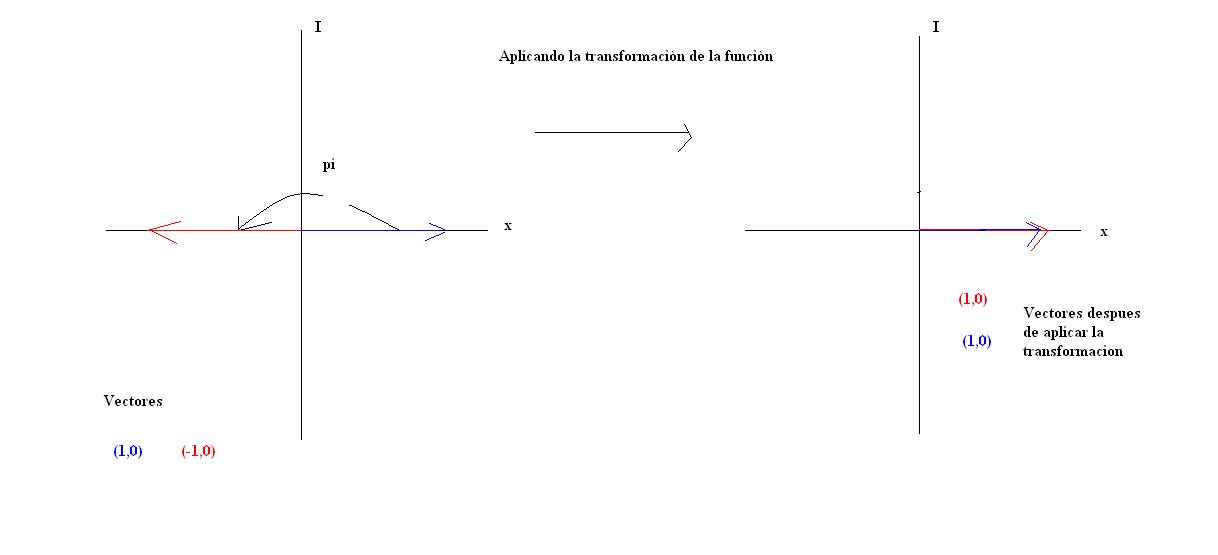
--Karla 16:55 7 dic 2009 (UTC)Karla

---

Compleja:ej-cap1.1 Compleja:ej-cap1.2 Compleja:ej-cap1.3 Compleja:ej-cap1.4

Compleja:ej-cap2.1 Compleja:ej-cap2.2 Compleja:ej-cap2.3 Compleja:ej-cap2.4 Compleja:ej-cap2.5

Compleja:ej-cap3.1 Compleja:ej-cap3.2 Compleja:ej-cap3.3 Compleja:ej-cap3.4