Compleja:ej-cap1.1

1. Demuestre que el producto de números complejos cumple con la ley asociativa

Sean Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z = a + i b, \quad w = c + i d, \quad s = e + i f \, \quad con $\quad a,b,c,d,e,f\in {\mbox{R}}$

Por demostrar $(zw)s=z(ws)\,$

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (zw)s = [(a + i b)(c + i d)](e + i f) = [(ac - bd) + i (bc + ad)](e + i f)\,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =[e(ac - bd) - f(bc + ad)] + i [e(bc + ad) + f(ac - bd) = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,

Por otra parte

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z(ws) = (a + i b)[(c + i d)(e + i f)] = (a + i b)[(ce - df) + i (de + cf)]\,

$=[a(ce-df)-b(de+cf)]+i[b(ce-df)+a(de+cf)]=(ace-bde-bcf-adf)+i(bce+ade+acf-bdf)\,$

Entonces se cumple $(zw)s=z(ws)\,$.

--Gabita 22:15 28 sep 2009 (UTC)

1.1.2

1. Demuestre que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left|\frac{z}{w}\right| = \frac{\left|z\right|}{\left|w\right|}

Sean Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z = a + i b \quad y \quad w = c + i d\,

$\left|{\frac {z}{w}}\right|=\left|{\frac {a+ib}{c+id}}\right|=\left|{\frac {(a+ib)(c-id)}{(c+id)(c-id)}}\right|$

$=\left|{\frac {(ac+bd)+i(bc-ad)}{c^{2}+d^{2}}}\right|={\sqrt {{\bigg (}{\frac {ac+bd}{c^{2}+d^{2}}}{\bigg )}^{2}+{\bigg (}{\frac {bc-ad}{c^{2}+d^{2}}}{\bigg )}^{2}}}={\frac {1}{c^{2}+d^{2}}}{\sqrt {(ac+bd)^{2}+(bc-ad)^{2}}}$

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =\frac{1}{c^2 + d^2}\sqrt{a^2 c^2 + a^2 d^2 + b^2 c^2 + b^2 d^2 } = \sqrt{\Bigg [\frac{a^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] + \Bigg [\frac{b^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] } = \sqrt{\frac{a^2 + b^2}{c^2 + d^2}}

Por otra parte

${\frac {\left|z\right|}{\left|w\right|}}={\frac {\left|a+ib\right|}{\left|c+id\right|}}={\sqrt {\frac {a^{2}+b^{2}}{c^{2}+d^{2}}}}=\left|{\frac {z}{w}}\right|$

--Gabita 22:15 28 sep 2009 (UTC)

---

2. Exprese ${\overline {\left({\frac {\left(2+3i\right)^{2}}{4+i}}\right)}}$de la forma $x+iy$

Por las propiedades ${\overline {\left({\frac {z}{w}}\right)}}={\frac {\bar {z}}{\bar {w}}}$ , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline{zw}=\bar{z}\bar{w}

${\frac {\overline {\left({2+3i}\right)^{2}}}{\overline {\left({4+i}\right)}}}={\frac {{\overline {\left({2+3i}\right)}}{\overline {\left({2+3i}\right)}}}{\overline {\left({4+i}\right)}}}={\frac {\left(2-3i\right)\left(2-3i\right)}{\left(4-i\right)}}$

Simplificando, se obtiene:

${\frac {4-6i-6i-9}{4-i}}={\frac {-5-12i}{4-i}}$

Resolviendo la divicion de números complejos, de la forma:

${\frac {z}{w}}={\frac {z{\bar {w}}}{w{\bar {w}}}}={\frac {z{\bar {w}}}{\left|w\right|^{2}}}$:

${\frac {\left(-5-12i\right)\left(4+i\right)}{\left(4-i\right)\left(4+i\right)}}={\frac {-20-5i-48i+12}{17}}={\frac {-8-53i}{17}}$

=$-{\frac {8}{17}}-{\frac {53}{17}}i$.

--Josua Da Vinci 23:00 28 sep 2009 (UTC)

---

5. Sean Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z_1 , z_2 , z_3 \in \mathbb{C} tales que cumplen ${\frac {z_{2}-z_{1}}{z_{3}-z_{1}}}={\frac {z_{1}-z_{3}}{z_{2}-z_{3}}}$, demuestre que estos tres puntos determinan un triángulo equilátero.

Archivo:Comp triang eq2.jpg

Figura 1

Tenemos que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left | \frac{z_2 - z_1}{z_3 - z_1} \right | = \left | \frac{z_1 - z_3}{z_2 - z_3} \right |,\qquad (1)

y, por lo tanto,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{|z_2 - z_1|}{|z_3 - z_1|} = \frac{|z_1 - z_3|}{|z_2 - z_3|}.\qquad (2)

De la Figura 1, vemos que cada una de esas normas de números complejos son exactamente los segmentos de recta que constituyen el triángulo ABC, a saber:

$\left.{\begin{matrix}|z_{2}-z_{1}|=A\\|z_{3}-z_{1}|=B=|z_{1}-z_{3}|\\|z_{2}-z_{3}|=C\\\end{matrix}}\right\}\qquad (3)$

De (2) y (3) tenemos que:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{A}{B} = \frac{B}{C}. \qquad (4)

Por triángulos semejantes, se tiene que el ángulo $\beta$ es igual al ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \gamma y éste a su vez al ángulo $\alpha$, es decir,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \alpha = \beta = \gamma. \qquad (5)

== 1.1.7 == Demuestre que en un paralelogramo la suma de los cuadrados de las diagonales es la suma de los cuadrados de los lados.

Recordando Pitágoras c^2 = a^2 + b^2 (para magnitudes reales)

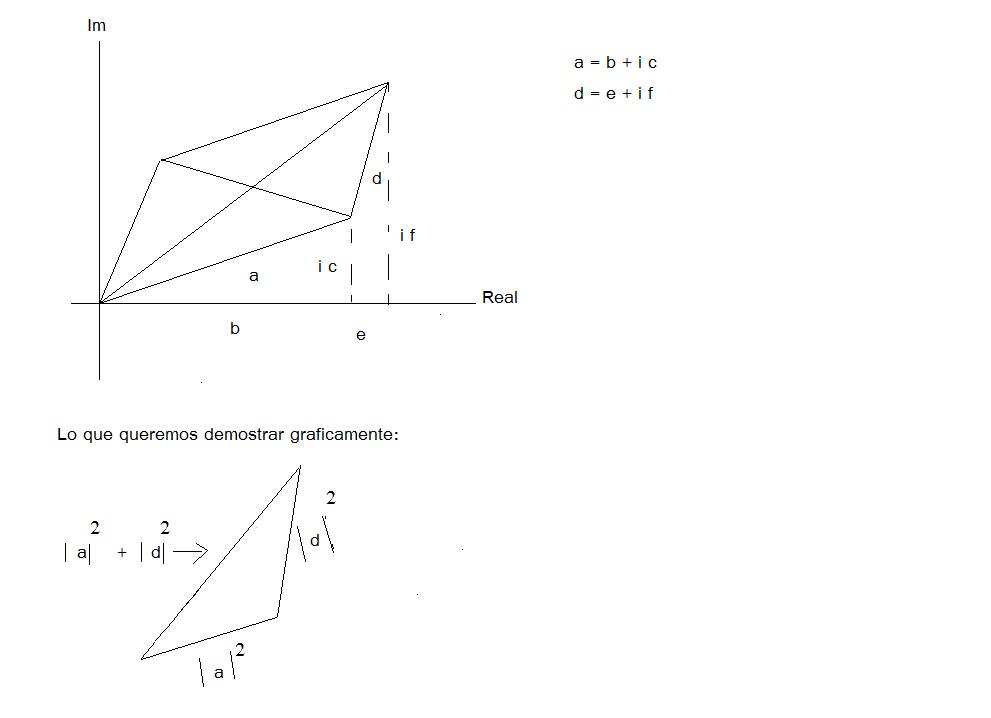
Tomamos dos numeros complejos

a = b + ic d = e + if

Para poder demostrar que la suma de los cuadrados de los lados sea igual a la suma del cuadrado de las diagonales necesitamos obtener la magnitud de los numeros complejos anteriores "a" y "d".

|a| = Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \sqrt{ b^2+c^2} que corresponde a la norma de "a". |d| = ${\sqrt {e^{2}+f^{2}}}$ que corresponde a la norma de "d".

si |a|^2 = b^2 + c^2

  |d|^2 = e^2 + f^2

Ahora definimos la diagonal como |h| con componentes |a| y|d| obtenemos la magnitud de |h| y tenemos

|h|= Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \sqrt{|a|^2+|d|^2}

reacomodando.

|h|^2 = |a|^2 + |d|^2 lo que queriamos demostrar

Por lo tanto tenemos que en un paralelogramo que la suma de los cuadrados de las diagonales son la suma de los cuadrados de los lados. Con lo anterior hemos concluido nuestra demostración.

--mfg-wiki 21:27 25 sep 2009 (UTC)

1.1.4

--mfg-wiki 21:27 25 sep 2009 (UTC)