Ondas contrapropagantes en musica: cuerdas de guitarra
Ondas estacionarias en cuerdas de guitarra
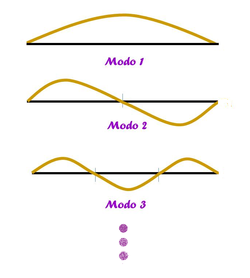
En instrumentos de cuerda, como las guitarras, las ondas sonoras en el aire son creadas por la resonancia transversal de ondas estacionarias en las cuerdas. La cuerda de una guitarra, a diferencia de la masa en un resorte, puede oscilar en muchas frecuencias o patrones de onda conocidos como modos de vibración (Figura 1). La definición de "onda estacionaria" viene de que cada modo de vibración tiene propiedades de "onda" (tales como longitud de onda, frecuencia, étc.) y debido a que esta no viaja de izquierda a derecha a través del espacio, sino que esta se mantiene oscilando de arriba a abajo en el mismo lugar, se le llama "estacionaria".
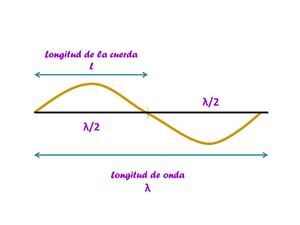
En las cuerdas de una guitarra hablamos de patrones de onda estacionaria (por su forma sinusoidal) ya que si analizamos su movimiento no es una onda completa; una onda parte del reposo, crece hasta su cresta, vuelve a la posición de equilibrio, decrece hasta un valle y vuelve a su posición de equilibrio en un ciclo completo; mientras que en una cuerda, la oscilación en la frecuencia fundamental, sólo se produce la mitad de una onda en toda la longitud de la cuerda. Por lo que la longitud de onda $\lambda$ es dos veces la longitud de la cuerda $L$.
A la frecuencia fundamental le llamamos primer modo de vibración, es el modo con la longitud de onda más larga y la frecuencia más baja. La frecuencia depende de la velocidad del sonido en la cuerda.
Si suponemos que esta velocidad es $V_{s}=107 \frac{m}{s}$, la longitud de la cuerda es $L=65 cm$ y dado que $\lambda=2L=1.3m$ entonces
\begin{equation} \ f=f_{1}=\frac{V_{s}}{\lambda}=\frac{107}{1.3}=82.3 Hz\label{eq:frecuencia1} \end{equation}
Esta es la frecuencia fundamental de la cuerda más baja, correspondiente a la nota Mi.
Ya que la longitud de onda es dos veces la longitud de la cuerda podemos expresar en forma general la ecuación (\ref{eq:frecuencia1}) como
\begin{equation} \ f=f_{1}=\frac{V_{s}}{2L}\label{eq:frecuencia1'} \end{equation}
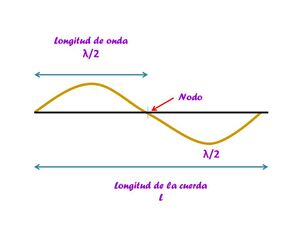
Para comprender el segundo modo de vibración tenemos que hablar del concepto de nodo, el cual se verá con mayor detalle en la siguiente sección, Armónicos. Para los fines de esta sección, supongamos que podemos ver a un nodo como un punto donde se parte a la cuerda en dos secciones iguales, podemos ver cada parte como dos cuerdas con longitudes de onda $\frac{\lambda}{2}$
Entonces, para este caso, podemos notar que la longitud de onda de la cuerda es igual a la longitud de la cuerda, ya que tenemos dos medios de $\lambda$ en toda la cuerda.
Así la frecuencia para el segundo modo de vibración es
\begin{equation}
\ f_{2}= 2\frac{V_{s}}{2L}= \frac{V_{s}}{L}=\frac{107}{0.65}=165 Hz\label{eq:frecuencia2}
\end{equation}
Para el 3er modo de vibración se añade otro nodo, cada nodo está igualmente espaciado a lo largo de la longitud de la cuerda, por lo que podemos ver que para este modo de vibración tenemos $ 3\frac{\lambda}{2}$ en toda la longitud de la cuerda
La frecuencia del tercer modo es \begin{equation} \ f_{3}= 3\frac{V_{s}}{2L}= 3\frac{107}{130}=247 Hz\label{eq:frecuencia3} \end{equation}
En este punto, es claro que no existe un límite para los posibles modos de vibración en los que puede oscilar la cuerda de una guitarra, creando cada uno de ellos los diferentes armónicos de un tono. El primer modo de vibración corresponde al primer armónico o tono fundamental, el segundo modo crea el segundo armónico y así sucesivamente. Cada frecuencia armónica es un múltiplo entero de la frecuencia fundamental.
Ecuación de onda
Armónicos
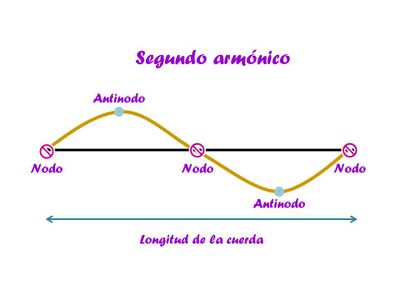
Se le llama armónicos a dos o más componentes de un tono si sus frecuencias son múltiplos enteros pequeños de una misma frecuencia fundamental. Por ejemplo, las ecuaciones (\ref{eq:frecuencia2}) y (\ref{eq:frecuencia3}) muestran frecuencias que son múltiplos enteros de la frecuencia fundamental que arroja la ecuación (\ref{eq:frecuencia1}) para la cuerda más baja de una guitarra. El primer modo corresponde al primer armónico o armónico fundamental, el segundo modo es el segundo armónico y así sucesivamente. Como vimos en la sección anterior los nodos hacen distintos a un modo de otro o, en otras palabras a un armónico de otro, sin embargo, no los hemos definido como tal. Los nodos son puntos donde la cuerda no se mueve, puntos de no desplazamiento, donde no importa cuanto esperemos no veremos a la cuerda oscilar. El primer armónico tiene dos nodos, los cuales son los extremos de la guitarra, su puente y las clavijas que sujetan a las cuerdas.
Entre cada dos nodos existe un antinodo, si en los nodos la amplitud de la onda es mínima (no hay amplitud realmente), en los antinodos la amplitud es máxima, ambos son puntos donde la velocidad de la cuerda es cero.
En la siguiente tabla podemos visualizar la relación que hay según el número de armónico, con las ondas en una cuerda de guitarra, cuántos nodos y antinodos hay, la longitud de onda y sus frecuencias utilizando la información para $v{_s}$ y $L$ de la sección anterior.
| Armónico | Ondas en la cuerda | #
De nodos |
#
De antinodos |
Longitud de onda
(cm) |
Frecuencia
(Hz) |
|---|---|---|---|---|---|
| $1$ | $\frac{1}{2}$ | $2$ | $1$ | $2L=130$ | $82.3$ |
| $2$ | $1$ | $3$ | $2$ | $L=65$ | $165$ |
| $3$ | $\frac{3}{2}$ | $4$ | $3$ | $\frac{2}{3}L=43.3$ | $247$ |
| $4$ | $2$ | $5$ | $4$ | $\frac{1}{2}L=32.5$ | $329$ |
| $5$ | $\frac{5}{2}$ | $6$ | $5$ | $\frac{2}{5}L=26$ | $416$ |
Ya hemos mencionado que las frecuencias de los armónicos son siempre múltiplos enteros de la frecuencia fundamental, este hecho hace que se puedan crear tonos consistentes con los componentes de vibración que son armónicos, estos componentes son ondas sinusoidales llamadas "partes" ya que un tono completo se compone de varias de estas. Cada componente sinusoidal es "parte" de una onda completa, las partes de un tono creado por una cuerda estirada son armónicas debido a esta relación entre las frecuencias de las partes, hecho que se enfatiza con la expresión \begin{equation} \ f_{n}= nf_{1}\label{eq:frecuenciaarm} \end{equation}
La cual determina la frecuencia de cualquier armónico o modo de vibración.
La ecuación del guitarrista
Para tocar melódica y armoniosamente un guitarrista debe tocar notas con una correcta frecuencia fundamental, la frecuencia fundamental de una nota o tono está relacionada con la velocidad del sonido en la cuerda y a su vez, la velocidad del sonido depende de la tensión en la cuerda $T$ y su densidad de masa lineal $ \mu$ de acuerdo con la expresión \begin{equation} \ v_{s}=\sqrt\frac{T}{\mu}\label{eq:velso} \end{equation}
Al sustiuir $v_{s}$ dada por (\ref{eq:velso}) en la ecuación (\ref{eq:frecuencia1'}) obtenemos la ecuación del guitarrista para la frecuencia fundamental de un tono \begin{equation} \ f_{1}=\frac{1}{2L}\sqrt\frac{T}{\mu}\label{eq:guitar'splayer} \end{equation}
Esta expresión muestra que la creación de un tono depende de las propiedades de la cuerda: Tensión $T$, Longitud $L$ y densidad lineal $\mu$.
Cabe mencionar que la expresión (\ref{eq:guitar'splayer}) es sólo la idealización de la realidad. Ya que considera que la tensión es la única fuerza que actúa sobre la cuerda, lo cual es falso. Analicemos un poco lo que pasa: Cuando tocamos la guitarra nuestros dedos hacen que la cuerda oscile, la fuerza restauradora es la que hace que la cuerda busque su posición de equilibrio, esta fuerza, en mayor medida, está compuesta por la tensión pero también contribuye la rigidez de la cuerda. Para comprender qué es la rigidez, imaginemos que le quitamos una cuerda a la guitarra, por tanto ya no hay tensión, si intentamos doblar por completo la cuerda encontraremos que existe cierta resistencia, esa resistencia es la rigidez. Para hablar de cuerdas reales necesitamos incluir la rigidez en nuestro razonamiento.