Ondas electromagneticas planas
Introducción
Se sabe que un campo electromagnético se propaga en el vacío con una velocidad igual a la de la luz en el vacío, es decir a una velocidad
\[ c=\frac{1}{\sqrt{\epsilon_{0}\mu_{0}}}\approx3*10^{8}\text{ms}^{-1}. \]
La existencia de dichas ondas había sido predicha por James Clerck Maxwell y confrimada por Heinrich Hertz. El trabajo de Maxwell lo llevó a sintetizar en 4 ecuaciones los fenómenos electromagnéticos clásicos; dichas ecuaciones, conocidas comunmente con el nombre de 'Ecuaciones de Maxwell', son las siguientes:
i) Ley de Gauss para campo eléctrico.
Forma integral:
\[ \oint_{s}\boldsymbol{\boldsymbol{\varepsilon}}\cdot\boldsymbol{u_{n}}\,dS=\frac{q}{\epsilon_{0}}. \]
Forma diferencial:
\[ \nabla\cdot\boldsymbol{\boldsymbol{\varepsilon}}=\frac{\rho}{\epsilon_{0}}. \]
ii) Ley de Gauss para campo magnético.
Forma integral:
\[ \oint_{s}\boldsymbol{B}\cdot\boldsymbol{u_{n}}\,dS=0. \]
Forma diferencial:
\[ \nabla\cdot\boldsymbol{\boldsymbol{B}}=0. \]
iii) Ley de Faraday-Henry.
Forma integral:
\[ \oint_{L}\boldsymbol{\boldsymbol{\varepsilon}}\cdot d\boldsymbol{l}=-\frac{d}{dt}\oint_{s}B\cdot\boldsymbol{u_{n}}\,dS. \]
Forma diferencial:
\[ \nabla\times\boldsymbol{\boldsymbol{\boldsymbol{\varepsilon}}}=-\frac{\partial\boldsymbol{B}}{\partial t}. \]
iv) Ley de Ampere-Maxwell.
Forma integral:
\[ \oint_{L}\boldsymbol{B}\cdot d\boldsymbol{l}=\mu_{0}\boldsymbol{I}+\epsilon_{0}\mu_{0}\frac{d}{dt}\oint_{s}\boldsymbol{\boldsymbol{\varepsilon}}\cdot\boldsymbol{u_{n}}\,dS. \]
Forma diferencial:
\[ \nabla\times\boldsymbol{B}=\mu_{0}\boldsymbol{j}+\epsilon_{0}\mu_{0}\frac{\partial\boldsymbol{\boldsymbol{\varepsilon}}}{\partial t}. \]
Así, se abordará el cuestionamiento sobre si las ecuaciones de Maxwell para el campo electromágetico admiten como solución particular, un campo eléctrico $\varepsilon$ y un campo magético B perpendiculares entre sí.
Ejemplos comunes de ondas electromagnéticas son las ondas de radios, las señales de televisión, los haces de radar y los rayos luminosos. Todas las formas de energía comparten tres características fundamentales: se desplazan a gran velocidad, adoptan al hacerlo propiedades de ondas e irradioan hacia fuera desde una fuente sin la ayuda de ningún vehículo discernible.
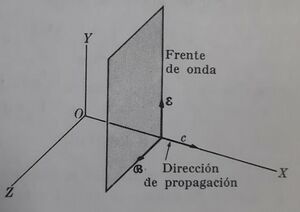
Ondas electromagnéticas planas en el vacío
Se aborda una situación particular en la que la dirección del campo eléctrico $\varepsilon$ y la dirección del campo magnético B son siempre perperdiculares entre sí, abordando de esta manera el concepto de ondas electromagnéticas planas. Tomaremos el eje Y paralelo al campo $\varepsilon$ y eje Z paralelo al campo B. En este caso particular:
\[ \varepsilon_{x}=0,\:\,\,\,\varepsilon_{y}=\varepsilon,\,\,\,\,\varepsilon_{z}=0, \]
y
\[ B_{x}=0,\:\,\,\,B_{y}=0,\,\,\,\,B_{z}=B. \]
Supondremos también que el campo se encuentra en el vacío, es decir,
que no hay cargas libre ni corrientes; esto implica que $\rho=0$
y $\boldsymbol{j}=0$, densidad de carga y densidad de corriente respectivamente.
En estas condiciones, las ecuaciones de Maxwell se expresan como:
(a) ley de Gauss para campo eléctrico,
\[ \frac{\partial\varepsilon}{\partial y}=0; \]
(b) ley de Gauss para campo magnético.
\[ \frac{\partial B}{\partial z}=0; \]
(c) ley de Faraday-Henry,
\[ \frac{\partial\varepsilon}{\partial z}=0, \]
\begin{equation} \frac{\partial\varepsilon}{\partial x}=-\frac{\partial B}{\partial t}; \end{equation}
(d) ley de Ampere-Maxwell,
\[ \frac{\partial\varepsilon}{\partial z}=0, \]
\begin{equation} -\frac{\partial B}{\partial x}=\epsilon_{0}\mu_{0}\frac{\partial\varepsilon}{\partial t}. \end{equation}
Las ecuaciones anteriores indican que ni $\varepsilon$ ni B dependen de Y o de Z. En consecuencia ambos cambos dependen sólo de X y de t, y en cada instante cada uno de ellos tiene el mismo valor sobre cualquier plano perpendicular al eje X. Por lo tanto nos quedan las ecuaciones distintas de ceron para deperminar las dependencias de los campos descritos con las variables X y t, posición y tiempo, respectivamente.
Derivando la ecuación (1) con respecto a x, obtenemos:
\[ \frac{\partial^{2}\varepsilon}{\partial x^{2}}=-\frac{\partial^{2}B}{\partial x\partial t}. \]
Análogamente, derivando la ecuación (2) con respecto a t, resulta
\[ -\frac{\partial^{2}B}{\partial x\partial t}=\epsilon_{0}\mu_{0}\frac{\partial{}^{2}\varepsilon}{\partial t^{2}}. \]
Combinando estos dos resultados se tiene
\[ \frac{\partial^{2}\varepsilon}{\partial t^{2}}=\frac{1}{\epsilon_{0}\mu_{0}}\frac{\partial^{2}\varepsilon}{\partial x^{2}}. \]
Inmediatamente se identifica la forma de una ecuación de onda
\[ \frac{\partial^{2}\psi}{\partial t^{2}}=\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial x^{2}}=\frac{1}{c^{2}}\frac{\partial^{2}\psi}{\partial x^{2}}. \]
en donde el campo eléctrico se propaga en la dirección del eje X con velocidad
\[ c=\frac{1}{\sqrt{\epsilon_{0}\mu_{0}}}, \]
por tanto se puede expresar de la forma
\[ \varepsilon(x,t)=\varepsilon(x-ct). \]
De manera análoga se tiene
\[ \frac{\partial^{2}B}{\partial t^{2}}=\frac{1}{\epsilon_{0}\mu_{0}}\frac{\partial^{2}B}{\partial x^{2}}, \]
de donde
\[ B(x,t)=B(x-ct). \]
Consideremos en particular el caso de las ondas armónicas de frecuencia $\nu=\frac{\omega}{2\pi}$ y longitud de onda $\lambda=\frac{2\pi}{k}$. En tal caso
\[ \varepsilon=\varepsilon_{0}\text{sin}k(x-ct)=\varepsilon_{0}\text{sin}(kx-\omega t) \]
y
\[ B=B_{0}\text{sin}k(x-ct)=B_{0}\text{sin}(kx-\omega t). \]
De donde observamos que
\[ k=\omega\sqrt{\mu_{0}\varepsilon_{0}}=\frac{\omega}{c}, \]
podemos además definir una contante llamada 'impedancia intrínseca del vacío' dada por:
\[ \eta_{0}=\sqrt{\frac{\mu_{0}}{\varepsilon_{0}}}=120\pi\simeq377\,\Omega; \]
por lo tanto podemos reescribir las ecuaciones de onda para campo eléctrico y magnético de manera vectorial como:
\[ \boldsymbol{\boldsymbol{\varepsilon}}=\varepsilon_{0}\text{sin}(kx-\omega t)\,\boldsymbol{a_{\varepsilon}}=\varepsilon_{0}\text{sin}(kx-\omega t)\,\boldsymbol{\widehat{j}}, \]
y
\[ \boldsymbol{B}=B_{0}\text{sin}(kx-\omega t)\,\boldsymbol{a_{B}}=B_{0}\text{sin}(kx-\omega t)\,\boldsymbol{\widehat{k}}=\frac{\varepsilon_{0}}{\eta_{0}}\text{sin}(kx-\omega t)\boldsymbol{\widehat{k}}. \]
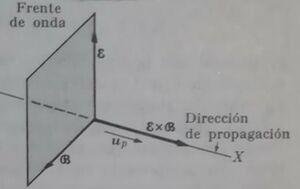
Al usar la notación de vectores canónicos unitarios, se puede observar claramente que ambos campos son siempre normales entre sí, tal que
\[ \boldsymbol{a_{\varepsilon}}\times\boldsymbol{a_{B}}=\boldsymbol{\widehat{k}}. \]
Esto significa que se sitúan en un plano transversal u ortogonal a esa dirección. Así, forma una onda electromagnética sin componentes de campo eléctrico y magnético a lo largo de la dirección de propagación, llamada 'onda electromagnética transversal (ET)'. $\varepsilon$ y B son a su vez, y por separado, una 'onda plana uniforme', puesto que $\varepsilon$ (o B) manientene igual magnitud a todo lo largo de un plano transversal, definido por x constante. La dirección en la que apunta el campo eléctrico es la polarización de una onda ET.
Derivando cada ecuación hallada respecto del tiempo, en el caso del campo magnético, y respecto a la posición, en el caso del campo eléctrico se tienen:
\[ \frac{d\boldsymbol{\boldsymbol{\varepsilon}}}{dx}=k\varepsilon_{0}\text{cos}k(x-ct), \]
y
\[ \frac{d\boldsymbol{B}}{dt}=-kc\varepsilon_{0}\text{cos}k(x-ct); \]
sustituyendo en la ecuación (1) se tiene:
\[ \frac{\partial\varepsilon}{\partial x}=-\frac{\partial B}{\partial t}\Rightarrow k\varepsilon_{0}\text{cos}k(x-ct)=-kc\varepsilon_{0}\text{cos}k(x-ct), \]
por lo tanto
\[ \varepsilon_{0}=cB_{0}\leftrightarrow B_{0}=\frac{1}{c}\varepsilon \]
Por otra parte, la existencia física de una onda plana uniforme es imposible, ya que se extendería al infinito y representaría una energía infinita. Pese a su simplicidad, no carece de importancia pues sirve como aproximación de ondas prácticas -las procedentes de una antena de radio, por ejemplo- alejadas de fuentes de radiación.