Pendulo
Introducción
Derivación de la ecuación del péndulo
Ecuación del movimiento en coordenadas polares
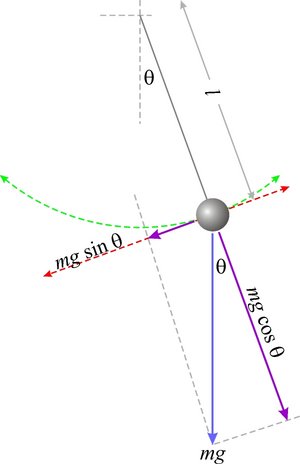
Tomamos un péndulo longitud , lo fijamos por el extremo superior y colocamos una partícula de masa en su extremo libre inferior. Situamos el origen del sistema de coordenadas en la posición de la partícula en equilibrio. Al desplazar la masa de su punto de equilibrio, oscila a ambos lados de dicha posición, realizando un movimiento armónico simple. En la posición de uno de los extremos, se produce un equilibrio de fuerzas. Para derivar las ecuaciones pertenecientes a un péndulo gravitacional se deben hacer las siguientes hipótesis:
- Hilo inextensible y sin peso
- Movimiento sin rozamiento del aire
La flecha azul representa la fuerza debido a la gravedad actuando sobre la masa. Las flechas en color violeta representan los componentes paralelo y perpendicular al movimiento instantáneo de la masa.
Ya que la masa está obligada a moverse en un trayecto circular (representado en color verde), el componente paralelo de esta fuerza es el responsable del movimiento de la masa y viene dado según la ecuación:
La fuerza perpendicular, que mantiene la masa en estado de equilibrio con la tensión del hilo es:
La aceleración lineal que sigue la línea marcada en color rojo está relacionada con el cambio en el ángulo por la fórmula para encontrar la longitud de arco:
De donde se deduce que la velocidad y la aceleración vienen dadas por:
Esta aceleración no toma en cuenta que el ángulo está disminuyendo. La ecuación de movimiento teniendo en cuenta que la aceleración tiene que llevar un signo negativo viene dada por:
Aplicamos la segunda ley de newton en forma diferencial.
Rescribimos la ecuación la ecuación como función de ángulo
reescribiendo esta ecuación sólo por notación tenemos que
de donde
\begin{equation} \ddot{\theta}= -{g\over \ell} \sin\theta \label{1} \end{equation}
que es la ecuación conocida del péndulo simple.
Solución aproximada(para ángulos pequeños)
Con deseos de encontrar una solución aproximada de la ecuación de movimiento, asumamos que es pequeña. En este caso
así que tenemos
ó
donde es la frecuencia de oscilación.
Algunas consideraciones extras
Recordemos que la solución a esta ecuación diferencial es
Donde , es la amplitud de la
oscilación y es el ángulo de desfasamiento. El movimiento es armónico simple, y el periodo de oscilación está dado por
Ecuación del movimiento en coordenadas cartesianas
Ahora tomamos la simetría del triángulo que forma la longitud del péndulo con el eje horizontal y el eje vertical
donde
Tenemos que la segunda derivada del ángulo con respecto al tiempo es
sustituimos en nuestra ecuación diferencial
y así
\begin{equation} \bigg(\frac{\ddot{x}(t) }{\sqrt{1-{x(t)^2 \over l^2}}} + \frac{\dot{x}(t)x(t) }{l^2(1-{x(t)^2 \over l^2})^{3\over 2}}\bigg)=-{g \over l}x(t) \label{2} \end{equation}
Que es exactamente igual a (\ref{2}) solo con una transformación de coordenadas.
Límite para ángulos pequeños
Para ángulos pequeños, es decir pequeños desplazamientos con respecto a la longitud del péndulo podemos hacer una serie de aproximaciones muy finas, pero si se suponen que los desplazamiento son lo suficientemente pequeños para justificar el porque se desprecian los términos de la forma
Entonces la ecuación (\ref{2}) se reduce a
y nos queda la ecuación homogénea diferencial de segundo orden del péndulo como función de las coordenadas cartesianas, donde la coordenada es función del tiempo.
Función Potencial de un péndulo
En el caso estacionario el parámetro es independiente del tiempo podemos determinar la energía potencial.
Por el teorema de trabajo energía establece la existencia de una función
la cual es llamada energía potencial entonces podemos determinar esta energía por
\begin{equation} V(x)=-\int F(x) dx \label{integral} \end{equation}
donde de la segunda ley de Newton
y sustituyendo en
finalmente
Consideraciones de la energía
Como la energía del sistema esta dada por la suma de la energía cinética más la energía potencial, entonces tenemos que
Cuando alcanza su amplitud máxima la velocidad de la masa es cero entonces
En el caso estudiado por galileo la constricción se introduce en el eje del péndulo sin realizar ningún trabajo sobre el sistema ; por lo tanto la energía se conserva
Para los dos estados estacionarios se obtiene la razón de sus amplitudes.
Péndulo de longitud variable
Algunas de la aportaciones mas importantes del principio del péndulo fue descubierto por el físico y astrónomo italiano Galileo, quien estableció que el periodo de la oscilación de un péndulo de una longitud dada puede considerarse independientemente de su amplitud, para amplitudes pequeñas(no obstante, cuando la amplitud es grande el periodo del péndulo si depende de ella). Galileo propone un experimento que utiliza un péndulo cercano de una pared, mientras este oscila , se introduce un clavo en la pared que se interpone en el camino que recorre la cuerda cuando pasa por la vertical.La longitud del péndulo cambia entonces de forma abrupta .Galileo, apoyándose en la nociones del momento e ímpetu que había concebido, explica que la altura máxima que alcanza el péndulo es idéntica en todos los casos. En aquella época no existía el concepto de energía que fue permeado años después, primero con la energía cinética, posteriormente con la energía potencial y finalmente distintas formas de energía cuyo valor total siempre se conserva.
En el lenguaje contemporáneo, el problema descrito por galileo se formula en términos de un oscilador armónico con un parámetro dependiente del tiempo(la longitud variable) y los invariantes asociados al sistema. A partir del ultimo tercio del siglo XX se revitalizo el interés por el oscilador armónico dependiente del tiempo, este debido a que se encontró un invariante exacto que es valido para variaciones lentas o rápidas.
Para el péndulo de longitud variable se describirá al sistema bajo tres condiciones:
• En el limite abrupto que es el invariante en un limite abrupto que abordo Galileo.
• En el limite adiabático que es el caso en el cual la variación de la longitud es muy lenta.
• En el caso más general del invariante exacto que debe ser válido para ambos casos particulares.
Longitud que varía con el tiempo
Si ahora consideramos a donde L es la longitud del péndulo como función del tiempo la ecuación diferencial toma la forma
Donde representa la posición horizontal del centro de masa del péndulo , es un parámetro dependiente el tiempo , es la longitud variable y es la contante gravitacional en la superficie terrestre.
Oscilaciones forzadas con amortiguamiento
En la física clásica un oscilador armónico simple un sistema físico en el cual, su movimiento es con respecto a una posición de equilibrio en el que ninguna fuerza actúa sobre el sistema y cuando se desplaza de su posición de equilibrio proporcional experimenta una única fuerza de compensación F proporcional al desplazamiento x y opuesta a la dirección del desplazamiento y este movimiento es periódico (se repite en un cierto intervalo de tiempo)
Algunos osciladores armónicos son:
Masas conectadas a un resorte
Péndulos con ángulos de desplazamientos pequeños
Cuando una fuerza actúa sobre un oscilador y sea única es un oscilador sea única es un oscilador armónico simple. Si existiera una fuerza de fricción digamos proporcional a la velocidad, el oscilador se llama amortiguado. Si existiera una fuerza externa dependiente del tiempo se dice que el oscilador es forzado
Veamos un sistema masa-resorte donde la única fuerza que actúa sobre la masa m es una fuerza de compensación F proporcional al desplazamiento x y opuesta a la dirección del desplazamiento de acuerdo con la ley Hooke
Donde k es una constante positiva
Por la segunda ley de Newton se tiene que
Donde
es la aceleración es decir
Por lo que
Y poniendo
la ecuación anterior se describe
La cual es una ecuación diferencial ordinaria de segundo orden y observamos que las soluciones de esta ecuación debe ser una función de
resolviendo
Con a y b constantes arbitrarios como solución general podemos escribir como
Con A y Φ otras constantes a las que se llaman Amplitud y fase del oscilador respectivamente ambos determinados por las condiciones iniciales la amplitud indica que tan fuerte es la oscilación y la fase dice en qué punto de la oscilación estaba el sistema Una oscilación se repite después de cada 2π/ω segundos a la cual se le conoce como frecuencia del oscilador
Podemos notar que la frecuencia del oscilador depende de k y m mientras más grande sea k más rígido será el resorte; se necesitara más fuerza y así la frecuencia será mayor. Hay otra cantidad que se usa en el movimiento ondulatorio
Ahora veremos a un oscilador físico, que se somete a una fuerza impulsora periódica mediante una agente externo. Para esto veremos un nuevo fenómeno llamada resonancia, la resonancia es un fenómeno de un oscilador impulsado exteriormente es el modo con que una fuerza periódica de un valor fijo produce diferentes resultados dependientes de su frecuencia. En particular, si la frecuencia impulsora se hace muy próxima a la frecuencia natural, entonces suele hacerse la amplitud de oscilación muy grande mediante aplicaciones repetidas de una fuerza muy pequeña.
Apoyándonos de ciertas ecuaciones podemos ver que
El valor de que representa la frecuencia angular natural del sistema, se designará por ω0 por lo tanto la ecuación de movimiento, en la forma
ma = fuerza neta, es:
O bien
\begin{equation}
m\frac{d^2x}{dt^2}+kx=F_0 \cos(\omega t)
\label{4}
\end{equation}
Consideramos la situación, si el oscilador se ve impulsado a partir de la posición de equilibrio y se le deja oscilar por sí mismo, oscilará con su frecuencia natural $\omega_0$ . Una fuerza impulsora periódica, sin embargo, intentara imponer su propia frecuencia ω al oscilador. La característica más importante del movimiento será gran respuesta en las proximidades de $\omega=\omega_0$, antes de resolver la ecuación (\ref{4}) señalaremos algunas características del movimiento en los casos extremos de valores muy altos o muy bajos de la frecuencia impulsora ω.
Si la fuerza impulsora es de frecuencia muy baja respecto a la frecuencia natural de las oscilaciones libres, es lógico que la partícula se mueva esencialmente en fase con la fuerza impulsora con una amplitud no muy diferente de desplazamiento que produciría una fuerza constante F0. Esto es equivalente a afirmar que el término en la ecuación 1 juega un papel relativamente pequeño comparado con el término kx a frecuencias muy bajas, o en otras palabras que la respuesta está controlada por la rigidez del muelle.
Para obtener la solución estacionaria de la ecuación (\ref{4}) podemos escribir
\begin{equation}
x=C \cos(\omega t)
\label{5}
\end{equation}
En otras palabras estamos admitiendo que el movimiento es armónico, de la misma frecuencia y fase que la fuerza impulsora, y que no están presentes las oscilaciones naturales del sistema.
No debemos olvidar que la ecuación (\ref{5}) es simplemente de tanteo y debemos estar preparados para rechazarla si no acertamos a encontrar un valor de la constante C, hasta ahora indeterminada, tal que satisfaga la ecuación (\ref{4}) para valores arbitrarios de ω y t derivando la ecuación (\ref{5}) dos veces respecto a t se tiene
Sustituyendo en la ecuación (\ref{4}) tenemos así
Y de aquí.
\begin{equation} C=\frac{F_0}{(k-(m \omega)^2 )}=\frac{(F_0/m)}{\omega_0^2-\omega^2} \label{6} \end{equation}
La ecuación (\ref{6}) define satisfactoriamente la ecuación a C de modo que la ecuación (\ref{4}) se satisface siempre. Así pues, podemos considerar que el movimiento forzado esta descrito por la ecuación (\ref{5}) con C dependiente de ω de acuerdo con la ecuación (\ref{6}).
El fenómeno de por sí mismo está representado por el hecho de que el valor de C, sin tener en cuenta el signo, resulta infinitamente grande cuando se cumple exactamente que $\omega= \omega_0$.
Otro procedimiento mejor de llegar al resultado, más de acuerdo con nuestra descripción general de los movimientos armónicos. Este método consiste en expresar x en función de una vibración sinusoidal que tenga una amplitud A, mediante la definición de una magnitud positiva y una fase α para t = 0
Esto implica la condición $A= |C|$ y que se dé a $\alpha$ uno u otro de los siguientes valores según la frecuencia impulsora $\omega$ sea menor o mayor que $\omega_0$:
El intervalo de $\omega$ viene entonces representado por curvas separadas para la mitad de la amplitud $A$ y para la fase $\alpha$. El valor infinito de $A$ para $\omega= \omega_0$ el salto discontinuo de cero a $\pi$ del valor de $\alpha$ cuando se pasa por $ω_0$ carece de significado físico, pero como veremos, representa un caso límite (matemáticamente) de lo que realmente ocurre en el sistema de amortiguamiento no nulo.
Utilizando el método del exponente complejo resultara ser muy ventajosa cuando la consideremos en el caso del oscilador amortiguado pero no nos meteremos con números complejos. Empecemos con la ecuación física del movimiento dada por la ecuación (\ref{4}).
Con esto entraremos de lleno con el tema de oscilaciones forzadas con amortiguamiento Consideremos ahora el resultado que se obtiene al actuar sobre un sistema una fuerza. El enunciado de Newton se convierte ahora en
o bien
\begin{equation} \frac{d^2x}{dt^2}+\frac{b}{m}\frac{dx}{dt}+\frac{k}{m}x=\frac{F_0}{m}\cos(\omega t) \label{7} \end{equation}
Haciendo ,esta expresión puede escribirse
Busquemos una solución estacionaria a esta ecuación.
Suponemos una solución de la forma:
(*)
Por lo tanto tenemos:
\begin{equation} A(\omega)=\frac{\frac{F_0}{m}}{[(\omega_0^2-\omega^2)^2+(\gamma\omega)^2]^{1/2}} \label{8} \end{equation}
Esta es la ecuación que nos ayudara a encontrar la frecuencia de resonancia y la constante de amortiguamiento para encontrar la constante de resonancia solamente despejaremos de la ecuación y haciendo que ω_0=ω por lo tanto queda que
Por lo tanto
Donde gama γ es la constante amortiguamiento
Para encontrar la frecuencia de la resonancia solamente derivamos la ecuación (\ref{8})
Donde $\omega$ es la frecuencia de resonancia
Aportación por Usuario: Yonatan Aldana Saldañas 20:49 28 mar 2012 (UTC)













































































![A(\omega)=\frac{\frac{F_0}{m}}{[(\omega_0^2-\omega^2)^2+(\gamma\omega)^2]^{1/2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9897a4a3c158c9c075d1766fa230dee8716e6cb8)

