Vibra: probs c2
Main cap.2
Problema 2.1
Un reloj hace tick 5 veces por segundo . Su rueda de equilibrio tiene un momento de inercia de $2\times10^{-6}\mathrm{kg\mathrm{m^{2}}}$. Calcular la rigidez trosional del resorte de balance . (Suponiendo que el periodo es de 2 ticks )
Tenemos que la frecuencia angular para vibraciones angulares esta dado por:
\begin{equation} \omega{}_{0}=\sqrt{\frac{c}{I}}=\frac{\sqrt{c}}{\sqrt{I}}...(1) \end{equation}
Donde: $\omega{}_{0}$ es la frecuencia angular, $c$ es la rigidez
torcional e $I$ es el momento de inercía .
Sustituimos la ecuación (1) en la expresión para en periodo y despejamos c
\[ T=\frac{2\pi}{\omega{}_{0}}=\frac{2\pi\sqrt{I}}{\sqrt{c}} \]
\begin{equation}
c=\frac{4\pi^{2}I}{T^{2}}
\end{equation}
Suistituimos los datos proporcionados en el ejercicio
\[ c=\frac{4\pi^{2}(2\times10^{-6}\mathrm{kg\mathrm{m^{2}}})}{(2\mathrm{s})^{2}}=1.9739\times10^{-5}\mathrm{kgm^{2}s^{-2}} \]
\[
c=1.9739\times10^{-5}\mathrm{kgm^{2}s^{-2}}
\]
Rosario Maya (Usuario discusión:Rosario Maya) 17:02 17 feb 2015 (MVR)
Luis Velázquez (Usuario discusión:Luis Velázquez) 11:37 17 feb 2015 (CST) Mario Moranchel (discusión) 04:16 22 ene 2014 (UTC)
Enuncié la expresión de periodo --Pablo (discusión) 22:38 19 feb 2015 (CST)
Problema 2.2
Un reloj de pared hace tick una vez por segundo . Muestre que la longitud del péndulo debe ser de al menos de $1m$ de altura
El periodo de un péndulo vibracional se define como:
\begin{equation} T=\frac{2\pi}{\omega{}_{0}} ...(1) \end{equation}
despejando $\omega_{0}$ de (1), tenemos
\begin{equation} \omega_{0}=\frac{2\pi}{T} ... (2) \end{equation}
donde la frecuencia angular para el péndulo vibracional está dada
por:
\begin{equation} \omega_{0}=\sqrt{\frac{g}{l}} ... (3) \end{equation}
Substituyendo la ecuación (3) en la ecuación (2)
\[ \frac{\sqrt{g}}{\sqrt{l}}=\frac{2\pi}{T} \]
Despejando $\sqrt{l}$, tenemos:
\[ \sqrt{l}=\frac{T\sqrt{g}}{2\pi} \]
\[
l=\frac{gT{}^{2}}{4\pi^{2}}
\]
Substituyendo los siguientes valores: $g=9.81\mathrm{ms^{-2}}$y $T=2s$,
el periodo es de 2s ya que la frecuencia de oscilación es de $0.5s^{-1}$ y ya que
el periodo es el inverso de la frecuencia de oscilación, tenemos que:
\[ l=\frac{(9.81\mathrm{ms^{-2}})(4s^{2})}{4\pi^{2}}=0.9939\mathrm{m} \]
\[
l\eqsim1\mathrm{m}
\]
Rosario Maya (Usuario discusión:Rosario Maya) 19:10 17 feb 2015 (MVR)
Otra forma de resolver el problema es la siguiente:
El problema nos habla de un reloj que hace tictac una vez por segundo y nos pide demostrar que el reloj es de 1m de altura.
El hecho de que haga tictac una vez por segundo nos dice que tiene una frecuencia de medio segundo.
Entonces con este dato podemos obtener la frecuencia angular del reloj despejando la siguiente ecuación:
\[ \nu=\frac{\omega}{2\pi} \]
De esta relación podemos despejar $\omega$
\[ \omega=2\pi\nu....(1) \]
La ecuación para un péndulo simple es:
\[ \omega=\left[\frac{g}{L}\right]^{\frac{1}{2}} \]
De aquí se puede despejar la longitud $L$ para obtener: \[ L=\frac{g}{\omega^{2}}....(2) \] Entonces al substituir $w$ de la ecuación (1) en la ecuación (2), queda: \[ L=\frac{g}{(2\pi\nu)^{2}} \] Ya que conocemos todos los datos de la ecuación podemos substituir todo y obtendremos:
\[ L=\frac{(9.81\mathrm{ms^{-2}})}{4\pi^{2}(0.5^{2})}=0.9939\mathrm{m}\eqsim1\mathrm{m} \]
--Daniel Olvera Moreno - 22:17 20 de feb 2014 --Pablo (discusión) 22:49 19 feb 2015 (CST) --A. Martín R. Rabelo (discusión) 18:02 22 feb 2015 (CST)
Problema 2.3
2.3. Show that the isotermal compressibility is equal to for a perfect gas. Estimate the percentage difference which the use of instead would make to the calculated value of for a flask containing air.
Muestra que la compresibilidad isotérmica es igual a para un gas perfecto. Estima la diferencia porcentual que el uso de en lugar de haría al calculo del valor de para un frasco que contiene aire.
Usamos la ecuación de gas perfecto para obtener una expresión para la compresibilidad isotérmica usando su definición termodinámica
. Primero despejamos de la ecuación de gas perfecto y derivamos:
Usando la ecuación de gas perfecto se reduce a:
Ahora sustituimos en la definición de
Entonces la expresión para la frecuencia angular, usando queda:
Por otro lado, la expresión de la frecuencia angular usando es:
Donde es la razón de las capacidades caloríficas y se uso la ecuación de gas perfecto en términos de la masa molar , .
Así la diferencia porcentual puede ser calculada con la razón de ambas frecuencias:
Y si usamos de nuevo la ecuación del gas perfecto, donde se tiene
Finalemente la diferencia porcentual se obtiene multiplicando por 100 el resultado anterior. Brenda Pérez Vidal (discusión) 23:15 16 feb 2014 (UTC)
Edgar Ortega Roano (discusión) 09:23 12 feb 2014 (UTC)
Brenda Pérez Vidal (discusión) 22:23 9 feb 2014 (UTC)
Problema 2.4
2.4. Estimate the approximate change in the pitch of the organ if the temperature in church falls by 20ºC (The pitch of a vibrator rises by one semitone every time its frequency rises by 5.9 percent).
Estima el cambio aproximado en el tono del órgano si la temperatura en la iglesia cae a 20ºC (el tono de un vibrador se eleva a un semitono cada vez que su frecuencia aumenta en un 5,9 por ciento).
Para resolver este problema, se considera el aire del ambiente bajo
condiciones normales de temperaturaa y presión, comportándose como
un gas ideal y obedeciendo la relación de los gases ideales:
\[ pV=RT \]
Para cambios adiabáticos en un gas ideal, se toma a $pV^{\gamma}$como
una constante en donde $\gamma=\frac{Cp}{Cv}$ con Cp: constante de
presión y Cv: constante de volúmen.
Se sabe que la compresibilidad del aire (k), se calucla ulilizando la siguiente relación:\ensuremath{\partial}
\begin{equation} K=-\frac{1}{V}(\frac{dV}{dp}) \end{equation}
Donde d representa una dreivada parcial.
De la relación anterior, se obtiene ks para la expresión $\frac{1}{\gamma p}.$
Al ocupar la siguiente relación: $\omega_{0}\thickapprox(a/lvpk)^{1/2}$ y escibir la ecuación del gasi ideal de la masa molar, el volumen y la constante R, se obtienen las siguientes relaciones:
\[ \rho=\frac{M}{V}=\frac{Mp}{RT} \]
\[
\rho KS=\frac{M}{\gamma RT}
\]
En donde$\rho ks$ representa la presión adiabática; al sustituir
las relaciónes anteriores en la definición que se dio de $\omega_{0},$se
obtiene:
\[ \omega_{0}\thickapprox\left[\left(\frac{a}{lv}\right)\left(\frac{\gamma RT}{M}\right)\right]^{1/2} \]
En donde $a=10^{-4}m^{2},v=10^{-3}m^{3},,l=5x10^{-2}m$ son datos
atmosféricos y valores típicos para las dimensiones de un cilindro.
$ $Y en la imágen que se muestra a continuación, se aprecian valores dados en el libro de Maine en la página 21:
\includegraphics[scale=0.1]{\string"../../Pictures/iPhoto biblioteca/Previews/2014/02/20/20140220-104005/1948027_10202466608239773_797720853_n\string".jpg}
Lo siguiente es calcular la frecuencia al ocupar la siguiente relación: $\nu=\frac{\omega}{2\Pi}$
Se calcula la frecuencia para dos casos, el de la temperatura inicial y el de la temperatura final, y se obitienen los siguientes resultados:
$\omega_{0i}=\left[\left(\frac{10^{-4}}{10^{-3}(5x10^{-2})}\right)\left(\frac{1.4(8.3)(300)}{0.029}\right)\right]^{1/2}=490.3$ rad/s $\nu_{i}=\frac{490.3}{2\Pi}$=78 Hz
$\omega_{0f}=\left[\left(\frac{10^{-4}}{10^{-3}(5x10^{-2})}\right)\left(\frac{1.4(8.3)(6.85)}{0.029}\right)\right]^{1/2}$=74.09rad/s $\nu_{f}=\frac{74.09}{2\Pi}=11.8$ Hz
Ahora se calcula la diferencia entre ambas frecuencias:
$ $$\Delta\nu=-66.2$
Que resulta negativo porque decrece.
Luis Velázquez (Usuario discusión:Luis Velázquez) 11:41 17 feb 2015 (CST)
Ana Alarid (discusión) 01:05 22 feb 2014 (UTC)
Para calcular el número de semitons, se divide la diferencia de frecuencias entre 0.59, y el número de semitonos es igual a -39.058.
Problema 2.5
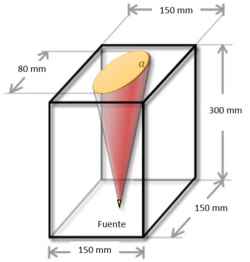
2.5. A miniature loudspeaker unit has a cone of diameter 80 mm mounted in a hole of the same diameter in a sealed cabinet of internal dimensions 150 mm X 150 mm X 300 mm. Yhe mass of the cone is 5.0 g, and the mounting is such that the stiffness of the suspension may be neglected. Estimate the free vibration frequency of the cone
Interpretación al español latino
Una unidad de altavoz en miniatura tiene un cono de 80 mm de diámetro montado en un agujero del mismo diámetro en un gabinete cerrado de dimensiones interiores 150 mm X 150 mm X 300 mm. La masa del cono es 5.0 g, y el montaje es tal que la rigidez de la suspensión puede ser despreciada. Estimar la frecuencia de vibración libre del cono.
Tenemos los siguientes datos: Diámetro de la base = $0.80[m]$; radio de la base del cono = $0.04 [m]$; masa del cono = $0.005 [kg]$; dimensiones de la suspensión= $0.15 [m] X 0.15 [m] X 0.3[m]$; suponiendo que $l=0.3 [m]$, es decir, la misma altura de la suspensión.
Se utilizan las siguientes ecuaciones base para determinar vibraciones acústicas: \begin{equation} \kappa=-\frac{1}{V}(\frac{\partial V}{\partial p}) ......(1) \end{equation}
donde $\kappa$ constante de compresibilidad del aire, $V$ es el volumen del cono, $p$ presión ejercida por el aire dentro del cono, $l$ altura del cono.
\begin{equation} \omega_{0}=(\frac{a}{lV\rho\kappa})^{\frac{1}{2}} ......(2) \end{equation}
donde $\omega_{0}$ la frecuencia libre, $a$ superficie transversal del cono (base circular), $\rho$ densidad del cono, $\kappa$ constante de compresibilidad del aire, $l$ altura del cono.
De acuerdo al problema, se nos pide encontrar la frecuencia libre del cono, entonces primeramente determinamos el volumen de nuestro objetivo y enseguida su densidad:
\begin{equation} V=\frac{1}{3}*\pi*r^2*l ......(3) \end{equation}
\begin{equation} V=(\frac{1}{3})(\pi)(0.04)^2(0.3) \end{equation}
\begin{equation} V=5.02*10^{-4}[m^3] \end{equation}
\begin{equation} \rho=\frac{m}{V}......(4) \end{equation}
\begin{equation} \rho=\frac{0.005}{5.02*10^{-4}} \end{equation}
\begin{equation} \rho=9.96 [\frac{kg}{m^3}] \end{equation}
Considerando que alguna partícula está dentro del altavoz posicionada en la fuente (origen), en reposo y con masa despreciable (como se indica en la figura) efectuará un movimiento uniforme cuando el impulso de sonido, originado en la fuente, produzca un frente de onda que lleve a la partícula perpendicularmente sobre la sección transversal denotada por $a$, entonces podemos determinar la aceleración del sonido en el cuerpo cónico:
Sabemos que la rapidez del sonido en el aire a 20[°C] es $v=343 [\frac{m}{s}]$
\begin{equation} (v_{f})^2=(v_{i})^22a(x_{f}-x_{i}); v_{i}=0, x_{i}=0 \end{equation}
Despejando a \begin{equation} a=\frac{(v_{f})^2}{2x_{f}} \end{equation}
\begin{equation} a=\frac{(343)^2}{2(0.3)} \end{equation}
\begin{equation} a=196.08*10^3 [\frac{m}{s^2}] \end{equation}
La fuerza se determina a través de la segunda ley de Newton: $F=m*a$, tenemos la aceleración del sonido, sin embargo también necesitamos la masa del medio, es decir del aire, para ello utilizaremos la expresión de densidad, pues conocemos el volumen del recipiente que contiene al gas y la densidad del mismo:
Densidad del aire \begin{equation} \rho= 1 [\frac{kg}{m^3}] \end{equation}
\begin{equation} \rho= \frac{m}{V} \end{equation}
\begin{equation} m=\rho*V \end{equation}
\begin{equation} m=(1)(5.02*10^{-4}) \end{equation}
\begin{equation} m=5.02*10^{-4}[kg] \end{equation}
Ahora sustituyendo en la segunda ley de Newton $F=m*a$:
\begin{equation} F=(5.02*10^{-4})(196.08*10^3 ) \end{equation}
\begin{equation} F=98.432 [N] \end{equation}
Ahora encontramos la presión que se ejerce sobre la superficie transversal $a$:
\begin{equation} p=\frac{F}{A} \end{equation}
Conocemos el radio de la base del cono, así podemos determinar el área de la sección transversal: $a=A=\pi*r^2$ entonces $A=5.026*10^{-3}$:
\begin{equation} p=\frac{98.432}{5.026*10^{-3}} \end{equation}
\begin{equation} p=19584.592 [Pa] \end{equation}
Utilizando las expresiones de densidad, fuerza y presión podremos encontrar $\kappa$ indicada con (1), $\kappa$ representa la propiedad relevante del aire: su compresibilidad. \begin{equation} \kappa=-\frac{1}{V}(\frac{\partial V}{\partial p}) \end{equation}
Para sustituir correctamente los datos en (1), es necesario poner el volumen en función de la presión debida al aire.
\begin{equation} p=\frac{F}{A}=\frac{F}{\pi*r^2} \end{equation} Despejando $r^2$
\begin{equation} r^2=\frac{F}{\pi*p} \end{equation}
Sustituyendo $r^2$ en el volumen
\begin{equation} V=\frac{1}{3}*\pi*r^2*l \end{equation}
\begin{equation} V=\frac{1}{3}Flp^{-1} \end{equation} Aplicando derivada parcial respecto de la presión:
\begin{equation} \frac{\partial V}{\partial p}=-\frac{1}{3}Flp^{-2} \end{equation}
\begin{equation} \frac{\partial V}{\partial p}=-\frac{Fl}{3p^{2}} \end{equation}
Ahora sólo sustituimos en (1)
\begin{equation} \kappa=-\frac{1}{V}(\frac{\partial V}{\partial p}) \end{equation}
\begin{equation} \kappa=-(\frac{1}{V})(-\frac{Fl}{3p^{2}}) \end{equation}
Evaluando
\begin{equation} \kappa=\frac{1}{5.02*10^{-4}}(\frac{(98.432)(0.3)}{3(19584.592)^{2}}) \end{equation}
\begin{equation} \kappa= 5.112*10^{-5} [\frac{ms^{2}}{kg}] \end{equation}
Finalmente sustituimos todos los valores en (2)
\begin{equation} \omega_{0}=(\frac{a}{lV\rho\kappa})^{\frac{1}{2}} \end{equation}
\begin{equation} \omega_{0}=(\frac{5.026*10^{-3}}{(0.39)(5.02*10^{-4})(9.96)})^{\frac{1}{2}} \end{equation}
El resultado es:
\begin{equation} \omega_{0}=255.867 [s^{-1}] \end{equation}
Luis Velázquez (Usuario discusión:Luis Velázquez) 11:50 17 feb 2015 (CST)
Angel Nahir Molina Guadarrama (discusión) 08:10 21 feb 2014 (UTC) --Pablo (discusión) 20:54 22 feb 2015 (CST)
Problema 2.6
2.6. Two masses and are joined by a spring of stiftness . They can vibrate along the line of their centres,moving alternately towards and away from each other. For this vibration, show that where
solucion:
consideremos la siguiente figura
en la figura dos cuerpos de masa mencionada estan unidos a un resorte de constante S y consideremos y las coordenadas de posicion de los cuerpos respecto a un sistema fijo de coordenadas.En este caso es la distancia desde los puntos hasta el bloque de masa y va de los puntos hasta , entonces la longitud del resorte sera y si su longitud para la deformacion nula es , el alargamiento del resorte es .
El movimiento de los bloques solo esta dado en una dirección en este
caso elegimos la dirección $\hat{i}$ y entonces el problema a tratar
es unidimensional
La fuerza que se ejerce sobre $m_{2}$es :
\[ F_{2}=-kx \]
y la fuerza sobre $m_{1}$es:
\[ F_{1}=-(-kx) \]
así las ecuaciones de movimiento para cada bloque es:
\begin{equation} \ddot{m_{1}x}_{1}=kx \end{equation}
\begin{equation}
m_{2}\ddot{x}_{2}=-kx
\end{equation}
para resolver las ecuaciones diferenciales miltiplicamos a $(1)$
por $m_{2}$ y a $(2)$ por $m_{1}$y así obtenemos:
\[ m_{1}m_{2}\ddot{x}_{1}=m_{2}kx\qquad,\qquad m_{1}m_{2}\ddot{x}_{2}=-m_{1}kx \]
y al restarlas llegamos a:
\[ m_{1}m_{2}(\ddot{x}_{2}-\ddot{x}_{1})=-kx(m_{1}+m_{2}) \]
pero sabemos que $x=x_{2}-x_{1}-d\qquad entonces\qquad\ddot{x}=\ddot{x}_{2}-\ddot{x}_{1}$
por lo tanto la ecuacion diferencial queda como
\[ \ddot{x}+(\frac{m_{1}+m_{2}}{m_{1}m_{2}})kx=0\qquad haciendo\qquad\mu=\frac{m_{1}+m_{2}}{m_{1}m_{2}} \]
\begin{equation}
\ddot{x}+\mu kx=0
\end{equation}
ahora, sí $m_{1}\ll m_{2}$encontramos que $\mu\approx m_{1}$y entonces
la ecuación diferencial sería la de un solo bloque.
Luis Miguel Sánchez Mtz. (discusión) 01:59 26 ene 2014 (UTC)
Problema 2.7
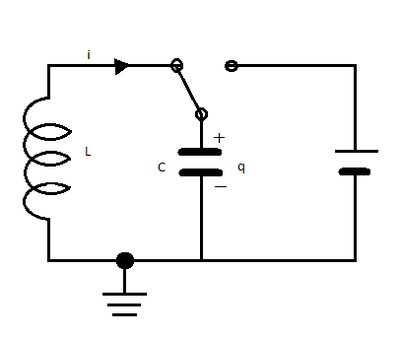
2.7. Shows an arrangement wicht could be used to set an LC circuit into oscilation. The capacitor is first charged to a voltage $V$ be means of the battery. At time $t=0$ the switch is thrown to connect the charged capacitor across the coil. Derive: a) the amplitude. b) the phase constant of the resulting oscilation.
2.7. Muestra un arreglo que podría ser usado para establecer un circuito LC en oscilación. El condensador está primero cargado a una voltaje $V$ con la batería. En el tiempo $t = 0$ el interruptor se cambia para conectar el condensador cargado a través de la bobina. Calcular:
a) La amplitud. b) La constante de fase de la oscilación resultante.
-El voltaje total en el circuito LC está dado por:
donde,
entonces,
Sea por lo que de la ec. (1.1'), al desconectar el circuito tendremos:
La solución general de la ec. (1.2) es,
su derivada, la corriente $I$:
Ahora, cuando el circuito se haya conectado, esto es, en $t=0$
la igualdad de la ecuación (1.4') se satisface:
Y, por último la ecuación (1.3) en $t=0$ es:
como y tenemos, entonces:
--Daniela López Martínez (discusión) 17:06 29 may 2013 (CDT) --A. Martín R. Rabelo (discusión) 16:45 22 feb 2015 (CST)
Problema 2.7.5
La figura 2.8 muestra un arreglo que puede ser usado para poner un circuito LC en oscilacion. El capacitor esta cargado inicialmente con un voltaje $V_{1}$en la bateria. En el tiempo $t=0$ el switch se cambia para conectar el capacitor cargado a lo largo del circuito. Derive (a) la amplitud y (b) la constante de fase de la oscilacion resultante.
La solución a este problema la realice de la siguiente manera:
Tenemos que la ecuación diferencial de este sistema está dada por:
\[ V_{1}+\varepsilon_{L}=0 \]
\[
L\frac{di}{dt}+\frac{q}{C}=0
\]
\[
L\frac{d^{2}q}{dt^{2}}+\frac{q}{C}=0
\]
Del polinomio característico de la ecuación y sabiendo que $\omega_{0}^{2}=\frac{1}{\sqrt{LC}}$,
tenemos que una solución para esta dada por:
\[ \psi(t)=Acos(\omega_{0}+\phi) \]
Notemos que, en nuestro caso, $\psi(t)=q(t)$ y $\frac{dq(t)}{dt}=i(t)$,
las cuales son la carga y la corriente respectivamente, luego, para
hallar (a) tenemos que:
\[ A=\frac{\psi(t)}{cos(\omega_{0}t+\phi)}=\frac{q(t)}{cos(\omega_{0}t+\phi)} \]
Para hallar (b), realicemos lo siguiente:
\[ \psi(t)=Acos(\omega_{0}t+\phi) \]
\[
\frac{d\psi(t)}{dt}=-A\omega_{0}sen(\omega_{0}t+\phi)
\]
Diviendo ambas ecuaciones entre sí tenemos que:
\[ \frac{\psi(t)}{\psi(t)}=-\frac{sen(\omega_{0}t+\phi)\omega_{0}}{cos(\omega_{0}t+\phi)}\Rightarrow\frac{\psi(t)}{\omega_{0}\psi(t)}=-tan(\omega_{0}t+\phi) \]
\[
\omega_{0}t+\phi=arctan\left(\frac{-i(t)}{\omega_{0}q(t)}\right)
\]
\[
\Rightarrow\phi=arctan\left(\frac{-i(t)}{\omega_{0}q(t)}\right)-\omega_{0}t
\]
--Cesar Ivan Avila Vasquez Traducción:Cesar Ivan Avila Vasquez 23:49 19 Feb 2014 (CDT)
Problema 2.8
2.8. Show that vertical vibrations of a mass m suspended on a spring of stiffness s whose other end is fixed have angular frequency (s/m)^1/2 .(Hint: measure displacements from the equilibrium position of the mass, where its weight is balanced by the spring force.)
Muestra que las vibraciones verticales de una masa m suspendida de un resorte de rigidez s, cuyo otro extremo está fijo, tienen una frecuencia angular de . (Consejo: Mide los desplazamientos de la posición de equilibrio de la masa, donde su peso está balanceado por la fuerza del resorte.)
Cuando la masa se cuelga del resorte y el sistema está en equilibrio, el resorte adquiere una longitud y ejerce una fuerza de restauración de la forma:
Usando la segunda ley de Newton, la suma de fuerzas en el equilibrio debe ser cero:
El momento en que el sistema oscila verticalmente la masa se desplaza una distancia de la posición de equilibrio y se ejerce una fuerza de restauración:
En este caso la segunda ley de Newton queda:
Pero del equilibrio sabemos que , entonces la segunda ley de Newton queda:
Al dividir la ecuación entre se tiene:
Que es la forma de la ecuación de oscilación armónica simple , de ahí concluimos que la frecuencia angular del sistema es:
Brenda Pérez Vidal (discusión) 20:42 9 feb 2014 (UTC)
La forma en que resolvería el problema es:
Cuando se cuelga una masa $m$ al resorte, ésta alcanza la posición de equilibrio $y_0$. En esta posición tenemos que la segunda ley de Newton es
\begin{equation} mg-sy_0=0.\qquad\qquad (1) \end{equation}
Ahora, si desplazamos la masa una cantidad $y$ desde la posición de equilibrio $y_0$, la segunda ley de Newton es \begin{eqnarray*} m\frac{d^2 y}{dt^2}&=& mg-s(y_0+y)\\ m\frac{d^2 y}{dt^2}&=&-sy,\qquad\qquad (2) \end{eqnarray*}
donde utilizamos $(1)$. La ec.de movimiento $(2)$ es igual a la ec. de movimiento en la dirección $x$, por tanto se tiene que $\omega^2=\frac{s}{m}$.
--Ernesto (discusión) 14:11 14 may 2013 (CDT)
--mfg-wiki (discusión) 15:09 2 may 2013 (CDT)
Problema 2.9
2.9. An astronaut on the surface of the moon weignts rock samples using light spring balance, wich was calibrated on earth, has a scale 100 mm long wich reads from 0 to 1.0 kg.He observes that certain rock gives a stady reading of 0.40 kg and, when disturbed, vibrates with a period of 1.0 s. What is the acceleration due to gravity on the moon?
2.9 Un astronauta sobre la superficie de la luna pesa muestras de roca utilizando un ligero dinamómetro. Ésta báscula, que fue calibrada en la tierra, tiene una escala de 100 mm de largo que lee de 0 a 1 kg. Él observa que cierta roca da una lectura estable de 0.40 kg y, cuando se le perturba, vibra con un periodo de 1.0 s. ¿ Cuál es la aceleración debido a la gravedad en la luna?
Sabemos por la redacción del problema que el dinamómetro utiliza en su interior un resorte ligero , así que tenemos:
La ecuación 1 también puede expresarse de la siguiente forma:
En la ecuación 2 el primer término corresponde a la fuerza de gravedad lunar, mientras que el segundo corresponde a la fuerza del resorte. La suma de ambas fuerzas da como resultado cero porque las fuerzas están en equilibrio.
Para resolver el problema necesitamos encontrar el valor de la la constante de proporcionalidad , y lo hacemos de la siguiente manera. Como sabemos que la roca al ser perturbada oscila armonicamente podemo utilizar la siguiente ecuación para la frecuencia angular (la frecuencia angular de un movimiento armónico simple).
\begin{equation}\omega=\sqrt{\frac{k}{m}} ...(3)\end{equation}
De la ecuación 3 despejamos k elevando al cuadrado ambos lados de la ecuación y obtenemos:
\begin{equation}k=m\omega^{2} ...(4)\end{equation}
El valor de la masa (de la roca) es un dato que nos proporciona el problema y como sabemos que la frecuencia angular para un movimiento armónico simple es:
\begin{equation}\omega = \frac{2\pi}{T} ...(5)\end{equation}
Por último par resolver el problema usamos la ecuación 1 y el hecho de que la segunda derivada de respespecto del tiempo es la aceleración de la gravedad lunar. Tendremos ahora una nueva ecuación, muy parecida a la ecuación 1:
\begin{equation}mg=kx...(6)\end{equation}
Despejamos g:
\begin{equation}g=\frac{kx}{m}...(7)\end{equation}
La solución queda:
\begin{equation}mg=m\omega^{2}x \end{equation}
\begin{equation}g=\frac{kx}{m}=\frac{(10kg/s^{2})(0.4m)}{(0.2533kg)}=1.57m/s^{2}\end{equation}
\begin{equation}g=\omega^{2}x=(\frac{2\pi}{T})^{2}x=1.57m/s^{2}\end{equation}
Pedro Pablo Ramírez Martínez (discusión) 21:48 16 feb 2014 (UTC)
Problema 2.11
2.11. A mass moves under a potential , where and are constants.(a)Find the position of stable equilibruim. (b)Show that the frecuency of small vibrations about this point is the same as it woudl be if the same mass was vibrating on a spring of stiffness .
Una masa se mueve bajo un potencial , donde y son constantes. a) Encuentre la posision de equilibrio b)Muestra que la frecuencia a amplitudes pequeñas al rededor de este punto es la misma que si se tratara de la misma masa cuando vibra en un resorte con constante .
a) De la ecuación 2.12 del libro se tiene que:
Entonces:
Dado que buscamos el punto de equilibrio se tiene cuando
luego:
para lo cual necesariamente:
Por lo tanto, el punto de equilibrio es:
b) De la ecuación 2.14 del libro se tiene que:
es decir
Por otra parte sabemos que:
por lo que:
para oscilaciones pequeñas
Entonces:
Finalmente:
Pérez Córdoba Sabino (discusión) 02:10 21 feb 2014 (UTC) Cesar Ivan Avila Vasquez (discusión) 17:30 25 Febrero 2014
2.11. A mass moves under a potential $V(x)=V_{0}\cosh(\frac{x}{x_0})$, where $V_0$ y $x_0$ are constants.(a) Find the position of stable equilibruim. (b) Show that the frecuency of small vibrations about this point is the same as it would be if the same mass was vibrating on a spring of stiffness $V_0/x_0^2$
(a) La posición de equilbrio es el punto en el que el potencial tiene un valor mínimo, es decir en el que su derivada es nula.
\begin{equation} \frac{ \mathrm{d}V(x)}{ \mathrm{d}x} = \frac{V_0}{x_0} \sinh(\frac{x}{x_0})=0 \; \Leftrightarrow \; x=0 \, , \, x\in \R \end{equation}
Por lo que $x=0$ es la posición de equilibrio estable del sistema.
(b) Primero considérese un sistema masa-resorte con $s=V_0/x_0^2$, entonces $\omega_0^2=s/m$, y la frecuencia es
\begin{equation} \label{1} \nu=\frac{\omega_0}{2 \, \pi}=\frac{1}{2 \, \pi} \sqrt{\frac{s}{m}}=\frac{1}{2 \, \pi} \sqrt{\frac{V_0}{m \, x_0^2}} \end{equation}
Por otra parte, de acuerdo a la ecuación (2.14) de libro (Main, Ian G.,Vibrations and Waves in Physics,1993),para un potencial $V(r)$, $ s \approx \left.\frac{d^2\,V(r)}{d\,r^2}\right|_{x=R}$ válido solo para oscilaciones $|\, \psi (t)\,|$ muy pequeñas, donde $R$ es la posición de equilibrio. Para nuestro potencial $V(x)$ en una dimensión tenemos que:
\begin{equation} \label{2} s= \left[ \frac{\mathrm{d^2}}{\mathrm{d}x^2}\,V_0 \cosh(\frac{x}{x_0}) \right]_{x=0}= \left. \frac{V_0}{x_0^2} \cosh(\frac{x}{x_0}) \right|_{x=0}= \frac{V_0}{x_0^2} \end{equation}
Como $\omega_0=\sqrt{s/m} $ y $\nu=\omega_0 / (2 \, \pi)$ y con $(2)$ obtenemos
\begin{equation} \label{3} \nu=\frac{\sqrt{s/m}}{2 \, \pi}=\frac{1}{2 \, \pi} \sqrt{\frac{V_0}{m \, x_0^2}} \end{equation}
La ec. $(1)$ muestra la frecuencia de vibración de una masa $m$ debida a un resorte con constante $s=V_0/x_0^2$, mientras que la $(3)$ es la frecuencia de oscilación de una masa debido a un potencial $V(x)$ alrededor de su punto mínimo o punto de equilibrio. Por lo tanto, como las frecuencias $(1)$ y $(3)$ son iguales, el potencial $V(x)=V_{0}\cosh(\frac{x}{x_0})$ es determinado o es equivalente a un sistema de una masa que realiza una vibración mediante $s=V_0/x_0^2$.
-- Adolfo Calderón Alcaraz (discusión) 18:33 17 feb 2015 (CST) --
Problema 2.12
2.12. Una masa que pesa 2 libras alarga 6 pulgadas un resorte. En t=0 se libera la masa desde un punto que esta 8 pulgadas abajo de la posición de equilibrio con una velocidad ascendente de 4/3 pie/seg. Determine la ecuación de movimiento.
Transformaremos las unidades
obtenemos esta ecuación
En el desplazamiento inicial y la velocidad se tiene que, y
donde
se tiene que
Por lo que la solución general de la ecuación diferencial es
Aplicando las condiciones iniciales x(t) y x'(t) obtenemos que y
por lo tanto la ecuación de movimiento es:
--David Alberto Rojas Solis (discusión) 04:10 6 jul 2013 (CDT)--A. Martín R. Rabelo (discusión) 18:12 22 feb 2015 (CST)
Problema II.I
When the electron in a hydrogen atom bound to the nucleus moves a small distance from its equilibrium position, a restoring force per unit distance is given by:
where $r=0.05nm$ may be taken as the radius of the atom. Show that the electron can oscillate with a simple harmonic motion with:
If the electron is forced to vibrate at this frequency, in which region of the electromagnetic spectrum would its radiation be found?:
Cuando el electrón en un átomo de hidrógeno ligado al núcleo se mueve una pequeña distancia de su posición de equilibrio, una fuerza restauradora por unidad de distancia está dada por:
donde $r=0.05nm$ puede tomarse como el radio del átomo. Muestre que el electrón puede oscilar en un movimiento armónico simple con:
Si el electrón es forzado a vibrar con ésta frecuencia, ¿en qué región del espectro electromagnético irradia?:
Al ser $s$ la fuerza restauradora por unidad de distancia, tenemos que la ecuación diferencial del oscilador puede escribirse como:
y proponiendo una solución del tipo:
tenemos que:
además:
y sustituyendo en la ecuación diferencial obtenemos:
de donde:
Luego, para obtener el valor de $\omega_0$, sustituímos a $s$:
y si aproximamos:
y lo sustituímos en la ecuación para $\omega_0$:
Por lo que podemos concluír que:
Ahora, obtenemos la frecuencia:
Y como:
Entonces, basados en la clasificación del espectro electromagnético, podemos concluír que el átomo irradia en el ultravioleta extremo.
Ivan de Jesús Pompa García (discusión) 15:50 14 feb 2015 (CST)
Problema II.II
Un circuito $L-C$, que contiene un conductor de $80mH$ y un capacitor de $1.25nF$, oscila con una corriente máxima de $0.75A$.
a) Calcule la carga máxima en el capacitor. b) Calcule la frecuencia de oscilación del circuito.
De la segunda ley de Kirchhoff es posible deducir la ecuación diferencial
Donde representa la carga.
Esta ecuación es de la misma forma que la ecuación “común” de el movimiento armónico
reescribiendo la ecuación (1) tenemos
, de donde se tiene ahora que
análogo a lo hecho cuando se trabajo
con la ecuación (2). De lo anterior se encuentra la solución de la ecuación (3)
Ahora considerando que,
Así que la corriente varía en el tiempo y sera máxima cuando el coeficiente trigonométrico sea 1 y con el valor absoluto queda
de (4) entonces
--Uziel Sanchez Gutierrez (discusión) 01:05 20 feb 2015 (CST)
Problema 2.9
2.9 Un astronauta sobre la superficie de la luna pesa muestras de roca utilizando un ligero dinamómetro. Ésta báscula, que fue calibrada en la tierra, tiene una escala de 100 mm de largo que lee de 0 a 1 kg. Él observa que cierta roca da una lectura estable de 0.40 kg y, cuando se le perturba, vibra con un periodo de 1.0 s. ¿ Cuál es la aceleración debido a la gravedad en la luna?
Solución
El problema plantea una báscula, esta tiene un dinamómetro y que a su vez contiene un resorte que se estira, para soportar cierta carga de rocas; como se ha visto en el capítulo 1, ejercicio1, sabemos que la ecuación de un movimiento armónico simple es:
- Error al representar (función desconocida «\varPsi»): \ddot{\varPsi}+\frac{s}{m}\varPsi=0
Esta ecuación diferencial se puede expresar también de la forma:
- Error al representar (función desconocida «\varPsi»): \ddot{\varPsi}+w^{2}\varPsi=0...(1)
donde:
y entonces, despejando se tiene:
Por otro lado la fuerza del resorte esta dado por:
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): F=s\varPsi...(3)
pero sabemos por el problema, que el astronauta esta posando en la superficie lunar , lo que nos habla de una fuerza gravitatoria que es:
Igualando ecuación (3) y (4) se tiene:
- Error al representar (función desconocida «\varPsi»): s\varPsi=mg...(5)
despejando “g” , y sustituyendo (2) en ecuación (5) , y reduciendo se tiene:
- Error al representar (función desconocida «\varPsi»): g=w^{2}\varPsi
sustituyendo los datos del problema y recordando que la frecuencia angular se puede escribir como , se tiene:
- Error al representar (función desconocida «\varPsi»): g=\left(\frac{2\pi}{T}\right)^{2}\varPsi
Ricardo García Hernández
--Pablo (discusión) 20:37 22 feb 2015 (CST)
Problema 2.10
Una butaca está montada sobre un resorte. Cuando se sienta una persona de 75 kg, oscila con una frecuencia de 1 Hz. Si sobre ella se sienta ahora otra persona de 50 kg,
a) ¿Cuál será la nueva frecuencia de vibración?
b) ¿Cuánto descenderá la butaca cuando alcance el equilibrio?'
Solución:
a) En el movimiento vertical, la fuerza resultante entre la fuerza recuperadora elástica y el peso es una fuerza recuperadora del tipo:
Y donde la frecuencia angular del sistema responde a la siguiente relación:
\[ \omega_{0}=\sqrt{\frac{k}{m}}\ldots(2) \]
Nos piden encontrar el valor de la nueva frecuencia y sabemos que:
\[ \upsilon_{0}=\frac{\omega_{0}}{2\pi}\ldots(3) \]
Definimos $M$ como la masa total $M=m_{1}+m_{2}=75kg+50kg=125kg$ y podemos entonces escribir la frecuencia resultante combinando las ecuaciones (3) y (2) como:
\[ \upsilon_{0}=\frac{1}{2\pi}\sqrt{\frac{k}{M}}\ldots(4) \]
pero no tenemos el valor de la constante del resorte $k$ la cual
podemos determinar si tomamos los valores de la frecuencia y masa
iniciales. Así que tomamos la ecuación (2) y despejando $k$ nos
queda de la forma:
\[ K=\omega_{0}^{2}\cdot m_{1} \]
Pero $\omega_{0}=2\pi\cdot\upsilon_{0}=(2\pi)(1Hz)=6.2831\frac{rad}{seg}$
por lo que:
\[ K=(6.2831\frac{rad}{seg})^{2}(75kg)=2,960.88\frac{N}{m} \]
Entonces ya podemos substituir todos nuestros valores en la ecuación
(4)...
\[ \upsilon_{0}=\frac{1}{2\pi}\sqrt{\frac{2,960.88\frac{N}{m}}{125kg}}=.7745Hz \]
b)Tomamos como posición de equilibrio la posición de resorte
cuando está encima la primera persona. Cuando se pone encima de ella
la segunda, al alcanzar el equilibrio la fuerza resultante será nula.
Por lo tanto, el peso sumado con la fuerza contraria al pesoque imprime el resorte se puede escribir como:
\[ \bar{P}_{eso}+\bar{F}_{el\acute{a}stica}=0 \]
Sabemos que el peso corresponde a la ecuación de la segunda ley de
newton donde $\bar{P}=-mg$
Al combinar esta ecuación con la ecuación (1) tenemos:
\[ \bigtriangleup m\cdot g=\bigtriangleup y\cdot k \]
entonces despejando $\bigtriangleup y$ nos queda:
\[ \bigtriangleup y=\frac{\bigtriangleup m\cdot g}{k}=\frac{(50kg)(9.8\frac{m}{s^{2}})}{2960\frac{N}{m}}=.1655m \] --A. Martín R. Rabelo (discusión) 16:16 22 feb 2015 (CST)











![\omega_{0}(k_{s})=[(\frac{a}{l v})(\frac{\gamma R T}{M})]^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4b48f1d795781e774b8aceb611670789e1e44d10)



![\frac{\omega_{0}(k_{t})}{\omega_{0}(k_{s})}=\frac{(\frac{P a}{l v \rho})^{1/2}}{[(\frac{a}{l v})(\frac{\gamma R T}{M})]^{1/2} }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2ab5bbc3b86b2265a8ad47111d9ca4bd7ff0f8c2)