Diferencia entre revisiones de «Vibra: probs c1»
| (No se muestran 42 ediciones intermedias de 4 usuarios) | |||
| Línea 1494: | Línea 1494: | ||
\theta=arctan\left(-\frac{B}{A}\right) | \theta=arctan\left(-\frac{B}{A}\right) | ||
\] | \] | ||
--Añadi un nuevo problema---- | ---- | ||
--Añadi un nuevo problema----[[Usuario:Evamontiel|Evamontiel]] ([[Usuario discusión:Evamontiel|discusión]]) | |||
---- | |||
== Problema I.I == | == Problema I.I == | ||
| Línea 1798: | Línea 1800: | ||
<math>\tau= | <math>\tau= \frac{2 \pi}{2.10x10^{3} \frac{rad}{s}} = 3.00x10^{-3} s = 3.00 ms </math> | ||
b) Para la velocidad usaremos la expresión (5): | b) Para la velocidad usaremos la expresión (5): | ||
| Línea 1811: | Línea 1813: | ||
[[Usuario:LeonardoFR|LeonardoFR]] ([[Usuario discusión:LeonardoFR|discusión]]) 17:28 9 jun 2020 (CDT) | [[Usuario:LeonardoFR|LeonardoFR]] ([[Usuario discusión:LeonardoFR|discusión]]) 17:28 9 jun 2020 (CDT) | ||
---- | |||
[[Usuario:Juan Daniel Rivera Bautista|Juan Daniel Rivera Bautista]] ([[Usuario discusión:Juan Daniel Rivera Bautista|discusión]]) 18:41 22 jun 2020 (CDT) arreglé el código de una expresión matemática | |||
---- | ---- | ||
| Línea 2324: | Línea 2328: | ||
[[Usuario:Rodrigo|Rodrigo]] ([[Usuario discusión:Rodrigo|discusión]]) 14:30 16 jun 2020 (CDT) | [[Usuario:Rodrigo|Rodrigo]] ([[Usuario discusión:Rodrigo|discusión]]) 14:30 16 jun 2020 (CDT) | ||
== | ==Problema propuesto 1.== | ||
si la posición, velocidad y aceleración iniciales de un objeto que se mueve con movimiento armónico simple son $ x_{0} $,$ v_{0} $, $ a_{0} $ y la frecuencia de oscilación es $ w $. Si la función para la posición del objeto del objeto se propone como se muestra a continuación: | si la posición, velocidad y aceleración iniciales de un objeto que se mueve con movimiento armónico simple son $ x_{0} $,$ v_{0} $, $ a_{0} $ y la frecuencia de oscilación es $ w^{2} = \frac{k}{m} $. Si la función para la posición del objeto del objeto se propone como se muestra a continuación: | ||
$x(t) = x_{0} cos(w t) + \frac{v_{0}}{w} sin(wt)$ | $x(t) = x_{0} cos(w t) + \frac{v_{0}}{w} sin(wt)$ | ||
| Línea 2332: | Línea 2336: | ||
$v(t) = -x_{0} w sin (w t ) + v_{0} cos (wt)$ | $v(t) = -x_{0} w sin (w t ) + v_{0} cos (wt)$ | ||
(b) si la amplitud del movimiento es $A$, demuestre que | (b) si la amplitud del movimiento es $A$, demuestre que | ||
$ | $ v_{0}^{2}-a_{0} x_{0}= A^{2} w^{2}$ | ||
Solución: | Solución: | ||
a) derivando la función de la posición del objeto con respecto al tiempo se tiene que | |||
$\frac{dx}{dt} = - x_{0} w sin(wt) + v_{0} cos(w t)$ | |||
se sabe que por definición la derivada de la posición con respecto al tiempo es la velocidad por lo tanto | |||
$v(t) =- x_{0} w sin(wt) + v_{0} cos(w t) $ | |||
b) la solución general de un movimiento armónico simple es: | |||
$x(t) = A cos (wt+ \phi)$ | |||
la expresión para la velocidad es | |||
$ v(t) = -A w sin(wt+ \phi)$ | |||
la expresión para la aceleración es | |||
$a(t) = -A w^{2} cos (wt+ \phi)$ | |||
evaluando en $t=0$ | |||
$v_{0} = - A w sin(\phi)$ | |||
$x_{0} = A cos(\phi)$ | |||
$a_{0} = - w^{2} x_{0}$ | |||
con lo anterior se llega a que | |||
$x_{0}^{2} + \frac{v_{0}^{2}}{w^{2}} = A^{2} (cos^{2}(\phi)+sin^{2}(\phi))$ | |||
recordemos que $ cos^{2}(\phi)+sin^{2}(\phi)=1 $, reescribiendo | |||
$w^{2} x_{0}^{2} +v_{0}^{2} = A^{2} w^{2}$ | |||
de $a_{0} = - w^{2} x_{0}$ se despeja $x_{0}$ | |||
$x_{0}=-\frac{a_{0}}{w^{2}}$ | |||
sustituyendo lo anterior en $w^{2} x_{0}^{2} +v_{0}^{2} = A^{2} w^{2}$, se llega finalmente a que: | |||
$A^{2}w^{2} = v_{0}^{2}-a_{0}x_{0}$ | |||
[[Usuario:Monicacruz|Monicacruz]] ([[Usuario discusión:Monicacruz|discusión]]) 14:31 18 jun 2020 (CDT) Monica Cruz | [[Usuario:Monicacruz|Monicacruz]] ([[Usuario discusión:Monicacruz|discusión]]) 14:31 18 jun 2020 (CDT) Monica Cruz | ||
== Problema propuesto 2== | |||
Muestre que la tasa de cambio en el tiempo de la energía mecánica correspondiente a un oscilador amortiguado sin accionamiento esta dada por $\frac{dE}{dt}=-bv^{2}$ y en consecuencia siempre es negativa. | |||
solución : | |||
obteniendo la diferencial de la energía mecánica $E=\frac{1}{2} m v^{2} + \frac{1}{2} k x^{2}$ | |||
$\frac{dE}{dt}= \frac{d}{dt}(\frac{1}{2} m v^{2} + \frac{1}{2} k x^{2})$ | |||
se obtiene | |||
$\frac{dE}{dt}=m v \frac{dv}{dt} + k x \frac{dx}{dt} $ | |||
$\frac{dE}{dt}=(m \frac{d^{2}x}{dt^{2}} + k x ) v $ | |||
se reescribe la expresión anterior | |||
$\frac{1}{v}\frac{dE}{dt} - k x =m \frac{d^{2}x}{dt^{2}} $ | |||
La ecuación de movimiento amortiguado: | |||
$ - k x - b \frac{dx}{dt}=m \frac{d^{2}x}{dt^{2}}$ | |||
igualando las dos ultimas expresiones se llega a: | |||
$ \frac{1}{v}\frac{dE}{dt} - k x = - k x - b \frac{dx}{dt} $ | |||
$\frac{1}{v}\frac{dE}{dt} =- b \frac{dx}{dt} $ | |||
finalmente se llega a que la derivada temporal de la energía mecánica de un oscilador amortiguado es siempre negativa ya que aunque la velocidad sea negativa su cuadrado siempre es positivo y $b$ es una constante positiva. | |||
$\frac{dE}{dt}=-bv^{2}$ | |||
[[Usuario:Monicacruz|Monicacruz]] ([[Usuario discusión:Monicacruz|discusión]]) 00:06 19 jun 2020 (CDT) | |||
== Problema propuesto 3== | |||
Se observa que para un dispositivo mecánico al cuál después de experimentar un impulso inesperado regresa al desplazamiento cero "posición de equilibrio" en un tiempo mínimo.suponga que el sistema tiene desplazamiento cero en $t=0$ | |||
a) encontrar la ecuación $x(t)$ y $v(t)$ | |||
b) el máximo desplazamiento antes de regresar al reposo. y el tiempo en que alcanza este máximo | |||
c)dibuje la grafica $x$ contra $t$ y use los valores en a) y b) | |||
solución: | |||
a) la soluciones generales para un movimiento amortiguado son | |||
$x_{1}(t)=B \rm e^{-\beta t} cos(\omega t + \phi)$ | |||
$x_{2}(t)=A \rm e^{-\beta t} sen(\omega t + \phi)$ | |||
evaluando en la condición inicial en ambas posibles soluciones para este problema en especifico, con $\phi=0$ | |||
$x_{1}(0)= B$ | |||
$x_{2}(0)= 0$ | |||
de esta manera se a que la solución adecuada es $ x_{2}$ llamaremos a la solución solo x(t) | |||
$x(t)=A \rm e^{-\beta t} sen(\omega t )$ | |||
derivamos para obtener la expresión de la velocidad | |||
$v(t)= A \omega \rm e^{-\beta t} cos(\omega t ) - A \beta \rm e^{-\beta t} sen(\omega t) $ | |||
b) el desplazamiento máximo se tiene cuando la función $\sin(\omega t)=1 $ | |||
tomando el primer valor donde la función seno es uno se obtiene lo siguiente | |||
$\omega t = \frac{\pi}{2}$ | |||
el tiempo en el cual alcanza el desplazamiento máximo es | |||
$t=\frac{\pi}{2 \omega }$ | |||
el desplazamiento máximo es | |||
$x_{max}(t=\frac{\pi}{2 \omega})= A \rm e^{\frac{-\beta \pi}{2 \omega}}$ | |||
c) Grafica de la posición vs timepo con $A=6$, $\beta=\frac{1}{2}$ y $\omega =3$ | |||
[[Archivo:Amortigado mov.png|thumb|800px|marco|centro|Gráfica de x, se han asignado valores a las constantes solo para poder visualizar la gráfica de la posición contra el tiempo ]] | |||
[[Usuario:Monicacruz|Monicacruz]] ([[Usuario discusión:Monicacruz|discusión]]) 10:09 19 jun 2020 (CDT) | |||
---- | |||
[[Usuario:Juan Daniel Rivera Bautista|Juan Daniel Rivera Bautista]] ([[Usuario discusión:Juan Daniel Rivera Bautista|discusión]]) 19:32 22 jun 2020 (CDT) ajusté el tamaño de la figura para que no se saliera del márgen | |||
---- | |||
== Problema propuesto 4== | |||
El sistema mostrado en la figura, consiste en un tubo doblado en forma de "U" cuya sección trasversal tiene área $A$. Este tubo contiene una columna de liquido de longitud $L$ y densidad $\rho$ y se pone en movimiento, encuentre: | |||
a) la ecuacion de movimiento para el tuvo contenido en el liquido | |||
b)la frecuencia | |||
[[Archivo:Captura de pantalla de 2020-06-27 12-45-00~3.png|derecha|tubo en forma de "U"]] | |||
la energía potencial esta dada por | |||
$U=mgy$ | |||
recordando la definición de densidad | |||
$\rho=\frac{m}{V}$, el volumen es $V= A y $ (se esta considerando solo el volumen que sube o baja, según el sistema de referencia elegido) | |||
una vez definido a la energía potencial en términos de los datos conocidos, se puede escribir: | |||
$U= A \rho g y^{2}$ | |||
la energia cinetica en terminos de las cantidades conocidas es: ($m= A \rho L$) | |||
$K=\frac{1}{2} \rho A L (v_{y})^{2}$ | |||
o bien $K=\frac{1}{2} \rho A L (\frac{d y}{dt})^{2}$ | |||
La energía total del sistema es: | |||
$E=\frac{1}{2} \rho A L (\frac{d y}{dt})^{2} + A \rho g y^{2}$ | |||
la energía del sistema es una constante por lo tanto al derivar con respecto al tiempo, se tiene lo siguiente | |||
$\frac{dE}{dt}=\frac{d}{dt}(\frac{1}{2} \rho A L (\frac{d y}{dt})^{2} + A \rho g y^{2}) = 0$ | |||
$\frac{dE}{dt}=\rho A L(\frac{dy}{dt})(\frac{d^{2}y}{dt^{2}})+ 2 A \rho g y (\frac{dy}{dt})=0$ | |||
$\frac{dy}{dt}(\rho A L(\frac{d^{2}y}{dt^{2}})+ 2 A \rho g y )=0$ | |||
$\rho A L(\frac{d^{2}y}{dt^{2}})+ 2 A \rho g y =0$ | |||
finalmente se obtiene la ecuación de movimiento armónico simple | |||
$\frac{d^{2}y}{dt^{2}}+\frac{2g}{L} y =0$ | |||
De la ecuacion de movimiento se puede ver que | |||
$\omega^{2} = \frac{2 g}{L}$ | |||
la frecuencia esta dada por | |||
$f=\frac{\omega}{2 \Pi}$ | |||
o bien | |||
$f= \sqrt{\frac{2g}{L}} \frac{1}{2\Pi}$ | |||
[[Usuario:Monicacruz|Monicacruz]] ([[Usuario discusión:Monicacruz|discusión]]) 14:13 27 jun 2020 (CDT) | |||
==Problema 4.7== | |||
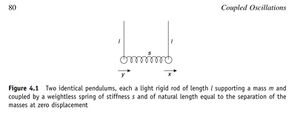
[[Archivo:Pendaco.jpg|miniaturadeimagen|Péndulos acoplados]] | |||
Cuando las masas de los péndulos acoplados de la figura 4.1 ya no son iguales, la ecuación de movimiento se convierte en: | |||
<math> m_1 \ddot{x} = - m_1 \left ( \frac{g}{l} \right ) x - s (x – y ) ... (1)</math> | |||
<math> m_2 \ddot{y} = - m_2 \left ( \frac{g}{l} \right ) y + s (x – y ) ...(2)</math> | |||
Mostrar que podemos elegir las coordenadas normales: | |||
<math> X = \frac{ m_1 x + m_2 y }{ m_1 + m_2 } </math> | |||
Con una frecuencia de modo normal $ \omega_{1}^{2} = \frac{ g }{ l } $ y $ Y = ( x – y )$ , con una frecuencia de modo normal $ \omega_{2}^{2} = \frac{ g }{ l } + s \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) $. Tenga en cuenta que $X$ es la coordenada del centro de masa del sistema, mientras que la masa efectiva en el modo $Y$ es la masa reducida $mu$ del sistema donde $\frac{ 1 }{ \mu\ } = \frac{1}{m_1} + \frac{1}{m_2}$. | |||
Solución: | |||
Si sumamos las ecuaciones (1) y (2): | |||
<math> m_1 \ddot{x} + m_2 \ddot{y} = - \left ( \frac{g}{l} \right ) (m_1 x + m_2 y) …………….(3)</math> | |||
Como el problema nos da las coordenadas normales: | |||
<math> X = \frac{ m_1 x + m_2 y }{ m_1 + m_2 } </math> | |||
Entonces: | |||
<math> \ddot{ X } = \frac{ m_1 \ddot{x} + m_2 \ddot{y} }{ m_1 + m_2 } </math> | |||
Hacemos un despeje para sustituir en (3): | |||
<math> m_1 \ddot{x} + m_2 \ddot{y} = \ddot{X} ( m_1 + m_2 )</math> | |||
<math> m_1 x + m_2 y = X ( m_1 + m_2 )</math> | |||
Sustituyendo en (3) obtenemos: | |||
<math> \ddot{X} ( m_1 + m_2 ) = - \frac{g}{l} ( m_1 + m_2 ) X </math> | |||
Multiplicamos por $ \frac {1}{m_1 + m_2}$ | |||
<math> \ddot{X}= - \frac{g}{l} X </math> | |||
Y podemos ver que en ésta ecuación la frecuencia de modo normal es $\omega_{1}^{2} = \frac{ g }{ l } $ | |||
Para comprobar la segunda parte , tomamos nuevamente (1) y (2), y despejamos $\ddot{x}$ y $\ddot{y}$ | |||
<math> \ddot{x} = - \left ( \frac{g}{l} \right ) x - \frac{s}{m_1} (x – y ) </math> | |||
<math> \ddot{y} = - \left ( \frac{g}{l} \right ) y + \frac{s}{m_2} (x – y ) </math> | |||
Y hacemos la resta $\ddot{x} - \ddot{y}$ | |||
\begin{matrix}\ddot{x} - \ddot{y} & = & - \frac{ g }{ l } x - \frac{ s }{ m_1 } ( x – y ) + \frac{ g }{ l } y - \frac{ s }{ m_2 } ( x – y ) \\ \ & = & -\frac{ g }{ l } ( x – y ) - 2 s ( x – y ) \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) \\ \ & = & ( x – y ) \left \lbrack - \frac{g}{l} – 2 s \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) \right \rbrack \end{matrix} | |||
Tomamos la coordenada normal $Y = x – y $ , vemos que $\ddot{Y}=\ddot{x}- \ddot{y}$, y hacemos una sustitución en $\ddot{x}- \ddot{y}$ | |||
<math> \ddot{Y} = \left \lbrack - \frac{g}{l} – s \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) \right \rbrack Y </math> | |||
<math> \ddot{Y} = - \left \lbrack \frac{g}{l} + s \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) \right \rbrack Y </math> | |||
De la última ecuación, podemos ver que la frecuencia de modo normal es $ \omega_{2}^{2} = \frac{ g }{ l } + s \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) $. | |||
En cada caso la variable elegida es una sola frecuencia de vibración, coordenadas normales, y corresponden cada uno a sus respectivos modos normales de vibración. | |||
Nota: Ejercicio 4.7 es del libro H. J. Pain. The Physics of Vibrations and Waves. Wiley, 2005. | |||
[[Usuario:Nayomi|Nayomi]] ([[Usuario discusión:Nayomi|discusión]]) 22:27 18 jun 2020 (CDT) Nayomi Russell | |||
==Problema 4.8== | |||
Deje que el sistema del problema 4.7 se ponga en movimiento con las condiciones iniciales $x = A$, $y = 0$, $\dot{x}=\dot{y}= 0$ en $t=0$. Muestra que las amplitudes del modo normal son $X_0=\left ( \frac{m_1}{M} \right)A$ y $Y_0=A$, para hacer: | |||
<math>x = \frac{A}{M} (m_1 cos \omega_1 t + m_2 cos \omega_2 t) </math> | |||
Y $y = \frac{m_1}{M} A ( cos \omega_1 t - cos \omega_2 t)$ | |||
Donde $M=m_1 + m_2$. Exprese estos desplazamientos como: | |||
<math>x =2 A cos \omega_m t cos \omega_a t + \frac{2A}{M}(m_1 – m_2 ) sen \omega_m t sen \omega_a t </math> | |||
Y $y =2 A \frac{m_1}{M} sen \omega_m t sen \omega_a t $ | |||
Dónde $\omega_m = (\omega_1 - \omega_2)/2$ y $ omega_a = (\omega_1 + \omega_2)/2$ | |||
Solución: | |||
Para las ecuaciones de movimiento en la coordenada normal tenemos que: | |||
<math>X =X_0 cos \omega_1 t </math> | |||
<math>Y =Y_0 cos \omega_2 t </math> | |||
Podemos decir que: | |||
<math>\frac{m_1 x + m_2 y}{m_1 + m_2} =X_0 cos \omega_1 t </math> | |||
<math>x - y =Y_0 cos \omega_2 t </math> | |||
Sustituimos las condiciones iniciales: $t=0$, $x=A$, y $y=0$ en las ecuaciones, y obtenemos que: | |||
<math>X_0 =\left ( \frac{m_1}{M} \right)A</math> | |||
<math>Y_0 =A</math> | |||
Dónde $M=m_1 + m_2$, por lo que las soluciones a las ecuaciones de movimiento en las coordenadas x y y son: | |||
<math>x = \frac{A}{M} (m_1 cos \omega_1 t + m_2 cos \omega_2 t) </math> | |||
Y $ y = \frac{m_1}{M} A ( cos \omega_1 t - cos \omega_2 t) $ | |||
Aquí $\omega_1=\omega_a-\omega_m$ y $\omega_2=\omega_a+\omega_m$ | |||
Recordamos que $\omega_m = (\omega_1 - \omega_2)/2$ y $ omega_a = (\omega_1 + \omega_2)/2$. Y sustituimos $\omega_1$ y $\omega_2$ en las soluciones de las ecuaciones de movimiento. | |||
\begin{matrix}x & = & \frac{ A }{ M } [m_1 cos (\omega_a - \omega_m)t + m_2 cos (\omega_a + \omega_m)t] \\ \ & = & \frac{ A }{ M} [m_1 (cos \omega_m t cos \omega_a t + sen\omega_a t \omega_m t) + m_2 (cos \omega_m t cos \omega_a t - sen\omega_a t \omega_m t)] \\ \ & = & \frac{ A }{ M } [(m_1 + m_2) cos \omega_m t cos\omega_a t + (m_1 - m_2)sen\omega_m t sen \omega_a t ]\end{matrix} | |||
Simplificando: | |||
<math>x =A cos \omega_m t cos \omega_a t + \frac{A}{M} (m_1 – m_2) sen \omega_m t sen \omega_a t </math> | |||
Y | |||
\begin{matrix}y & = & A\frac{ m_1 }{ M } [ cos (\omega_a - \omega_m)t - cos (\omega_a + \omega_m)t] \\ \ & = & 2A\frac{ m_1 }{ M} sen \omega_m t sen \omega_a t \end{matrix} | |||
Nota: Ejercicio 4.8 es del libro H. J. Pain. The Physics of Vibrations and Waves. Wiley, 2005. | |||
[[Usuario:Nayomi|Nayomi]] ([[Usuario discusión:Nayomi|discusión]]) 21:10 19 jun 2020 (CDT) Nayomi Russell | |||
Revisión del 20:14 25 abr 2021
--Jose de jesus (discusión) 18:03 25 feb 2015 (CST)--Luis Santos (discusión) 00:27 1 feb 2015 (CST)Problemas del capítulo uno [1] mfg-wiki (discusión) 18:42 16 ene 2014 (UTC)
- ↑ Iain G. Main Vibrations and waves in physics, CUP 3rd. ed. 1994
Problema 1.1
Solución 1
If the system shown in fig 1.1 has m= 0.010kg and s= 36 N/m , calculate (a) the angular frequency, (b) the frequency, and (c) the period.
Si el sistema mostrado en la figura 1.1 tiene m=0.010 kg y s=36 N/m, calcula (a) la frecuencia angular, (b) la frecuencia y (c) el período.
-
Solución propuesta:
- El sistema de la figura 1.1 es perturbado al mover a la masa de su posición de equilibrio, al efectuar esta perturbación el resorte ejerce una fuerza de restauración (opuesta al desplazamiento de la masa) hacia la posición de equilibrio, esto provoca que el sistema varíe armónicamente y tome la forma de una vibración. La masa provoca una aceleración que usando la segunda ley de Newton se ve como sigue:
- Este movimiento armónico se repite a sí mismo una cantidad infinita de veces en una secuencia que repite ciclos idénticos cada que el ángulo de fase se incrementa . El número de ciclos por unidad de tiempo se conoce como frecuencia y está dado como sigue:
- Estos ciclos, es decir cantidades como el desplazamiento, la velocidad y la dirección se repiten cada vez que el ángulo de fase se incrementa , esto sucede cada que es conocido como el período .
--Brenda Pérez Vidal (discusión) 07:10 24 ene 2014 (UTC)
--Luis Santos (discusión) 00:27 1 feb 2015 (CST)
--Ivan de Jesús Pompa García (discusión) 22:34 3 feb 2015 (CST)
--Pablo (Usuario discusión:Pablo) 17:47 7 feb 2015 (CST)
--Ricardo Garcia Hernandez (discusión) 18:40 22 feb 2015 (CST)
Rodrigo (discusión) 09:59 16 jun 2020 (CDT)
Solución 2
Si el sistema mostrado en la figura 1.1 tiene m=0.010 kg y s=36 N/m, calcula (a) la frecuencia angular, (b) la frecuencia y (c) el período.
Solución propuesta:
- Error al representar (función desconocida «\varPsi»): {\displaystyle F\left(\varPsi\right)=-s\varPsi...(1)}
- Error al representar (función desconocida «\varPsi»): U\left(\varPsi\right)=\frac{1}{2}s\varPsi^{2}...(2)
- Error al representar (función desconocida «\varPsi»): F\left(\varPsi\right)=-\frac{dU}{d\varPsi}
- Error al representar (función desconocida «\varPsi»): -s\varPsi=m\ddot{\varPsi}
- Error al representar (función desconocida «\varPsi»): \ddot{\varPsi}+\frac{s}{m}\varPsi=0...(4)
- Error al representar (función desconocida «\varPsi»): \ddot{\varPsi}=-\frac{s}{m}\varPsi...(5)
- Error al representar (función desconocida «\varPsi»): {\displaystyle \varPsi\left(t\right)=\cos\left(wt\right) }
- Error al representar (función desconocida «\varPsi»): {\displaystyle \dot{\varPsi}\left(t\right)=-w \mathrm{sen}\left(wt\right) }
- Error al representar (función desconocida «\varPsi»): {\displaystyle \ddot{\varPsi}(t)=-w^{2}\cos\left(wt\right) }
Ricardo García Hernández--Ricardo Garcia Hernandez (discusión) 23:10 22 feb 2015 (CST) Entendí y me gustó más esta forma de resolver el ejercicio--Esther Sarai (discusión) 23:31 19 feb 2015 (CST)Esther Sarai García Gonzalez Sólo cambié la notación Juan Daniel Rivera Bautista (discusión) 19:37 8 jun 2020 (CDT) Rodrigo (discusión) 10:04 16 jun 2020 (CDT) Rodrigo (discusión) 14:32 16 jun 2020 (CDT)
Problema 1.2
For the same vibrator as in problem 1.1 at time t=0, the mass is observed to be displaced 50 mm to the right of its equilibrium position and to be moving to the right at speed 1.7 m s^-1. Calcule a) the amplitude b) the phase constant c) the energy
Por el mismo vibrador como en el problema 1.1 en el tiempo t = 0 , se observa la masa ser desplazada 50 mm a la derecha de su posición de equilibrio y estar moviéndose hacia la derecha a una velocidad de 1.7 ms^-1 Calcule:
(a) la amplitud
(b) la constante de fase
(c) la energía
__________________________________Corrección del ejercicio 1.2___________________________________________
(a) La amplitud
Usamos la ecuación de la energía de un oscilador armónico simple, dada por:
\begin{equation} E=T+V=\mathrm{constante} \end{equation}
Donde $T$ es la energía cinética y $V$ es la energía potencial
\begin{equation} E=\frac{1}{2}m\dot{\psi}^{2}+\frac{1}{2}s\psi^{2}=\frac{1}{2}sA_{\psi}^{2} \end{equation}
De las condiciones iniciales del problema se conocen
\[ \psi(0)=0.05m \]
\[
\dot{\psi(0)}=1.7ms{}^{-1}
\]
Despejando $A{}_{\psi}$de la ecuación (2), tenemos
\begin{equation} A{}_{\psi}{}^{2}=\frac{m\dot{\psi}^{2}+s\psi^{2}}{s} \end{equation}
Sustituyendo los datos en (3)
\[ A{}_{\psi}{}^{2}=\frac{(0.01kg)(1.7ms{}^{-1})^{2}+(36Nm{}^{-1})(0.05m)^{2}}{36Nm{}^{-1}}=\frac{0.0289Nm+0.09Nm}{36Nm{}^{-1}}=\frac{0.118Nm}{36Nm{}^{-1}}=0.00327m^{2} \]
\[
A{}_{\psi}=\sqrt{0.00327m^{2}}=0.0571m
\]
b) El ángulo de fase $\phi$
Ahora consideremos las ecuaciones
\begin{equation} \psi(t)=A{}_{\psi} \cos(\omega t+\phi) \end{equation}
\begin{equation} \dot{\psi(t)}={-}\omega A{}_{\psi}\mathrm{sen}(\omega t+\phi) \end{equation}
Dividiende (5)entre (4) y evaluando en $t=0$:
\[ \frac{\dot{\psi(0)}}{\psi (0)}=\frac{{-}\omega A{}_{\psi}\mathrm{sen}(\omega t+\phi)}{A{}_{\psi}\cos(\omega t+\phi)} =-\omega \tan (\omega t+\phi)=\frac{1.7}{.05}=-34 \]
\[
\tan (\omega t+\phi)=\frac{34}{\omega}=\frac{-34}{60}=-0.5666
\]
\[ \omega t+\phi=\arctan(-0.5666) \] Hay que recordar que estamos evaluando en $t=0$ por lo que
\[ \phi=\arctan(-0.5666) \]
\[ \phi=-0.52rad \]
\[
\phi=30°
\]
c) La energía
Usamos la energía del oscilador armónico simple del inciso a)
\begin{equation} E=\frac{1}{2}sA{}_{\psi}^{2} \end{equation}
Entonces,
\[ E=\frac{1}{2}(36Nm{}^{-1})(0.057m)^{2}=0.059J. \]
--Luis Santos (discusión) 11:13 12 feb 2015 (CST)
--Luis Santos (discusión) 11:53 12 feb 2015 (CST)
--Ricardo Garcia Hernandez (discusión) 17:13 26 feb 2015 (CST)
Para la misma vibración que en el problema 1.1 , en el tiempo $t=0$ , se observa la masa a se desplaza $50mm$ a la derecha de su posición de equilibrio y se mueve hacia la derecha a una velocidad de $1.7ms{}^{-1}$. Calcúlese (a) la amplitud, (b) el ángulo de fase, y (c) la energía.
(a) La amplitud
Usamos la ecuación de la energía de un oscilador armónico simple, dada por:
\begin{equation} E=T+V=\mathrm{constante} \end{equation}
Donde $T$ es la energía cinética y $V$ es la energía potencial:
\begin{equation} E=\frac{1}{2}m\dot{\psi}^{2}+\frac{1}{2}s\psi^{2}=\frac{1}{2}sA_{\psi}^{2} \end{equation}
De las condiciones iniciales del problema se conocen:
\[ \psi(0)=0.05m \]
\[
\dot{\psi(0)}=1.7ms{}^{-1}
\]
Despejando $A{}_{\psi}$de la ecuación (2), tenemos:
\begin{equation} A{}_{\psi}{}^{2}=\frac{m\dot{\psi}^{2}+s\psi^{2}}{s} \end{equation}
Sustituyendo los datos en (3):
\[ A{}_{\psi}{}^{2}=\frac{(0.01kg)(1.7ms{}^{-1})^{2}+(36Nm{}^{-1})(0.05m)^{2}}{36Nm{}^{-1}}=\frac{0.0289Nm+0.09Nm}{36Nm{}^{-1}}=\frac{0.1189Nm}{36Nm{}^{-1}}=3.30277x10^{-3}m^{2} \]
\[
A{}_{\psi}=\sqrt{3.30277x10^{-3}m^{2}}=0.0571m
\]
b) el ángulo de fase $\phi$
Ahora consideremos la solución:
\begin{equation} \psi(t)=A{}_{\psi}\mathrm{sen}(\omega t+\phi) \end{equation}
Tenemos todo lo necesario para despejar el ángulo de fase de la ecuación
(4)
\[ \psi(0)=(0.0571m)\mathrm{sen}\left[\left(60s{}^{-1}\right)(0)+\phi\right]=0.05m \]
\[
\phi=\mathrm{arcsen}(\frac{0.05m}{0.0571m})=61.122\text{°}
\]
c) La energía
Usamos la energía del oscilador armónico simple del inciso a)
\begin{equation} E=\frac{1}{2}sA{}_{\psi}^{2} \end{equation}
Entonces,
\[ E=\frac{1}{2}(36Nm{}^{-1})(3.2604x10^{-3}m^{2})=0.0586J. \]
Ejercicio corregido por Maya Velasco, Definitivamente me equivoque
al hacer los cálculos numéricos en el cálculo de la amplitud algo
que agradezco mucho que mi compañero Luis Velázquez haya notado. Posteriormente
revisando la solución que dio mi compañero y la que yo propuse note
lo siguiente:
\[ \psi(t)=A{}_{\psi}\cos(\omega t+\phi) \]
Al derivar la expresión anterior obtenemos:
\[ \dot{\psi(t)}=-A{}_{\psi}\mathrm{sen}(\omega t+\phi) \]
Después mi compañero dividió ambas expresiones de la siguiente manera:
\[ \frac{\dot{\psi(t)}}{\psi(t)}=\frac{-A{}_{\psi}\omega \mathrm{sen}(\omega t+\phi)}{A{}_{\psi}\cos(\omega t+\phi)}=-\omega \tan(\omega t+\phi) \]
Posteriormente el ángulo $\phi$ es
\[ \phi=-29.53\text{°}\eqsim-30\text{°} \]
No encuentro otro error en el trabajo de mi compañero a excepción' del signo, y después de su revisión sobre mi trabajo pues creo que aparentemente el mio también es correcto pero los valores en el ángulo de fase son diferentes y puedo explicar por que:
Ambas soluciones de la ecuación del oscilador armónico simple son correctas, sin embargo es más común usar la expresión que involucra la función coseno, ahora puedo mostrar que ambas soluciones son equivalentes desfasadas por un cierto ángulo.
Se sabe que la función seno esta desfasada de la función coseno por $\frac{\pi}{2}$ ó 90°, hagamos lo siguiente, a la solución de mi compañero pongamos le el ángulo de fase que calculé yo que es de aproximadamente 61° y restemos le el desfase de los 90° .
\[ \psi(t)=A{}_{\psi}\cos(\omega t+61\text{°}-90\text{°}) \]
\[
\psi(t)=A{}_{\psi}\cos(\omega t-29\text{°})
\]
Esta es la respuesta de mi compañero que es correcta, entonces podemos
concluir que ambos resultados son equivalentes. Si alguien más nota
algún otro error mucho les agradeceré que me lo hagan notar, gracias.
Ejercicio resuelto por Rosario Maya. Martes 10 de febrero 2015 --Rosario Maya
Ejercicio corregido por Rosario Maya el 12.02.15 a las 22:56 pm
"El problema 1.2 está correcto; sobre todo al proponer dos formas diferentes de cómo calcular el ángulo de fase". --Ricardo Garcia Hernandez (discusión) 20:46 22 feb 2015 (CST)
--A. Martín R. Rabelo (discusión) 07:28 19 feb 2015 (CST)
Juan Daniel Rivera Bautista (discusión) 19:59 8 jun 2020 (CDT) Cambios en la notación
Problema 1.3
An identical system is set into vibration with the same amplitude as the vibrator in problem 1.2, but with a phase advance of 90°. Calculate (a) the displacement, and (b) the velocity this second vibrator at time t = 0. (c) At what time will it come to rest.
Un sistema idéntico se pone en vibración con la misma amplitud que el vibrador en el problema 1.2, pero con un avance de fase de 90°. Calcule a) el desplazamiento y b) la velocidad de este segundo vibrador en el tiempo t=0. c) ¿A qué hora va a llegar al reposo?
(a)
Tenemos como ecuación de movimiento a: \[ \psi(t)=Acos(\omega t + \phi - \frac{\pi}{2}) \] La cual puede escribise como: \[ \psi(t)=Asin(\omega t + \phi) --------(1)\]
Para t=0 se tiene:
\[
\psi(t=0s) = (57mm ) sin(-0.52) =-28mm
\]
(El signo indica que el desplazamiento es hacia la izquierda)
(b)
Al derivar (1) se tiene la ecuación para la velocidad
\[ \dot{\psi}(t)=A \omega cos(\omega t + \phi) \] Para t=0 \[ \dot{\psi}(t=0)= A\omega cos\phi=(0.057m)(60s^{-1})cos(-0.52) \]
\[ \dot{\psi}(t=0)=3 m s^{-1} \]
(c)
La velocidad del sistema es nula en los extremos, es decir, cuando \[\psi(t)=A\] \[ Asin(\omega t + \phi)=A \] \[ \omega t + \phi = 1.57 \]
\[ t=\frac{1.57-\phi}{\omega}= \frac{1.57+0.52}{60} \] \[ t=35 ms \]
Luis Velázquez (Usuario discusión:Luis Velázquez) 11:23 17 feb 2015 (CST)
Pablo (Usuario discusión:Pablo) 19:03 07 feb 2015 (CST)
--Luis Santos (discusión) 13:17 12 feb 2015 (CST)
"El problema 1.3, te sugiero que les des una descripción física a los resultados que obtuviste." --Ricardo Garcia Hernandez (discusión) 22:01 22 feb 2015 (CST)
Problema 1.4
El sistema mostrado al principio en la figura podría ser puesto en vibración dándole a la masa un repentino impulso hacia la izquierda; tocándolo por un martillo, por ejemplo. Si la magnitud de el impulso es y es dado al tiempo , encontrar a) la amplitud y b) la fase constante del consecuente movimiento.
Aplicando la segunda Ley de Newton se tiene:
\[ m\ddot{\psi}=p_{1}-k\psi...(1) \]
Al dividir la ecuación (1) entre la masa y ordenarla, nos resulta una ecuación de segundo orden no homogénea:
\[
\ddot{\psi}+\frac{k}{m} \psi=p_{1}...(2)
\]
donde tenemos definida a y a como:
\[\omega^{2}\equiv \dfrac{k}{m}\] \[p_{1}\equiv Ft\]
Como se pondrá en movimiento con una fuerza que actuará sólo un instante de tiempo, se emplea la función delta de Dirac para describir el impulso, por lo cual la ecuación queda expresada como:
\[ \ddot{\psi}+\omega^{2} \psi=\frac{F}{m}\delta(t-t_0)...(3) \]
Aplicando la transformada de Laplace
\[
\mathcal{L} \lbrace\ddot{x}\rbrace + \omega ^{2} \mathcal {L}\lbrace x \rbrace= \frac{F}{m} \mathcal{L}{\delta\lbrace (t-t_0)}\rbrace
\]
\[ s^2 X(s) -sx(0)-\dot {x} (0) + \omega ^2 X(s) = \frac{F}{m}e^{-st_0} \]
Donde las condiciones iniciales son:
\[x(0)=0 \] \[\dot{x}(0)=0\]
Por lo que la ecuación queda expresada como:
\[ X(s) = \frac{F}{m \omega} \frac{\omega}{s^2 + \omega ^2} e^{-st_0} ...(4)\]
Aplicando ahora la transformada inversa en la ecuación (4) \[ \mathcal{L}^{-1} \lbrace X(s)\rbrace = \frac{F}{m \omega}\mathcal{L}^{-1}\lbrace\frac{\omega}{s^2 + \omega ^2} e^{-st_0}\rbrace \]
Resulta \[ x(t)=\frac{F}{m\omega}sin(\omega (t-t_0))\mathcal{U}(t-t_0)...(5) \]
Y como \[t_0 =0\]
Entonces \[ x(t)=\frac{F}{m\omega} sin(\omega t) \mathcal{U}(t)...(6) \]
La cual es equivalente a: \[ x(t)=\frac{F}{m \omega} cos(\omega t + \frac{\pi}{2})..(7) \]
haciendo una analogía de la ecuación (7) y la ecuación \[x(t) = A\cos(\omega t -\phi)\] se puede observar que la amplitud es:
\[ A= \frac{p}{m \omega} \] y la fase
\[ \phi=\frac{\pi}{2} \]
Otra solución:
El impuso que se le imprime se convertirá en energía cinética, por lo que: \[ E=\frac{1}{2m\dot{x}^2} = \frac{1}{2 k_e A^2} \] LeonardoFR (discusión) 17:16 9 jun 2020 (CDT) Luego: \[ A^2=\frac{m\dot{x}^2}{\omega_0 ^2 m}=\frac{m^2 \dot{x}^2 }{\omega_0 ^2m^2}=\frac{p^2}{\omega_0 ^2 m^2} \] Finalmente :
\[ A=\frac{p}{\omega_0 m} \] --Luis Santos (discusión) 01:27 8 mar 2015 (CST)
Le di un poco de orden al problema y corregí faltas de ortografía
--Esther Sarai (discusión) 22:01 18 feb 2015 (CST)Esther Sarai García González
--Luis Santos (discusión) 01:07 13 feb 2015 (CST) --Pablo (discusión) 22:54 18 feb 2015 (CST) --Ricardo Garcia Hernandez (discusión) 21:00 22 feb 2015 (CST)
--Esther Sarai (discusión) 20:27 17 feb 2015 (CST)
Problema 1.5
The system shown at rest in fig 1.1(a) could be set into motion by giving it an initial displacement $A_{1}$ and an initial velocity $v_{1}$ (both to the right, say). Assuming that the motion is started in this way at time $t=0$, show that the amplitude $A$ and the phase constant $\phi$ are given by:
El sistema en reposo mostrado en la figura 1.1(a) puede ser puesto en movimiento dándole un desplazamiento inicial $A_{1}$ y una velocidad inicial $v_{1}$ (ambos a la derecha). Suponiendo que el movimiento se inicia de esta manera en el momento t=0, mostrar que la amplitud $A$ y la constante de fase $\phi$ están dados por:
\begin{equation} A=[A_{1}^{2}+(\frac{v_{1}}{\omega_{0}})^{2}]^{\frac{1}{2}} \end{equation}
\begin{equation} tan\phi=-\frac{v_{1}}{A_{1}\omega_{0}} \end{equation}
Ecuación de Movimiento Armónico Simple:
\begin{equation} \psi(t)=A\cos{(w_{0}t+\Phi)}.....(I) \end{equation}
De acuerdo con la condición inicial del problema $(t=0)$ llamaremos $A_{1}$ al desplazamiento y $v_{1}$ a la velocidad, así obtenemos las siguientes identidades:
\begin{equation}
A_{1}= A \cos{\phi}.....(1)
\end{equation}
\begin{equation} v_{1}=-Aw_{0} sen{\phi}.....(2) \end{equation}
Sabemos que el Movimiento Armónico Simple está descrito por la ecuación $(I)$, es por ello que en el problema podemos utilizar las relaciones (1) y (2) para cumplir el objetivo.
Para mostrar que la amplitud del problema está dado por , elevamos al cuadrado las ecuaciones (1) y (2), obteniendo: \begin{equation} {A_{1}}^2=A^2 \cos^2{ \phi}.....(3) \end{equation}
\begin{equation} {v_{1}}^2=A^2 {w_{0}}^2sen^2{\phi}.....(4) \end{equation}
La ecuación (4) la dividimos por ${w_{0}}^2$ en ambos lados:
\begin{equation} \frac{{v_{1}}^2}{{w_{0}}^2}={A}^2 sen^2{\phi}.....(5) \end{equation}
De lo anterior podemos simplificar las ecuaciones (3) y (5), y sumando de la siguiente manera: \begin{equation} {A_{1}}^2 +\frac{{v_{1}}^2}{{w_{0}}^2}=A^2 \cos^2{ \phi} + {A}^2 sen^2{\phi}.....(6) \end{equation}
De la ecuación (6) factorizamos $A^2$
\begin{equation} {A_{1}}^2 +\frac{{v_{1}}^2}{{w_{0}}^2}=A^2 (\cos^2{ \phi} + sen^2{\phi}).....(7) \end{equation}
Hemos llegado a una identidad trigonométrica básica, la cual está dada por $\cos^2{ \phi} + sen^2{\phi}=1$, de esta identidad sustituiremos la suma de las funciones trigonométricas elevadas al cuadrado por su igualdad, obteniendo:
\begin{equation} {A_{1}}^2 +\frac{{v_{1}}^2}{{w_{0}}^2}=A^2.....(8) \end{equation}
Entonces, sólo despejamos $A$ de la ecuación (8) y tenemos el siguiente resultado: \begin{equation} \boxed{A=[{A_{1}}^2 +(\frac{v_{1}}{\omega_{0}})^{2}]^\frac{1}{2}}.....(9) \end{equation}
la amplitud Q.E.D.
Para demostrar que el ángulo de fase está dado por $\tan{\phi}={-\frac{v_{1}}{A_{1}w_{0}}}$, primero se toma la ecuación (2) dividiéndola entre $-w_{0}$ para obtener: \begin{equation} -\frac{{v_{1}}}{{w_{0}}}={A}sen{\phi}.....(10) \end{equation}
Ahora se toman las ecuaciones (1) y (10), dividiendo la ecuación (10) entre la ecuación (1)
\begin{equation}
\frac{A sen{\phi}}{ A \cos{\phi}}=\frac{\frac{-v_{1}}{w_{0}}}{A_{1}}.....(11)
\end{equation}
En el bando izquierdo de la ecuación (10) la división de la amplitud $A$ entre la misma amplitud $A$ hacen la unidad y por conocimientos previos sobre trigonometría, sabemos que $\frac{sen{\phi}}{\cos{\phi}}= \tan{\phi}$ y por parte del bando derecho se resuelve la división entre fracciones: \begin{equation} \boxed{\tan{\phi}={-\frac{v_{1}}{A_{1}w_{0}}}}.....(12) \end{equation}
Por lo tanto la ecuación de constante de fase también queda demostrada.
Angel Nahir Molina Guadarrama (discusión) 05:59 31 ene 2014 (UTC) Angel Nahir Molina Guadarrama (discusión) 11:39 26 ene 2014 (UTC)
--Andrés Arturo Cerón Téllez (discusión) 23:11 15 may 2013 (CDT)
Otra forma de hacerlo
Tenemos las funciones que definen al desplazamiento y la velocidad
\[x(t)=C_{1}cos\omega t+ C_{2}sin\omega t \] \[\dot{x}(t)=-C_{1}\omega sin \omega t + C_{2} \omega cos \omega t \]
Entonces tenemos como condiciones inciales \[x(0)=0 \] \[\dot{x}(0)=0\]
Lo que resulta
\[x(0)=C_{1}cos\omega (0) + C_{2}sin\omega (0)= C_{1} cos (0) + C_{2} sin (0) = C_{1} \] \[\dot{x}(0)=-C_{1}\omega sin \omega (0) + C_{2} \omega cos \omega (0) = -C_{1}\omega sin (0) + C_{2}\omega cos (0) = C_2\omega \]
de donde
\[C_{1}= A_{0} \]
\[C_{2}= \dfrac{v_{0}}{\omega_{0}} \] Y finalmente se obtiene
\[x(t)= A_{0}cos\omega t + \dfrac{v_{0}}{\omega_{0}} sen \omega t \] La cual se puede escribir de las siguientes formas:
\[x(t)= A sin (\omega + \phi)\] o bien \[x(t)= Acos(\omega - \phi)\]
Esto se demuetra por las siguentes identidades: \[C_{1}cos \omega t + C_{2} sen \omega t = A sen (\omega t+ \phi) = A (sen\omega t cos\phi + sen\phi cos \omega t)\]
Y luego usamos las siguientes identidades también:
\[ A (sen\omega t cos\phi + sen\phi cos \omega t)= (A cos\phi)sen \omega t + (Asen \phi)cos\omega =
(A sen\phi)cos\omega t + (A cos\phi )sen\omega t \]
\[ Asen \phi = C_{1}\] y \[A cos\phi = C_{2}\]
\[ C_{1}^{2} + C_{2}^{2} = A^{2}sen^{2}\phi + A^{2}cos^{2}\phi = A^{2}(sen^{2}\phi + cos^{2}\phi)= A^{2}\]
\[A= \sqrt{C_{1}^{2} + C_{2}^{2}}\]
por lo tanto \[\phi = arctan\dfrac{C_{1}}{C_{2}}\] y como \[C_{1}= A_{0} \]
\[C_{2}= \dfrac{v_{0}}{\omega_{0}} \]
entonces tenemos que
\[A= [A_{0}^{2}+\dfrac{v_{0}^{2}}{\omega^{2}}]^{\dfrac{1}{2}}\]
\[ tan\phi = \dfrac{A_{0} \omega}{v_{0}}\]
O bien
\[ tan\phi = - \dfrac{v_{0}}{A_{0}\omega}\]
Por lo tanto la ecuación de constante de fase queda demostrada por este método alternativo.
--Esther Sarai (discusión) 20:27 17 feb 2015 (CST)Esther Sarai Garcia Gonzalez (UAM-I) --Pablo (discusión) 21:27 19 feb 2015 (CST -- La solución es correcta, me parece que es lo mas cercano a explicar este fenómeno físico al problema que se plantea--Ricardo Garcia Hernandez (discusión) 23:07 22 feb 2015 (CST)
Solución alternativa utilizando energías
Para demostrar la primera identidad se tiene que la energía mecánica del sistema es igual a la suma de la energía cinética y potencial:
$ W = K + U.....(eq.1)$
Donde $W$, $K$, y $U$ son la energía mecánica, la cinética y la potencial, respectivamente. Tenemos que estas están dadas por:
$W = {1\over 2}{s}{A}^{2}....(eq.2)$
$K = {1\over 2}{m}{v_{1}^{2}}.....(eq.3)$
$U = {1\over 2}{s}{A_{1}^{2}}.....(eq.4)$
Donde $s$ es la constante del resorte. Si reemplaza las ecuaciones $2, 3, 4$ en la ecuación $1$ se tiene:
${1\over 2}{s}{A}^{2} = {1\over 2}{m}{v_{1}^{2}} + {1\over 2}{s}{A_{1}^{2}}.....(eq. 5)$
Despejando A de esta última ecuación se tiene:
$A^{2} = {m \over s}{v_{1}^{2}} + {A_{1}^{2}}$
$A^{2} = (\frac{v_{1}}{\omega_{0}})^{2} + {A_{1}}^{2}$
$A = {[(\frac{v_{1}}{\omega_{0}})^{2} + {A_{1}}^{2}]}^{1/2}$
Para la segunda identidad se utilizará las ecuaciones de posición y velocidad del cuerpo oscilante:
$\psi(t)=A\cos{(\omega_{0}t+\phi)}.....(eq. 6)$
$\dot{\psi}(t)={-}\omega_{0}A\sin{(\omega_{0}t+\phi)}.....(eq. 7)$
Reemplazando en las ecuaciones los valores iniciales, se tiene que en $t = 0$ la posición es $A_{1}$ y la velocidad es $v_{1}$. Entonces:
$A_{1} = Acos{\phi}.....(eq.7)$
$v_{1} = {-}{A}{\omega_{0}}{sin{\phi}}.....(eq.8)$
Despejando $A$ de ambas ecuaciones, la ecuación 7 y 8 se convierten en:
$A = {A_{1} \over cos{\phi}}.....(eq.9)$
$A = {{-}{v_{1} \over {\omega_{0}}{sin{\phi}}}}.....(eq.10)$
Respectivamente. Ahora solo se igualan estas dos ecuaciones y se tiene:
${A_{1} \over cos{\phi}} = {{-}{v_{1} \over {\omega_{0}}{sin{\phi}}}}$
Y esta igualdad se puede convertir en:
${sin{\phi} \over cos{\phi}} = {{-}{v_{1}} \over {{A_{1}}{\omega_{0}}}}$
$tan{\phi} = {{-}{v_{1}} \over {{A_{1}}{\omega_{0}}}}$
Resolviendo el Problema.
--Gustavo.uami12 (discusión) 09:55 9 jun 2020 (CDT) --Propuse una solución alternativa mucho más corta que las dos anteriores.
Problema 1.6
Calculate (a)the amplitude, (b)the phase constant, and (c)the complex amplitud, for the vibration by $\psi=\left(10mm\right)\cos\left(\omega_{0}t\right)+\left(17mm\right)\sin\left(\omega_{0}t\right)$
Calcular: a) La amplitud.
b) La constante de fase.
c) La amplitud compleja para la vibración dada: $\psi=\left(10mm\right)\cos\left(\omega_{0}t\right)+\left(17mm\right)\sin\left(\omega_{0}t\right)$.
Solución: (a)La solución general del movimiento armónico simple considerando las condiciones iniciales, está dada por:
donde $\mathit{A_{0}}$ es la amplitud que queremos encontrar.
Desarrollando la función en términos de seno: \[A_{0}\sin\left(\omega_{0}t\text{+}\phi\right)=A_{0}\sin\left(\omega_{0}t\right)\cos\left(\phi\right)+A_{0}\sin\left(\phi\right)\cos\left(\omega_{0}t\right)\]
Igualando se obtiene entonces que: \[A\cos\omega_{0}t+B\sin\omega_{0}t=A_{0}\sin\left(\omega_{0}t\right)\cos\left(\phi\right)+A_{0}\sin\left(\phi\right)\cos\left(\omega_{0}t\right)\]
De aquí obtenemos las siguientes dos ecuaciones:
\[A=A_{0}\cos\left(\phi\right)................ (1) \]
\[B=A_{0}\sin\left(\phi\right)................ (2) \]
Se identifica, $A=10 \, mm$ y $B= 17 \, mm$.
Elevamos al cuadrado (1) y (2), y sumamos:
\[A^{2}+B^{2}=A_{0}^{2}\cos^{2}\left(\phi\right)+A_{0}^{2}\sin^{2}\left(\phi\right)\]
- dado que
Procedemos a sustituir y operar, lo que resulta
(b) Tomemos nuevamente las ecuaciones (1) y (2)
dividimos $\frac{B}{A}=\tan\left(\phi\right)$
y despejando $\phi$ obtenemos:
\[\phi=\arctan\left(\frac{B}{A}\right)\]
Sustituyendo tenemos que:
\[\phi=\arctan\left(\frac{17}{10}\right)\]
Por tanto, $\phi=59.5$
(c) Por la relación matemática que existe entre los números complejos y las vibraciones (ver fasores) podemos ver que la amplitud compleja será:
\[A_{0}=A+iB=10mm+i(17mm)\]
En el enunciado del problema 1.6 lo reescribí en español Israel López (discusión) 21:51 27 ene 2014 (UTC)
Creo que hay un error en las ecuaciones 1 y 2, los valores de A y B estan intercambiados Pérez Córdoba Sabino (discusión) 13:32 17 feb 2014 (UTC)
Pablo (discusión) 23:22 18 feb 2015 (CST)
Corregí algunas faltas de ortografía y poco de la teoría--Esther Sarai (discusión) 23:16 19 feb 2015 (CST)Esther Sarai García Gonzalez
Esta muy bien desarrollado y la teoría explica el planteamiento del ejercicio Ricardo Garcia Hernandez (discusión) 23:19 22 feb 2015 (CST)
Corregi algunas ecuaciones y edite un poco. --Adolfo Calderón Alcaraz (discusión) 23:43 22 feb 2015 (CST)
Problema 1.7
Solución 1
During a vibration with a frecuency of 50 Hz, the displacement is observed to be 30 mm at time t=0, and -14 mm at t=12 ms. Find the complex amplitude.
Durante una vibración con una frecuencia de 50 hz, el desplazamiento obeservado es de 30 mm al tiempo t=0,-14 mm al t=12 s.Encuentre la amplitud compleja
A partir de la expresión para el desplazamiento, se busca obtener los valores que constituyen la expresión anterior:
Desarrollando:
Sean:
Sustituyendo las constantes:
Se toma la siguiente condición:
para la ecuación (1.2).
Por tanto, es 0.03m.
Ahora, para para la ec. (1.3'). Dado que la frecuencia es 50 Hz, y de la relación
Entonces,
. Sustituyendo en la ecuación (1.3')
Finalmente, al sustituir en ecuación (1.1). La amplitud compleja es:
--Daniela López Martínez (discusión) 18:53 15 may 2013 (CDT)
Solución 2
Fe de erratas. Correcciones sobre el problema 1.7.
En efecto, la frecuencia angular está dada por:
al sustituir las cantidades,
Y, además, haciendo una conversión:
Así, pues, dadas las condiciones iniciales
entonces, tomando la siguiente condición
se obtiene.
Dado que
por tanto, en la ec. (1.1), resulta:
En el 1.7 realicé la traducción Aura Yazmin Bejarano Olvera (discusión)
Solución 3
La solución a este problema la realice de la siguiente manera: Tenemos que:
\[ \psi(t)=Acos(\omega_{0}t+\phi) \]
\&
\[ \omega_{0}=\nu_{0}2\pi \]
Luego, con las condiciones iniciales $\psi(0s)=x_{1}=30$ mm y $\psi(12ms)=x_{2}=-14$mm
tendremos que:
\[ \psi(0s)=x_{1}=Acos(\phi) \]
\[
\psi(0.012s)=x_{2}=Acos(\omega_{0}(12ms)+\phi)
\]
\[
x_{2}=Acos(\phi)cos(\omega_{0}(0.012s))-Asen(\phi)sen(\omega_{0}(0.012s))
\]
Pero $Acos(\phi)=x_{1}$, asi:
\[ x_{2}=x_{1}cos(2\pi\nu_{0}(0.012s))-Asen(\phi)sen(2\pi\nu_{0}(0.012s)) \]
Tenemos también que:
\[ cos(2\pi(50Hz)(0.012s))\cong0.99 \]
\[
sen(2\pi(50Hz)(0.012s))\cong0.06
\]
Asi:
\[ -0.014m=(0.03m)(0.99)-Asen(\phi)(0.06) \]
\[
Asen(\phi)(0.06)=0.029m+0.014m
\]
\[
Asen(\phi)=\frac{0.043m}{0.06}=0.071m
\]
Por lo cual la amplitud compleja es igual a:
\[ D=0.03m+i0.071m \]
La nueva solución fue realizada por: Cesar Ivan Avila Vasquez el 19 de Febrero de 2014.
Solución 4
During a vibration with frequency of $50 Hz$, the displacement is observed to be $30 mm$ at time $t=0$, and $-14 mm$ at $t=12 \, ms$. Find the complex amplitude.
Durante una vibración de frecuencia $50 Hz$, el desplazamiento observado es $30 mm$ al tiempo $t=0$, y $-14 mm$ al tiempo $t=12 \, ms$. Encuentre la amplitud compleja.
Para empezar tenemos que calcular la frecuencia angular a partir de la frecuencia dada.
$w_0=2 \pi v=2 \pi (50 Hz) =100 \pi \,s^{-1}$
Luego sabemos que la forma compleja (forma D en el Main, Iain G., Vibrations and Waves in Physics, 1993) es $ \psi (t)=Re[D \, e^{i w_0 t}] $, donde $D=a+i \, b$. Además sabemos dos condiciones iniciales, por lo que podemos determinar dos constantes $a$ y $b$.
\begin{equation} \label{1} \psi (0 \, s)=30 \, mm \end{equation}
\begin{equation} \label{2} \psi (12 \, ms)= \psi (.012\,s)=-14 \, mm \end{equation}
De la ec. $(1)$ obtenemos la constante $a$.
$\psi (0)=Re[D e^{i w_0 (0)}]=Re[(a+ib) (1)]=30\,mm$
Evaluando la parte real, entonces... \begin{equation} \label{3} a=30\,mm \end{equation}
Si utilizamos la ec. $(2)$, encontraremos la constante faltante, $b$. $\psi (.012 \,s)=Re[D \, e^{i (100 \pi \, s^{-1}) (0.012 \, s)}]=-14 \, mm$ $Re[(a+ib)(cos(1.2 \pi)+i\,sen(1.2 \pi))]=-14 \, mm$
De nuevo se evalua la parte real del número complejo y luego se despeja $b$. $ a \, cos(1.2 \pi)-b \, sen(1.2 \pi)=-14 \, mm $ $ b=\frac{14\,mm+(30\,mm)\,cos(1.2 \pi)}{sen(1.2 \pi)} $ \begin{equation} \label{4} \, b \approx 17.47323498\,mm \end{equation}
Si juntamos $(3)$ y $(4)$, la amplitud compleja es $D=30\,mm+i\,17.47323498\,mm$ Y la función es
\begin{equation} \label{5} \psi (t)=Re[(30\,mm+i\,17.47323498\,mm)\, e^{i\, (100\pi \,s^{-1}) \, t}] \end{equation}
La comprobación se realiza evaluando la ecuación $(5)$ a los tiempos $t=0 \, s$ y $t=0.012 \, s$, lo cual nos da las condiciones iniciales de $(1)$ y $(2)$. $ \, $
Solución realizada por: Adolfo Calderón Alcaraz(discusión) el 14 de Febrero de 2014
Separé la solución de César Iván e hice algunas correcciones ortográficas. --Pablo (discusión) 21:56 19 feb 2015 (CST)
Algunas correciones --Adolfo Calderón Alcaraz (discusión) 23:32 20 feb 2015 (CST)
Falta un poco de teoría del planteamiento del problema--Ricardo Garcia Hernandez (discusión) 23:23 22 feb 2015 (CST)
Agregado un nuevo subíndice, espero que no sea confuso.--Adolfo Calderón Alcaraz (discusión) 23:48 22 feb 2015 (CST)
Arreglé el código porque varias expresiones matemáticas no salían bien Juan Daniel Rivera Bautista (discusión) 20:26 8 jun 2020 (CDT)
Problema 1.8
Calculate the maximum acceleration (in units of $g$) of pickup stylus reproducing a frequency of $16 kHz$, with an amplitude of $0.01mm$.
Calcule la aceleración máxima (en unidades de $g$) de una aguja que reproduce una frecuencia de $16 kHz$, con una amplitud de $0,01 mm$.
El problema nos proporciona los siguientes datos: $f =16kHz = 16000Hz$ $A = 0.01mm = 0.00001m$
Resultado:
Sabemos que podemos expresar la frecuencia angular como la frecuencia por $2\pi$: \[ \omega=2\pi f...(1) \]
Ahora sustituimos el valor de la frecuencia($f =16000Hz$) en la ecuación 1:
\[\omega=2\pi(16000Hz)\]
Luego obtenemos una nueva ecuación ya con el valor de $f$ evaluado:
\[\omega=32000\pi \frac{rad}{s}\]
\[{\color{black}{\color{blue}\omega=100530.9649\frac{rad}{s}}}...(2)\]
Un dato importante en este momento, es la expresión para la aceleración máxima en el movimiento armónico simple:
\[ \frac{d^2x}{dt^2} = a(t) = -\omega^2x\]
Donde $x$ es la solución para el movimiento armónico simple ,osea , $x(t) = A \cos(\omega t + \phi)$. El valor de $x$ será máximo cuando el $\cos(\omega t + \phi)=1$ alcance su valor máximo y esto sucede cuando es igual uno. Por tal razón podemos expresar la aceleración máxima como sigue:
\[\left\Vert a_{max}\right\Vert =A\omega^{2}\]
Finalmente sustituimos el valor de $\omega$ elevado al cuadrado proveniente de la ecuación 2:
\[\left\Vert a_{max}\right\Vert =(0.00001m)(100530.9649\frac{rad}{s})^{2}\]
\[\left\Vert a_{max}\right\Vert =101064.749\frac{m}{s^{2}}\]
Ahora hay que dividir el resultado obtenido en la ecuación 3 entre $g$ para expresarlo en unidades de $g$.Usamos primero:
\[g=9.8\frac{m}{s^2}\]
Y obtenemos la aceleración máxima en unidades de $g$:
\[\left\Vert a_{max}\right\Vert =10312.729g\]
Pedro Pablo Ramírez Martínez (discusión) 04:51 21 feb 2014 (UTC) --A. Martín R. Rabelo (discusión) 20:22 18 feb 2015 (CST)
--Entendible y bien desarrollado----Ricardo Garcia Hernandez (discusión) 23:32 22 feb 2015 (CST)
Problema 1.9
1.9.- Un oscilador armónico se compone de una masa de 100 gramos sujeta a un muelle de constante de recuperación de 4 dinas/cm. Se desplaza la masa una distancia de 3 cm. soltando desde el reposo. Calcular: a) la frecuencia propia y el periodo, b) la energía total y c) la velocidad máxima.
$\;$
Se sabe que el bloque fue estirado 3cm, además debido a que se desprecía la fricción entre el bloque y la superficie en la que se encuentra ya sabemos que la amplitud máxima del sistema es de 3cm.
$\;$
Por otro lado, al tratarse de un oscilador armónico simple y al saber que la única fuerza que actuá en la misma línea de acción del movimiento es la fuerza del resorte, entonces tenemos: La energia potencial correspondiente a dicha fuerza es:
La fuerza y la energia potencial estan relacionadas por :
Ahora , aplicando la segunda ley de Newton: :
Ahora, dividiendo entre “m” e igualando la expresion a cero, se tiene :
\begin{equation} \ddot{x}+\frac{k}{m}x=0 \end{equation}
y al resolver la ecuación diferencial obtenemos como solución
\[ x(t)=ACos(wt)+BSen(wt)\;\;\;\;;\;\;\; w=\sqrt{\frac{k}{m}} \]
Además de las condiciones iniciales tenemos:
$\;$
Cuando $t=0$ la posición inicial es $x(t=0)=3cm$ y cuando $t=0$ la velocidad inicial es $\dot{x}(t=0)=0$
\[ x(t=0)=A=3\;\;\;;\;\;\;\dot{x}(t=0)=B=0 \]
\[
\therefore\;\;\; x(t)=3Cos(wt)
\]
de aquí podemos decir que el bloque estará oscilando en $-3\leq x(t)\leq3$
y que la velocidad máxima del bloque es justamente cuando el bloque
no esta elongado, es decir cuando $x(t=t_{0})=0$
$\;$
Ahora por otro lado, sabemos que cuando el bloque tiene velocidad máxima justo en ese instante la energía del sistema es en su totalidad energía cinética ya que al no estar el bloque elongado este no tiene energía potencial.
\[ E_{T}=T+U=\frac{1}{2}m\dot{x}^{2}+\frac{1}{2}kx^{2}\;\;\quad al\; sustituir\;\; x(t)\;\; y\;\;\dot{x}(t)\;\quad llegamos\; a \]
\begin{equation}
E_{T}=\frac{1}{2}kA^{2}\; con\; A=3
\end{equation}
entonces al igualar la energía total con la energá cinética máxima
obtenemos la velocidad máxima
\begin{equation} \frac{1}{2}kA^{2}=\frac{1}{2}m\dot{x}_{max}^{2}\Rightarrow\dot{x}_{max}=A\sqrt{\frac{k}{m}} \end{equation}
a) La frecuencia propia esta dada por $f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$
y haciendo la conversion correcta al SI tenemos $f=1.59\frac{1}{s}$
y en de forma inmediata el periodo es $T=\frac{1}{f}\;\;\Rightarrow T=0.63s$
b) La energía total del sistema esta dada por $(2)$
\[ E_{T}=4.5\times10^{-3}Joules \]
c) La velocidad máxima que experimenta el bloque esta dada por $(3)$
\[ \dot{x}_{max}=0.3\frac{m}{s} \]
Luis Miguel Sánchez Mtz. (discusión) 21:59 25 ene 2014 (UTC)
--Falta explicar como obtiene la ecuación diferencial del oscilador armonico simple, y como obtiene las condiciones iniciales partiendo del problema----Ricardo Garcia Hernandez (discusión) 23:35 22 feb 2015 (CST)
--Solo cambio y completo mas la teoría de como obtiene la ecuación diferencial del oscilador----Ricardo Garcia Hernandez (discusión) 00:03 23 feb 2015 (CST)
Problema 1.10
1.10 Comprobar que la ecuación diferencial $\frac{d^{2}x}{dt^{2}} =-kx$ tiene por solución $y=Acos(kx)+Bsen(kx)$ siendo A y B constantes arbitrarias. Demostrar también que esta solución puede escribirse en la forma $y=Ccos(kx+\alpha)=C$ $\mathbb{R}\epsilon\left[e^{i(kx+\alpha)}\right]=\mathbb{R\epsilon}\left[(Ce^{i\alpha})e^{ikx}\right]$ y expresar C y \textgreek{a} en función de A y B.
SOLUCIÓN:
Por segunda ley de Newton tenemos:
\[ |\overrightarrow{F}|=m|\vec{a}|\rightarrow-kx=m\frac{d^{2}x}{dt^{2}} \]
entonces derivamos dos veces a $y=Acos(kx)+Bsen(kx)$
\[ \frac{dy}{dx}=-kAsen(kx)+kBcos(kx) \]
\[ \frac{d^{2y}}{dx^{2}}=y=-k^{2}Acos(kx)-k^{2}Bsen(kx)=-k^{2}\left[Acos(kx)+Bsen(kx)\right]=-k^{2}y \]
donde
\[ y=Acos(kx)+Bsen(kx) \]
Sean \begin{equation} A=Ccos(\theta) \end{equation}
\begin{equation} B=-Csen(\theta) \end{equation}
Entoces:
\[ y=Acos(kx)+Bsen(kx)=Ccos(\theta)cos(kx)-Csen(\theta)sen(kx) \]
Aplicando la propiedad trigonometrica de la suma de los ángulos del coceno
\[ cos\left(a+b\right)=cos\left(a\right)cos\left(b\right)-sen\left(a\right)sen\left(b\right) \]
tenemos:
\[ =C[cos(kx)cos(\theta)-Csen(kx)sen(\theta)]=C[cos(kx+\theta)] \]
quedando asi demostrada la primera parte.
Ahora demostraremod que $y=Ccos(kx+\alpha)=C\mathbb{R}\epsilon\left[e^{i(kx+\alpha)}\right]=\mathbb{R\epsilon}\left[(Ce^{i\alpha})e^{ikx}\right]$
De los números complejos sabemos que:
\[ z=e^{i\alpha}=cos(\alpha)+isen(\alpha) \]
aplicando propiedades de los expenontes, y teniendo en cuenta que la parte real de $z=cos(\alpha)$ y el resultado anterior tenemos que:
\[ y=C\mathbb{R}\left[e^{i(kx+\alpha)}\right]=\mathbb{R}\left[Ce^{i(kx+\alpha)}\right]=\mathbb{R}\left[(Ce^{i\alpha})e^{ikx}\right] \]
demoatrando lo pedido.
Por último expresaremos C y \textgreek{a} en función de A y B.
Si elevamos al cuadrado las ecuaciones 1 y 2 tenemos que
\[ A^{2}+B^{2}=C^{2}cos^{2}\left(\theta\right)+\left(-C\right)^{2}sen^{2}\left(\theta\right)=\left[C^{2}(cos^{2}\left(\theta\right)+sen^{2}\left(\theta\right))\right]=C^{2} \]
entonces
\begin{equation} C^{2}=\sqrt{A^{2}+B^{2}} \end{equation}
para \textgreek{j} tenemos que:
\[ tan\left(\theta\right)=\frac{A}{B}=\frac{-Csen(\theta)}{Ccos(\theta)}=-tan\left(\theta\right) \]
\[ \theta=arctan\left(-\frac{B}{A}\right) \]
--Añadi un nuevo problema----Evamontiel (discusión)
Problema I.I
A piston executes harmonic motion with an amplitude of $0.1m$. If it passes through the center of its motion with a speed of $0.5m/s$, what is the period of oscillation?
Un pistón realiza un movimiento armónico con una amplitud de $0.1m$. Si pasa por el centro de su movimiento con una velocidad de $0.5m/s$, ¿cuál es su periodo de oscilación?.
Sabemos que para el movimiento armónico simple(MAS), podemos proponer una solución del tipo:
por lo que, al derivar la función de posición, obtenemos la velocidad como función del tiempo:
Ahora bien, dadas las condiciones del problema, tenemos que resolver las ecuaciones para la posición y la velocidad de manera simultanea. Por lo tanto, tenemos el siguiente sistema de ecuaciones:
y sustituyendo las condiciones de frontera del problema, tenemos:
Para que se cumpla la primera ecuación, la única posibilidad es que $\cos(\omega t + \phi) = 0$ y para ello, $\omega t + \phi = (2n-1) \pi / 2$ con $i = 1,2,3,\ldots$.
Si tomamos ahora la segunda ecuación:
Pero al estar resolviendo un sistema de ecuaciones, debemos considerar la condición de que $\omega t + \phi = (2n-1) \pi / 2$ con $i = 1,2,3,\ldots$. Y bajo las condiciones anteriores, $\sin(\omega t + \phi) = \pm 1$, por lo que la segunda ecuación queda como:
Tomando $|\omega|$ y la definición de $T=2\pi / \omega \Rightarrow T = 2\pi / (5s^{-1})$, con lo que tendremos la solución deseada:
Ivan de Jesús Pompa García (discusión) 13:09 14 feb 2015 (CST)
Problema I.II
A particle undergoes harmonic motion with a frequency of $10$Hz. Find the displacement $\psi$ at any time $t$ for the following initial condition: $t=0$, $\psi=0.25m$, $\dot{\psi}=0.1m/s$.
Una partícula sigue un movimiento armónico con una frecuencia de $10Hz$. Encuentre el desplazamiento $\psi$ para cualquier tiempo $t$ con las condiciones iniciales: $\psi(t=0)=0.25m,\dot{\psi}(t=0)=0.1m/s$.
Proponemos la siguiente solución:
con lo que la velocidad será:
y aplicando las condiciones iniciales y sabiendo que $\omega = 2\pi \nu = 2\pi (10Hz) = 20\pi s^{-1}$ tendremos lo siguiente:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \psi(t=0) = A\cos(\phi) = 0.25m \\ \dot{\psi}(t=0) = -(2\pi)(10Hz) A\sin(\phi) = 0.1m/s
Y dividiendo la ecuación (2) entre la (1):
y realizando los cálculos:
Retomando la ecuación para el desplazamiento y el valor de $\phi$:
De tal forma que la función $\psi(t)$ se puede escribir como:
Ivan de Jesús Pompa García (discusión) 13:39 14 feb 2015 (CST) --Esther Sarai (discusión) 21:27 19 feb 2015 (CST)Esther Sarai García Gonzalez --Ricardo Garcia Hernandez (discusión) 17:26 26 feb 2015 (CST)
Solución vectorial del oscilador armónico del capítulo 1
En esta parte lo que pretendo es llegar a la solución vectorial del oscilador armónico de la forma:
- para la ecuación diferencial de segundo orden
Descomponiendo esta ecuación en un sistema de ecuaciones de primer orden
A este sistema le asociamos una matriz
Los valores propios para esta matriz son:
Buscamos ahora los vectores propios para los valores de . De hecho,
sólo podemos tomar el valor positivo ya que para valor propio complejo su vector propio asociado viene en par conjugado
El vector propio asociado a
- es
Entonces formando la matriz
Su inversa de es
Ahora para desacoplar el sistema de ecuaciones (1) y (2) calculamos
Que es una diagonalización y la matriz
La utilizamos para calcular
Esta es la solución vectorial para la ecuación
Resuelto por Hector resendiz --Héctor Reséndiz (discusión) 22:22 17 feb 2015 (CST)
--Pablo (discusión) 21:35 19 feb 2015 (CST)
--A. Martín R. Rabelo (discusión) 08:48 21 feb 2015 (CST)
Problema l.lll
Una partícula de 12.3 Kg experimenta un movimiento armónico simple con una amplitud de 1.86mm. Su aceleración máxima es . a)Encuentre el periodo de movimiento. b)¿Cúal es la velocidad máxima? c) Calcule la energía mecánica total de este oscilador armónico simple.
Tratándose de un movimiento armónico simple recurriremos a la siguiente expresión diferencial, que modela el movimiento armónico simple :
Donde es el coeficiente de restitución y la aceleración.
Al dividir la ecuación (1) por obtenemos que:
Donde la expresión (2) queda satisfecha por: \[ \psi(t)=Acos(\omega t + \phi) \]
Donde es la frecuencia angular. Al calcular la primera derivada de obtenemos la velocidad y la aceleración al volverla a derivar por segunda vez, es decir que: \[\dot{\psi}(t)=-A \omega Sen(\omega t + \phi)...(3)\] \[\ddot{\psi}(t)=-A \omega^2 Cos(\omega t + \phi)...(4)\]
Analizando las ecuaciones (3) y (4), notamos que las funciones seno y coseno oscilan entre , por lo que los valores extremos para la velocidad son . De una forma análoga para la aceleración, los valores extremos que puede tomar son , en consecuencia los valores máximos para la aceleración y la velocidad:
\[\dot{\psi}(t)= A \omega ...(5)\] \[\ddot{\psi}(t)= A \omega^2 ...(6)\]
La energía ó Ondas: conservacion está dada por: \begin{equation} W = T + V =Cte \end{equation}
Donde $T$ es la energía cinética y $V$ es la energía potencial, por lo que podemos redefinirla como:
a) El periodo del movimiento es el intervalo de tiempo requerido para que la partícula realize un ciclo completo de su movimiento, por lo que:
Como tenemos los valores de la aceleración máxima y la amplitud, despejamos a de la ecuación (6), luego sustituimos los valores conocidos para obtener el valor de . \[\omega= \sqrt{\ddot{\psi} \over A} = \sqrt{7.93x10^3 {m \over s^2} \over 1.8x10^{-3} m} = 2.10x10^{3} \frac{rad}{s} \]
por lo que al sustituir el valor de en (8) obtenemos que:
b) Para la velocidad usaremos la expresión (5): \[\dot{\psi}(t)= A \omega = (1.86x10^{-3}m)(2.10x10^{3} \frac{rad}{s})=3.90 {m \over s} \]
c) Para la enegía mecánica total usaremos la expresion (7):
--Pablo (discusión) 20:33 19 feb 2015 (CST)
LeonardoFR (discusión) 17:28 9 jun 2020 (CDT)
Juan Daniel Rivera Bautista (discusión) 18:41 22 jun 2020 (CDT) arreglé el código de una expresión matemática
Problema 1-12, French
Un punto se mueve en una circunferencia con una celeridad constante de 50 cm/s. El periodo de una vuelta completa es 6 seg. Para t=0 la recta que va del punto al centro de la circunferencia forma un angulo 30° con el eje x.
(a) Obtener la ecuación de la coordenada x del punto en función del tiempo en la forma , conocidos los valores numéricos de A, y
(b) Hallar los valores de $x$, y para t=2 s
Dado que el punto tarda 6 seg en dar una vuelta completa y este se mueve con una velocidad de 50 cm/s; la circunferencia mide,
y dado que...
el resultado anterior es la máxima distancia del punto en el eje x, es decir es la amplitud.
Ahora,
Dado que en $t=0$ el punto forma un ángulo de
con en eje x, y pensando que el ángulo fue medido de la forma normal, anti-horaria se tiene que
y,
Ahora se calculara su posición, velocidad y aceleración en $t=2 s$.
Para calcular la posición primero sustituimos $t=2$
Después de simplificar el argumento del argumento del coseno, calcular el resultado es trivial:
Para la velocidad, primero debemos derivar la función de la posición,
Después de simplificar nos queda:
Sustituimos $t=2s$,simplificamos el argumento del seno y calcular el resultado es trivial,
Para la aceleración primero derivamos la velocidad
Sustituimos $t=2s$, simplificamos en argumento del coseno y calcular el resultado se hace trivial:
--Uziel Sanchez Gutierrez (discusión) 02:10 20 feb 2015 (CST) --A. Martín R. Rabelo (discusión) 08:28 21 feb 2015 (CST)
Sólo reescribí la solución de los últimos cálculos explicando un poco másJuan Daniel Rivera Bautista (discusión) 21:30 8 jun 2020 (CDT)
Problema 11-21, Física general Sears-Zemansky Ed. 4ta
Una masa $m$ oscila en el extremo de un resorte vertical con una frecuencia de 1 Hz y una amplitud de 5 cm. Cuando se añade otra masa de 300 g, la frecuencia de oscilación es de 0,5 Hz. Determine:
a) El valor de la masa m y de la constante recuperadora del resorte.
b) El valor de la amplitud de oscilación en el segundo caso si la energía mecánica del sistema es la misma en ambos casos
Solución:
Por la relación \[ \omega_{0}=(\frac{k}{m})^{\frac{1}{2}}...(a) \]
y \[ \upsilon_{0}=\frac{\omega_{0}}{2\pi}...(b) \]
donde $\omega{}_{0}$ es la frecuencia angular y $\upsilon_{0}$ la frecuencia; se puede sustituir (a) en (b) para obtener:
\[ \upsilon_{0}=\frac{1}{2\pi}\sqrt{\frac{k}{m}} \]
donde $k$ en la constante del resorte respectivo y $m$ la masa.
Del problema conocemos la frecuencia, antes y después de ser agregada la segunda masa,
la cual también conocemos, y la amplitud.
a)Por lo tanto se puede expresar :
\[ \upsilon_{1}^{2}=\frac{k}{4\pi^{2}m}\ldots(1) \]
\[ \upsilon_{2}^{2}=\frac{k}{4\pi^{2}(m+.3kg)}\ldots(2) \]
Donde $\upsilon_{1}$ y $\upsilon_{2}$ representan las frecuencias antes y después de colocar la segunda masa.
De las ecs. (1) y (2), podemos despejar $k$ e igualar de la siguiente manera:
\[ \upsilon_{1}^{2}4\pi^{2}m=\upsilon_{2}^{2}4\pi^{2}(m+.3) \]
y despejando $m$ queda
\[ m=\frac{.3*.5^{2}}{(1^{2}-.5{}^{2})}=.1 \]
Por lo tanto $m=100g$ y despejando $k$ de (1) tenemos
\[ k=\upsilon_{1}^{2}4\pi^{2}m\ldots\ldots(3) \]
\[ k=1^{2}4\pi^{2}(.1)=3.947 \]
Entonces $K=3.947N/m$
(b)Para calcular la amplitud en la segunda situación tenemos la relación siguiente:
Conocemos...
\[ E_{m1}=\frac{1}{2}kA_{1}^{2}\ldots\ldots\ldots(\alpha) \]
Y también sabemos que:
\[ E_{m2}=\frac{1}{2}kA_{2}^{2}\ldots\ldots\ldots(\beta) \]
Pero como como $E_{m1}=E_{m2}$ entonces al igualar ($\alpha$) y ($\beta$) sabremos que:
\[ A_{1}^{2}=A_{2}^{2} \]
Por lo que $A_{2}^{2}=.05m$
--A. Martín R. Rabelo (discusión) 07:54 21 feb 2015 (CST)
Problema oscilador armónico
El desplazamiento de una partícula viene dado por:
- $x$ en metros y $t$ en segundos.
a) Determinar la frecuencia, el periodo, la amplitud, la pulsación y la fase inicial.
b) ¿Dónde se encuentra la partícula en $t$ = 1s?
c) Calcula la velocidad y la aceleración en un instante cualquiera $t$.
d) Calcula la posición y velocidad inicial.
- Solución:
a) Observamos que se trata de un movimiento armónico simple, cuya ecuación general viene dada por:
Comparando directamente tenemos que $A=0.3 m$ , $\omega =2Hz$ , $\phi = \frac{\pi}{6} rad$
La frecuencia se obtiene a partir de la pulsación:
el periodo se calcula como la inversa de la frecuencia:
b) Para saber dónde se encuentra la partícula en el instante $t$ = 1s es suficiente substituir en la ecuación del movimiento:
c) La velocidad y la aceleración se pueden obtener de la posición derivando respecto del tiempo (una vez para obtener la velocidad, dos para la aceleración).
d) únicamente tenemos que substituir t = 0 en las expresiones adecuadas:
--Luis Martínez (discusión) 14:59 22 feb 2015 (CST)
Corregí el código porque algunas expresiones matemáticas que no se veían bien Juan Daniel Rivera Bautista (discusión) 21:40 8 jun 2020 (CDT)
Problema propuesto en relación al capitulo I
Se encontró experimentalmente que un peso de estira un resorte de . Si el peso se suelta desde la posición de equilibrio con una velocidad dirigida hacia abajo de , determine:
a) La ecuación diferencial y condiciones iniciales que describen el movimiento.
b) La ecuación de movimiento.
c) El periodo y la frecuencia.
Solución
Recordando que , realizando las conversiones respectivos, se tiene:
Inicialmente el peso está en una posición de reposo , y después se suelta desde la posición de equilibrio (reposo) .
Además .
problema propuesto vibraciones y ondas
si la posición, velocidad y aceleración de un objeto que se mueve con movimiento armónico simple son $v_{0}$
Entonces, por la ley de Hooke y sustituyendo los datos se tiene:
a) La ecuación diferencial que describe el movimiento es:
Sustituyendo los datos se tiene:
con las condiciones iniciales y
b) La ecuación auxiliar de (1) es , cuyas raíces son . La solución general de (1) es:
derivando dos veces la solución general se tiene:
Para conocer y , sustituímos las condiciones iniciales en (2) y (3)
c) La posición, velocidad y aceleración del peso 2 segundos después, está dado por:
Lo cual indica que el cuerpo se encuentra a arriba de la posición de equilibrio moviendose hacia arriba.
Bibliografía
José Ventura Becerril y David Elizarraraz, ecuaicones diferenciales técncas de solución y aplicaciones, 1ra edición, Universidad Autónoma Metrpolitana Azcapotzalco, México, 2004.
--Ricardo García Hernández----Ricardo Garcia Hernandez (discusión) 00:51 23 feb 2015 (CST)
Problema del serwey
un bloque de conectado a un resorte ligero tiene una constante de fuerza de es libre de oscilar sobre una superficie horizontal sin friccion. El bloque se desplaza desde el equilibrio y se libera del reposo.
a) Hallar el periodo de movimiento
primero hay que encontrar la frecuencia angular con la siguiente ecuación
el periodo esta dado por .
b) Hallar (velocidad) y (aceleracion) máxima A=.05m c) Exprese la posición, velocidad y aceleración como funciones del tiempo en unidades del SI para un tiempo inicial igual a cero la fase es 0
- --
--Jose de jesus (discusión) 18:03 25 feb 2015 (CST)jose de jesus Arizpe flores 24/02/15 18:03
Problema 2.8, The Physics of Vibrations and Waves, A. Pain
A plasma consists of an ionized gas of ions and electrons of equal number densities ($n_i = n_e = n$)having charges of opposite sign $\pm e$, and masses $m_i$ and $m_e$ , respectively, where $m_i > m_e$. Relative displacement between the two species sets up a restoring electric field which returns the electrons to equilibrium, the ions being considered stationary. In the diagram, a plasma slab of thickness $l$ has all its electrons displaced a distance $x$ to give a restoring electric field $E=nex/\epsilon_0$ where $\epsilon_0$ is a constant. Show that the restoring force per unit area on the electrons is $xn^2e^2l/\epsilon_0$ and that they oscillate simple harmonically with angular frequency $\omega^2_e = ne^2/m_e\epsilon_0$. This frequency is called the electron plasma frequency, and only those radio waves of frequency $\omega > \omega_e$ will propagate in such an ionized medium. Hence the reflection of such waves from the ionosphere.
Un plasma consiste en gas ionizado formado por iones y electrones con densidades iguales ($n_i = n_e = n$) teniendo cargas del signo opuesto $\pm e$, y masas $m_i$ y $m_e$ respectivamente, donde $m_i > m_e$. El desplazamiento relativo entre dos especies establece un campo eléctrico restaurador que regresa a los electrones al equilibrio, donde los iones se consideran estacionarios. En el diagrama, un bloque de plasma de ancho $l$ tiene todos sus electrones desplazados una distancia $x$, proporcionando un campo eléctrico restaurador $E=nex/\epsilon_0$ donde $\epsilon_0$ es una constante. Muestre que la fuerza restauradora por unidad de área en los electrones es $xn^2e^2l/\epsilon_0$ y que ellos oscilan de manera armónica simple con frecuencia angular $\omega^2_e = ne^2/m_e\epsilon_0$. Esta frecuencia es llamada frecuencia de plasma y sólo aquellas ondas de radio con frecuencia $\omega > \omega_e$ se propagarán a través del medio ionizado. De este mode se da la reflección de tales ondas desde la ionósfera.
Sabemos que la densidad lineal de los electrones en el plasma está dada por $n_e = n$, entonces, para encontrar la carga de los electrones por unidad de área en el plasma, tenemos que multiplicar por la longitud del bloque($l$) y por la carga de cada electrón($-e$):
Ahora, si se quiere calcular la fuerza restauradora por unidad de área, tomamos la definición de la fuerza eléctrica:
y luego sustimos la expresión dada para el campo eléctrico restaurador y la expresión encontrada para la carga:
lo cual es el resultado buscado. También es necesario mostrar que los electrones oscilan de manera armónica simple. Para ello, escribimos las fuerzas involucradas en el sistema. Una es la fuerza de restaurauración por unidad de área y la otra es la aceleración de los electrones por su masa por unidad de área. La masa por unidad de área de los electrones se encuentra multiplicando la densidad lineal $l$, por la masa de cada electrón $m_e$, por el ancho del bloque de plasma. Lo anterior nos da:
Donde simplificando la ecuación anterior, tenemos:
lo anterior demuestra que es un movimiento armónico simple.
Ivan de Jesús Pompa García (discusión) 11:56 3 mar 2015 (CST)
ejercicio vibra 1
Durante una vibración con una frecuencia de 50 hz, el desplazamiento obeservado es de 30 mm al tiempo t=0,-14 mm al t=12 s.Encuentre la amplitud compleja
A partir de la expresión para el desplazamiento, se busca obtener los valores que constituyen la expresión anterior:
Desarrollando:
Sean:
Sustituyendo las constantes:
Se toma la siguiente condición:
para la ecuación (1.2).
Por tanto, es 0.03m.
Ahora, para para la ec. (1.3'). Dado que la frecuencia es 50 Hz, y de la relación
Entonces,
. Sustituyendo en la ecuación (1.3')
Finalmente, al sustituir en ecuación (1.1). La amplitud compleja es:
--Luisa Alejandra Vega Sanchez (discusión) 17:40 30 mar 2015 (CDT)luisa alejandra vega sanchez
Ejercicio 1
Un oscilador está formado por un bloque de masa $m=0.5 kg$ conectado a un resorte ideal. Cuando es puesto en oscilación con una amplitud de $A=35 cm$, el oscilador repite su movimiento cada $0.5s$. Encontrar:
Solución propuesta:
- Si el tiempo se mide desde que el sistema se suelta estando el bloque en una posición igual a la amplitud, entonces el ángulo de fase es nulo y la ecuación de movimiento es:
- $x(t)=A\cos(wt)$
(a) Como el periodo es el tiempo en que el movimiento se repite, entonces:
- $T=0.5s$
(b) Como la frecuencia es igual al inverso del periodo, entonces:
- $f=\frac{1}{T}=\frac{1}{0.5s}=2.0Hz$
(c) La frecuencia angular es $w=2πf$, entonces:
- $w=2πf=\frac{2π}{T}=4π=12.57rad/s$
(d) La constante del resorte es $k=mw^{2}$, entonces:
- $k=mw^{2}=(0.5kg)(12.57rad/s)^{2}=78.96 N/m$
(e) La magnitud de la velocidad máxima es $v_{max}=wA$.
- $v_{max}=wA=(12.57rad/s)(0.35m)=4.40m/s$
(f) Usando la segunda ley de Newton, la fuerza máxima es:
- $F_{max}=ma_{max}=m(w^{2}A)=(78.96N/m)(0.35m)=27.64 N.$
(g) La energía mecanica del sistema es:
- $E=\frac{1}{2}kA^{2}=(0.5)(78.96N/m)(0.35m)^{2}=4.84J$
Rodrigo (discusión) 14:30 16 jun 2020 (CDT)
Problema propuesto 1.
si la posición, velocidad y aceleración iniciales de un objeto que se mueve con movimiento armónico simple son $ x_{0} $,$ v_{0} $, $ a_{0} $ y la frecuencia de oscilación es $ w^{2} = \frac{k}{m} $. Si la función para la posición del objeto del objeto se propone como se muestra a continuación: $x(t) = x_{0} cos(w t) + \frac{v_{0}}{w} sin(wt)$
(a) demuestre que la velocidad del objeto para todo tiempo puede escribirse como:
$v(t) = -x_{0} w sin (w t ) + v_{0} cos (wt)$
(b) si la amplitud del movimiento es $A$, demuestre que
$ v_{0}^{2}-a_{0} x_{0}= A^{2} w^{2}$
Solución:
a) derivando la función de la posición del objeto con respecto al tiempo se tiene que
$\frac{dx}{dt} = - x_{0} w sin(wt) + v_{0} cos(w t)$
se sabe que por definición la derivada de la posición con respecto al tiempo es la velocidad por lo tanto
$v(t) =- x_{0} w sin(wt) + v_{0} cos(w t) $
b) la solución general de un movimiento armónico simple es:
$x(t) = A cos (wt+ \phi)$
la expresión para la velocidad es
$ v(t) = -A w sin(wt+ \phi)$
la expresión para la aceleración es
$a(t) = -A w^{2} cos (wt+ \phi)$
evaluando en $t=0$
$v_{0} = - A w sin(\phi)$
$x_{0} = A cos(\phi)$
$a_{0} = - w^{2} x_{0}$
con lo anterior se llega a que
$x_{0}^{2} + \frac{v_{0}^{2}}{w^{2}} = A^{2} (cos^{2}(\phi)+sin^{2}(\phi))$
recordemos que $ cos^{2}(\phi)+sin^{2}(\phi)=1 $, reescribiendo
$w^{2} x_{0}^{2} +v_{0}^{2} = A^{2} w^{2}$
de $a_{0} = - w^{2} x_{0}$ se despeja $x_{0}$
$x_{0}=-\frac{a_{0}}{w^{2}}$
sustituyendo lo anterior en $w^{2} x_{0}^{2} +v_{0}^{2} = A^{2} w^{2}$, se llega finalmente a que:
$A^{2}w^{2} = v_{0}^{2}-a_{0}x_{0}$
Monicacruz (discusión) 14:31 18 jun 2020 (CDT) Monica Cruz
Problema propuesto 2
Muestre que la tasa de cambio en el tiempo de la energía mecánica correspondiente a un oscilador amortiguado sin accionamiento esta dada por $\frac{dE}{dt}=-bv^{2}$ y en consecuencia siempre es negativa.
solución :
obteniendo la diferencial de la energía mecánica $E=\frac{1}{2} m v^{2} + \frac{1}{2} k x^{2}$
$\frac{dE}{dt}= \frac{d}{dt}(\frac{1}{2} m v^{2} + \frac{1}{2} k x^{2})$
se obtiene $\frac{dE}{dt}=m v \frac{dv}{dt} + k x \frac{dx}{dt} $
$\frac{dE}{dt}=(m \frac{d^{2}x}{dt^{2}} + k x ) v $
se reescribe la expresión anterior
$\frac{1}{v}\frac{dE}{dt} - k x =m \frac{d^{2}x}{dt^{2}} $
La ecuación de movimiento amortiguado:
$ - k x - b \frac{dx}{dt}=m \frac{d^{2}x}{dt^{2}}$
igualando las dos ultimas expresiones se llega a:
$ \frac{1}{v}\frac{dE}{dt} - k x = - k x - b \frac{dx}{dt} $
$\frac{1}{v}\frac{dE}{dt} =- b \frac{dx}{dt} $
finalmente se llega a que la derivada temporal de la energía mecánica de un oscilador amortiguado es siempre negativa ya que aunque la velocidad sea negativa su cuadrado siempre es positivo y $b$ es una constante positiva.
$\frac{dE}{dt}=-bv^{2}$
Monicacruz (discusión) 00:06 19 jun 2020 (CDT)
Problema propuesto 3
Se observa que para un dispositivo mecánico al cuál después de experimentar un impulso inesperado regresa al desplazamiento cero "posición de equilibrio" en un tiempo mínimo.suponga que el sistema tiene desplazamiento cero en $t=0$
a) encontrar la ecuación $x(t)$ y $v(t)$
b) el máximo desplazamiento antes de regresar al reposo. y el tiempo en que alcanza este máximo
c)dibuje la grafica $x$ contra $t$ y use los valores en a) y b)
solución:
a) la soluciones generales para un movimiento amortiguado son
$x_{1}(t)=B \rm e^{-\beta t} cos(\omega t + \phi)$
$x_{2}(t)=A \rm e^{-\beta t} sen(\omega t + \phi)$
evaluando en la condición inicial en ambas posibles soluciones para este problema en especifico, con $\phi=0$
$x_{1}(0)= B$
$x_{2}(0)= 0$
de esta manera se a que la solución adecuada es $ x_{2}$ llamaremos a la solución solo x(t)
$x(t)=A \rm e^{-\beta t} sen(\omega t )$
derivamos para obtener la expresión de la velocidad
$v(t)= A \omega \rm e^{-\beta t} cos(\omega t ) - A \beta \rm e^{-\beta t} sen(\omega t) $
b) el desplazamiento máximo se tiene cuando la función $\sin(\omega t)=1 $ tomando el primer valor donde la función seno es uno se obtiene lo siguiente
$\omega t = \frac{\pi}{2}$
el tiempo en el cual alcanza el desplazamiento máximo es
$t=\frac{\pi}{2 \omega }$
el desplazamiento máximo es
$x_{max}(t=\frac{\pi}{2 \omega})= A \rm e^{\frac{-\beta \pi}{2 \omega}}$
c) Grafica de la posición vs timepo con $A=6$, $\beta=\frac{1}{2}$ y $\omega =3$
Monicacruz (discusión) 10:09 19 jun 2020 (CDT)
Juan Daniel Rivera Bautista (discusión) 19:32 22 jun 2020 (CDT) ajusté el tamaño de la figura para que no se saliera del márgen
Problema propuesto 4
El sistema mostrado en la figura, consiste en un tubo doblado en forma de "U" cuya sección trasversal tiene área $A$. Este tubo contiene una columna de liquido de longitud $L$ y densidad $\rho$ y se pone en movimiento, encuentre:
a) la ecuacion de movimiento para el tuvo contenido en el liquido
b)la frecuencia
la energía potencial esta dada por $U=mgy$
recordando la definición de densidad
$\rho=\frac{m}{V}$, el volumen es $V= A y $ (se esta considerando solo el volumen que sube o baja, según el sistema de referencia elegido)
una vez definido a la energía potencial en términos de los datos conocidos, se puede escribir:
$U= A \rho g y^{2}$
la energia cinetica en terminos de las cantidades conocidas es: ($m= A \rho L$)
$K=\frac{1}{2} \rho A L (v_{y})^{2}$ o bien $K=\frac{1}{2} \rho A L (\frac{d y}{dt})^{2}$
La energía total del sistema es:
$E=\frac{1}{2} \rho A L (\frac{d y}{dt})^{2} + A \rho g y^{2}$
la energía del sistema es una constante por lo tanto al derivar con respecto al tiempo, se tiene lo siguiente
$\frac{dE}{dt}=\frac{d}{dt}(\frac{1}{2} \rho A L (\frac{d y}{dt})^{2} + A \rho g y^{2}) = 0$
$\frac{dE}{dt}=\rho A L(\frac{dy}{dt})(\frac{d^{2}y}{dt^{2}})+ 2 A \rho g y (\frac{dy}{dt})=0$
$\frac{dy}{dt}(\rho A L(\frac{d^{2}y}{dt^{2}})+ 2 A \rho g y )=0$
$\rho A L(\frac{d^{2}y}{dt^{2}})+ 2 A \rho g y =0$
finalmente se obtiene la ecuación de movimiento armónico simple
$\frac{d^{2}y}{dt^{2}}+\frac{2g}{L} y =0$
De la ecuacion de movimiento se puede ver que
$\omega^{2} = \frac{2 g}{L}$
la frecuencia esta dada por
$f=\frac{\omega}{2 \Pi}$
o bien
$f= \sqrt{\frac{2g}{L}} \frac{1}{2\Pi}$
Monicacruz (discusión) 14:13 27 jun 2020 (CDT)
Problema 4.7
Cuando las masas de los péndulos acoplados de la figura 4.1 ya no son iguales, la ecuación de movimiento se convierte en:
Error al representar (error de sintaxis): {\displaystyle m_1 \ddot{x} = - m_1 \left ( \frac{g}{l} \right ) x - s (x – y ) ... (1)}
Error al representar (error de sintaxis): {\displaystyle m_2 \ddot{y} = - m_2 \left ( \frac{g}{l} \right ) y + s (x – y ) ...(2)}
Mostrar que podemos elegir las coordenadas normales:
Con una frecuencia de modo normal $ \omega_{1}^{2} = \frac{ g }{ l } $ y $ Y = ( x – y )$ , con una frecuencia de modo normal $ \omega_{2}^{2} = \frac{ g }{ l } + s \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) $. Tenga en cuenta que $X$ es la coordenada del centro de masa del sistema, mientras que la masa efectiva en el modo $Y$ es la masa reducida $mu$ del sistema donde $\frac{ 1 }{ \mu\ } = \frac{1}{m_1} + \frac{1}{m_2}$. Solución:
Si sumamos las ecuaciones (1) y (2):
Error al representar (error de sintaxis): {\displaystyle m_1 \ddot{x} + m_2 \ddot{y} = - \left ( \frac{g}{l} \right ) (m_1 x + m_2 y) …………….(3)}
Como el problema nos da las coordenadas normales:
Entonces:
Hacemos un despeje para sustituir en (3):
Sustituyendo en (3) obtenemos:
Multiplicamos por $ \frac {1}{m_1 + m_2}$
Y podemos ver que en ésta ecuación la frecuencia de modo normal es $\omega_{1}^{2} = \frac{ g }{ l } $
Para comprobar la segunda parte , tomamos nuevamente (1) y (2), y despejamos $\ddot{x}$ y $\ddot{y}$
Error al representar (error de sintaxis): {\displaystyle \ddot{x} = - \left ( \frac{g}{l} \right ) x - \frac{s}{m_1} (x – y ) }
Error al representar (error de sintaxis): {\displaystyle \ddot{y} = - \left ( \frac{g}{l} \right ) y + \frac{s}{m_2} (x – y ) }
Y hacemos la resta $\ddot{x} - \ddot{y}$
\begin{matrix}\ddot{x} - \ddot{y} & = & - \frac{ g }{ l } x - \frac{ s }{ m_1 } ( x – y ) + \frac{ g }{ l } y - \frac{ s }{ m_2 } ( x – y ) \\ \ & = & -\frac{ g }{ l } ( x – y ) - 2 s ( x – y ) \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) \\ \ & = & ( x – y ) \left \lbrack - \frac{g}{l} – 2 s \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) \right \rbrack \end{matrix}
Tomamos la coordenada normal $Y = x – y $ , vemos que $\ddot{Y}=\ddot{x}- \ddot{y}$, y hacemos una sustitución en $\ddot{x}- \ddot{y}$
Error al representar (error de sintaxis): {\displaystyle \ddot{Y} = \left \lbrack - \frac{g}{l} – s \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) \right \rbrack Y }
De la última ecuación, podemos ver que la frecuencia de modo normal es $ \omega_{2}^{2} = \frac{ g }{ l } + s \left ( \frac{1}{m_1} + \frac{1}{m_2} \right ) $.
En cada caso la variable elegida es una sola frecuencia de vibración, coordenadas normales, y corresponden cada uno a sus respectivos modos normales de vibración.
Nota: Ejercicio 4.7 es del libro H. J. Pain. The Physics of Vibrations and Waves. Wiley, 2005.
Nayomi (discusión) 22:27 18 jun 2020 (CDT) Nayomi Russell
Problema 4.8
Deje que el sistema del problema 4.7 se ponga en movimiento con las condiciones iniciales $x = A$, $y = 0$, $\dot{x}=\dot{y}= 0$ en $t=0$. Muestra que las amplitudes del modo normal son $X_0=\left ( \frac{m_1}{M} \right)A$ y $Y_0=A$, para hacer:
Y $y = \frac{m_1}{M} A ( cos \omega_1 t - cos \omega_2 t)$
Donde $M=m_1 + m_2$. Exprese estos desplazamientos como:
Error al representar (error de sintaxis): {\displaystyle x =2 A cos \omega_m t cos \omega_a t + \frac{2A}{M}(m_1 – m_2 ) sen \omega_m t sen \omega_a t }
Y $y =2 A \frac{m_1}{M} sen \omega_m t sen \omega_a t $
Dónde $\omega_m = (\omega_1 - \omega_2)/2$ y $ omega_a = (\omega_1 + \omega_2)/2$
Solución:
Para las ecuaciones de movimiento en la coordenada normal tenemos que:
Podemos decir que:
Sustituimos las condiciones iniciales: $t=0$, $x=A$, y $y=0$ en las ecuaciones, y obtenemos que:
Dónde $M=m_1 + m_2$, por lo que las soluciones a las ecuaciones de movimiento en las coordenadas x y y son:
Y $ y = \frac{m_1}{M} A ( cos \omega_1 t - cos \omega_2 t) $
Aquí $\omega_1=\omega_a-\omega_m$ y $\omega_2=\omega_a+\omega_m$ Recordamos que $\omega_m = (\omega_1 - \omega_2)/2$ y $ omega_a = (\omega_1 + \omega_2)/2$. Y sustituimos $\omega_1$ y $\omega_2$ en las soluciones de las ecuaciones de movimiento.
\begin{matrix}x & = & \frac{ A }{ M } [m_1 cos (\omega_a - \omega_m)t + m_2 cos (\omega_a + \omega_m)t] \\ \ & = & \frac{ A }{ M} [m_1 (cos \omega_m t cos \omega_a t + sen\omega_a t \omega_m t) + m_2 (cos \omega_m t cos \omega_a t - sen\omega_a t \omega_m t)] \\ \ & = & \frac{ A }{ M } [(m_1 + m_2) cos \omega_m t cos\omega_a t + (m_1 - m_2)sen\omega_m t sen \omega_a t ]\end{matrix}
Simplificando:
Error al representar (error de sintaxis): {\displaystyle x =A cos \omega_m t cos \omega_a t + \frac{A}{M} (m_1 – m_2) sen \omega_m t sen \omega_a t }
Y
\begin{matrix}y & = & A\frac{ m_1 }{ M } [ cos (\omega_a - \omega_m)t - cos (\omega_a + \omega_m)t] \\ \ & = & 2A\frac{ m_1 }{ M} sen \omega_m t sen \omega_a t \end{matrix}
Nota: Ejercicio 4.8 es del libro H. J. Pain. The Physics of Vibrations and Waves. Wiley, 2005.
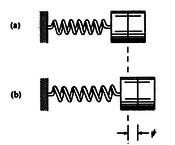
























![A=[A_{1}^{2}+(\frac{v_{1}}{\omega_{0}})^{2}]^{\frac{1}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/37820c4bdecde528e9bc197adbda815fd72ec562)