Vibra: oscilador forzado
=Solución del oscilador forzado no amortiguado y con fuerza motriz senoidal y amortiguado con fuerza motriz de un pulso ==
===== Caso de frecuencias diferentes=====
A continuación, en esta sección,se resuelve el oscilador forzado sin amortiguación sometido a una fuerza motriz senoidal. la ecuación es: \begin{equation} y^{"}+\omega_{0}y=F_{0}\sin (\omega t) \end{equation} y las condiciones iniciales son: $y(0)=0$ y $y^{'}(0)=0$. en la primera parte se resuelve para cuando las frecuencias de oscilación de la fuerza motriz y del oscilador no son iguales, para ello se emplea el método de la transformada de Laplace.
Aplicando la transformada de laplace a ambos lados de (1):
\begin{equation} s^2Y(s)-sy(0)-y^{'}(0)+\omega_{0}Y(s)=F_{0}\frac{\omega}{s^2+\omega^2} \end{equation}
sustituyendo condiciones iniciales , simplificando y despejando $Y(s)$ \begin{equation} Y(s)=\frac{F_{0}}{(s^2+\omega_{0}^{2})}\frac{\omega}{(\omega^{2}+s^{2})} \end{equation} y aplicando el método de fracciones parciales a la ecuación (2) \begin{equation} \frac{F_{0}}{(s^2+\omega_{0}^{2})}\frac{\omega}{(\omega^{2}+s^{2})}=\frac{As+B}{s^{2}+\omega^{2}}+\frac{Cs+D}{s^{2}+\omega_{0}^{2}} \end{equation} continuando con el desarrollo del método de fracciones parciales: \begin{equation} (As+B)(s^{2}+\omega_{0}^{2})+(Cs+D)(s^{2}+\omega_{0}^{2})=F_{0}\omega \end{equation} se rescribe asi: \begin{equation} s^3(A+C)+s^2(B+D)+s(A\omega_{0}^{2}+C\omega^{2})+B\omega_{0}^{2}+D\omega^{2}=F_{0}\omega \end{equation} Resulta el siguiente sistema de ecuaciones simultaneas: \begin{equation} A+C=0 \end{equation} \begin{equation} B+D=0 \end{equation} \begin{equation} A\omega_{0}^{2}+C\omega^{2}=0 \end{equation} \begin{equation} B\omega_{0}^{2}+D\omega^{2}=0 \end{equation} resolviendo simultáneamente para A,B,C,D: $A=0$,$B=-\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}$,$C=0$ y $D=\frac{F_{0}\omega}{{\omega^{2}-\omega_{0}^{2}}}$. Sustituyendo A,B,C,D en (4) y luego en (3): \begin{equation} Y(s)=-\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}\frac{1}{s^{2}+\omega^{2}}+\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}(\frac{\omega_{0}}{\omega_{0}})\frac{1}{s^{2}+\omega_{o}^{2}} \end{equation} Aplicando ahora la transformada inversa de Laplace: $y(t)=\mathcal{L}^{-1}{Y(s)}$, entonces se obtiene: \begin{equation} y(t)==-\frac{F_{0}\omega}{\omega^{2}-\omega_{0}^{2}}\sin \omega t+\frac{F_{0}\omega}{(\omega^{2}-\omega_{0}^{2})\omega_{0}}\sin \omega_{0} t \end{equation} se puede rescribir asi: \begin{equation} y(t)=\frac{\omega F_{0}}{\omega^{2}-\omega_{0}^{2}} (\frac{\sin \omega_{0} t }{\omega_{0}}-\frac{\sin \omega t }{\omega}) \end{equation} esto fue para el caso de frecuencias ddel oscilador y de la fuerza externa diferentes.
===== caso de frecuencias casi iguales o iguales =====
Partiendo de la ec (3) pero haciendo $\omega=\omega_{0}$: \begin{equation} Y(s)=\frac{\omega_{0} F_{0}} {(s^{2}+\omega_{0}^{2})(s^{2}+\omega_{0}^{2})} \end{equation} por fracciones parciales: \begin{equation} \frac{\omega_{0} F_{0}} {(s^{2}+\omega_{0}^{2})(s^{2}+\omega_{0}^{2})}=\frac{As+B}{s^{2}+\omega_{0}^{2}}+\frac{Cs+D}{(s^{2}+\omega_{0}^{2})^{2}} \end{equation} se puede rescribir asi: \begin{equation} (As+B)(s^{2}+\omega_{0}^{2})+{(Cs+D)}=F_{0} \omega_{0} \end{equation} Efectuando operaciones,desarrollando y factorizando términos: \begin{equation} s^{3}A+s^{2}B+s(A\omega_{0}^{2}+C)+(B \omega_{0}^{2}+D)=\omega_{0} F_{0} \end{equation} Despejando las incógnitas A,B,C,D: $A=B=C=0$, $D=F_{0 } \omega_{0}$ por lo tanto: \begin{equation} Y(s)=\frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})^{2}} \end{equation} pero rescribiendo: \begin{equation} \frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})^{2}}=\frac{F_{0}\omega_{0}}{(s^{2}+\omega_{0}^{2})} \frac{\omega_{0}}{\omega_{0}(s^{2}+\omega_{0}^{2})} \end{equation} Aplicando ahora la transformada inversa de Laplace: , entonces se obtiene: \begin{equation} Y(s)=\frac{F_{0}}{\omega_{0}}\sin (\omega_{0} t) \sin (\omega_{0} t ) \end{equation} Aplicando el teorema de la convolución: \begin{equation} \frac{F_{0}}{\omega_{0}}\int_0^t \sin \omega\tau\sin(t-\tau)d\tau=\frac{F_{0}}{2\omega_{0}}(\sin \omega_{0}t-\omega_{0} t \cos \omega_{0} t) \end{equation}
o sea: \begin{equation} y(t)=\frac{F_{0}}{2\omega_{0}}(\sin \omega_{0}t-\omega_{0} t \cos \omega_{0} t) \end{equation}
===== Oscilador amortiguado forzado con fuerza motriz puntual =====
A continuación se resuelve el caso de un Oscilador Amortiguado sometido a una fuerza de un pulso empleando la transformada de Laplace, para ello se hace uso del delta de dirac para modelar la fuerza de un pulso en este caso unitario, posteriormente en el desarrollo del método de Laplace se hace uso del teorema de traslación para pasar del dominio de la frecuencia al dominio del tiempo. La ecuación general del oscilador amortiguado sometido a la fuerza de un pulso (golpe) unitario es: \begin{equation} y"(t)+by'(t)+\omega_{0}^{2}y(t)=\delta(t-a) \end{equation} con las siguientes condiciones iniciales: $y'(0)=0$, es decir con velocidad inicial cero, y $y(0)=0$, o sea parte de la posición de equilibrio. Aplicando la transformada de Laplace para la primera y segunda derivada que dice: \begin{equation} \mathcal{L}(y"(t))=s^{2}Y(s)-sy(0)-y'(0) \end{equation} y \begin{equation} \mathcal{L}(y'(t))=Y(s)-y(0) \end{equation} y aplicando la transformada de laplace al delta de dirac: \begin{equation} \mathcal{L}(\delta(t-a)=e^{-sa} \end{equation} Aplicando (24) y (25) y (26) a (23) simplificando y reescribiendo: \begin{equation} Y(s)=\frac{e^{-sa}}{(s^2+bs+\omega_{0}^{2})} \end{equation} Acompletando el binomio cuadrado en el denominador y rescribiendo: \begin{equation} Y(s)=\frac{e^{-sa}}{(s+b/2)^{2}+(\sqrt{\omega_{0}^{2}-b^{2}/4})^{2}} \end{equation} Por inspección y aplicando el teorema de la traslación de Laplace a (28): \begin{equation} y(t)=H(t-a)\frac{\sin{((\sqrt{\omega_{0}^{2}-b^2/4})(t-a))} }{\sqrt{\omega_{0}^{2}-b^2/4}}e^{-b(t-a)/2} \end{equation} donde $H(t-a)$ es la función de Heaviside.
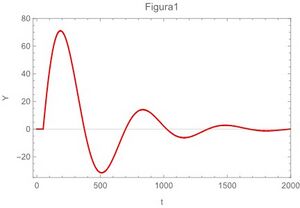
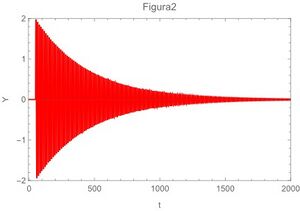
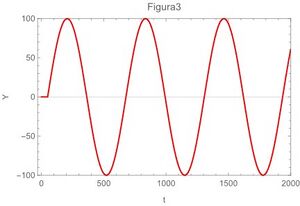
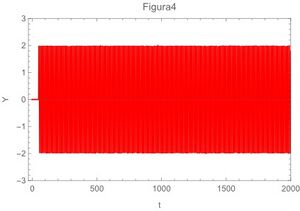
En términos físicos,la letra $a$ se refiere a el momento en que se propina el golpe o pulso, a partir de este momento se inicia la perturbación y dado que es un movimiento amortiguado con frecuencia propia de oscilación en algún momento se detendrá el movimiento después de varias oscilaciones.
La letra $b$ se refiere a el coeficiente de fricción en el que está inmerso el oscilador, cuando este numero es cero se trata de un oscilador que oscila libremente por tiempo indefinido.
La letra $\omega_{0}$ se refiere a la frecuencia angular natural propia del oscilador y que en el caso de un resorte oscilador depende del cociente de su constante de rigidez entre su masa.
A continuación las gráficas de la ecuación (29) para los 4 casos extremos
.
. Bibliografía:
- Ecuaciones Diferenciales con problemas con valores en la frontera, Dennis G. Zill,Warren S. Wright, 8ava. edición, CENGAGE Learning,2015
- Vibrations and Waves in Physics,Ian G. Main, 3rd Edition,Cambridge University Press,1993.
- software Graficación: MATHEMATICA, Wolfram