Diferencia entre revisiones de «Transformación Bilineal»
| Línea 56: | Línea 56: | ||
Para facilitar tomamos el primer termino | Para facilitar tomamos el primer termino | ||
\[ | \[ | ||
w=\frac{1}{T}\log (z) | w=\frac{1}{T}\log (z)\approx \frac{2}{T}\left(\frac{z-1}{z+1}\right) | ||
\] | \] | ||
Que sera conocida como la '''Transformación Bilineal'''. | Que sera conocida como la '''Transformación Bilineal'''. | ||
Ahora veamos como se comporta ante el mapeo de circunferencias de diversos radios para verificar que realmente mapée el circulo unitario al semiplano izquierdo. | Ahora veamos como se comporta ante el mapeo de circunferencias de diversos radios para verificar que realmente mapée el circulo unitario al semiplano izquierdo. | ||
Sea: | |||
\[ | |||
z=R\,e^{i\theta}\;\;\;\;\;\;\;\;R \in \mathbb{R}^{+} \;\;\;\theta \in [-\pi,\pi) | |||
\] | |||
\[ | |||
w=\frac{2}{T}\left(\frac{z-1}{z+1}\right)=\frac{2}{T}\left(\frac{R\,e^{i\theta}-1}{R\,e^{i\theta}+1}\right)=\frac{2}{T}\left(1-\frac{2}{R\,e^{i\theta}+1}\right)=\frac{2}{T}\left(1-\frac{2}{R\,\cos(\theta)+1+i\,R\,\sin(\theta)}\frac{R\,\cos(\theta)+1-i\,R\,\sin(\theta)}{R\,\cos(\theta)+1-i\,R\,\sin(\theta)}\right) | |||
\] | |||
\[ | |||
w=\frac{2}{T}\left( 1-2 \frac{R\,\cos(\theta)+1-i\,R\,\sin(\theta)}{(R^\,\cos(\theta)+1)^2+(R\,\sin(\theta))^2} \right)=\frac{2}{T}\left( 1-2 \frac{R\,\cos(\theta)+1-i\,R\,\sin(\theta)}{R^2+2R\,\cos(\theta)+1} \right) | |||
\] | |||
Resulta complicado ver que forma tiene, pero dado que $R$ sera constante en cada evaluación y que solo nos interesa que para $R<1 0\leq Re(w)$, $R>1 Re(w)\leq 0$, tomamos: | |||
\[ | |||
Re(w)=\frac{2}{T}\left( 1-2 \frac{R\,\cos(\theta)+1}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{R^2+2R\,\cos(\theta)+1-2R\,\cos(\theta)-2}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{R^2+1-2}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{R^2-1}{R^2+2R\,\cos(\theta)+1} \right) | |||
\] | |||
Para $R=1$ | |||
\[ | |||
Re(w)=\frac{2}{T}\left( \frac{R^2-1}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{1-1}{1+2\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{0}{1+2\cos(\theta)+1} \right)=0 | |||
\] | |||
\[ | |||
Im(w)=\frac{2}{T}\left( \frac{2R\,\sin(\theta)}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{2\sin(\theta)}{1+2cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{\sin(\theta)}{cos(\theta)+1} \right) | |||
\] | |||
El numerador varia en signo y magnitud, el denominador varia de 0 a 2; es decir que el cociente uede ser positivo o negativo (por el signo del numerador), tan grande como se desee (por que tan cerca del 0 este el denominador) y tan pequeño como se desee (dependiendo de que tan cerca del 0 este el numerador). Para $R=1$ $w$ es el eje imaginario. | |||
Para $R<1$ | |||
\[ | |||
Re(w)=\frac{2}{T}\left( \frac{R^2-1}{R^2+2R\,\cos(\theta)+1} \right) | |||
\] | |||
El término $R^2<R<1$, por lo que el numerador siempre sera negativo. En el denominador si $R\to 0$ este tenderá a 1, y si $R\to 1$ este tenderá a $2(\cos (\theta)+1)$ que siempre es positivo, por lo que el denominador siempre sera positvo. | |||
Y por lo tanto $w$ permanecera en el semiplano izquierdo como buscamos. | |||
Para $R>1$ | |||
\[ | |||
Re(w)=\frac{2}{T}\left( \frac{R^2-1}{R^2+2R\,\cos(\theta)+1} \right) | |||
\] | |||
El término $R^2>R>1$, por lo que el numerador siempre sera positivo. En el denominador si $R\to 1$ este tenderá a $2(\cos (\theta)+1)$ que siempre es positivo, y si tiende a infinito: | |||
\[ | |||
\lim_{R\to\infty} Re(w)=\lim_{R\to\infty}\frac{2}{T}\left( \frac{1-\frac{1}{R^2}}{1+\frac{2}{R}\,\cos(\theta)+\frac{1}{R^2}} \right)=\frac{2}{T}\left( \frac{1+0}{1+0+0} \right)=\frac{2}{T} | |||
\] | |||
Que es positivo y por lo que el denominador siempre sera positvo. Y $w$ permanecera en el semiplano derecho como buscamos. | |||
--[[Usuario:Tlacaelel Cruz|Tlacaelel Cruz]] ([[Usuario discusión:Tlacaelel Cruz|discusión]]) 11:52 3 jul 2015 (CDT) | --[[Usuario:Tlacaelel Cruz|Tlacaelel Cruz]] ([[Usuario discusión:Tlacaelel Cruz|discusión]]) 11:52 3 jul 2015 (CDT) | ||
Revisión del 23:04 3 jul 2015
Transformación Bilineal
En Teoría de Control para analizar las propiedades de sistemas, se recurre a la transformada de Laplace, que permite (entre otras cosas) transformar sistemas de ecuaciones diferencial a sistemas de ecuaciones algebraicos; lo más habitual es relacionar cada sistema con una función de transferencia, que comúnmente (cuando el sistema es lineal) es un cociente de polinomios, para ser representada mediante bloques. Esta representación es ampliamente usada para diseñar sistemas de control como P, Pi, PID,PI-PD, etc. y funciona bastante bien cuando se trata de sistemas continuos. Para el tratamiento de sistemas discretos, se emplea la transformada Z, para llevar de una representación a otra basta con mapear $z=e^{sT}$, donde $T$ es el tiempo de muestreo. Dado el amplio desarrollo en el dominio de Laplace de estrategias de control (principalmente de estabilidad) resultaría deseable recuperar algunas de estas propiedades. Y aquí es donde surge la necesidad de esta transformación.
Información en una función de Transferencia
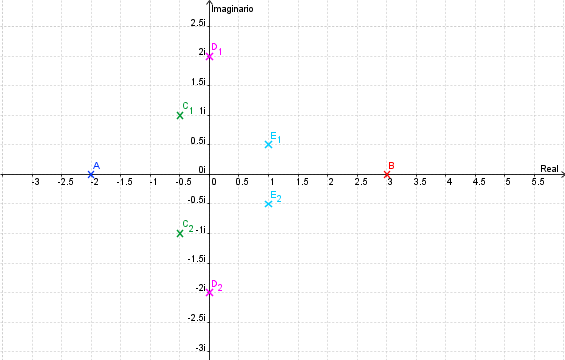
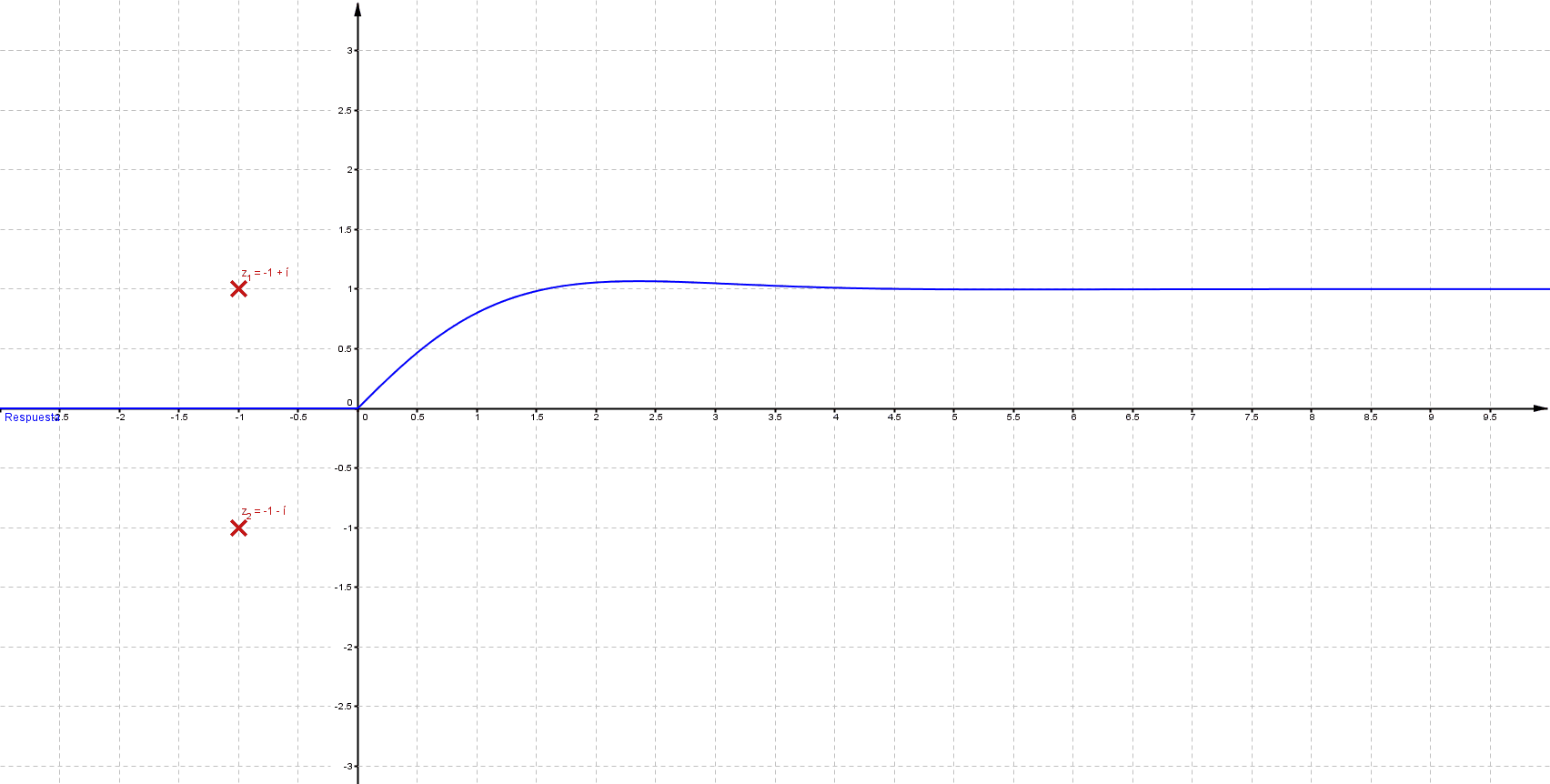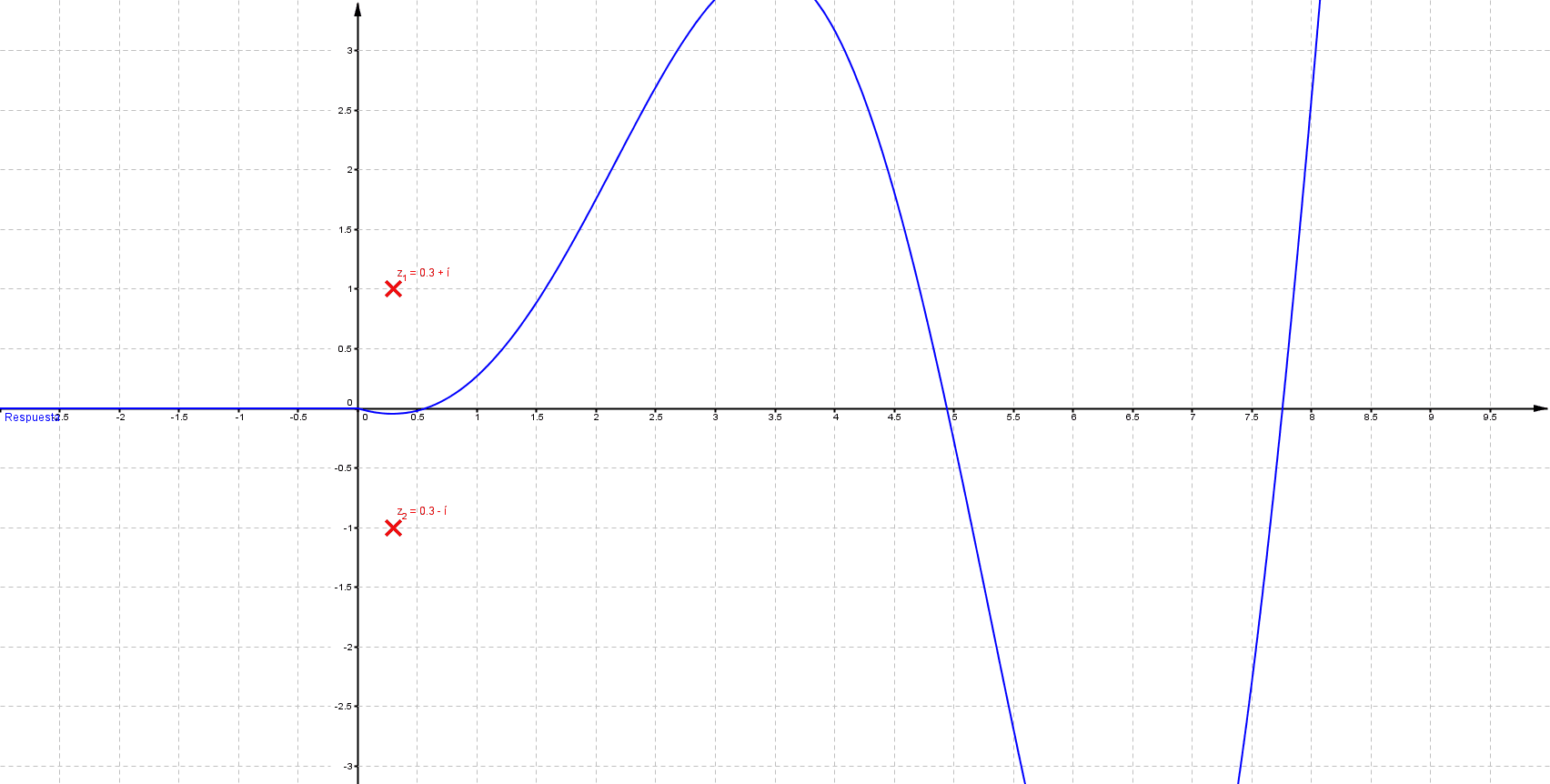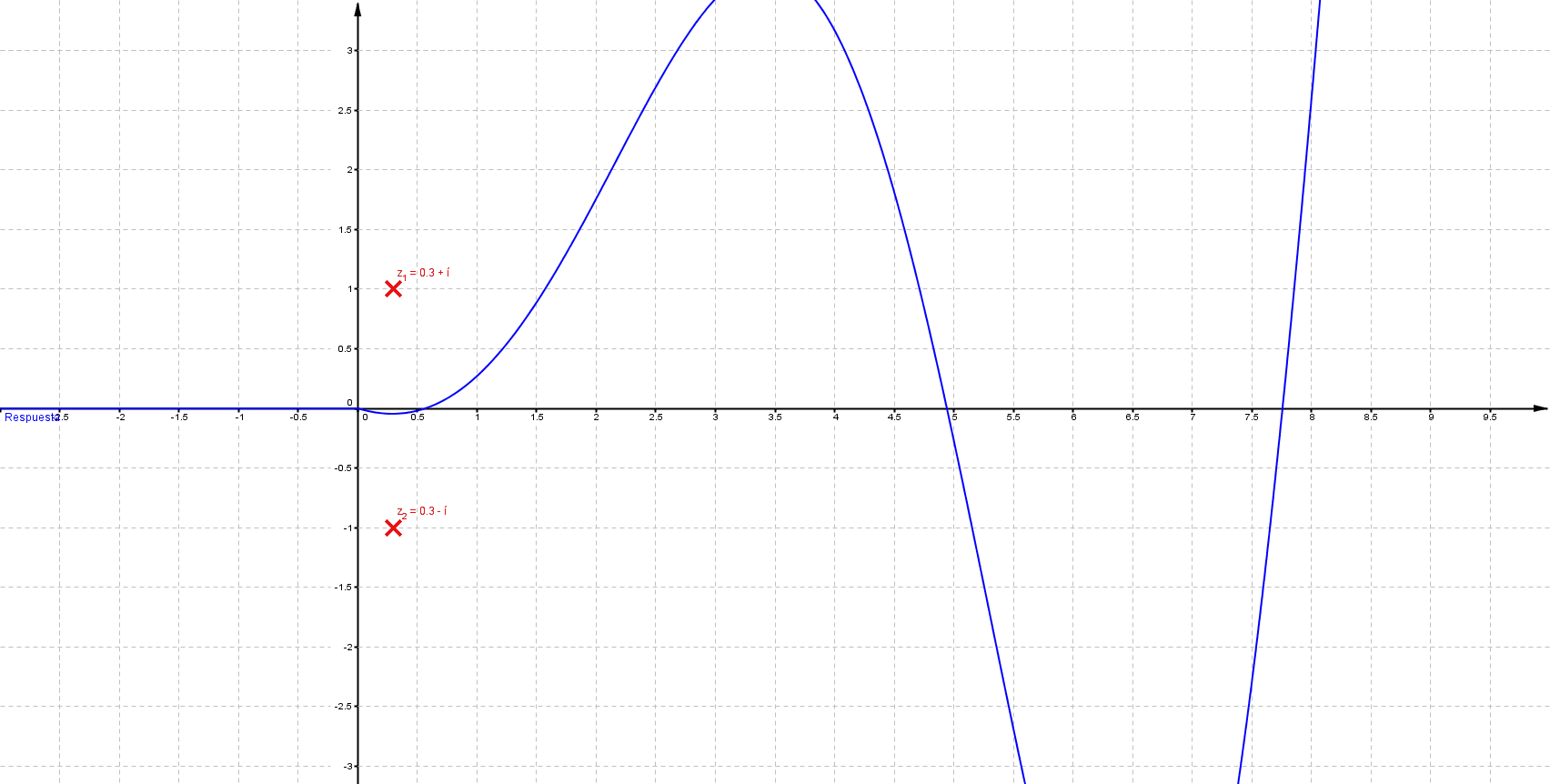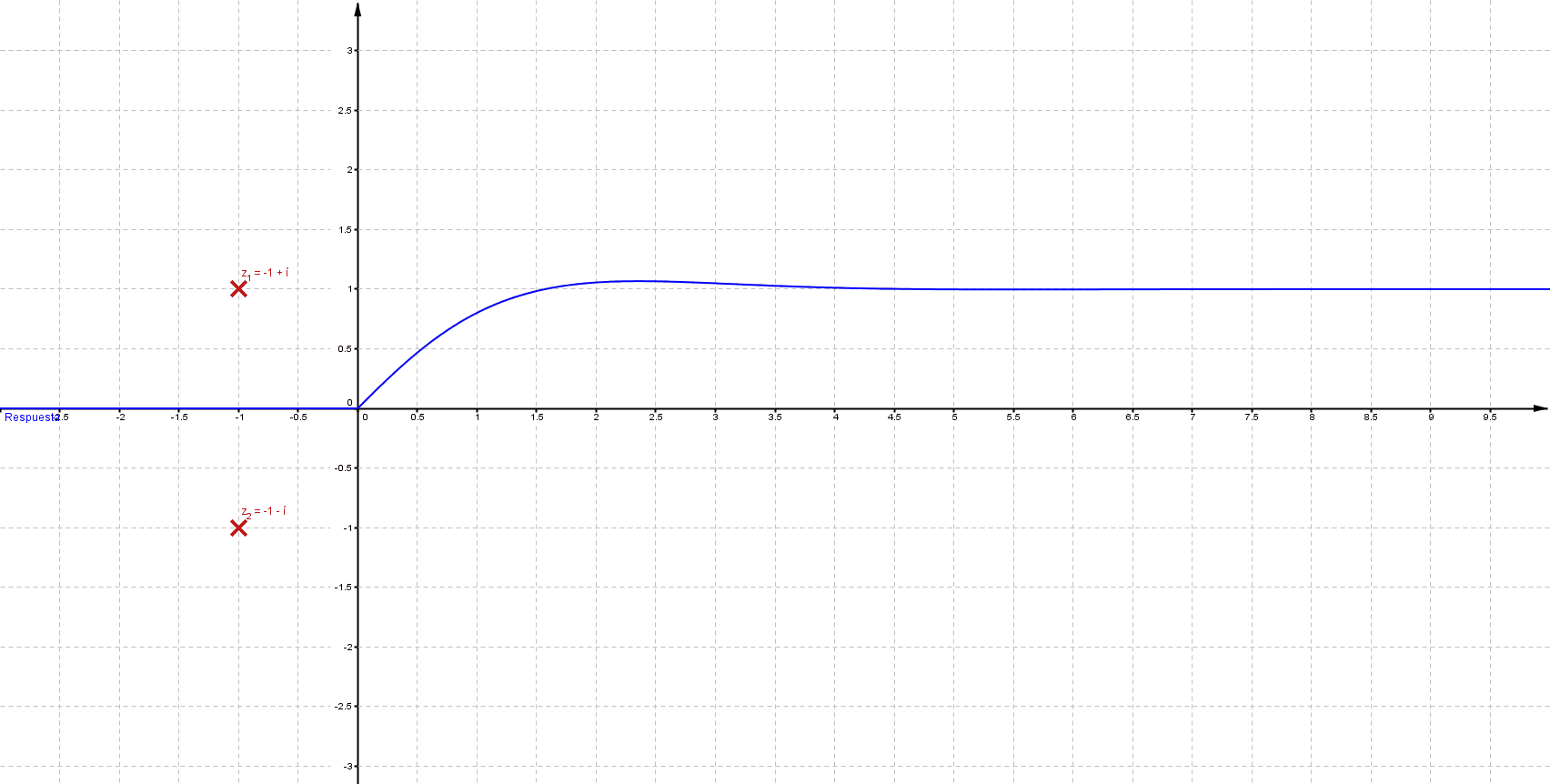
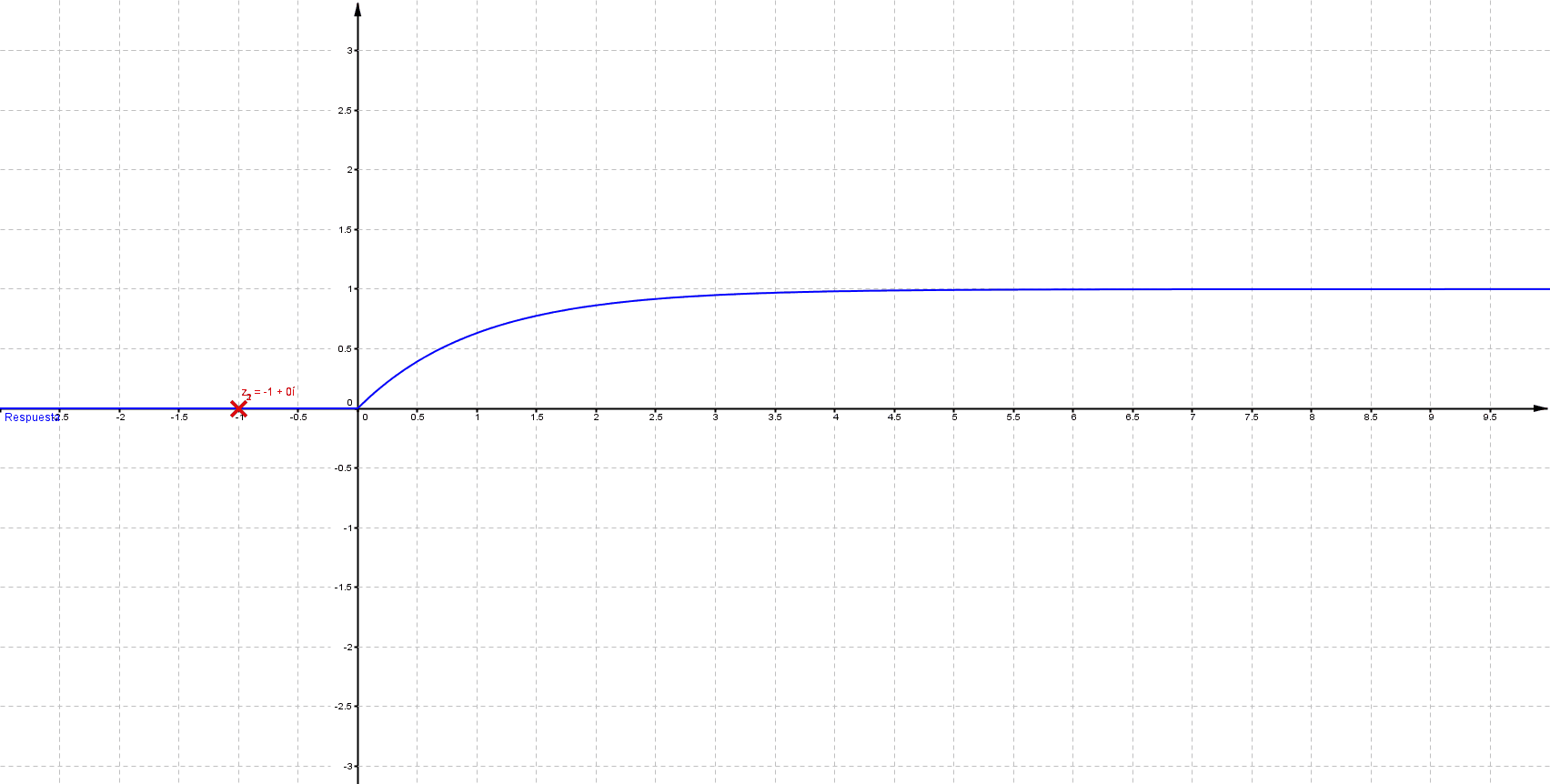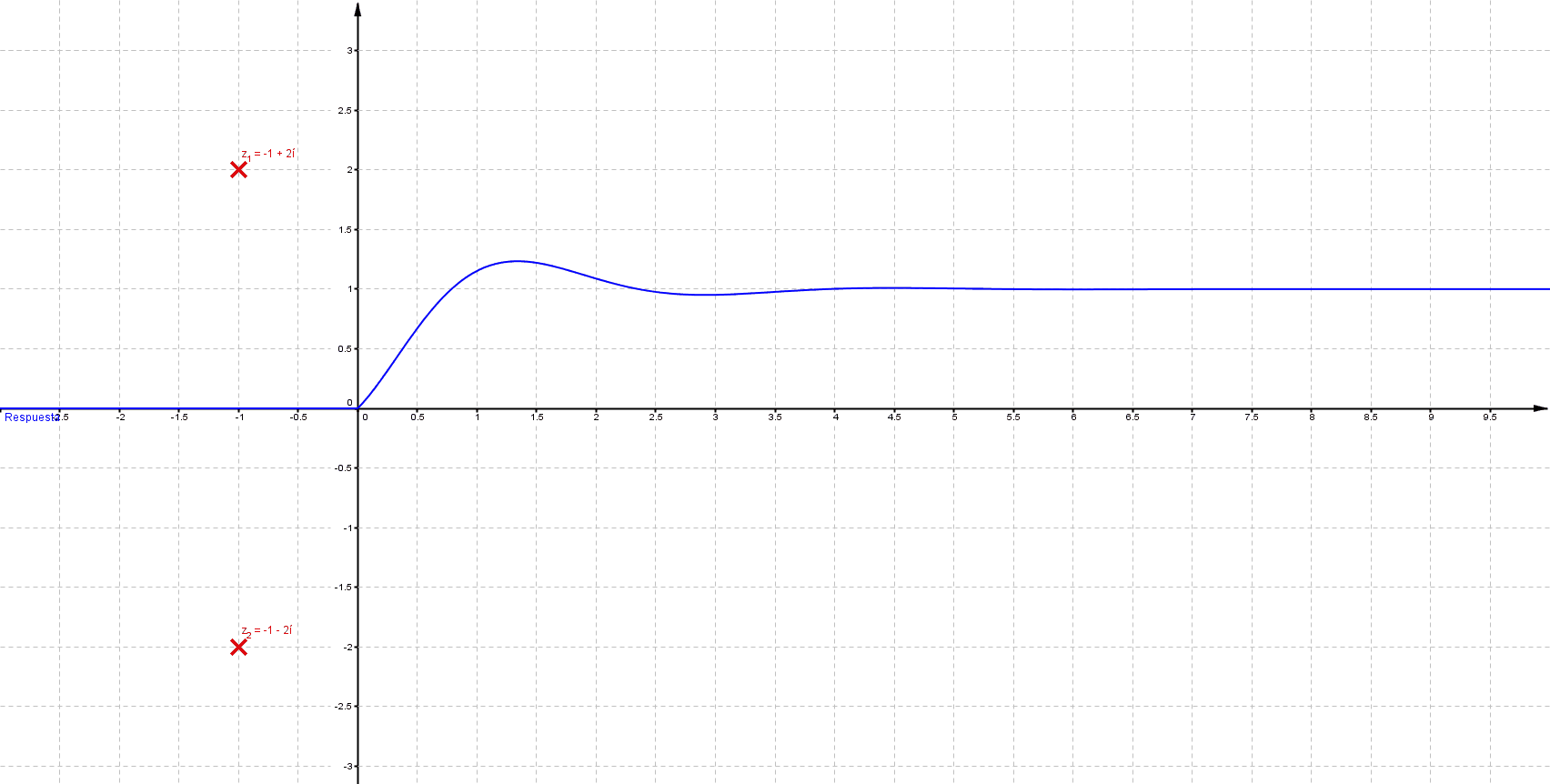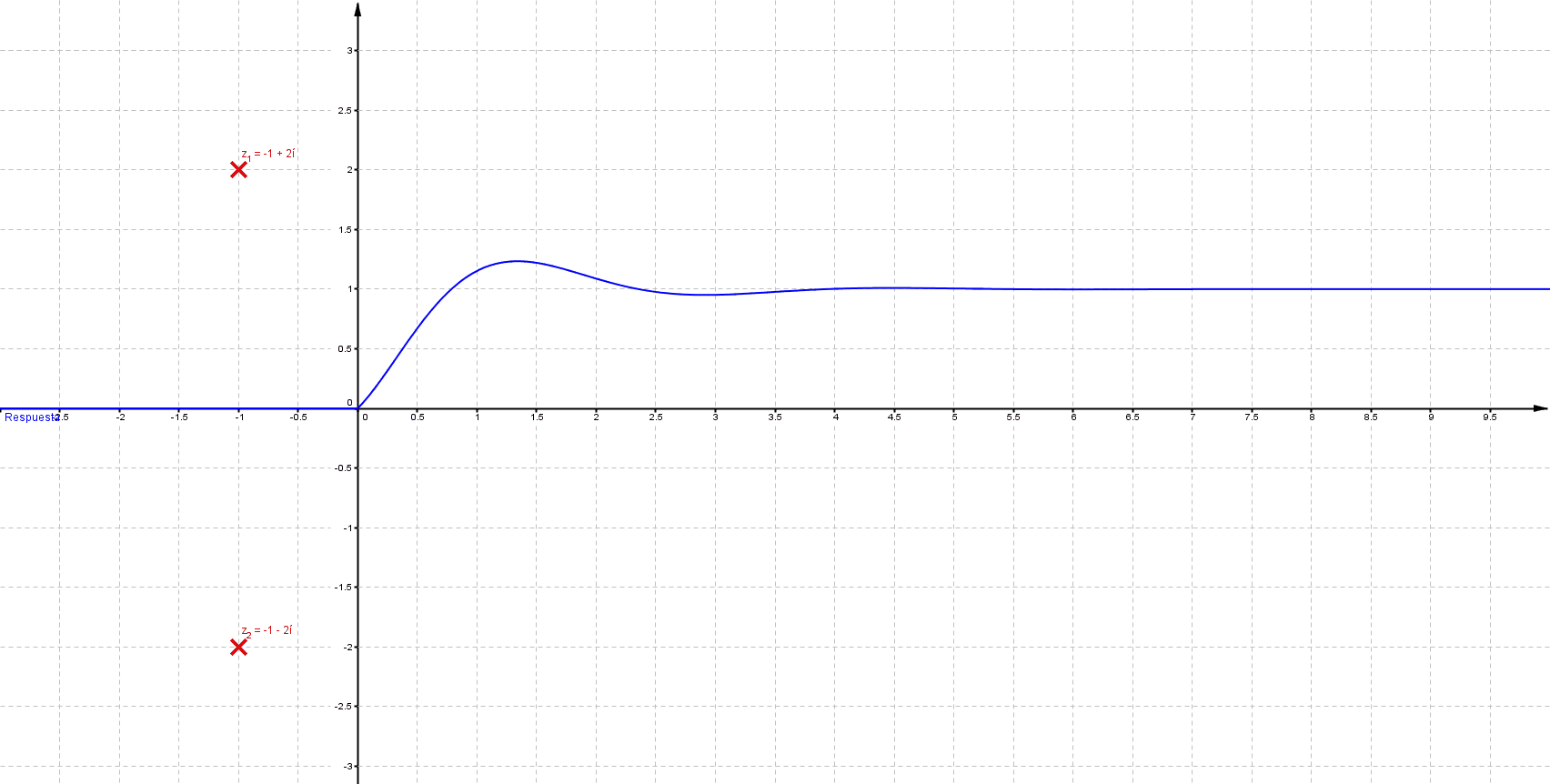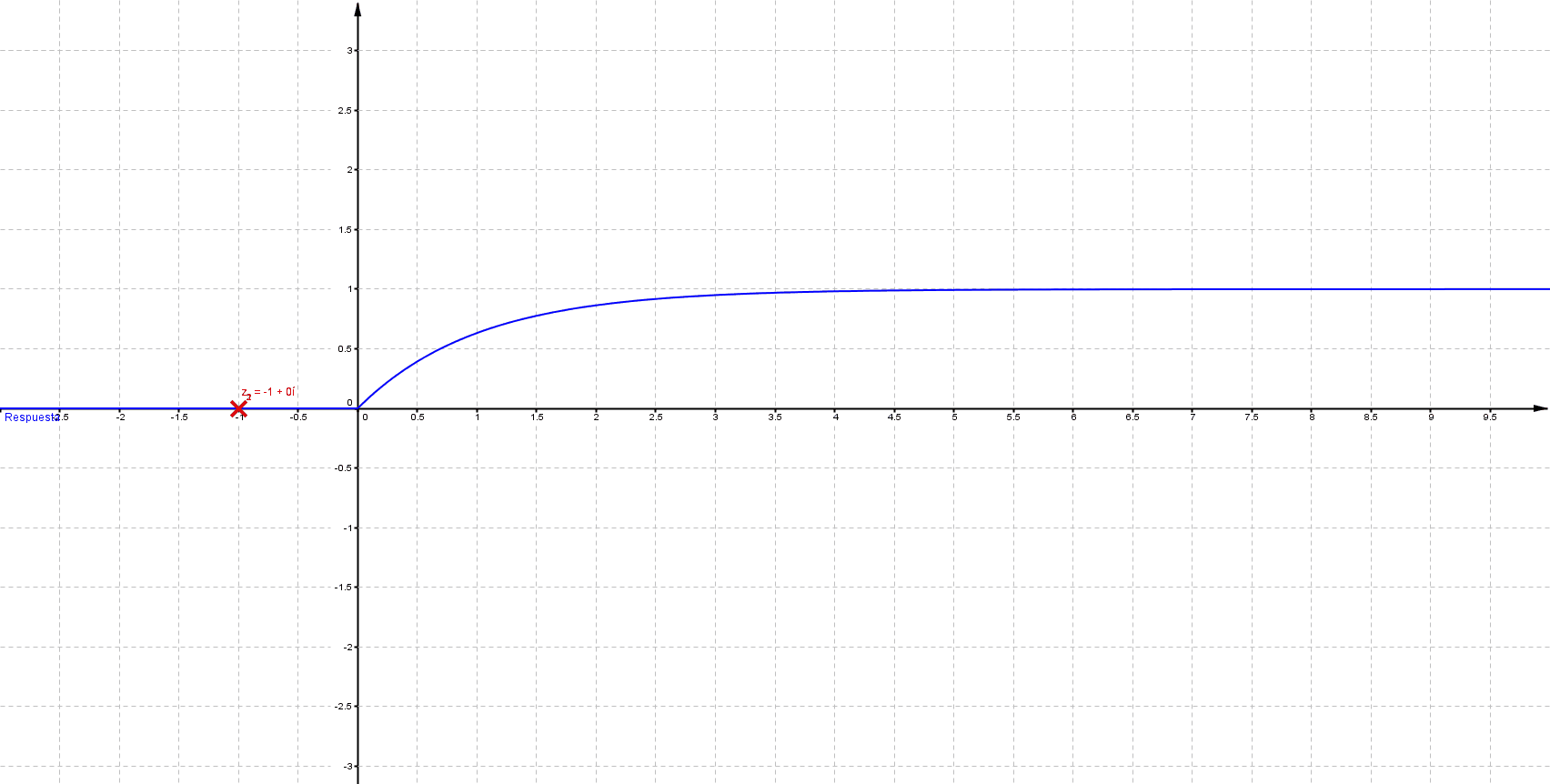
Primeramente me gustaría enunciar algunas propiedades que se presentan en un sistema LTI (lineal e invariante en el tiempo); estos sistemas se representan del siguiente modo: \[ F(s)=\frac{\sum_{k=0}^{m} {a_k \, s^k}}{\sum_{k=0}^{n} {a_k \, s^k}}\;\;\;\;\;\; \] Donde $n$, $m$ $\in \mathbb{N}$ tal que $m\leq n$ Las raíces del numerador son ceros y las del denominador polos; los polos determinan la estabilidad del sistema, a continuación se muestra comportamiento habitual para una entrada de tipo escalón
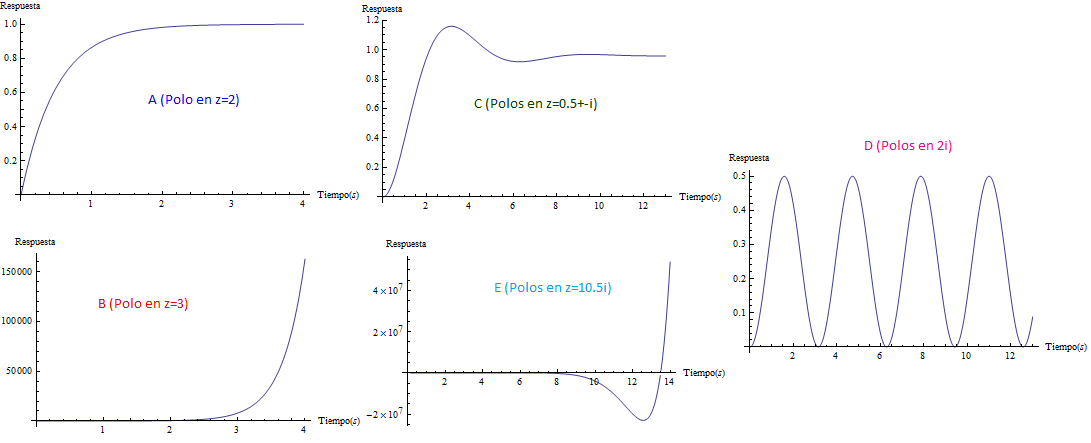
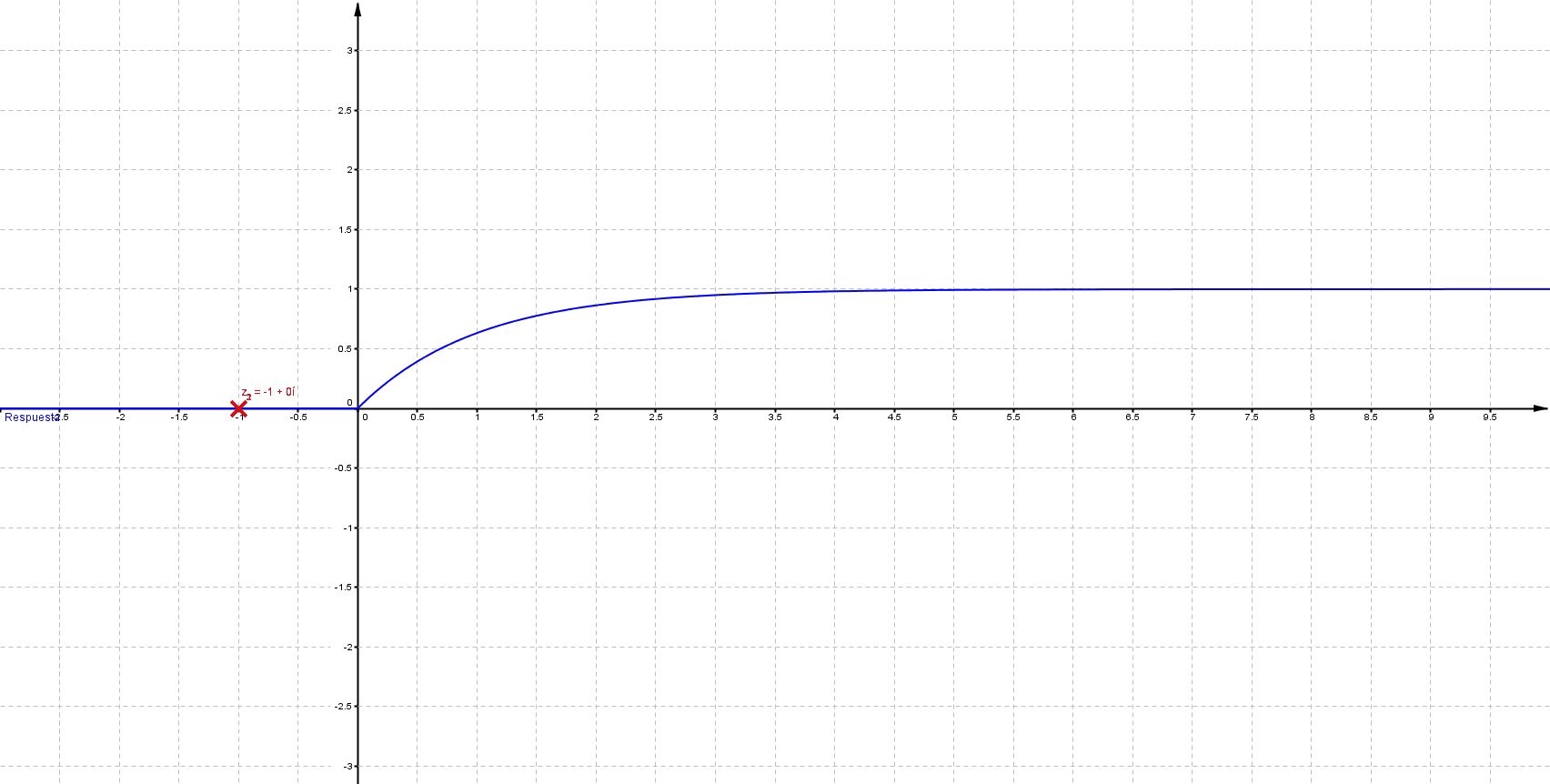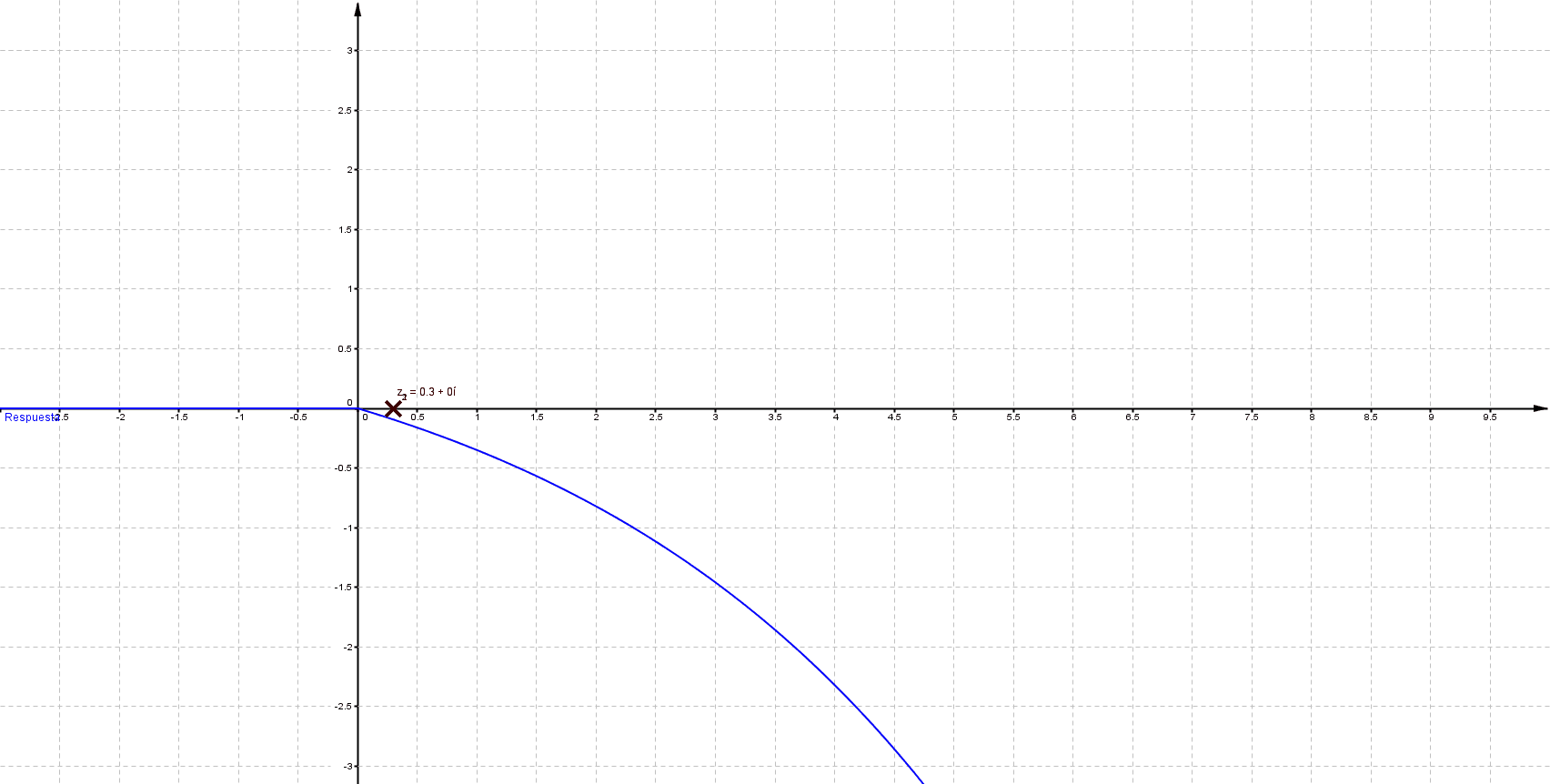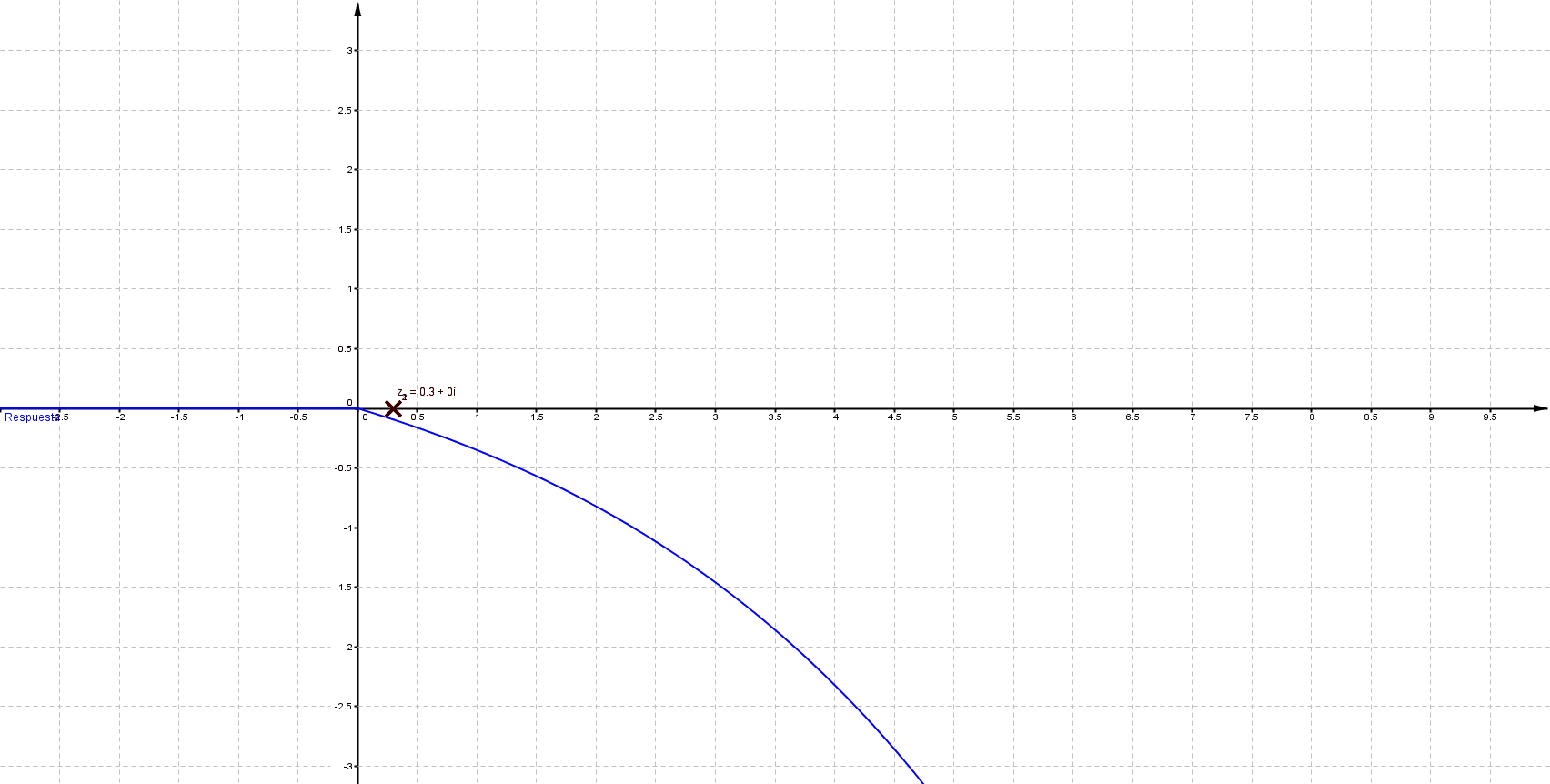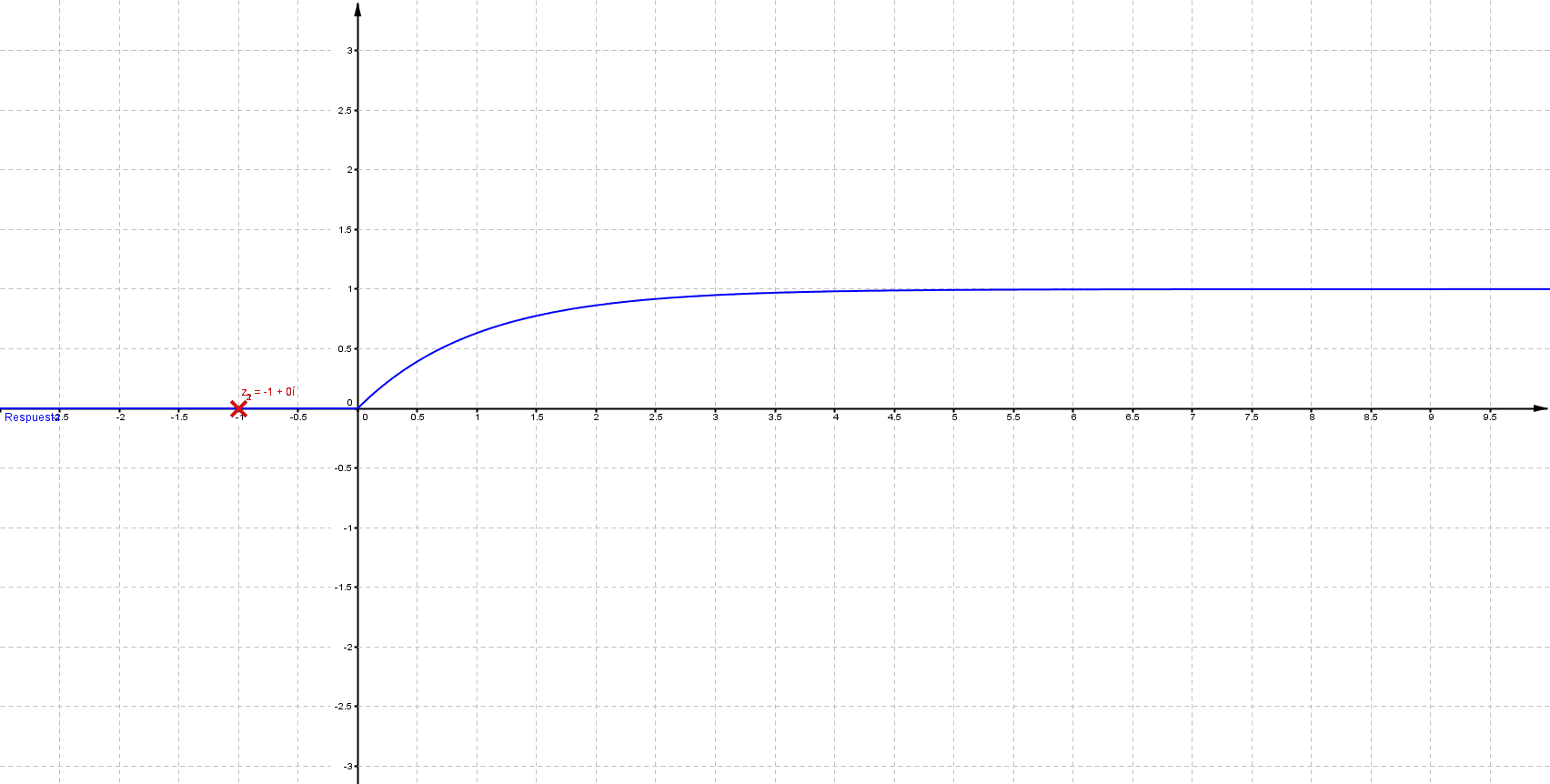
Mientras que sus respuestas en el tiempo son:
Puede verificarse que cuando las singularidades (polos) están del lado izquierdo (semiplano izquierdo), los sistemas son estables, las componentes imaginarias del valor del polo indican oscilaciones (cuando los polos son puramente imaginarios se denomina marginalmente estable).
En las siguiente animaciones se observan estos cambios:
Los sistemas se transforman
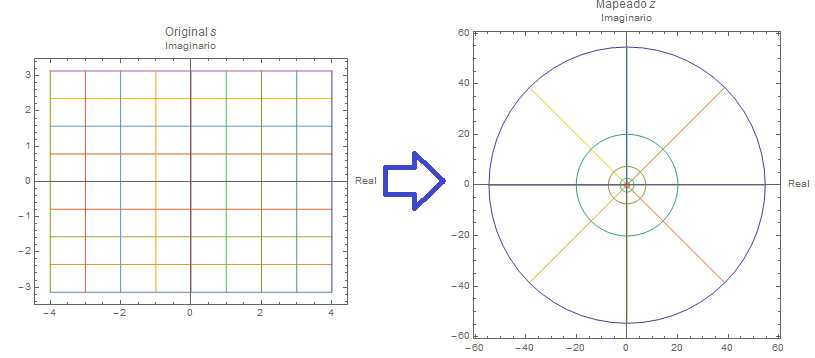
Cuando pasamos del continúo al discreto, el comportamiento de los sistemas es el mismo, pero solo podemos ver como se encuentran en instantes de muestreo, por lo que el dominio de Laplace no es adecuado para el análisis de estos, se emplea la transformada z, para convertir un sistema en s a otro en z basta con evaluar $z=e^{sT}$, siendo $T$ el tiempo de muestreo y añadir un ROC (Retenedor de Orden Cero) que hace lo que efectúa un muestreador y retenedor (como están constituidos los dispositivos electrónicos de adquisición de datos). A continuación veremos los efectos de este mapeo. Las rectas verticales ($s=a_0+ib$) se mapean: \[ z=e^{(a_0+ib)T}=e^{T\,a_0}\left[\cos{(T\,b)}+i\sin{(T\,b)}\right] \] En circunferencias de radio $e^{T\,a_0}$ Las rectas horizontales ($s=a+ib_0$) se mapean: \[ z=e^{(a+ib_0)T}=e^{T\,a}\left[\cos{(T\,b_0)}+i\sin{(T\,b_0)}\right] \] En rayos de recta con un angulo de ${T\,b_0}$ respecto a la horizontal.
Ahora la estabiidad se encuentra dentro del circulo unitario.
Transformación Bilineal
Dado que es relativamente sencillo determinar si las raíces son positivas o negativas con herramientas como el criterio de Routh-Hurwitz; no obstante calcular si esta dentro o fuera del circulo unitario, resulta más complicado de aplicar el criterio de Jury. Para esto se busca recuperar la forma que se tenía en el dominio de Laplace (aplicar la operación inversa), es decir, hacer $w=\frac{1}{T}\log z$, esto carecería de sentido por complejidad, la transformada z entre otras cosas linealiza los retardos (cuando estos sean múltiplos enteros del periodo de muestreo). Así que se busca una función que haga esto sin ser tan complicada. \[ \log (z)=\log\left( \frac{2z}{2} \right)=\log \left( \frac{z+1+z-1}{z+1-z+1} \right)=\log \left( \frac{\frac{z+1+z-1}{z+1}}{\frac{z+1-z+1}{z+1}} \right)=\log \left( \frac{1+\frac{z-1}{z+1}}{1-\frac{z-1}{z+1}} \right)=2\left[\frac{\log \left(1+\frac{z-1}{z+1}\right)}{2} -\frac{\log \left(1-\frac{z-1}{z+1}\right)}{2}\right] \] De la expansión en forma exponencial, puede decirse que: \[ \arctan (w)=\frac{\log \left(1+w\right)}{2} -\frac{\log \left(1-w\right)}{2}=2\left[ w+\frac{w^3}{3}+\frac{w^5}{5}+\frac{w^7}{7}+\ldots \right] \] $\therefore$ \[ \log (z)=2\arctan \left( \frac{z-1}{z+1} \right)=2\left[ \frac{z-1}{z+1}+\frac{\frac{z-1}{z+1}^3}{3}+\frac{\frac{z-1}{z+1}^5}{5}+\frac{\frac{z-1}{z+1}^7}{7}+\ldots \right] \] y \[ \frac{1}{T}\log (z)=\frac{2}{T}\left[ \frac{z-1}{z+1}+\frac{\frac{z-1}{z+1}^3}{3}+\frac{\frac{z-1}{z+1}^5}{5}+\frac{\frac{z-1}{z+1}^7}{7}+\ldots \right] \] Para facilitar tomamos el primer termino \[ w=\frac{1}{T}\log (z)\approx \frac{2}{T}\left(\frac{z-1}{z+1}\right) \] Que sera conocida como la Transformación Bilineal.
Ahora veamos como se comporta ante el mapeo de circunferencias de diversos radios para verificar que realmente mapée el circulo unitario al semiplano izquierdo. Sea: \[ z=R\,e^{i\theta}\;\;\;\;\;\;\;\;R \in \mathbb{R}^{+} \;\;\;\theta \in [-\pi,\pi) \] \[ w=\frac{2}{T}\left(\frac{z-1}{z+1}\right)=\frac{2}{T}\left(\frac{R\,e^{i\theta}-1}{R\,e^{i\theta}+1}\right)=\frac{2}{T}\left(1-\frac{2}{R\,e^{i\theta}+1}\right)=\frac{2}{T}\left(1-\frac{2}{R\,\cos(\theta)+1+i\,R\,\sin(\theta)}\frac{R\,\cos(\theta)+1-i\,R\,\sin(\theta)}{R\,\cos(\theta)+1-i\,R\,\sin(\theta)}\right) \] \[ w=\frac{2}{T}\left( 1-2 \frac{R\,\cos(\theta)+1-i\,R\,\sin(\theta)}{(R^\,\cos(\theta)+1)^2+(R\,\sin(\theta))^2} \right)=\frac{2}{T}\left( 1-2 \frac{R\,\cos(\theta)+1-i\,R\,\sin(\theta)}{R^2+2R\,\cos(\theta)+1} \right) \] Resulta complicado ver que forma tiene, pero dado que $R$ sera constante en cada evaluación y que solo nos interesa que para $R<1 0\leq Re(w)$, $R>1 Re(w)\leq 0$, tomamos: \[ Re(w)=\frac{2}{T}\left( 1-2 \frac{R\,\cos(\theta)+1}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{R^2+2R\,\cos(\theta)+1-2R\,\cos(\theta)-2}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{R^2+1-2}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{R^2-1}{R^2+2R\,\cos(\theta)+1} \right) \]
Para $R=1$ \[ Re(w)=\frac{2}{T}\left( \frac{R^2-1}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{1-1}{1+2\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{0}{1+2\cos(\theta)+1} \right)=0 \] \[ Im(w)=\frac{2}{T}\left( \frac{2R\,\sin(\theta)}{R^2+2R\,\cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{2\sin(\theta)}{1+2cos(\theta)+1} \right)=\frac{2}{T}\left( \frac{\sin(\theta)}{cos(\theta)+1} \right) \] El numerador varia en signo y magnitud, el denominador varia de 0 a 2; es decir que el cociente uede ser positivo o negativo (por el signo del numerador), tan grande como se desee (por que tan cerca del 0 este el denominador) y tan pequeño como se desee (dependiendo de que tan cerca del 0 este el numerador). Para $R=1$ $w$ es el eje imaginario.
Para $R<1$ \[ Re(w)=\frac{2}{T}\left( \frac{R^2-1}{R^2+2R\,\cos(\theta)+1} \right) \] El término $R^2<R<1$, por lo que el numerador siempre sera negativo. En el denominador si $R\to 0$ este tenderá a 1, y si $R\to 1$ este tenderá a $2(\cos (\theta)+1)$ que siempre es positivo, por lo que el denominador siempre sera positvo. Y por lo tanto $w$ permanecera en el semiplano izquierdo como buscamos.
Para $R>1$ \[ Re(w)=\frac{2}{T}\left( \frac{R^2-1}{R^2+2R\,\cos(\theta)+1} \right) \] El término $R^2>R>1$, por lo que el numerador siempre sera positivo. En el denominador si $R\to 1$ este tenderá a $2(\cos (\theta)+1)$ que siempre es positivo, y si tiende a infinito: \[ \lim_{R\to\infty} Re(w)=\lim_{R\to\infty}\frac{2}{T}\left( \frac{1-\frac{1}{R^2}}{1+\frac{2}{R}\,\cos(\theta)+\frac{1}{R^2}} \right)=\frac{2}{T}\left( \frac{1+0}{1+0+0} \right)=\frac{2}{T} \] Que es positivo y por lo que el denominador siempre sera positvo. Y $w$ permanecera en el semiplano derecho como buscamos.
--Tlacaelel Cruz (discusión) 11:52 3 jul 2015 (CDT)