Rendijas

Rendijas

La difracción en rendijas es un fenómeno amplia mente estudiado, este fenómeno se lleva a cabo mediante una luz incidente en una

apertura con dimensiones variables o en su caso varias aperturas. La difracción ocurre cuando la longitud de onda de la luz

incidente en la apertura tiene dimensiones de longitud muy parecidas.

En los párrafos siguientes se muestra el calculo de la difracción en en cuatro diferentes aberturas (tres de ellos en 1D Y uno mas en dos dimensiones) y como se llega a la irradianza.

Para una sola rendija

Se considera una fuente puntual (circulo azul), la radiación pasara por la rendija de ancho

2a y una vez que interactue con la abertura sera detectada en una pantalla (Figura 1).

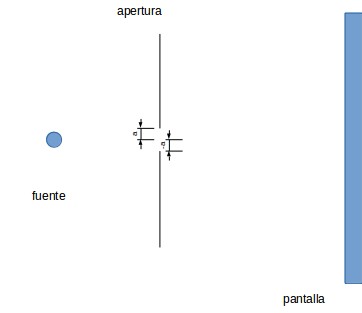
Figura 1: En la figura se muestra el intervalo [a,-a]

La solución se muestra de la siguiente manera, donde $l_{1}$ y $l_{2}$ son los limites de la rendija por donde pasara la luz.

$\Psi (P)=c\int \limits _{l_{1}}^{l_{2}}e^{i\kappa \alpha \xi }\,d\xi$

con base a la figura 1. se observa que los limites de integracion seran $a$ en el limite superior y $-a$ en el limite inferior.

$\Psi (P)=c{\frac {e^{-i\kappa \alpha \xi }}{-i\kappa \alpha }}|_{-a}^{\;a}$

Evaluando.

$\Psi (P)={\frac {c}{-i\kappa \alpha }}(e^{-i\kappa \alpha a}-e^{i\kappa \alpha a})$

multiplicando por 2/2.

$\Psi (P)={\frac {2c}{\kappa \alpha }}({\frac {e^{i\kappa \alpha a}-e^{-i\kappa \alpha a}}{2i}})$

Recordando que $Sen(x)={\frac {e^{ix}-e^{-ix}}{2i}}$

$\Psi (P)={\frac {2c}{\kappa \alpha }}Sen(\kappa \alpha a)$

$\Psi (P)=2ca{\frac {Sen(\kappa \alpha a)}{\kappa \alpha a}}$

Se nombra.

$\gamma =\kappa \alpha a$

Haciendo el cambio de variable se llega a.

$\Psi (P)=2ca{\frac {Sen(\gamma )}{\gamma }}$

Elevando al cuadrado. $|\Psi (P)|=4c^{2}a^{2}({\frac {Sen\gamma }{\gamma }})^{2}=I(p)$

Apertura rectangular

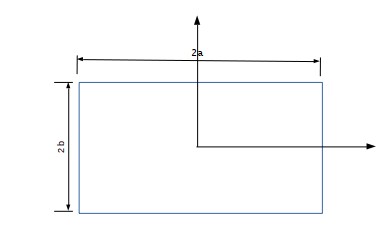
Figura 2: En la figura se muestran las dimensiones del rectángulo

Para una apertura rectangular se considera un rectángulo de lados 2a y 2b, utilizando la integral de difracción de Fraunhofer

$\Psi (P)=c\int \limits _{-a}^{a}\int \limits _{-b}^{b}e^{-i\kappa (p\xi +q\eta )}d\xi d\eta =c\{\int \limits _{-a}^{a}e^{-i\kappa p\xi }d\xi \int \limits _{-b}^{b}e^{-i\kappa q\eta }d\eta \}$

En la figura 2 se muestran las dimensiones de la apertura donde los ejes ahora son llamados con otro nombre, en el eje x se tiene $\xi$ y en el eje "y" la letra $\eta$

Observando solo la primera integral con los limites entre a y -a se procede a resolver y evaluar de la siguiente forma.

$\Psi (P)=\int \limits _{-a}^{a}e^{-i\kappa p\xi }d\xi =-{\frac {1}{i\kappa p}}\{e^{-i\kappa pa}-e^{-i\kappa qb}\}=2{\frac {Sen(\kappa pa)}{\kappa pa}}$

De igual forma se realiza la otra integral. La intensidad esta dada por.

$I(P)=|\Psi (P)|^{2}=({\frac {Sen\kappa pa}{\kappa pa}})^{2}({\frac {Sen\kappa qb}{\kappa qb}})^{2}$

Doble rendija

Utilizando la misma idea de una sola rendija vista anteriormente, se escribe la solución de la siguiente manera.

se puede observar en la figura 3. la simetría que se encuentra al tomar las distancias de la manera en que se muestra

para posteriormente hacer la integral y reducir factores.

Figura 3: En la figura se muestra los intervalos de integración (superior e inferior)

$\Psi (P)=c\{\int \limits _{-d-a}^{-d+a}e^{-i\kappa \alpha \xi }\,d\xi +\int \limits _{d-a}^{d+a}e^{-i\kappa \alpha \xi }\,d\xi \}$

$\Psi (P)=c\{{\frac {e^{-i\kappa \alpha \xi }}{-i\kappa \alpha \xi }}|_{-d-a}^{-d+a}+{\frac {e^{-i\kappa \alpha \xi }}{-i\kappa \alpha \xi }}|_{d-a}^{d+a}\}$

$\Psi (P)=c{\frac {1}{-i\kappa \alpha }}\{e^{-i\kappa \alpha (-d+a)}-e^{-i\kappa \alpha (-d-a)}+e^{-i\kappa \alpha (d+a)}-e^{-i\kappa \alpha (d-a)}\}$

Multiplicando por un factor 2\2.

$\Psi (P)={\frac {2c}{2}}{\frac {1}{-i\kappa \alpha }}\{e^{i\kappa \alpha (d-a)}-e^{-i\kappa \alpha (-d-a)}+e^{i\kappa \alpha (-d-a)}-e^{-i\kappa \alpha (d-a)}\}$

Haciendo un Re acomodando los términos de la suma de exponenciales.

$\Psi (P)={\frac {2c}{2}}{\frac {1}{-i\kappa \alpha }}\{(e^{i\kappa \alpha (d-a)}-e^{-i\kappa \alpha (d-a)})-(e^{i\kappa \alpha (d+a)}-e^{-i\kappa \alpha (d+a)})\}$

$\Psi (P)=-2c{\frac {1}{\kappa \alpha }}\{{\frac {(e^{i\kappa \alpha (d-a)}-e^{-i\kappa \alpha (d-a)})}{2i}}-{\frac {(e^{i\kappa \alpha (d+a)}-e^{-i\kappa \alpha (d+a)})}{2i}}\}$

$\Psi (P)=-2c{\frac {1}{\kappa \alpha }}\{Sen(\kappa \alpha (d-a))-Sen(\kappa \alpha (d+a))\}$

Usando la identidad.

$Sen(a)-Sen(b)=2Cos({\frac {1}{2}}(a+b)Sen{\frac {1}{2}}(a-b))$

Entonces.

$Sen(\kappa \alpha (d-a))-Sen(\kappa \alpha (d+a))=\{2Cos({\frac {1}{2}}(\kappa \alpha d-\kappa \alpha a+\kappa \alpha d+\kappa \alpha a))Sen({\frac {1}{2}}(\kappa \alpha d-\kappa \alpha a-\kappa \alpha d-\kappa \alpha a))\}$

haciendo las sumas y eliminando términos se obtiene.

$\Psi (P)={\frac {4c}{\kappa \alpha }}\{Sen(\kappa \alpha a)Cos(\kappa \alpha d)\}$

Con un cambio de variable se obtiene.

$\Psi (P)=4ca\{{\frac {Sen(\gamma )}{\gamma }}Cos(\delta )\}$

N Rendijas

Para n rendijas se tiene se tiene la solución construida de la

siguiente manera, se puede observar el arreglo de las n rendijas

en la figura 4.

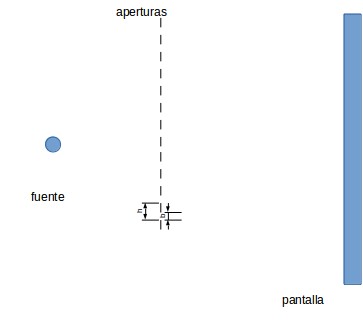
Figura 4: En la figura se muestra los intervalos de integración (superior e inferior), buscando una simetria entre todos ellos.

$\Psi (p)=c\{\int \limits _{0}^{b}e^{i\kappa \alpha \xi }\,d\xi +\int \limits _{h}^{h+b}e^{i\kappa \alpha \xi }\,d\xi +\int \limits _{2h}^{2h+b}......+\int \limits _{(n-1)h}^{(n-1)h+b}e^{i\kappa \alpha \xi }\,d\xi \}$

Donde cada uno de los sumandos representan la solución a la rejilla individual, para cada una de las integrales se observa .

$\int \limits _{l_{1}}^{l_{2}}e^{i\kappa \alpha \xi }\,d\xi ={\frac {e^{i\kappa \alpha \xi }}{\kappa \alpha \xi }}|_{l_{1}}^{l_{2}}={\frac {1}{\kappa \alpha }}{\frac {e^{i\kappa \alpha l_{2}}-e^{i\kappa \alpha l_{1}}}{i}}$

Resolviendo la primera integral, segunda y n-ada integral.

$1={\frac {1}{\kappa \alpha }}{\frac {e^{i\kappa \alpha b}-1}{i}}$

$2={\frac {1}{\kappa \alpha }}{\frac {e^{i\kappa \alpha (h+b)}-e^{i\kappa \alpha h}}{i}}$

.

.

.

$n={\frac {1}{\kappa \alpha }}{\frac {e^{i\kappa \alpha (n-1)h+b}-e^{i\kappa \alpha (n-1)h}}{i}}$

La segunda ecuación se puede reescribir de la siguiente manera.

${\frac {1}{\kappa \alpha }}e^{i\kappa \alpha h}{\frac {(e^{i\kappa \alpha b}-1)}{i}}$

Para la eneada ecuación.

${\frac {1}{\kappa \alpha }}(e^{i\kappa \alpha (n-1)h})({\frac {e^{i\kappa \alpha b}-1}{i}})$

Donde se puede observar un termino común en todas los términos, se puede reescribir la ecuación como sigue.

$\Psi (p)=c\{{\frac {1}{\kappa \alpha }}{\frac {e^{i\kappa \alpha b}-1}{i}}\}\{1+e^{i\kappa \alpha h}+e^{i\kappa \alpha 2h}+...e^{i\kappa \alpha (n-1)h}\}$

Recordando.

$\sigma =1+x+x^{2}+...+x^{n-1}$

$\sigma x=x+x^{2}+x^{3}+...+x^{n}$

Restando las dos ecuaciones anteriores.

$x\sigma -\sigma =x^{n}-1$

$\sigma (x-1)=x^{n}-1$

$\sigma ={\frac {x^{n}-1}{x-1}}$

Si se observa la ecuación se reescribe.

$\sigma ={\frac {x^{n}-1}{x-1}}={\frac {e^{i\kappa \alpha nh}-1}{e^{i\kappa \alpha h}-1}}$

en la ecuación.

$\Psi (P)=c{\frac {e^{i\kappa \alpha b}-1}{\kappa \alpha }}\{{\frac {e^{i\kappa \alpha nh}-1}{e^{i\kappa \alpha h}-1}}\}$

$\Psi (P)={\frac {2c}{\kappa \alpha }}e^{i\kappa \alpha {\frac {b}{2}}}({\frac {e^{i\kappa \alpha {\frac {b}{2}}}-e^{-i\kappa \alpha {\frac {b}{2}}}}{2i}}){\frac {e^{i\kappa \alpha n{\frac {h}{2}}}({\frac {e^{i\kappa \alpha n{\frac {h}{2}}}-e^{-i\kappa \alpha n{\frac {h}{2}}}}{2i}})}{e^{i\kappa \alpha {\frac {h}{2}}}({\frac {e^{i\kappa \alpha {\frac {h}{2}}}-e^{-i\kappa \alpha {\frac {h}{2}}}}{2i}})}}$

$\Psi (P)={\frac {2c}{\kappa \alpha }}e^{i\kappa \alpha {\frac {b}{2}}}(Sen({\frac {\kappa \alpha b}{2}})){\frac {e^{i\kappa \alpha n{\frac {h}{2}}}(Sen({\frac {\kappa \alpha nh}{2}}))}{e^{i\kappa \alpha {\frac {h}{2}}}(Sen({\frac {\kappa \alpha nh}{2}}))}}$

$\Psi (P)=cbe^{i\kappa \alpha {\frac {b}{2}}}e^{i\kappa \alpha (n-1){\frac {h}{2}}}{\frac {(Sen({\frac {\kappa \alpha b}{2}}))}{\frac {\kappa \alpha b}{2}}}{\frac {Sen(n\kappa \alpha {\frac {h}{2}})}{Sen(\kappa \alpha {\frac {h}{2}})}}$

$\Psi (P)=c\{n\}{\frac {Sen(\beta )}{\beta }}{\frac {Sen(n\beta )}{n\beta }}$

$|\Psi (P)|=I_{0}({\frac {Sen(\beta )}{\beta }})^{2}({\frac {Sen(n\beta )}{n\beta }})^{2}$