Radiacion: reflexion y refraccion en conductores

Concepto de medio conductor

La característica sobresaliente de los medios conductores es la presencia de un numero de cargas eléctricas libres, es decir que no están ligadas por lo tanto son capaces de circular por todas partes dentro del material. Para los metales estas cargas son por supuesto los electrones y su movimiento constituye una corriente. Los metales son medios isótropos que tienen como característica que su conductividad, sigma, es distinta de cero.

Para un dieléctrico no hay electrones libres o de conducción y $\sigma =0$, mientras que para los metales reales $\sigma$ es diferente de cero y finita. En contraste un conductor ideal tendría una conductividad infinita. Esto equivale a decir que los electrones impulsados a oscilar por una onda armónica, simplemente seguiría las alteraciones del campo. No habría fuerza de restauración, ni frecuencias naturales, ni absorción, solamente remisión. En metales reales los electrones de conducción sufren colisiones con la red agitada térmicamente o con imperfecciones y al hacerlo así convierten energía electromagnética de forma irreversible como calor de joule. La absorción de energía radiante de un material es una función de su conductividad.

Aproximaciones

La justificación para trabajar con vectores complejos nos viene dada al definir nuestra función como $\phi =\mathbf {A} cos(kz-\omega t)$ que representa a nuestra onda plana que como hemos explicado antes, debe ser amortiguada al entrar al medio 2 por lo cual buscamos una función que evaluada en la interfaz sea cero y que su derivada sea negativa. La función que cumple perfectamente esto es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \mathbf{e}^{-|pz|} donde al reescribir $\phi$ en termino de exponenciales encontramos que$\phi =\mathbf {Ae} ^{-|pz|}\mathbf {e} ^{i(kz-\omega t)}=\mathbf {Ae} ^{i(kz+i|pz|-\omega t)}$ que como podemos ver a continuación se puede escribir como un numero complejo, lo cual justifica su uso en la descripción de una onda amortiguada $\phi =\mathbf {Ae} ^{i[(k+ip)z-\omega t]}=\mathbf {Ae} ^{i({\tilde {k}}z-\omega t)}$. Con la tilde diferenciáremos a los números complejos en este trabajo.

Medios conductores

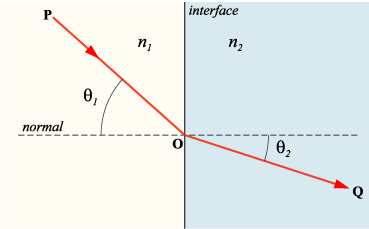
En esta imagen el lado izquierdo representa un medio dieléctrico y el derecho el medio conductor, por lo que n1 es real y n2 es complejo.

Utilizando la información recolectada al estudiar la incidencia en un medio dieléctrico sobre otro dieléctrico propondremos el uso de la misma estructura en las ecuaciones mostradas a continuación, primero para el caso de incidencia normal, que como vemos son muy sencillas y luego ya en función del ángulo de incidencia que es el caso más general. Donde obtenemos la amplitud de la onda reflejada y refractada en función de la amplitud de la onda incidente.

Incidencia normal:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): E^{\prime\prime}_{b} = E_{a}\frac{{n_{1}-n_{2}}}{{n_{1}+n_{2}}}  ; $E_{b}^{\prime }=E_{a}{\frac {2n_{1}}{n_{1}+n_{2}}}$

Las amplitudes que no están etiquetadas con el símbolo primado son las del campo de incidente, las biprimas son las reflejadas y las primas las transmitidas.

Incidencia oblicua:

Con el campo eléctrico perpendicular al plano

$E_{0}^{\prime \prime }=E_{0}{\frac {n_{1}cos\theta _{1}-n_{2}cos\theta _{2}}{n_{1}cos\theta _{1}+n_{2}cos\theta _{2}}}$

 ;

$E_{0}^{\prime }=E_{0}{\frac {2n_{1}cos\theta _{1}}{n_{1}cos\theta _{1}+n_{2}cos\theta _{2}}}$

Con el campo eléctrico paralelo al plano

$E_{0}^{\prime \prime }=E_{0}{\frac {n_{1}cos\theta _{2}-n_{2}cos\theta _{1}}{n_{1}cos\theta _{2}+n_{2}cos\theta _{1}}}$

 ;

$E_{0}^{\prime }=E_{0}{\frac {2n_{1}cos\theta _{2}}{n_{1}cos\theta _{2}+n_{2}cos\theta _{1}}}$

Donde como interesa calcular lo que se refleja y/o transmite, definimos los coeficientes de Fresnel como:

Para la incidencia normal

$r_{F}=-{\frac {E_{b}}{E_{a}}}={\frac {-n_{1}+n_{2}}{n_{1}+n_{2}}}$ Coeficiente de reflexión de Fresnel.

$t_{F}={\frac {E_{b}^{\prime }}{E_{a}}}={\frac {2n_{1}}{n_{1}+n_{2}}}$ Coeficiente de transmisión de Fresnel.

Para cualquier ángulo de incidencia y el campo eléctrico perpendicular al plano

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): r_{F} =\frac{{-n_{1}cos \theta_{1}+n_{2} cos \theta_{2}}}{{n_{1}cos \theta_{1}+n_{2} cos \theta_{2}}}

$t_{F}={\frac {2n_{1}cos\theta _{1}}{n_{1}cos\theta _{1}+n_{2}cos\theta _{2}}}$

Siendo r y t amplitudes de reflexión y transmisión, que nos dan los coeficientes de reflexión (intensidad de reflexión) y transmisión (intensidad de transmisión) que a continuación presentamos

$R={|r_{F}|}^{2}$

$T={|t_{0}|}^{2}$

donde $t_{0}={\sqrt {\frac {n_{2}}{n_{1}}}}t_{F}={\frac {2{\sqrt {n_{2}n_{1}}}}{n_{1}+n_{2}}}$

La suma de estos coeficientes es ${R+T=1}$

Medio conductor.

Para el caso dieléctrico/conductor haremos que en el medio dos, que es donde la onda incide, los vectores sean complejos, ya que la reflexión cuando la luz incide sobre un medio isótropo de conductividad no nula tiene el índice de refracción del segundo medio complejo, donde n' y k (coeficiente de extinción) son constantes reales y positivas relacionadas con la constante dieléctrica y la conductividad del medio. La amplitud decae en dirección K.

Perpendicular al plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): E^{\prime\prime}_{0} = E_{0}\frac{{n_{1}cos \theta_{1}-\tilde n_{2} cos \tilde \theta_{2}}}{{n_{1}cos \theta_{1}+\tilde n_{2} cos \tilde \theta_{2}}}  ; $E_{0}^{\prime }=E_{0}{\frac {2n_{1}cos\theta _{1}}{n_{1}cos\theta _{1}+{\tilde {n}}_{2}cos{\tilde {\theta }}_{2}}}$

Paralelo al plano reincidencia $E_{0}^{\prime \prime }=E_{0}{\frac {n_{1}cos{\tilde {\theta }}_{2}-{\tilde {n}}_{2}cos\theta _{1}}{n_{1}cos{\tilde {\theta }}_{2}+{\tilde {n}}_{2}cos\theta _{1}}}$ ; $E_{0}^{\prime }=E_{0}{\frac {2n_{1}cos{\tilde {\theta }}_{2}}{n_{1}cos{\tilde {\theta }}_{2}+{\tilde {n}}_{2}cos\theta _{1}}}$

Para saber cuánto vale ${\tilde {n}}^{\prime }$ utilicemos la ecuación extraída de el tratamiento de las ecuaciones de Maxwell y las condiciones de frontera del campo eléctrico y magnético.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \nabla^2 \mathbf{E}(\mathbf{r},t)-\epsilon\mu\frac{\partial^2\mathbf{E}(\mathbf{r},t)}{\partial t^2}-\sigma \mu \frac{{\partial\mathbf{E}(\mathbf{r},t )}}{{\partial t}}= 0 ...(1)

Representando el vector de campo eléctrico como

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \mathbf{E}(\mathbf{r},t)=\mathbf{E}(\mathbf{r})\mathbf{e}^{-i \omega t}= E_{0}\mathbf{e}^{i(\mathbf{\tilde k} \cdot \mathbf{r} -\omega t)}

Sustituimos en la ecuación 1 para obtener

$\nabla ^{2}\mathbf {E} (\mathbf {r} )\mathbf {e} ^{-i\omega t}+\omega ^{2}\epsilon \mu \mathbf {E} (\mathbf {r} )\mathbf {e} ^{-i\omega t}-i\omega \sigma \mu \mathbf {E} (\mathbf {r} )\mathbf {e} ^{-i\omega t}=0$...(2)

Utilizando $\nabla e^{i(\mathbf {k\cdot r} )}=i\mathbf {k}$ podemos proponer el operador Laplaciano de una onda plana en este caso como

$\nabla ^{2}=i\mathbf {\tilde {k}} \cdot i\mathbf {\tilde {k}} =-{\tilde {k}}^{2}$

y sustituimos en la ecuación 2 nuestros resultados

$-{\tilde {k}}^{2}\mathbf {E} (\mathbf {r} )\mathbf {e} ^{-i\omega t}+\omega ^{2}\epsilon \mu \mathbf {E} (\mathbf {r} )\mathbf {e} ^{-i\omega t}+i\omega \sigma \mu \mathbf {E} (\mathbf {r} )\mathbf {e} ^{-i\omega t}=0$

Factorizamos $\mathbf {E} (\mathbf {r} )\mathbf {e} ^{-i\omega t}$ de la ecuación anterior y sustituimos ${\tilde {k}}^{2}={\tilde {k}}^{\prime 2}$ para que sea más consistente con nuestra notación ya que los valores primados son los que viven en el medio dos, nuestro conductor. Por ser un medio que consideramos magnético haremos $\mu =\mu _{0}$

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): -\tilde k^{\prime 2}+\omega^2\epsilon\mu+i\omega \sigma \mu=0

${\tilde {k}}^{\prime 2}=\omega ^{2}\epsilon \mu _{0}+i\omega \sigma \mu _{0}$

Multiplicando por 1 escrito como Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac {c^2}{\omega^2}* \frac {\omega^2}{c^2} para poder llevar la ecuación a su forma ${\tilde {k}}^{\prime }={\frac {\omega }{c}}{\tilde {n}}^{\prime }$ y de esta manera identificar el valor de ${\tilde {n}}^{\prime }$, donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): c^2= \frac {1}{\epsilon_0 \mu_0} .

${\tilde {k}}^{\prime 2}=(\omega ^{2}\epsilon \mu _{0}{\frac {c^{2}}{\omega ^{2}}}+i\omega \sigma \mu _{0}{\frac {c^{2}}{\omega ^{2}}}){\frac {\omega ^{2}}{c^{2}}}=({\frac {\epsilon }{\epsilon _{0}}}+{\frac {i\sigma }{\omega \epsilon _{0}}}){\frac {\omega ^{2}}{c^{2}}}$

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \tilde k^\prime =\frac {\omega}{c} \sqrt{\frac {\epsilon}{\epsilon_0} + \frac {i \sigma}{\omega\epsilon_0}}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \tilde n^\prime = \sqrt{\frac {\epsilon}{\epsilon_0} + \frac {i \sigma}{\omega\epsilon_0}}

Renombremos ${\frac {\epsilon }{\epsilon _{0}}}=k$ y recordando que definimos ${\tilde {n}}^{\prime }=n^{\prime }+i\eta ^{\prime }$ despejemos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): n^\prime Y $\eta ^{\prime }$

$n^{\prime }={\sqrt {{\frac {1}{2}}(k+{\sqrt {k^{2}+{({\frac {\sigma }{\omega \epsilon _{0}}})}^{2}}}}}$

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \eta ^\prime=\sqrt{\frac {1}{2}(-k +\sqrt{k^2+ {(\frac {\sigma}{\omega\epsilon_0})}^2}}

Valores para las ecuaciones del medio conductor

Como podemos ver las ecuaciones que arriba hemos puesto nos da los valores que conformar a ${\tilde {n}}^{\prime }$ pero aun no sabemos cual es el angulo complejo que aparece, por lo tanto propondremos

${\tilde {n}}^{\prime }cos{\tilde {\theta }}^{\prime }=p+iq$

Tomando en cuenta que la ley de Snell tambien se cumple.

$n\sin \theta ={\tilde {n}}^{\prime }\sin {\tilde {\theta }}^{\prime }$

Elevamos al cuadrado ambas partes de la ecuación y descomponemos el coseno para encontrar un término donde podamos aplicar la ley de Snell, con esto lograremos poner todo en función de el ángulo de incidencia y el medio 1, datos que siempre tenemos.

${\tilde {n}}^{\prime 2}cos^{2}{\tilde {\theta }}^{\prime }=p^{2}-q^{2}+i2pq$

${\tilde {n}}^{\prime 2}(1-sin{\tilde {\theta }}^{\prime })^{2}=p^{2}-q^{2}+i2pq$

${\tilde {n}}^{\prime 2}-({\tilde {n}}sin{\tilde {\theta }}^{\prime })^{2}=p^{2}-q^{2}+i2pq$

Aplicamos ley de Snell $n^{\prime 2}-\eta ^{\prime 2}+i2n^{\prime }\eta ^{\prime }-(nsin\theta )^{2}=p^{2}-q^{2}+i2pq$

Tomemos la parte reale de la ecuacion anterior $n^{\prime 2}-\eta ^{\prime 2}-(nsin\theta )^{2}=p^{2}-q^{2}$

Podemos ahora despejar $p$ y $q$.

Observe que si el angulo incidente es cero $p=n^{\prime }$ y $q=\eta ^{\prime }$

$p={\sqrt {{\frac {1}{2}}({k-{\frac {\sigma \sin ^{2}\theta }{\omega \epsilon _{0}}}})+{\sqrt {(k-{{\frac {\sigma \sin \theta }{\omega \epsilon _{0}}})^{2}}+({\frac {\sigma }{\omega \epsilon _{0}}})^{2}}}}}$

$q={\sqrt {{\frac {1}{2}}({-k-{\frac {\sigma \sin ^{2}\theta }{\omega \epsilon _{0}}}})+{\sqrt {(k-{{\frac {\sigma \sin \theta }{\omega \epsilon _{0}}})^{2}}+({\frac {\sigma }{\omega \epsilon _{0}}})^{2}}}}}$

Resultados de la incidencia sobre un medio conductor.

Para entender mejor los resultados hagamos un ejemplo.

perpendicular al plano $E_{0}^{\prime \prime }=E_{0}{\frac {ncos\theta -{\tilde {n}}^{\prime }cos{\tilde {\theta }}^{\prime }}{ncos\theta +{\tilde {n}}^{\prime }cos{\tilde {\theta }}^{\prime }}}=E_{0}{\frac {ncos\theta -(p+iq)}{ncos\theta +(p+iq)}}$ ;

$E_{0}^{\prime }=E_{0}{\frac {2ncos\theta }{ncos\theta +{\tilde {n}}^{\prime }cos{\tilde {\theta }}^{\prime }}}=E_{0}{\frac {2ncos\theta }{ncos\theta +(p+iq)}}$

Supongamos que una onda plana, que se propaga en un medio dieléctrico, por ejemplo el aire (n=1), se encuentra con la superficie de un conductor. Puesto que la óptica de medios conductores puede desarrollarse como los dieléctricos isótropos, pero con índice de refracción complejo.

Ahora si la incidencia es normal podemos escribir en lugar de p y q, n y $\eta$

perpendicular al plano $E_{0}^{\prime \prime }=E_{0}{\frac {n-{\tilde {n}}^{\prime }cos{\tilde {\theta }}^{\prime }}{n+{\tilde {n}}^{\prime }cos{\tilde {\theta }}^{\prime }}}=E_{0}{\frac {n-(n^{\prime }+i\eta ^{\prime })}{n+(n^{\prime }+i\eta ^{\prime })}}$ ;

$E_{0}^{\prime }=E_{0}{\frac {2n}{n+{\tilde {n}}^{\prime }cos{\tilde {\theta }}^{\prime }}}=E_{0}{\frac {2n}{n+(n^{\prime }+i\eta ^{\prime })}}$

Donde la reflexión sera

$R={\frac {({n-(n^{\prime }+i\eta ^{\prime })})^{2}}{({n+(n^{\prime }+i\eta ^{\prime })})^{2}}}={\frac {({1-(n^{\prime }+i\eta ^{\prime })})^{2}}{({1+(n^{\prime }+i\eta ^{\prime })})^{2}}}$

si tomamos en el cobre que es un excelente conductor $n^{\prime }=\eta ^{\prime }$

$R={\frac {({1-n^{\prime }-i\eta ^{\prime }})^{2}}{({1+n^{\prime }+i\eta ^{\prime }})^{2}}}={\frac {1-2n^{\prime }-2in^{\prime }+2in^{\prime 2}}{1+2n^{\prime }+2in^{\prime }+2in^{\prime 2}}}$

Que como podemos ver no nos dará una reflexión de 1 es decir, no es posible que sea reflejada toda la luz que incide sobre un medio conductor.

En el caso del cobre sera del 90%