DIPOLO ELECTRICO
Un dipolo eléctrico está conformado por un par de cargas eléctricas
de igual magnitud pero de signos opuestos  y
y  separadas
por una distancia
separadas
por una distancia  generalmente muy pequeña, como se muestra en la siguiente figura. Son sistemas físicos
muy importantes pues desde las moléculas hasta las antenas de televisión
pueden ser descritos como tales.
generalmente muy pequeña, como se muestra en la siguiente figura. Son sistemas físicos
muy importantes pues desde las moléculas hasta las antenas de televisión
pueden ser descritos como tales.
Una cantidad con que se caracterizan los dipolos eléctricos es la denominada momento dipolar eléctrico expresado como el producto entre la carga eléctrica  y la distancia de separación entre cargas
y la distancia de separación entre cargas  . Es una cantidad vectorial dirigida de la carga negativa a la positiva.
. Es una cantidad vectorial dirigida de la carga negativa a la positiva.
Es costumbre tomar la distancia entre cargas como  y medir la distancia
y medir la distancia  desde el centro de separación entre cargas.
Junto con el campo eléctrico hay asociado un potencial eléctrico el cual está dado por:
desde el centro de separación entre cargas.
Junto con el campo eléctrico hay asociado un potencial eléctrico el cual está dado por:

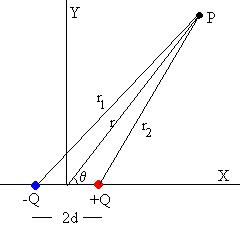
expresamos  y
y  en funcion de
en funcion de  y
y  , que es la posicion del punto
, que es la posicion del punto  expresada en coordenadas polares
expresada en coordenadas polares


teniendo en cuenta que  es pequeño frente a
es pequeño frente a  podemos obtener una buena aproximacion empleando el desarrollo en serie
podemos obtener una buena aproximacion empleando el desarrollo en serie

despreciando los terminos de orden superior a 


Que en función de la distancia  y del ángulo θ se expresa por:
y del ángulo θ se expresa por:

Esta expresión es válida para d pequeña y para 
Y puede simplificarse utilizando el concepto del momento dipolar. Primero se identifica el segmento vectorial dirigido de  a
a  con la letra
con la letra  , luego se define el momento dipolar como
, luego se define el momento dipolar como  y se le asigna el simbolo
y se le asigna el simbolo  . De manera que,
. De manera que,

Y como
 se obtiene entonces
se obtiene entonces

Obsérvese que el potencial disminuye con el inverso del cuadrado de la distancia  en vez de la inversa de distancia
en vez de la inversa de distancia  como es el caso de una carga puntual.
como es el caso de una carga puntual.
Ahora bien, como se sabe el campo electrico esta dado por: 
y si se utiliza esta ecuación en coordenadas esféricas,

se obtiene


haciendo valer  obtenemos el caso del campo electrico para una sola carga
obtenemos el caso del campo electrico para una sola carga
La intensidad del campo eléctrico disminuye como el cubo de la distancia  .
.
A continuación aplicamos estos conceptos al caso de antenas de dipolo.
RADIACION POR UN DIPOLO ELECTRICO
La radiación procedente de una antena de dipolo se denomina radiación dipolar eléctrica. Muchas ondas electromagnéticas presentan las características de la radiación dipolar eléctrica. Una característica importante de este tipo de radiación es que la intensidad de la onda electromagnética radiada por una antena dipolar es cero a lo largo del eje de la antena y máxima en las direcciones perpendiculares al eje de la misma.
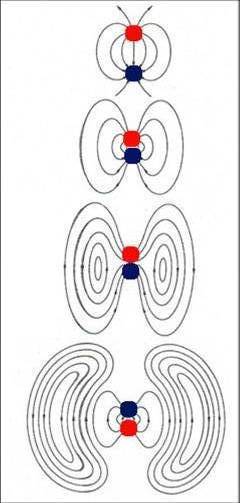
El esquema de una antena dipolar eléctrica, consta de dos varillas conductoras dobladas que se alimentan mediante un generador de corriente alterna. En el instante t = 0, los extremos de las varillas se encuentran cargados y existe un campo eléctrico cerca de las varillas paralelo a ellas. También existe un campo magnético que rodea las varillas y que se debe a la corriente que circula por ellas. Estos campos se mueven alejándose de las varillas con la velocidad de la luz. Al cabo de un cuarto de periodo a t = T/4, las varillas se encuentran descargadas y en sus proximidades el campo eléctrico es nulo. Para t = T/2, las varillas se encuentran cargadas de nuevo, pero las cargas son opuestas a las que había en t = 0. Los campos eléctrico y magnético a grandes distancia de esta antena transmisora son muy diferentes de los que existen cerca de la misma. Lejos de la antena, los campos eléctrico y magnético oscila en fase con un movimiento armónico simple, perpendicular el uno del otro y a la dirección de propagación de la onda. La siguiente figura muestra los campos eléctricos y magnéticos lejos de una antena dipolar eléctrica.
Para determinar el campo electromagnético de un dipolo elemental se siguen los siguientes tres pasos:
1. Determinar el potencial Magnético A de una distribución de corriente J
siendo J una distribución de corriente conocida o supuesta en la antena.
2. Encontrar el campo magnético a partir de A
3. Encontrar el campo eléctrico
Donde
Este potencial magnético A se debe pasar a coordenadas esféricas:
Después de hallado el potencial magnético podemos hallar el campo magnético:
Después de hallado el campo magnético podemos hallar el campo eléctrico:
Al considerar el desarrollo multipolar de una distribución cualquiera de corriente y, tomando en cuenta la ecuación de continuidad (conservación de carga), se puede obtener como valor para el potencial dipolar eléctrico ( ), la expresión:
), la expresión:

Y la expresión para el campo dipolar eléctrico, a partir del vector potencial se calcula

Si

Sustituimos en la ecuacion para el campo electrico

mediante la identidad que dice que

llegamos a

Si utilizamos la fórmula 
la ecuación anterior se reduce a
![=i(\frac{c^{2}}{\omega})[\nabla\times\overrightarrow{\boldsymbol{B}}+\nabla^{2}\overrightarrow{\boldsymbol{A}}+(\frac{\omega^{2}}{c^{2}})\overrightarrow{\boldsymbol{A}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/be2f9b4e8bee144107566eb7badf0cb51fe85860)
y como esta ecuación satisface la ecuación de onda tenemos que
![=i(\frac{c^{2}}{\omega})[\nabla\times\overrightarrow{\boldsymbol{B}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/31274a65984b4fad1c20751c8dd9c2163454c626)
En donde ![\overrightarrow{\boldsymbol{B}}=-\frac{\mu_{0}k^{2}\omega\boldsymbol{p}_{0}}{4\pi}[\frac{1}{kr}+\frac{i}{(kr)^{2}}]\sin\theta e^{i(kr-\omega t)}\hat{\phi}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c4eeccc6105a2cba0a29dca430ca1608c747debf)
Haciendo la sustitución y resolviendo, llegamos a
![\overrightarrow{\boldsymbol{E}}=-\frac{k^{3}\boldsymbol{p}_{0}}{4\pi\epsilon_{0}}\{[\frac{2i}{(kr)^{2}}-\frac{2}{(kr)^{3}}]\cos\theta\hat{r}+[\frac{1}{kr}+\frac{1}{(kr)^{2}}-\frac{1}{(kr)^{3}}]\sin\theta\hat{\theta}\}e^{i(kr-\omega t)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/00515ec142d3d7f627c7ed9d88f4a44d70d5549b)
Para la zona de radiación  , por lo que
de los sumandos para los campos
, por lo que
de los sumandos para los campos  y
y  , sólo
son apreciables los que corresponden a
potencias tipo
, sólo
son apreciables los que corresponden a
potencias tipo 

Estas ecuaciones de campo magnético y campo eléctrico corresponden a un dipolo de longitud finita. Estas expresiones son bastante complicadas, sin embargo en los problemas de antenas lo que mas interesa son los campos a distancias muy lejanas de la antena, es decir, regiones donde  . En estas circunstancias (en las zonas lejanas) podemos despreciar los términos ya que tienden a cero.
. En estas circunstancias (en las zonas lejanas) podemos despreciar los términos ya que tienden a cero.
Finalmente los campos se reducen a:


DENSIDAD DE POTENCIA INSTANTÁNEA
El flujo de energía que se transforma en el campo, se puede medir en función de la rapidez , con la que fluye la energía por unidad de superficie, se conoce como vector de Poynting y esta dado por:

Queremos obtener la densidad de potencia instantánea .La expresión instantánea del vector de Poynting o vector de densidad de potencia es :
![\mathbf{S}(\bar{r},t)=Re[\mathbf{E}(\bar{r},t)]\times Re[\mathbf{H}(\bar{r},t)]...\left(2\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f732ed78eac68644a4cae81a11e84aa167abb12a)
Calcularemos la densidad de potencia instantánea para los campos de radiación para el dipolo eléctrico .Los campos de radiación son:


Tomando la parte real de cada uno de ellos, puesto que es la que efectivamente radia la antena, y corresponde al flujo de potencia que atraviesa una unidad de área esférica, mientras que la imaginaria corresponde a aquella que se disipa alrededor de la antena en forma de calor:


Resolviendo la ecuación (2) en base a las ecuaciones (5) y (6) tenemos :

Que es la densidad de potencia instantánea (véase A-1).
Nos interesa calcular la densidad de potencia media(irradiancia), esta se obtiene en un tiempo promedio sobre un ciclo completo donde  que es el periodo temporal de la onda (Intervalo de tiempo para que se repita la forma de la onda)
que es el periodo temporal de la onda (Intervalo de tiempo para que se repita la forma de la onda)

Resolviendo la ecuación (8) para la densidad de potencia instantánea obtenida en la ecuación (7) tenemos (véase A-2):

En el caso general podemos calcular la intensidad de potencia media en una onda que se propaga:

Nos damos cuenta que la energía radial por carga se mueve arbitrariamente en función de su momento dipolar eléctrico P.
CONCLUSION
El vector poynting equivale a la densidad instantánea de potencia que suministra una antena. Esta densidad instantánea de potencia se compone de una parte real (densidad promedio de potencia radiada) y una parte imaginaria (densidad promedio de potencia reactiva). La densidad de potencia radiada es la que efectivamente radia la antena, y corresponde al flujo de potencia que atraviesa una unidad de área esférica, mientras que la reactiva corresponde a aquella que se disipa alrededor de la antena en forma de calor.
A frecuencias Ópticas la densidad instantánea es una función extremadamente rápida variando en función del tiempo, por lo tanto se emplea el promedio temporal, que absorbe la energía radiante en un intervalo de tiempo finito utilizado, por ejemplo: la película de la placa de la retina del ojo humano.
APÉNDICE A
A-1
![\mathbf {S}(\bar{r},t)=Re[\mathbf{E_{\theta}}(\bar{r},t)]\times Re[\mathbf{H_{\phi}}(\bar{r},t)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1e2da45ae373792e1d64558767e483dac421aedd)


El producto cruz es una multiplicación de vectores .Dados dos vectores A y B, el producto cruz se denota A B (“A cruzB ”) que es otro vector definido por :
Donde es el ángulo más pequeño entre los vectores A y B y es un vector unitario normal (perpendicular ) al plano que contiene A y B. Por lo tanto , el producto cruz A
B (“A cruzB ”) que es otro vector definido por :
Donde es el ángulo más pequeño entre los vectores A y B y es un vector unitario normal (perpendicular ) al plano que contiene A y B. Por lo tanto , el producto cruz A B produce otro vector cuya dirección se obtiene por la regla de la mano derecha al girar de A a B.
B produce otro vector cuya dirección se obtiene por la regla de la mano derecha al girar de A a B.

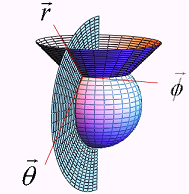
Un punto  en coordenadas esféricas se especifica como la intersección de tres superficies siguientes: una superficie esférica centrada en el origen con el radio
en coordenadas esféricas se especifica como la intersección de tres superficies siguientes: una superficie esférica centrada en el origen con el radio  ; un cono circular recto con sus vértices en el origen , su eje coincidente con el eje +z y un ángulo mitad
; un cono circular recto con sus vértices en el origen , su eje coincidente con el eje +z y un ángulo mitad  ; y un semiplano con el eje z como arista y que forma un ángulo
; y un semiplano con el eje z como arista y que forma un ángulo con el plano xz.
con el plano xz.
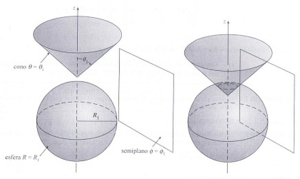
superficie esferica, un cono circular recto y un semi plano que contiene el eje z 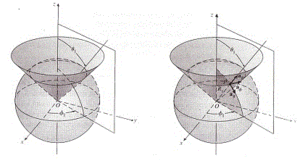
La intersección de la esfera, el cono y el semiplano especifican el punto P Observe que el vector base  en P es radial desde el origen .El vector base
en P es radial desde el origen .El vector base  está en el plano
está en el plano  y es tangencial a la superficie esférica , mientras que el vector de base
y es tangencial a la superficie esférica , mientras que el vector de base  es el mismo que las coordenadas cilíndricas (tangencial a la superficie del cono medio)
es el mismo que las coordenadas cilíndricas (tangencial a la superficie del cono medio)
ESTA GRÁFICA MUESTRA MEJOR LAS COORDENADAS ESFÉRICAS
Usando el sistema de la regla de la mano derecha tenemos :
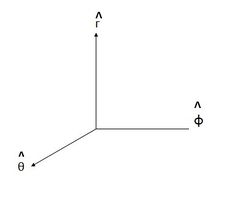
Es el nuevo plano en coordenadas esféricas



A-2
La integral se resuelve :


Ocupando la propiedad trigonométrica



para resolver la integral del lado derecho , hacemos un cambio de variable




DONDE:
Finalmente solo queda el termino de un medio :

Referencias
Classical Electromagnetic Radiation, Jerry B. Marion, Second Edition
Introduction to electrodynamics , David.J.Griffithis, Third Edition
Optics, Hecht, Third Edition
--Diana Rodriguez Almaraz. 06:47 23 jul 2012 (UTC)





































![=i(\frac{c^{2}}{\omega})[\nabla\times\overrightarrow{\boldsymbol{B}}+\nabla^{2}\overrightarrow{\boldsymbol{A}}+(\frac{\omega^{2}}{c^{2}})\overrightarrow{\boldsymbol{A}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/be2f9b4e8bee144107566eb7badf0cb51fe85860)
![=i(\frac{c^{2}}{\omega})[\nabla\times\overrightarrow{\boldsymbol{B}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/31274a65984b4fad1c20751c8dd9c2163454c626)
![\overrightarrow{\boldsymbol{B}}=-\frac{\mu_{0}k^{2}\omega\boldsymbol{p}_{0}}{4\pi}[\frac{1}{kr}+\frac{i}{(kr)^{2}}]\sin\theta e^{i(kr-\omega t)}\hat{\phi}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c4eeccc6105a2cba0a29dca430ca1608c747debf)
![\overrightarrow{\boldsymbol{E}}=-\frac{k^{3}\boldsymbol{p}_{0}}{4\pi\epsilon_{0}}\{[\frac{2i}{(kr)^{2}}-\frac{2}{(kr)^{3}}]\cos\theta\hat{r}+[\frac{1}{kr}+\frac{1}{(kr)^{2}}-\frac{1}{(kr)^{3}}]\sin\theta\hat{\theta}\}e^{i(kr-\omega t)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/00515ec142d3d7f627c7ed9d88f4a44d70d5549b)









![\mathbf{S}(\bar{r},t)=Re[\mathbf{E}(\bar{r},t)]\times Re[\mathbf{H}(\bar{r},t)]...\left(2\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f732ed78eac68644a4cae81a11e84aa167abb12a)









![\mathbf {S}(\bar{r},t)=Re[\mathbf{E_{\theta}}(\bar{r},t)]\times Re[\mathbf{H_{\phi}}(\bar{r},t)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1e2da45ae373792e1d64558767e483dac421aedd)