Diferencia entre revisiones de «Radiacion: Potencial de Lienard Wiechert»
Sin resumen de edición |
|||
| (No se muestran 30 ediciones intermedias de 3 usuarios) | |||
| Línea 2: | Línea 2: | ||
El potencial escalar y el potencial vectorial para campos estáticos se puede calcular con las ecuaciones: | El potencial escalar y el potencial vectorial para campos estáticos se puede calcular con las ecuaciones: | ||
\begin{equation} | |||
\Phi(\mathbf{r})=\int\limits_v\frac{\rho(\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|}\,\mathrm{d}v' | |||
\label{1} | |||
\end{equation} | |||
\begin{equation} | |||
\mathbf{A}(\mathbf{r})=\frac{1}{c}\int\limits_v\frac{\mathbf{J}(\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|}\mathrm{d}v' | |||
\label{2} | |||
\end{equation} | |||
En estas ecuaciones esta explícitamente indicado que el potencial será evaluado en la posición designada por el radio | En estas ecuaciones esta explícitamente indicado que el potencial será evaluado en la posición designada por el radio | ||
vector <math>\mathbf{r}</math>. La distancia entre el punto de integración <math>r'</math> y el punto en que serán evaluados <math>\Phi</math> y <math>\mathbf{A}</math> es <math>|r-r'|</math> y <math>dv'</math> es el elemento de volumen en <math>\mathbf{r'}</math> | vector <math>\mathbf{r}</math>. La distancia entre el punto de integración <math>r'</math> y el punto en que serán evaluados <math>\Phi</math> y <math>\mathbf{A}</math> es <math>|r-r'|</math> y <math>dv'</math> es el elemento de volumen en <math>\mathbf{r'}</math> | ||
Consideremos el cálculo del potencial escalar en una posición R al tiempo t. No podemos calcular <math>\Phi(r,t)</math> de (1) si las cargas están en | Consideremos el cálculo del potencial escalar en una posición $R$ al tiempo $t$. No podemos calcular <math>\Phi(r,t)</math> de (\ref{1}) si las cargas están en | ||
movimiento arbitrario por que el campo eléctrico asociado con las cargas se propaga a una velocidad finita c. | movimiento arbitrario por que el campo eléctrico asociado con las cargas se propaga a una velocidad finita $c$. | ||
Para ello debemos saber la posición de las cargas, no a un tiempo t, si no a un tiempo anterior <math>t-|r-r'|/c</math> el cual corresponde a los tiempos en el cual los campos eléctricos fueron emitidos de las cargas en las posiciones indicadas por r' para llegar a r al tiempo t. | Para ello debemos saber la posición de las cargas, no a un tiempo t, si no a un tiempo anterior <math>t-|r-r'|/c</math> el cual corresponde a los tiempos en el cual los campos eléctricos fueron emitidos de las cargas en las posiciones indicadas por r' para llegar a $r$ al tiempo $t$. | ||
Los cálculos de los campos individuales deben realizarse a tiempos retardados: | Los cálculos de los campos individuales deben realizarse a tiempos retardados: | ||
tiempo retardado | |||
\begin{equation} | |||
\text{tiempo retardado} = t-\frac{|\mathbf{\mathbf{r}-\mathbf{r'}|}}{c} | |||
\label{3} | |||
\end{equation} | |||
Por lo tanto, en el caso general debemos modificar la expresión para <math>\Phi</math> y <math>A</math> | Por lo tanto, en el caso general debemos modificar la expresión para <math>\Phi</math> y <math>A</math> | ||
\begin{equation} | |||
\Phi(\mathbf{r},t)=\int\limits_v\frac{\rho(\mathbf{r'},t-|\mathbf{r}-\mathbf{r'}|/c)}{|\mathbf{r}-\mathbf{r'}|} | |||
\label{4} | |||
\end{equation} | |||
\begin{equation} | |||
\mathbf{A}(\mathbf{r},t)=\frac{1}{c}\int\limits_v\frac{\mathbf{J}(\mathbf{r'},t-|\mathbf{r}-\mathbf{r'}|/c)}{|\mathbf{r}-\mathbf{r}|}\,\mathrm{d}v' | |||
\label{5} | |||
\end{equation} | |||
Estos potenciales son conocidos como Potenciales Retardados, notemos que <math>\mathbf{J(r')}</math> y <math>\rho(\mathbf{r'})</math> han de ser evaluados en el tiempo retardado. | Estos potenciales son conocidos como Potenciales Retardados, notemos que <math>\mathbf{J(r')}</math> y <math>\rho(\mathbf{r'})</math> han de ser evaluados en el tiempo retardado. | ||
| Línea 31: | Línea 51: | ||
Para una carga puntual, la localización es una función delta en el tiempo, | Para una carga puntual, la localización es una función delta en el tiempo, | ||
[[Archivo:Trayectoria.png|300x200px|thumb|rigth|<center>Fig (1) Geometría de una carga en movimiento</center>]] | [[Archivo:Trayectoria.png|300x200px|thumb|rigth|<center>Fig (1) Geometría de una carga en movimiento</center>]] | ||
== Potencial de Lienard-Wiechert == | == Potencial de Lienard-Wiechert == | ||
Consideremos una partícula cargada en movimiento a lo largo de la trayectoria descrita por el radio vector <math>\mathbf{r}_{e}(t')</math> , para una sola carga su ubicación está dada por una función delta en el tiempo, con esto podemos escribir el potencial retardado como una integral sobre el tiempo en lugar del volumen: | Consideremos una partícula cargada en movimiento a lo largo de la trayectoria descrita por el radio vector <math>\mathbf{r}_{e}(t')</math> , para una sola carga su ubicación está dada por una función delta en el tiempo, con esto podemos escribir el potencial retardado como una integral sobre el tiempo en lugar del volumen: | ||
\begin{equation} | |||
\Phi(\mathbf{r},t)=e\int\limits_{-\infty}^\infty\frac{\delta(t'-t+|\mathbf{r}-\mathbf{r_{e}}|/c)}{|\mathbf{r}-\mathbf{r_{e}}|}\,\mathrm{d}t' | |||
\label{6} | |||
\end{equation} | |||
Para resolver la integral hacemos un cambio de variable de tal manera que la variable de integración sea el mismo que el argumento de la función delta. La integral es entonces sólo el valor del integrando tomada en el momento que es permitido por la función delta. Definimos entonces una nueva variable <math>t''</math> igual al argumento de la función delta: | Para resolver la integral hacemos un cambio de variable de tal manera que la variable de integración sea el mismo que el argumento de la función delta. La integral es entonces sólo el valor del integrando tomada en el momento que es permitido por la función delta. Definimos entonces una nueva variable <math>t''</math> igual al argumento de la función delta: | ||
Diferenciamos la ecuación y hacemos <math>dt=0</math> puesto que t es el tiempo fijo de observación, obtenemos entonces: | |||
\begin{equation} | |||
t''=t'-t+|\mathbf{r}-\mathbf{r_{e}(t')}|/c | |||
\label{7} | |||
\end{equation} | |||
Diferenciamos la ecuación y hacemos <math>dt=0</math> puesto que $t$ es el tiempo fijo de observación, obtenemos entonces: | |||
\begin{equation} | |||
dt''=dt'(1+\frac{1}{c}\frac{d}{dt}|\mathbf{r}-\mathbf{r_{e}(t')}|) | |||
\label{8} | |||
\end{equation} | |||
La cantidad <math>|\mathbf{r}-\mathbf{r_{e})}|</math> es solo | La cantidad <math>|\mathbf{r}-\mathbf{r_{e})}|</math> es solo | ||
donde el subíndice <math>r_{e}</math> indica que el gradiente será tomado respecto de las coordenadas de la carga. El operador gradiente | \begin{equation} | ||
|\mathbf{r}-\mathbf{r_{e}}(t')|=\sqrt{\sum_{i}(x_{i}-x_{e,i})^2} | |||
\label{9} | |||
\end{equation} | |||
donde <math>x_{e,i}=x_{e,i}(t')</math> depende implícitamente de $t'$ y <math>x_{i}</math> está fijo. Entonces la derivada en (\ref{8}) es: | |||
<center> | |||
<math>\frac{1}{c}\frac{d}{dt'}|\mathbf{r}-\mathbf{r_{e}}(t')|=\frac{1}{c}\sum_{i}(\frac{\partial}{\partial x_{e,i}}|\mathbf{r}-\mathbf{r_{e}(t')|})\frac{dx_{e,i}}{dt'}=\frac{1}{c}(\mathbf{grad_{r_{e}}}|\mathbf{r}-\mathbf{r_{e}}|)\frac{d\mathbf{r}_{e}}{dt'}</math> | |||
</center> | |||
Donde el subíndice <math>r_{e}</math> indica que el gradiente será tomado respecto de las coordenadas de la carga. El operador gradiente también puede ser expresado como: | |||
\begin{equation} | |||
\mathbf{grad}_{r_{e}}|\mathbf{r}-\mathbf{r}_{e}|=-\frac{|\mathbf{r}-\mathbf{r}_{e}|}{|\mathbf{r}-\mathbf{r}_{e}|}=-\frac{\mathbf{R}}{R} | |||
\label{10} | |||
\end{equation} | |||
La derivada de <math>r_{e}</math> con respecto a t es justamente la velocidad de la partícula <math>\mathbf{u}</math>. Definimos | La derivada de <math>r_{e}</math> con respecto a $t$ es justamente la velocidad de la partícula <math>\mathbf{u}</math>. Definimos | ||
<center> | <center> | ||
| Línea 75: | Línea 113: | ||
</center> | </center> | ||
\begin{equation} | |||
dt''=dt'(1+\frac{1}{c}\frac{d}{dt}|\mathbf{r}-\mathbf{r_{e}(t')}|)=dt'(1-\frac{\beta\cdot \mathbf{R}}{R}) | |||
\label{11} | |||
\end{equation} | |||
ó | |||
<center> | <center> | ||
<math>dt | <math>dt'=\frac{R}{R-\beta\cdot\mathbf{R}}dt''</math> | ||
</center> | </center> | ||
== Partícula cargada | Con el cambio de variable definido, la ecuación para <math>\Phi(\mathbf{r},t)</math> se convierte en | ||
Supongamos que tenemos una partícula cargada en una órbita circular (radio <math>\rho</math>), | |||
<math>\ | \begin{equation} | ||
\Phi(\mathbf{r},t)=e\int\limits_{-\infty}^\infty\frac{\delta(t'')}{R(t')}(\frac{R(t')}{R(t')-\beta(t')\cdot\mathbf{R}})dt'' | |||
\label{12} | |||
\end{equation} | |||
Es ahora fácil resolver la integral si sabemos que la integral delta sobre todo el espacio vale uno. | |||
\begin{equation} | |||
\Phi(\mathbf{r},t)=\frac{e}{R(t')-\beta(t')\cdot\mathbf{R}}|_{t''=0} | |||
\label{13} | |||
\end{equation} | |||
Pero <math>t''=0</math> implica <math>t'=t-\mathbf{R}(t')/c</math> el cual es el tiempo retardado. Entonces: | |||
\begin{equation} | |||
\Phi(\mathbf{r},t)=\frac{e}{R-\beta\cdot\mathbf{R}} | |||
\label{14} | |||
\end{equation} | |||
Haciendo un procedimiento análogo encontramos el potencial vectorial: | |||
\begin{equation} | |||
\mathbf{A}(\mathbf{r},t)=\frac{e\beta}{R-\beta\cdot\mathbf{R}} | |||
\label{15} | |||
\end{equation} | |||
Las ecuaciones (\ref{14}) y (\ref{15}) que exhiben explícitamente la dependencia de la velocidad de la partícula en el potencial, son conocidos como los ''potenciales de Liénard-Wiechert'' | |||
Ahora para obtener los campos, basta aplicar las ecuaciones de Maxwel a los potenciales. | |||
== Campos Retardados== | |||
La derivación de éstos resultados se encuentra en [[Radiacion: campos retardados|campos retardados]]. | |||
Los campos retardados de ''Liénard-Wiechert'' son | |||
<center> | |||
<math>\mathbf{B}=e((\frac{\beta\times \mathbf{n})(\alpha-\beta^2)}{(1-\beta\cdot\mathbf{n})^3R^2})+\frac{(\mathbf{\alpha\cdot n})(\beta\times \mathbf{n})}{c^2 (1-\beta\cdot\mathbf{n})^3R}+\frac{(\alpha\times \mathbf{n})}{c^2 (1-\beta\cdot\mathbf{n})^2 R}</math> | |||
</center> | |||
<center> | |||
<math>\mathbf{E}=\frac{e}{\epsilon }\frac{\mathbf {(n-\beta)(1-\beta^2) }}{(1-\mathbf{\beta\cdot n})^3 R^2}+\frac{e}{\epsilon c}\frac{\mathbf {n\times((n-\beta)\times\alpha) }}{(1-\mathbf{\beta\cdot n})^3 R}</math> | |||
</center> | |||
con <math>\mathbf{n}=\frac{\mathbf{R}}{R}</math> | |||
El campo eléctrico puede ser separado en dos términos. El primero que involucra a la velocidad, pero no a la aceleración de la partícula, el cual se reduce al campo coulombiano para bajas velocidades. Y el segundo término es proporcional a la aceleración de la partícula | |||
== Partícula cargada confinada a movimiento circular == | |||
[[Archivo:Spherical.jpg|400x350px|thumb|rigth|<center>Fig (2) Carga en movimiento circular</center>]] | |||
Supongamos que tenemos una partícula cargada en una órbita circular (radio <math>\rho</math>),el vector de aceleración <math>\alpha</math>esta dirigido hacia el centro de la órbita y es perpendicular a la velocidad <math>\mathbf{\beta}</math> | |||
<center> | |||
<math>\omega=\beta_{0}/\rho</math> | |||
<math>\alpha_{0}=\rho \omega^2</math> | |||
</center> | |||
<math></math> | <math></math> | ||
El campo eléctrico | El campo eléctrico retardado esta dado por: | ||
<center> | |||
<math>\mathbf{E}=\frac{e}{\epsilon }\frac{\mathbf {(n-\beta)(1-\beta^2) }}{(1-\mathbf{\beta\cdot n})^3 R^2}+\frac{e}{\epsilon c}\frac{\mathbf {n\times((n-\beta)\times\alpha) }}{(1-\mathbf{\beta\cdot n})^3 R}</math> | |||
</center> | |||
Donde el primer término representa el campo de velocidad y el segundo el campo de aceleración. | |||
<math>\mathbf{ | Para el cálculo de los campos, usamos coordenadas esféricas para describir la posición del observador, las componentes del vector <math>\mathbf{R}</math> en coordenadas cartesianas están dadas por: | ||
<center> | |||
<math>x=r\cos\theta\cos\phi</math> | <math>x=r\cos\theta\cos\phi</math> | ||
</center> | </center> | ||
<center> | |||
<math>y=r\sin\theta\cos\phi</math> | <math>y=r\sin\theta\cos\phi</math> | ||
</center> | </center> | ||
| Línea 100: | Línea 203: | ||
</center> | </center> | ||
--[[Usuario:Carlos López Cobá|Carlos López Cobá]] 00:59 22 jul 2012 (UTC) | El vector de velocidad y aceleración están sobre el plano XZ con componentes: | ||
<center> | |||
<math>\beta=\beta_{0}(\cos\omega t,0,\sin\omega t)</math> | |||
<math>\alpha=\alpha_{0}(-\sin\omega t,0,\cos\omega t)</math> | |||
</center> | |||
de tal manera que se verifica que <math>\beta\bot\alpha</math>. | |||
Veámos como cambia el campo eléctrico de aceleración,a medida que variamos los ángulos <math>\phi</math> y <math>\theta</math>. | |||
Primero Analicemos el caso en el que <math>\beta</math> y R son coplanares. Para esto hacemos que el vector de velocidad apunte en dirección al eje x, haciendo <math>t=\pi/\omega</math> por lo que se verifica que <math>\beta=\beta_{0}(\cos\pi t,0,0)</math> y hacemos <math>\theta=\pi</math>, con esto el vector R esta en el plano (-X,Z). | |||
=== Gráficas campo E aceleración === | |||
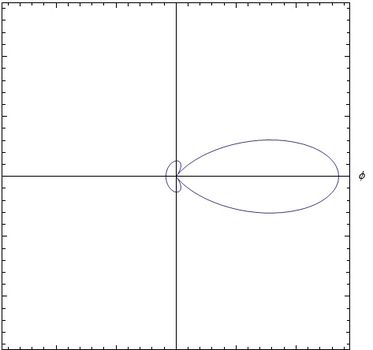
En todas las gráficas, la velocidad está en dirección del eje <math>-x</math> y la aceleración es es perpendicular a esta. A medida que se incrementa la velocidad, el Campo de aceleración, aumenta en la perpendicular. esto es en <math>\phi</math>=0,<math>\theta=\pi</math> que es el eje y positivo. | |||
{| | |||
|- | |||
| [[Archivo:CampoEFig1.jpg|400x350px|thumb|left|<center>Fig (3) <math>\beta=0.1</math></center>]] | |||
| [[Archivo:CampoEFig4.jpg|400x350px|thumb|rigth|<center>Fig (4) <math>\beta=0.4</math></center>]] | |||
|- | |||
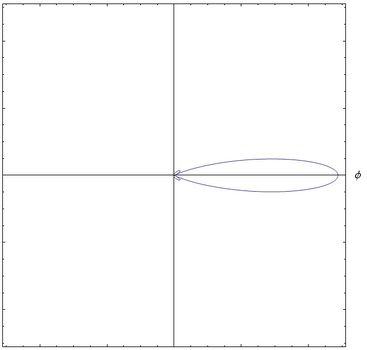
| [[Archivo:CampoEFig6.jpg|400x350px|thumb|left|<center>Fig (5) <math>\beta=0.6</math></center>]] | |||
| [[Archivo:CampoEFig9.jpg|400x350px|thumb|rigth|<center>Fig (6) <math>\beta=0.9</math>, para velocidades relativistas, el campo E aumenta en gran medida en la perpendicular a la aceleración</center>]] | |||
|} | |||
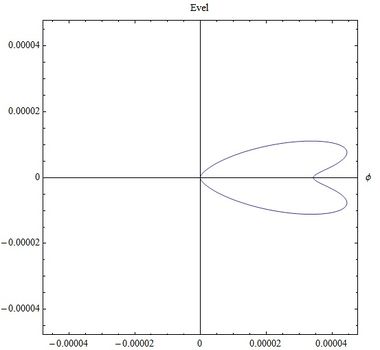
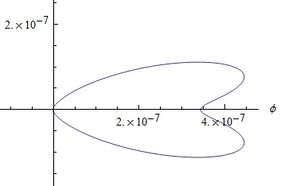
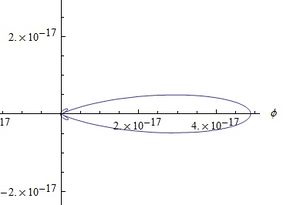
=== Gráficas campo E velocidad === | |||
{| | |||
|- | |||
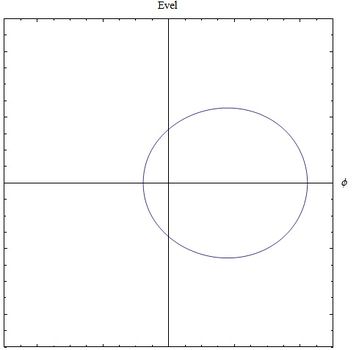
| [[Archivo:CampoVFig1.jpg|400x350px|thumb|left|<center>Fig (7) <math>\beta=0.1</math> para velocidades bajas, el campo de velocidad se reduce al de Coulomb</center>]] | |||
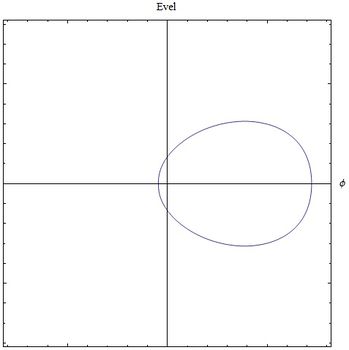
| [[Archivo:CampoVFig4.jpg|400x350px|thumb|rigth|<center>Fig (8) <math>\beta=0.4</math></center>]] | |||
|- | |||
| [[Archivo:CampoVFig6.jpg|400x350px|thumb|left|<center>Fig (9) <math>\beta=0.6</math></center>]] | |||
| [[Archivo:CampoVFig9.jpg|400x350px|thumb|rigth|<center>Fig (10) <math>\beta=0.9</math></center>]] | |||
|} | |||
=== Gráficas campo E total === | |||
Veamos ahora como es el comportamiento del campo eléctrico total, en distancias cortas y grandes. | |||
{| | |||
|- | |||
| [[Archivo:Lejano1.jpg|thumb|left|<center>Fig (11) <math>\beta=0.9,r=1</math></center>]] | |||
| [[Archivo:Lejano2.jpg|thumb|rigth|<center>Fig (12) <math>\beta=0.9, r=1000000</math></center>]] | |||
|} | |||
Observamos que justamente, para campo lejano, el campo de aceleración es el que domina. | |||
En este último ejemplo, hemos hecho <math>\theta=\pi/2</math> | |||
{| | |||
|- | |||
| [[Archivo:EtotFig1.jpg|400x350px|thumb|left|<center>Fig (11) <math>\beta=0.5 </math></center>]] | |||
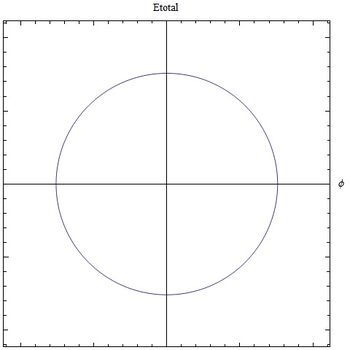
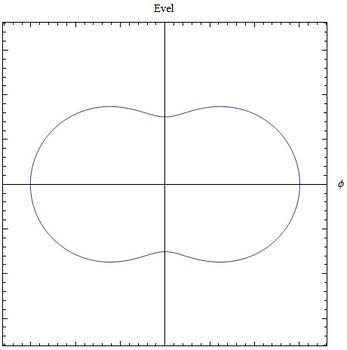
| [[Archivo:EtotFig2.jpg|400x350px|thumb|rigth|<center>Fig (12) <math>\beta=0.5</math> el campo E es máximo para <math>\phi=0</math> <math>\beta\bot R</math></center>]] | |||
|} | |||
== Referencias == | |||
Mark A. Heald,Jerry B. Marion ''Classical Electromagnetic Radiation'',Third Edition pp290 | |||
---- | |||
Aportación por usuario: [[Usuario:Carlos López Cobá|Carlos López Cobá]] 00:59 22 jul 2012 (UTC) | |||
---- | |||
[[categoría:Radiacion]] | |||
[[categoría:Cursos]] | |||
Revisión actual - 18:39 23 sep 2023
Potenciales Retardados
El potencial escalar y el potencial vectorial para campos estáticos se puede calcular con las ecuaciones:
\begin{equation}
\Phi(\mathbf{r})=\int\limits_v\frac{\rho(\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|}\,\mathrm{d}v'
\label{1}
\end{equation}
\begin{equation}
\mathbf{A}(\mathbf{r})=\frac{1}{c}\int\limits_v\frac{\mathbf{J}(\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|}\mathrm{d}v'
\label{2}
\end{equation}
En estas ecuaciones esta explícitamente indicado que el potencial será evaluado en la posición designada por el radio vector . La distancia entre el punto de integración y el punto en que serán evaluados y es y es el elemento de volumen en
Consideremos el cálculo del potencial escalar en una posición $R$ al tiempo $t$. No podemos calcular de (\ref{1}) si las cargas están en movimiento arbitrario por que el campo eléctrico asociado con las cargas se propaga a una velocidad finita $c$. Para ello debemos saber la posición de las cargas, no a un tiempo t, si no a un tiempo anterior el cual corresponde a los tiempos en el cual los campos eléctricos fueron emitidos de las cargas en las posiciones indicadas por r' para llegar a $r$ al tiempo $t$. Los cálculos de los campos individuales deben realizarse a tiempos retardados:
tiempo retardado
\begin{equation} \text{tiempo retardado} = t-\frac{|\mathbf{\mathbf{r}-\mathbf{r'}|}}{c} \label{3} \end{equation}
Por lo tanto, en el caso general debemos modificar la expresión para y
\begin{equation} \Phi(\mathbf{r},t)=\int\limits_v\frac{\rho(\mathbf{r'},t-|\mathbf{r}-\mathbf{r'}|/c)}{|\mathbf{r}-\mathbf{r'}|} \label{4} \end{equation}
\begin{equation}
\mathbf{A}(\mathbf{r},t)=\frac{1}{c}\int\limits_v\frac{\mathbf{J}(\mathbf{r'},t-|\mathbf{r}-\mathbf{r'}|/c)}{|\mathbf{r}-\mathbf{r}|}\,\mathrm{d}v'
\label{5}
\end{equation}
Estos potenciales son conocidos como Potenciales Retardados, notemos que y han de ser evaluados en el tiempo retardado.
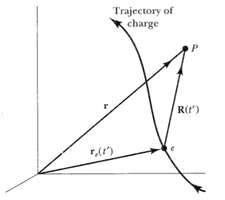
Consideremos una carga puntual moviéndose a lo largo de la trayectoria descrita por el radio vector como se muestra: Para una carga puntual, la localización es una función delta en el tiempo,
Potencial de Lienard-Wiechert
Consideremos una partícula cargada en movimiento a lo largo de la trayectoria descrita por el radio vector , para una sola carga su ubicación está dada por una función delta en el tiempo, con esto podemos escribir el potencial retardado como una integral sobre el tiempo en lugar del volumen:
\begin{equation} \Phi(\mathbf{r},t)=e\int\limits_{-\infty}^\infty\frac{\delta(t'-t+|\mathbf{r}-\mathbf{r_{e}}|/c)}{|\mathbf{r}-\mathbf{r_{e}}|}\,\mathrm{d}t' \label{6} \end{equation}
Para resolver la integral hacemos un cambio de variable de tal manera que la variable de integración sea el mismo que el argumento de la función delta. La integral es entonces sólo el valor del integrando tomada en el momento que es permitido por la función delta. Definimos entonces una nueva variable igual al argumento de la función delta:
\begin{equation}
t''=t'-t+|\mathbf{r}-\mathbf{r_{e}(t')}|/c
\label{7}
\end{equation}
Diferenciamos la ecuación y hacemos puesto que $t$ es el tiempo fijo de observación, obtenemos entonces:
\begin{equation} dt''=dt'(1+\frac{1}{c}\frac{d}{dt}|\mathbf{r}-\mathbf{r_{e}(t')}|) \label{8} \end{equation}
La cantidad es solo
\begin{equation}
|\mathbf{r}-\mathbf{r_{e}}(t')|=\sqrt{\sum_{i}(x_{i}-x_{e,i})^2}
\label{9}
\end{equation}
donde depende implícitamente de $t'$ y está fijo. Entonces la derivada en (\ref{8}) es:
Donde el subíndice indica que el gradiente será tomado respecto de las coordenadas de la carga. El operador gradiente también puede ser expresado como:
\begin{equation} \mathbf{grad}_{r_{e}}|\mathbf{r}-\mathbf{r}_{e}|=-\frac{|\mathbf{r}-\mathbf{r}_{e}|}{|\mathbf{r}-\mathbf{r}_{e}|}=-\frac{\mathbf{R}}{R} \label{10} \end{equation}
La derivada de con respecto a $t$ es justamente la velocidad de la partícula . Definimos
con
Por lo que
\begin{equation}
dt''=dt'(1+\frac{1}{c}\frac{d}{dt}|\mathbf{r}-\mathbf{r_{e}(t')}|)=dt'(1-\frac{\beta\cdot \mathbf{R}}{R})
\label{11}
\end{equation}
ó
Con el cambio de variable definido, la ecuación para se convierte en
\begin{equation}
\Phi(\mathbf{r},t)=e\int\limits_{-\infty}^\infty\frac{\delta(t'')}{R(t')}(\frac{R(t')}{R(t')-\beta(t')\cdot\mathbf{R}})dt''
\label{12}
\end{equation}
Es ahora fácil resolver la integral si sabemos que la integral delta sobre todo el espacio vale uno.
\begin{equation} \Phi(\mathbf{r},t)=\frac{e}{R(t')-\beta(t')\cdot\mathbf{R}}|_{t''=0} \label{13} \end{equation}
Pero implica el cual es el tiempo retardado. Entonces:
\begin{equation} \Phi(\mathbf{r},t)=\frac{e}{R-\beta\cdot\mathbf{R}} \label{14} \end{equation}
Haciendo un procedimiento análogo encontramos el potencial vectorial:
\begin{equation} \mathbf{A}(\mathbf{r},t)=\frac{e\beta}{R-\beta\cdot\mathbf{R}} \label{15} \end{equation}
Las ecuaciones (\ref{14}) y (\ref{15}) que exhiben explícitamente la dependencia de la velocidad de la partícula en el potencial, son conocidos como los potenciales de Liénard-Wiechert Ahora para obtener los campos, basta aplicar las ecuaciones de Maxwel a los potenciales.
Campos Retardados
La derivación de éstos resultados se encuentra en campos retardados.
Los campos retardados de Liénard-Wiechert son
con
El campo eléctrico puede ser separado en dos términos. El primero que involucra a la velocidad, pero no a la aceleración de la partícula, el cual se reduce al campo coulombiano para bajas velocidades. Y el segundo término es proporcional a la aceleración de la partícula
Partícula cargada confinada a movimiento circular
Supongamos que tenemos una partícula cargada en una órbita circular (radio ),el vector de aceleración esta dirigido hacia el centro de la órbita y es perpendicular a la velocidad
El campo eléctrico retardado esta dado por:
Donde el primer término representa el campo de velocidad y el segundo el campo de aceleración.
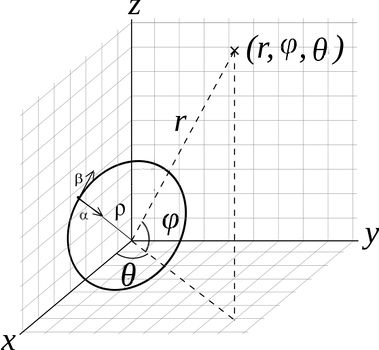
Para el cálculo de los campos, usamos coordenadas esféricas para describir la posición del observador, las componentes del vector en coordenadas cartesianas están dadas por:
El vector de velocidad y aceleración están sobre el plano XZ con componentes:
de tal manera que se verifica que .
Veámos como cambia el campo eléctrico de aceleración,a medida que variamos los ángulos y . Primero Analicemos el caso en el que y R son coplanares. Para esto hacemos que el vector de velocidad apunte en dirección al eje x, haciendo por lo que se verifica que y hacemos , con esto el vector R esta en el plano (-X,Z).
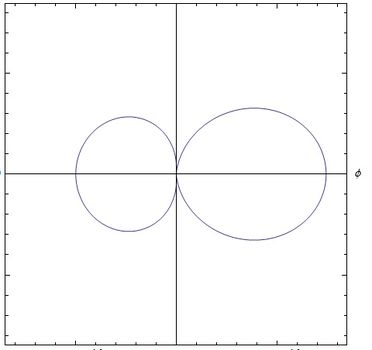
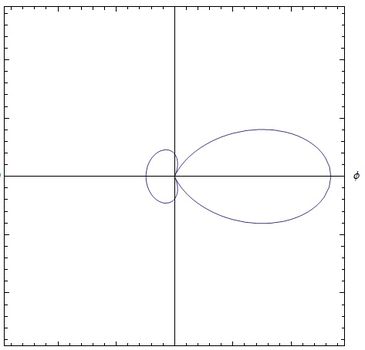
Gráficas campo E aceleración
En todas las gráficas, la velocidad está en dirección del eje y la aceleración es es perpendicular a esta. A medida que se incrementa la velocidad, el Campo de aceleración, aumenta en la perpendicular. esto es en =0, que es el eje y positivo.
Gráficas campo E velocidad
Archivo:CampoVFig1.jpg |
|
Gráficas campo E total
Veamos ahora como es el comportamiento del campo eléctrico total, en distancias cortas y grandes.
Observamos que justamente, para campo lejano, el campo de aceleración es el que domina.
En este último ejemplo, hemos hecho
Referencias
Mark A. Heald,Jerry B. Marion Classical Electromagnetic Radiation,Third Edition pp290
Aportación por usuario: Carlos López Cobá 00:59 22 jul 2012 (UTC)