Radiacion: Dispersion en dielectricos

Introducción

La interacción de ondas con la materia concierne la interacción de radiación electromagnética con electrones, átomos y moléculas. Para estudiar esta interacción reemplazaremos la materia por un conjunto de osciladores clásicos, electrones en particular, algunas veces sostenidas por fuerzas de resortes a los núcleos, y oscilando en respuesta a una fuerza electromagnética que actúa sobre ellos.

Ondas electromagnéticas en dieléctricos

Nos encargaremos a estudiar la respuesta de materiales dieléctricos o aislantes a los campos electromagnéticos.

El efecto neto de introducir un dieléctrico isótropo y homogéneo en una región del espacio libre es cambiar $\epsilon _{0}$ por $\epsilon$ y $\mu _{0}$ por $\mu$ en las ecuaciones de Maxwell. La velocidad de fase en el medio pasa a ser

$v=1/{\sqrt {\epsilon \mu }}\qquad (1)$

El cociente entre la velocidad de la onda electromagnética en el vacío y en la materia se denomina índice de refracción absoluto $n$:

$n={\frac {c}{v}}={\sqrt {\frac {\epsilon \mu }{\epsilon _{0}\mu _{0}}}}\qquad (2)$

En términos de permitividad y permeabilidad relativas del medio, $n$ pasa a ser:

$n={\sqrt {\epsilon _{r}\mu _{r}}}\qquad (3)$

donde $\mu =\mu _{r}\mu _{0}$ y $\epsilon =\epsilon _{r}\epsilon _{0}$.

Existen sustancias magnéticas que resultan ser transparentes en las regiones infrarroja y de microondas de espectro. Sin embargo, nosotros estamos principalmente interesados en los materiales que son transparentes en el visible y todos estos son esencialmente no-magnéticos. $\mu _{r}$ generalmente no se desvía de 1 en más que unas pocas partes de $10^{4}$. Poniendo $\mu _{r}=1$ en la fórmula para $n$ resulta una expresión denominada relación de Maxwell, es decir

$n={\sqrt {\epsilon _{r}}}\qquad (4)$

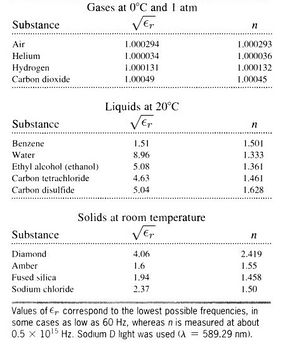
donde $\epsilon _{r}$ se supone que es la constante dieléctrica estática. Como se indica en la tabla 1 esta relación parece funcionar bien sólo para algunos gases simples. La dificultad surge porque $\epsilon _{r}$ y, por lo tanto, $n$ dependen realmente de la frecuencia. La dependencia de $n$ con la longitud de onda de la luz es un efecto conocido con el nombre de dispersión. Surge a nivel microscópico, y por lo tanto en las ecuaciones de Maxwell casi no se da cuenta de ello. Hace más de 300 años, Isaac Newton utilizó unos prismas para dispersar la luz blanca en sus colores constituyentes, y el fenómeno era ya entonces, sino bien entendido, si bien conocido.

Tabla 1. Relaciones de Maxwell

La teoría de Maxwell considera la materia como continua, representando sus respuestas eléctricas y magnéticas a los campos aplicados $\mathbf {E}$ y $\mathbf {B}$ en términos de constantes $\epsilon$ y $\mu$. Por consiguiente, $\epsilon _{r}$ y $\mu _{r}$ son también constantes mientras que $n$ es, por lo tanto, de forma no realista, independiente de la frecuencia. Para poder analizar teóricamente la dispersión, es necesario incorporar la naturaleza atómica de la materia y aprovechar algún aspecto de la misma que depende de la frecuencia.

Cuando un dieléctrico está sujeto a un campo eléctrico aplicado, la distribución de la carga interna se distorsiona. Esto se debe a la generación de momentos dipolares eléctricos que, a su vez, contribuyen al campo interno total. De manera más sencilla, el campo externo separa las cargas negativas de las positivas del medio y luego ellas aportan un componente adicional del campo. El momento dipolar resultante por unidad de volumen se denomina polarización eléctrica $\mathbf {P}$. Para la mayoría de los materiales $\mathbf {P}$ y $\mathbf {E}$ son proporcionales y pueden relacionarse satisfactoriamente con

$\mathbf {P=\mathrm {\chi _{\mathit {e}}} E} \qquad (5)$

si,

$\epsilon =\epsilon _{0}(1+\chi _{e}),$

por lo tanto

$\mathbf {P} =(\epsilon -\epsilon _{0})\mathbf {E} \qquad (6)$

Dispersión

La dispersión corresponde al fenómeno en el cual el indice de refracción de un medio es dependiente de la frecuencia. Todos los medios materiales son dispersivos; únicamente el vació es no dispersivo.

Dispersión en gases

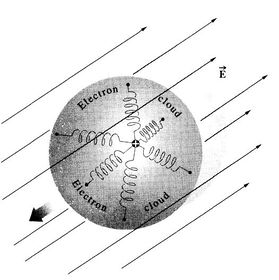
Un medio material se presenta como una agrupación, en el vacío, de un número muy elevado de átomos polarizables, cada uno de los cuales es pequeño (con respecto a longitud de onda de la luz) y está cerca de sus vecinos. Cuando una onda luminosa incide en dicho medio, cada átomo puede considerarse como una oscilador forzado amortiguado clásico que está siendo excitado por un campo eléctrico variable en el tiempo $\mathbf {E} (t)$ de la onda. La figura 1 es una representación mecánica de tal oscilador el medio isótropo donde la capa de carga negativa esta atada a un núcleo positivo estacionario por muelles idénticos. Aun en la luz brillante del sol, la amplitud de las oscilaciones no será mayor de unos $10^{17}$m. La fuerza $\mathbf {F} _{E}$ ejercida sobre un electrón de carga $q_{e}$ y por el campo $\mathbf {E} (t)$ de una onda armónica de frecuencia $\omega$, tiene la forma

Figura 1. Modelo del oscilador mecánico para un medio isótropo, todos los muelles son iguales y el oscilador puede vibrar por igual en todas las direcciones

$\mathbf {F} _{E}=q_{e}\mathbf {E} (t)=q_{e}\mathbf {E} _{0}e^{i\omega t}\qquad (7)$

Por consiguiente, la segunda ley de Newton proporciona la ecuación de movimiento; es decir, la suma de las fuerzas es igual a la masa por la aceleración

$q_{e}\mathbf {E} _{0}e^{i\omega t}-m_{e}\omega _{0}^{2}\mathbf {r} -m_{e}\gamma {\frac {d\mathbf {r} }{dt}}=m_{e}{\frac {d^{2}\mathbf {r} }{dt^{2}}}\qquad (8)$

Es el primer término de la izquierda es la fuerza impulsora y el segundo es la fuerza restablecedora opuesta, donde; $\omega _{0}$ es la frecuencia de resonancia o natural a la que el electrón oscilará alrededor de su punto de equilibrio, después de haber sido perturbado momentáneamente por la fuerza, que viene dada por $\omega _{0}={\sqrt {k/m_{e}}}$ donde $m_{e}$ es su masa, la tercera representa la fuerza de amortiguamiento que es proporcional a la velocidad donde $\gamma$ es el factor de amortiguamiento. Para satisfacer la ecuación 8, $\mathbf {r}$ tendrá que ser una función cuya segunda derivada temporal no sea muy distinta a $\mathbf {r}$. Así que proponemos la solución a la ecuación de la forma:

$\mathbf {r} (t)=\mathbf {r} _{0}e^{i\omega t}$

y la reemplazamos en la ecuación 8 para calcular la amplitud $\mathbf {r} _{0}$.

Calculamos primero

${\frac {d\mathbf {r} }{dt}}=\mathbf {r} _{0}i\omega e^{i\omega t}$

y después

${\frac {d^{2}\mathbf {r} }{dt^{2}}}=-\omega ^{2}\mathbf {r} _{0}e^{i\omega t}$

sustituyendo

$q_{e}\mathbf {E} _{0}e^{i\omega t}-m_{e}\omega _{0}^{2}\mathbf {r} _{0}e^{i\omega t}-m_{e}\gamma \mathbf {r} _{0}i\omega e^{i\omega t}=-m_{e}\omega ^{2}\mathbf {r} _{0}e^{i\omega t}$

despejamos $\mathbf {r} _{0}$ y queda

$\mathbf {r} _{0}={\frac {q_{e}/m_{e}}{(\omega _{0}^{2}-\omega ^{2}+i\gamma \omega )}}\mathbf {E} _{0}$

De esta manera encontramos que

$\mathbf {r} (t)={\frac {q_{e}/m_{e}}{(\omega _{0}^{2}-\omega ^{2}+i\gamma \omega )}}\mathbf {E} _{0}e^{i\omega t}\qquad (9)$

o,

$\mathbf {r} (t)={\frac {q_{e}/m_{e}}{(\omega _{0}^{2}-\omega ^{2}+i\gamma \omega )}}\mathbf {E} (t)\qquad (10)$

Éste es el desplazamiento relativo entre la nube negativa y el núcleo positivo. Tradicionalmente, se deja $q_{e}$ positiva y se habla del desplazamiento del oscilador.

El momento dipolar equivale a la carga $q_{e}$ multiplicada por su desplazamiento y esta dado por $\mathbf {p} =q_{e}\mathbf {r}$, o

$\mathbf {p} ={\frac {q_{e}^{2}/m_{e}}{(\omega _{0}^{2}-\omega ^{2}+i\gamma \omega )}}\mathbf {E} \qquad (11)$

y ahora suponemos que existen un número de electrones $N$ por unidad de volumen. No todos los electrones, sin embargo, tienen la misma constante de resorte y de ahí la misma frecuencia natural $\omega _{0}$. Sea $f_{1}$ la fracción con frecuencia $\omega _{01}$, $f_{2}$ la fracción con frecuencia $\omega _{02}$, así cada una con unos osciladores $f_{j}$ que tienen unas frecuencias naturales $\omega _{0j}$ donde j=1,2,3... En este caso, la polarización eléctrica o el momento dipolar eléctrico por unidad de volumen es

$\mathbf {P} =\sum _{i}Nf_{j}\mathbf {p} _{j}\qquad (12)$

Por lo tanto

$\mathbf {P} ={\frac {q_{e}^{2}N}{m_{e}}}\sum _{j}{\frac {f_{j}}{(\omega _{0}^{2}-\omega ^{2}+i\gamma _{j}\omega )}}\mathbf {E} \qquad (13)$

donde $\gamma _{j}$ es el factor de amortiguamiento del j-ésimo grupo de electrones oscilando.

Ahora de la ecuación 6

$\epsilon =\epsilon _{0}+\mathbf {\frac {P}{E}} =\epsilon _{0}+{\frac {q_{e}^{2}N}{m_{e}}}\sum _{j}{\frac {f_{j}}{(\omega _{0}^{2}-\omega ^{2}+i\gamma _{j}\omega )}}\qquad (14)$

y de la ecuación 4 utilizamos el hecho de que $n^{2}=\epsilon _{r}=\epsilon /\epsilon _{0}$, podemos llegar a una expresión para n como función de $\omega$, que se conoce como ecuación de dispersión

$n^{2}(\omega )=1+{\frac {q_{e}^{2}N}{\epsilon _{0}m_{e}}}\sum _{j}{\frac {f_{j}}{(\omega _{0}^{2}-\omega ^{2}+i\gamma _{j}\omega )}}\qquad (15)$

Dispersión en materiales densos

Uno podría pensar que nuestra ecuación 15 es correcta para medios enrarecidos como los gases, y también para dieléctricos como líquidos y sólidos. Pero esto no es, porque el campo $\mathbf {E}$ en esta ecuación actúa sobre un átomo dado que debe incluir el campo eléctrico producido por todos los átomos vecinos, y en la materia densa este puede ser muy grande.

Para proceder con este problema, imaginemos entonces que el medio se polariza por medio de un campo eléctrico $\mathbf {E}$ (para sustancias polares que tienen momentos dipolares permanentes, son excluidas de nuestra consideración), denotemos el campo eléctrico promedio en cualquier punto del medio denso por $\mathbf {E}$. Para encontrar el campo $\mathbf {E} _{local}$ sobre el lugar de un átomo dado, quitamos del átomo de su sitio, de otra manera el campo que nosotros mediríamos allí sería una superposición de $\mathbf {E} _{local}$ deseado y el autocampo de la partícula polarizada. La supresión dejará un agujero vacío y nuestra tarea es calcular $\mathbf {E} _{local}$ dentro de ahí. Note que $\mathbf {E} _{local}$ es mayor que la $\mathbf {E}$ solamente porque en el agujero no hay los dipolos que se oponen el campo aplicado. Si el vacío dejado por el átomo estuviera en la forma de una ranura larga y perpendicular orientado al campo, entonces el campo eléctrico dentro de la ranura sería $\mathbf {E} _{local}=\mathbf {E} +(\mathbf {P} /\epsilon _{0})$. Esto, sin embargo, al suponer que el campo dentro de nuestro hueco es de esta forma sería irrazonable. El retiro de un dipolo desde dentro una distribución arbitraria de dipolos vecinos es mejor aproximado por huecos esféricos como están ilustrados en la figura 2. Entonces, por el principio de superposición, podemos escribir el campo $\mathbf {E}$ promedio del dieléctrico como la suma del campo eléctrico dentro del hueco esférico más el campo eléctrico debido a la polarización de la superficie de este, denotaremos este último $\mathbf {E} _{p}$ entonces,

Archivo:Dieléctricos.png

Figura 2. El campo electrico $\mathbf {E} _{local}$ en varios huecos de distintas formas, (a) las cargas no estan polarizadas, por lo tanto $E_{local}=E$, cuando la el hueco esta como en (b) se induce una carga polarizada sobre las superfies arriba y abajo, de modo que $E_{local}=E+{\frac {P}{\epsilon _{0}}}$, (c) para el caso del agujero esférico $E_{local}=E+{\frac {P}{3\epsilon _{0}}}.)$

$\mathbf {E} =\mathbf {E} _{local}+\mathbf {E} _{p}$

pero

$\mathbf {E} _{p}=-{\frac {\mathbf {P} }{3\epsilon _{0}}}$

y entonces

$\mathbf {E} _{local}=\mathbf {E} +{\frac {\mathbf {P} }{3\epsilon _{0}}}\qquad (16)$

Ahora, lo que sigue es simple. Tenemos que reemplazar en la ecuación 13 el campo eléctrico $\mathbf {E}$ por $E_{local}$ dado en la ecuación 16, quedando

$\mathbf {P} ={\frac {q_{e}^{2}N}{m_{e}}}\sum _{j}{\frac {f_{j}}{(\omega _{0}^{2}-\omega ^{2}+i\gamma _{j}\omega )}}\mathbf {E} _{local}=\left[{\frac {q_{e}^{2}N}{m_{e}}}\sum _{j}{\frac {f_{j}}{(\omega _{0}^{2}-\omega ^{2}+i\gamma _{j}\omega )}}\right](\mathbf {E} +{\frac {\mathbf {P} }{3\epsilon _{0}}})\qquad (17)$

que también es igual a

$\mathbf {P} =\chi (\mathbf {E} +{\frac {\mathbf {P} }{3\epsilon _{0}}})\qquad (18)$

donde el símbolo $\chi$, representa la cantidad entre corchetes cuadrados. Este resultado puede ser arreglado en términos de $\chi$ como

$\mathbf {P} ={\frac {\chi }{1-(\chi /3\epsilon _{0})}}\mathbf {E}$

demostrando una vez más que la polarización $\mathbf {P}$ es directamente proporcional al campo eléctrico $\mathbf {E}$. Comparando este resultado con el de la ecuación 5 vemos que

$\epsilon _{0}(K_{E}-1)={\frac {\chi }{1-({\frac {\chi }{3\epsilon _{0}}})}}$

haciendo álgebra

$\chi (3\epsilon _{0})=\epsilon _{0}(\epsilon _{r}-1)(3\epsilon _{0}-\chi )$

y reordenando los términos encontramos que

${\frac {(\epsilon _{r}-1)}{(\epsilon _{r}+2)}}=({\frac {\chi }{3\epsilon _{0}}})\qquad (19)$

y ya que $\epsilon _{r}=n^{2}$, entonces

${\frac {n^{2}-1}{n^{2}+2}}={\frac {Nq_{e}^{2}}{3\epsilon _{0}m_{e}}}\sum _{j}{\frac {f_{j}}{\omega _{0j}^{2}-\omega ^{2}+i\gamma _{j}\omega }}\qquad (20)$

La cual es conocida como la ecuación de Clausius-Mossotti. Obsérvese que para gases donde $n^{2}$ no está muy lejos de la unidad, esta ecuación se vuelve idéntica a la ecuación 15.

La ecuación 20 demuestra ser extraordinariamente exacta para una amplia variedad de sustancias. El lado derecho de la ecuación es proporcional a $N$, el número de electrones por unidad de volumen, y por lo tanto proporcional al número de átomos por unidad de volumen y de ahí el radio de masa de densidad $\rho$ a el peso molecular $W$ del material, eso significa que

$\left({\frac {n^{2}-1}{n^{2}+2}}\right){\frac {W}{\rho }}=constante\,A\qquad (21)$

donde $A$ es conocido como la refractividad molar. La refractividad molar trata del comportamiento refractivo a nivel molecular, ésta ecuación dice que si uno conoce el indice de refracción $n_{1}$ de una sustancia cuando su densidad es $\rho _{1}$, uno puede determinar su indice $n_{2}$ cuando está en un estado diferente $\rho _{2}$, simplemente resolviendo la ecuación

${\frac {A}{W}}={\frac {(n_{1}^{2}-1)}{\rho _{1}(n_{1}^{2}+2)}}={\frac {(n_{2}^{2}-1)}{\rho _{2}(n_{2}^{2}+2)}}\qquad (22)$

Esto funciona extraordinariamente bien, tan bien que uno de los estado puede ser líquido y el otro vapor. Obsérvese además que la ecuación 20 puede ser usada para calcular el indice de refracción de una mezcla.

Tipos de dispersión

Hasta ahora hemos analizado, casi exclusivamente, osciladores electrónicos; sin embargo el mismo resultado se hubiera podido aplicar también a iones enlazados con posiciones atómicas fijas.

Las implicaciones de un índice complejo de refracción no se analizaran aquí , así que limitamos la discusión a las situaciones en las que la absorción es despreciable (es decir, $\omega _{0j}^{2}-\omega ^{2}>>i\gamma _{j}\omega$) y $n$ es real, por lo tanto

${\frac {n^{2}-1}{n^{2}+2}}={\frac {Nq_{e}^{2}}{3\epsilon _{0}m_{e}}}\sum _{j}{\frac {f_{j}}{\omega _{0j}^{2}-\omega ^{2}}}\qquad (23)$

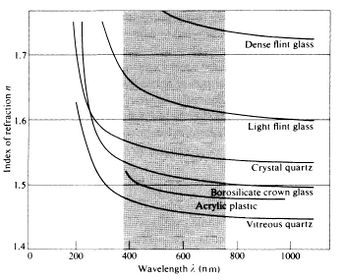
Las frecuencias características de los materiales incoloros y transparentes se hallan fuera de la región visible del espectro (Por esta razón, son de hecho, incoloros y transparentes ). En concreto, las frecuencias naturales de los vidrios están por encima de la región visible, en el ultravioleta, donde se vuelven opacos. En los casos en que $\omega _{0j}^{2}>>\omega ^{2}$, puede despreciarse $\omega ^{2}$ en la ecuación 23, dando un índice de refracción esencialmente constante en esa región de frecuencias. Por ejemplo, las frecuencias características de los vidrios se encuentran en una longitud de onda de unos 100 nm. La mitad del rango visible es aproximadamente cinco veces más grande que ese valor, y ahí, $\omega _{0j}^{2}>>\omega ^{2}$. Obsérvese que mientras $\omega$ va aumentando hacia $\omega _{0j}$, ($\omega _{0j}^{2}-\omega ^{2}$) disminuye y $n$ incrementa gradualmente con la frecuencia, como se pone de manifiesto la figura 3. Esto se denomina dispersión normal.

Figura 3. Dependencia con la longitud de onda con el índice de refracción)

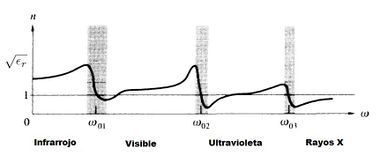
En la región ultravioleta, al acercarse $\omega$ a una frecuencia natural los osciladores empezarán a resonar. Sus amplitudes aumentarán considerablemente, y esto estará acompañado de amortiguación y de una fuerte absorción de energía de la onda incidente. Cuando $\omega _{0j}=\omega$ en la ecuación 20 , el término de amortiguación se hará dominante. Las regiones que se hayan alrededor de las diferentes $\omega _{0j}$ en la figura se denominan bandas de absorción. Ahí $dn/d\omega$ es negativo, y se dice que el proceso es de dispersión anómala (es decir, anormal, Figura 4). Cuando la luz blanca pasa a través de un prisma de vidrio, la componente azul tiene un índice más elevado que la roja, por lo tanto se desvía por un ángulo más grande. Por el contrario, cuando se utiliza un prisma de celda para líquidos que contenga una disolución de colorante con una banda de absorción en el rango visible, el espectro se altera considerablemente. Todas las sustancias poseen unas bandas de absorción en algún sitio dentro del espectro de frecuencias electromagnéticas, así que terminó dispersión anómala que se remonta a finales del siglo XIX, es con toda seguridad una denominación errónea.

Figura 4. Índice de refracción frente a la frecuencia)

Conclusión

Notemos que a través del proceso anterior hemos obtenido algo muy interesante. Porque no solo tenemos un número para el indice de refracción que puede calcularse a través de las cantidades atómicas básicas, sino que también hemos aprendido como varía el indice de refracción con la frecuencia $\omega$ de la luz. Esto es algo que nunca entenderíamos de la simple afirmación que “la luz se propaga más lentamente en un material transparente”.

---

Aportación de: Nahum Mendez Alba

---