Prueba
Amortiguamiento
El amortiguamiento se define como la perdida de energía en un sistema que oscila o que vibra.
Este se comporta como una fuerza proporcional a la velocidad, como lo son las fuerzas de rozamiento con fluídos como el aire, el agua, etc... Si no se considerara el amortiguamiento tendríamos un sistema con energía infinita ya que no se tomaría en cuenta la perdida de energía del sistema y nunca dejaría de vibrar o de oscilar.
Atennuación
función de respuesta como $\alpha$
\[ R\left(\omega\right)\equiv\frac{\gamma^{2}\omega^{2}}{\left(\Omega^{2}-\omega^{2}\right)^{2}+\gamma^{2}\omega^{2}} \]
Mfgwi (discusión) 09:44 10 sep 2020 (CDT) modif Mfgwi (discusión) 20:46 25 sep 2020 (CDT)
Mfgwi (discusión) 17:35 30 mar 2021 (CDT)
Prueba Wiki - Vibraciones Mecánicas
Una vibración es un movimiento oscilatorio de pequeña amplitud, el cual es representado por medio de una señal sinusoidal.
Introducción al movimiento armónico.
Un oscilador es un objeto que se puede mover de arriba hacia abajo, de derecha a izquierda, o de un lado al otro una y otra vez.
Fuerza Restauradora
Voy a modificarlo!
Mfgwi (discusión) 09:01 1 sep 2020 (CDT)
La fuerza restauradora trata de restaurar el sistema a su posición de equilibrio, esta fuerza es proporcional al desplazamiento.
\[ F = -Kx \]
14:58 26 may 2020 (CDT)
Probando wiki 1 - Ondas acústicas
Podemos ver que las ondas acústicas como un fenómeno físico que consiste en la alteración mecánica de las partículas de un medio elástico, producida por un elemento en vibración, que es capaz de provocar una sensación auditiva.
Archivo:Audio-prueba.ogg audioprueba
Explicación Main [#Main1994, p.18]
Sabemos que el aire a temperatura ambiente y a presión atmosférica se comporta como un gas ideal. Para procesos adiabáticos en un gas perfecto $ pV^γ $ es una constante donde $ γ=C_{p}/C_{v} $ es la razón de las capacidades caloríficas. De esta forma utilizando la ecuación \[ κ= {-1 \over V} ( {∂V\over ∂p} ) \] Podemos obtener para $ κ_{s} $ la expresión $ 1 \over γp $ , necesitamos el producto $ ρκ_{s} $ el cual es requerido en la ecuación \[ ω_{0}= ( {a\over lvρκ} )^1/2 \]
Intento 1.0
sabemos que $ sen^2 + cos^2 = 1 $
Intentando mejorar el intento: \[ X = \sqrt{\pi \over 2} \]
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Exponencial, seno y coseno
Partiendo de una posible solución:
$x(t)=C_{1}e^{i\omega t}+C_{2}e^{-i\omega t}$
las exponenciales se pueden escribir como:
$e^{\pm i\omega t}=cos(\omega t) \pm i sen(\omega t)$
sustituyendo en la primera función, nos queda
$x(t)=(C_{1}+C_{2})cos(\omega t)+ i (C_{1}-C_{2})sen(\omega t)$
Sabemos que la suma de constantes nos da como resultado otra constante por lo tanto las nombro $B_1$, $B_2$.
$x(t)=B_{1}cos(\omega t)+ i B_{2}sen(\omega t)$
Juan Daniel Rivera Bautista
14:50 26 may 2020 (CDT)
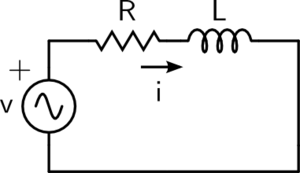
Circuitos LR
Se muestra un ciruito donde un resitor y un inductor L estan conectados en serie. Se cuentan con dispositivos adecuados para medir las diferencias de voltaje a traves del resitor ${(\Delta V_R)}$ y el inductor ${(\Delta V_L)}$
El inductor produce una FEM inducida ${(\varepsilon_L)}$ que se opone al incremento de la corriente. Matematicamente se establece que: \[ \varepsilon = i R + L \frac{di}{dt} \] Buscando una solución para ${\textit{i}}$ \[ \varepsilon -i R = L \frac{di}{dt} \] Separando variables, podemos obtener la siguiente expresión, pero para saber de que variables hablamos al final de la ecuación vamos a primar cada una de las variables, por tanto \[ \frac{di´}{\varepsilon-i´ R}=\frac{dt´}{L} \] integrando de ambos lados \[ \int_{0}^{i} \frac{di´}{\varepsilon-i´ R}=\int_{0}^{t} \frac{dt´}{L} \] \[ \int_{0}^{i} \frac{di´}{\varepsilon-i´ R}= \frac{1}{L}\int_{0}^{t}dt´ \] Usando un cambio de variable del lado izquierdo, por tanto la integral a resolver será \[ -\frac{1}{R}\int_{\varepsilon}^{\varepsilon - i´ R} \frac{du}{u}=\frac{1}{L}\int_{0}^{t}dt' \] donde ${u=\varepsilon - i´ R}$, $du=-Rdi´$, por lo tanto $di´=-\frac{du}{R}$
Resolviendo la integral y evaluando en los limites de las integrales obtenemos: \[ -\frac{1}{R}[In (\varepsilon - i R)- In (\varepsilon)]=\frac{t}{L} \] Ahora sabemos que por propiedades de los logaritmos obtenemos que: \[ -\frac{1}{R}[In (\frac{\varepsilon - i R}{\varepsilon})]=\frac{t}{L} \] finalmente debemos despejar ${\textit{i}}$: \[ In (\frac{\varepsilon - i R}{\varepsilon})=-\frac{R}{L} t \] \[ \frac{\varepsilon - i R}{\varepsilon}=e^{-\frac{R}{L} t} \] \[ \varepsilon - i R=\varepsilon e^{-\frac{R}{L} t} \] \[ i R=\varepsilon -\varepsilon e^{-\frac{R}{L} t} \] \[ i R=\varepsilon (1-e^{-\frac{R}{L} t}) \] Por tanto obtuvimos una ${\textit{i}}$ que es una funcion del tiempo: \[ i =\frac{\varepsilon}{R} (1-e^{-\frac{R}{L} t}) \] Y esto nos hace pensar en que cuando ${t=0}$ entonces ${i\Longrightarrow 0}$ y cuando ${t=\infty}$ entonces ${i\Longrightarrow \frac{\varepsilon}{R}}$
un sistema RLC se comporta como un oscilador amortiguado, este puede ser ligeramente, críticamente o fuertemente el valor que tengan las raíces determinan de que sistema se trata
Ésta es una página de prueba
Vibraciones y ondas If the system shown in fig. has m= 0.010kg and s= 36 N/m , calculate (a) the angular frequency, (b) the frequency, and (c) the period. hola --mfg-wiki (discusión) 12:53 8 mayo 2015 (CDT)
$ F = \sqrt{s \over m}$
Mfgwi (discusión) 16:51 14 may 2020 (CDT)
$ \nabla^{2}\mathbf{V}=\frac{1}{c}\frac{\partial^{2}\mathbf{V}}{\partial t^{2}}. $
titulo primer nivel
aqui va un texto Deducción de la ecuacion de movimiento del OAS (Método energía)
Para un sistema masa resorte podemos aplicar que:
$E_{K}+E_{P}=cte$
la energia mecanica es una constante, por lo que al deivar se tiene:
$\frac{d}{dt}(E_{K}+E_{P})=0$
Entonces sabemos:
$\frac{1}{2}mv^{2}+\frac{1}{2}kx^{2}=cte$
$\frac{d}{dt}(\frac{1}{2}mv^{2}+\frac{1}{2}kx^{2}=cte)$
$\frac{2}{2}mv\frac{dv}{dt}+\frac{2}{2}kx\frac{dx}{dt}=0$
$mv\frac{d^{2}x}{dt^{2}}+kx\frac{dx}{dt}=0$
Sabemos que $\frac{dt}{dx}$no siempre es cero por lo tanto sugerimos:
dividir todo entre m entonce:
$v\frac{d^{2}x}{dt^{2}}+\frac{k}{m}x\frac{dx}{dt}=0$
sabemos que $\frac{dx}{dt}=v$ entonces:
$\frac{dx}{dt}(\frac{d^{2}t}{dt^{2}}+\frac{k}{m}x)=0$
Por otro lado sabemos que $\omega_{0}^{2}=\frac{k}{m}$entonces :
$\frac{d^{2}x}{dt}+\omega^{2}x=0$
La solución de la ecuacion deferencial de segundo orden es:
$x(t)=Acos(\omega t+\phi)$
y podemos deducir la velocidad y la aceleración de la siguiente manera:
$v_{x}(t)=\frac{dx}{dt}=-\omega Asen(\omega t+\phi)$
$a_{x}(t)=\frac{dv}{dt}=-\omega^{2}Acos(\omega t+\phi)$
subtitulo de segundo nivel
\[ f = {1 \over 2\pi} \sqrt{s \over m} = 9.5 Hz \]
(c) $ T= { 2\pi} \sqrt{m \over s} = 0.10 s $
d) $ H= {{\phi} \sqrt{\lambda} \over g} +2 $ --Fernando Vazquez V. (discusión) 18:48 8 mayo 2015 (CDT)
Medios estratificados - Ecuación diferencial
Holografía
Sesebasi (discusión) 15:13 30 nov 2018 (CST)
Alejandro Juárez Toribio (discusión) 16:48 10 jul 2015 (CDT)
Campo Eléctrico
Para iniciar con conceptos de la electricidad, comenzaremos definiendo las ecuaciones que satisfacen la electrostática son
De donde podemos ver que su rotacional es cero, por lo tanto, su campo eléctrico es conservativo.
El campo eléctrico de las ecuaciones de Maxwell para un medio estático,
isotrópico y lineal es
En ausencia de cargas y corrientes
Mientras que si el medio esté estratificado en la direccién ,
entonces .
Si el campo es TE y la propagación en el plano y-z , entonces .
puesto que y entonces .
Si escribimos explécitamente el laplaciano y la dependencia monocromética
donde . ésta ecuacién \eqref{eq: Hy wave eq strat} es el punto de partida del tratamiento que en el B\&W se obtiene de las ecs. de Maxwell en primeras derivadas.
Considere que se pueden separar las variables
de manera que se obtiene
donde hay dos partes que dependen solamente de z y y respectivamente. Dado que éstas variables son independientes, cada una debe cumplirse para cualquier valor de la otra variable
constante . La existencia de ésta cantidad invariante es la generalizacién de la relacién de Snell para medios inhomogéneos. Las ecuaciones son
entonces para la variable y
y para la variable en z
El parametro variable sufre un corrimiento respecto al caso unidimensional para incidencia normal.
Representacién de amplitud y fase
Si se considera un medio no magnético , entonces la
ecuacién \eqref{eq: ode u} se simplifica a
La ecuación del movimiento armónico simple es: si derivamos x respecto de t, obtenemos la velocidad y si derivamos v respecto a t, ó si sacamos la doble derivada de x respecto de t obtenemos la aceleración del sistema
cuando calculamos la posición, velocidad o aceleración máxima estamos diciendo que seno o coseno(según sea el caso) están llegando a su máximo, es decir
si esto sucede, entonces tenemos una posición máxima, velocidad máxima y aceleración máxima como sigue
--Letti GZ (discusión) 22:10 4 may 2013 (CDT)
Invariante
Sean dos soluciones linealmente independientes
Del producto de \eqref{eq: U der V 2} por menos \eqref{eq: U der V 1}por
se obtiene
De manera anéloga
y
De la diferencia \eqref{eq: U V ders}-\eqref{eq:V U ders} de éstas
dos ecuaciones
Coeficientes de reflexión y transmisión
Sean , y las amplitudes complejas del campo eléctrico incidente, reflejado y transmitido.
Continuidad de las contribuciones tangenciales de los campos
y , asi como la relación entre ellos para una onda plana
Para una onda TM (transverso eléctrico) plana
Es decir, al incidir en el medio estratificado que inicia en existe una onda incidente y una reflejada. Nótese que es el campo eléctrico independiente del tiempo como se describe en la ecuación (5) \cite[sec. 1.6.1, p.52 ]{Born75}. Sin embargo, B\&W se refiere a las amplitudes complejas \cite[sec. 1.6.3, p.59-60]{Born75} iguales a los campos.
El campo en la ec. (46) \cite[sec. 1.6.3, p.60]{Born75} se escribe el argumento de como que es la última capa; nosotros preferimos escribir (la última capa) donde ya solamente hay onda transmitida.
La primera derivada de \eqref{eq: ode U} se puede eliminar mediante
la transformación , entonces la primera derivada es
mientras que la segunda derivada es
que podemos reagrupar como
La ecuacién diferencial\eqref{eq: ode U} es entonces\begin{multline*} \frac{\partial^{2}u}{\partial z^{2}}+\frac{\partial\ln\mu}{\partial z}\frac{\partial u}{\partial z}+\left(\frac{1}{4}\left(\frac{\partial\ln\mu}{\partial z}\right)^{2}+\frac{1}{2}\frac{\partial^{2}\ln\mu}{\partial z^{2}}\right)u\\ -\frac{\partial\ln\mu}{\partial z}\left(\frac{\partial u}{\partial z}+\frac{1}{2}u\frac{\partial\ln\mu}{\partial z}\right)+\left(n^{2}k_{0}^{2}-\sigma^{2}k_{0}^{2}\right)u=0,\end{multline*}
que simplifica a
--Kanon1106 20:56 20 ene 2009 (CST)
Maxwell
Comencemos con las ecuaciones de Maxwell para un medio arbitrario (unidades del SI)
donde es el desplazamiento eléctrico, el desplazamiento magnético, el campo magnético y el campo eléctrico. En la ausencia de cargas libres pero permitiendo la existencia de corrientes, las ecuaciones anteriores devienen
donde las ecuaciones \ref{eq:div B} y \ref{eq:rot E} permanecen inalteradas.
relaciones constitutivas
Establecen la relación entre los campos y los desplazamientos. La permitividad y permeabilidad son:
- independientes del campo para medios lineales o campos con amplitud pequeña
- escalares para medios isotrópicos
- independientes del espacio para medios homogéneos
- independientes del tiempo para medios no dispersivos
- cantidades puramente reales para medios sin abosorción
Consideremos un medio isotrópico:
De la ecuación (div D =0}), se obtiene:
Un resultado análogo es cierto para la permeabilidad puesto que y el rotacional de ésta expresión puede reescribirse como:
Las ecuaciones de Maxwell pueden entonces combinarse para obtener:
características del medio
Si el medio es magnéticamente homogéneo, independiente del tiempo y el campo, el gradiente de la permeabilidad y su derivada temporal son cero creo que que que que
para un medio no magnético la permeabilidad es aquella del vacío .
Si la permitividad es independiente del tiempo, se obtiene
Para un medio homogéneo
se obtiene la ecuación de onda.
Funcion bicontinua: se dice que una funcion es bicontinua si tanto ella como su inversa son continuas --Wendy 03:25 29 oct 2010 (UTC)
We present an identity of products that reduces to Lagrange’s identity when a series expansion to fourth order terms are considered. Sixth and higher order terms produce other series identities.
Gsfwiki (discusión) 11:12 25 sep 2018 (CDT)
Sesebasi (discusión) 22:17 2 dic 2018 (CST)
introduction
Normed division algebras require that the norm of the product is equal to the product of the norms. Lagrange’s identity exhibits this equality. Due to Hurwitz theorem, it admits this interpretation only for algebras isomorphic to the real numbers , complex numbers , quaternions and octonions . If divisors of zero are allowed, many other algebraic structures in are possible. Two such possibilities for hyperbolic numbers has been introduced by Fjelstad and Gal and more recently by Catoni et al. . Another approach has been presented in the context of a deformed Lorentz metric. This latter proposal is based on a transformation stemming from the product operation and magnitude definition in hyperbolic scator algebra . The product identity used as a starting point here, is a consequence of the equality for scator algebras.
Lagrange’s identity can be proved in a variety of ways . Most derivations use the identity as a starting point and prove in one way or another that the equality is true. In the present approach, Lagrange’s identity is actually derived without assuming it a priori. The pseudo-norm of the product identity used in the derivation has the strength to imply an infinite number of identities. An example when sixth order terms are retained is shown here. The ease of the derivation has induced us to present it for complex numbers.
Lagrange’s identity for complex numbers
Let be complex numbers and the overbar represents complex conjugate.
The product identity reduces to the complex Lagrange’s identity when fourth order terms, in a series expansion, are considered.
Expand the product on the LHS of the product identity in terms of series[1] up to fourth order
i=1n(1-ai|ai-bi|bi+ai|aibi|bi)=1-i=1n(ai|ai+bi|bi)+i=1nai|aibi|bi
+i<jn(ai|aiaj|aj+bi|bibj|bj)+i<jn(ai|aibj|bj+aj|ajbi|bi)+O5+.[eq:series LHS complex O5]
The two factors on the RHS are also written in terms of series
i=1n(1-ai|ai)i=1n(1-bi|bi)=(1-i=1nai|ai+i<jnai|aiaj|aj+O5+)
(1-i=1nbi|bi+i<jnbi|bibj|bj+O5+).
The product of this expression up to fourth order is
i=1n(1-ai|ai)i=1n(1-bi|bi)=1-i=1n(ai|ai+bi|bi)
+(i=1nai|ai)(i=1nbi|bi)+i<jn(ai|aiaj|aj+bi|bibj|bj)+O5+.[eq:series RHS complex O5]
Substitution of eq:series LHS complex O5 and eq:series RHS complex O5 in the product identity give The product of two conjugates series can be expressed as series involving the product of conjugate terms[2], thus
(i=1naibi)(i=1naibi)-i<jn(aibi|aj|bj+|ai|biajbj)+i<jn(ai|aibj|bj+aj|ajbi|bi)
=(i=1nai|ai)(i=1nbi|bi).
The terms of the last two series on the LHS are grouped as in order to obtain the complex Lagrange’s identity In terms of the modulii,
other identities
The non trivial identities for real numbers obtained to sixth order series expansion of the product identity are and its counterpart, obtained by interchanging the variables and .'
Expand the product identity in series up to sixth order. The LHS is
i=1n(1-ai2-bi2+ai2bi2)=1+i=1n(-ai2-bi2+ai2bi2)
+i<jn(-ai2-bi2+ai2bi2)(-aj2-bj2+aj2bj2)
+i<j<kn(-ai2-bi2+ai2bi2)(-aj2-bj2+aj2bj2)(-ak2-bk2+ak2bk2)+O7+.
Consider only the sixth order terms
O6(LHS)=-i<jn[ai2aj2(bi2+bj2)+bi2bj2(ai2+aj2)]-i<j<knai2aj2ak2+bi2bj2bk2
-i<j<kn(ai2aj2bk2+ai2bj2ak2+bi2aj2ak2)-i<j<kn(ai2bj2bk2+bi2aj2bk2+bi2bj2ak2)
The RHS of the product identity is similarly expanded in series up to sixth order
i=1n(1-ai2)i=1n(1-bi2)=(1-i=1nai2+i<jnai2aj2-i<j<knai2aj2ak2+O7+)
(1-i=1nbi2+i<jnbi2bj2-i<j<knbi2bj2bk2+O7+),
and only sixth order terms retained
O6(RHS)=-i<j<knai2aj2ak2-i<j<knbi2bj2bk2-(i=1nai2)(i<jnbi2bj2)-(i=1nbi2)(i<jnai2aj2).
These two results are equated for equal powers of . The terms and give trivial identities whereas the terms involving and give the non trivial sixth order identities
Prueba 1
Ecuaciones de Maxwell
--Tlacaelel Cruz (discusión) 21:26 8 mayo 2015 (CDT)
Prueba de arhivos(.svg)
Nota: el formato de archivo permitivo es (.svg) otra extension de archivos vectoriales es (.svgz) pero no lo soporta la pagina
--Tlacaelel Cruz (discusión) 18:51 26 nov 2015 (CST)
Relación estadística-termodinámica
La relación entre estados microscópicos y macroscópicos (es decir, la termodinámica) viene dada por la famosa fórmula de Ludwig Boltzmann de la entropía:
donde $\Omega$ es el número de estados microscópicos compatibles con una energía, volumen y número de partículas dado y $k_{B}$ es la constante de Boltzmann.
En el término de la izquierda tenemos la termodinámica mediante la entropía definida en función de sus variables naturales, lo que da una información termodinámica completa del sistema. A la derecha tenemos las configuraciones microscópicas que definen la entropía mediante esta fórmula. Estas configuraciones se obtienen teniendo en cuenta el modelo que hagamos del sistema real a través de su hamiltoniano mecánico.
Esta relación, propuesta por Ludwig Boltzmann, no la aceptó inicialmente la comunidad científica, en parte debido a que contiene implícita la existencia de átomos, que no estaba demostrada hasta entonces. Esa respuesta del medio científico, dicen, hizo que Boltzmann, desahuciado, decidiera quitarse la vida.
Actualmente esta expresión no es la más apropiada para realizar cálculos reales. Ésta es la llamada ecuación puente en el Colectivo Micro Canónico. Existen otros colectivos, como el Colectivo Canónico o el Colectividad macrocanónica, que son de más interés práctico.
Criterios de segunda derivada
Suponga que $f(x,y)$ tiene segundas derivadas parciales continuas en una vecindad de $(x_{0},y_{0})$ y que $\nabla f(x_{0},y_{0})=0$.
Sea $D=D(x_{0},y_{0})=f_{xx}(x_{0},y_{0})f_{yy}(x_{0},y_{0})-f_{xy}^{2}(x_{0},y_{0})$ (el cual es el determinante/Hessiano):
a) Si $D>0$ y $f_{xx}(x_{0},y_{0})<0,$entonces $f(x_{0},y_{0})$ es un valor máximo local.
b) Si $D>0$ y $f_{xx}(x_{0},y_{0})>0,$entonces $f(x_{0},y_{0})$ es un valor mínimo local.
c) Si $D<0$, entonces $f(x_{0},y_{0})$ no es un valor extremo, $(x_{0},y_{0})$ es un punto silla.
d) Si $D=0$, el criterio no es concluyente
Funciones vectoriales
Una función vectorial de una variable real, es una funciónde la forma $\gamma:D\subseteq\mathbb{R}\longrightarrow\mathbb{R}^{n}$ tal que para cada $t\in D$, $\gamma\left(t\right)\in\mathbb{R}^{n}$
Dado que $\gamma\left(t\right)\in\mathbb{R}^{n}$ , para cada $t$ perteneciente a $D$, este tiene n-coordenadas, las cuales suelen ser, funciones de la variable $t$. Así. podemos escribir
\[ \gamma\left(t\right)=\left(\gamma_{1}\left(t\right),\gamma_{2}\left(t\right),\gamma_{3}\left(t\right),\ldots,\gamma_{n}\left(t\right)\right) \]
donde $\gamma_{i}\left(t\right):D\subseteq\mathbb{R}\longrightarrow\mathbb{R},i=1,2,3,\ldots,n$
son funciones de la variable $t$, llamadas funciones coordenadas
de $\gamma$(o funciones componentes de $\gamma$)
El dominio de $\gamma$ con funciones componentes $\gamma_{i}$ es:
\[ Dom\left(\gamma\right)=\cap_{i=1}^{n}Dom\left(\gamma_{i}\right) \]
Particularmente, para $n=3$, una función $f:D\subseteq\mathbb{R}\longrightarrow\mathbb{R}^{3}$,
puede ser escrita como $f\left(t\right)=f_{1}\left(t\right)\hat{i}+f_{2}\left(t\right)\hat{j}+f_{3}\left(t\right)\hat{k}$
para cada $t$ perteneciente a $D$; donde $f_{1},f_{2},f_{3}$ son
las funciones componentes de $f$. Su dominio es:
\[ Dom\left(f\right)=Dom\left(f_{1}\right)\cap Dom\left(f_{2}\right)\cap Dom\left(f_{3}\right) \]
Teorema de Fubini
Sea f una función tal que $f:I\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ con $I:=\{(x,y)\mid a\leq x\leq b;c\leq y\leq d\}.$ Entonces:
\[ \underset{I}{\iint}f(x,y)dxdy=\mathop{\int}_{a}^{b} dx\mathop{\int}_{c}^{d}f(x,y)dy=\mathop{\int}_{c}^{d}dy\mathop{\int}_{a}^{b}f(x,y)dx \]
Máximos y mínimos locales
Definición
Diremos que sea una función f con dominio D. Diremos que $x_{o}$ es un máximo local interior de f en D, si:
- $x_{o}$ es un punto interior de D.
- Existe $r>0$ tal que $∀ x ∈ B_{r}(x_{o})$.
- $f(x_{o}) ≥ f(x)$
Definición
Sea f una función con dominio D. Diremos que $x_{o}$ es un mínimo local interior de f en D, si:
- $x_{o}$ es un punto interior de D.
- Existe $r>0$ tal que $∀ x ∈ B_{r}(x_{o})$.
- $f(x_{o}) ≤ f(x)$.
Resuelva: Hallar los máximos y mínimos locales de: $f(x,y)=\frac{x^{3}-6xy}{y^{3}}$
Rodrigo (discusión) 15:31 4 jul 2020 (CDT)
Campo magnético
Típicamente representamos el campo magnético de dos maneras diferentes:
- Describimos matemáticamente el campo magnético como un campo vectorial. Podemos representar directamente este campo como un conjunto de vectores dibujados en una cuadrícula. Cada vector apunta en la dirección en la que lo haría una brújula y su magnitud depende de la fuerza magnética. Arreglar muchas brújulas en un patrón de cuadrícula y colocar este patrón en un campo magnético ilustra esta técnica. La única diferencia en este caso es que una brújula no muestra la intensidad del campo.
- Una forma alternativa para representar la información contenida en un campo vectorial es por medio de las lineas de campo. En esta representación, omitimos la cuadrícula y conectamos los vectores con líneas suaves. Podemos dibujar tantas líneas como queramos.
conclusions
Lagrange’s identity for complex numbers has been obtained from a straight-forward product identity. The procedure is elementary and very economical. A derivation for the reals is obviously even more succinct. In a wider context, this product identity can be seen as a consequence of the relationship for scator algebras. Since the Cauchy–Schwarz inequality is a particular case of Lagrange’s identity , this proof is yet another way to obtain the CS inequality.
Vibraciones en la naturaleza
Muchas veces nos preguntamos para que nos sirve estudiar vibraciones y ondas, o para que nos útiles, esto tiene una respuesta muy simple. Vivimos en un universo lleno de vibraciónes, nuestrop planeta está repleto de ellas y si queremos entender y conocer un poquito más lo que nos rodea sería bueno estudiar este tema. Debemos tomar en cuenta que , algunas vibraciones son audibles como el aleteo de un mosquito pero otras no como el sonido que emiten los murciélagos ya que estos son ultrasónicos y emitidos con una frecunca de 110.000 Hz, un dato interesante es que cuando se frota suavemente los dedos pulgar e índice se genera una fricción que genera una señal ultrasónica, que los murciélagos consiguen captar[3].
Se sabe también que los elefantes también se comunican por medio de sus pisadas, con ayuda de herramientas diseñadas para detectar terremotos, investigadores descubrieron que los elefantes crean diferentes “firmas sísmicas” en el suelo durante distintas actividades, como caminar, correr, resoplar y gruñir. Según un estudio publicado en la revista Current Biology, estas vibraciones viajan, en algunos casos, más lejos por el suelo que por el aire, así estos animales tienen una variedad de métodos poderosos para la comunicación a larga distancia, estudios han demostrado que es posible para los elefantes monitorear vibraciones en el suelo a través de sus cuerpos, una característica más comúnmente asociada con criaturas pequeñas como escorpiones e insectos. Por ejemplo, se ha observado a los elefantes huir a terrenos más elevados antes de la llegada de tsunamis distantes, y que una madre elefante que se siente amenazada pisará fuerte el suelo para advertir a los demás. Al sugerir que los elefantes no solo provocan vibraciones distintas con actividades diferentes, sino que pueden percibir la diferencia desde grandes distancias, la investigación expande las posibilidades de lo que pueden estarse comunicando los animales entre sí.[4]
Por lo general las vibraciones de un objeto grande suele ser más lento compardo al de los objetos pequeños. Cabe destacar que el cuerpo humano vibran todo el tiempo, "nuestros corazones laten, nuestros pulmones socilan, cuando nos da fiebre no es más que el resultado de la vibración de las moléculas que conforman nuestro cuerpo."[5] Y claro no es para menos, una vibración podemos definirla como un movimiento repetitivo, es decir un movimiento periódico.
Algo maravilloso es que todo esto lo podemos describir con el poderoso lenguaje de las matemáticas, y es aquí en donde nos remontamos al estudio de las vibraciones y ondas, donde podemos describir movimientos periódicos utilizando funciones seno y coseno, que a su vez tienen una amplitud (A), un periodo (T), una frecuencia "nu" (ν), y claro las relaciónes entre fuerza, aceleración y masa que Newton decribe en su obra Philosophiæ naturalis principia matemática.
Método de Langevin al movimiento Browniano
Para dar inicio a esta sección es necesario que en primera instancia se considere el problema de MB como un proceso determinista en el cual no está involucrado una fuerza fluctuante $f(t)$ esto permitirá encontrar los valores para una partícula en términos de su velocidad y de su posición, con ello se conocerán los posibles caminos que puede tomar dicha PB además será sencillo realizar una comparativa de resultados cuando ésta interactúa con un ruido externo. Se parte de la segunda ley de Newton
\begin{equation} m\frac{dv}{dt}= -\alpha v \end{equation}
\begin{equation} m\frac{d^{2}x}{dt^{2}}= -\alpha \frac{dx}{dt} \end{equation}
\begin{equation} m\frac{d^{2}x}{dt^{2}}+\alpha \frac{dx}{dt}=0 \end{equation}
Al dividir sobre la masa, es posible plantear una ecuación que permita escribirla en la forma de un polinomio característico y de modo que se encontrara una forma más sencilla una solución a esta ecuación diferencial.
\begin{equation} \frac{d^{2}x}{dt^{2}}+\frac{\alpha}{m}\frac{dx}{dt}=0 \end{equation}
Con ello, al coeficiente descrito por $\frac{\alpha}{m}$ lo renombramos $\gamma$ lo que nos permite reescribir de la siguiente forma
\begin{equation} r^{2}+ \gamma r \end{equation}
Dicha ecuación nos presenta un conjunto de soluciones para la variable $r$, con lo que es posible conocer la solución al problema como a continuación se presenta de forma que la ecuación a desarrollar es la siguiente
\begin{equation} x(t)=C_{1}+C_{2}e^{-\gamma t} \end{equation}
Para conocer el valor de las constantes $C_{1}$ y $C_{2}$ es necesario hacer estas consideraciones $x(0)= x_{0}$ y $\dot{x}(0)= v_{0}$ bajo estas condiciones iniciales es posible dar una solución dando como resultado el valor tanto para $C_{1}$ así como para $C_{2}$
\begin{equation} C_{1}=x_{0}+\frac{v_{0}}{\gamma} \end{equation}
\begin{equation} C_{2}=-\frac{v_{0}}{\gamma} \end{equation}
Con los resultados anteriores para las dos variables es posible dar una solución general al problema determinista, utilizando el valor de las constantes y se sustituyen sus respectivos valores dando una función de movimiento para la función $x(t)$ de manera que también se conocerá el valor para su velocidad $v(t)$ dando como resultado
\begin{equation} x(t)=x_{0}+\frac{v_{0}}{\gamma}-\frac{v_{0}}{\gamma}e^{-\gamma t} \end{equation}
\begin{equation} v(t)=\frac{v_{0}}{\gamma}e^{-\gamma t} \end{equation}
Asimismo se construirá la ecuación diferencial, tomando la ideología planteada por Langevin en donde únicamente los resultados estarán basados en el conocimiento de su promedio y de su desviación estándar de las PB lo que conlleva a utilizar plenamente la ec.1 de la cual daremos una solución al problema cuando éste interacciona con una fuerza fluctuante. Inicialmente se considera la ec.1, de donde al hacer un promedio para cada uno de los términos que contiene obtendremos la siguiente forma
\begin{equation} m\langle x \frac{d^{2}x}{dt^{2}}\rangle =-\alpha \langle x \frac{dx}{dt} \rangle+ \langle x \Gamma(t) \rangle \end{equation}
Al colocar el promedio para la función mostrado con $x$ conseguiremos que el valor determinado por $\langle x \Gamma(t) \rangle$ sea 0, ¿Por qué ocurre esto ? dada la naturaleza de las interacciones internas entre la PB y el fluido son de tal forma que medidas en un tiempo pequeño las fuerzas ejercidas sobre ella serán exactamente las mismas de un lado que del otro dando como resultado que para cada instante el promedio de la fuerza estocástica se anule o en otras palabras significa que la fuerza aleatoria es independiente de una trayectoria media. Esto nos ayudara a iniciar el desarrollo de su ecuación planteándola de la siguiente manera
\begin{equation}
m\langle x \frac{d^{2}x}{dt^{2}}\rangle =-\alpha \langle x \frac{dx}{dt} \rangle
\end{equation}
En este apartado es importante realizar el desarrollo para las diferenciales mostradas ya que serán de gran ayuda para poder modelar una ecuación que describa el comportamiento de una PB, en ambos lados tenemos derivadas temporales las que habrá de describir individualmente, en primer lugar, tenemos el lado izquierdo
\begin{equation}
m\langle x \frac{d^{2}x}{dt^{2}}\rangle=\frac{d}{dx}\frac{dx^{2}}{dt}=\frac{d}{dt}(2x\frac{dx}{dt})
\end{equation}
\begin{equation}
=2x\frac{d^{2}x}{dt^{2}}+2\frac{d}{dt}\frac{d}{dt}
\end{equation}
\begin{equation}
=2x\frac{d^{2}x}{dt^{2}}+2v^{2}
\end{equation}
Al factorizar los valores para el último párrafo se mostrará el resultado para la parte izquierda de la
\begin{equation}
m\langle x \frac{d^{2}x}{dt^{2}}\rangle= \frac{m}{2}\langle\frac{d^{2}x^{2}}{dt^{2}}\rangle-m\langle v^{2}\rangle
\end{equation}
Ahora es necesario encontrar una solución para el lado derecho de modo que al desarrollarla encontramos lo siguiente
\begin{equation}
\langle x \frac{dx}{dt} \rangle=\frac{1}{2}\frac{d\langle x^{2}\rangle}{dt}
\end{equation}
Se observa de esta manera que al combinar las soluciones obtendremos una nueva forma de reescribir que permitirá proponer un nuevo tipo de modelo matemático basándose en los diferentes componentes obtenidos, al hacer dicha unión se encuentra lo siguiente
\begin{equation}
\frac{m}{d}\frac{d^{2}\langle x^{2} \rangle}{dt^{2}}-m\langle v^{2}\rangle= \frac{\alpha}{m}\frac{d\langle x^{2} \rangle}{dt}
\end{equation}
al hacer un reacomodo de la ecuación anterior conseguiremos plantear una nueva forma que permita la simplificación de esta, una vez realizado esto se definirán nuevos valores para esta nueva formulación de modo que
\begin{equation} \frac{d^{2}\langle x^{2} \rangle}{dt^{2}}=\frac{\alpha}{m}\frac{d\langle x^{2} \rangle}{dt}+2\langle v^{2}\rangle \end{equation}
Tomando en cuenta las diferenciales que aparecen en la ec.10 proponemos lo siguiente, un cambio de variable en términos de $y$
\begin{equation} y=\frac{d\langle x^{2} \rangle}{dt} \end{equation}
\begin{equation} \frac{dy}{dt}=\frac{d^{2}\langle x^{2} \rangle}{dt^{2}} \end{equation}
\begin{equation} \gamma=\frac{\alpha}{m} \end{equation}
Por otro lado, también encontraremos una variable que será definida por la relación que existe entre la energía cinética promedio y el teorema de equipartición propuesto por Boltzmann de donde esto se realiza bajo un equilibrio termodinámico de modo que al considerar esta hipótesis planteada por Langevin conseguiremos lo siguiente
\begin{equation} \frac{1}{2}m\langle v^{2} \rangle= \frac{1}{2}KbT \end{equation}
Pero el interés sobre esta ecuación esta sobre la velocidad que al despejarla del punto anterior conoceremos su valor que quedara en termino de $Kbt$ y $m$ que al plantearla nuevamente obtendremos
\begin{equation} \langle v^{2} \rangle=\frac{2KbT}{m}=c \end{equation}
Esta relación encontrada la podremos definir como una constante que se vamos a definir con la letra $C$ y con esto podremos platear lo siguiente con las nuevas definiciones que encontramos lo que nos generara una nueva ecuación diferencial que describe la idea principal planteada por Langevin, la cual esta descrita de la siguiente manera
\begin{equation} \frac{dy}{dt}-\gamma y = c \end{equation}
El planteamiento anterior permite realizar una separación de variables que va a proporcionar una manera más sencilla de resolución en donde se debe encontrar el valor para $y$, al realizar la operación antes mencionada observaremos una ecuación que al encontrar su valor se conseguirá dar el desplazamiento cuadrático medio bajo la formulación Newtoniana
\begin{equation} \int_{yo}^{y}\frac{dy}{c-\gamma y}=\int_{0}^{t}dt \end{equation}
Al realizar las debidas integrales para cada lado se encontrarán sus debidos valores lo que permite reducir algebraicamente de la siguiente forma
\begin{equation} \frac{c-\gamma y }{c-\gamma y_{0}}= e^{-\gamma t} \end{equation}
\begin{equation} -\gamma y = e^{-\gamma t} (c-\gamma y_{0})-c \end{equation}
Dando como resultado el valor de la variable $y$ que será de gran utilidad para las descripciones siguientes
\begin{equation} y= [ y_{0}-\frac{c}{\gamma}]e^{-\gamma t}+\frac{c}{\gamma} \end{equation}
En este punto el desarrollo que se ha realizado es para poder describir el DCP, como se puede observar aquí se encontró el valor $y$ lo que muestra una relación existente ya mostrada cuando se realizó un cambio de variable, y fue este cambio lo que hará posible determinar el valor de $\langle x^{2}\rangle$ que representa el DCP
\begin{equation} y=\frac{d\langle x^{2} \rangle}{dt} \end{equation}
En la definición encontrada para $y$ conocimos su valor lo que nos permite relacionar la ecuación quedando de la siguiente forma
\begin{equation} \frac{d\langle x^{2} \rangle}{dt}=[ y_{0}-\frac{c}{\gamma}]e^{-\gamma t}+\frac{c}{\gamma} \end{equation}
Al realizar nuevamente una separación de variables encontraremos el comportamiento de la solución en donde tomaremos en cuenta algunos postulados planteados por Langevin que le ayudaron a obtener el mismo resultado obtenido por Einstein, de tal modo que al separar e integrar dará como resultado lo que a continuación de muestra
\begin{equation} \int_{x_{0}}^{x}d \langle x^{2}\rangle = \int_{0}^{t} ([y_{0}-\frac{c}{\gamma}]e^{-\gamma t}+\frac{c}{\gamma})dt \end{equation}
\begin{equation} \langle x^{2}\rangle-\langle x_{0}^{2}\rangle=(y_{0}-\frac{c}{\gamma})(-\frac{1}{\gamma})(e^{-\gamma t}-1)+\frac{ct}{\gamma} \end{equation}
Bajo las siguientes condiciones iniciales definidas por $\langle x_{0}^{2}\rangle=0$ y $y_{0}=0$, es posible simplificar la ecuación anterior para así reducirla y encontrar las partes útiles para la descripción del fenómeno, bajo esta idea reescribimos nuestra ecuación con sus condiciones, obteniendo lo siguiente
\begin{equation} \langle x(t)^{2}\rangle=\frac{c}{\gamma}t-\frac{c}{\gamma^{2}}(1-e^{-\gamma t}) \end{equation}
Al llegar a este punto cabe mencionar que es necesario volver a las definiciones que se hicieron al inicio tanto para $c$ así como para $\gamma$ y al tener dichos valores
de modo que
\begin{equation} c=\frac{2K_{b}t}{m} \end{equation}
Una vez retomando este valor podemos realizar una sustitución en nuestra ec.12 dando como resultado esta expresión
\begin{equation} \langle x^{2}\rangle=(\frac{2K_{b}t}{m \gamma})T-\frac{2K_{b}t}{m \gamma^{2}}(1-e^{-\gamma t}) \end{equation}
\begin{equation} \gamma t \gg 1 \end{equation}
Al proponer esta solución para tiempos muy grandes tales que est0s tienden a infinito de modo que para el sistema se consigue plantear
\begin{equation}
\langle x^{2}\rangle=(\frac{2K_{b}t}{m \gamma})T-\frac{2K_{b}t}{m \gamma^{2}}
\end{equation}
\begin{equation}
(\frac{2K_{b}t}{m \gamma})T \gg \frac{2K_{b}t}{m \gamma^{2}}
\end{equation}
Como se observa el lado izquierdo de la ecuación anterior tiene un término extra $T$ lo que provoca que al multiplicarlas por las constantes genere la eliminación del término derecho ya que con respecto a la otra es imperceptible y por lo tanto se desprecia lo que conlleva a obtener la misma ecuación que predijo Einstein en su trabajo
\begin{equation}
\langle x^{2}\rangle=(2\frac{K_{b}t}{m \gamma})T
\end{equation}
\begin{equation}
\langle x^{2}\rangle= 2D_{e}T
\end{equation}
De esta manera fue como Langevin consiguió llegar al mismo termino obtenido por Einstein bajo otra metodología.
Cristian-MaHe (discusión) 22:18 21 jun 2020 (CDT)
La vida, una máquina termodinámica
El segundo principio de la termodinámica es descrito por el modelo matemático:
\[ dS=dQ/T \].
donde S es la medida de entropía, Q la transferencia de calor y T la temperatura de equilibrio del sistema. Este nos dice que existe cierta irreversibilidad en los procesos termodinámicos. La energía y la materia tienden a desordenarse, a carecer de una forma definida, a ser homogéneas en el espacio que las contiene, a eso se le llama entropía. Pues bien, la vida parece desobedecer al principio de la entropía. ¿Por qué? Pues la respuesta es que la vida, es en sí misma un catalizador de la entropía. Producir actividades que parecen inútiles desde el punto de vista evolutivo darwiniano, como jugar ajedéz, sentir amor, u odio son formas en las que la energía se consume y se dispersa al ambiente en forma de calor y radiación, siendo imposible recuperarla para su consiguiente reciclaje. Si consideramos que la razón del universo es producir vida (postura biocentrista), entonces la razón real del universo es dispersar la energía y hacerla homogénea en todo el espacio.
Prueba Wiki- Intengral "$e^{-x^2}$".
Sea $I$ la integral
\begin{equation} I = \int_{- \infty}^{\infty} e^{-x^{2}} \end{equation}
Resolvamos la integral sin recurrir a la función error de Gauss.
Definimos a $I^2$ como una función equivalente, de dos variables.
Entonces:
\begin{equation} I^2 = \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{-x^{2}-y^{2}} dx dy \end{equation}
Notemos que es igual a escribir:
\begin{equation} \int_{- \infty}^{\infty} e^{-x^{2}} dx \int_{- \infty}^{\infty} e^{-y^{2}} dy \end{equation}
Por lo que:
\begin{equation} I^2 = \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{-x^{2}-y^{2}} dx dy= \int_{- \infty}^{\infty} e^{-x^{2}} dx \int_{- \infty}^{\infty} e^{-y^{2}} dy \end{equation}
Podemos nombrar a $r^2 = x^2 + y^2$ ; $dxdy= r dr d\theta$, por lo qu ahora escribimos:
\begin{equation} \int_{0}^{2 \pi} \int_{0}^{\infty} e^{-r^{2}} r dr d\theta \end{equation}
\begin{equation} = 2\pi \int_{0}^{\infty} e^{-r^{2}} r dr = -\pi \int_{0}^{\infty} e^{-r^{2}} (-2r) dr = -\pi e^{-r^{2}} |_{0}^{\infty} = -\pi (0 -1) \end{equation}
Finalmente
\begin{equation} I^2 = \pi \Longrightarrow I = \int_{- \infty}^{\infty} e^{-x^{2}} dx = \sqrt{\pi} \end{equation}
Andrés (discusión) 19:10 10 jun 2020 (CDT)
Electrónvolt como unidad de energía
La unidad de energía en el Sistema Internacional (SI) es el Joule (J). Sin embargo en la física atómica y nuclear, hay otra unidad que se emplea mucho. Se le define en términos de la energía que adquiere una carga de magnitud $e$ al pasar por una diferencia de potencial de un volt:
Un electrónvolt (eV) es la energía adquirida por una carga de magnitud $e$ al pasar por una diferencia de potencial de un volt
Para ver como se relaciona el electrónvolt con el joule, hay que recordar que la energía que adquiere una carga $q$ al pasar por una diferencia de potencial $V_{AB}$ es:
Energía en joules $= qV_{AB}$
Esta energía es $1$ eV cuando $q = e = 1.602 x 10^{-19}$ C y $V_{AB} = 1$ eV. En consecuencia $1$eV $=(1.602 x 10^{-19} $C$)(1 $V$) = 1.602 x 10^{-19} $J$$
Yolasilvaa (discusión) 17:54 26 jun 2020 (CDT)
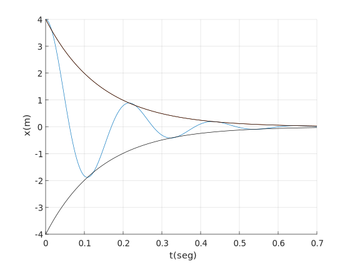
Movimiento amortiguado
Los muelles y péndulos que oscilan libremente se detienen al cabo de un tiempo debido a la pérdida de energía mecánica disipada por las fuerzas de rozamiento. A este tipo de movimiento se le denomina amortiguado. Dependiendo del grado de amortiguamiento del sistema oscilatorio se pueden distinguir tres tipos de movimientos amortiguados: Subamortiguado donde la fricción es pequeña y el sistema oscila con amplitudes decrecientes con el tiempo hasta alcanzar la posición de equilibrio. Sobreamortiguado donde la fricción es grande y el sistema tiende a la posición de equilibrio sin oscilar. Existe una situación frontera entre los dos casos anteriores que se conoce como amortiguamiento crítico donde el sistema no llega a realizar una oscilación completa, tendiendo hacia la posición de equilibrio más rápidamente que en el caso sobreamortiguado.
Ley del movimiento (2ª ley de Newton)
La fuerza de fricción en este movimiento responde a la expresión:
donde o $c$es el llamado coeficiente de amortiguamiento, cuyas unidades son (). Esta fuerza se opone al movimiento, por lo que el trabajo que realiza es negativo y hace disminuir la energía mecánica del sistema.
La ecuación del movimiento amortiguado (o ecuación diferencial del movimiento) para un sistema en el que una masa esta ligada a un muelle de constante k se deduce de la segunda ley de Newton cuando se considera que la masa sujeta al muelle está en un medio resistente , puede ser la misma resistencia del aire y, en consecuencia, tiene aplicada, además, la fuerza de rozamiento proporcional a su velocidad.
Dicha ecuación diferencial, ordenada, queda de la forma:
Dividiendo por queda en la forma:
o también
donde recibe el nombre de índice de amortiguamiento
y es la frecuencia angular del movimiento oscilatorio sin rozamiento.
Esta ecuación diferencial de segundo orden que expresa la dinámica del movimiento del oscilador , tiene tres posibles formas de solución según sea el movimiento, subamortiguado,amortiguado crítico o sobreamortiguado.
Solución en el tiempo
Según la relación entre los valores de la pulsación y del índice de amortiguamiento aparecen los diferentes tipos de solución en el tiempo, dependiendo de si el amortiguamiento es menor, igual o mayor que la pulsación libre $\omega_0$
| Subamortiguado | |
| Amortiguado Crítico | |
| Sobreamortiguado |
Denis (discusión) 20:18 1 jul 2020 (CDT)
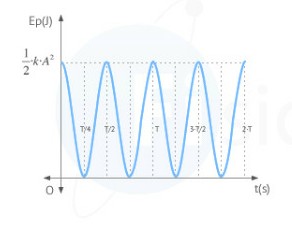
Energía del movimiento armónico simple
Para estudiar las componentes energéticas del movimiento armónico simple podemos suponer que no hay fuerzas de fricción o rozamiento (fuerzas no conservativas) y por tanto la energía mecánica, compuesta principalmente de energía cinética y energía potencial elástica.
Energía cinética en el Movimiento Armónico Simple
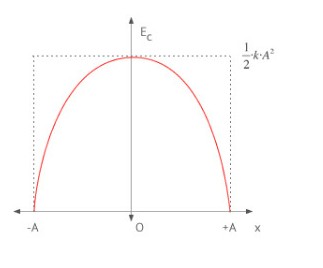
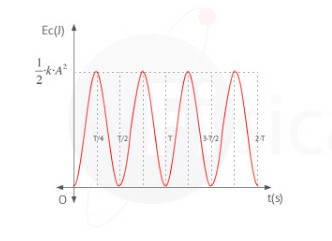
La energía cinética en un movimiento armónico simple en un punto está asociada a la velocidad que el cuerpo tiene en dicho punto. Recuerda que la velocidad en un oscilador armónico es máxima en la posición de equilibrio y 0 en los extremos.
La energía cinética $E_c$ en un movimiento armónico simple varía de manera periódica entre un valor mínimo en los extremos y un valor máximo en la posición de equilibrio. Su valor puede venir expresado en función de la elongación x o en función del tiempo t. En función de x: \begin{equation} E_c=\frac{1}{2}k(A^2−x^2) \end{equation} En función de t: \begin{equation} E_c=\frac{1}{2} k A^2 \sin^2(\omega t + \phi_0) \end{equation}
Donde: \begin{equation} E_c: Energía cinética. [J] \end{equation}
\begin{equation} A:Amplitud. [m] \end{equation}
\begin{equation} w:Frecuencia angular. [rad/s] \end{equation}
\begin{equation} \phi_0: Fase inicial. [rad] \end{equation}
\begin{equation} k: Constante de amortiguamiento. [N/m] \end{equation}
El valor máximo de la energía cinética es $E_c=\frac{1}{2}kA^2$ y el valor mínimo es 0.
Energía Potencial en el Movimiento Armónico Simple
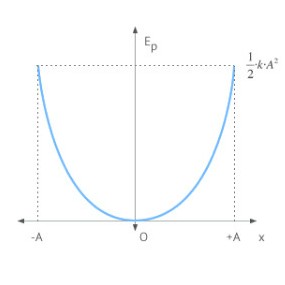
La fuerza restauradora o elástica es una fuerza conservativa. El trabajo realizado por las fuerzas conservativas depende unicamente de los puntos inicial y final, y no del camino elegido. Por ello, las fuerzas conservativas dan lugar a la energía potencial. En este caso se trata de energía potencial elástica, al ser la fuerza responsable la fuerza recuperadora o elástica.
La energía potencial <math>E_p<math> en un movimiento armónico simple varía de manera periódica entre un valor mínimo en la posición de equilibrio y un valor máximo en los extremos. Su valor puede venir expresado en función de la elongación x o en función del tiempo t. En función de x: \begin{equation} E_p=\frac{1}{2}kx^2 \end{equation} En función de t: \begin{equation} E_p=\frac{1}{2}kA^2\cos^2(wt+\phi_0) \end{equation}
Donde: \begin{equation} E_p: Energía potencial. [J] \end{equation}
\begin{equation} A:Amplitud. [m] \end{equation}
\begin{equation} w:Frecuencia angular. [rad/s] \end{equation}
\begin{equation} \phi_0: Fase inicial. [rad] \end{equation}
\begin{equation} k: Constante de amortiguamiento. [N/m] \end{equation}
El valor máximo de la energía potencial es $E_c=\frac{1}{2}kA^2$ y el valor mínimo es 0.
Denis (discusión) 22:13 12 jul 2020 (CDT)
El hallazgo de Bartlett: la representación mental del conocimiento
El psicólogo y filósofo británico Frederic Bartlett (1886-1969), precursor de la psicología cognitiva contemporánea, dio un paso de gigante en los estudios de la memoria en la década de 1930 al estudiar en grupos de control la manera en que las personas memorizamos y olvidamos. Bartlett se interesó por la antropología, la psicología social y la psicología experimental de la memoria, que se planteo estudiar en toda su complejidad y en situaciones de la vida cotidiana.
La tradición, que venía comienzos del siglo xx, abanderada por el psicólogo Hermann Ebbinghaus, se centraba en experimento muy controlados, pero que versaban sobre cuestiones limitadas y poco relevantes, como la capacidad de recordar sílabas sin significado (por ejemplo,\textbf{\textit{Bal}). El propio Ebbinghaus se aprendió hasta 169 listas de 13 silabas sin significado cada una, y analizo el ritmo al que las iba olvidando. Consignaba los olvidos que se producían al repetir las listas al cabo de 20 minuto, al cabo de un día, al cabo de dos... hasta llegar a los 31 días. Concluyo que el volumen de información olvidada era alarmante el primer día pero disminuía a medida que pasaba el tiempo, y constató también que esa información olvidada quedaba en cualquier caso en una especie de latencia, pues meses más tarde resultaba relativamente fácil aprenderla de nuevo. El ejemplo clásico es el del idioma que recuperamos, sin tener que partir de cero, despues de un tiempo sin emplearlo.
Pero Bartlett le pareció que el estudio sobre el recuerdo de silabas sin significado no nos aportaba información fiable sobre cómo opera nuestra memoria. De hecho, tomó el camino contrario: enfatizó la importancia del significado y de las redes de significado y acuño el término \textbf{\textit{esquemas}}, para designar las estructuras mentales que organizan nuestro conocimiento sobre el mundo. En uno de sus experimentos más conocidos, explicaba a un grupo de personas un relato popular norteamericano, <La guerra de los fantasmas>, y les pedía que lo repitieran un cuarto de hora después, unos días después e incluso unos años después. La conclusión de estos estudios fue que las personas tendemos a racionalizar, a dotar de un significado concreto, las informaciones que memorizamos; las llevamos a nuestra zona de confort, a nuestra experiencia, a nuestros conocimientos. Por eso, cada miembro del grupo de control recordaba unos detalles concretos y no otros de la historia, priorizaba aquellos que se habían incorporado más fácilmente a alguno de sus <esquemas> semánticos.
Texto extraído del libro: Somos nuestra memoria recordar y olvidar, Emilio García Garcia,(2018), página 30.
Carlosmiranda (discusión) 04:19 11 sep 2020 (CDT)
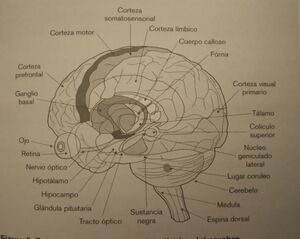
Las bases cerebrales de las memorias explícita e implícita
Desde los descubrimientos pioneros de Brenda Milner hasta la actualidad, los conocimientos sobre las bases cerebrales de las distintas memorias han avanzado espectacularmente gracias a la investigación experimental en animales, la investigación clínica con seres humanos, el análisis de los trastornos de las memorias relacionados con lesiones cerebrales especificas y los estudios con tecnologías de neuroimagen de personas sanas o afectadas por algún trastorno de la memoria.
Como hemos visto en el caso del paciente H.M., el hipocampo, una parte del sistema límbico que se halla en la cara inferior del lóbulo temporal, desempeña un papel clave en la estabilización de la memoria explicita. Pero hay otras áreas cerebrales implicadas en los procesos de memorización declarativa: la amigdala, las cortezas etorrinal, parahipocampal y perirrinal, el bulbo olfativo y la corteza prefrontal son los sistemas más comprometidos. También se incluyen núcleos del tálamo que son centros de conexión entre la corteza temporal y la corteza prefrontal. Asimismo esta memoria recibe información del neocórtex, que le avisa de las consecuencias negativas o positivas de los estímulos, y del tronco encefálico.
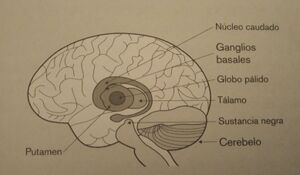
En cambio, en la memoria implícita, los ganglios basales son fundamentales, pues a ellos se debe el carácter inconsciente de las respuestas. Estos ganglios son núcleos situados bajo la corteza cerebral con conexiones con toda la corteza y proyecciones de estas al tálamo y al córtex premotor pero que, en determinadas funciones, puede no recibir retroalimentación de la corteza, como sucede durante los procesos de la memoria implícita. Los ganglios basales reciben también conexiones de la sustancia negra, una región del mesencéfalo responsable de la transmisión de neurotransmisores como la dopamina, necesaria para el adecuado funcionamiento de estos ganglios, y responsable de la automatización de la conducta.
El transtorno más común y más conocido derivado de un mal funcionamiento de los ganglios basales es la enfermedad de Parkinson. Los sintomas más reconocibles de este transtorno son los temblores en reposo, acompañados de rigidez muscular y pérdida de movimientos espontáneos. Estos enfermos sufren déficits en la memoria implícita, aunque por lo general conservan buena memoria para sucesos y datos.
Texto imágenes de dominio público extraídas del libro: Somos nuestra memoria recordar y olvidar, Emilio García Garcia,(2018), página 34 y35.
Carlosmiranda (discusión) 04:19 11 sep 2020 (CDT)
Primera prueba de wiki
Introduciendo ecuaciones
\[y=y_0+v_{0y}t+\frac{1}{2}at^{2}\]
Rodrigo corrales (discusión) 05:33 16 sep 2020
Probando la página de Prueba
Escribiré una ecuación de Shcrödinger independiente del tiempo en coordenadas esféricas: \[ \frac{-\hbar^2}{2m}\nabla^2 \psi(r,\theta,\phi)+V \psi(r,\theta,\phi)=E \psi(r,\theta,\phi) \] donde \[ \nabla^2 \psi=\frac{1}{r^2}\frac{\partial}{\partial r}\left( r\frac{\partial\psi}{\partial r}\right)+\frac{1}{r^2 \sin \theta}\frac{\partial}{\partial \theta}\left( \sin \theta \frac{\partial \psi}{\partial\theta}\right)+ \frac{1}{r^2 \sin^2 \theta } \frac{\partial^2\psi}{\partial \phi^2} \]
Haciendo pruebas de como usar la wiki
////\newline
\\ \\\\ --- =
mckfkdnñafndjakñlfm dlsñanfkñladsnfk dnafñjndsakñ
++
- ↑ Recall that products of the form can be expanded in terms of sums as where means terms with order three or higher in .
- ↑ The conjugate series product is .
- ↑ https://www.biobiochile.cl/noticias/2015/12/15/5-sonidos-que-probablemente-no-logres-escuchar.shtml
- ↑ https://www.nytimes.com/es/2018/05/10/espanol/elefantes-conservacion-pies.html
- ↑ R.E.D. Bishop, Vibration, Cambridge University Press, N.Y. 1965. Una descripción general viva y fascinante de las vibraciones con referencia especial a los problemas técnicos
























![\frac{\partial^{2}u}{\partial z^{2}}+\left[n^{2}k_{0}^{2}-\sigma^{2}k_{0}^{2}\right]u=0.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8937a0cabae793e15ba0e2248562604a188192ea)
































![\frac{\partial^{2}U}{\partial z^{2}}=\mu^{\frac{1}{2}}\left[\frac{\partial^{2}u}{\partial z^{2}}+\frac{\partial\ln\mu}{\partial z}\frac{\partial u}{\partial z}+\left(\frac{1}{4}\left(\frac{\partial\ln\mu}{\partial z}\right)^{2}+\frac{1}{2}\frac{\partial^{2}\ln\mu}{\partial z^{2}}\right)u\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9112cb11423432735b834ad2e6a8ab3a36b4dddb)
![\frac{\partial^{2}u}{\partial z^{2}}+\left[n^{2}k_{0}^{2}-\sigma^{2}k_{0}^{2}+\left(\frac{1}{2}\frac{\partial^{2}\ln\mu}{\partial z^{2}}-\frac{1}{4}\left(\frac{\partial\ln\mu}{\partial z}\right)^{2}\right)\right]u=0.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/84ae1198b4f4efe478103f709d506fa3f080501a)































![\sum_{i<j}^{n}\left[a_{i}^{2}a_{j}^{2}\left(b_{i}^{2}+b_{j}^{2}\right)\right]+\sum_{i<j<k}^{n}\left[a_{i}^{2}a_{j}^{2}b_{k}^{2}+a_{i}^{2}b_{j}^{2}a_{k}^{2}+b_{i}^{2}a_{j}^{2}a_{k}^{2}\right]=\left(\sum_{i=1}^{n}b_{i}^{2}\right)\left(\sum_{i<j}^{n}a_{i}^{2}a_{j}^{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f4d986e198b3c514044f2fe2a28d787007d3ffc3)